Testing the Steady-State Fluctuation Relation in the Solar Photospheric Convection
Abstract
1. Introduction
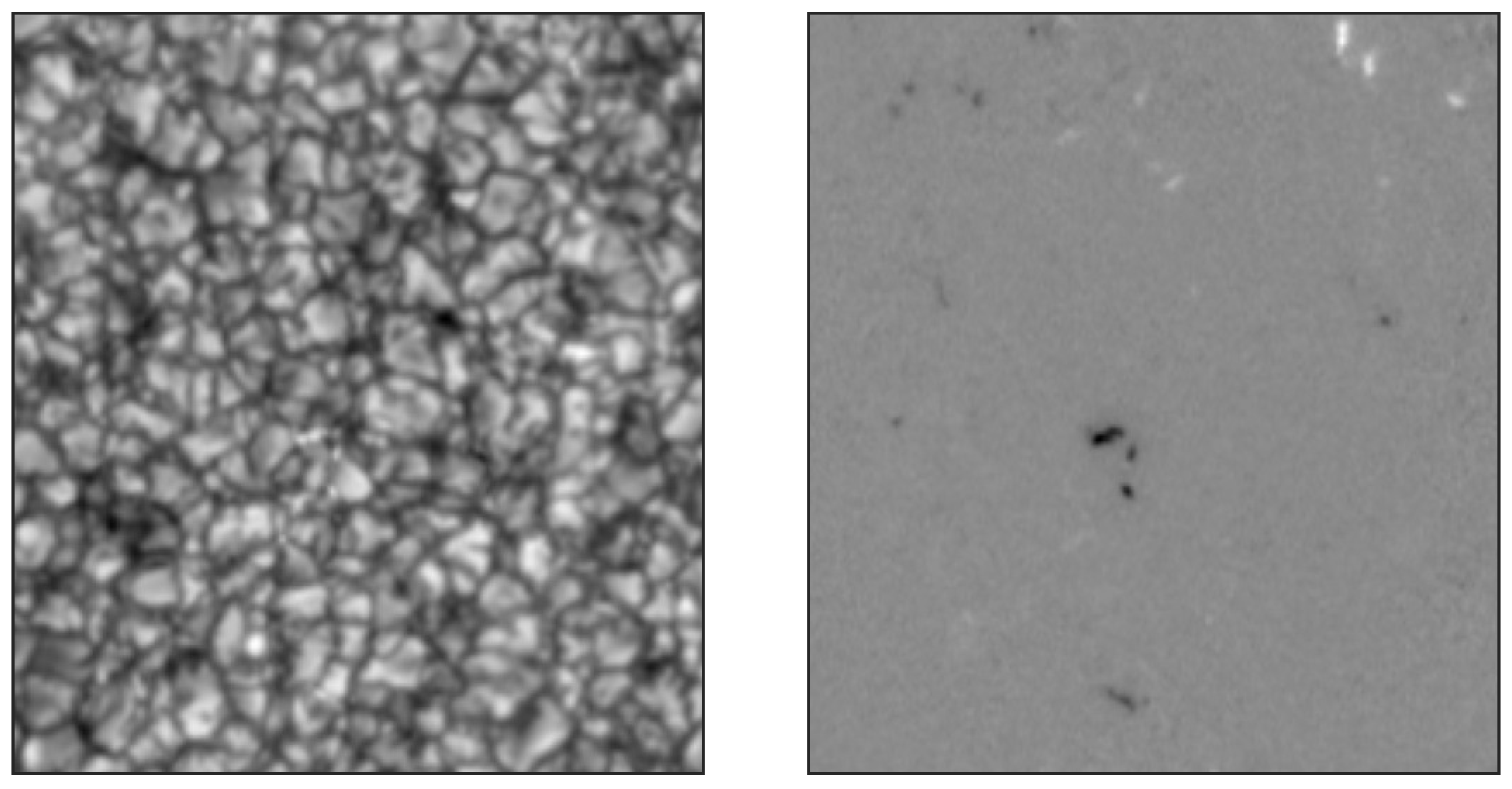
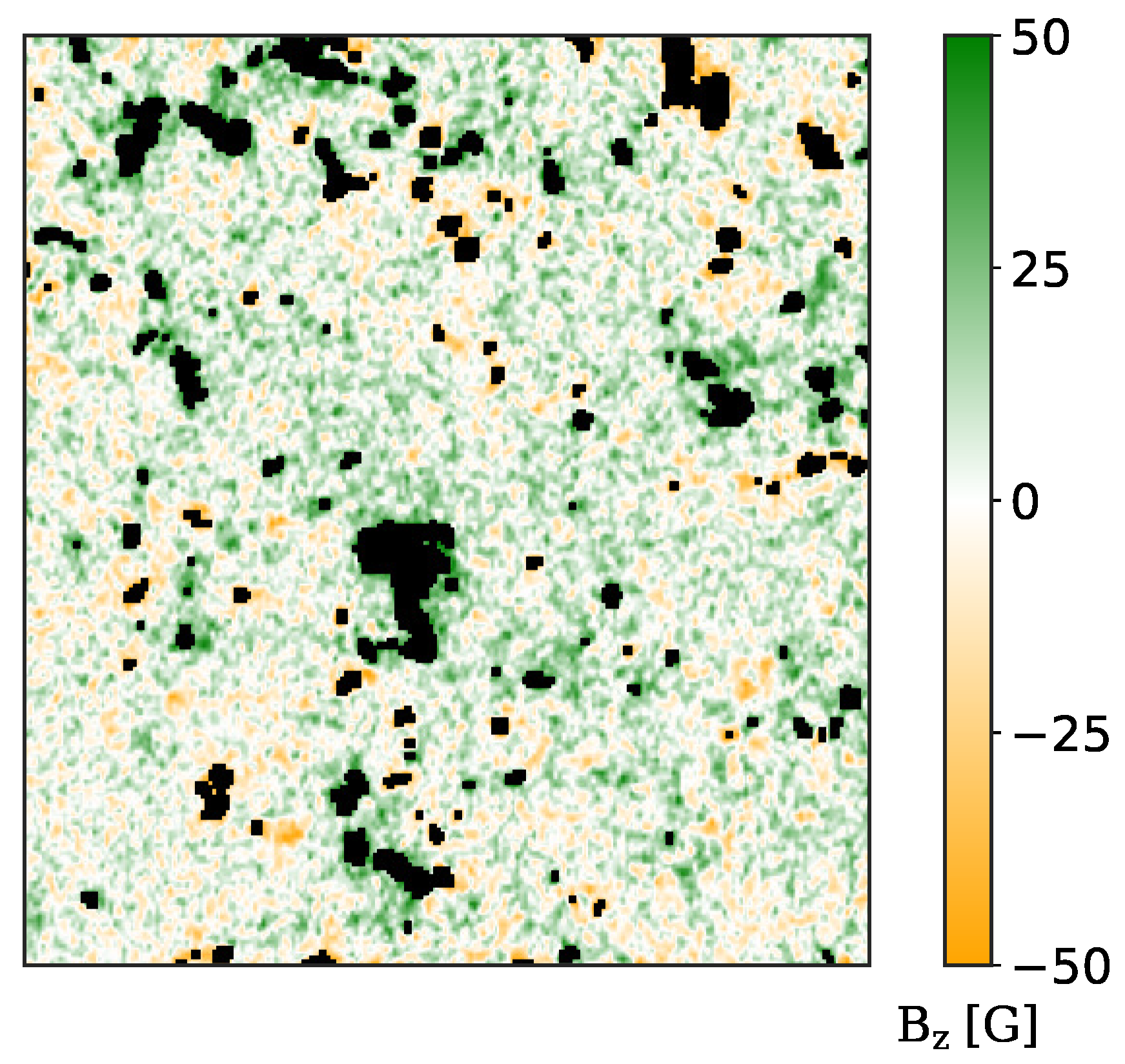
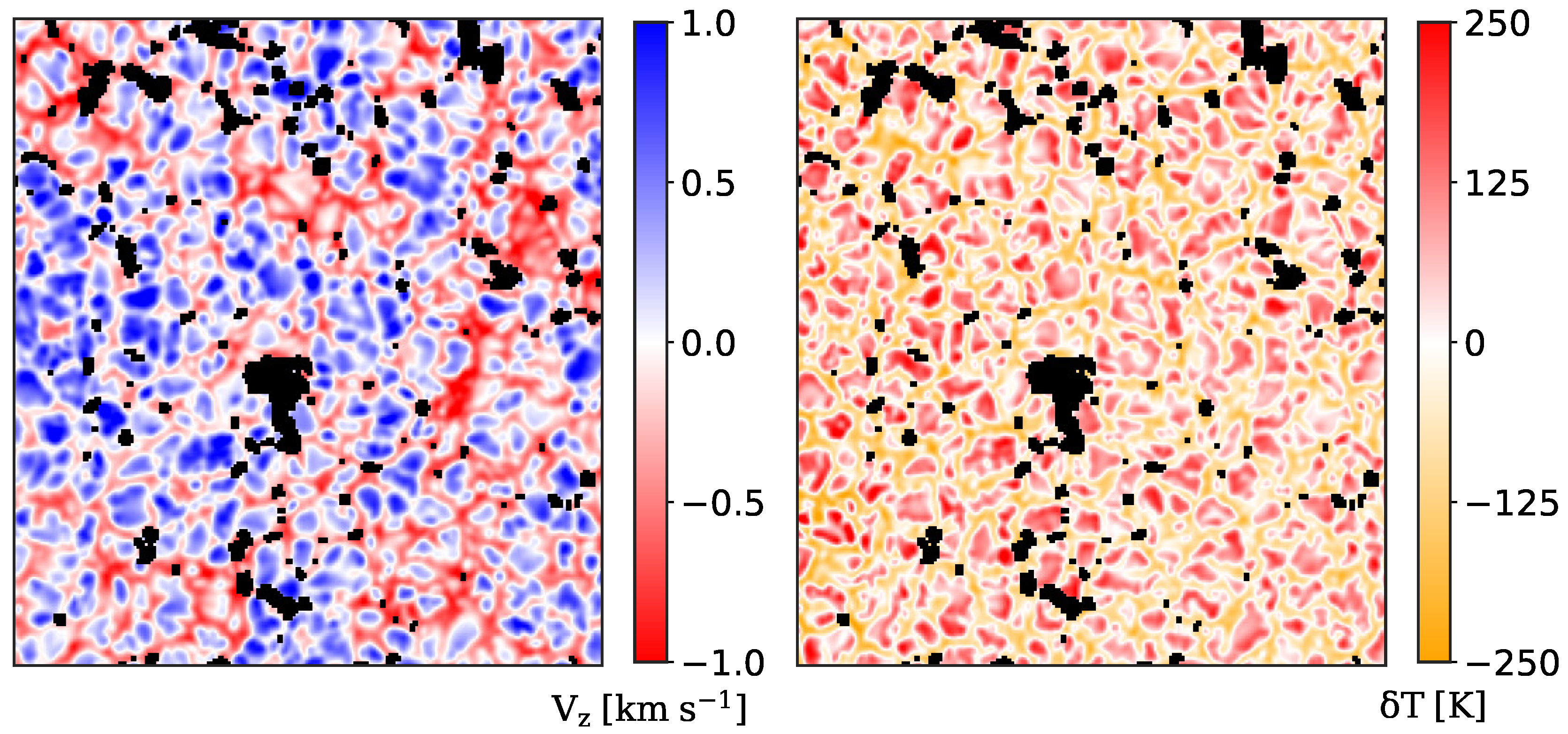
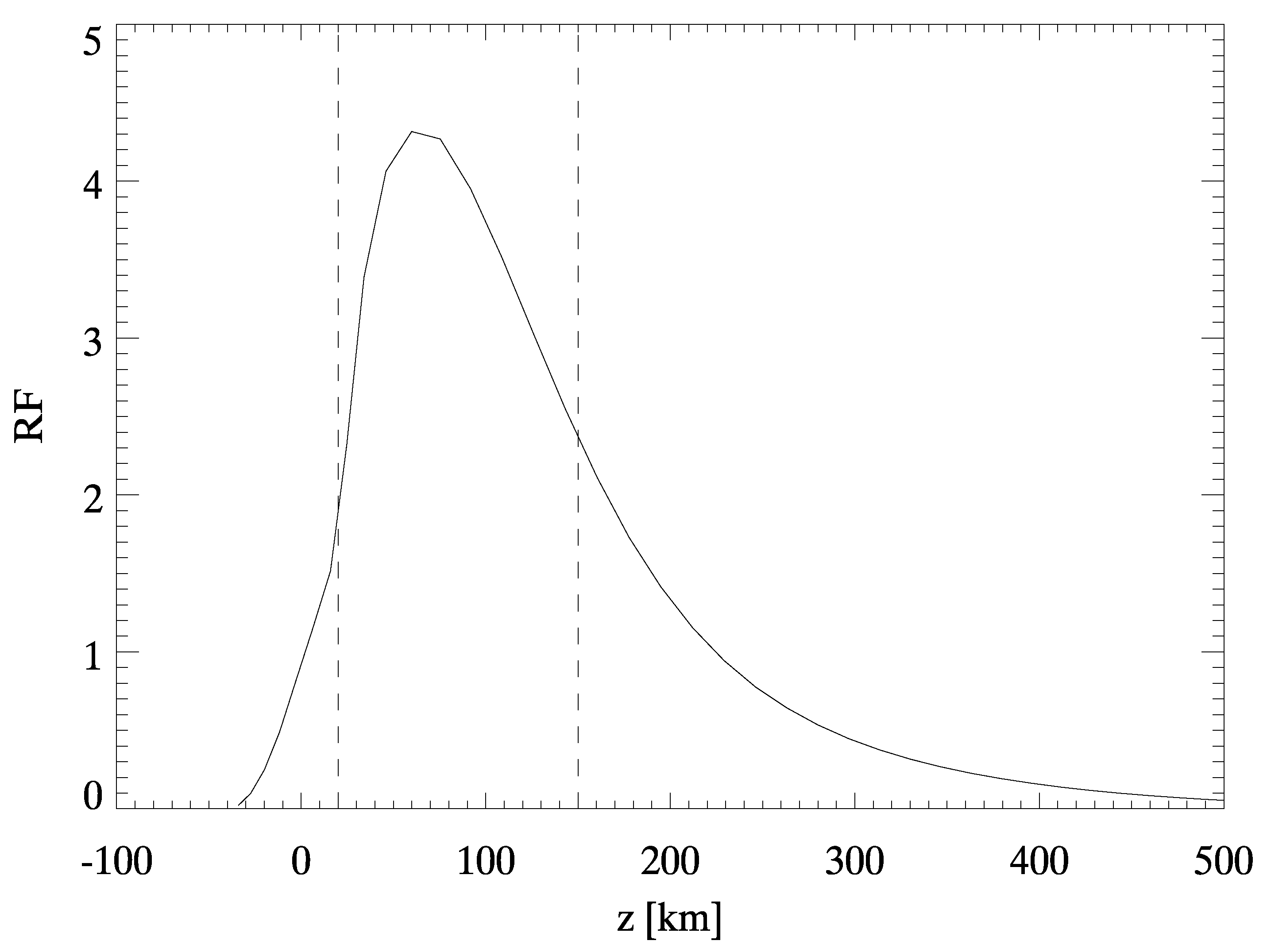
2. Dataset and Methods
3. Data Analysis and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NESS | Non Equlibrium Stationary States |
| FR | Fluctuation Relation |
| GCFR | Gallavotti–Cohen Fluctuation Relation |
| LoS | Line-of-Sight |
| NSO | National Solar Observatory |
| DST | Dunn Solar Telescope |
| IBIS | Interferometric BIdimensional Spectropolarimeter |
| FoV | Field-of-View |
| CoG | Center of Gravity |
| PDFs | Probability Density Functions |
References
- Groot, S.R.D.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications, Inc.: New York, NY, USA, 1984. [Google Scholar]
- Gallavotti, G. Nonequilibrium and Irreversibility; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Gallavotti, G.; Cohen, E.G.D. Dynamical Ensembles in Nonequilibrium Statistical Mechanics. Phys. Rev. Lett. 1995, 74, 2694–2697. [Google Scholar] [CrossRef] [PubMed]
- Gallavotti, G.; Cohen, E.G.D. Dynamical ensembles in stationary states. J. Stat. Phys. 1995, 80, 931–970. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Spohn, H. A Gallavotti-Cohen-Type Symmetry in the Large Deviation Functional for Stochastic Dynamics. J. Stat. Phys. 1999, 95, 333–365. [Google Scholar] [CrossRef]
- Bonetto, F.; Gallavotti, G. Reversibility, Coarse Graining and the Chaoticity Principle. Commun. Math. Phys. 1997, 189, 263–275. [Google Scholar] [CrossRef]
- Gallavotti, G. Breakdown and regeneration of time reversal symmetry in nonequilibrium statistical mechanics. Phys. D Nonlinear Phenom. 1998, 112, 250–257. [Google Scholar] [CrossRef]
- Gallavotti, G. Nonequilibrium and Fluctuation Relation. J. Stat. Phys. 2019. [Google Scholar] [CrossRef]
- Gallavotti, G. Ensembles, turbulence and fluctuation theorem. Eur. Phys. J. E 2020, 43, 37. [Google Scholar] [CrossRef]
- Ciliberto, S.; Garnier, N.; Hernandez, S.; Lacpatia, C.; Pinton, J.F.; Ruiz Chavarria, G. Experimental test of the Gallavotti-Cohen fluctuation theorem in turbulent flows. Phys. A Stat. Mech. Its Appl. 2004, 340, 240–250. [Google Scholar] [CrossRef][Green Version]
- Gallavotti, G. A local fluctuation theorem. Phys. A Stat. Mech. Its Appl. 1999, 263, 39–50. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. The Fluctuation Theorem. Adv. Phys. 2002, 51, 1529–1585. [Google Scholar] [CrossRef]
- Shang, X.D.; Tong, P.; Xia, K.Q. Test of steady-state fluctuation theorem in turbulent Rayleigh-Bénard convection. Phys. Rev. E 2005, 72, 015301. [Google Scholar] [CrossRef] [PubMed]
- Hurtado, P.I.; Pérez-Espigares, C.; del Pozo, J.J.; Garrido, P.L. Symmetries in fluctuations far from equilibrium. Proc. Natl. Acad. Sci. USA 2011, 108, 7704–7709. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, M.L.; Toomre, J. Correlation Tracking of Mesogranules from SOI-MDI Doppler Images to Reveal Supergranular Flow Fields. In Structure and Dynamics of the Interior of the Sun and Sun-Like Stars; Korzennik, S., Ed.; ESA Special Publication: Noordwijk, The Netherlands, 1998; Volume 418, p. 753. [Google Scholar]
- Roudier, T.; Rieutord, M.; Malherbe, J.M.; Vigneau, J. Determination of horizontal velocity fields at the sun’s surface with high spatial and temporal resolution. Astron. Astrophys. 1999, 349, 301–311. [Google Scholar]
- Cattaneo, F.; Lenz, D.; Weiss, N. On the Origin of the Solar Mesogranulation. Astrophys. J. Lett. 2001, 563, L91–L94. [Google Scholar] [CrossRef]
- Rast, M.P. The Scales of Granulation, Mesogranulation, and Supergranulation. Astrophys. J. 2003, 597, 1200–1210. [Google Scholar] [CrossRef]
- De Rosa, M.L.; Toomre, J. Evolution of Solar Supergranulation. Astrophys. J. 2004, 616, 1242–1260. [Google Scholar] [CrossRef][Green Version]
- Del Moro, D.; Berrilli, F.; Duvall, T.L.; Kosovichev, A.G. Dynamics and Structure of Supergranulation. Sol. Phys. 2004, 221, 23–32. [Google Scholar] [CrossRef]
- Berrilli, F.; Scardigli, S.; Giordano, S. Multiscale Magnetic Underdense Regions on the Solar Surface: Granular and Mesogranular Scales. Sol. Phys. 2013, 282, 379–387. [Google Scholar] [CrossRef][Green Version]
- Giannattasio, F.; Berrilli, F.; Biferale, L.; Del Moro, D.; Sbragaglia, M.; Bellot Rubio, L.; Gošić, M.; Orozco Suárez, D. Pair separation of magnetic elements in the quiet Sun. Astron. Astrophys. 2014, 569, A121. [Google Scholar] [CrossRef]
- Giannattasio, F.; Stangalini, M.; Berrilli, F.; Del Moro, D.; Bellot Rubio, L. Diffusion of Magnetic Elements in a Supergranular Cell. Astrophys. J. 2014, 788, 137. [Google Scholar] [CrossRef]
- Berrilli, F.; Scardigli, S.; Del Moro, D. Magnetic pattern at supergranulation scale: The void size distribution. Astron. Astrophys. 2014, 568, A102. [Google Scholar] [CrossRef][Green Version]
- Caroli, A.; Giannattasio, F.; Fanfoni, M.; Del Moro, D.; Consolini, G.; Berrilli, F. Turbulent convective flows in the solar photospheric plasma. J. Plasma Phys. 2015, 81, 495810514. [Google Scholar] [CrossRef]
- Giovannelli, L.; Giannattasio, F.; Del Moro, D.; Caroli, A.; Berrilli, F. Diffusion of emerging bipolar magnetic pairs in solar photosphere. Nuovo C. C Geophys. Space Phys. C 2019, 42, 3. [Google Scholar] [CrossRef]
- Müller, D.A.N.; Steiner, O.; Schlichenmaier, R.; Brandt, P.N. Time-slice diagrams of solar granulation. Sol. Phys. 2001, 203, 211–232. [Google Scholar] [CrossRef]
- Berrilli, F.; Consolini, G.; Pietropaolo, E.; Caccin, B.; Penza, V.; Lepreti, F. 2-D multiline spectroscopy of the solar photosphere. Astron. Astrophys. 2002, 381, 253–264. [Google Scholar] [CrossRef][Green Version]
- Hirzberger, J. On the brightness and velocity structure of solar granulation. Astron. Astrophys. 2002, 392, 1105–1118. [Google Scholar] [CrossRef]
- Nesis, A.; Hammer, R.; Roth, M.; Schleicher, H. Dynamics of the solar granulation. VIII. Time and space development. Astron. Astrophys. 2002, 396, 1003–1010. [Google Scholar] [CrossRef]
- Roudier, T.; Malherbe, J.M.; Mein, P.; Muller, R.; Coutard, C.; Lafon, M.; Grimaud, F. High spatial resolution capabilities of Doppler measurements with the Pic du Midi MSDP spectrograph. Astron. Astrophys. 2003, 409, 793–797. [Google Scholar] [CrossRef]
- Del Moro, D. Solar granulation properties derived from three different time series. Astron. Astrophys. 2004, 428, 1007–1015. [Google Scholar] [CrossRef]
- Berrilli, F.; Del Moro, D.; Consolini, G.; Pietropaolo, E.; Duvall, T.L.; Kosovichev, A.G. Structure Properties of Supergranulation and Granulation. Sol. Phys. 2004, 221, 33–45. [Google Scholar] [CrossRef]
- Nesis, A.; Hammer, R.; Roth, M.; Schleicher, H. Dynamics of the solar granulation. IX. A global approach. Astron. Astrophys. 2006, 451, 1081–1089. [Google Scholar] [CrossRef][Green Version]
- November, L.J. Mesogranulation and Supergranulation in the Sun. Ph.D. Thesis, University of Colorado Boulder, Boulder, CO, USA, 1980. [Google Scholar]
- Hart, A.B. Motions in the Sun at the photospheric level. VI. Large-scale motions in the equatorial region. Mon. Not. R. Astron. Soc. 1956, 116, 38. [Google Scholar] [CrossRef]
- Leighton, R.B.; Noyes, R.W.; Simon, G.W. Velocity Fields in the Solar Atmosphere. I. Preliminary Report. Astrophys. J. 1962, 135, 474. [Google Scholar] [CrossRef]
- Simon, G.W.; Leighton, R.B. Velocity Fields in the Solar Atmosphere. III. Large-Scale Motions, the Chromospheric Network, and Magnetic Fields. Astrophys. J. 1964, 140, 1120. [Google Scholar] [CrossRef]
- Stein, R.F.; Nordlund, Å. Simulations of Solar Granulation. I. General Properties. Astrophys. J. 1998, 499, 914–933. [Google Scholar] [CrossRef]
- Nordlund, Å.; Stein, R.F.; Asplund, M. Solar Surface Convection. Living Rev. Sol. Phys. 2009, 6, 2. [Google Scholar] [CrossRef]
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Astrophys. 1958, 46, 108. [Google Scholar]
- Canuto, V.M.; Mazzitelli, I. Stellar Turbulent Convection: A New Model and Applications. Astrophys. J. 1991, 370, 295. [Google Scholar] [CrossRef]
- Getling, A. Rayleigh-Benard Convection: Structures And Dynamics; World Scientific Publishing Co Pte Ltd.: Singapore, 1998. [Google Scholar]
- Berrilli, F.; Del Moro, D.; Russo, S.; Consolini, G.; Straus, T. Spatial Clustering of Photospheric Structures. Astrophys. J. 2005, 632, 677–683. [Google Scholar] [CrossRef]
- Giannattasio, F.; Del Moro, D.; Berrilli, F.; Bellot Rubio, L.; Gošić, M.; Orozco Suárez, D. Diffusion of Solar Magnetic Elements up to Supergranular Spatial and Temporal Scales. Astrophys. J. 2013, 770, L36. [Google Scholar] [CrossRef]
- Cavallini, F.; Berrilli, F.; Cantarano, S.; Egidi, A. IBIS: A new instrument for solar bidimensional spectroscopy. Mem. Soc. Astron. Ital. 2001, 72, 554–557. [Google Scholar]
- Cavallini, F. IBIS: A New Post-Focus Instrument for Solar Imaging Spectroscopy. Sol. Phys. 2006, 236, 415–439. [Google Scholar] [CrossRef]
- Viticchié, B.; Del Moro, D.; Berrilli, F.; Bellot Rubio, L.; Tritschler, A. Imaging Spectropolarimetry with IBIS: Evolution of Bright Points in the Quiet Sun. Astrophys. J. Lett. 2009, 700, L145–L148. [Google Scholar] [CrossRef]
- Del Moro, D.; Giannattasio, F.; Berrilli, F.; Consolini, G.; Lepreti, F.; Gošić, M. Super-diffusion versus competitive advection: A simulation. Astron. Astrophys. 2015, 576, A47. [Google Scholar] [CrossRef]
- Viavattene, G.; Berrilli, F.; Collados Vera, M.; Del Moro, D.; Giovannelli, L.; Ruiz Cobo, B.; Zuccarello, F. Remote sensing of the solar photosphere: A tale of two methods. J. Phys. Conf. Ser. 2018, 956, 012006. [Google Scholar] [CrossRef]
- Del Moro, D.; Giovannelli, L.; Pietropaolo, E.; Berrilli, F. JP3D compression of solar data-cubes: Photospheric imaging and spectropolarimetry. Exp. Astron. 2017, 43, 23–37. [Google Scholar] [CrossRef]
- Viticchié, B.; Del Moro, D.; Criscuoli, S.; Berrilli, F. Imaging Spectropolarimetry with IBIS. II. On the Fine Structure of G-band Bright Features. Astrophys. J. 2010, 723, 787–796. [Google Scholar] [CrossRef]
- Cattaneo, F.; Emonet, T.; Weiss, N. On the Interaction between Convection and Magnetic Fields. Astrophys. J. 2003, 588, 1183–1198. [Google Scholar] [CrossRef]
- Rees, D.E.; Semel, M.D. Line formation in an unresolved magnetic element—A test of the centre of gravity method. Astron. Astrophys. 1979, 74, 1–5. [Google Scholar]
- Viavattene, G.; Berrilli, F.; Consolini, G.; Del Moro, D.; Giannattasio, F.; Giovannelli, L.; Penza, V. Evaluating a proxy of the local entropy production rate on the solar photosphere. J. Phys. Conf. Ser. 2019, 1226, 012004. [Google Scholar] [CrossRef]
- Viavattene, G.; Berrilli, F.; Consolini, G.; Del Moro, D.; Giannattasio, F.; Giovannelli, L.; Penza, V. Statistical behaviour of a proxy of the entropy production rate of the solar photosphere. Nuovo C. C Geophys. Space Phys. C 2019, 42, 8. [Google Scholar] [CrossRef]
- Rodriguez Hidalgo, I.; Collados, M.; Vazquez, M. Centre-to-limb variation of solar granulation along the equator and the central meridian. Astron. Astrophys. 1992, 264, 661–672. [Google Scholar]
- Caccin, B.; Penza, V. Line-Depth and Teff Variations with the Solar Cycle due to Possible Size-Changes of Photospheric Granulation. In The Solar Cycle and Terrestrial Climate, Solar and Space Weather; Wilson, A., Ed.; ESA Special Publication: Noordwijk, The Netherlands, 2000; Volume 463, p. 293. [Google Scholar]
- Judge, P.G.; Kleint, L.; Uitenbroek, H.; Rempel, M.; Suematsu, Y.; Tsuneta, S. Photon Mean Free Paths, Scattering, and Ever-Increasing Telescope Resolution. Sol. Phys. 2015, 290, 979–996. [Google Scholar] [CrossRef][Green Version]
- Caccin, B.; Gomez, M.T.; Marmolino, C.; Severino, G. Response functions and contribution functions of photospheric lines. Astron. Astrophys. 1977, 54, 227–231. [Google Scholar]
- Penza, V.; Caccin, B.; Del Moro, D. The sensitivity of the C I 538.0 nm Fe I 537.9 nm and Ti II 538.1 nm lines to solar active regions. Astron. Astrophys. 2004, 427, 345–351. [Google Scholar] [CrossRef]
- Penza, V.; Caccin, B.; Ermolli, I.; Centrone, M. Comparison of model calculations and photometric observations of bright “magnetic” regions. Astron. Astrophys. 2004, 413, 1115–1123. [Google Scholar] [CrossRef]
- Cristaldi, A.; Ermolli, I. 1D Atmosphere Models from Inversion of Fe I 630 nm Observations with an Application to Solar Irradiance Studies. Astrophys. J. 2017, 841, 115. [Google Scholar] [CrossRef]
- Ruiz Cobo, B.; del Toro Iniesta, J.C. Inversion of Stokes Profiles. Astrophys. J. 1992, 398, 375. [Google Scholar] [CrossRef]
- Kurucz, R.L. Model atmospheres for g, f, a, b, and o stars. Astrophys. J. Suppl. Ser. 1979, 40, 1–340. [Google Scholar] [CrossRef]
- Title, A.M.; Tarbell, T.D.; Topka, K.P.; Ferguson, S.H.; Shine, R.A.; SOUP Team. Statistical properties of solar granulation derived from the SOUP instrument on Spacelab 2. Astrophys. J. 1989, 336, 475–494. [Google Scholar] [CrossRef]
- Shang, X.D.; Qiu, X.L.; Tong, P.; Xia, K.Q. Measured Local Heat Transport in Turbulent Rayleigh-Bénard Convection. Phys. Rev. Lett. 2003, 90, 074501. [Google Scholar] [CrossRef] [PubMed]
- Shang, X.D.; Qiu, X.L.; Tong, P.; Xia, K.Q. Measurements of the local convective heat flux in turbulent Rayleigh-Bénard convection. Phys. Rev. E 2004, 70, 026308. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Phys. D Nonlinear Phenom. 2002, 166, 43–62. [Google Scholar] [CrossRef]
- Kippenhan, R.; Weigert, A. Stellar Structure and Evolution; Springer: Heidelberg, Germany, 1994. [Google Scholar]
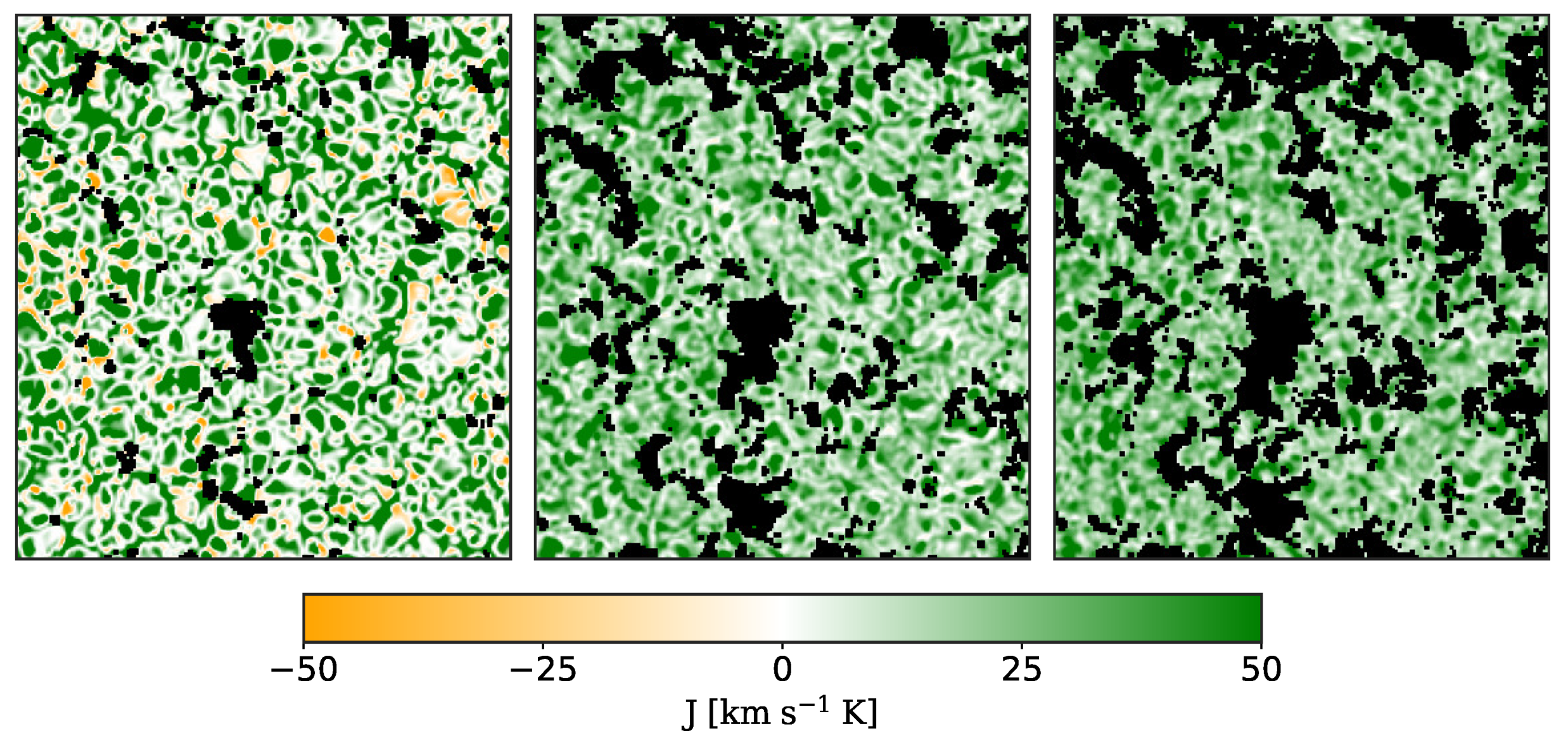
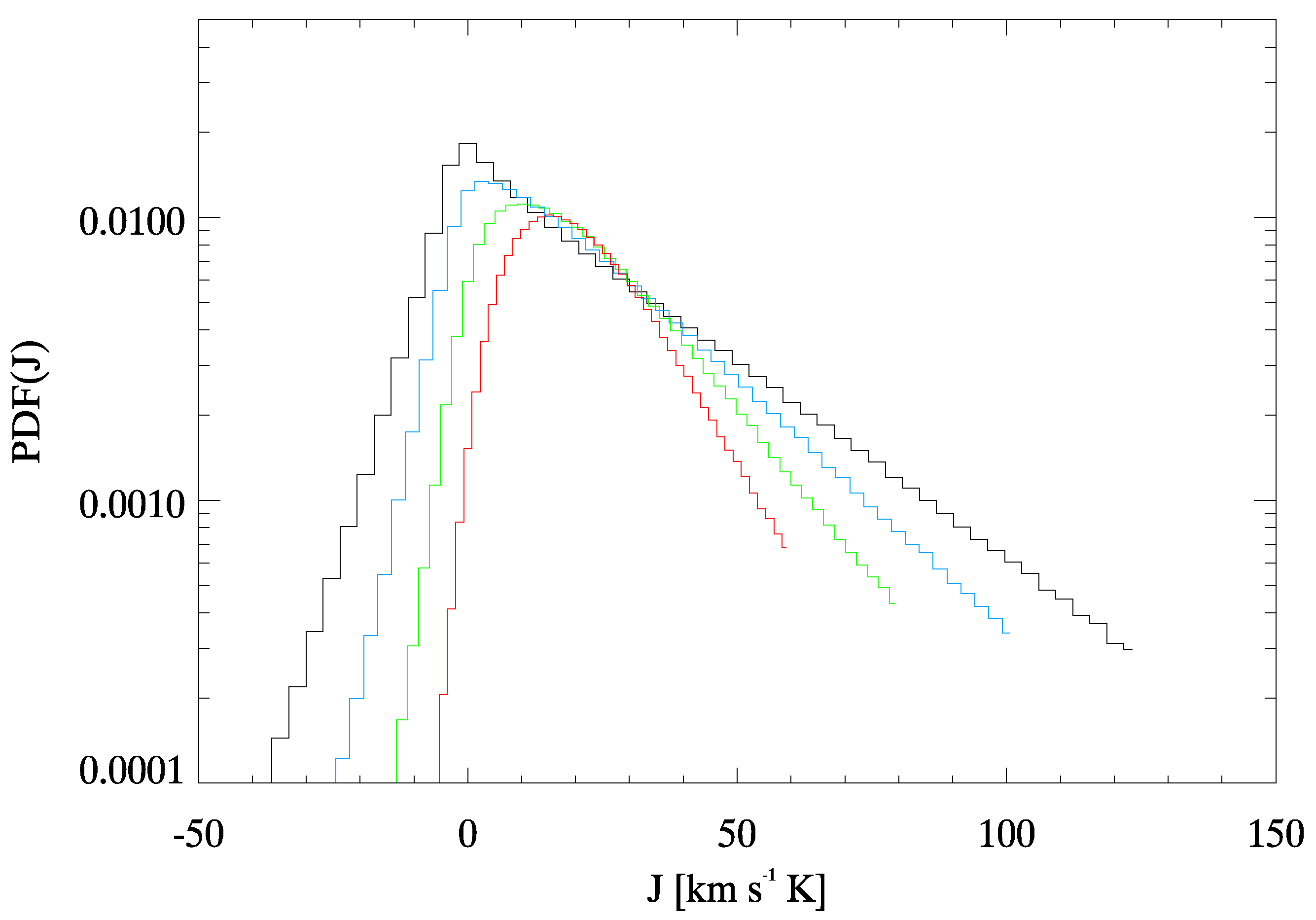
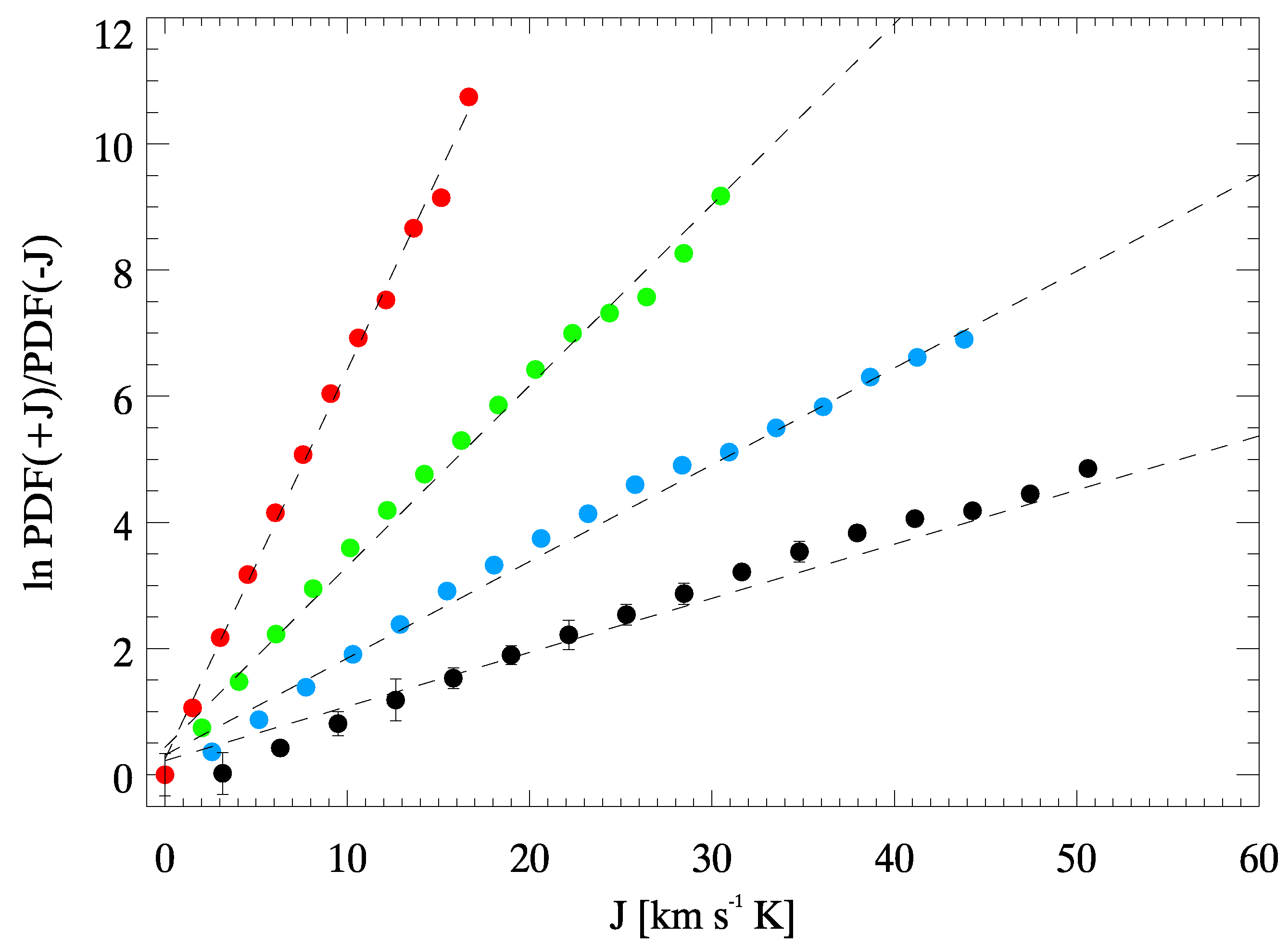
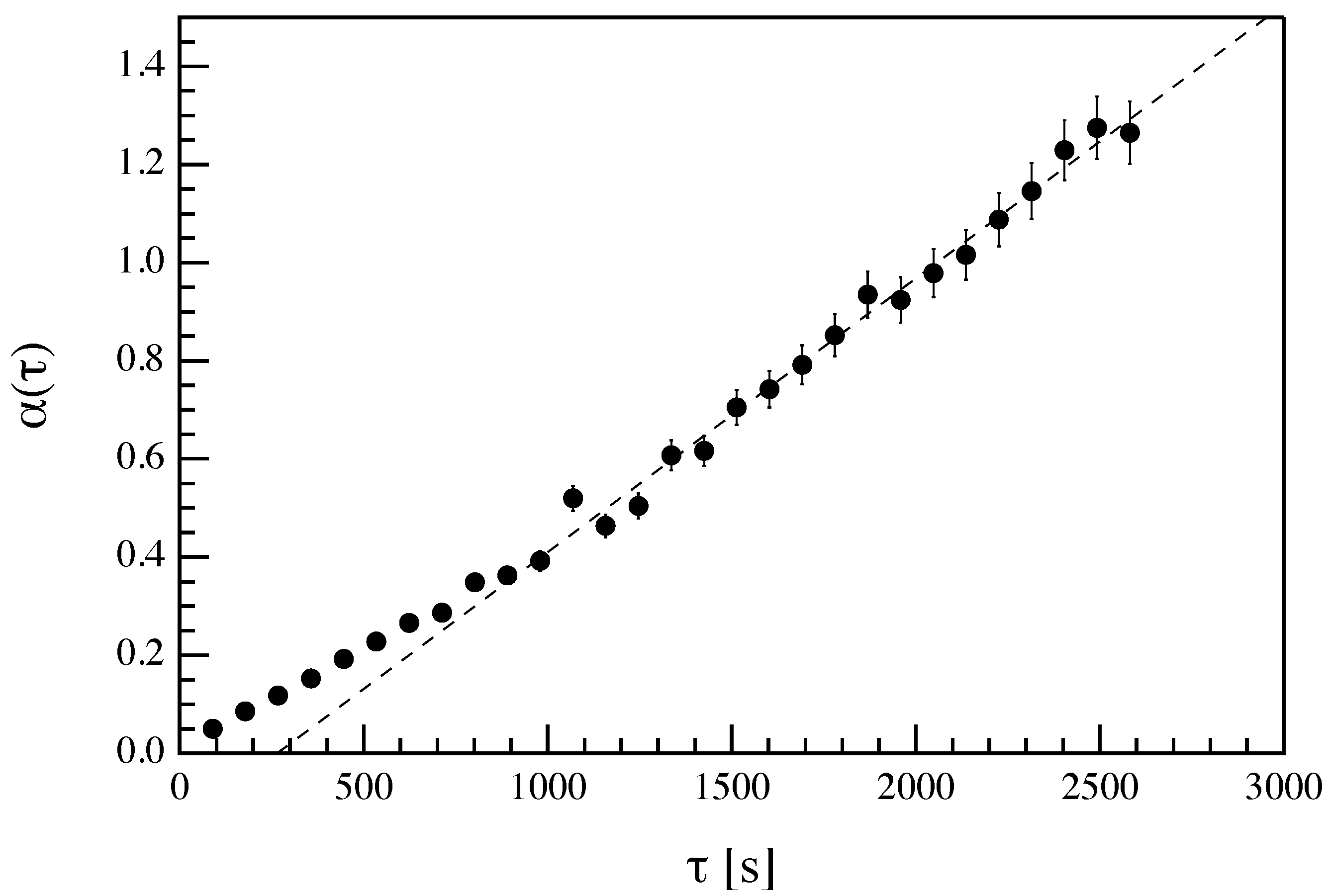
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viavattene, G.; Consolini, G.; Giovannelli, L.; Berrilli, F.; Del Moro, D.; Giannattasio, F.; Penza, V.; Calchetti, D. Testing the Steady-State Fluctuation Relation in the Solar Photospheric Convection. Entropy 2020, 22, 716. https://doi.org/10.3390/e22070716
Viavattene G, Consolini G, Giovannelli L, Berrilli F, Del Moro D, Giannattasio F, Penza V, Calchetti D. Testing the Steady-State Fluctuation Relation in the Solar Photospheric Convection. Entropy. 2020; 22(7):716. https://doi.org/10.3390/e22070716
Chicago/Turabian StyleViavattene, Giorgio, Giuseppe Consolini, Luca Giovannelli, Francesco Berrilli, Dario Del Moro, Fabio Giannattasio, Valentina Penza, and Daniele Calchetti. 2020. "Testing the Steady-State Fluctuation Relation in the Solar Photospheric Convection" Entropy 22, no. 7: 716. https://doi.org/10.3390/e22070716
APA StyleViavattene, G., Consolini, G., Giovannelli, L., Berrilli, F., Del Moro, D., Giannattasio, F., Penza, V., & Calchetti, D. (2020). Testing the Steady-State Fluctuation Relation in the Solar Photospheric Convection. Entropy, 22(7), 716. https://doi.org/10.3390/e22070716






