Optimal Encoding in Stochastic Latent-Variable Models
Abstract
1. Introduction
2. Results
2.1. RBMs as a Statistical Machine-Learning Analogue of Stochastic Spiking Communication
2.2. RBMs Provide an Energy-Based Interpretation of Spiking Population Codes
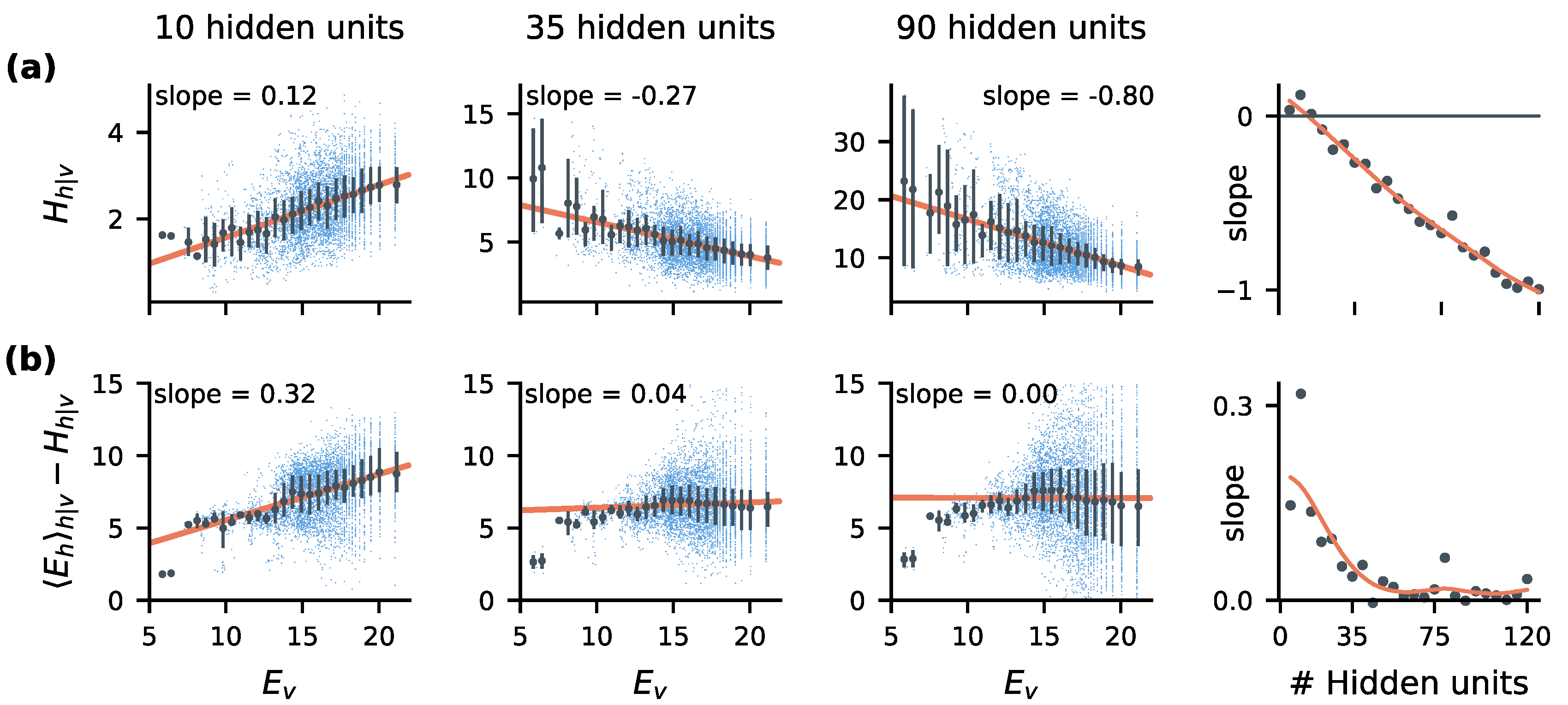
2.3. Stimulus-Dependent Variability Suppression Is a Key Feature of Optimal Encoding
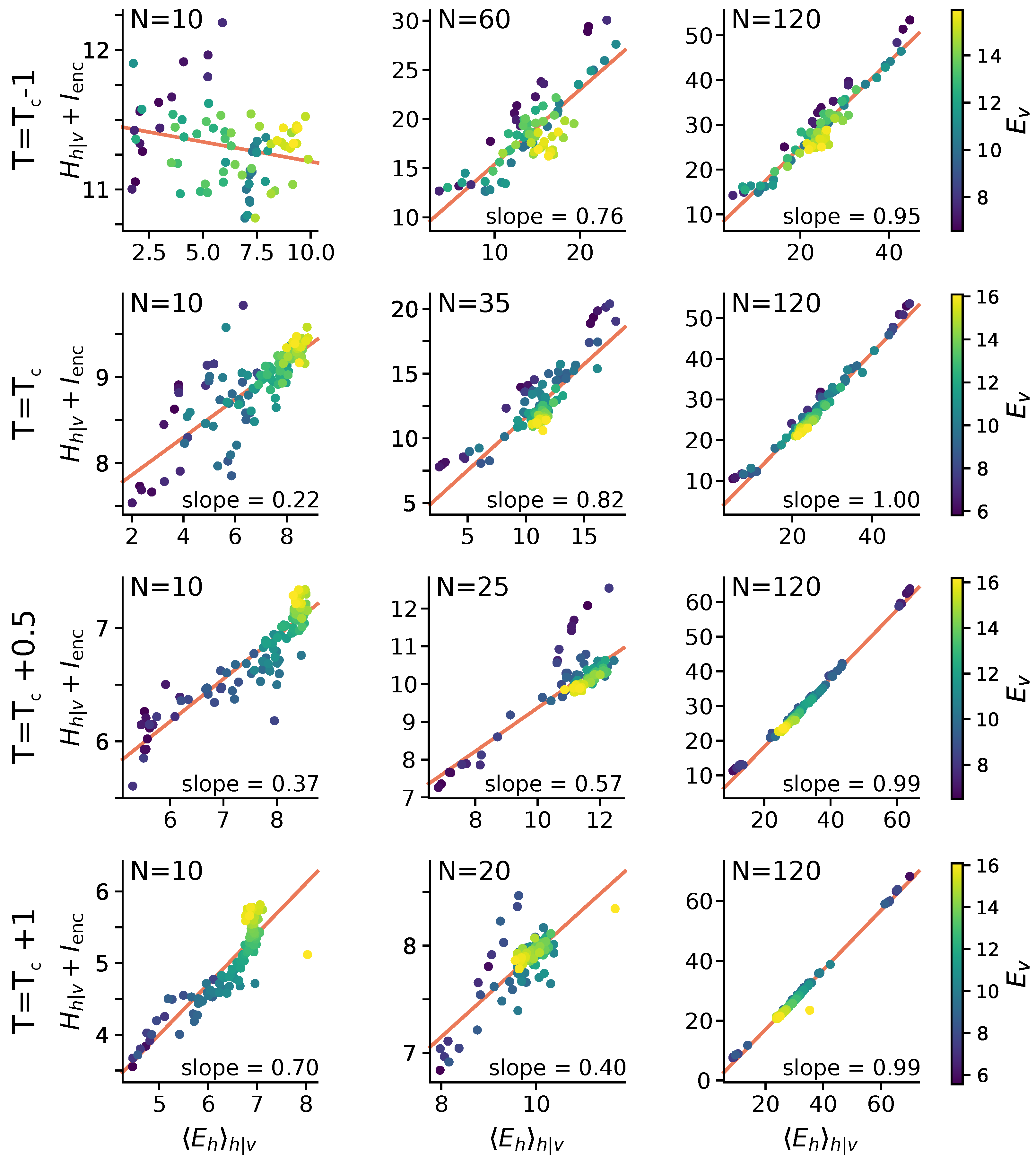
2.4. Optimal Codes Exhibit Statistical Criticality
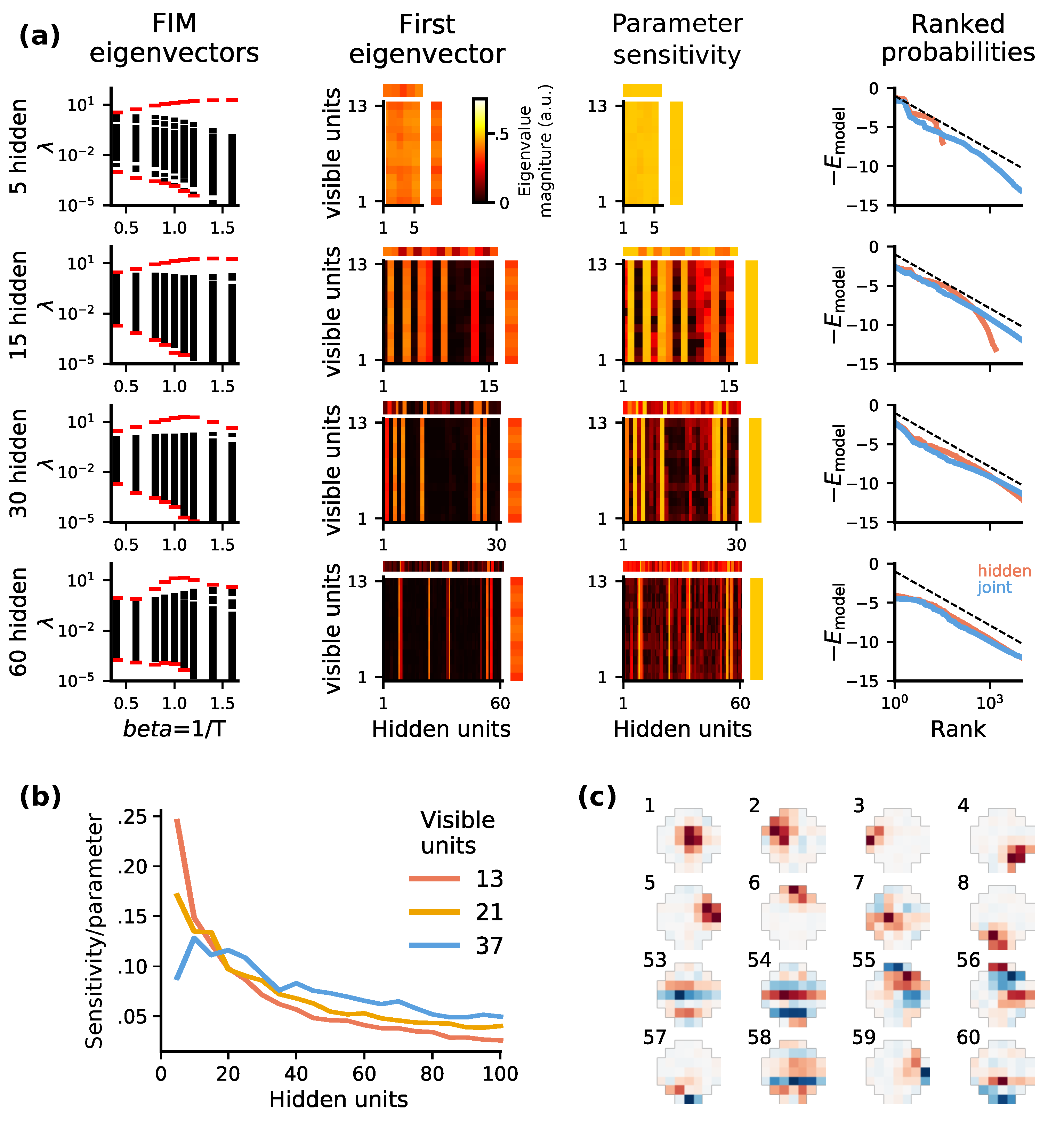
2.5. Statistical Correlates of the Size-Accuracy Trade-Off
3. Discussion
4. Materials and Methods
4.1. Datasets
4.2. Restricted Boltzmann Machines
4.3. Energy and Entropy
4.4. Fisher Information
4.5. Free Energy in RBMs
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RBM | Restricted Boltzmann Machine |
| FIM | Fisher Information Matrix |
| v | ‘Visible stimulus’ pattern, the input to a neural sensory encoder |
| h | ‘Hidden activation’ pattern of stimulus-driven binary neural activity (interpreted as spiking) |
| W | The weight matrix for an RBM mapping visible activations to hidden-unit drive |
| The biases on the hidden units for an RBM | |
| The biases on the visible units for an RBM | |
| Parameters associated with an RBM model | |
| E | ‘Energy’, defined here as negative log-probability |
| H | ‘Entropy’, in the Shannon sense |
| The log-probability of simultaneously observing stimulus v and neural pattern h | |
| The entropy of the distribution of neural patterns h evoked by stimulus v | |
| Set of input stimuli with similar energy (log-probability i.e., bitrate) | |
| The critical temperature of an RBM interpreted as an Ising spin model | |
| Inverse temperature |
References
- Barlow, H.B. Single units and sensation: A neuron doctrine for perceptual psychology? Perception 1972, 1, 371–394. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication, Part I, Part II. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Field, D.J. Relations between the statistics of natural images and the response properties of cortical cells. Josa A 1987, 4, 2379–2394. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed]
- Vinje, W.E.; Gallant, J.L. Sparse coding and decorrelation in primary visual cortex during natural vision. Science 2000, 287, 1273–1276. [Google Scholar] [CrossRef] [PubMed]
- Churchland, M.M.; Byron, M.Y.; Cunningham, J.P.; Sugrue, L.P.; Cohen, M.R.; Corrado, G.S.; Newsome, W.T.; Clark, A.M.; Hosseini, P.; Scott, B.B.; et al. Stimulus onset quenches neural variability: A widespread cortical phenomenon. Nat. Neurosci. 2010, 13, 369–378. [Google Scholar] [CrossRef] [PubMed]
- Orbán, G.; Berkes, P.; Fiser, J.; Lengyel, M. Neural variability and sampling-based probabilistic representations in the visual cortex. Neuron 2016, 92, 530–543. [Google Scholar] [CrossRef]
- Prentice, J.S.; Marre, O.; Ioffe, M.L.; Loback, A.R.; Tkačik, G.; Berry, M.J. Error-robust modes of the retinal population code. PLoS Comput. Biol. 2016, 12, e1005148. [Google Scholar] [CrossRef]
- Loback, A.; Prentice, J.; Ioffe, M.; Berry, M., II. Noise-Robust Modes of the Retinal Population Code Have the Geometry of “Ridges” and Correspond to Neuronal Communities. Neural Comput. 2017, 29, 3119–3180. [Google Scholar] [CrossRef]
- Destexhe, A.; Sejnowski, T.J. The Wilson–Cowan model, 36 years later. Biol. Cybern. 2009, 101, 1–2. [Google Scholar] [CrossRef]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Shlens, J.; Field, G.D.; Gauthier, J.L.; Grivich, M.I.; Petrusca, D.; Sher, A.; Litke, A.M.; Chichilnisky, E. The structure of multi-neuron firing patterns in primate retina. J. Neurosci. 2006, 26, 8254–8266. [Google Scholar] [CrossRef] [PubMed]
- Köster, U.; Sohl-Dickstein, J.; Gray, C.M.; Olshausen, B.A. Modeling higher-order correlations within cortical microcolumns. PLoS Comput. Biol. 2014, 10, e1003684. [Google Scholar] [CrossRef] [PubMed]
- Tkačik, G.; Mora, T.; Marre, O.; Amodei, D.; Palmer, S.E.; Berry, M.J.; Bialek, W. Thermodynamics and signatures of criticality in a network of neurons. Proc. Natl. Acad. Sci. USA 2015, 112, 11508–11513. [Google Scholar] [CrossRef]
- Hinton, G.E.; Brown, A.D. Spiking boltzmann machines. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2000; pp. 122–128. [Google Scholar]
- Nasser, H.; Marre, O.; Cessac, B. Spatio-temporal spike train analysis for large scale networks using the maximum entropy principle and Monte Carlo method. J. Stat. Mech. Theory Exp. 2013, 2013, P03006. [Google Scholar] [CrossRef]
- Zanotto, M.; Volpi, R.; Maccione, A.; Berdondini, L.; Sona, D.; Murino, V. Modeling retinal ganglion cell population activity with restricted Boltzmann machines. arXiv 2017, arXiv:1701.02898. [Google Scholar]
- Gardella, C.; Marre, O.; Mora, T. Blindfold learning of an accurate neural metric. Proc. Natl. Acad. Sci. USA 2018, 115, 3267–3272. [Google Scholar] [CrossRef]
- Turcsany, D.; Bargiela, A.; Maul, T. Modelling Retinal Feature Detection with Deep Belief Networks in a Simulated Environment. In Proceedings of the 28th European Conference on Modelling and Simulation (ECMS), Brescia, Italy, 27–30 May 2014; pp. 364–370. [Google Scholar]
- Shao, L.Y. Linear-Nonlinear-Poisson Neurons Can Do Inference on Deep Boltzmann Machines. In Proceedings of the 1st International Conference on Learning Representations, ICLR 2013, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Schwab, D.J.; Nemenman, I.; Mehta, P. Zipf’s law and criticality in multivariate data without fine-tuning. Phys. Rev. Lett. 2014, 113, 068102. [Google Scholar] [CrossRef]
- Mastromatteo, I.; Marsili, M. On the criticality of inferred models. J. Stat. Mech. Theory Exp. 2011, 2011, P10012. [Google Scholar] [CrossRef]
- Beggs, J.M.; Timme, N. Being critical of criticality in the brain. Front. Physiol. 2012, 3, 163. [Google Scholar] [CrossRef]
- Aitchison, L.; Corradi, N.; Latham, P.E. Zipf’s Law Arises Naturally When There Are Underlying, Unobserved Variables. PLoS Comput. Biol. 2016, 12, e1005110. [Google Scholar] [CrossRef] [PubMed]
- Touboul, J.; Destexhe, A. Power-law statistics and universal scaling in the absence of criticality. Phys. Rev. E 2017, 95, 012413. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E. A practical guide to training restricted Boltzmann machines. In Neural Networks: Tricks of the Trade; Springer: Berlin, Germany, 2012; pp. 599–619. [Google Scholar]
- Hinton, G.E.; Dayan, P.; Frey, B.J.; Neal, R.M. The “wake-sleep” algorithm for unsupervised neural networks. Science 1995, 268, 1158–1161. [Google Scholar] [CrossRef]
- Dayan, P.; Hinton, G.E.; Neal, R.M.; Zemel, R.S. The Helmholtz Machine. Neural Comput. 1995, 7, 889–904. [Google Scholar] [CrossRef]
- Mora, T.; Bialek, W. Are Biological Systems Poised at Criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef]
- Sorbaro, M.; Herrmann, J.M.; Hennig, M. Statistical models of neural activity, criticality, and Zipf’s law. In The Functional Role of Critical Dynamics in Neural Systems; Springer: Berlin, Germany, 2019; pp. 265–287. [Google Scholar]
- Bradde, S.; Bialek, W. PCA meets RG. J. Stat. Phys. 2017, 167, 462–475. [Google Scholar] [CrossRef]
- Meshulam, L.; Gauthier, J.L.; Brody, C.D.; Tank, D.W.; Bialek, W. Coarse graining, fixed points, and scaling in a large population of neurons. Phys. Rev. Lett. 2019, 123, 178103. [Google Scholar] [CrossRef]
- Stringer, C.; Pachitariu, M.; Steinmetz, N.; Carandini, M.; Harris, K.D. High-dimensional geometry of population responses in visual cortex. Nature 2019, 571, 361–365. [Google Scholar] [CrossRef]
- Ioffe, M.L.; Berry, M.J., II. The structured ‘low temperature’ phase of the retinal population code. PLoS Comput. Biol. 2017, 13, e1005792. [Google Scholar] [CrossRef]
- Tyrcha, J.; Roudi, Y.; Marsili, M.; Hertz, J. The effect of nonstationarity on models inferred from neural data. J. Stat. Mech. Theory Exp. 2013, 2013, P03005. [Google Scholar] [CrossRef]
- Nonnenmacher, M.; Behrens, C.; Berens, P.; Bethge, M.; Macke, J.H. Signatures of criticality arise from random subsampling in simple population models. PLoS Comput. Biol. 2017, 13, e1005718. [Google Scholar] [CrossRef] [PubMed]
- Saremi, S.; Sejnowski, T.J. On criticality in high-dimensional data. Neural Comput. 2014, 26, 1329–1339. [Google Scholar] [CrossRef] [PubMed]
- Swendsen, R.H.; Wang, J.S. Nonuniversal critical dynamics in Monte Carlo simulations. Phys. Rev. Lett. 1987, 58, 86. [Google Scholar] [CrossRef]
- Stephens, G.J.; Mora, T.; Tkačik, G.; Bialek, W. Statistical Thermodynamics of Natural Images. Phys. Rev. Lett. 2013, 110, 018701. [Google Scholar] [CrossRef]
- Bedard, C.; Kroeger, H.; Destexhe, A. Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 2006, 97, 118102. [Google Scholar] [CrossRef] [PubMed]
- Prokopenko, M.; Lizier, J.T.; Obst, O.; Wang, X.R. Relating Fisher information to order parameters. Phys. Rev. E 2011, 84, 041116. [Google Scholar] [CrossRef] [PubMed]
- Daniels, B.C.; Chen, Y.J.; Sethna, J.P.; Gutenkunst, R.N.; Myers, C.R. Sloppiness, robustness, and evolvability in systems biology. Curr. Opin. Biotechnol. 2008, 19, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Gutenkunst, R.N.; Waterfall, J.J.; Casey, F.P.; Brown, K.S.; Myers, C.R.; Sethna, J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007, 3, e189. [Google Scholar] [CrossRef]
- Panas, D.; Amin, H.; Maccione, A.; Muthmann, O.; van Rossum, M.; Berdondini, L.; Hennig, M.H. Sloppiness in spontaneously active neuronal networks. J. Neurosci. 2015, 35, 8480–8492. [Google Scholar] [CrossRef]
- Schneidman, E.; Puchalla, J.L.; Segev, R.; Harris, R.A.; Bialek, W.; Berry, M.J. Synergy from silence in a combinatorial neural code. J. Neurosci. 2011, 31, 15732–15741. [Google Scholar] [CrossRef] [PubMed]
- White, B.; Abbott, L.F.; Fiser, J. Suppression of cortical neural variability is stimulus-and state-dependent. J. Neurophysiol. 2012, 108, 2383–2392. [Google Scholar] [CrossRef] [PubMed]
- Festa, D.; Aschner, A.; Davila, A.; Kohn, A.; Coen-Cagli, R. Neuronal variability reflects probabilistic inference tuned to natural image statistics. BioRxiv 2020. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- LaMont, C.H.; Wiggins, P.A. Correspondence between thermodynamics and inference. Phys. Rev. E 2019, 99, 052140. [Google Scholar] [CrossRef] [PubMed]
- Aitchison, L.; Hennequin, G.; Lengyel, M. Sampling-based probabilistic inference emerges from learning in neural circuits with a cost on reliability. arXiv 2018, arXiv:1807.08952. [Google Scholar]
- Song, J.; Marsili, M.; Jo, J. Resolution and relevance trade-offs in deep learning. J. Stat. Mech. Theory Exp. 2018, 2018, 123406. [Google Scholar] [CrossRef]
- Cubero, R.J.; Jo, J.; Marsili, M.; Roudi, Y.; Song, J. Statistical criticality arises in most informative representations. J. Stat. Mech. Theory Exp. 2019, 2019, 063402. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features From Tiny Images. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rule, M.E.; Sorbaro, M.; Hennig, M.H. Optimal Encoding in Stochastic Latent-Variable Models. Entropy 2020, 22, 714. https://doi.org/10.3390/e22070714
Rule ME, Sorbaro M, Hennig MH. Optimal Encoding in Stochastic Latent-Variable Models. Entropy. 2020; 22(7):714. https://doi.org/10.3390/e22070714
Chicago/Turabian StyleRule, Michael E., Martino Sorbaro, and Matthias H. Hennig. 2020. "Optimal Encoding in Stochastic Latent-Variable Models" Entropy 22, no. 7: 714. https://doi.org/10.3390/e22070714
APA StyleRule, M. E., Sorbaro, M., & Hennig, M. H. (2020). Optimal Encoding in Stochastic Latent-Variable Models. Entropy, 22(7), 714. https://doi.org/10.3390/e22070714




