Assessment of Airflow and Oximetry Signals to Detect Pediatric Sleep Apnea-Hypopnea Syndrome Using AdaBoost
Abstract
1. Introduction
2. Database
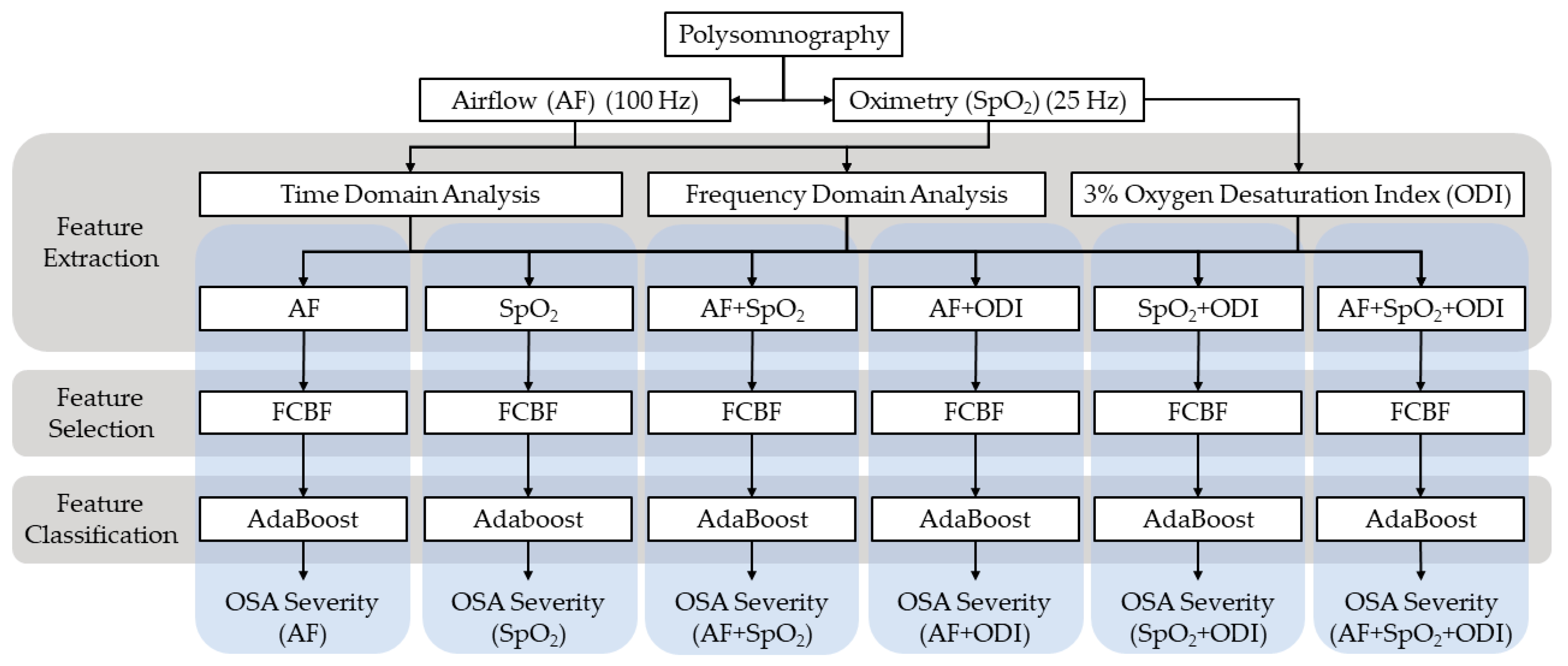
3. Methods
3.1. Preprocessing
3.2. Feature Extraction: Time and Frequency Domain Analyses
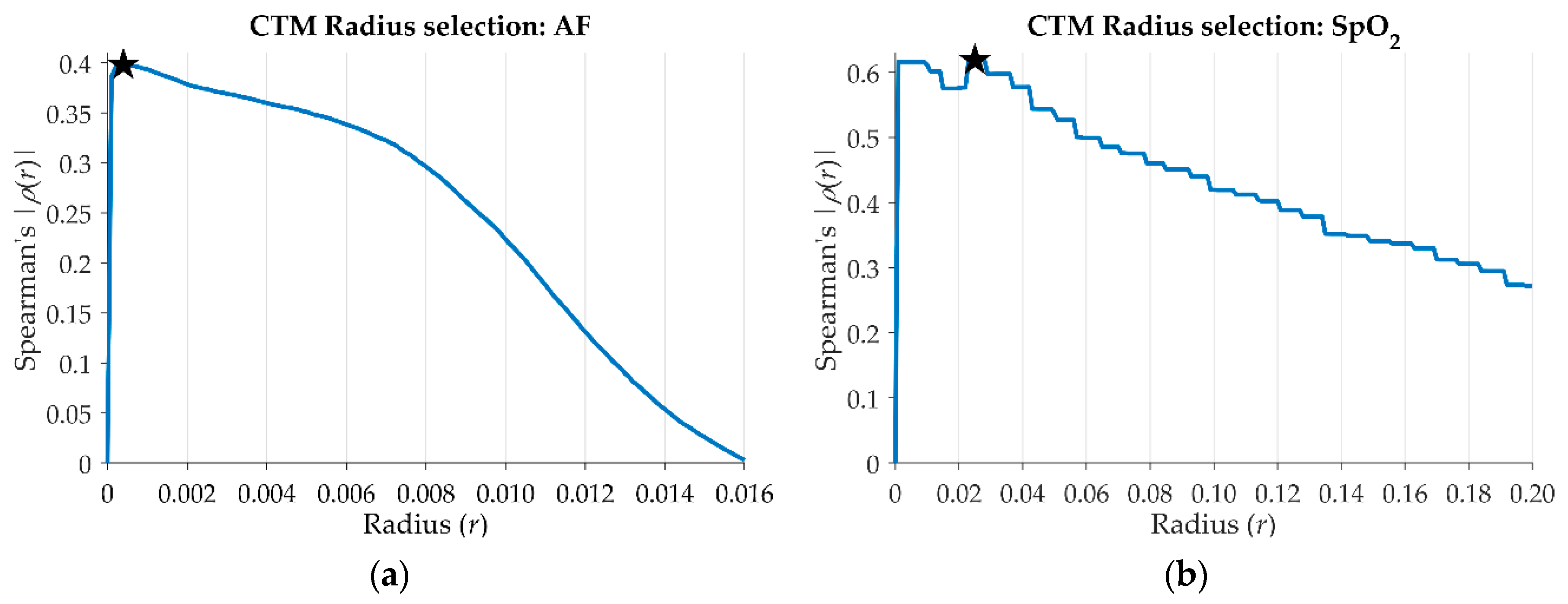
3.2.1. Time-Domain Moments and Nonlinear Analysis
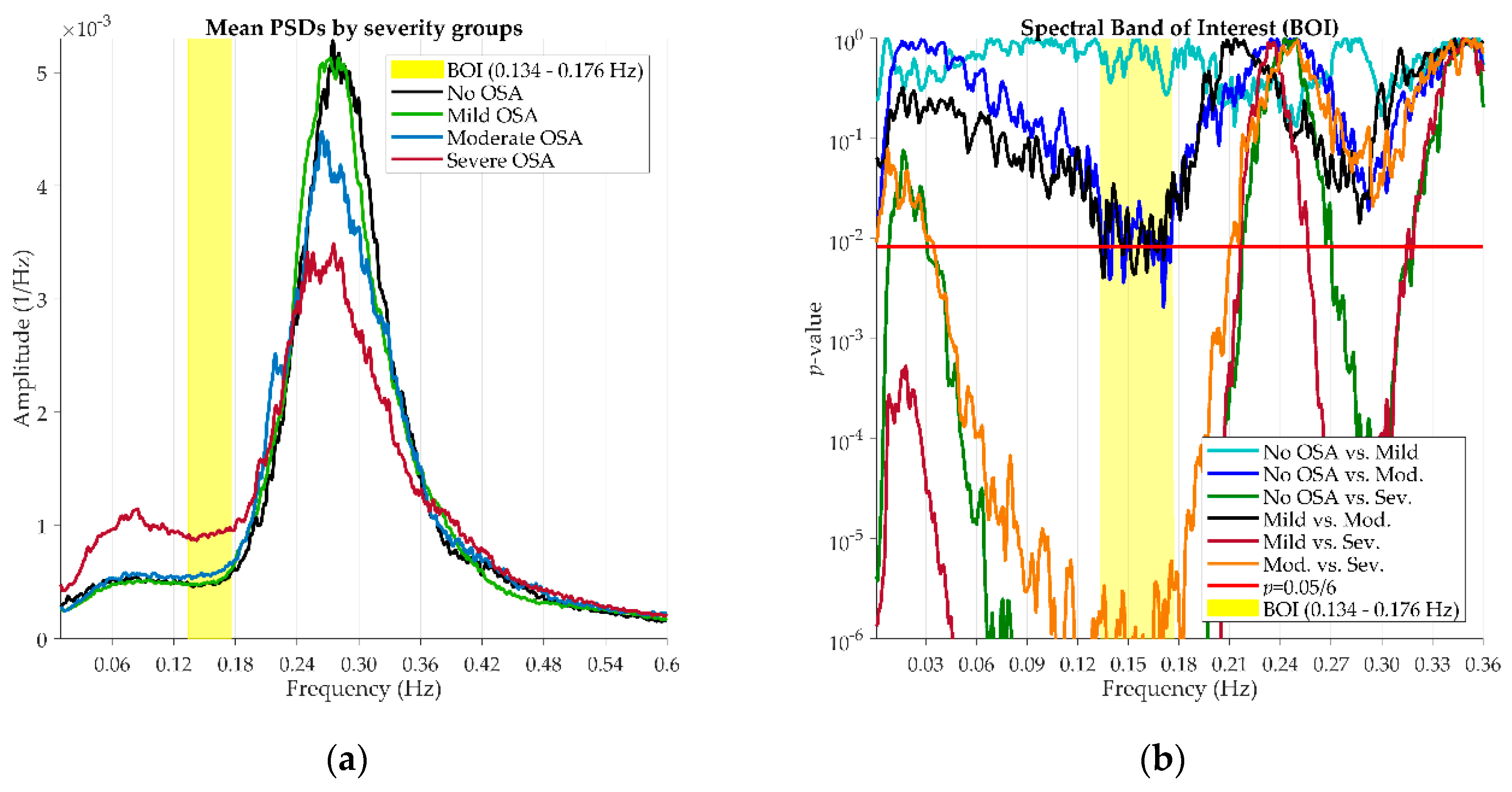
3.2.2. Spectral Analysis
3.2.3. Oxygen Desaturation Index
3.3. Feature Selection: Fast Correlation-Based Filter
3.4. Classification: Multiclass AdaBoost
3.5. Model Optimization and Training
3.6. Statistical Analysis
4. Results
4.1. Preprocessing. Parameters Optimization in the Training Set
4.2. Statistical Analysis in the Training Set: Individual Features
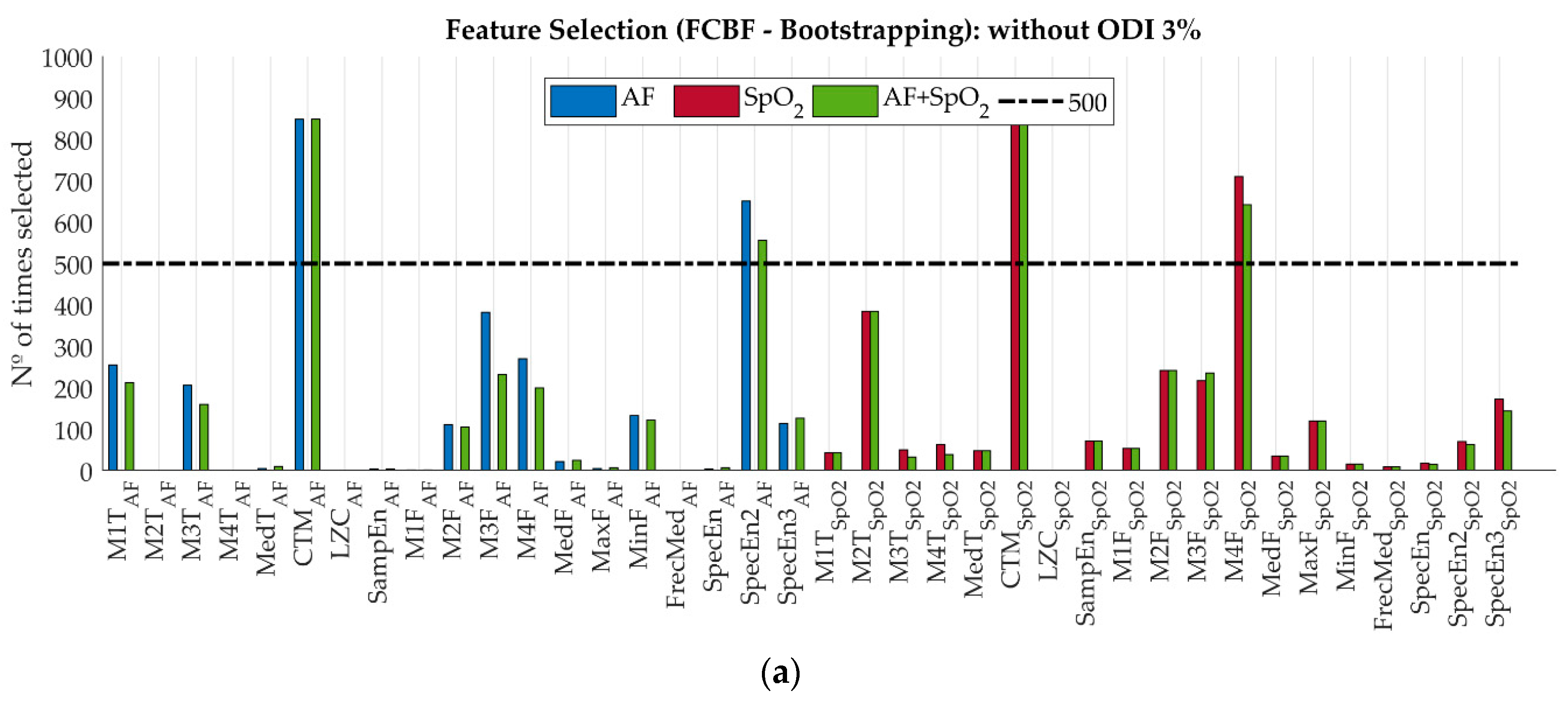
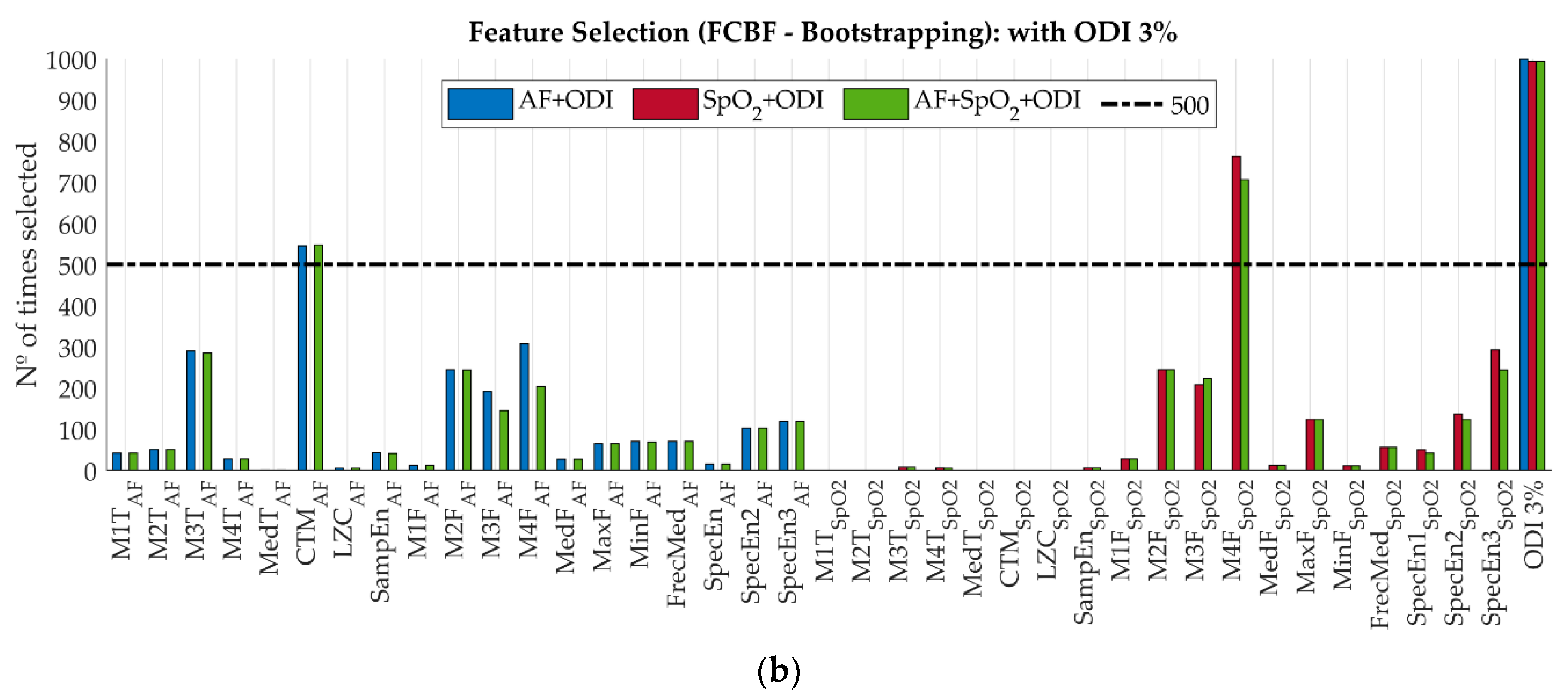
4.3. Feature Selection in the Training Set
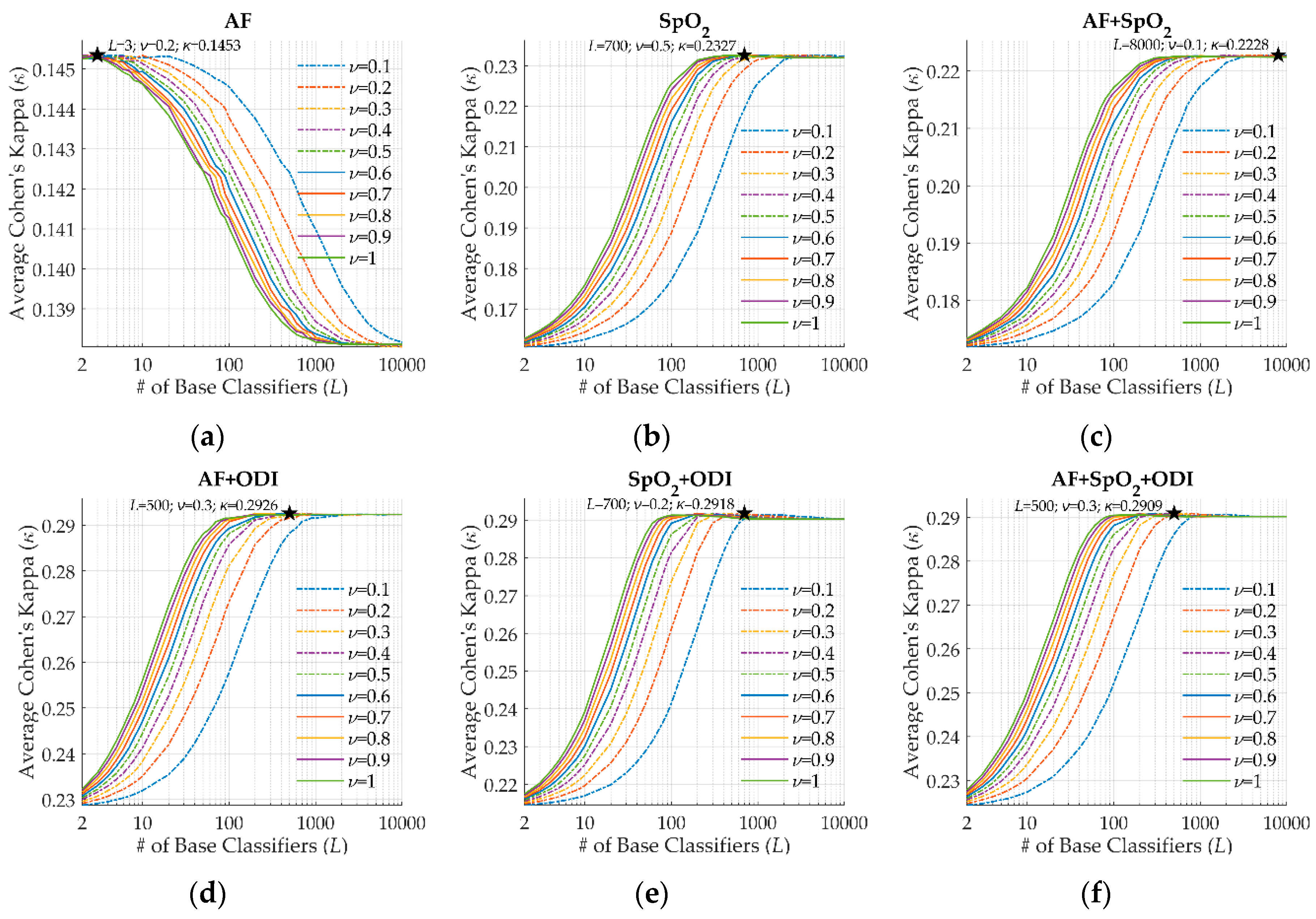
4.4. Model Optimization in the Training Set
4.5. Diagnostic Ability Assessment in the Test Set
5. Discussion
5.1. Feature Extraction and Selection
5.2. Diagnostic Ability and Comparison with Previous Studies
5.3. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tauman, R.; Gozal, D. Obstructive sleep apnea syndrome in children. Expert Rev. Respir. Med. 2011, 5, 425–440. [Google Scholar] [CrossRef] [PubMed]
- Marcus, C.L.; Brooks, L.J.; Ward, S.D.; Draper, K.A.; Gozal, D.; Halbower, A.C.; Jones, J.; Lehmann, C.; Schechter, M.S.; Sheldon, S.; et al. Diagnosis and Management of Childhood Obstructive Sleep Apnea Syndrome. Pediatrics 2012, 130, e714–e755. [Google Scholar] [CrossRef] [PubMed]
- DelRosso, L.M. Epidemiology and Diagnosis of Pediatric Obstructive Sleep Apnea. Curr. Probl. Pediatr. Adolesc. Health Care 2016, 46, 2–6. [Google Scholar] [CrossRef] [PubMed]
- Hunter, S.J.; Gozal, D.; Smith, D.L.; Philby, M.F.; Kaylegian, J.; Kheirandish-Gozal, L. Effect of Sleep-disordered Breathing Severity on Cognitive Performance Measures in a Large Community Cohort of Young School-aged Children. Am. J. Respir. Crit. Care Med. 2016, 194, 739–747. [Google Scholar] [CrossRef] [PubMed]
- Blechner, M.; Williamson, A.A. Consequences of Obstructive Sleep Apnea in Children. Curr. Probl. Pediatr. Adolesc. Health Care 2016, 46, 19–26. [Google Scholar] [CrossRef]
- Brockmann, P.E.; Schaefer, C.; Poets, A.; Poets, C.F.; Urschitz, M.S. Diagnosis of obstructive sleep apnea in children: A systematic review. Sleep Med. Rev. 2013, 17, 331–340. [Google Scholar] [CrossRef]
- Tan, H.-L.; Kheirandish-Gozal, L.; Gozal, D. Pediatric Home Sleep Apnea Testing. Chest 2015, 148, 1382–1395. [Google Scholar] [CrossRef]
- Tan, H.-L.; Bandla, H.P.R.; Ramirez, H.M.; Gozal, D.; Kheirandish-Gozal, L. Overnight Polysomnography versus Respiratory Polygraphy in the Diagnosis of Pediatric Obstructive Sleep Apnea. Sleep 2014, 37, 255–260. [Google Scholar] [CrossRef]
- Kaditis, A.G.; Alonso Alvarez, M.L.; Boudewyns, A.; Alexopoulos, E.I.; Ersu, R.; Joosten, K.; Larramona, H.; Miano, S.; Narang, I.; Trang, H.; et al. Obstructive sleep disordered breathing in 2- to 18-year-old children: Diagnosis and management. Eur. Respir. J. 2016, 47, 69–94. [Google Scholar] [CrossRef]
- Alonso-Álvarez, M.L.; Terán-Santos, J.; Ordax Carbajo, E.; Cordero-Guevara, J.A.; Navazo-Egüia, A.I.; Kheirandish-Gozal, L.; Gozal, D. Reliability of Home Respiratory Polygraphy for the Diagnosis of Sleep Apnea in Children. Chest 2015, 147, 1020–1028. [Google Scholar] [CrossRef]
- Stehling, F.; Keull, J.; Olivier, M.; Große-Onnebrink, J.; Mellies, U.; Stuck, B.A. Validation of the screening tool ApneaLink® in comparison to polysomnography for the diagnosis of sleep-disordered breathing in children and adolescents. Sleep Med. 2017, 37, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Kaditis, A.; Kheirandish-Gozal, L.; Gozal, D. Pediatric OSAS: Oximetry can provide answers when polysomnography is not available. Sleep Med. Rev. 2016, 27, 96–105. [Google Scholar] [CrossRef]
- Van Eyck, A.; Verhulst, S.L. Improving the diagnosis of obstructive sleep apnea in children with nocturnal oximetry-based evaluations. Expert Rev. Respir. Med. 2018, 12, 165–167. [Google Scholar] [CrossRef] [PubMed]
- Berry, R.B.; Budhiraja, R.; Gottlieb, D.J.; Gozal, D.; Iber, C.; Kapur, V.K.; Marcus, C.L.; Mehra, R.; Parthasarathy, S.; Quan, S.F.; et al. Rules for Scoring Respiratory Events in Sleep: Update of the 2007 AASM Manual for the Scoring of Sleep and Associated Events. J. Clin. Sleep Med. 2012, 8, 597–619. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.B.; Chow, C.M.; Su, S.W. Classification methods to detect sleep apnea in adults based on respiratory and oximetry signals: A systematic review. Physiol. Meas. 2018, 39, 03TR01. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, F.; Mostafa, S.S.; Ravelo-García, A.G.; Morgado-Dias, F.; Penzel, T. A Review of Obstructive Sleep Apnea Detection Approaches. IEEE J. Biomed. Health Inform. 2019, 23, 825–837. [Google Scholar] [CrossRef]
- del Campo, F.; Crespo, A.; Cerezo-Hernández, A.; Gutiérrez-Tobal, G.C.; Hornero, R.; Álvarez, D. Oximetry use in obstructive sleep apnea. Expert Rev. Respir. Med. 2018, 12, 665–681. [Google Scholar] [CrossRef]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Marcos, J.V.; Del Campo, F.; Hornero, R. Pattern recognition in airflow recordings to assist in the sleep apnoea-hypopnoea syndrome diagnosis. Med. Biol. Eng. Comput. 2013, 51, 1367–1380. [Google Scholar] [CrossRef]
- Gutierrez-Tobal, G.C.; Alvarez, D.; del Campo, F.; Hornero, R. Utility of AdaBoost to Detect Sleep Apnea-Hypopnea Syndrome From Single-Channel Airflow. IEEE Trans. Biomed. Eng. 2016, 63, 636–646. [Google Scholar] [CrossRef]
- Álvarez, D.; Hornero, R.; Víctor Marcos, J.; Delcampo, F. Multivariate analysis of blood oxygen saturation recordings in obstructive sleep apnea diagnosis. IEEE Trans. Biomed. Eng. 2010, 57, 2816–2824. [Google Scholar] [CrossRef] [PubMed]
- Marcos, J.V.; Hornero, R.; Álvarez, D.; Aboy, M.; Del Campo, F. Automated Prediction of the Apnea-Hypopnea Index from Nocturnal Oximetry Recordings. IEEE Trans. Biomed. Eng. 2012, 59, 141–149. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Crespo, A.; Del Campo, F.; Hornero, R. Evaluation of Machine-Learning Approaches to Estimate Sleep Apnea Severity From At-Home Oximetry Recordings. IEEE J. Biomed. Health Inform. 2019, 23, 882–892. [Google Scholar] [CrossRef] [PubMed]
- Garde, A.; Dehkordi, P.; Karlen, W.; Wensley, D.; Ansermino, J.M.; Dumont, G.A. Development of a Screening Tool for Sleep Disordered Breathing in Children Using the Phone OximeterTM. PLoS ONE 2014, 9, e112959. [Google Scholar] [CrossRef]
- Garde, A.; Hoppenbrouwer, X.; Dehkordi, P.; Zhou, G.; Rollinson, A.U.; Wensley, D.; Dumont, G.A.; Ansermino, J.M. Pediatric pulse oximetry-based OSA screening at different thresholds of the apnea-hypopnea index with an expression of uncertainty for inconclusive classifications. Sleep Med. 2019, 60, 45–52. [Google Scholar] [CrossRef]
- Álvarez, D.; Alonso-Álvarez, M.L.; Gutiérrez-Tobal, G.C.; Crespo, A.; Kheirandish-Gozal, L.; Hornero, R.; Gozal, D.; Terán-Santos, J.; Del Campo, F. Automated Screening of Children With Obstructive Sleep Apnea Using Nocturnal Oximetry: An Alternative to Respiratory Polygraphy in Unattended Settings. J. Clin. Sleep Med. 2017, 13, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Philby, M.F.; Alonso-Álvarez, M.L.; Álvarez, D.; Dayyat, E.A.; Xu, Z.; Huang, Y.-S.; Tamae Kakazu, M.; et al. Nocturnal Oximetry-based Evaluation of Habitually Snoring Children. Am. J. Respir. Crit. Care Med. 2017, 196, 1591–1598. [Google Scholar] [CrossRef]
- Crespo, A.; Álvarez, D.; Gutiérrez-Tobal, G.C.; Vaquerizo-Villar, F.; Barroso-García, V.; Alonso-Álvarez, M.L.; Terán-Santos, J.; Hornero, R.; Campo, F.D. Multiscale Entropy Analysis of Unattended Oximetric Recordings to Assist in the Screening of Paediatric Sleep Apnoea at Home. Entropy 2017, 19, 284. [Google Scholar] [CrossRef]
- Álvarez, D.; Crespo, A.; Vaquerizo-Villar, F.; Gutiérrez-Tobal, G.C.; Cerezo-Hernández, A.; Barroso-García, V.; Ansermino, J.M.; Dumont, G.A.; Hornero, R.; del Campo, F.; et al. Symbolic dynamics to enhance diagnostic ability of portable oximetry from the Phone Oximeter in the detection of paediatric sleep apnoea. Physiol. Meas. 2018, 39, 104002. [Google Scholar] [CrossRef]
- Vaquerizo-Villar, F.; Álvarez, D.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Barroso-García, V.; Crespo, A.; del Campo, F.; Gozal, D.; Hornero, R. Detrended fluctuation analysis of the oximetry signal to assist in paediatric sleep apnoea–hypopnoea syndrome diagnosis. Physiol. Meas. 2018, 39, 114006. [Google Scholar] [CrossRef]
- Gutiérrez-Tobal, G.C.; Alonso-Álvarez, M.L.; Álvarez, D.; del Campo, F.; Terán-Santos, J.; Hornero, R. Diagnosis of pediatric obstructive sleep apnea: Preliminary findings using automatic analysis of airflow and oximetry recordings obtained at patients’ home. Biomed. Signal Process. Control 2015, 18, 401–407. [Google Scholar] [CrossRef]
- Barroso-García, V.; Gutiérrez-Tobal, G.; Kheirandish-Gozal, L.; Álvarez, D.; Vaquerizo-Villar, F.; Crespo, A.; del Campo, F.; Gozal, D.; Hornero, R. Irregularity and Variability Analysis of Airflow Recordings to Facilitate the Diagnosis of Paediatric Sleep Apnoea-Hypopnoea Syndrome. Entropy 2017, 19, 447. [Google Scholar] [CrossRef]
- Barroso-García, V.; Gutiérrez-Tobal, G.C.; Kheirandish-Gozal, L.; Álvarez, D.; Vaquerizo-Villar, F.; Núñez, P.; del Campo, F.; Gozal, D.; Hornero, R. Usefulness of recurrence plots from airflow recordings to aid in paediatric sleep apnoea diagnosis. Comput. Methods Programs Biomed. 2020, 183, 105083. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-García, J.; Gutiérrez-Tobal, G.C.; García, M.; Álvarez, D.; Barroso-García, V.; Vaquerizo-Villar, F.; Martín-Montero, A.; Del Campo, F.; Kheirandish-Gozal, L.; Gozal, D.; et al. Evaluación de la información espectral de las señales de flujo aéreo y saturación de oxígeno en sangre para la ayuda al diagnóstico de la apnea del sueño infantil. In Proceedings of the XXXVII Congreso Anual de la Sociedad Española de Ingeniería Biomédica, Santander, Spain, 27–29 November 2019; pp. 25–28. [Google Scholar]
- Álvarez, D.; Cerezo-Hernández, A.; Crespo, A.; Gutiérrez-Tobal, G.C.; Vaquerizo-Villar, F.; Barroso-García, V.; Moreno, F.; Arroyo, C.A.; Ruiz, T.; Hornero, R.; et al. A machine learning-based test for adult sleep apnoea screening at home using oximetry and airflow. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Rosen, C.L.; D’andrea, L.; Haddad, G.G. Adult Criteria for Obstructive Sleep Apnea Do Not Identify Children with Serious Obstruction. Am. Rev. Respir. Dis. 1992, 146, 1231–1234. [Google Scholar] [CrossRef]
- Chang, L.; Wu, J.; Cao, L. Combination of symptoms and oxygen desaturation index in predicting childhood obstructive sleep apnea. Int. J. Pediatr. Otorhinolaryngol. 2013, 77, 365–371. [Google Scholar] [CrossRef]
- Wu, D.; Li, X.; Guo, X.; Qin, J.; Li, S. A simple diagnostic scale based on the analysis and screening of clinical parameters in paediatric obstructive sleep apnoea hypopnea syndrome. J. Laryngol. Otol. 2017, 131, 363–367. [Google Scholar] [CrossRef] [PubMed]
- Gil, E.; Bailon, R.; Vergara, J.M.; Laguna, P. PTT Variability for Discrimination of Sleep Apnea Related Decreases in the Amplitude Fluctuations of PPG Signal in Children. IEEE Trans. Biomed. Eng. 2010, 57, 1079–1088. [Google Scholar] [CrossRef] [PubMed]
- Lazaro, J.; Gil, E.; Vergara, J.M.; Laguna, P. Pulse Rate Variability Analysis for Discrimination of Sleep-Apnea-Related Decreases in the Amplitude Fluctuations of Pulse Photoplethysmographic Signal in Children. IEEE J. Biomed. Heal. Inform. 2014, 18, 240–246. [Google Scholar] [CrossRef]
- Crespo, A.; Álvarez, D.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Cerezo-Hernández, A.; Gozal, D.; Hornero, R.; del Campo, F. Assessment of oximetry-based statistical classifiers as simplified screening tools in the management of childhood obstructive sleep apnea. Sleep Breath. 2018, 22, 1063–1073. [Google Scholar] [CrossRef]
- Vaquerizo-Villar, F.; Álvarez, D.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Barroso-García, V.; Crespo, A.; del Campo, F.; Gozal, D.; Hornero, R. Wavelet analysis of oximetry recordings to assist in the automated detection of moderate-to-severe pediatric sleep apnea-hypopnea syndrome. PLoS ONE 2018, 13, e0208502. [Google Scholar] [CrossRef]
- Xu, Z.; Gutiérrez-Tobal, G.C.; Wu, Y.; Kheirandish-Gozal, L.; Ni, X.; Hornero, R.; Gozal, D. Cloud algorithm-driven oximetry-based diagnosis of obstructive sleep apnoea in symptomatic habitually snoring children. Eur. Respir. J. 2019, 53, 1801788. [Google Scholar] [CrossRef] [PubMed]
- Vaquerizo-Villar, F.; Álvarez, D.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Barroso-García, V.; Crespo, A.; del Campo, F.; Gozal, D.; Hornero, R. Utility of bispectrum in the screening of pediatric sleep apnea-hypopnea syndrome using oximetry recordings. Comput. Methods Programs Biomed. 2018, 156, 141–149. [Google Scholar] [CrossRef] [PubMed]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann/Elsevier: Burlington, MA, USA, 2011; ISBN 978-0-12-374856-0. [Google Scholar]
- Xie, B.; Minn, H. Real-time sleep apnea detection by classifier combination. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 469–477. [Google Scholar] [CrossRef] [PubMed]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2014; ISBN 9781118914540. [Google Scholar]
- Cohen, M.E.; Hudson, D.L.; Deedwania, P.C. Applying continuous chaotic modeling to cardiac signal analysis. IEEE Eng. Med. Biol. Mag. 1996, 15, 97–102. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Alcaraz, R.; Rieta, J.J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms. Biomed. Signal Process. Control 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Yu, L.; Liu, H. Efficient Feature Selection via Analysis of Relevance and Redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
| All | Training Set | Test Set | |
|---|---|---|---|
| N° of Subjects | 974 | 584 (60%) | 390 (40%) |
| Age (years) | 6.00 [3.00, 8.00] | 6.00 [3.00, 8.00] | 5.50 [3.00, 9.00] |
| N° of Males | 599 (61.50%) | 346 (59.25%) | 253 (64.87%) |
| N° of Females | 375 (38.50%) | 238 (40.75%) | 137 (35.13%) |
| BMI z-score | −0.22 [−0.60, 0.37] | −0.24 [−0.61, 0.43] | −0.17 [−0.58, 0.27] |
| AHI (events/hour) | 3.80 [1.53, 9.35] | 4.08 [1.71, 10.00] | 3.30 [1.40, 7.87] |
| N° of No OSA | 171 (17.56%) | 96 (16.44%) | 75 (19.23%) |
| N° of Mild OSA | 398 (40.86%) | 229 (39.21%) | 169 (43.33%) |
| N° of Moderate OSA | 176 (18.07%) | 113 (19.35%) | 63 (16.15%) |
| N° of Severe OSA | 229 (23.51%) | 146 (25.00%) | 83 (21.28%) |
| AF | SpO2 | |||||
|---|---|---|---|---|---|---|
| m = 1 | m = 2 | m = 3 | m = 1 | m = 2 | m = 3 | |
| r = 0.05 | −0.0872 | −0.1187 | 0.0026 | 0.5502 | 0.5516 | 0.5586 |
| r = 0.10 | −0.0753 | −0.0863 | −0.1168 | 0.5123 | 0.5118 | 0.5134 |
| r = 0.15 | −0.0777 | −0.0802 | −0.0914 | 0.4786 | 0.4786 | 0.4784 |
| r = 0.20 | −0.0832 | −0.0824 | −0.0886 | 0.4395 | 0.4381 | 0.4399 |
| r = 0.25 | 0.0897 | −0.0880 | −0.0910 | 0.3895 | 0.3899 | 0.3900 |
| r = 0.30 | 0.0983 | −0.0951 | −0.0966 | 0.3341 | 0.3350 | 0.3367 |
| Feature | AF | SpO2 | ||||
|---|---|---|---|---|---|---|
| Spearman | Kruskal–Wallis | Spearman | Kruskal–Wallis | |||
| ρ | p-Value | p-Value | ρ | p-Value | p-Value | |
| M1T | 0.1693 | <<0.01 | 0.0061 * | −0.4135 | <<0.01 | <<0.01 |
| M2T | −0.2481 | <<0.01 | <<0.01 | 0.5145 | <<0.01 | <<0.01 |
| M3T | −0.1655 | <<0.01 | 0.0024 * | −0.1879 | <<0.01 | <<0.01 |
| M4T | 0.3580 | <<0.01 | <<0.01 | 0.0968 | 0.0194 | 0.0103 * |
| MedT | 0.2070 | <<0.01 | <<0.01 | −0.3467 | <<0.01 | <<0.01 |
| CTM | 0.3979 | <<0.01 | <<0.01 | −0.6187 | <<0.01 | <<0.01 |
| LZC | −0.0660 | 0.1111 | 0.0409 * | 0.3871 | <<0.01 | <<0.01 |
| SampEn | −0.1187 | <0.01 | 0.0270 * | 0.5586 | <<0.01 | <<0.01 |
| M1F | 0.3492 | <<0.01 | <<0.01 | 0.6773 | <<0.01 | <<0.01 |
| M2F | 0.2979 | <<0.01 | <<0.01 | 0.6352 | <<0.01 | <<0.01 |
| M3F | −0.1418 | <<0.01 | <<0.01 | 0.0184 | 0.6574 | 0.4893 * |
| M4F | −0.0967 | 0.0195 | 0.0112* | 0.0356 | 0.3899 | 0.4643 * |
| MedF | 0.3591 | <<0.01 | <<0.01 | 0.6753 | <<0.01 | <<0.01 |
| MaxF | 0.3245 | <<0.01 | <<0.01 | 0.6646 | <<0.01 | <<0.01 |
| MinF | 0.3588 | <<0.01 | <<0.01 | 0.6504 | <<0.01 | <<0.01 |
| FreqM | −0.1280 | <0.01 | 0.0117 * | 0.1209 | <0.01 | 0.0073 * |
| SpecEn | 0.3464 | <<0.01 | <<0.01 | 0.0060 | 0.8842 | 0.9340 * |
| SpecEn2 | 0.2741 | <<0.01 | <<0.01 | 0.1247 | <0.01 | 0.0234 * |
| SpecEn3 | 0.1304 | <0.01 | 0.0024 * | 0.1075 | <0.01 | 0.0742 * |
| ODI 3% | — | — | — | 0.6918 | <<0.01 | <<0.01 |
| AdaBoost (Without ODI 3%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Severity Levels | Estimated: AF | Estimated: SpO2 | Estimated: AF + SpO2 | ||||||||||
| No | Mild | Mod. | Sev. | No | Mild | Mod. | Sev. | No | Mild. | Mod. | Sev. | ||
| Actual | No | 1 | 55 | 16 | 3 | 17 | 50 | 8 | 0 | 19 | 47 | 8 | 1 |
| Mild | 1 | 97 | 53 | 18 | 19 | 119 | 30 | 1 | 21 | 111 | 35 | 2 | |
| Mod. | 1 | 29 | 22 | 11 | 5 | 29 | 24 | 5 | 6 | 24 | 27 | 6 | |
| Sev. | 0 | 25 | 25 | 33 | 3 | 12 | 34 | 34 | 2 | 8 | 36 | 37 | |
| Acc4 = 39.23%; κ = 0.1143 | Acc4 = 49.74%; κ = 0.2646 | Acc4 = 49.74%; κ = 0.2781 | |||||||||||
| AdaBoost (With ODI 3%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Severity Levels | Estimated: AF + ODI | Estimated: SpO2 + ODI | Estimated: AF + SpO2 + ODI | ||||||||||
| No | Mild | Mod. | Sev. | No | Mild | Mod. | Sev. | No | Mild | Mod. | Sev. | ||
| Actual | No | 27 | 44 | 3 | 1 | 26 | 45 | 3 | 1 | 28 | 43 | 3 | 1 |
| Mild | 23 | 115 | 30 | 1 | 23 | 113 | 32 | 1 | 25 | 113 | 30 | 1 | |
| Mod. | 2 | 24 | 32 | 5 | 7 | 18 | 32 | 6 | 7 | 18 | 33 | 5 | |
| Sev. | 0 | 9 | 22 | 52 | 1 | 8 | 22 | 52 | 2 | 8 | 21 | 52 | |
| Acc4 = 57.95%; κ = 0.3930 | Acc4 = 57.18%; κ = 0.3864 | Acc4 = 57.95%; κ = 0.3984 | |||||||||||
| ODI 3% | |||||
|---|---|---|---|---|---|
| Severity Levels | Estimated | ||||
| No | Mild | Mod. | Sev. | ||
| Actual | No | 65 | 7 | 1 | 2 |
| Mild | 110 | 35 | 11 | 13 | |
| Mod. | 18 | 14 | 8 | 23 | |
| Sev. | 6 | 6 | 3 | 68 | |
| Acc4 = 45.13%; κ = 0.2833 | |||||
| Cutoff | Subset | Se | Sp | Acc | PPV | NPV | LR+ | LR- |
|---|---|---|---|---|---|---|---|---|
| 1 e/h | AF | 99.37% | 1.33% | 80.51% | 80.88% | 33.33% | 1.0071 | 0.4762 |
| SpO2 | 91.43% | 22.67% | 78.21% | 83.24% | 38.64% | 1.1823 | 0.3782 | |
| AF + SpO2 | 90.79% | 25.33% | 78.21% | 83.63% | 39.58% | 1.2160 | 0.3634 | |
| AF + ODI | 92.06% | 36.00% | 81.28% | 85.80% | 51.92% | 1.4385 | 0.2205 | |
| SpO2 + ODI | 90.16% | 34.67% | 79.49% | 85.29% | 45.61% | 1.3800 | 0.2839 | |
| AF + SpO2 + ODI | 89.21% | 37.33% | 79.23% | 85.67% | 45.16% | 1.4235 | 0.2891 | |
| ODI 3% | 57.46% | 86.67% | 63.08% | 94.76% | 32.66% | 4.3095 | 0.4908 | |
| 5 e/h | AF | 62.33% | 63.11% | 62.82% | 50.28% | 73.68% | 1.6898 | 0.5969 |
| SpO2 | 66.44% | 84.02% | 77.44% | 71.32% | 80.71% | 4.1567 | 0.3995 | |
| AF + SpO2 | 72.60% | 81.15% | 77.95% | 69.74% | 83.19% | 3.8511 | 0.3376 | |
| AF + ODI | 76.03% | 85.66% | 82.05% | 76.03% | 85.66% | 5.3002 | 0.2799 | |
| SpO2 + ODI | 76.71% | 84.84% | 81.79% | 75.17% | 85.89% | 5.0589 | 0.2745 | |
| AF + SpO2 + ODI | 76.03% | 85.66% | 82.05% | 76.03% | 85.66% | 5.3002 | 0.2799 | |
| ODI 3% | 69.86% | 88.93% | 81.79% | 79.07% | 83.14% | 6.3135 | 0.3389 | |
| 10 e/h | AF | 39.76% | 89.58% | 78.97% | 50.77% | 84.62% | 3.8144 | 0.6725 |
| SpO2 | 40.96% | 98.05% | 85.90% | 85.00% | 86.00% | 20.9598 | 0.6021 | |
| AF + SpO2 | 44.58% | 97.07% | 85.90% | 80.43% | 86.63% | 15.2062 | 0.5710 | |
| AF + ODI | 62.65% | 97.72% | 90.26% | 88.14% | 90.63% | 27.4768 | 0.3822 | |
| SpO2 + ODI | 62.65% | 97.39% | 90.00% | 86.67% | 90.61% | 24.0422 | 0.3835 | |
| AF + SpO2 + ODI | 62.65% | 97.72% | 90.26% | 88.14% | 90.63% | 27.4768 | 0.3822 | |
| ODI 3% | 81.93% | 87.62% | 86.41% | 64.15% | 94.72% | 6.6189 | 0.2063 |
| Study | N | Signal | Methods (Extraction/Selection/Classification) | Validation | Cutoff | Se | Sp | Acc |
|---|---|---|---|---|---|---|---|---|
| Chang et al. (2013) [36] | 141 | SpO2 | ODI, questionnaires/-/LR | -- | 5 | 60.0 | 86.0 | 76.6 |
| Wu et al. (2017) [37] | 311 | — | Clinical parameters/-/Stepwise LR | Holdout | 5 | 94.8 | 25.0 | 78.2 |
| Gil et al. (2010) [38] | 21 | PPG | DAP events, HRV, PTTV/Wrapper/LDA | -- | 5 | 75.0 | 85.7 | 80.0 |
| Lázaro et al. (2014) [39] | 21 | PPG | DAP events, spectral analysis of PRV/Wrapper/LDA | -- | 5 | 100 | 71.4 | 86.6 |
| Garde et al. (2014) [23] | 146 | SpO2, PRV | Time, frequency, nonlinear/-/LDA | Four-fold | 5 | 88.4 | 83.6 | 84.9 |
| Garde et al. (2019) [24] | 207 | SpO2, PRV | Time, frequency, ODI (SpO2); standard spectral bands (PRV)/-/LR (3 binary models) | Holdout | 1 | 68.0 | 86.0 | 71.0 |
| 5 | 58.0 | 89.0 | 78.0 | |||||
| 10 | 90.0 | 87.0 | 88.0 | |||||
| Álvarez et al. (2018) [28] | 142 | SpO2 | Time domain, ODI, symbolic dynamics/FSLR/LR | Bootstrap | 5 | 73.5 | 89.5 | 83.3 |
| Barroso-Garcia et al. (2017) [31] | 501 | AF | CTM and SpecEn/FSLR/LR (3 binary models) | Holdout | 1 | 60.5 | 58.6 | 60.0 |
| 5 | 65.0 | 80.6 | 76.0 | |||||
| 10 | 83.3 | 79.0 | 80.0 | |||||
| Crespo et al. (2018) [40] | 176 | SpO2 | Time, frequency, nonlinear, ODI/FCBF/LDA, QDA, LR (3 binary models) | Bootstrap | 1 | 93.9 | 37.8 | 84.3 |
| 5 | 70.0 | 91.4 | 82.7 | |||||
| Hornero et al. (2017) [26] | 4191 | SpO2 | Time, frequency, nonlinear, ODI/FCBF/MLP regression | Holdout | 1 | 84.0 | 53.2 | 75.2 |
| 5 | 68.2 | 87.2 | 81.7 | |||||
| 10 | 68.7 | 94.1 | 90.2 | |||||
| Xu et al. (2019) [42] | 432 | SpO2 | ODI, M3F/-/MLP regression | Direct validation | 1 | 95.3 | 19.1 | 79.6 |
| 5 | 77.8 | 80.5 | 79.4 | |||||
| 10 | 73.5 | 92.7 | 88.2 | |||||
| Vaquerizo-Villar et al. (2018) [29] | 981 | SpO2 | DFA, ODI/FCBF/MLP regression | Holdout | 1 | 97.1 | 23.3 | 82.7 |
| 5 | 78.8 | 83.7 | 81.9 | |||||
| 10 | 77.1 | 94.8 | 91.1 | |||||
| Barroso-García et al. (2020) [32] | 946 | AF, ODI | Recurrence plots, ODI/FCBF/Bayesian MLP regression | Holdout | 1 | 97.7 | 22.2 | 83.2 |
| 5 | 78.7 | 78.3 | 78.5 | |||||
| 10 | 78.8 | 94.3 | 91.0 | |||||
| This Study | 974 | AF, SpO2 | Time, Frequency, Nonlinear, ODI/FCBF/Multiclass AdaBoost | Holdout | 1 | 92.1 | 36.0 | 81.3 |
| 5 | 76.0 | 85.7 | 82.1 | |||||
| 10 | 62.7 | 97.7 | 90.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-García, J.; Gutiérrez-Tobal, G.C.; García, M.; Kheirandish-Gozal, L.; Martín-Montero, A.; Álvarez, D.; del Campo, F.; Gozal, D.; Hornero, R. Assessment of Airflow and Oximetry Signals to Detect Pediatric Sleep Apnea-Hypopnea Syndrome Using AdaBoost. Entropy 2020, 22, 670. https://doi.org/10.3390/e22060670
Jiménez-García J, Gutiérrez-Tobal GC, García M, Kheirandish-Gozal L, Martín-Montero A, Álvarez D, del Campo F, Gozal D, Hornero R. Assessment of Airflow and Oximetry Signals to Detect Pediatric Sleep Apnea-Hypopnea Syndrome Using AdaBoost. Entropy. 2020; 22(6):670. https://doi.org/10.3390/e22060670
Chicago/Turabian StyleJiménez-García, Jorge, Gonzalo C. Gutiérrez-Tobal, María García, Leila Kheirandish-Gozal, Adrián Martín-Montero, Daniel Álvarez, Félix del Campo, David Gozal, and Roberto Hornero. 2020. "Assessment of Airflow and Oximetry Signals to Detect Pediatric Sleep Apnea-Hypopnea Syndrome Using AdaBoost" Entropy 22, no. 6: 670. https://doi.org/10.3390/e22060670
APA StyleJiménez-García, J., Gutiérrez-Tobal, G. C., García, M., Kheirandish-Gozal, L., Martín-Montero, A., Álvarez, D., del Campo, F., Gozal, D., & Hornero, R. (2020). Assessment of Airflow and Oximetry Signals to Detect Pediatric Sleep Apnea-Hypopnea Syndrome Using AdaBoost. Entropy, 22(6), 670. https://doi.org/10.3390/e22060670








