Special Characteristics and Synchronizations of Multi Hybrid-Order Chaotic Systems
Abstract
1. Introduction
2. Mathematical Background
3. Characteristics Analysis of Hybrid Order Chaotic Systems
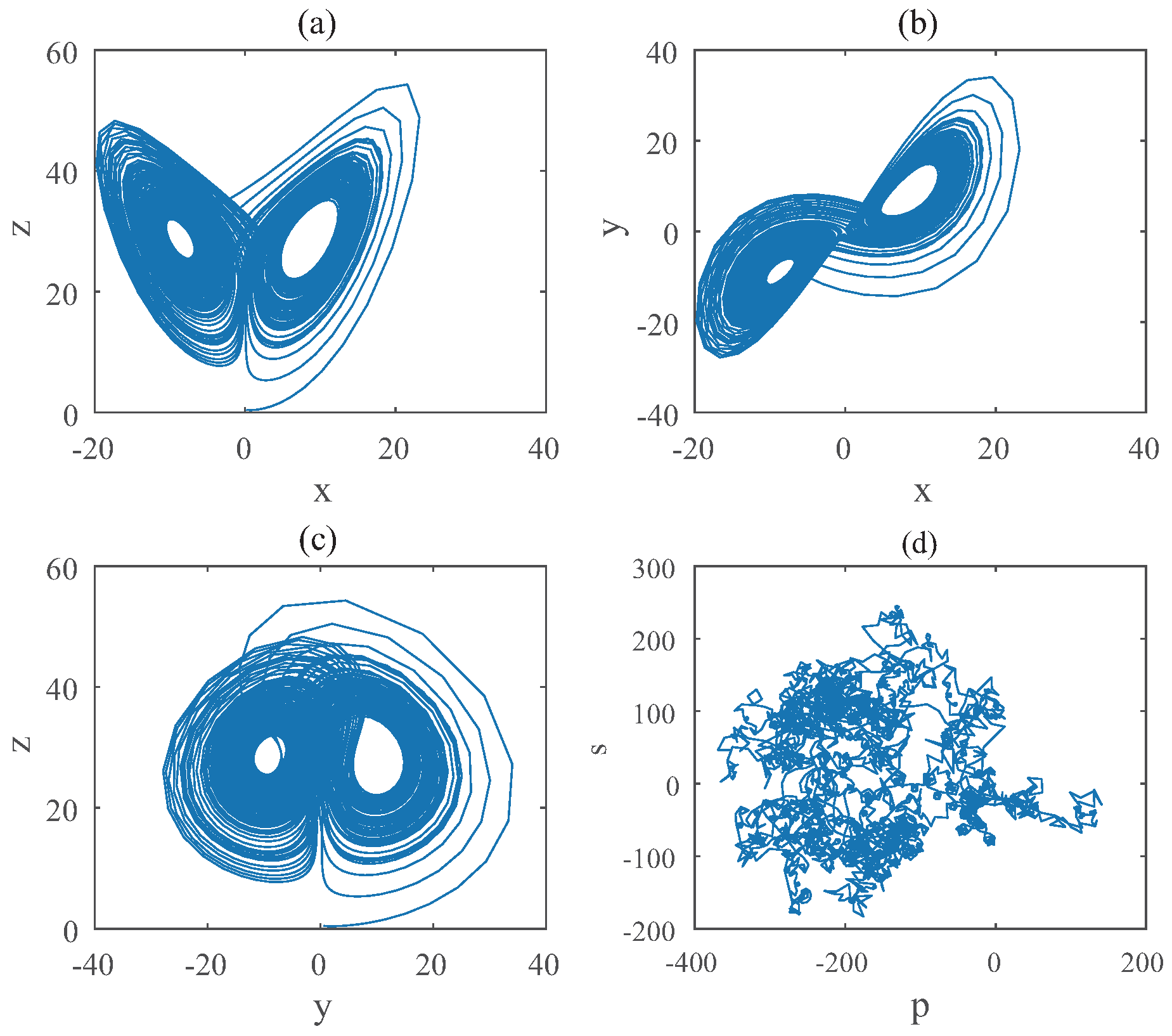
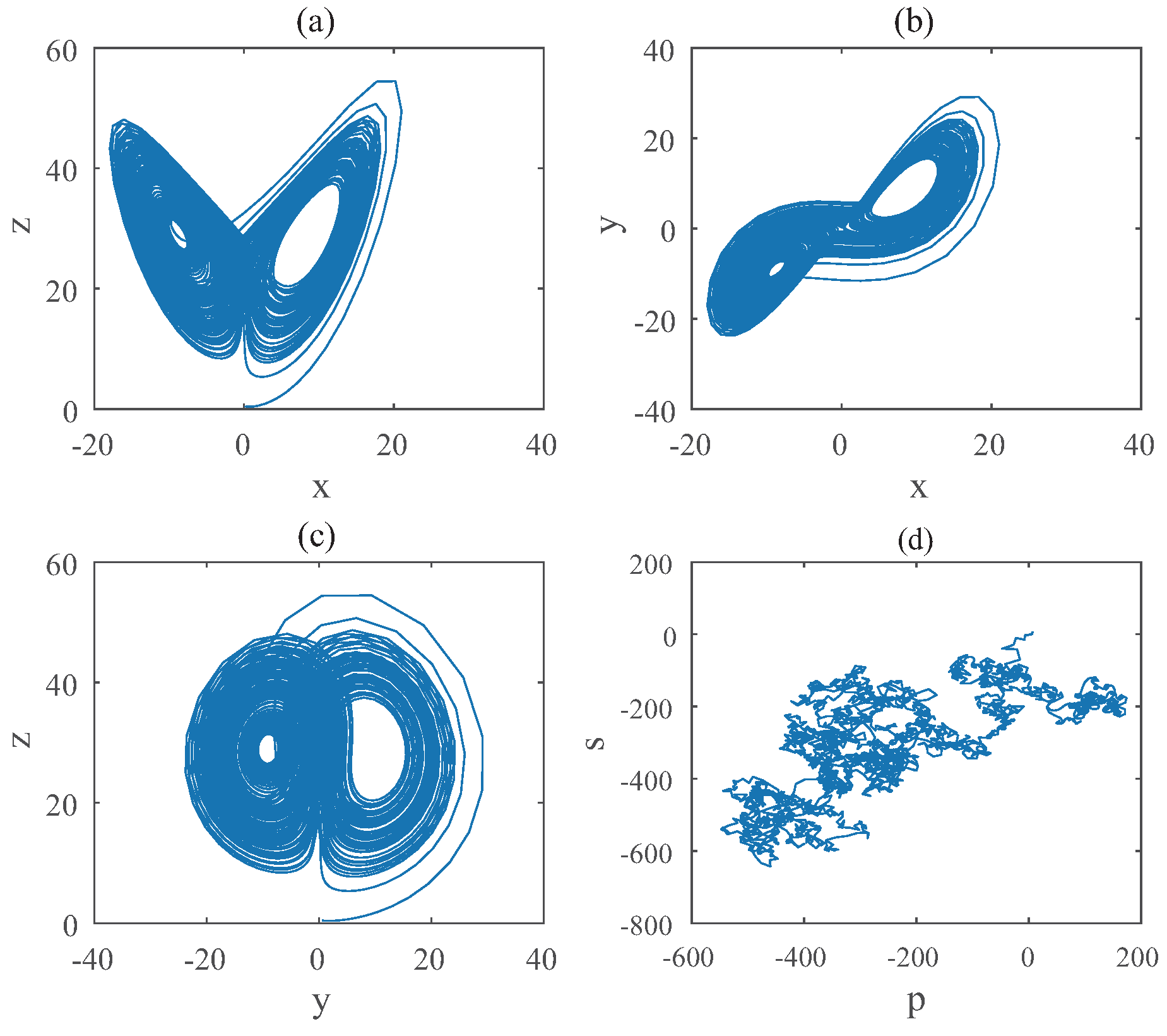
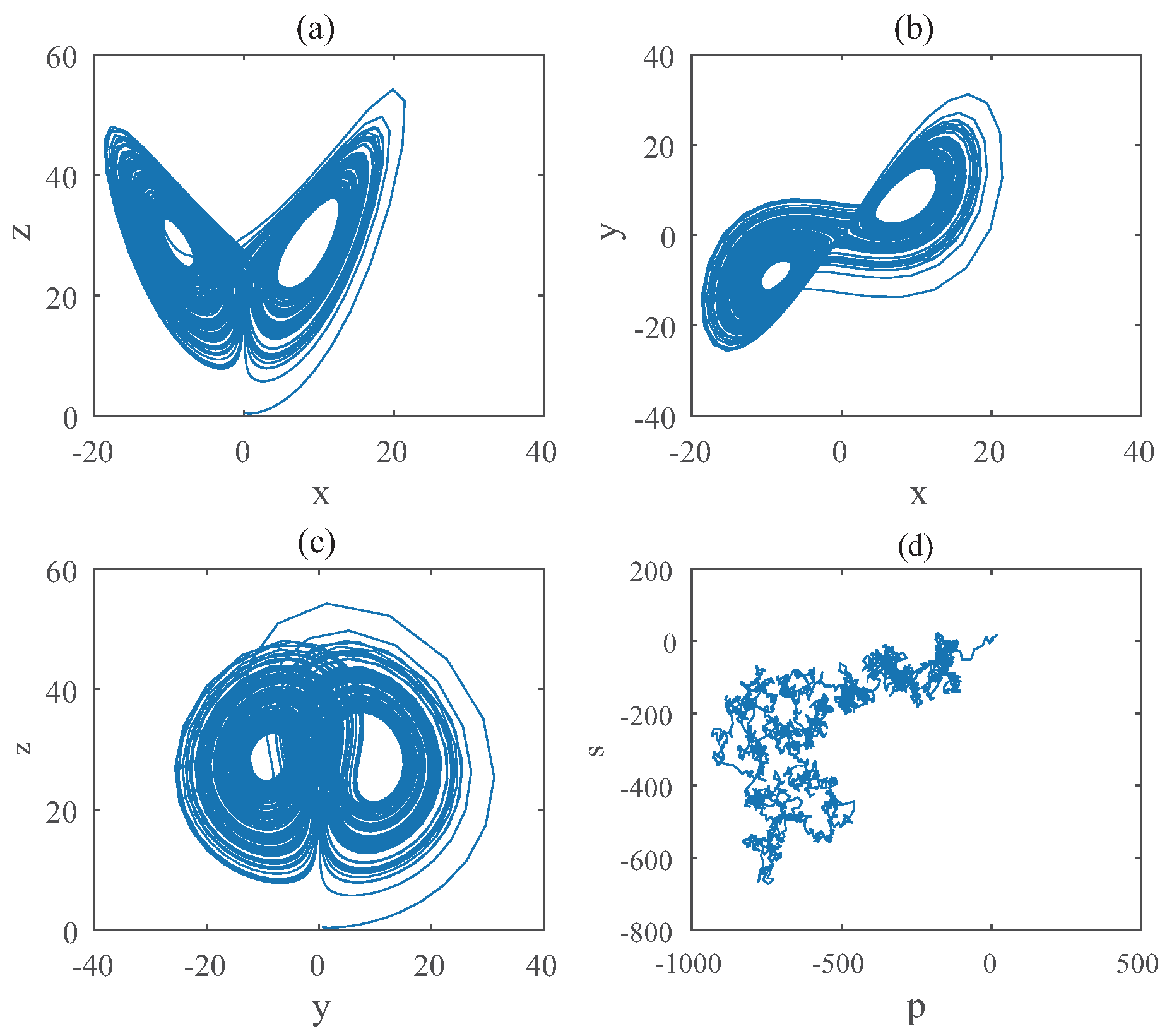
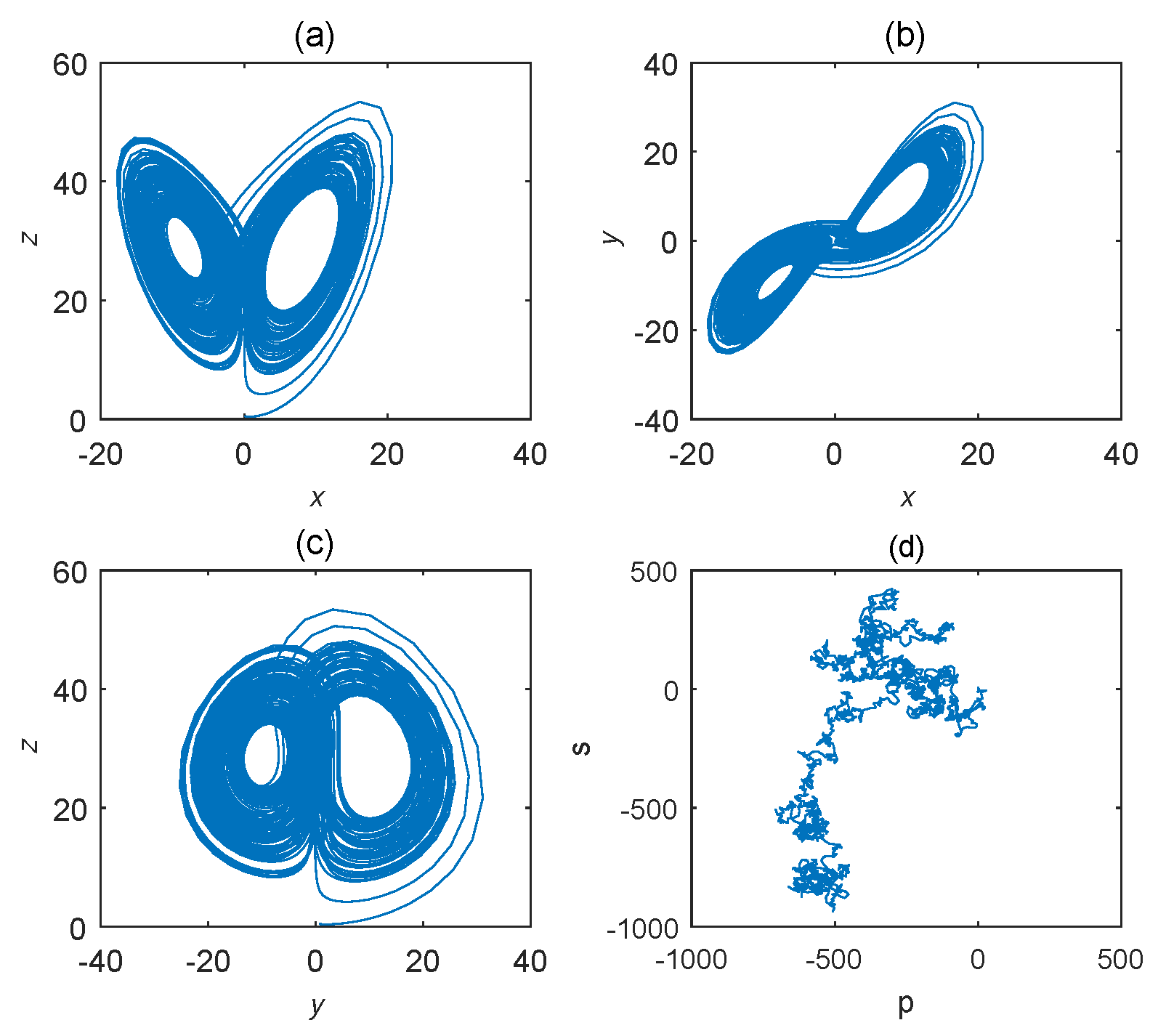
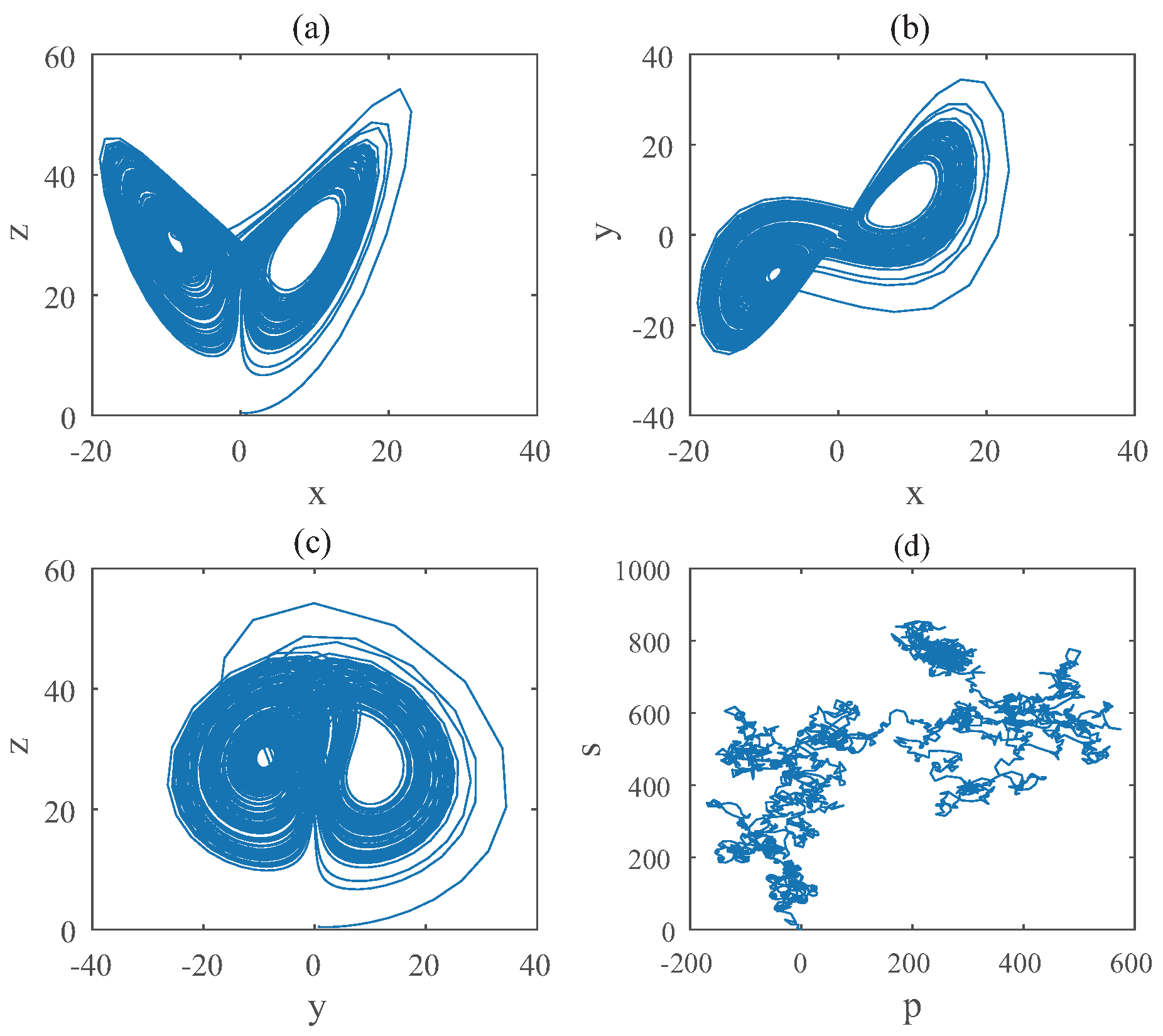
3.1. Hybrid Order Lorenz Systems
3.1.1. Dissipativeness and the Existence of Equilibriums
3.1.2. Equilibriums and Stability
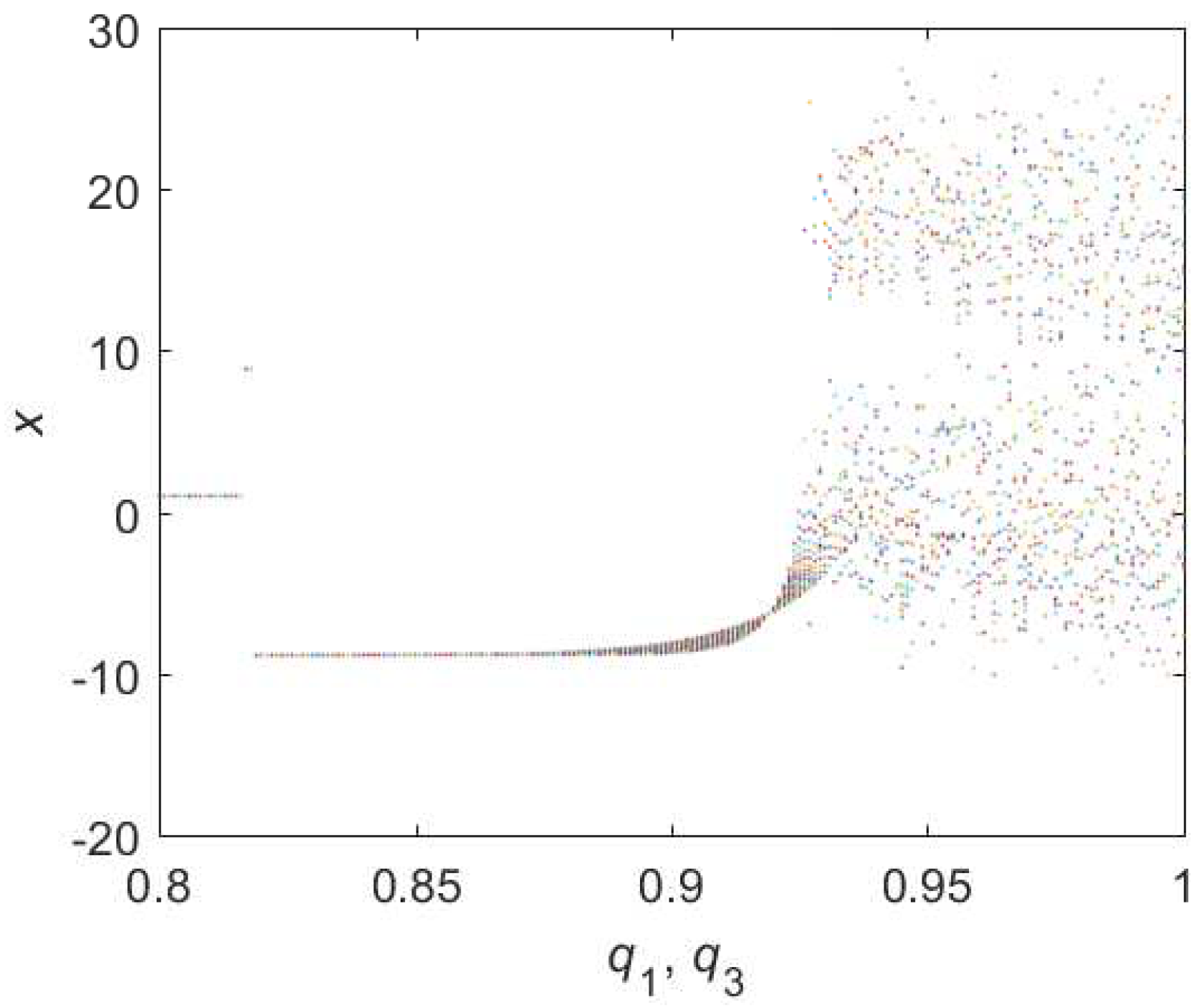
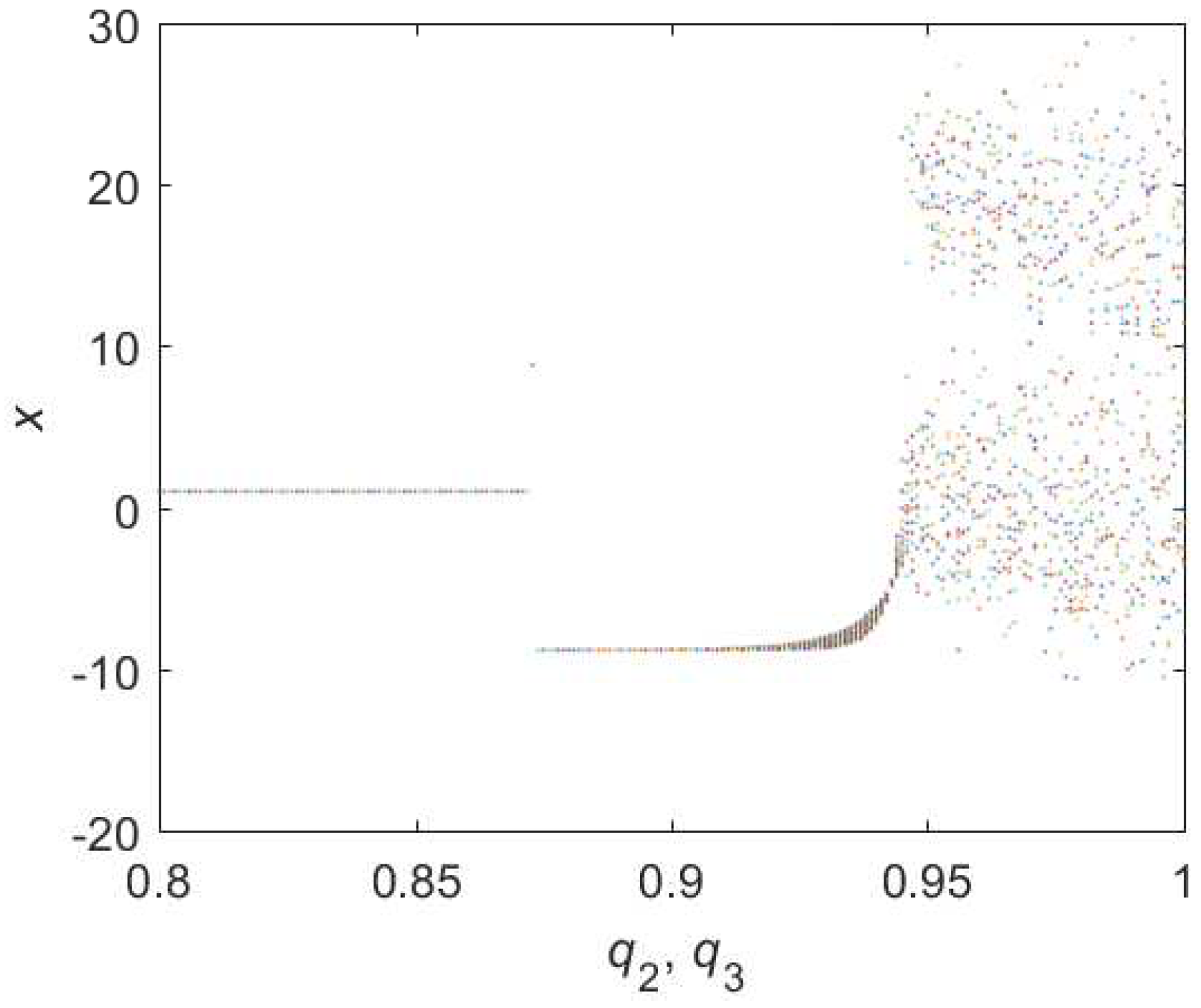
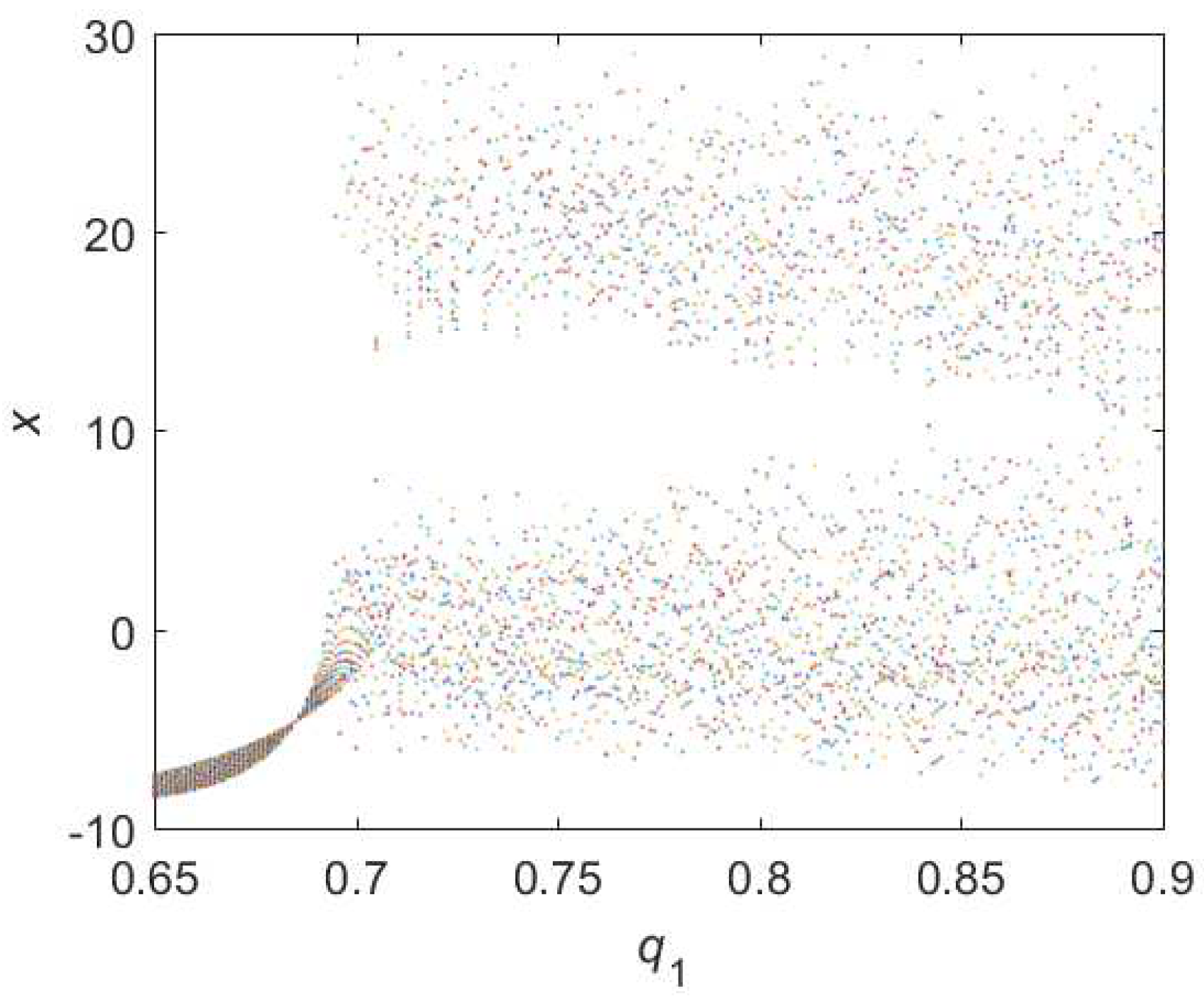
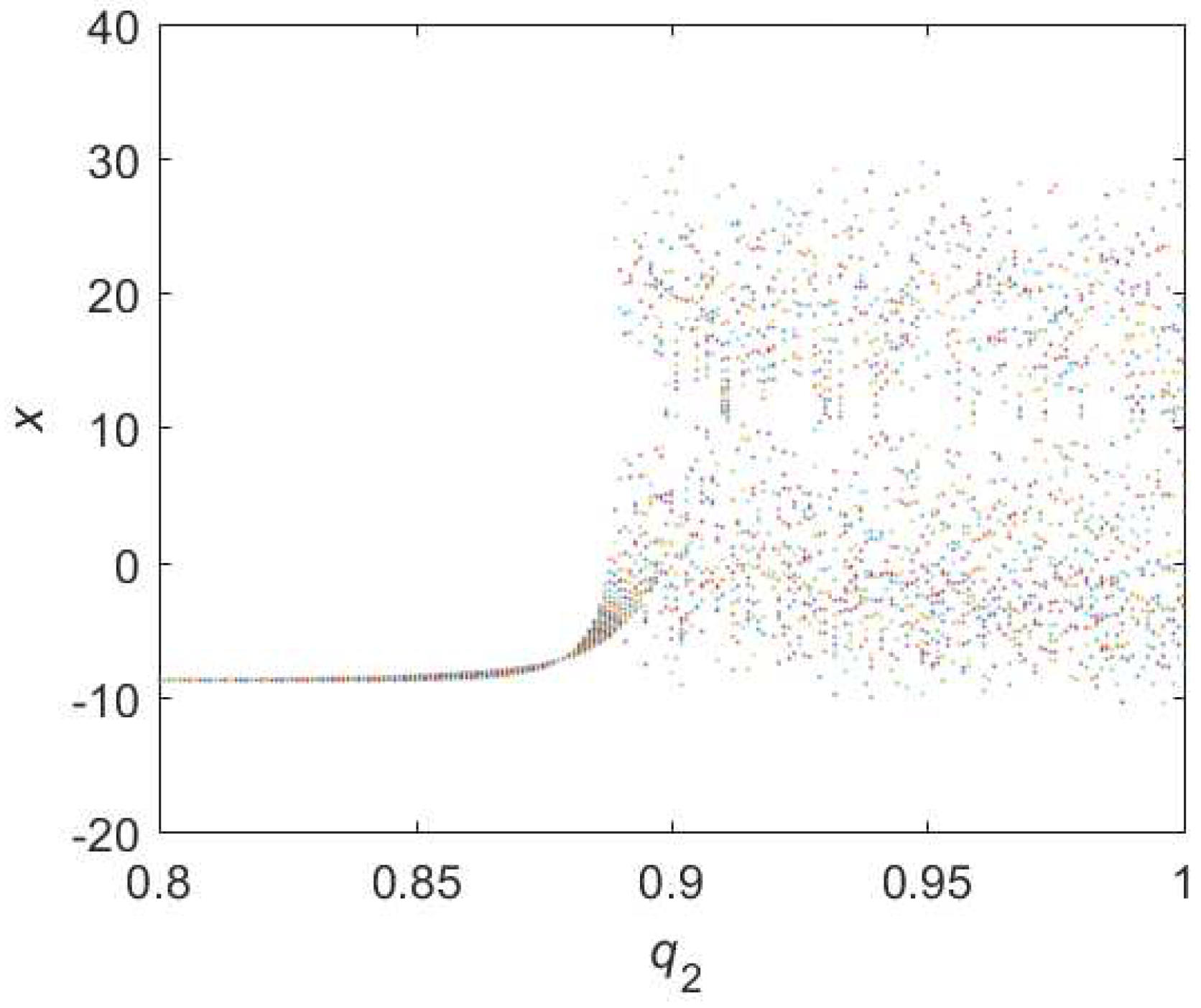
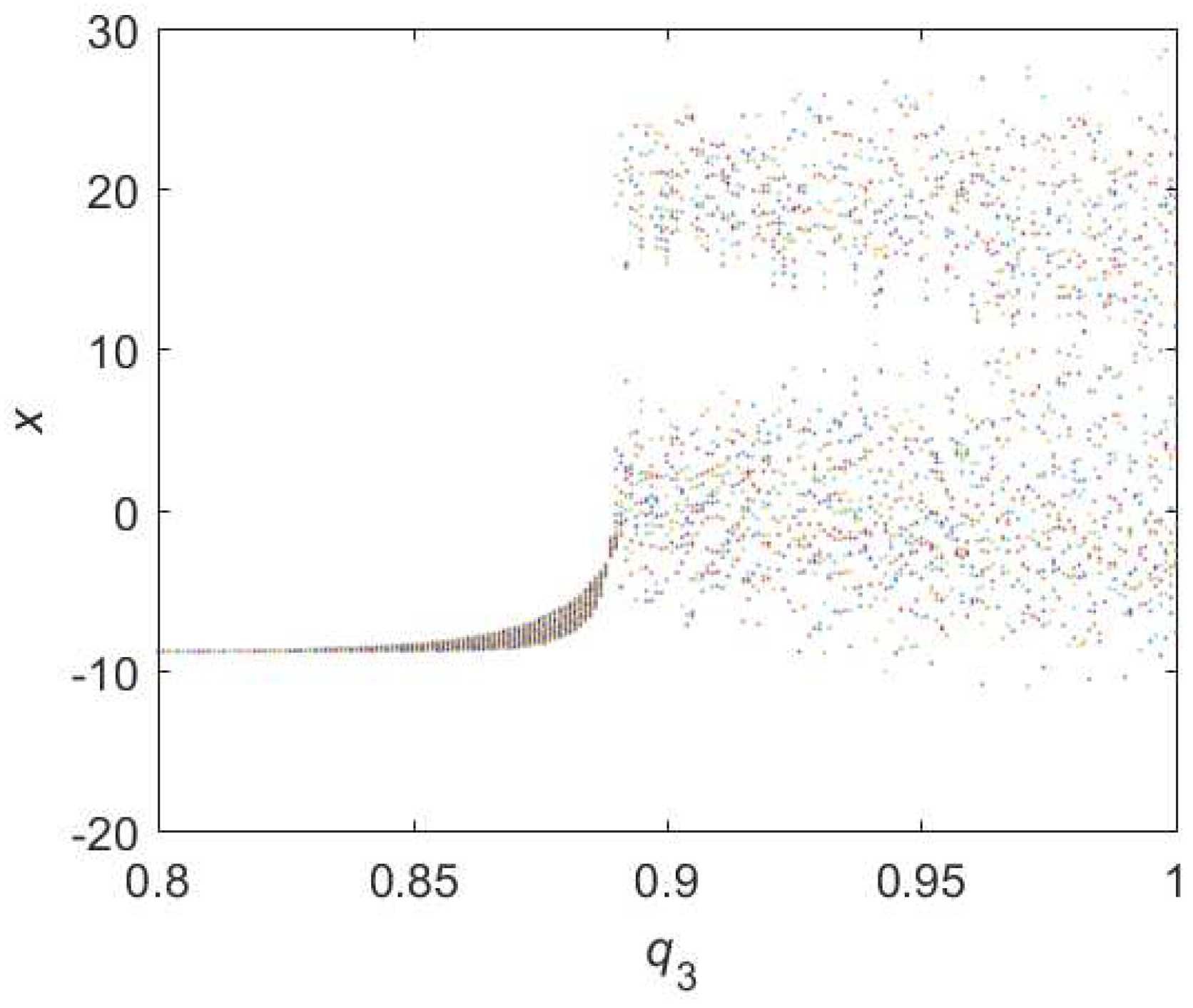
3.1.3. Bifurcations of Hybrid Order Lorenz Systems
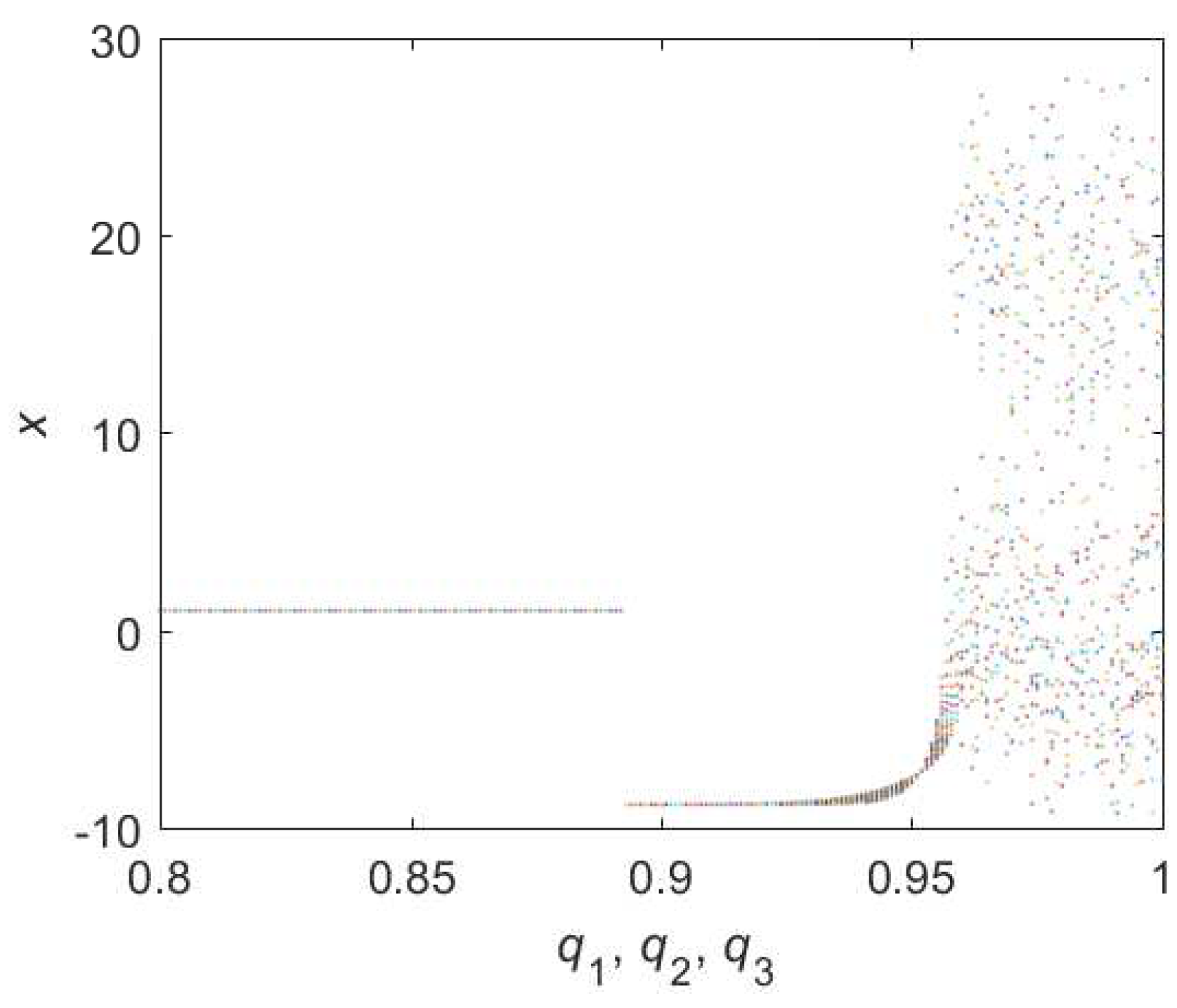
3.1.4. Relations of Different Chaotic Parameters in Hybrid Lorenz Systems
3.2. Other Classic Hybrid Order Chaotic ystems
3.2.1. Hybrid Order Chen Systems
3.2.2. Hybrid Order Lü Systems
3.2.3. Hybrid Order Complex Lorenz Systems
3.3. A Relation between Chaotic Parameters for Different Hybrid Order Chaotic Systems
- (1)
- always has inverse ratio relation with the lowest when .
- (2)
- Compared with complete fractional chaotic systems , we can always find lower in hybrid order systems.
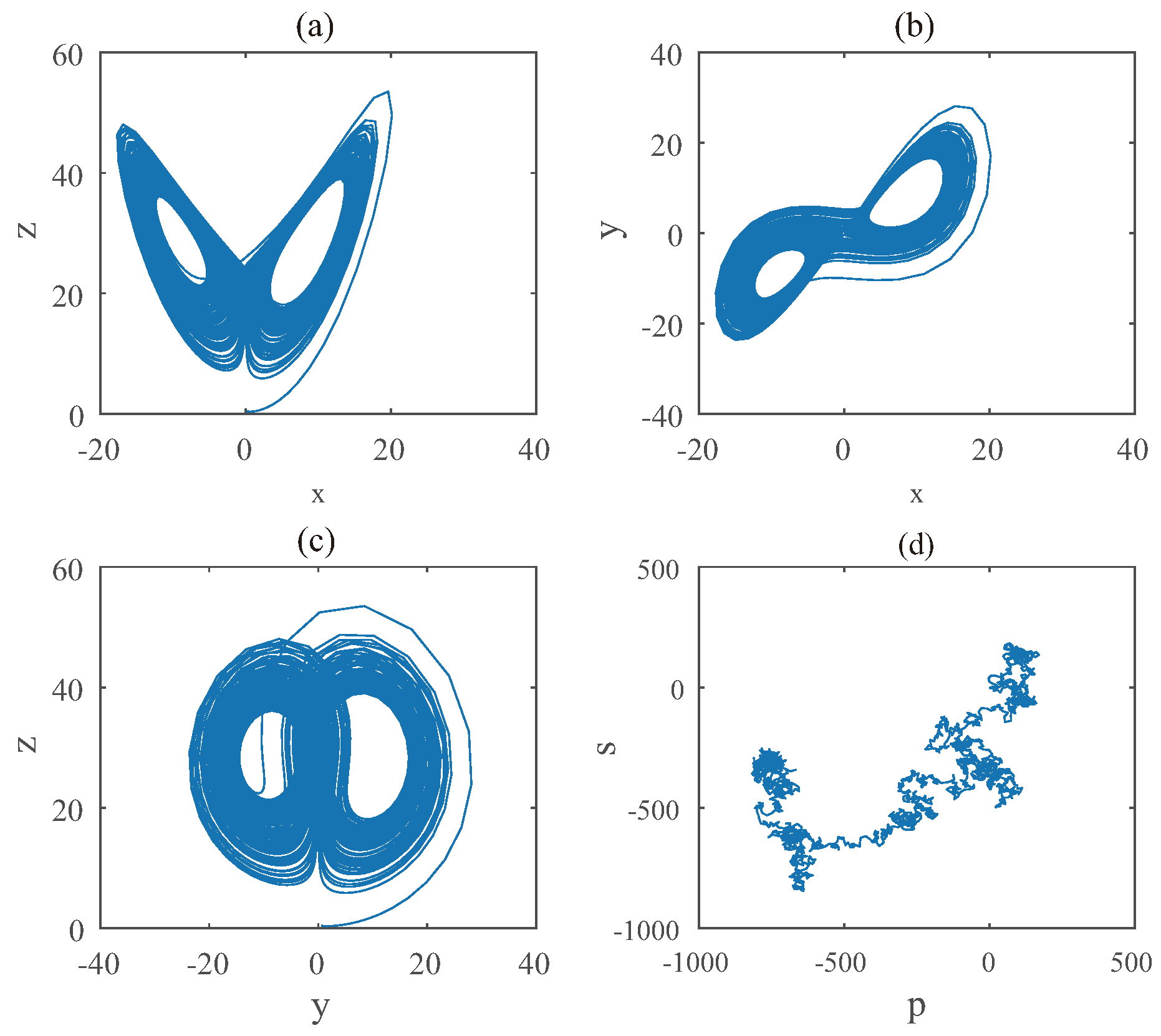
4. Combination Synchronization of Hybrid Order Chaotic Systems
4.1. Combination Synchronization
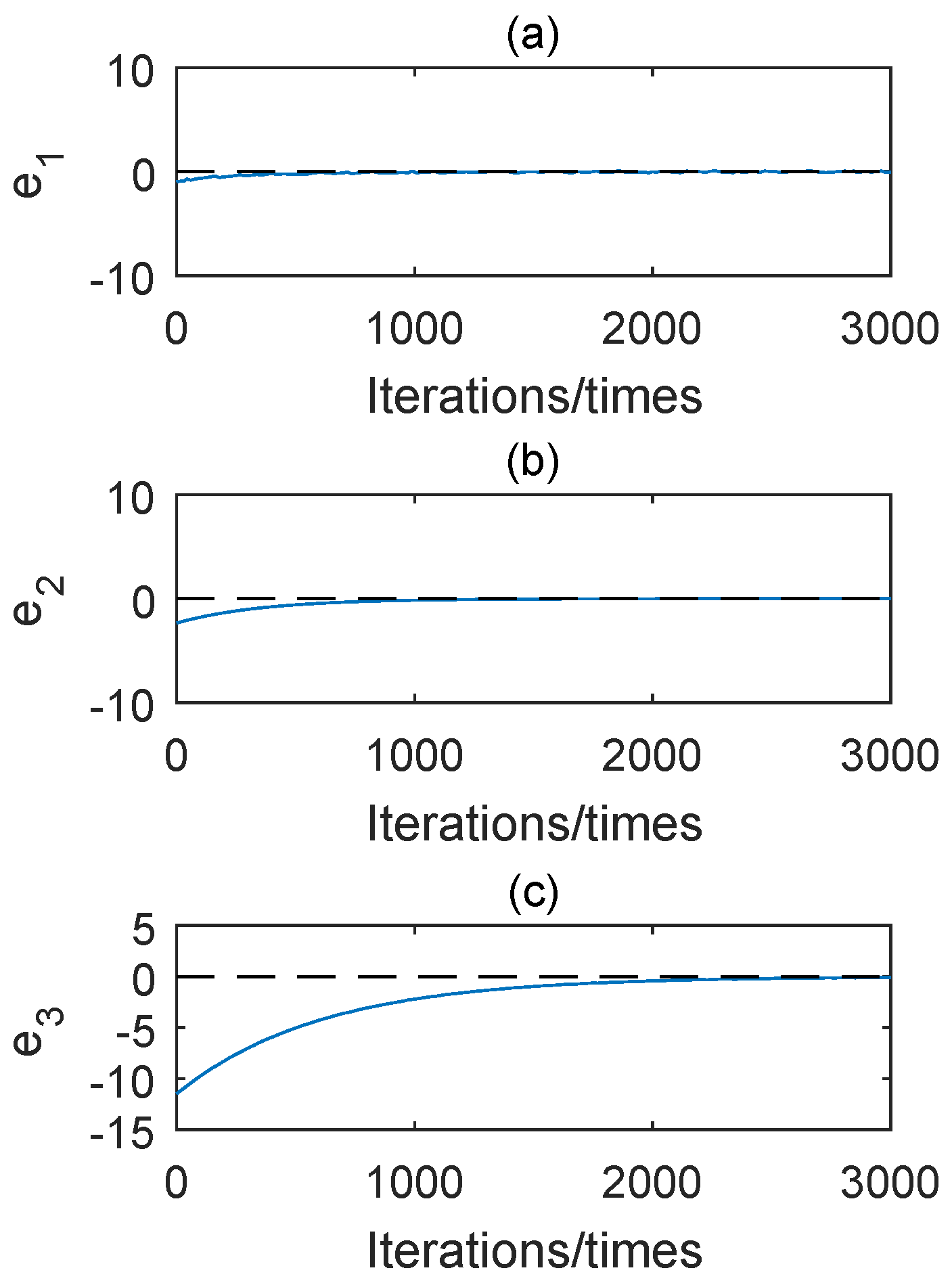
4.2. Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure communication of fractional complex chaotic systems based on fractional difference function synchronization. Complexity 2019, 2019, 7242791. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine chaotification model for enhancing chaos and its hardware implementation. IEEE Trans. Ind. 2018, 66, 1273–1284. [Google Scholar] [CrossRef]
- Zhang, F.; Li, M.; Leng, S.; Liu, J. Linear correlation of complex vector space and its application on complex parameter identification. J. Qilu Univ. Technol. 2019. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Bao, B.C. Two-Dimensional Sine Chaotification System with Hardware Implementation. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Wang, W.; Jia, X.; Luo, X.; Kurths, J.; Yuan, M. Fixed-time synchronization control of memristive MAM neural networks with mixed delays and application in chaotic secure communication. Chaos Solitons Fractals 2019, 126, 85–96. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Localization of hidden Chuas attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Moattar, M.H. Color image encryption based on hybrid chaotic system and DNA sequences. Multimed. Tools Appl. 2020, 79, 1497–1518. [Google Scholar] [CrossRef]
- Dukhan, A.; Jayalath, D.; van Heijster, P.; Senadji, B.; Banks, J. A generalized multilevel-hybrid chaotic oscillator for low-cost and power-efficient short-range chaotic communication systems. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 23. [Google Scholar] [CrossRef]
- Man, Z.; Li, J.; Di, X.; Bai, O. An Image Segmentation Encryption Algorithm Based on Hybrid Chaotic System. IEEE Access 2019, 7, 103047–103058. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, H. A fractional-order differential equation model of HIV infection of CD4+ T-cells. Math. Comput. Model. 2009, 50, 386–392. [Google Scholar] [CrossRef]
- Laskin, N. Fractional market dynamics. Physica A 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Bagley, R.L.; Calico, R. Fractional order state equations for the control of viscoelasticallydamped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Hartley, T.T.; Lorenzo, C.F.; Qammer, H.K. Chaos in a fractional order Chua’s system. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 485–490. [Google Scholar] [CrossRef]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 034101. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 549–554. [Google Scholar] [CrossRef]
- Lu, J.G. Chaotic dynamics of the fractional-order Lü system and its synchronization. Phys. Lett. A 2006, 354, 305–311. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X. Chaos in the fractional-order complex Lorenz system and its synchronization. Nonlinear Dyn. 2013, 71, 241–257. [Google Scholar] [CrossRef]
- Xu, F. A Class of Integer Order and Fractional Order Hyperchaotic Systems via the Chen System. Int. J. Bifurc. Chaos 2016, 26, 1650109. [Google Scholar] [CrossRef]
- Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive control for fractional order induced chaotic fuzzy cellular neural networks and its application to image encryption. Inf. Sci. 2019, 491, 74–89. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]
- Farah, M.A.B.; Guesmi, R.; Kachouri, A.; Samet, M. A novel chaos based optical image encryption using fractional Fourier transform and DNA sequence operation. Opt. Laser Technol. 2020, 121, 105777. [Google Scholar] [CrossRef]
- Lin, Z.; Yu, S.; Lu, J.; Cai, S.; Chen, G. Design and ARM-Embedded Implementation of a Chaotic Map-Based Real-Time Secure Video Communication System. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 1203–1216. [Google Scholar]
- Zhou, P.; Huang, K. A new 4-D non-equilibrium fractional-order chaotic system and its circuit implementation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2005–2011. [Google Scholar] [CrossRef]
- Li, H.; Liao, X.; Luo, M. A novel non-equilibrium fractional-order chaotic system and its complete synchronization by circuit implementation. Nonlinear Dyn. 2012, 68, 137–149. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A.K. FPGA implementation of novel fractional-order chaotic systems with two equilibriums and no equilibrium and its adaptive sliding mode synchronization. Nonlinear Dyn. 2017, 87, 2281–2304. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Mainieri, R.; Rehacek, J. Projective synchronization in three-dimensional chaotic systems. Phys. Rev. Lett. 1999, 82, 3042. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X. Function projective synchronization between two identical chaotic systems. Int. J. Mod. Phys. C 2007, 18, 883–888. [Google Scholar] [CrossRef]
- Fang-Fang, Z.; Shu-Tang, L.; Wei-Yong, Y. Modified projective synchronization with complex scaling factors of uncertain real chaos and complex chaos. Chin. Phys. B 2013, 22, 120505. [Google Scholar]
- Mohadeszadeh, M.; Pariz, N. Hybrid control of synchronization of fractional order nonlinear systems. Asian J. Control 2019. [Google Scholar] [CrossRef]
- Xu, F.; Lai, Y.; Shu, X. Chaos in integer order and fractional order financial systems and their synchronization. Chaos Solitons Fractals 2018, 117, 125–136. [Google Scholar] [CrossRef]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent—II. Geophys. J. R. Astron. Soc. 1966, 19, 529–539. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the CESA’96 IMACS Multi Conference (Computational Engineering in Systems Applications), Lille, France, 9–12 July 1996; Volume 2, pp. 963–968. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. Chaotic attractors in incommensurate fractional order systems. Physica D 2008, 237, 2628–2637. [Google Scholar] [CrossRef]
- Runzi, L.; Yinglan, W.; Shucheng, D. Combination synchronization of three classic chaotic systems using active backstepping design. Chaos 2011, 21, 043114. [Google Scholar] [CrossRef] [PubMed]

| System | |||
|---|---|---|---|
| Integer order | 3 | 1 | 3 |
| Equation (16) | 0 | 0.97 | 2.91 |
| Equation (8) | 1 | 0.91 | 2.82 |
| Equation (9) | 1 | 0.93 | 2.86 |
| Equation (10) | 1 | 0.95 | 2.9 |
| Equation (11) | 2 | 0.7 | 2.7 |
| Equation (12) | 2 | 0.89 | 2.89 |
| Equation (13) | 2 | 0.89 | 2.89 |
| Type | Model | |||
|---|---|---|---|---|
| Complete | ||||
| fractional | 0 | 0.78 | 2.34 | |
| Chen | ||||
| Hybrid | ||||
| order | 1 | 0.68 | 2.36 | |
| Chen | ||||
| 1 | 0.79 | 2.58 | ||
| 1 | 0.995 | 2.99 | ||
| 2 | 0.68 | 2.68 | ||
| 2 | 0.96 | 2.96 | ||
| 2 | 0.275 | 2.275 | ||
| Type | Model | |||
|---|---|---|---|---|
| Complete | ||||
| fractional | 0 | 0.78 | 2.34 | |
| Lü | ||||
| Hybrid | ||||
| order | 1 | 0.653 | 2.306 | |
| Lü | ||||
| 1 | 0.77 | 2.54 | ||
| 1 | 0.994 | 2.988 | ||
| 2 | 0.66 | 2.66 | ||
| 2 | 0.995 | 2.995 | ||
| 2 | 0.277 | 2.277 | ||
| Type | Model | |||
|---|---|---|---|---|
| Fractional | ||||
| complex | 0 | 0.959 | 2.877 | |
| Lorenz | ||||
| Hybrid | ||||
| order | 1 | 0.908 | 2.816 | |
| Lorenz | ||||
| 1 | 0.94 | 2.88 | ||
| 1 | 0.955 | 2.91 | ||
| 2 | 0.531 | 2.531 | ||
| 2 | 0.823 | 2.823 | ||
| 2 | 0.925 | 2.925 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, Z.; Zhang, F.; Yin, Y.; Ma, F. Special Characteristics and Synchronizations of Multi Hybrid-Order Chaotic Systems. Entropy 2020, 22, 664. https://doi.org/10.3390/e22060664
Liu J, Wang Z, Zhang F, Yin Y, Ma F. Special Characteristics and Synchronizations of Multi Hybrid-Order Chaotic Systems. Entropy. 2020; 22(6):664. https://doi.org/10.3390/e22060664
Chicago/Turabian StyleLiu, Jiaxun, Zuoxun Wang, Fangfang Zhang, Yankai Yin, and Fengying Ma. 2020. "Special Characteristics and Synchronizations of Multi Hybrid-Order Chaotic Systems" Entropy 22, no. 6: 664. https://doi.org/10.3390/e22060664
APA StyleLiu, J., Wang, Z., Zhang, F., Yin, Y., & Ma, F. (2020). Special Characteristics and Synchronizations of Multi Hybrid-Order Chaotic Systems. Entropy, 22(6), 664. https://doi.org/10.3390/e22060664





