Abstract
Constructal optimization of a plate condenser with fixed heat transfer rate and effective volume in ocean thermal energy conversion (OTEC) system is performed based on constructal theory. Optimizations of entropy generation rate () in heat transfer process and total pumping power () due to friction loss are two conflicting objectives for a plate condenser. With the conventional optimization method, the plate condenser is designed by taking a composite function (CF) considering both and as optimization objectives, and employing effective length, width, and effective number of heat transfer plates as design variables. Effects of structural parameters of the plate condenser and weighting coefficient of CF on design results are investigated. With a multi-objective genetic algorithm, the plate condenser is designed by simultaneously optimizing and , and the Pareto optimal set is obtained. The results demonstrate that CFs after primary and twice-constructal optimizations are respectively reduced by 7.8% and 9.9% compared with the initial CF, and the effective volume of the plate condenser has a positive impact on the twice minimum CF. Furthermore, the Pareto optimal set can provide better selections for performance optimizations of plate condensers.
1. Introduction
With the increasing demand for energy, it is urgent to find new energy. Ocean thermal energy which has the characteristics of a large reserve, renewability, and sustainability has been receiving wide attention. The ocean thermal energy conversion (OTEC) system was proposed by D’Arsonval [1], then many scholars performed plenty of research on it [2,3,4,5,6,7,8,9]. The closed OTEC system outputs energy (power and electricity) by utilizing the low boiling point refrigerant to exchange heats with the warm and cold seawaters to form the thermodynamic cycle. Therefore, the heat exchanger (HE) is an indispensable component of the OTEC system.
The condenser is one of the HEs in the OTEC system, and it usually adopts the plate HE [10,11,12,13,14,15,16] due to the constraints of the limited space volume and the small temperature difference between the warm and cold seawaters. It has been an important work to analyze the performance and optimize the structure for the plate condenser. By using the classical method, Nakaoka and Uehara [17] studied the heat transfer characteristic of a shell-and-plate-type condenser in an OTEC system, and proposed the empirical correlations to predict the heat transfer coefficients (HTCs) on the water side and condensation side. Yan et al. [18] researched the condensation pressure drop and HTC of a plate HE with refrigerant R134a, and analyzed the influences of refrigerant mass flux and vapor quality on the performance of the plate HE. Wang et al. [19] conducted an investigation on the flow characteristic for a plate HE under the conditions of partial condensation and complete condensation, and obtained the condensation pressure drop from the experimental data. Han et al. [20] proposed the formulas to calculate the friction factor and Nusselt number of the plate HE by considering the corrugation angle and corrugation wavelength. García-Cascales et al. [21] analyzed the calculation formulas of condensation HTCs in different plate HEs, and found that calculated results and experimental results are in good agreement. Longo et al. [22] found that the condensation HTC of the plate HE with refrigerant HFO1234ze (E) is less affected by saturation temperature while greatly affected by the refrigerant mass flux. Comparing the refrigerant HFO1234ze (E) with HFC134a, it was found that the HFC134a shows higher HTC and lower friction pressure drop. According to further experimental analyses and researches, Longo et al. [23] put forward a new formula to predict the condensation HTC of the plate HE with forced convection. Eldeeb et al. [24] and Shon et al. [25] compared the condensation HTCs of the plate HE with different working fluids, and found that ammonia shows higher heat transfer performance than other working fluids. Shon et al. [26] proposed the empirical correlations to predict the condensation pressure drop and HTC of the plate HE with refrigerant R-1233zd (E).
Constructal theory [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] was put forward by Professor Bejan in 1996. The corresponding constructal law [27,28] is “For a finite-size flow system to persist in time (to live), its configuration must change in time such that it provides easier and easier access to its currents.” The structural designs for living and non-living systems can be performed by applying constructal theory, including the structural designs of HEs. Vargas and Bejan [48] conducted an optimization for the aspect ratio of a crossflow HE, and analyzed the influences of smooth and finned heat transfer surfaces on the aspect ratio. It was found that the optimal constructs of the HE with two heat transfer surfaces are approximately the same. Bejan [49] constructed a multistage HE with the aim of the minimum pumping power and maximum heat exchange quantity, and found that the optimal spacings of the first-construct and elemental channels will lead the total pumping power to be minimum. Sotoodeh et al. [50] carried out a comparison between the ordinary single-scale plate-fin HE and constructal multi-scale plate-fin HE with the same volume and heat transfer area, and found that the constructal multi-scale plate-fin HE has higher heat recovery ability than the ordinary single-scale plate-fin HE. Xie et al. [51] optimized the pin-fins of the HE and obtained its optimal diameter, length, and shape. At the same time, it was found that the heat storage capacity of the HE after constructal optimization improves by 10.2%. Bejan et al. [52] obtained the optimal construct of a crossflow HE at the maximum heat transfer rate (HTR), and found that the optimal construct changes with the total flow-channel number and total volume of the HE. Besides the crossflow HE, Bejan et al. [53] also studied the HEs with different sizes, and found that the thermodynamic loss of flow structure can be reduced by simultaneously optimizing the shape and size of the HE. Feng et al. [54] conducted a constructal design for the disc-shaped HE, and obtained the optimal tube length at the maximum thermal efficiency. Feng et al. [55] and Cai et al. [56] investigated the performance characteristics of the shell-and-tube HEs with working fluids of R245fa and ammonia–water, respectively. And the results indicated the overall performances of the HEs after constructal designs were improved. Wu et al. [57] applied the plate HE to the evaporator of OTEC system, and obtained the optimal width of the heat transfer plate (HTP) by optimizing the total pumping power due to friction loss. Hajabdollahi [58] carried out multi-objective optimization for a plate-fin HE by simultaneously maximizing the thermal effectiveness and minimizing the annual cost, and discovered the optimal effectiveness of constructal plate-fin HE was higher than 0.747. Feng et al. [59] conducted an optimization for superheater in the supercharged boiler with the fixed total HE area, and found that the optimization objective was decreased by 2.6% after optimizing the tube outer diameter. Ariyo and Bello-Ochende [60] optimized the structural and flow parameters of a microchannel HE with the fixed total volume, and obtained the constructal microchannel HE with the minimum thermal resistance.
There are lots of studies about the performance analyses of the plate HE, but fewer optimizations in respect to the construct of the plate HE, especially in the case of the plate HE being applied to an OTEC system. However, the construct determines the performance of the plate HE, which has a crucial influence on an OTEC system. To enhance the comprehensive performance and find the optimal construct of the plate condenser, this paper will establish a composite function (CF) which considers both entropy generation rate (EGR) in heat transfer process and total pumping power due to friction loss as optimization objective, and apply constructal theory to optimize the HTP effective length, width, and effective number when the effective volume and total HTR of the plate condenser are fixed. Then the impacts of some parameters on the constructal optimization results (CORs) will be dissected. Furthermore, Pareto optimal set of the plate condenser based on the multi-objective genetic algorithm will be given by simultaneously minimizing the EGR in heat transfer process and the total pumping power due to friction loss. The obtained results can be applied to guide the designs for plate condensers in OTEC system.
2. Plate Condenser and Its Performance
Figure 1 shows a schematic diagram of the closed OTEC system, which takes the cold and warm seawaters as the heat sink and heat source, respectively. Because of the low temperatures of seawater, the OTEC system chooses the low boiling point substance as the working fluid. Based on References [13,15,16,61,62,63], ammonia is chosen as the working fluid for OTEC system after synthetically considering the environmental protection and thermodynamic performance. In Figure 2, the solid line in the cycle T-s diagram represents the condensation process. The cold seawater absorbs heat from the working fluid, and its temperatures are and at the inlet and outlet of the plate condenser, respectively. The working fluid releases heat to the cold seawater and occurs a phase transition in the plate condenser. The condensation pressure and temperature of the working fluid are and , respectively.
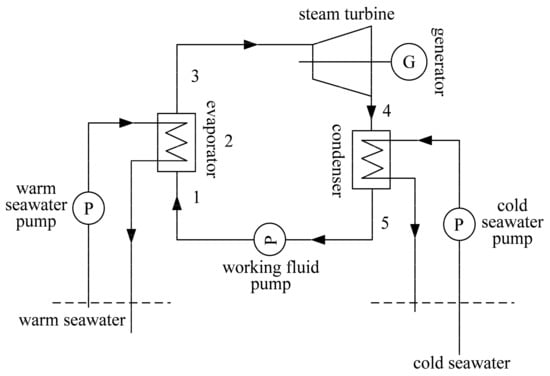
Figure 1.
Schematic diagram of the closed ocean thermal energy conversion (OTEC) system.
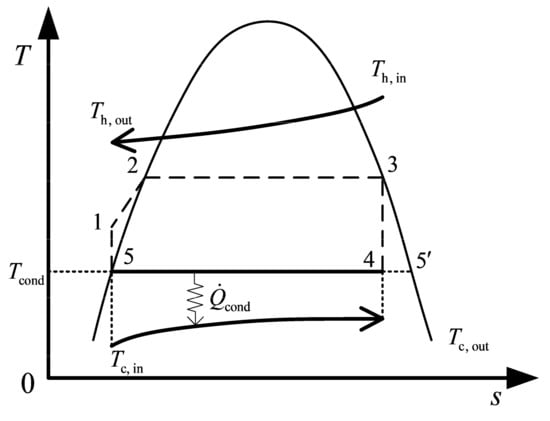
Figure 2.
T-s diagram of the organic Rankine cycle in OTEC system.
2.1. Structure of Plate Condenser
The plate HE has the advantages of the high HTC, small area, large logarithmic mean temperature difference, and small terminal temperature difference, therefore the plate HE is applied to the condenser in OTEC system. Currently, the stainless steel HE is the most widely used in the plate HEs, but it is not resistant to corrosion. While the OTEC system needs the plate material to be corrosion resistant. Although titanium has strong corrosion resistance, its price is too expensive. Researchers have found that the service life of the brazed aluminum HE can reach more than 30 years under the high-temperature seawater corrosion condition. Thus, the brazed aluminum is chosen as the plate material in the OTEC system [10,64,65]. Figure 3 depicts the flow schematic diagram of a plate HE. Plate heat exchangers are usually counterflow when the heat sink and working fluid are both single phases. While when the working fluid undergoes phase transition in the plate condensers, its pressure is constant after ignoring the flow pressure drop. At this time, the pressure drop and discharge of the heat sink are considered more than the flooding of the working fluid. If the plate condensers are still counterflow, its bottom has much heat sink, which leads to the large temperature difference and large flow pressure drop. Moreover, the counterflow will reduce the condensation temperature and lower heat exchange efficiency. Thus, the flow channels of cold seawater and working fluid in plate condenser both adopt the down-flow and single flow path configuration [12] to reduce the pressure drop and facilitate the condensate discharge. The combined forms of flow channels for working fluid and cold seawater are configured as , where and (equals to ) are the flow channel numbers of working fluid and cold seawater, respectively. Figure 4 depicts the structure diagram of a chevron plate HE, and the structural parameters , , , , , , , and are the length, effective length, width, corrugation angle, corrugation wavelength, corrugation pitch, adjacent plate spacing, and thickness of the HTP, respectively. The relationship among , , and is .
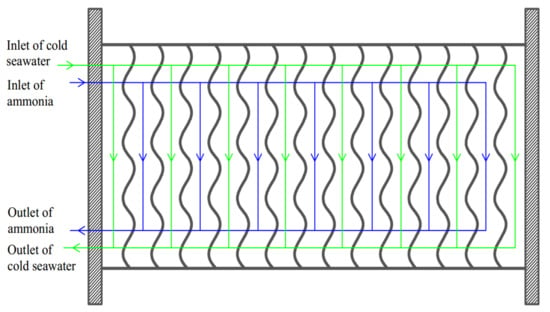
Figure 3.
Flow schematic diagram of a plate heat exchanger (HE).
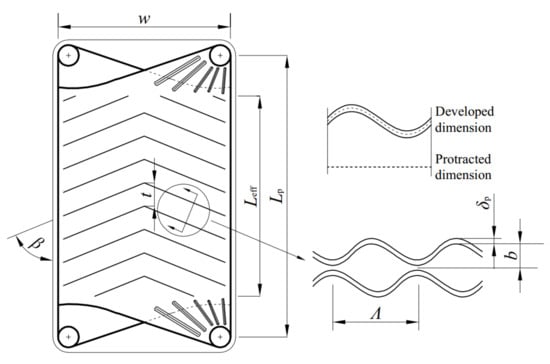
Figure 4.
Structure diagram of a chevron plate HE.
For the chevron plate HE, the hydraulic diameter () is:
where is the surface enlargement factor, i.e., the ratio of developed dimension to protracted dimension in Figure 4. When HTP corrugation section is sinusoidal, is approximately expressed as:
where (equals ) is the HTP dimensionless corrugation parameter.
The protracted area () of the single HTP is:
And the heat transfer area () (i.e., developed area) of the single HTP is:
The total heat transfer area () and effective volume of the plate condenser are:
where (equals ) is the HTP effective number.
2.2. Assumptions of Model
There are some assumptions to simplify the model and its calculations based on References [11,66,67]:
- (1)
- The flow in the plate condenser is a stable state and homogeneous for flow direction.
- (2)
- The working fluid is a two-phase state at the inlet of the plate condenser.
- (3)
- Considering that the cold seawater is enough, the working fluid will be cooled to a saturated liquid state (SLS).
- (4)
- The pressure drops at the manifolds and ports are ignored because only the HTP structure is studied in this paper. The influences of the manifolds and ports on the pressure drops and overall performance of OTEC system will be studied in future work.
2.3. Performance of Plate Condenser on Working Fluid Side
The vapor quality () of the working fluid changes continuously in the condensation process, and it has a significant impact on the performance of the plate condenser. Therefore, calculating the performance of the plate condenser by applying the average vapor quality () of the working fluid in the condensation process will lead to a big error. When the condensation process is equally divided into several small condensation sections, the calculation error of the total performance of the plate condenser can be reduced. In this paper, the condensation process of the working fluid is divided into small condensation sections, and the average vapor quality () of the working fluid in each section is:
where is the vapor quality of the working fluid at cyclic state point 4, and equals .
Adopting the computation formulas of condensation Nusselt number and friction factor in [19,23,68,69,70], the Nusselt number () and friction factor () in each small condensation section of working fluid side are:
where is the Prandtl number of the working fluid in the SLS, and the equivalent Reynolds number of the working fluid in each small condensation section is:
where is the dynamic viscosity of the working fluid in the SLS, and the equivalent mass flow rate (MFR) of the working fluid per cross-sectional area in each small condensation section is:
where and are the densities of the working fluid in the SLS and saturated vapor state, respectively, and MFR of the working fluid per cross-sectional area is:
where is the MFR of the working fluid and (equals ) is the cross-sectional area of the single flow channel in the plate condenser.
According to Reference [70], the surface HTC () in each small condensation section of the working fluid side is:
where is the thermal conductivity of the working fluid in the SLS. And the average surface HTC () on the working fluid side is:
The pressure drop () of each small condensation section on the working fluid side can be obtained based on Equations (11)–(16):
2.4. Performance of Plate Condenser on Cold Seawater Side
Although the cold seawater absorbs heat, it does not undergo a phase transition and its temperature changes small. Adopting the computation formulas of Nusselt number and friction factor in Reference [71], the Nusselt number () and friction factor () on the cold seawater side are:
where and are the cold-seawater Prandtl number and dynamic viscosity, respectively, and the cold-seawater Reynolds number is:
where the cold-seawater MFR per cross-sectional area is:
where is the cold-seawater MFR.
The surface THC () and pressure drop () on the cold seawater side are:
where is the cold-seawater density.
2.5. Overall Performance of Plate Condenser
The total HTC () of the plate condenser is:
where and are the fouling resistances on working fluid and cold seawater sides, and is the HTP thermal conductivity.
The pumping power () due to friction loss on the working fluid side is:
where is the efficiency of the working fluid pump, and the density () of the working fluid in each small condensation section is:
The pumping power () due to friction loss on the cold seawater side is:
where is the efficiency of the cold seawater pump.
The total pumping power () due to friction loss can be obtained based on Equations (27)–(29):
The plate condenser is treated as an isolated system. For an isolated system with the pure heat transfer process, the entropy generation is:
where and are the entropy changes of the isolated system in heat release and absorption processes, respectively. The entropy change rate () of the working fluid in heat release process is:
And the entropy change rate () of the cold seawater in heat absorption process is:
Combining Equations (31)–(33) yields the EGR () in heat transfer process:
According to the HE theory, the total HTR () of the plate condenser is:
where is the cold-seawater specific heat, and is a logarithmic mean temperature difference. When the plate condenser adopts down-flow configuration, can be calculated as:
3. Constructal Design for Plate Condenser with Conventional Optimization Method
3.1. Optimization Objective of Constructal Design
The plate condenser is an exothermic device in OTEC system. When the heat absorption of OTEC system is constant, the increase of the total HTR () of the plate condenser will lead to a decrease in cycle thermal efficiency. Thus, it is inapposite to take as the performance evaluation index of the plate condenser. The total pumping power () due to friction loss reflects the fluid flow characteristic of the plate condenser, it can be chosen as one of the performance evaluation criteria of the plate condenser. Besides, the EGR () [72,73,74,75,76,77,78,79,80] in heat transfer process can also be chosen as one of the performance evaluation criteria because it represents the heat transfer characteristic of the plate condenser. Although the irreversibility due to friction loss will lead to entropy generation, the friction loss has been reflected by . Thus, the EGR due to friction loss is not calculated to avoid double-counting, which is also too small compared with that due to heat transfer.
Singly optimizing or cannot fully reflect the performance of the plate condenser. Therefore, a composite function (CF) which synthetically considers and is established by applying the linear weighting method [81,82,83]:
where is the weighting coefficient, and and are the pumping power and EGR calculated by the initial design of the plate condenser. reflects the comprehensive performance of the plate condenser. When the effective volume () and total HTR () of the plate condenser are fixed, is a function of the HTP effective length (), width (), and effective number (). The constructal design of the plate condenser will be conducted by employing as an optimization objective and , , and as optimal design variables. Furthermore, the influences of the structural parameters and on CORs will be analyzed.
3.2. Optimization Procedure of Constructal Design
The constraint relationship between the condensation temperature () and total HTC () can be established based on Equation (35) when the total HTR () of the plate condenser and MFR () of the cold seawater are given. Then and can be obtained according to the constraint of the fixed effective volume () of the plate condenser. And then the MFR () of the working fluid, total pumping power () due to friction loss, and EGR () in heat transfer process can be obtained. Table 1 lists the values of some parameters in the calculations. To perform the constructal design for the plate condenser, the optimization procedure with conventional single-objective optimization method is given as follows:

Table 1.
Values and variation ranges of partial parameters.
- (1)
- The single variable optimization is carried out. The relationship between the CF () and HTP effective length () is obtained with the given HTP width () and effective number (). The relationships between and as well as between and are obtained by applying a similar method.
- (2)
- The double variable optimization is carried out by releasing the constraint of on the basis of singly optimizing . The relationships among , , and are obtained with the given .
- (3)
- The three variable optimization is carried out by releasing constraint of on the basis of step 2. The relationships among , , , and are obtained.
- (4)
- On the basis of step 3, the CORs of the plate condenser with different structural parameters and weighting coefficient are obtained. The subscripts “m” and “mm” mean the primary and twice minimizations, respectively, and the subscripts “opt” and “oo” mean the primary and twice optimizations, respectively.
The optimizations mentioned above are performed in MATLAB software, in which the ‘fsolve’ function is used.
3.3. Results of Constructal Designs
3.3.1. Single Variable Optimization
Figure 5, Figure 6 and Figure 7 reflect the effects of MFR () of the cold seawater on the characteristics of CF () versus HTP effective length (), versus HTP width (), and versus HTP effective number (), respectively. In the figures, no matter what value takes, always has the minimum value. Namely, with a given , there is always a primary optimal HTP effective length (), a primary optimal HTP width (), and a primary optimal HTP effective number () to make reach the primary minimum value (), respectively. And with the increase of , gradually decreases, while the corresponding first diminishes and then augments. It infers that there is an optimal MFR () of the cold seawater to make reach the twice minimum value (). At the same time, with the increase of , , and gradually increase, and their corresponding also gradually increase. These indicate that the influences of on , , and their corresponding are different from those of on and its corresponding . Furthermore, with the increase of , the curve of maintains a similar trend, while the curves of and gradually appear the maximum values, which significantly increase with the increase of . These results show that has both qualitative and quantitative influences on the curves of and , and only has a quantitative effect on the curve of . The explanation is that as increases, the total pumping power () due to friction loss augments while the EGR () in heat transfer process diminishes, which causes the shape of curve to gradually approximate curve and keep away from curve. Besides the above reason, it can be found from the calculations that the curves of and are both monotones. Both the curves of and only have the minimum points, and the curves of and both have the maximum and minimum points. Therefore, only has a quantitative influence on curve, while it has both quantitative and qualitative influences on the curves of and .
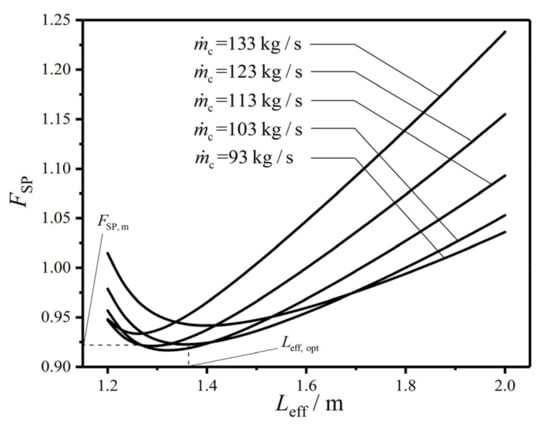
Figure 5.
Effect of on versus .
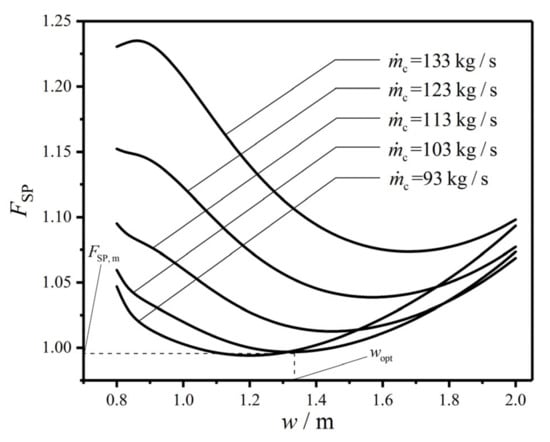
Figure 6.
Effect of on versus .
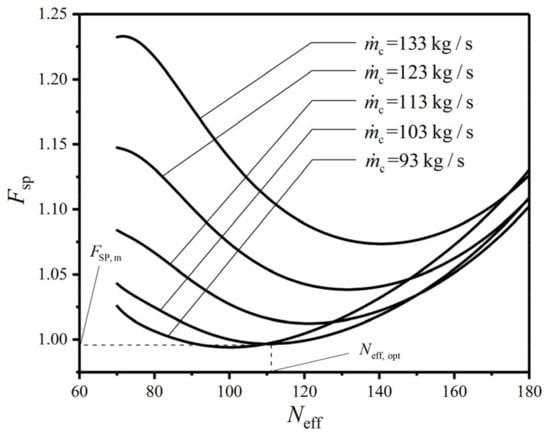
Figure 7.
Effect of on versus .
When is equal to 103 kg/s, first decreases and then increases with the increases of , , and in Figure 5, Figure 6 and Figure 7. There is a primary optimal HTP effective length (), a primary optimal HTP width (), and a primary optimal HTP effective number () to make reach , which are 0.922, 0.997, and 0.997, respectively. And they diminish by 7.8%, 0.3%, and 0.3% compared with the initial design of plate condenser. Thus, the result of singly optimizing is superior to those of singly optimizing and . The explanation for the decrease of is that diminishes 46.64%, 9.25%, and 7.47%, respectively, while augments 5.21%, 2.66%, and 2.04%, respectively. The decrease of is the main contribution to the decrease of . Finally, the plate condenser after constructal optimization greatly reduces the total flow pressure drops, and improve its comprehensive performance.
3.3.2. Double Variable Optimization
Figure 8 gives a three-dimensional diagram of the CF () versus effective length () and width () of the HTP. In the figure, there is always a primary optimal HTP effective length () to make reach the primary minimum () for any curve with a given . Figure 9 gives two-dimensional relationships between and as well as between and . One can know from the figure that as increases, first diminishes and then augments, while monotonically decreases. There is a primary optimal HTP width () to make be the twice minimum (), and the twice optimal HTP effective length () is 1.15 m. Compared with the plate condenser after singly optimizing , after simultaneously optimizing and diminishes 2.3%. The reason for the decrease of is that the total pumping power () due to friction loss diminishes 19.82%, while the EGR () in heat transfer process augments 3.77%. Thus, the decrease of is the main contribution to the decrease of . Besides, the result also indicates that further optimizing on the basis of singly optimizing can significantly improve the comprehensive performance of the plate condenser.
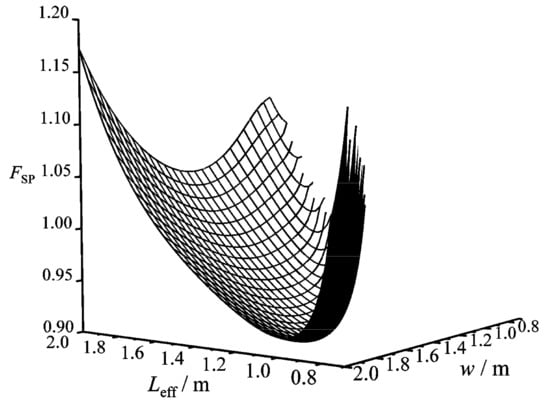
Figure 8.
Three-dimensional diagram of versus and .
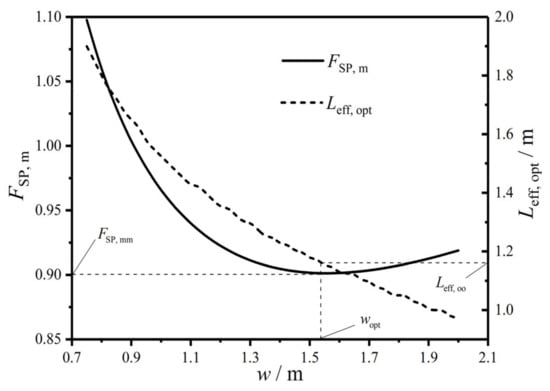
Figure 9.
Relationships of and versus .
3.3.3. Three Variable Optimization
Figure 10 gives the relationships between the twice minimum CF () and HTP effective number (), between the twice optimal HTP effective length () and , and between the primary optimal HTP width () and . One can know from the figure that with the increase of , remains stable, while monotonically decreases and has a wide variation. slowly diminishes with the growth of , and the variation of is small. The results show that further optimizing on the basis of the twice optimization cannot significantly improve the comprehensive performance of the plate condenser. When , is equal to 0.900, and when , is equal to 0.899. has little change in the range of . Thus, it is meaningless to further increase the HTP effective number when . The reasons for the low dependency of on are as follows: (1) has little effects on HTCs of the HTP on the working fluid and cold seawater sides, as shown in Figure 11. Thus, the EGR () which reflects the heat transfer characteristic of the plate condenser has a small effect. (2) has little effects on the MFRs ( and ) of the working fluid and cold-seawater per cross-sectional area because remains stable and the effective volume () is fixed. , , and are three key parameters to determine the fluid flow characteristic of the plate condenser. Their small changes make the total pumping power () less affected by .
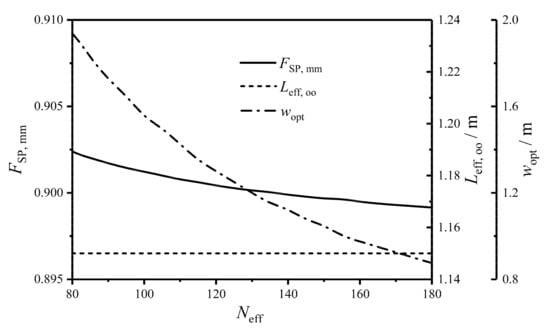
Figure 10.
Relationships of , , and versus .
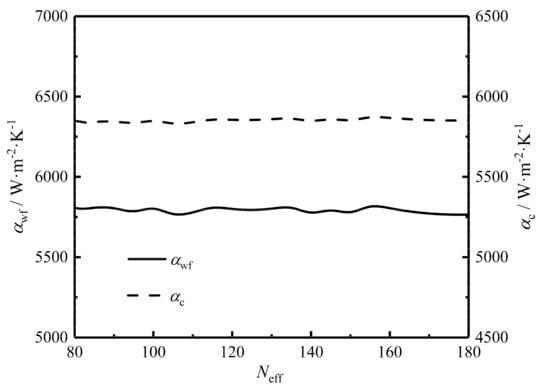
Figure 11.
Relationships of and versus .
3.3.4. Effects of Design Parameters on Optimization Results
Figure 12 gives the relationships of the twice minimum CF (), twice optimal HTP effective length (), and primary optimal HTP width () versus HTP corrugation angle () when equals to 150. One can know from the figure that grows with the increase of , and the optimal performance is significantly affected by . As increases, the fluid distribution tends to be uniform, and the fluid flow along the corrugating trough decreases. Moreover, with the increase of , the three-dimensional turbulence forms, and the eddy current density gradually increases. These reasons make the pressure drops of the working fluid and cold seawater increase, which leads to the augmentation of . On the other hand, the fluid flow state transits from the crossflow to zigzag flow with the increase of , leading to the enhancement of turbulence intensity and the increase of the total HTC. Thus, the outlet temperature () of the cold seawater increases when the total HTR () of the plate condenser is fixed. With the increase of , the EGR () in heat transfer process increases and further augments. With the increase of , the variation trend of is opposite to that of . When varies from to , gradually increases, while gradually decreases. When varies from to , gradually decreases, while gradually increases, and the variation of is larger than that of . Therefore, has significant impacts on the CORs of the plate condenser.
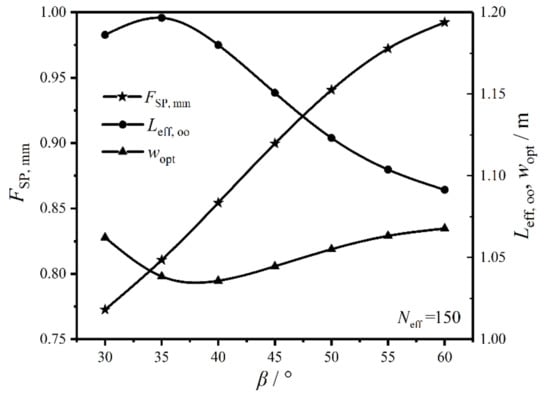
Figure 12.
Relationships of , , and versus .
Figure 13 gives the relationships of the twice minimum CF (), twice optimal HTP effective length (), and primary optimal HTP width () versus HTP corrugation wavelength () under the condition of . In the figure, near linearly augments with the enlargement of , which demonstrates can significantly affect the optimal performance of the plate condenser. The reason is that can make condensation temperature () increase, and the entropy change rate of the working fluid in heat transfer process increases, which causes to augment. When varies from 7 mm to 12 mm, gradually increases, while significantly decreases. When varies from 12 mm to 13 mm, sharply decreases, while remains stable. Therefore, has great influences on the CORs of the plate condenser.
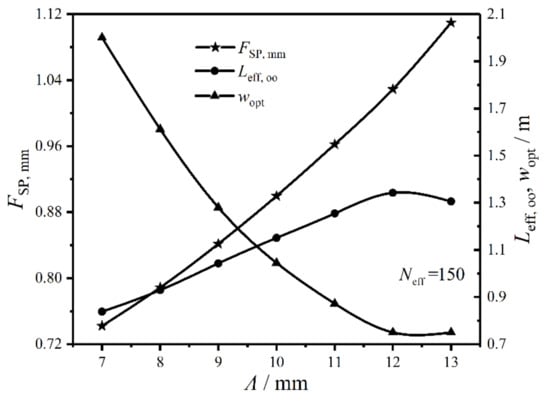
Figure 13.
Relationships of , , and versus .
Figure 14 gives the relationships of the twice minimum CF (), twice optimal HTP effective length (), and primary optimal HTP width () versus effective volume () of the plate condenser under the condition of . In the figure, near linearly diminishes with the increase of , which demonstrates the comprehensive performance of the plate condenser can be enhanced by increasing . The reason is that the cross-sectional area enlarges with the increase of , which leads to reducing the flow pressure drops and EGR () in heat transfer process. When increases from to , and gradually increase, and the variation trend of the latter is larger than that of the former. Therefore, has great effects on and . Moreover, it has a remarkable influence on the optimal performance of the plate condenser, and the main reason is that and the total pumping power () due to friction loss vary in the same direction with the increase of .
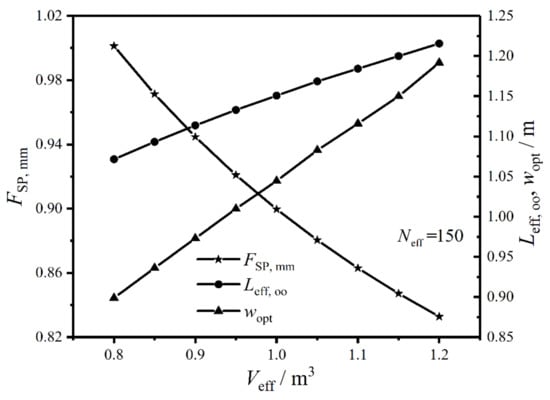
Figure 14.
Relationships of , , and versus .
Figure 15 gives the relationships of the twice minimum CF (), twice optimal HTP effective length (), and primary optimal HTP width () versus weighting coefficient () under the condition of . One can obtain from the figure that the plate condenser has the optimal performance and optimal construct in the range of . When varies from 0.45 to 0.95, the proportion of EGR () in heat transfer process increases, and the proportion of total pumping power () due to friction loss decreases. With the increase of , augments and its variation amplitude gradually diminishes, increases and its variation amplitude gradually increases, while near linearly decreases. Therefore, has remarkable influences on the CORs of the plate condenser.
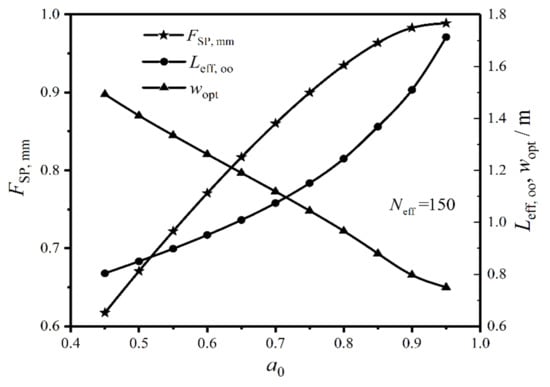
Figure 15.
Relationships of , , and versus .
All of the above research is important and helpful for OTEC system. The obtained optimal performance of the plate condenser can provide guidelines for the overall performance evaluation of OTEC system, and the obtained optimal construct of the plate condenser can be applied to design the plate condensers. Moreover, the above research considers the actual situation in which some parameters may deviate from the specific values, and analyze the impacts of variable parameters on the CORs. The obtained optimization results with different parameters can provide wide guidelines to design condensers under different operating conditions.
4. Constructal Design for Plate Condenser with Multi-Objective Genetic Algorithm
The above studies take the linear weighting method, which converts two optimization objectives into a single optimization objective, to solve the multi-objective optimization issue. However, the optimization objective may not be a linear weighting of two objective functions. To provide a wider selection for optimization and make the calculation results guide the designs of the plate condensers better, a multi-objective genetic algorithm [84,85,86,87] that is an intelligent algorithm provided by MATLAB software is adopted further.
4.1. Optimization Procedure of Multi-Objective Genetic Algorithm
The non-dominated sorting genetic algorithm II (NSGA-II), which is one of the multi-objective optimization algorithms, has strong points of high operation efficiency and good distribution of solution sets. Besides, NSGA-II is good at solving the low-dimensional optimization problem. In this paper, the optimal design variables are and , thus, NSGA-II is very suitable. Figure 16 gives a flowchart of NSGA-II, in which the following parameters are set: the size of the population is set as 300, the evolution generation is set as 500, and “PlotFcns” is chosen as “gaplotpareto”. The basic idea of NSGA-II is given as follows:
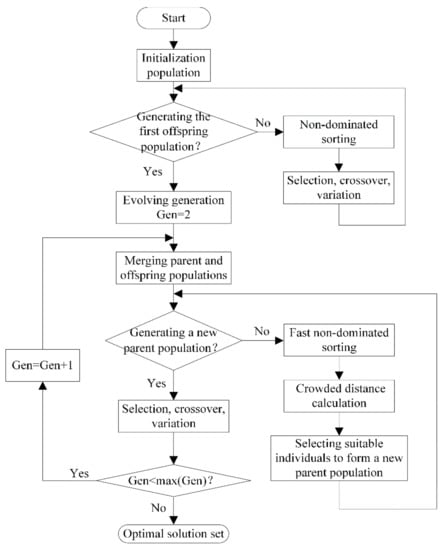
Figure 16.
Flowchart of non-dominated sorting genetic algorithm II (NSGA-II).
- (1)
- An initial population with scale is randomly generated, and the first offspring population is obtained through selection, crossover, and variation after non-dominated sorting.
- (2)
- The parent and offspring populations start to merge from the second generation. At the same time of performing the fast non-dominated sorting, the crowded distance of each individual in the non-dominated layer is calculated. A new parent population is formed by selecting suitable individuals based on the non-dominated relationship and the crowded distance of the individual.
- (3)
- A new offspring population is generated through selection, crossover, and variation of the parent population, and to circulate repeatedly until the ending conditions are satisfied. In this paper, the size of the population is set as 300, the evolution generation is set as 500, and “PlotFcns” is chosen as “gaplotpareto”.
4.2. Results of Constructal Design
Figure 17 gives Pareto front of the plate condenser based on multi-objective optimization of the minimum dimensionless EGR () and minimum dimensionless total pumping power (). One can know from the figure that the minimum and the minimum are two conflicting and influencing objective functions for the plate condenser. Each point in Pareto front is an optimal solution for the plate condenser, and at least one objective function ( or ) of the Pareto optimal solution is better than that of the solution outside the Pareto set. Namely, if (or ) decreases on the basis of the optimal solution, (or ) must be increased. Therefore, the optimal solution in the Pareto front has the least objective conflict compared with other solutions. In the figure, the ideal point at the lower-left corner is the minimum point that or should reach, but it cannot be reached in engineering because and cannot reach minimums simultaneously. Points and can be regarded as the optimal solutions of independently optimizing and , respectively. Point is the optimal solution of the plate condenser with CF () as an optimization objective, and it is also one of the optimal solutions in the Pareto front. Therefore, the Pareto front provides better selections for performance optimizations of the plate condenser.
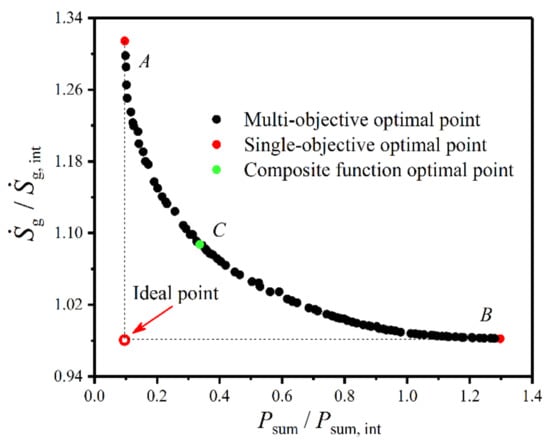
Figure 17.
Pareto front of the plate condenser based on multi-objective optimization.
5. Conclusions
The condenser is a crucial component in an OTEC system. This paper applies constructal theory to conduct constructal optimization for the plate condenser by optimizing the HTP effective length (), width (), and effective number (). The CORs of the plate condenser are obtained. The effects of different parameters on the CORs are analyzed and compared. Moreover, Pareto optimal set of the plate condenser is depicted by using NSGA-II. The obtained results are:
- (1)
- There is a primary optimal HTP effective length (), a primary optimal HTP width (), and a primary optimal HTP effective number () to make respectively reach 0.922, 0.997, and 0.997. has a more significant effect than and , and it can be chosen as the main design parameter to improve the performance of the plate condenser.
- (2)
- Continuing to optimize on the basis of singly optimizing can partly improve the comprehensive performance of the plate condenser. The twice minimum CF () after simultaneously optimizing and is 0.901, which is 2.3% less than after singly optimizing . The twice optimal HTP effective length () and are and , respectively.
- (3)
- Further optimizing the HTP effective number () on the basis of twice optimization cannot significantly improve the comprehensive performance of the plate condenser. The corrugation angle (), corrugation wavelength (), effective volume (), and weighting coefficient () have different influences on the optimal performance and optimal construct. gradually augments with the increases of , , and , and gradually diminishes with the increase of .
- (4)
- Pareto optimal set can provide better choices for the performance optimizations of the plate condenser.
- (5)
- and are two important parameters of the plate condenser. Single, double, and three variable optimizations, as well as the Pareto optimal set, all provide the optimal design values of the plate condenser, and they can be an important basis and criteria for designers to design the plate condensers.
The thermal efficiency and power output are two important performance indexes for OTEC system, and they are interesting to researchers. However, this paper took the plate condenser as a research objective, thus only the performance of the plate condenser was optimized. The influences of the plate condenser on the overall performance of OTEC system will be studied in the future system study. Moreover, the research methods and obtained conclusions herein are important for overall performance evaluation and experimental platform establishment of OTEC system. To test and verify these optimization results, the related experiment will be carried out in the next studies.
Author Contributions
Z.W., H.F., L.C., and Y.G. commonly finished the manuscript. All authors have read and approved the final version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos. 51779262 and 51506220) and Independent Project of Naval University of Engineering (No. 425317Q017).
Acknowledgments
The authors wish to thank the reviewers for their careful, unbiased, and constructive suggestions, which led to this revised manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| heat transfer area, | |
| heat transfer area of single heat transfer plate, | |
| projected area, | |
| cross-sectional area of single flow channel, | |
| plate spacing between two adjacent plates, | |
| specific heat at constant pressure, | |
| hydraulic diameter, | |
| composite function | |
| friction factor | |
| mass flow rate per cross-sectional area, | |
| enthalpy, | |
| total heat transfer coefficient, | |
| length, | |
| mass, | |
| number of heat transfer plates or flow channels | |
| Nusselt number | |
| quantity of condensation sections | |
| pumping power, | |
| pressure, | |
| Prandtl number | |
| quantity of heat transfer, | |
| fouling resistance, | |
| Reynolds number | |
| entropy generation, | |
| temperature, | |
| corrugation pitch, | |
| volume, | |
| width, | |
| dimensionless corrugation parameter of heat transfer plate | |
| vapor quality | |
| Greek letters | |
| surface heat transfer coefficient, | |
| corrugation angle, | |
| thickness, | |
| surface enlargement factor of heat transfer plate | |
| pump efficiency | |
| thermal conductivity, | |
| density, | |
| dynamic viscosity, | |
| corrugation wavelength, | |
| logarithmic mean temperature difference, | |
| pressure drop, | |
| Subscripts | |
| ave | average value |
| c | cold seawater |
| cond | condenser |
| eq | equivalent value |
| eff | effective value |
| sequence number of each small condensation section | |
| in | inlet |
| int | initial value |
| ios | isolated system |
| l | saturated liquid state |
| m | primary minimum value |
| mm | twice minimum value |
| opt | primary optimal value |
| oo | twice optimal value |
| out | outlet |
| p | heat transfer plate |
| sum | total |
| v | saturated vapor state |
| wf | working fluid |
| cyclic state points | |
| Superscript | |
| rate, | |
Abbreviations
| CF | composite function |
| COR | constructal optimization result |
| EGR | entropy generation rate |
| HE | heat exchanger |
| HRSG | heat recovery steam generator |
| HTC | heat transfer coefficient |
| HTP | heat transfer plate |
| HTR | heat transfer rate |
| MFR | mass flow rate |
| OTEC | ocean thermal energy conversion |
| SLS | saturated liquid state |
References
- D’Arsonval, A. Utilisation des forces naturelles, avenir de l’électricité. Rev. Sci. 1881, 17, 370–372. [Google Scholar]
- Claude, G. Power from the tropical seas. Mech. Eng. 1930, 52, 1039–1044. [Google Scholar]
- Lennard, D. Ocean thermal energy conversion—Past progress and future prospects. IEEE Proc. A Phys. Sci. Meas. Instrum. Manag. Educ. Rev. 1987, 134, 381. [Google Scholar] [CrossRef]
- Yeh, R.-H.; Su, T.-Z.; Yang, M.-S. Maximum output of an OTEC power plant. Ocean Eng. 2005, 32, 685–700. [Google Scholar] [CrossRef]
- Semmari, H.; Stitou, D.; Mauran, S. A novel Carnot-based cycle for ocean thermal energy conversion. Energy 2012, 43, 361–375. [Google Scholar] [CrossRef]
- Ikegami, Y.; Yasunaga, T.; Morisaki, T. Ocean Thermal Energy Conversion Using Double-Stage Rankine Cycle. J. Mar. Sci. Eng. 2018, 6, 21. [Google Scholar] [CrossRef]
- Wu, Z.X.; Feng, H.J.; Chen, L.G.; Xie, Z.J.; Cai, C.G.; Xia, S.J. Optimal design of dual-pressure turbine in OTEC system based on constructal theory. Energy Convers. Manag. 2019, 201, 112179. [Google Scholar] [CrossRef]
- Wu, Z.X.; Feng, H.J.; Chen, L.G.; Tang, W.; Shi, J.C.; Ge, Y.L. Constructal thermodynamic optimization for ocean thermal energy conversion system with dual-pressure organic Rankine cycle. Energy Convers. Manag. 2020, 210, 112727. [Google Scholar] [CrossRef]
- Yasunaga, T.; Ikegami, Y. Finite-Time Thermodynamic Model for Evaluating Heat Engines in Ocean Thermal Energy Conversion. Entropy 2020, 22, 211. [Google Scholar] [CrossRef]
- Uehara, H.; Kusuda, H.; Monde, M.; Nakaoka, T.; Sumitomo, H. Shell-and-Plate-Type Heat Exchangers for OTEC Plants. J. Sol. Energy Eng. 1984, 106, 286–290. [Google Scholar] [CrossRef]
- Uehara, H.; Ikegami, Y. Optimization of a Closed-Cycle OTEC System. J. Sol. Energy Eng. 1990, 112, 247–256. [Google Scholar] [CrossRef]
- Chen, B.H.; Li, X.R. Technical Application Manual for Plate Heat Exchanger and Heat Exchanger Device; China Architecture & Building Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Yamada, N.; Hoshi, A.; Ikegami, Y. Performance simulation of solar-boosted ocean thermal energy conversion plant. Renew. Energy 2009, 34, 1752–1758. [Google Scholar] [CrossRef]
- Wang, M.; Jing, R.; Zhang, H.; Meng, C.; Li, N.; Zhao, Y. An innovative Organic Rankine Cycle (ORC) based Ocean Thermal Energy Conversion (OTEC) system with performance simulation and multi-objective optimization. Appl. Therm. Eng. 2018, 145, 743–754. [Google Scholar] [CrossRef]
- Bernardoni, C.; Manzolini, G.; Giostri, A. Techno-economic analysis of closed OTEC cycles for power generation. Renew. Energy 2019, 132, 1018–1033. [Google Scholar] [CrossRef]
- Fontaine, K.; Yasunaga, T.; Ikegami, Y. OTEC Maximum Net Power Output Using Carnot Cycle and Application to Simplify Heat Exchanger Selection. Entropy 2019, 21, 1143. [Google Scholar] [CrossRef]
- Nakaoka, T.; Uehara, H. Performance test of a shell-and-plate-type condenser for OTEC. Exp. Therm. Fluid Sci. 1988, 1, 275–281. [Google Scholar] [CrossRef]
- Yan, Y.-Y.; Lio, H.-C.; Lin, T.-F. Condensation heat transfer and pressure drop of refrigerant R-134a in a plate heat exchanger. Int. J. Heat Mass Transf. 1999, 42, 993–1006. [Google Scholar] [CrossRef]
- Wang, L.K.; Sunden, B.; Yang, Q.S. Pressure Drop Analysis of Steam Condensation in a Plate Heat Exchanger. Heat Transf. Eng. 1999, 20, 71–77. [Google Scholar] [CrossRef]
- Han, D.H.; Lee, K.J.; Kim, Y.H. The characteristics of condensation in brazed plate heat exchangers with different chevron angles. J. Korean Phys. Soc. 2003, 43, 66–73. [Google Scholar]
- García-Cascales, J.R.; García, F.V.; Corberan, J.M.; Maciá, J.G. Assessment of boiling and condensation heat transfer correlations in the modelling of plate heat exchangers. Int. J. Refrig. 2007, 30, 1029–1041. [Google Scholar] [CrossRef]
- Longo, G.A.; Zilio, C.; Righetti, G.; Brown, J.S. Condensation of the low GWP refrigerant HFO1234ze(E) inside a Brazed Plate Heat Exchanger. Int. J. Refrig. 2014, 38, 250–259. [Google Scholar] [CrossRef]
- Longo, G.A.; Righetti, G.; Zilio, C. A new computational procedure for refrigerant condensation inside herringbone-type Brazed Plate Heat Exchangers. Int. J. Heat Mass Transf. 2015, 82, 530–536. [Google Scholar] [CrossRef]
- Eldeeb, R.; Aute, V.; Radermacher, R. A survey of correlations for heat transfer and pressure drop for evaporation and condensation in plate heat exchangers. Int. J. Refrig. 2016, 65, 12–26. [Google Scholar] [CrossRef]
- Shon, B.H.; Jeon, S.W.; Kim, Y.; Kang, Y.T. Review: Condensation and Evaporation Characteristics of Low GWP Refrigerants in Plate Heat Exchangers. Int. J. Air-Conditioning Refrig. 2016, 24, 1630004. [Google Scholar] [CrossRef]
- Shon, B.H.; Jung, C.W.; Kwon, O.J.; Choi, C.K.; Kang, Y.T. Characteristics on condensation heat transfer and pressure drop for a low GWP refrigerant in brazed plate heat exchanger. Int. J. Heat Mass Transf. 2018, 122, 1272–1282. [Google Scholar] [CrossRef]
- Bejan, A. Street network theory of organization in nature. J. Adv. Transp. 1996, 30, 85–107. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kim, S.; Lorente, S.; Bejan, A. Design with Constructal Theory: Vascularized Composites for Volumetric Cooling; Wiley: Hoboken, NJ, USA, 2008; pp. 437–444. [Google Scholar]
- Chen, L.G. Progress in study on constructal theory and its applications. Sci. China Ser. E Technol. Sci. 2012, 55, 802–820. [Google Scholar] [CrossRef]
- Bejan, A. Constructal Law: Optimization as Design Evolution. J. Heat Transf. 2015, 137, 061003. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H. Multi-Objective Constructal Optimizations for Fluid Flow, Heat and Mass Transfer Processes; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Chen, L.G.; Feng, H.J.; Xie, Z.H. Generalized Thermodynamic Optimization for Iron and Steel Production Processes: Theoretical Exploration and Application Cases. Entropy 2016, 18, 353. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H. Multi-disciplinary, multi-objective and multi-scale constructal optimizations for heat and mass transfer processes performed in Naval University of Engineering, a review. Int. J. Heat Mass Transf. 2017, 115, 86–98. [Google Scholar] [CrossRef]
- Miguel, A.F.; Rocha, L.A.O. Tree-Shaped Fluid Flow and Heat Transfer; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Chen, L.G.; Xiao, Q.H.; Feng, H.J. Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering: A Review. Entropy 2018, 20, 74. [Google Scholar] [CrossRef]
- Bejan, A. Constructal law, twenty years after. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inform. Sci. 2018, 18, 309–311. [Google Scholar]
- Rocha, L.A.O.; Lorente, S.; Bejan, A. Constructal Theory in Heat Transfer. Handb. Therm. Sci. Eng. 2018, 329–360. [Google Scholar] [CrossRef]
- You, J.; Feng, H.J.; Chen, L.G.; Xie, Z.H. Constructal optimization for cooling a nonuniform heat generating disc-shaped area by conduction. Entropy 2018, 20, 685. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H.; Sun, F.R. Progress of constructal theory in China over the past decade. Int. J. Heat Mass Transf. 2019, 130, 393–419. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A. Current trends in constructal law and evolutionary design. Heat Transfer-Asian Res. 2019, 48, 3574–3589. [Google Scholar] [CrossRef]
- Bejan, A. Freedom and Evolution: Hierarchy in Nature, Society and Science; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Chen, L.G.; Yang, A.B.; Feng, H.J.; Ge, Y.L.; Xia, S.J. Constructal design progress for eight types of heat sinks. Sci. China Ser. E Technol. Sci. 2020, 63, 879–911. [Google Scholar] [CrossRef]
- Bejan, A.; Gunes, U.; Sahin, B. University Rankings: Quality, Size and Permanence. Eur. Rev. 2020, 1–22. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Feng, H.J.; Chen, L.G.; You, J.; Xie, Z.J. Constructal Design of an Arrow-Shaped High Thermal Conductivity Channel in a Square Heat Generation Body. Entropy 2020, 22, 475. [Google Scholar] [CrossRef]
- Wang, R.; Xie, Z.H.; Yin, Y.; Chen, L.G. Constructal design of elliptical cylinders with heat generating for entropy generation minimization. Entropy 2020, 22, 651. [Google Scholar] [CrossRef]
- Vargas, J.; Bejan, A. Thermodynamic optimization of finned crossflow heat exchangers for aircraft environmental control systems. Int. J. Heat Fluid Flow 2001, 22, 657–665. [Google Scholar] [CrossRef]
- Bejan, A. Dendritic constructal heat exchanger with small-scale crossflows and larger-scales counterflows. Int. J. Heat Mass Transf. 2002, 45, 4607–4620. [Google Scholar] [CrossRef]
- Sotoodeh, A.F.; Amidpour, M.; Ghazi, M. Developing of constructal theory concept for plate fin heat exchanger modeling, design and optimization. Int. J. Exergy 2015, 18, 22–45. [Google Scholar] [CrossRef]
- Xie, G.; Song, Y.; Asadi, M.; Lorenzini, G. Optimization of Pin-Fins for a Heat Exchanger by Entropy Generation Minimization and Constructal Law. J. Heat Transf. 2015, 137, 061901. [Google Scholar] [CrossRef]
- Bejan, A.; Alalaimi, M.; Sabau, A.; Lorente, S. Entrance-length dendritic plate heat exchangers. Int. J. Heat Mass Transf. 2017, 114, 1350–1356. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S.; Martins, L.; Meyer, J.P. The constructal size of a heat exchanger. J. Appl. Phys. 2017, 122, 064902. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xia, S.J. Constructal design for disc-shaped heat exchanger with maximum thermal efficiency. Int. J. Heat Mass Transf. 2019, 130, 740–746. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Wu, Z.X.; Xie, Z.J. Constructal design of a shell-and-tube heat exchanger for organic fluid evaporation process. Int. J. Heat Mass Transf. 2019, 131, 750–756. [Google Scholar] [CrossRef]
- Cai, C.G.; Feng, H.J.; Chen, L.G.; Wu, Z.X.; Xie, Z.J. Constructal design of a shell-and-tube evaporator with ammonia-water working fluid. Int. J. Heat Mass Transf. 2019, 135, 541–547. [Google Scholar] [CrossRef]
- Wu, Z.X.; Feng, H.J.; Chen, L.G.; Xie, Z.J.; Cai, C.G. Pumping power minimization of an evaporator in ocean thermal energy conversion system based on constructal theory. Energy 2019, 181, 974–984. [Google Scholar] [CrossRef]
- Hajabdollahi, H. Multi-objective optimization of plate fin heat exchanger using constructal theory. Int. Commun. Heat Mass Transf. 2019, 108, 104283. [Google Scholar] [CrossRef]
- Feng, H.J.; Xie, Z.J.; Chen, L.G.; Wu, Z.X.; Xia, S.J. Constructal design for supercharged boiler superheater. Energy 2020, 191, 116484. [Google Scholar] [CrossRef]
- Ariyo, D.O.; Bello-Ochende, T. Constructal design of subcooled microchannel heat exchangers. Int. J. Heat Mass Transf. 2020, 146, 118835. [Google Scholar] [CrossRef]
- Ganić, E.; Wu, J. On the selection of working fluids for OTEC power plants. Energy Convers. Manag. 1980, 20, 9–22. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Xiao, H.; Owen-Jones, M.; David, W.I.F.; Bowen, P. Ammonia for power. Prog. Energy Combust. Sci. 2018, 69, 63–102. [Google Scholar] [CrossRef]
- Chen, F.; Liu, L.; Peng, J.; Ge, Y.; Wu, H.; Liu, W. Theoretical and experimental research on the thermal performance of ocean thermal energy conversion system using the rankine cycle mode. Energy 2019, 183, 497–503. [Google Scholar] [CrossRef]
- Eldred, M.P.; Van Ryzin, J.C.; Rizea, S.; Chen, I.C.; Loudon, R.; Nagurny, N.J.; Maurer, S.; Jansen, E.; Plumb, A.; Eller, M.R.; et al. Heat exchanger development for Ocean Thermal Energy Conversion. OCEANS’11 MTS/IEEE KONA 2011, 1–9. [Google Scholar] [CrossRef]
- Manuel, A.J.L.; Orlando, E.R.; José, A.M. Ocean Thermal Energy Conversion: Heat Exchanger Evaluation and Selection. Mater. Challenges Altern. Renew. Energy 2011, 224, 219. [Google Scholar]
- Wang, M.; Chen, Y.; Liu, Q.; Yuanyuan, Z. Thermodynamic and thermo-economic analysis of dual-pressure and single pressure evaporation organic Rankine cycles. Energy Convers. Manag. 2018, 177, 718–736. [Google Scholar] [CrossRef]
- Du, Y.; Yang, Y.; Hu, D.; Hao, M.; Wang, J.; Dai, Y. Off-design performance comparative analysis between basic and parallel dual-pressure organic Rankine cycles using radial inflow turbines. Appl. Therm. Eng. 2018, 138, 18–34. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’Haeseleer, W.D. Comparison of shell-and-tube with plate heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 87, 227–237. [Google Scholar] [CrossRef]
- Soontarapiromsook, J.; Mahian, O.; Dalkilic, A.S.; Wongwises, S. Effect of surface roughness on the condensation of R-134a in vertical chevron gasketed plate heat exchangers. Exp. Therm. Fluid Sci. 2018, 91, 54–63. [Google Scholar] [CrossRef]
- Tao, X.; Nuijten, M.P.; Ferreira, C.A.I. Two-phase vertical downward flow in plate heat exchangers: Flow patterns and condensation mechanisms. Int. J. Refrig. 2018, 85, 489–510. [Google Scholar] [CrossRef]
- Muley, A.; Manglik, R.M. Experimental Study of Turbulent Flow Heat Transfer and Pressure Drop in a Plate Heat Exchanger With Chevron Plates. J. Heat Transf. 1999, 121, 110–117. [Google Scholar] [CrossRef]
- Wu, Z.X.; Chen, L.G.; Feng, H.J. Thermodynamic Optimization for an Endoreversible Dual-Miller Cycle (DMC) with Finite Speed of Piston. Entropy 2018, 20, 165. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.G.; Xia, S.J.; Wang, C.; Sun, F.R. Entropy Generation Minimization for Reverse Water Gas Shift (RWGS) Reactors. Entropy 2018, 20, 415. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhang, L.; Xia, S.J.; Sun, F.R. Entropy generation minimization for CO2 hydrogenation to light olefins. Energy 2018, 147, 187–196. [Google Scholar] [CrossRef]
- Shi, H.N.; Xie, Z.H.; Chen, L.G.; Sun, F.R. Constructal optimization for line-to-line vascular based on entropy generation minimization principle. Int. J. Heat Mass Transf. 2018, 126, 848–854. [Google Scholar] [CrossRef]
- Chen, L.G.; Wang, C.; Xia, S.J.; Sun, F.R. Thermodynamic analysis and optimization of extraction process of CO2 from acid seawater by using hollow fiber membrane contactor. Int. J. Heat Mass Transfer. 2018, 124, 1310–1320. [Google Scholar] [CrossRef]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Zhang, L. Entropy Generation Rate Minimization for Methanol Synthesis via a CO2 Hydrogenation Reactor. Entropy 2019, 21, 174. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, S.J.; Chen, L.G.; Ge, Y.L.; Wang, C.; Feng, H.J. Entropy generation rate minimization for hydrocarbon synthesis reactor from carbon dioxide and hydrogen. Int. J. Heat Mass Transf. 2019, 137, 1112–1123. [Google Scholar] [CrossRef]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Zhang, L.; Kong, R.; Ge, Y.L.; Feng, H.J. Entropy generation rate minimization for steam methane reforming reactor heated by molten salt. Energy Rep. 2020, 6, 685–697. [Google Scholar] [CrossRef]
- Feng, H.J.; You, J.; Chen, L.G.; Ge, Y.L.; Xia, S.J. Constructal design of a non-uniform heat generating disc based on entropy generation minimization. Eur. Phys. J. Plus 2020, 135, 1–19. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhang, J.M.; Wu, C.; Sun, F.R. Analysis of multi-objective decision-making for marine steam turbine stage. Int. J. Power Energy Syst. 1998, 18, 96–101. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Liu, X.; Xie, Z.H. Constructal design for an iron and steel production process based on the objectives of steel yield and useful energy. Int. J. Heat Mass Transf. 2017, 111, 1192–1205. [Google Scholar] [CrossRef]
- Gulotta, T.M.; Guarino, F.; Cellura, M.; Lorenzini, G. Constructal law optimization of a boiler. Int. J. Heat Tech. 2017, 35, 297–305. [Google Scholar] [CrossRef]
- Ganjehkaviri, A.; Jaafar, M.N.M. Energy Analysis and Multi-Objective Optimization of an Internal Combustion Engine-Based CHP System for Heat Recovery. Entropy 2014, 16, 5633–5653. [Google Scholar] [CrossRef]
- Avendaño, P.; Souza, J.A.; Adamatti, D. Construction of conductive pathways using Genetic Algorithms and Constructal Theory. Int. J. Therm. Sci. 2018, 134, 200–207. [Google Scholar] [CrossRef]
- Valencia, G.; Núñez, J.; Duarte, J. Multiobjective optimization of a plate heat exchanger in a waste heat recovery organic Rankine cycle system for natural gas engines. Entropy 2019, 21, 655. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.G.; Xia, S.J.; Ge, Y.L.; Wang, C.; Feng, H.J. Multi-objective optimization for helium-heated reverse water gas shift reactor by using NSGA-II. Int. J. Heat Mass Transf. 2020, 148, 119025. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).