Estimation of Dynamic Bivariate Correlation Using a Weighted Graph Algorithm
Abstract
1. Introduction
2. Methods
2.1. Method # 1—Sliding-Window (SW) Technique
2.2. Method # 2—Dynamic Conditional Correlation
- 1st step:
- Estimate using GARCH(1,1)
- DE-GARCH data:
- 2nd step:
- Estimate quasi-correlation matrix , where
- 3rd step:
- Rescale to get a proper correlation matrix:
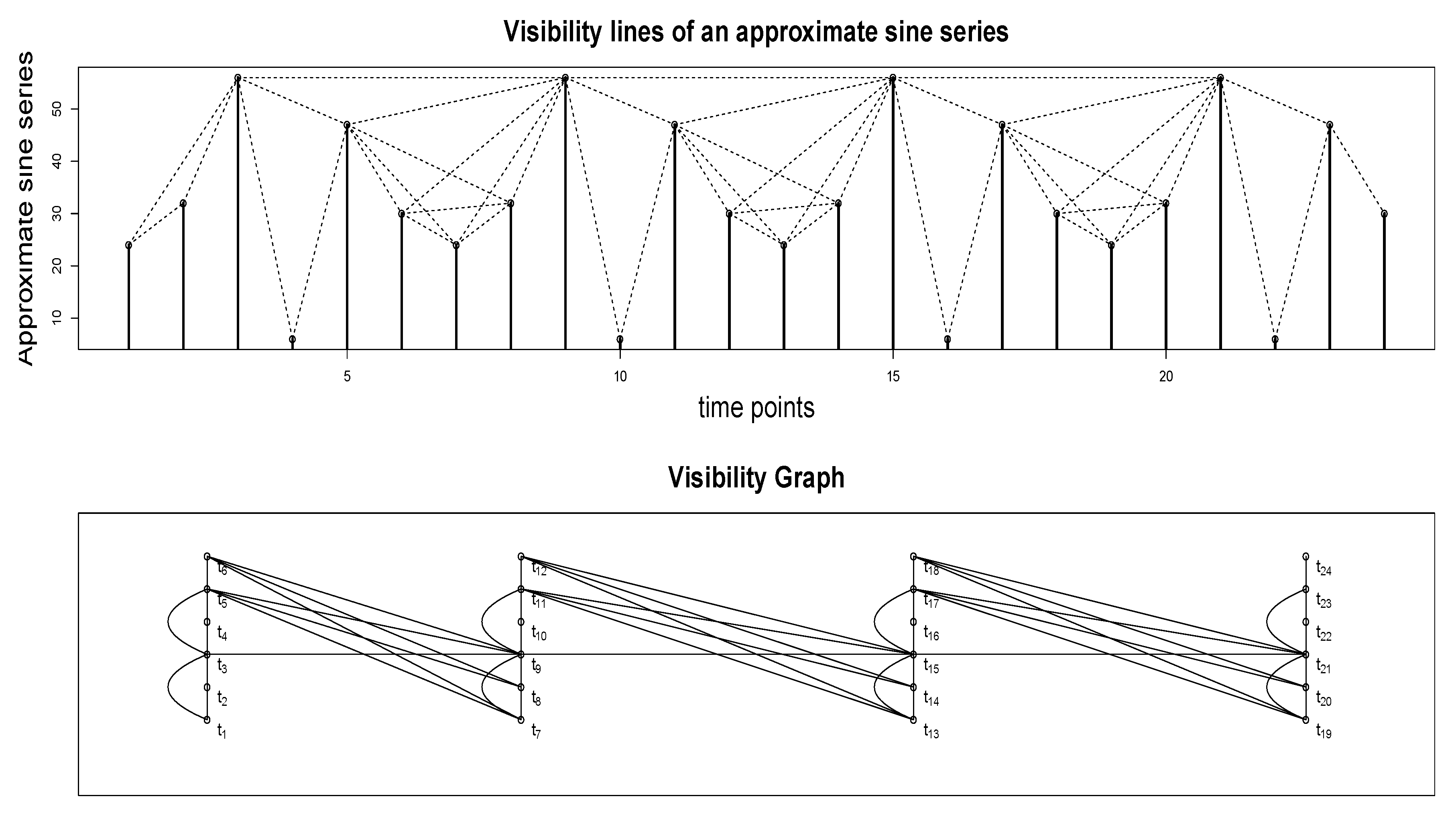
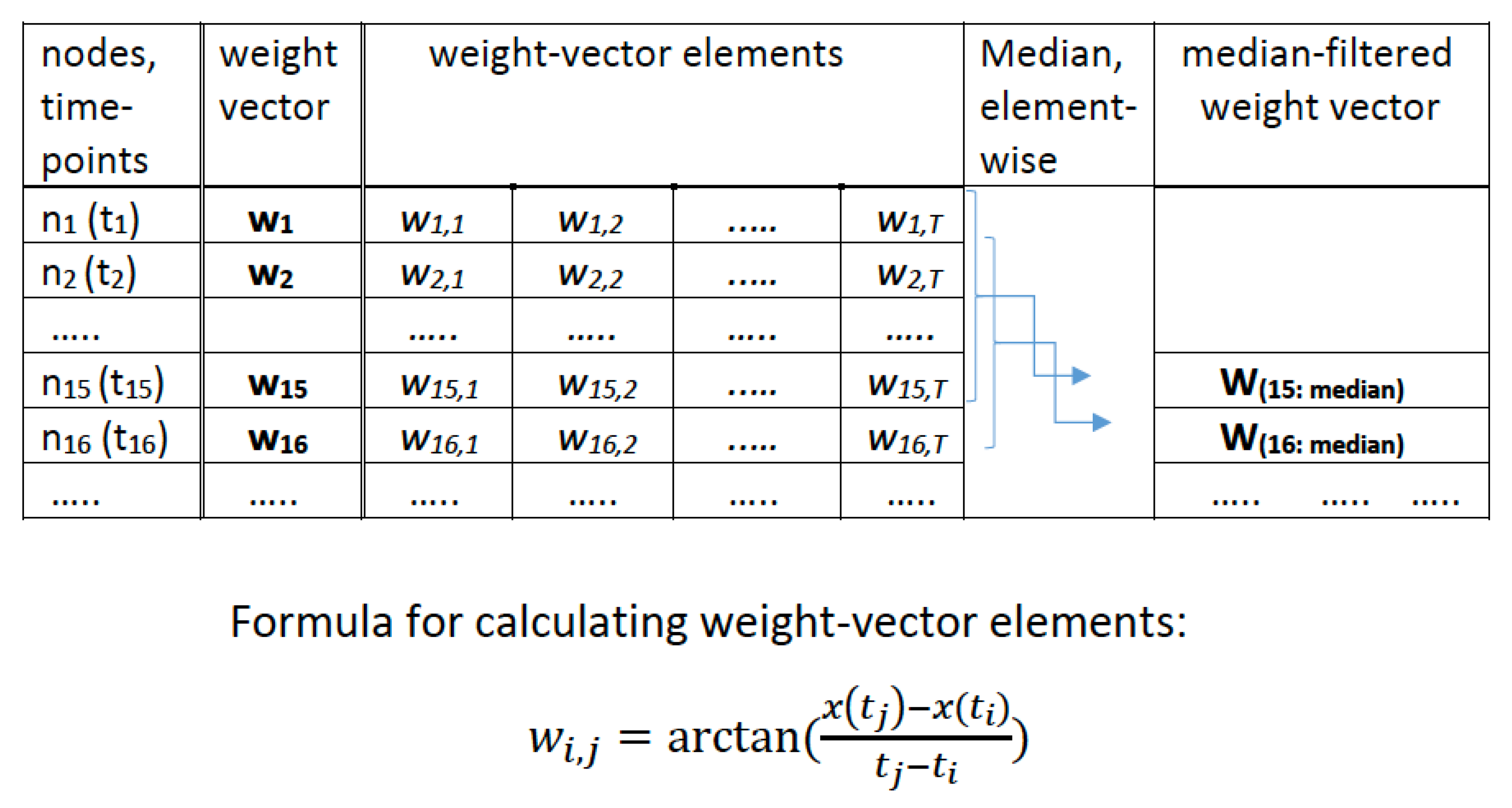
2.3. Method # 3—Weighted Graph Algorithm (WGA)
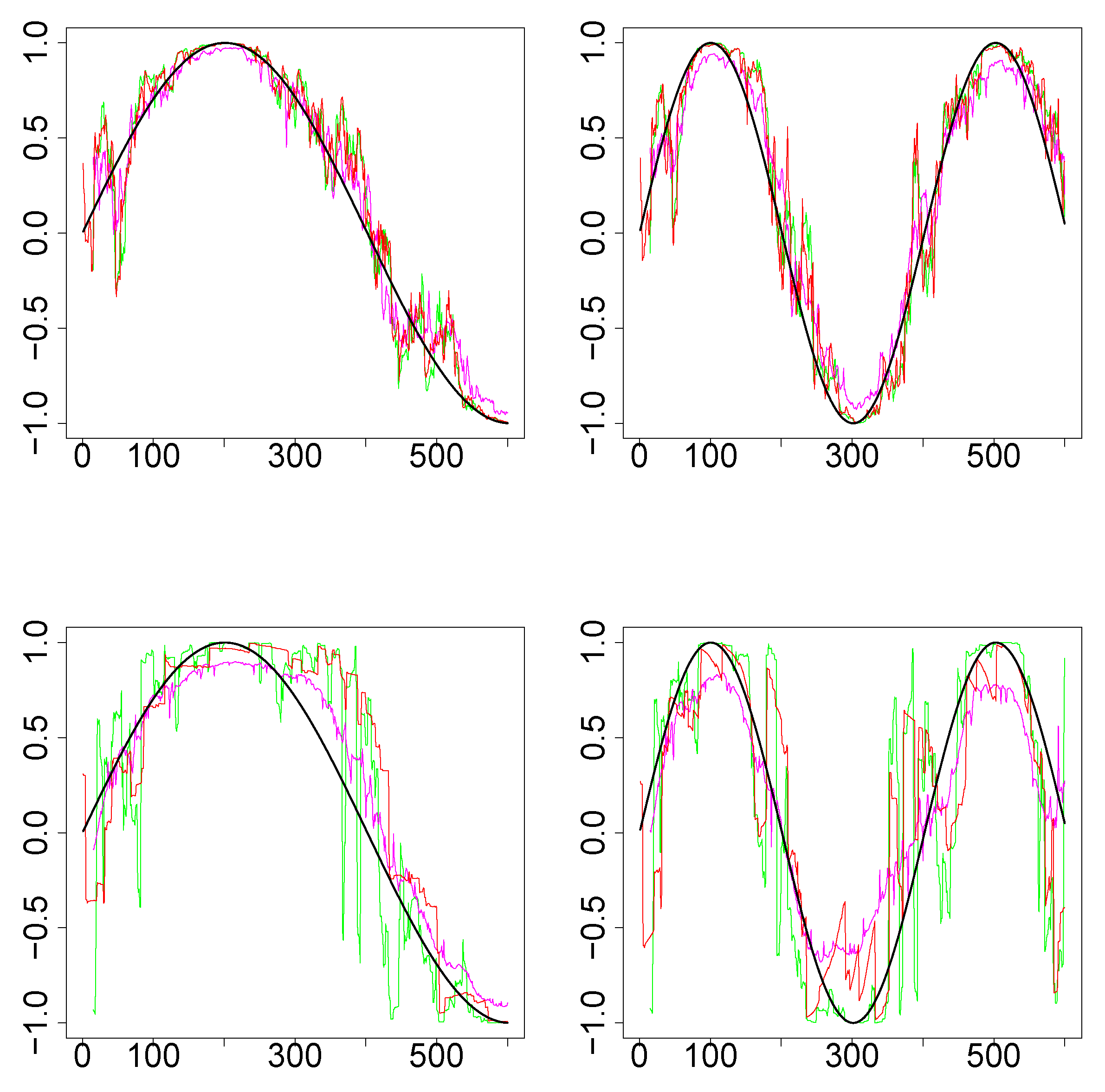
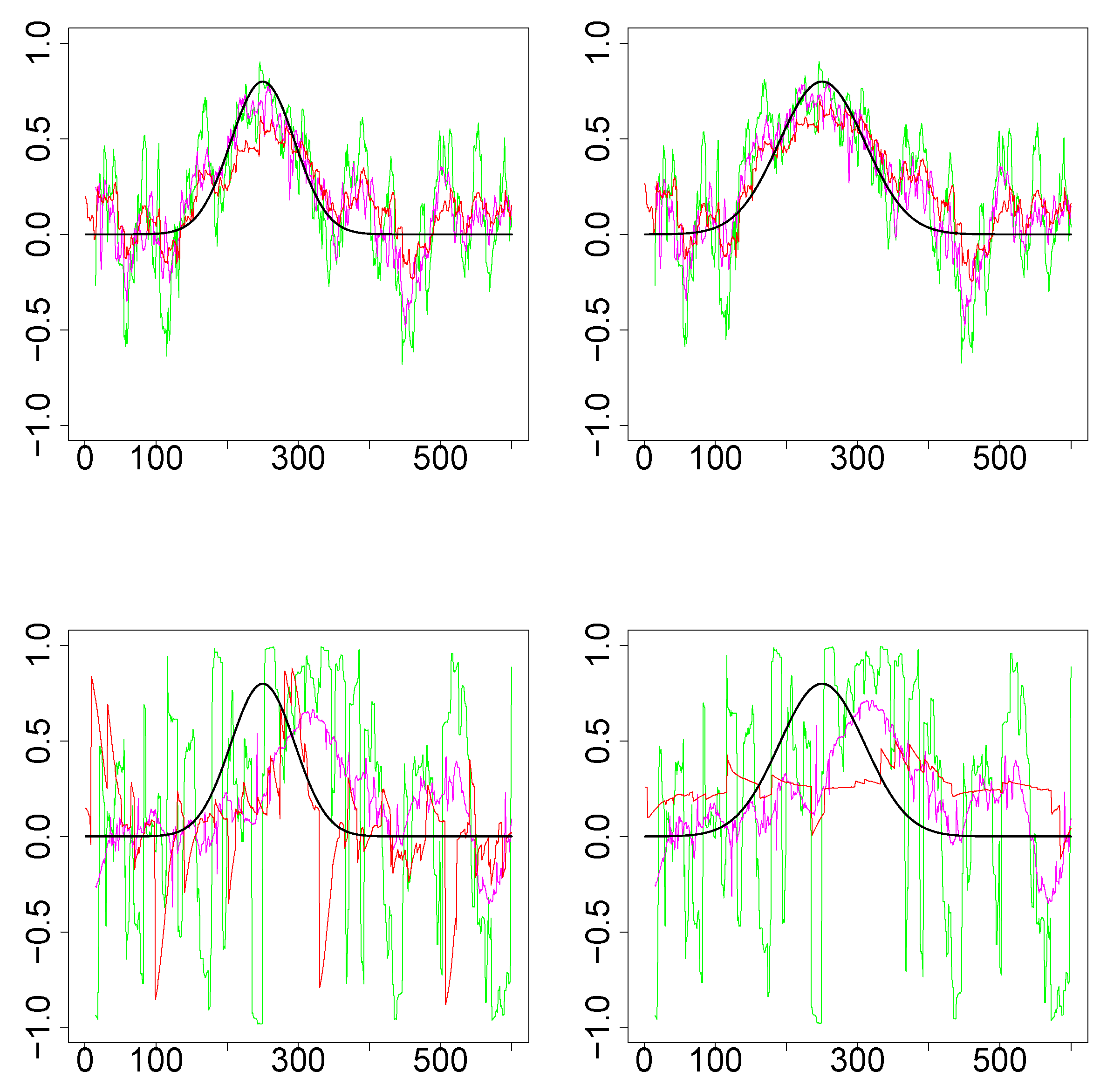
2.4. Simulation Design
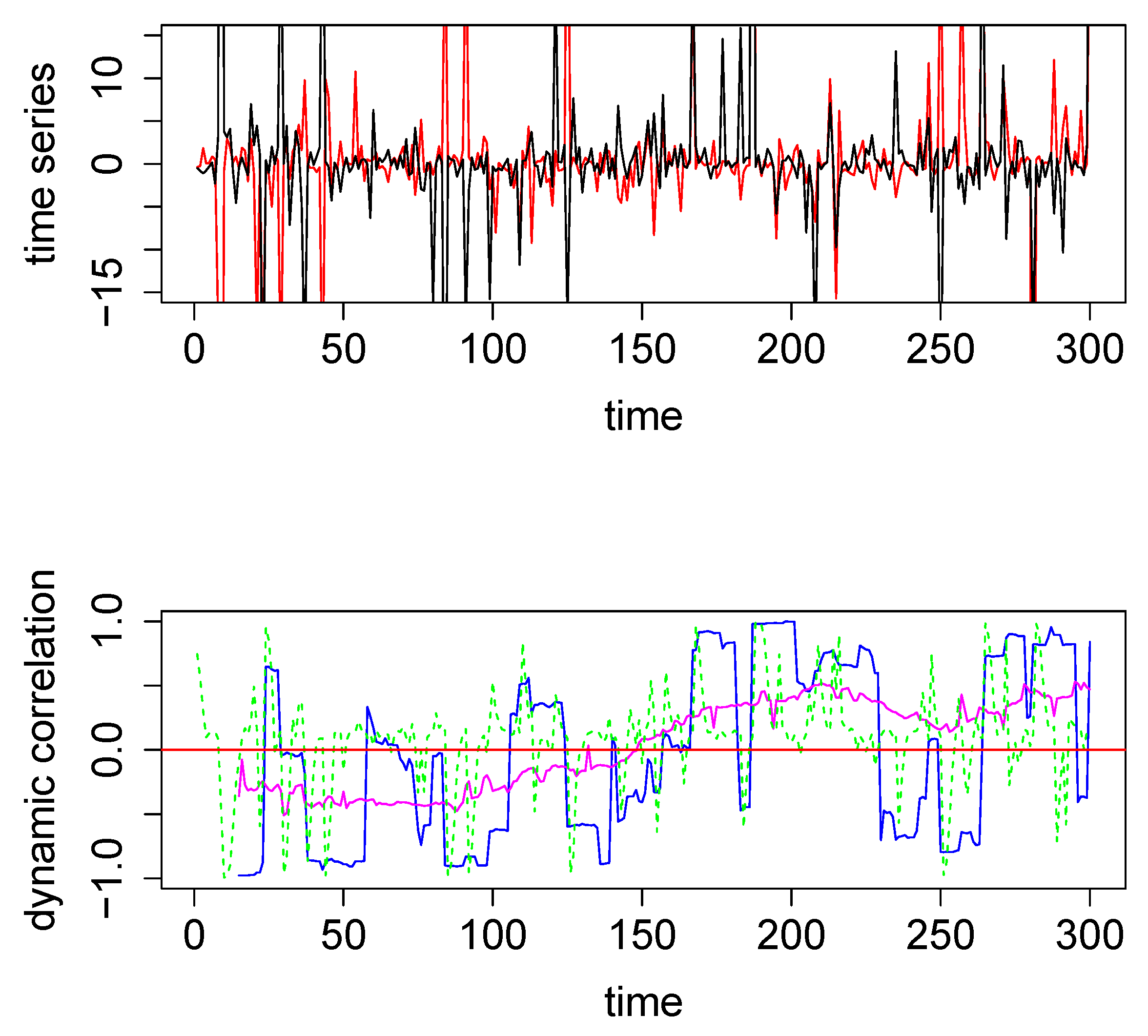
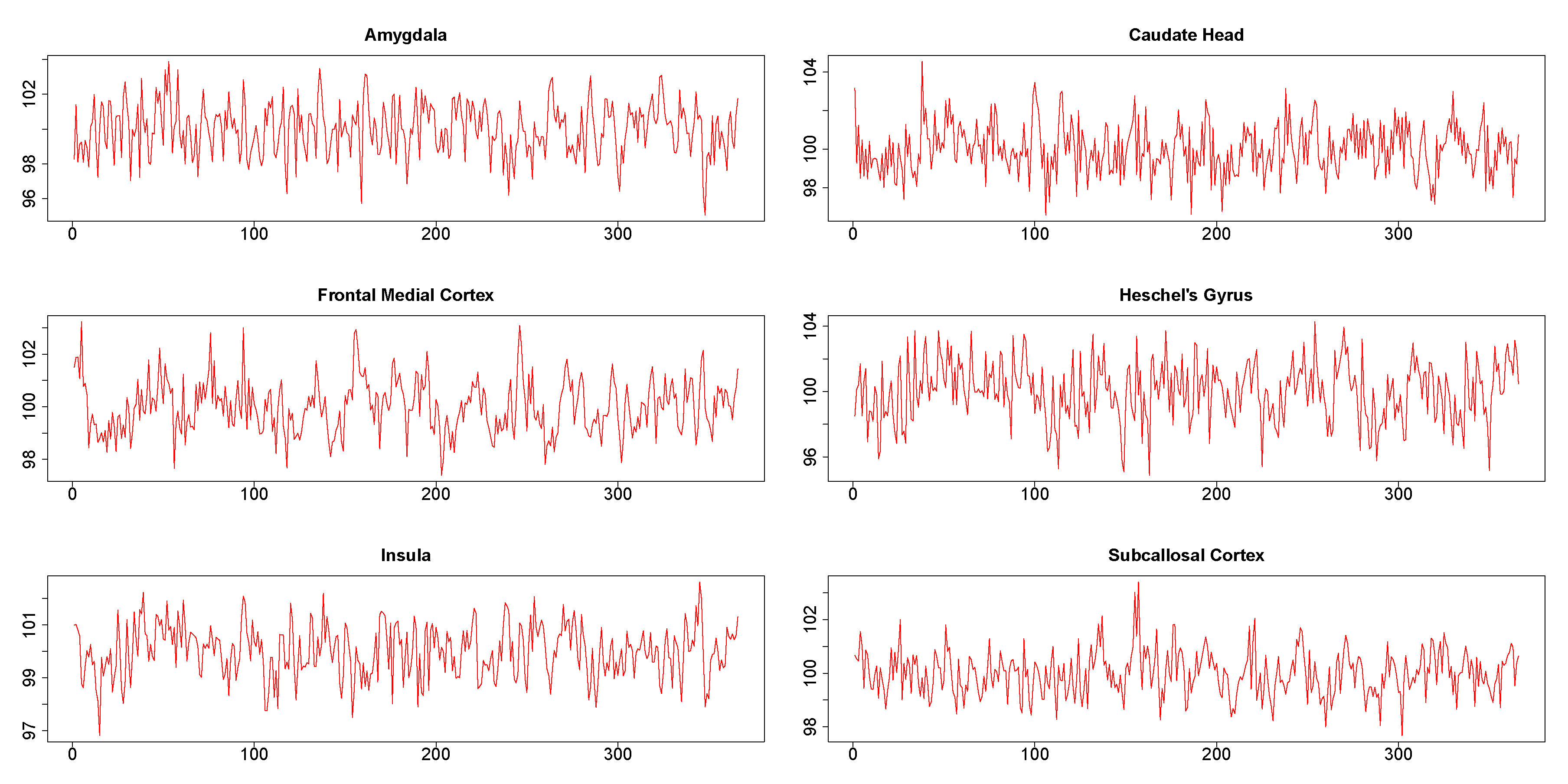
2.5. Real Data Analysis
3. Results
3.1. Simulations Results
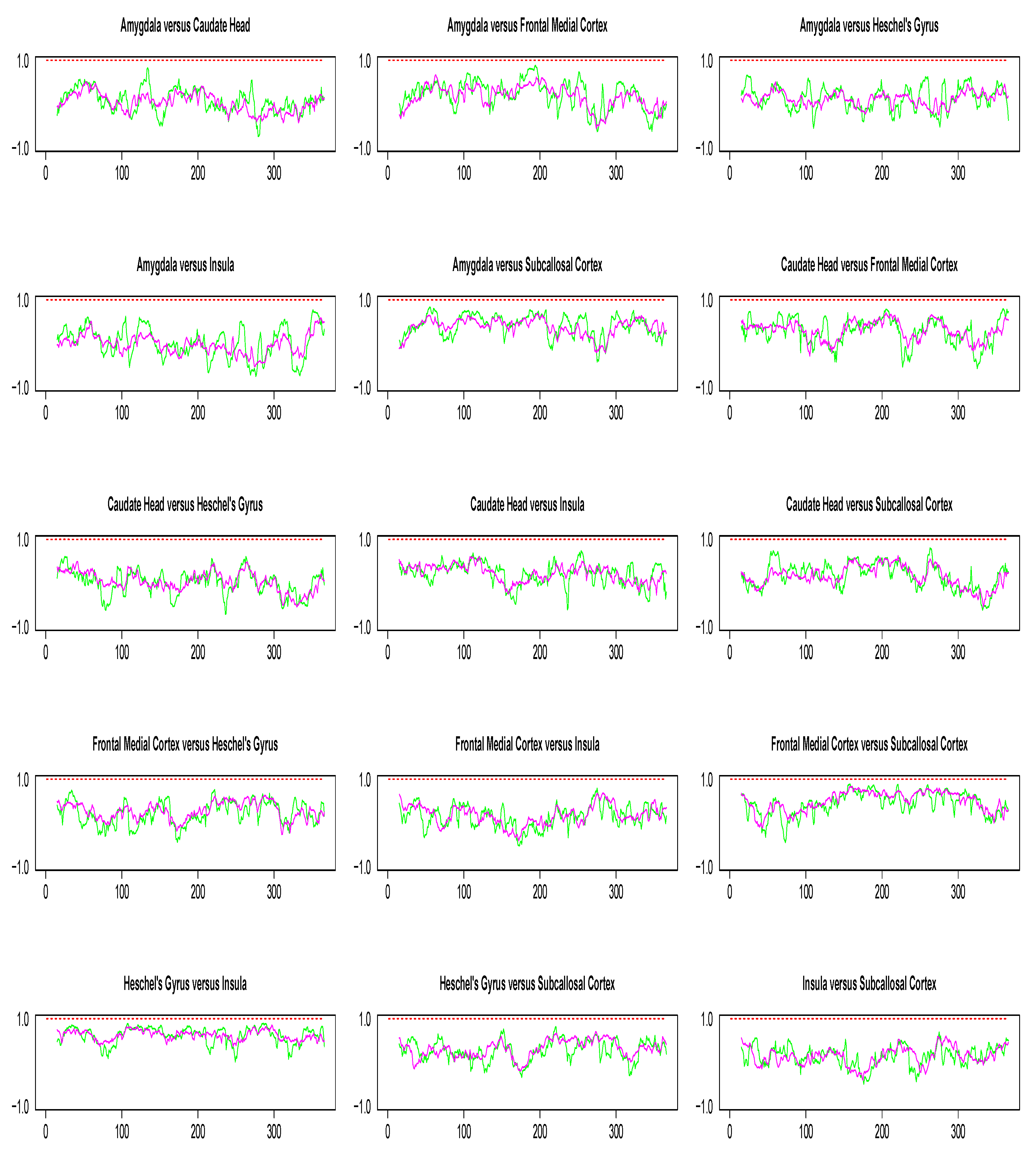
3.2. Stroop Task Data Results
4. Quantifying Uncertainty and Testing Hypothesis
4.1. Confidence Intervals
- Step 1:
- Let denote the centered where the centering for elements in and in are done separately.
- Step 2:
- Compute where L denotes the lower left matrix in Cholesky decomposition () of .
- Step 3:
- Let be the standardized version of obtained by subtracting the mean and dividing by the standard deviation (SD). Here mean and SD are computed from all elements in .
- Step 4:
- Generate by performing i.i.d resampling from .
- Step 5:
- Compute . Split into two separate vectors with containing the first T elements and containing the last T elements of .
- Step 6:
- Add mean of to each element of to obtain . Similarly, add mean of to each element of to obtain . The pair of vectors and are the bootstrap sample pair outputted.
- Step 1:
- Divide the data matrix X into K adjacent blocks, where each block is a matrix.
- Step 2:
- For each block run the MLPB algorithm to get a bootstrap sample pair corresponding to that block.
- Step 3:
- Combine the K adjacent blocks of bootstrap sample pairs and apply the WGA algorithm on the combined bootstrap sample pair.
- Step 4:
- Repeat the above steps B times to get B dynamic correlation time series based on the WGA algorithm.
- Step 5:
- At each time point calculate the 2.5th and 97.5th percentiles among the bootstrap samples to obtain the bootstrap based 95% confidence interval.
4.2. Hypothesis Testing
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Figures and Tables
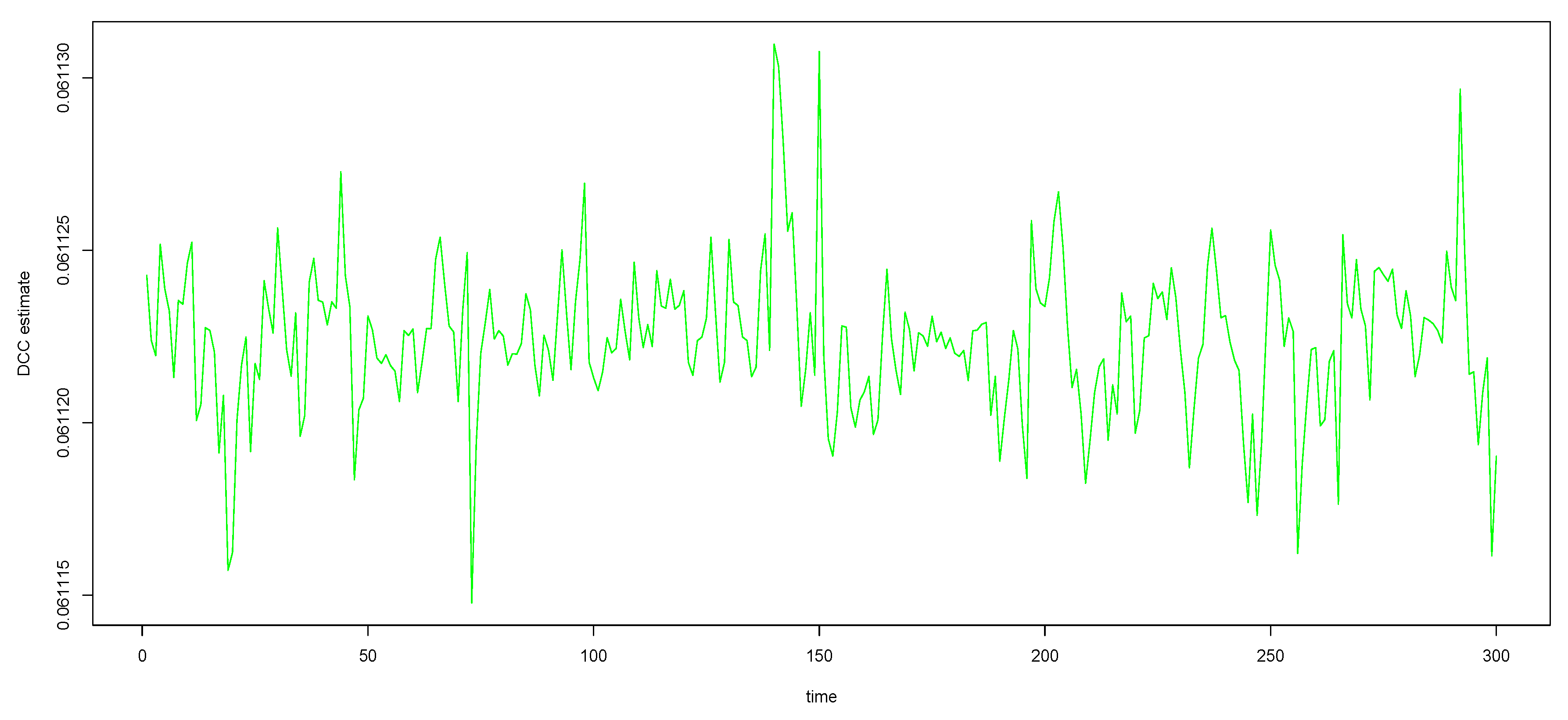
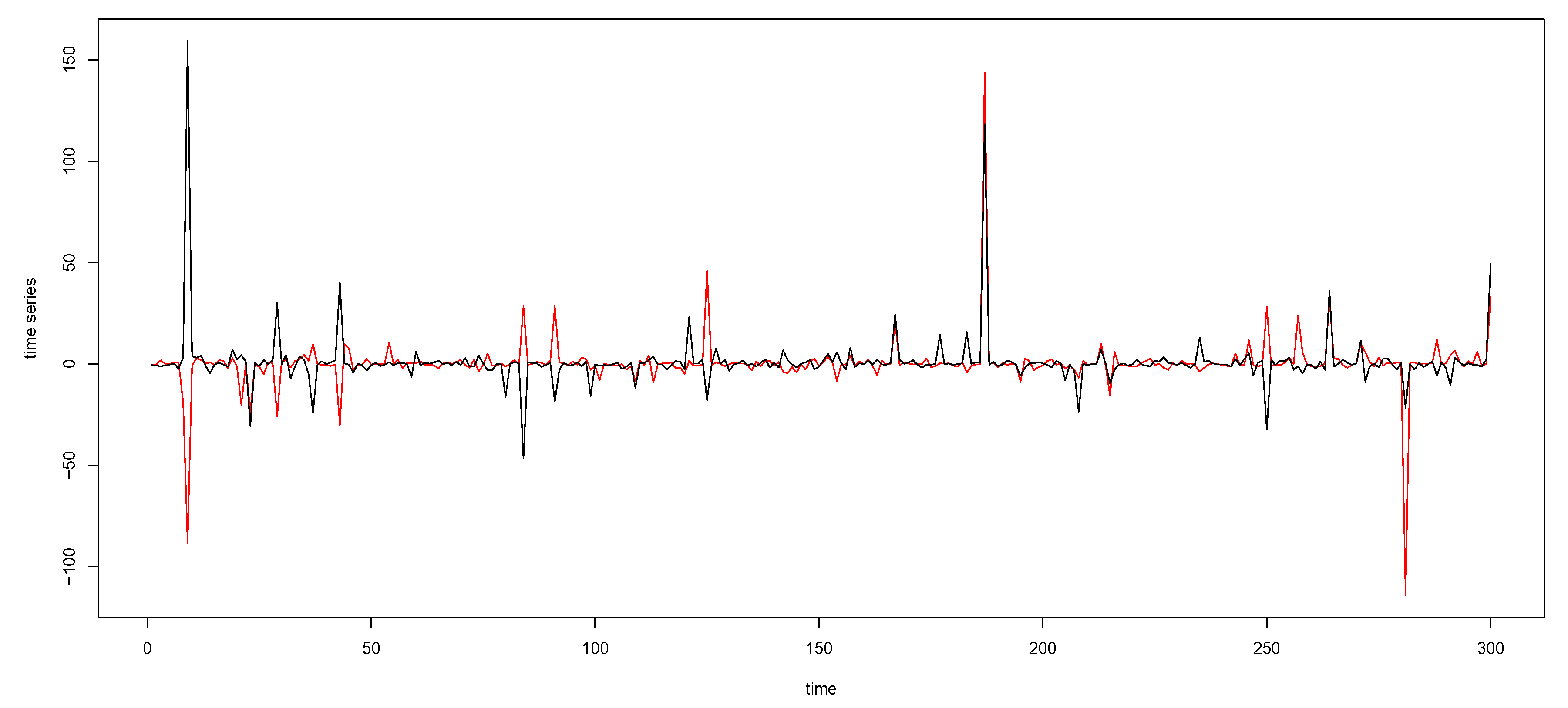
| Maximum Value of Correlations Across Time | |||
|---|---|---|---|
| SW | WGA | DCC | |
| Amygdala vs. Caudate Head | |||
| Amygdala vs. Frontal Medial Cortex | |||
| Amygdala vs. Heschel’s Gyrus | |||
| Amygdala vs. Insula | |||
| Amygdala vs. Subcallosal Cortex | |||
| Caudate Head vs. Frontal Medial Cortex | |||
| Caudate Head vs. Heschel’s Gyrus | |||
| Caudate Head vs. Insula | |||
| Caudate Head vs Subcallosal Cortex | |||
| Frontal Medial Cortex vs. Heschel’s Gyrus | |||
| Frontal Medial Cortex vs. Insula | |||
| Frontal Medial Cortex vs. Subcallosal Cortex | |||
| Heschel’s Gyrus vs. Insula | |||
| Heschel’s Gyrus vs. Subcallosal Cortex | |||
| Insula versus Subcallosal Cortex | |||
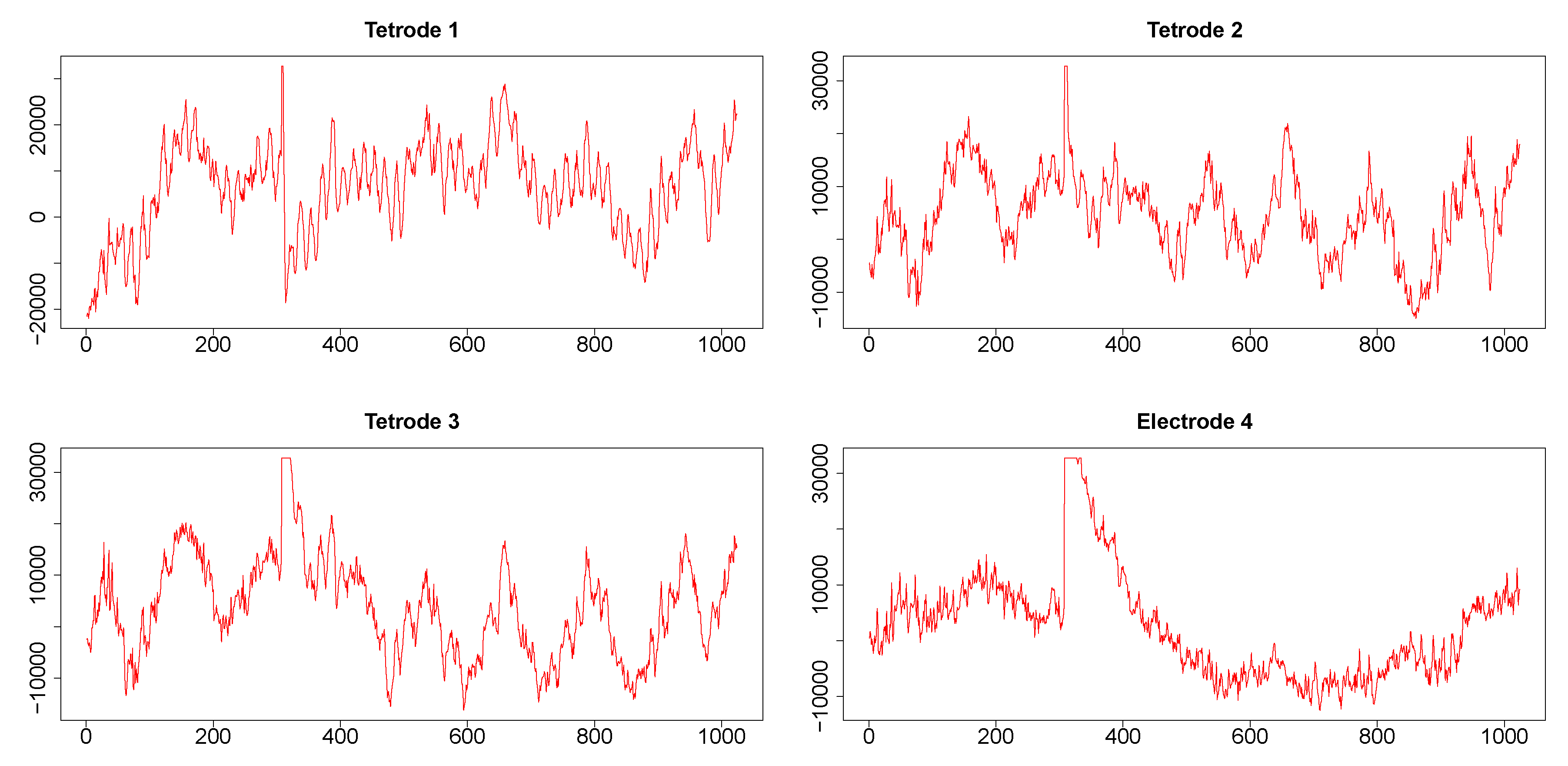
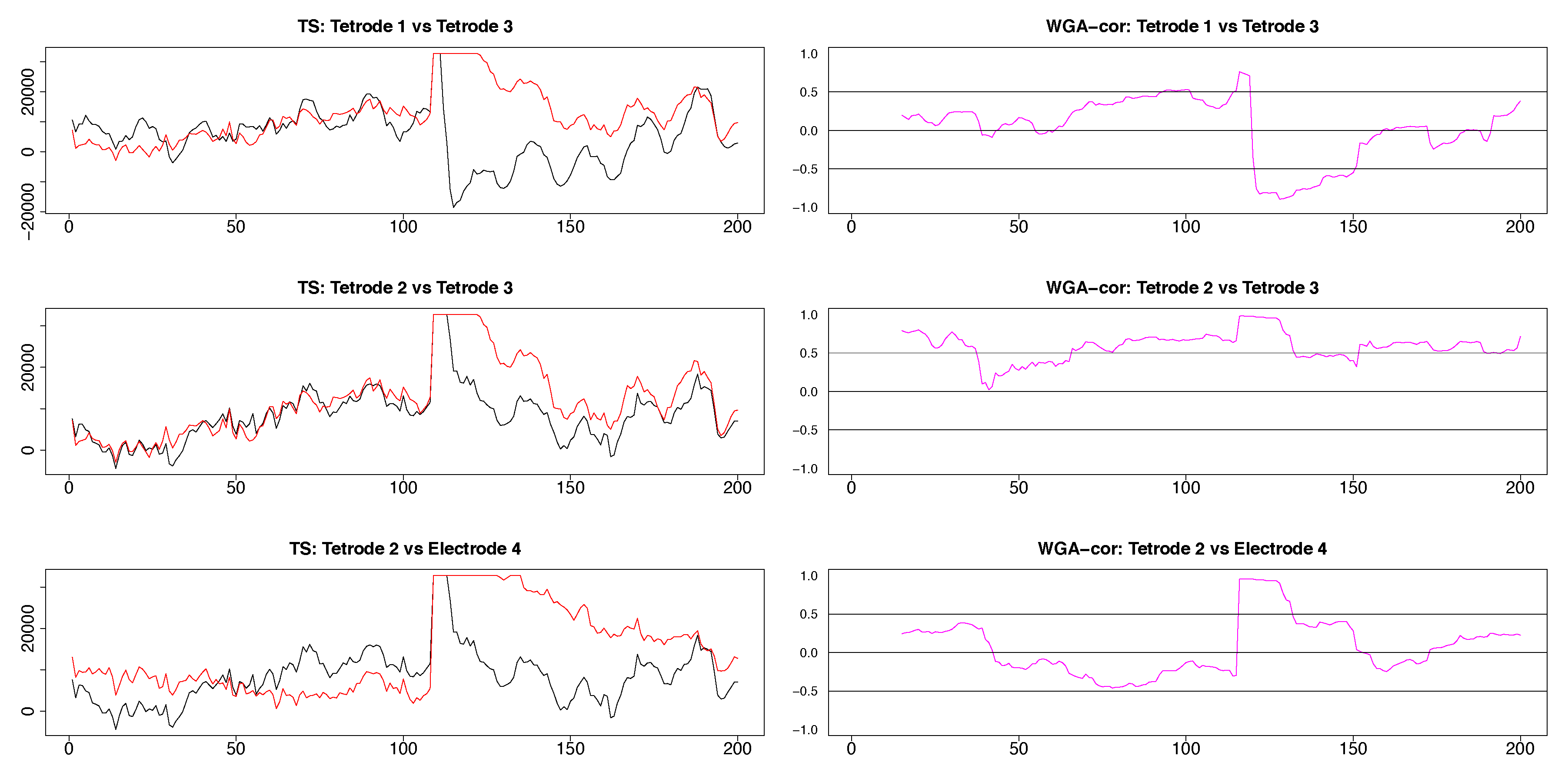
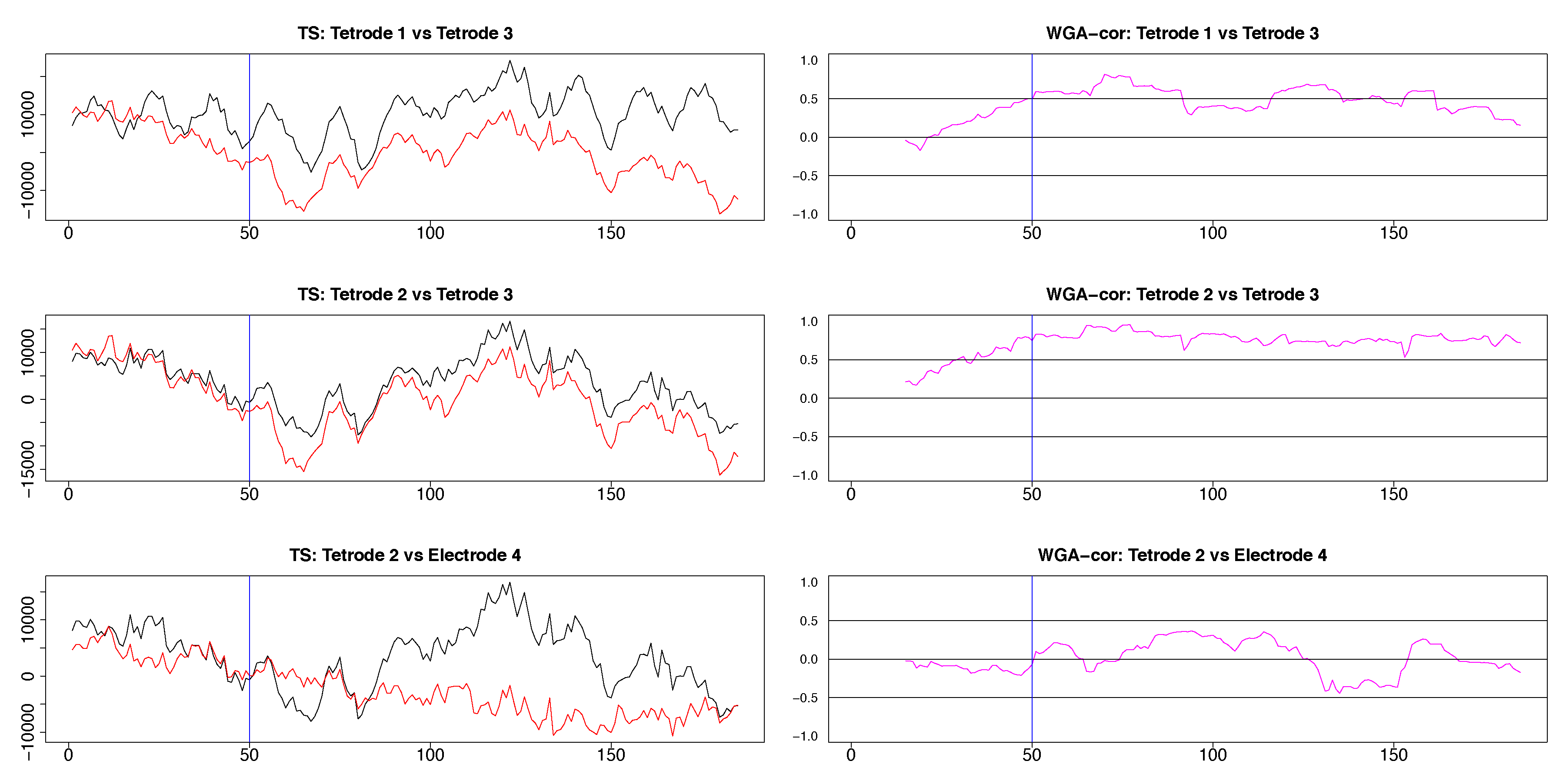
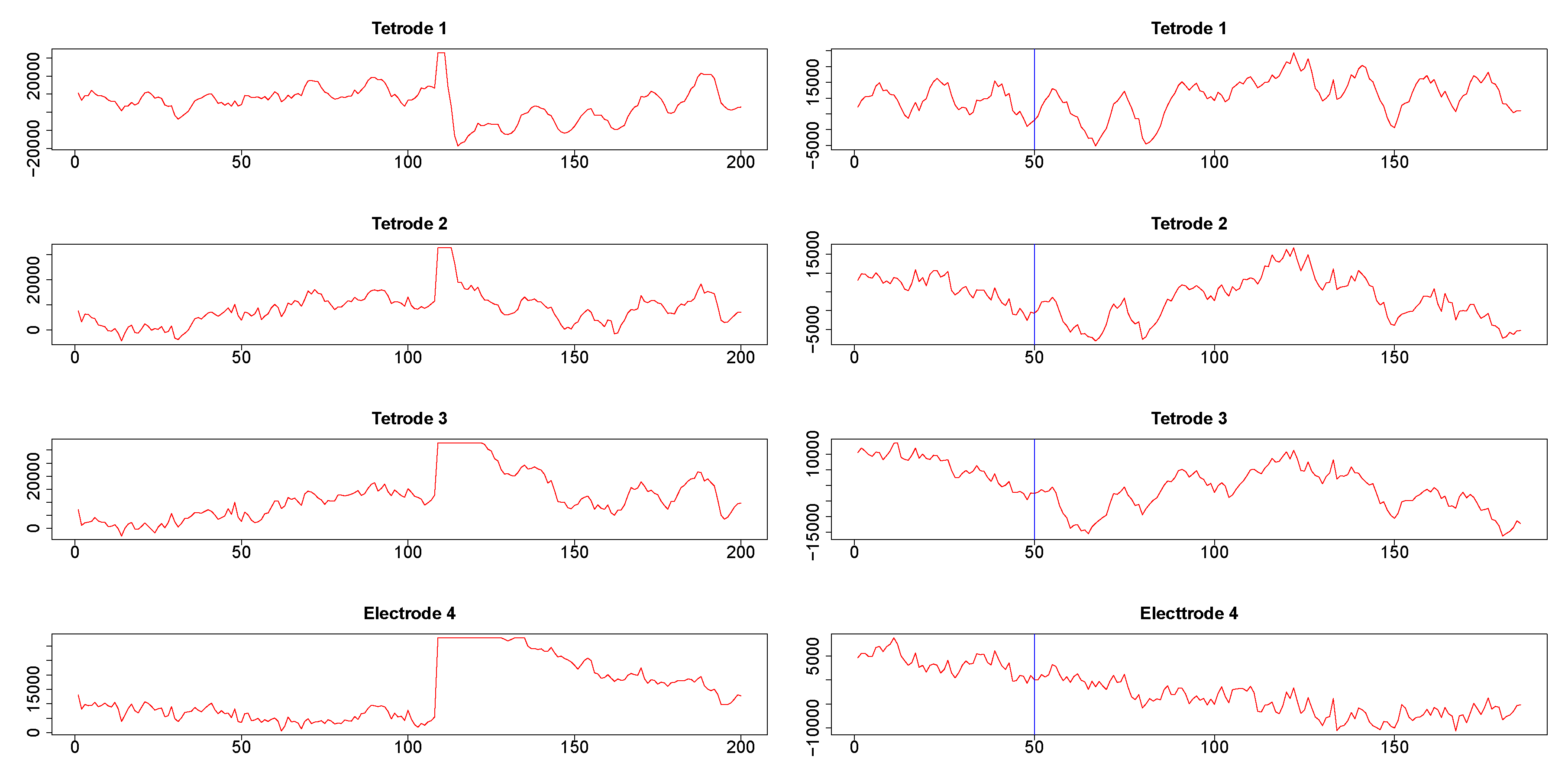
Appendix B. Visibility Criteria
Schematic Diagram
Appendix C. Theoretical Considerations
Appendix C.1. Heuristic Justification
Appendix C.2. A Theoretical Framework
References
- Allen, E.A.; Damaraju, E.; Plis, S.M.; Erhardt, E.B.; Eichele, T.; Calhoun, V.D. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex. Available online: http://dx.doi.org/10.1093/cercor/bhs352 (accessed on 1 August 2017). [CrossRef] [PubMed]
- Chang, C.; Glover, G.H. Time—frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 2010, 50, 81–98. [Google Scholar] [CrossRef] [PubMed]
- Cribben, I.; Haraldsdottir, R.; Atlas, L.Y.; Wager, T.D.; Lindquist, M.A. Dynamic connectivity regression: Determining state-related changes in brain connectivity. Neuroimage 2012, 61, 907–920. [Google Scholar] [CrossRef] [PubMed]
- Handwerker, D.A.; Roopchansingh, V.; Gonzalez-Castillo, J.; Bandettini, P.A. Periodic changes in fMRI connectivity. Neuroimage 2012, 63, 1712–1719. [Google Scholar] [CrossRef]
- Hutchison, R.M.; Womelsdorf, T.; Allen, E.A.; Bandettini, P.A.; Calhoun, V.D.; Corbetta, M.; Penna, S.D.; Duyn, J.; Glover, G.; Gonzalez-Castillo, J.; et al. Dynamic functional connectivity: Promises, issues, and interpretations. NeuroImage 2013, 80, 360–378. [Google Scholar] [CrossRef]
- Jones, D.T.; Vemuri, P.; Murphy, M.C.; Gunter, J.L.; Senjem, M.L.; Machulda, M.M.; Przybelski, S.A.; Gregg, B.E.; Kantarci, K.; Knopman, D.S.; et al. Non-stationarity in the “resting brain’s” modular architecture. PLoS ONE 2012, 7, e39731. [Google Scholar] [CrossRef]
- Kiviniemi, V.; Vire, T.; Remes, J.; Elseoud, A.A.; Starck, T.; Tervonen, O.; Nikkinen, J. A sliding time-window ICA reveals spatial variability of the default mode network in time. Brain Connect. 2011, 1, 339–347. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Engle, R.F.; Sheppard, K. Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate Garch; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2001. [Google Scholar]
- Lindquist, M.A.; Xu, Y.; Nebel, M.B.; Caffo, B.S. Evaluating dynamic bivariate correlations in resting-state fMRI: A comparison study and a new approach. NeuroImage 2014, 101, 531–546. [Google Scholar] [CrossRef]
- Engle, R.F. Anticipating Correlations; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econ. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Francq, C.; Zakoian, J.-M. GARCH Models: Structure, Statistical Inference and Financial Applications; Wiley: Hoboken, NJ, USA, 2010; ISBN 978-0-470-68391-0. [Google Scholar]
- Purdon, P.L.; Solo, V.; Weisskoff, R.M.; Brown, E.N. Locally regularized spatiotemporalmodeling and model comparison for functional MRI. Neuroimage 2001, 14, 912–923. [Google Scholar] [CrossRef] [PubMed]
- Supriya, S.; Siuly, S.; Wang, H.; Cao., J.; Zhang, Y. Weighted visibility graph with complex network features in the detection of epilepsy. IEEE Access. 2016, 4, 6554–6566. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibilty graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Small, M. Complex network from pseudoperiodic time series: Topology versus dynamics. Phys. Rev. Lett. 2006, 96, 238701. [Google Scholar] [CrossRef] [PubMed]
- Wuertz, D.; Setz, T.; Chalabi, Y. fMultivar: Rmetrics-Analysing and Modeling Multivariate Financial Return Distributions. Available online: https://CRAN.R-project.org/package=fMultivar (accessed on 1 August 2017).
- Stroop, J.R. Studies of interference in serial verbal reactions. Available online: https://psycnet.apa.org/record/1936-01863-001 (accessed on 1 August 2017).
- Verstynen, T.D. The organization and dynamics of corticostriatal pathways link the medial orbitofrontal cortex to future behavioral responses. J. Neurophysiol. 2014, 112, 2457–2469. [Google Scholar] [CrossRef][Green Version]
- Legatt, A.D.; Arezzo, J.; Vaughan, H.G., Jr. Averaged multiple unit activity as an estimate of phasic changes in local neuronal activity: Effects of volume-conducted potentials. J. Neurosci. Methods 1980, 2, 203–217. [Google Scholar] [CrossRef]
- Gray, C.M.; Maldonado, P.E.; Wilson, M.; McNaughton, B. Tetrodes markedly improve the reliability and yield of multiple single-unit isolation from multi-unit recordings in cat striate cortex. J. Neurosci. Methods 1995, 63, 43–54. [Google Scholar] [CrossRef]
- Kiparizoska, S.; Ikuta, T. Disrupted Olfactory Integration in Schizophrenia: Functional Connectivity Study. Int. J. Neuropsychopharmacol. 2017, 20, 740–746. [Google Scholar] [CrossRef]
- Palaniyappan, L.; Liddle, P.F. Does the salience network play a cardinal role in psychosis? An emerging hypothesis of insular dysfunction. J. Psychiatry Neurosci. 2012, 37, 17–27. [Google Scholar] [CrossRef]
- Pang, L.; Kennedy, D.; Wei, Q.; Lv, L.; Gao, J.; Li, H.; Quan, M.; Li, X.; Yang, Y.; Fan, X.; et al. Decreased Functional Connectivity of Insular Cortex in Drug Naïve First Episode Schizophrenia: In Relation to Symptom Severity. PLoS ONE 2017, 12, e0167242. [Google Scholar] [CrossRef]
- Leitman, D.I.; Hoptman, M.J.; Foxe, J.J.; Saccente, E.; Wylie, G.R.; Nierenberg, J.; Jalbrzikowski, M.; Lim, K.O.; Javitt, D.C. The neural substrates of impaired prosodic detection in schizophrenia and its sensorial antecedents. Am. J. Psychiatry 2007, 164, 474–482. [Google Scholar] [CrossRef] [PubMed]
- Jentsch, C.; Politis, D.N. Covariance matrix estimation and linear process bootstrap for multivariate time series of possibly increasing dimension. Ann. Stat. 2015, 43, 1117–1140. [Google Scholar] [CrossRef]
- Kudela, M.; Harezlak, J.; Lindquist, M.A. Assessing uncertainty in dynamic functional connectivity. NeuroImage 2017, 149, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Hindriks, R.; Adhikari, M.H.; Murayama, Y.; Ganzetti, M.; Mantini, D.; Logothetis, N.K.; Deco, G. Can sliding-window correlations reveal dynamic functional connectivity in resting-state fMRI? NeuroImage 2016, 127, 242–256. [Google Scholar] [CrossRef]
- Zalesky, A.; Fornito, A.; Cocchi, L.; Gollo, L.L.; Breakspear, M. Time-resolved resting-state brain networks. Proc. Natl. Acad. Sci. USA 2014, 111, 10341–10346. [Google Scholar] [CrossRef]
- Pawitan, Y. All Likelihood, 1 ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Lee, N.; Kim, J.-M. Dynamic functional connectivity analysis of resting-state fMRI based on copula time-varying correlation. J. Neurosci. Methods 2019, 323, 32–47. [Google Scholar] [CrossRef]
- Sklar, A. Random variables, joint distribution functions, and copulas. Kybernetika 1973, 9, 449–460. [Google Scholar]
- Lacasa, L.; Nicosia, V.; Latora, V. Network structure of multivariate time series. Sci. Rep. 2015, 5, 15508. [Google Scholar] [CrossRef]
- Sannino, S.; Stramaglia, S.; Lacasa, L.; Marinazzo, D. Multiplex temporal graphs and their modulations across resting-state networks. Network Neurosci. 2017, 1, 208–221. [Google Scholar] [CrossRef]
- Sanchez-Romero, R.; Cole, M.W. Combining Multiple Functional Connectivity Methods to Improve Causal Inferences. Available online: https://www.biorxiv.org/content/10.1101/841890v1.abstract (accessed on 25 May 2020).
- Reid, A.T.; Headley, D.B.; Mill, R.D.; Sanchez-Romero, R.; Uddin, L.Q.; Marinazzo, D.; Lurie, D.J.; Valdés-Sosa, P.A.; Hanson, S.J.; Biswal, B.B.; et al. Advancing functional connectivity research from association to causation. Nat. Neurosci. 2019, 1–10. [Google Scholar] [CrossRef]
- Nunez, A.; Lacasa, L.; Luque, B. Visibility Algorithms: A Short Review. Graph Theory (Edited by Intech). Available online: https://www.researchgate.net/publication/221926613_Visibility_Algorithms_A_Short_Review (accessed on 1 August 2017).
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
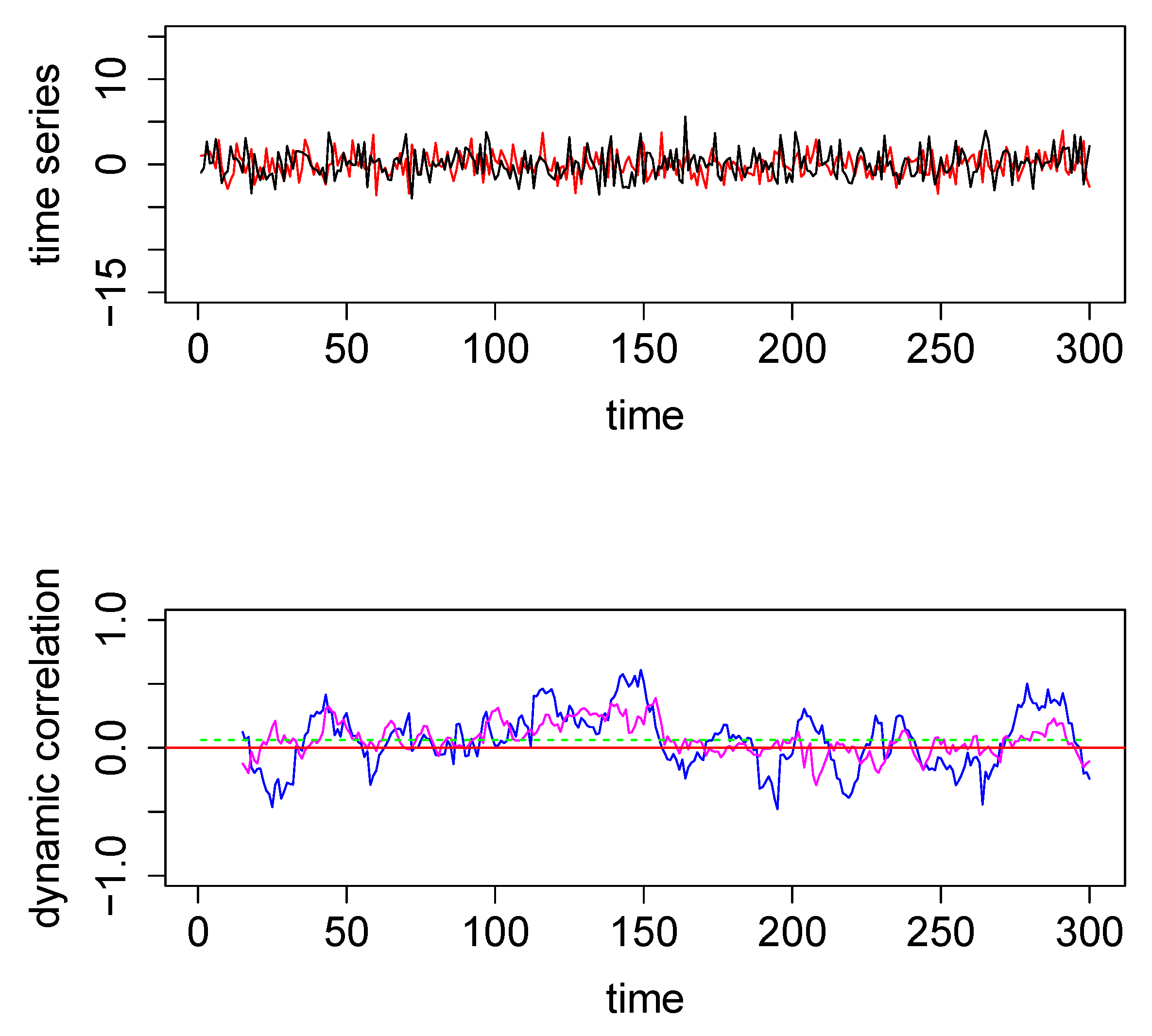
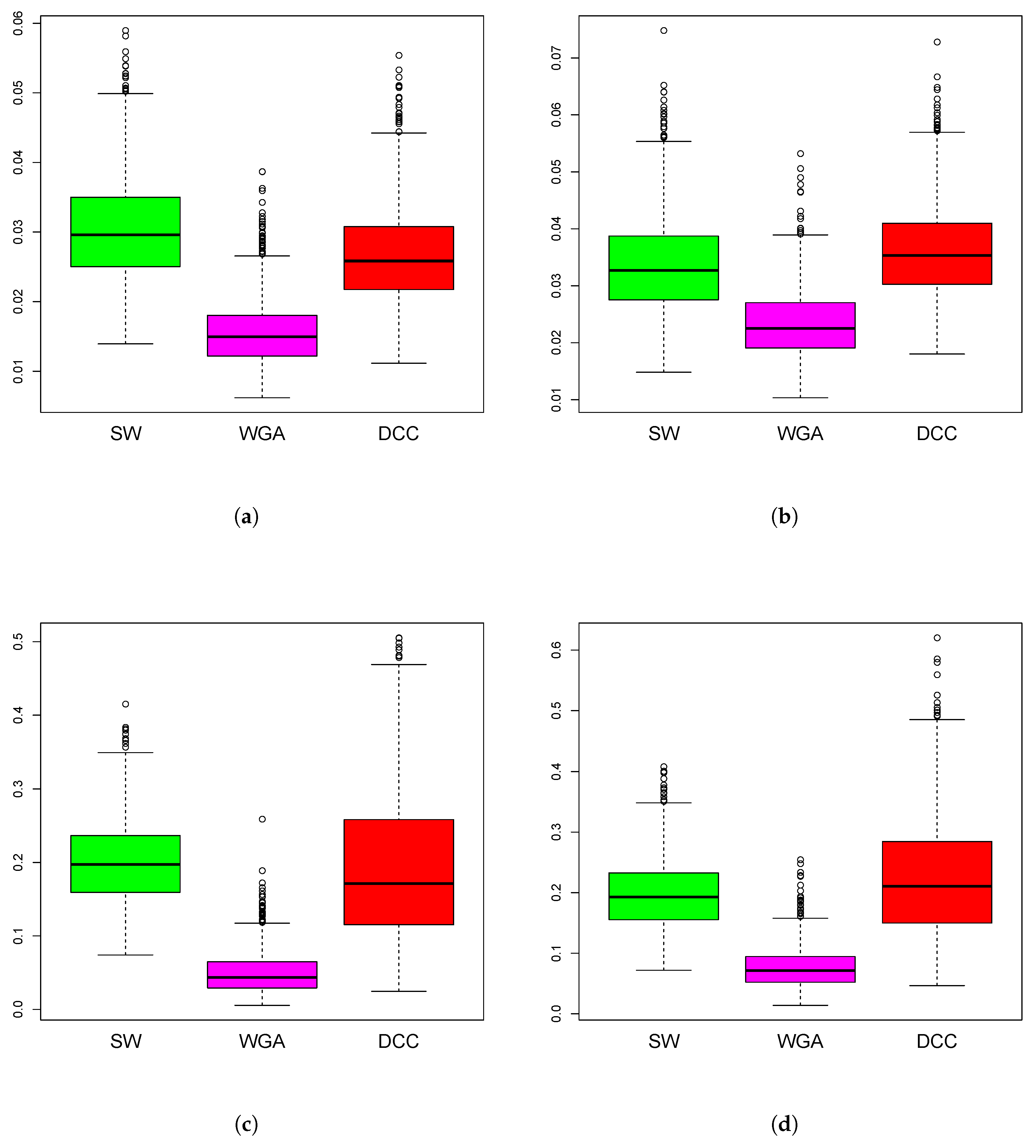
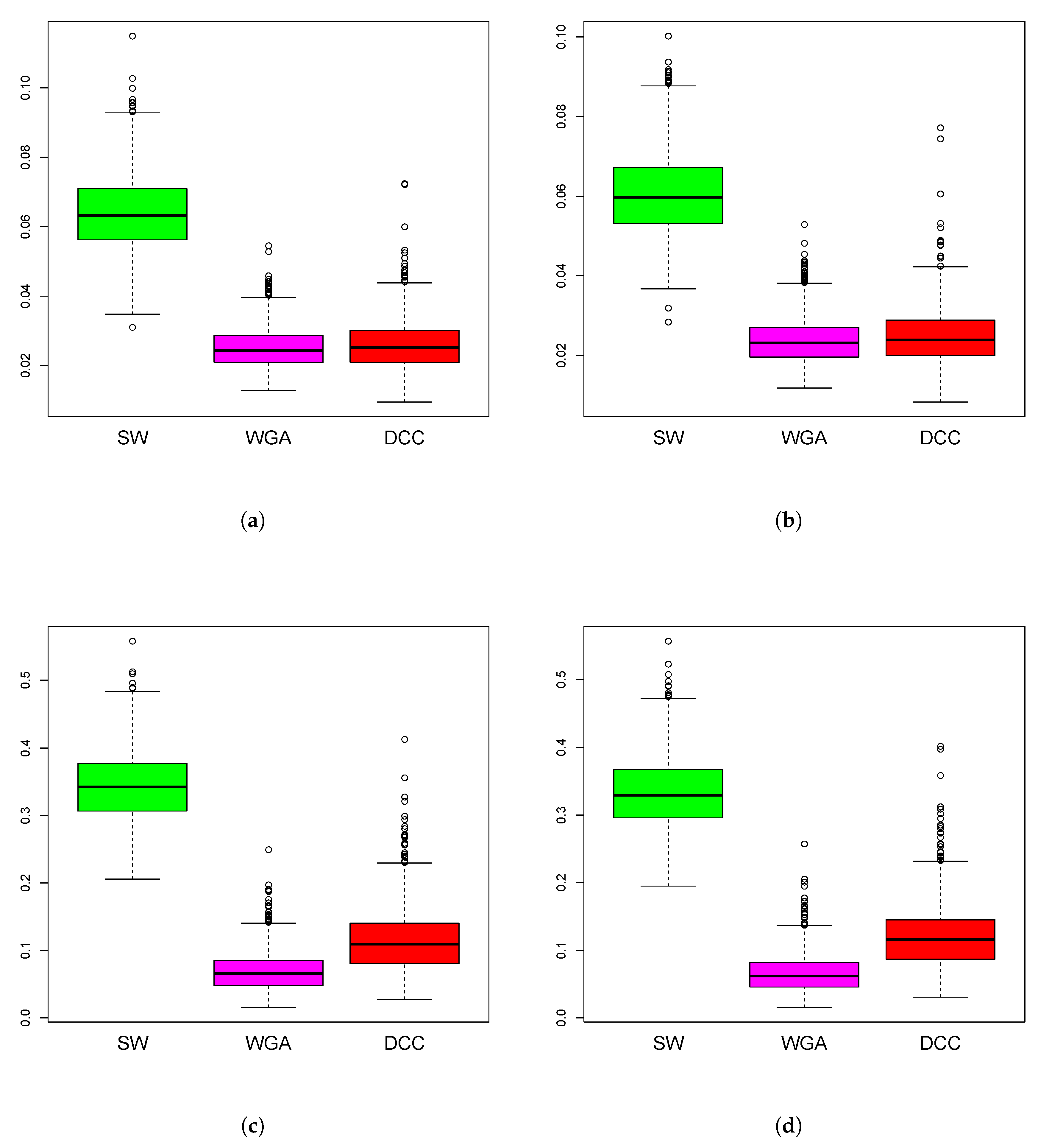
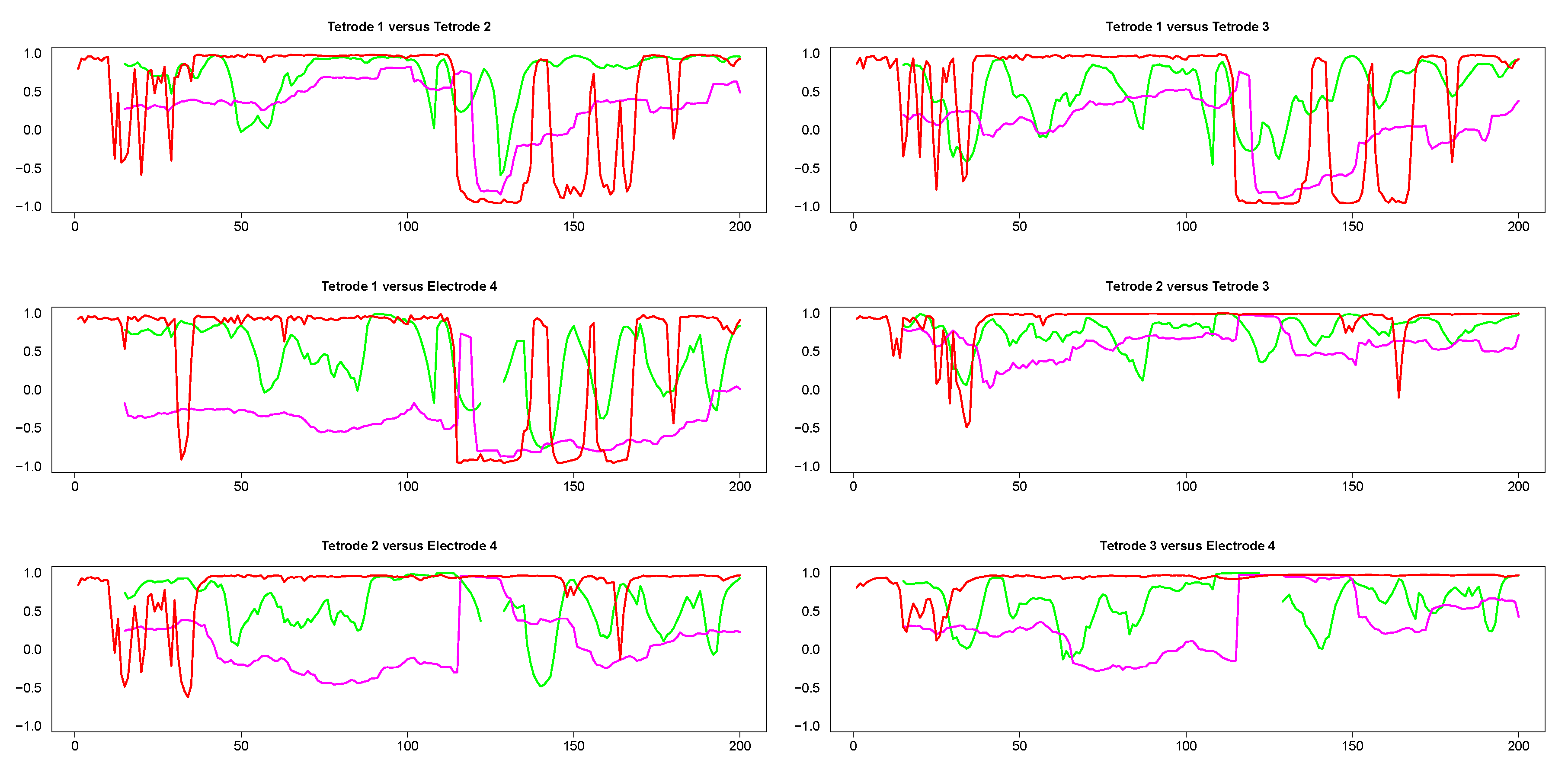
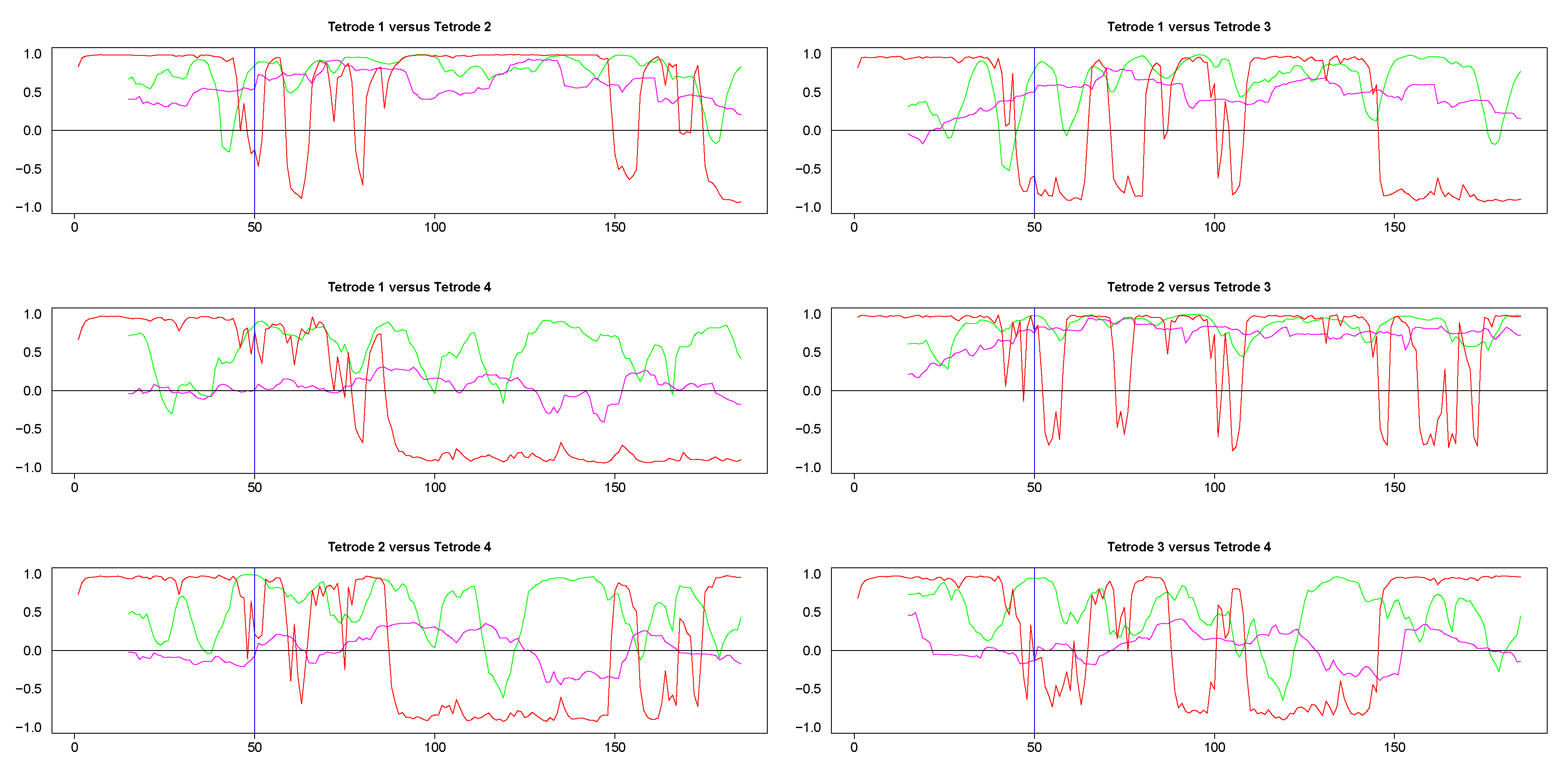
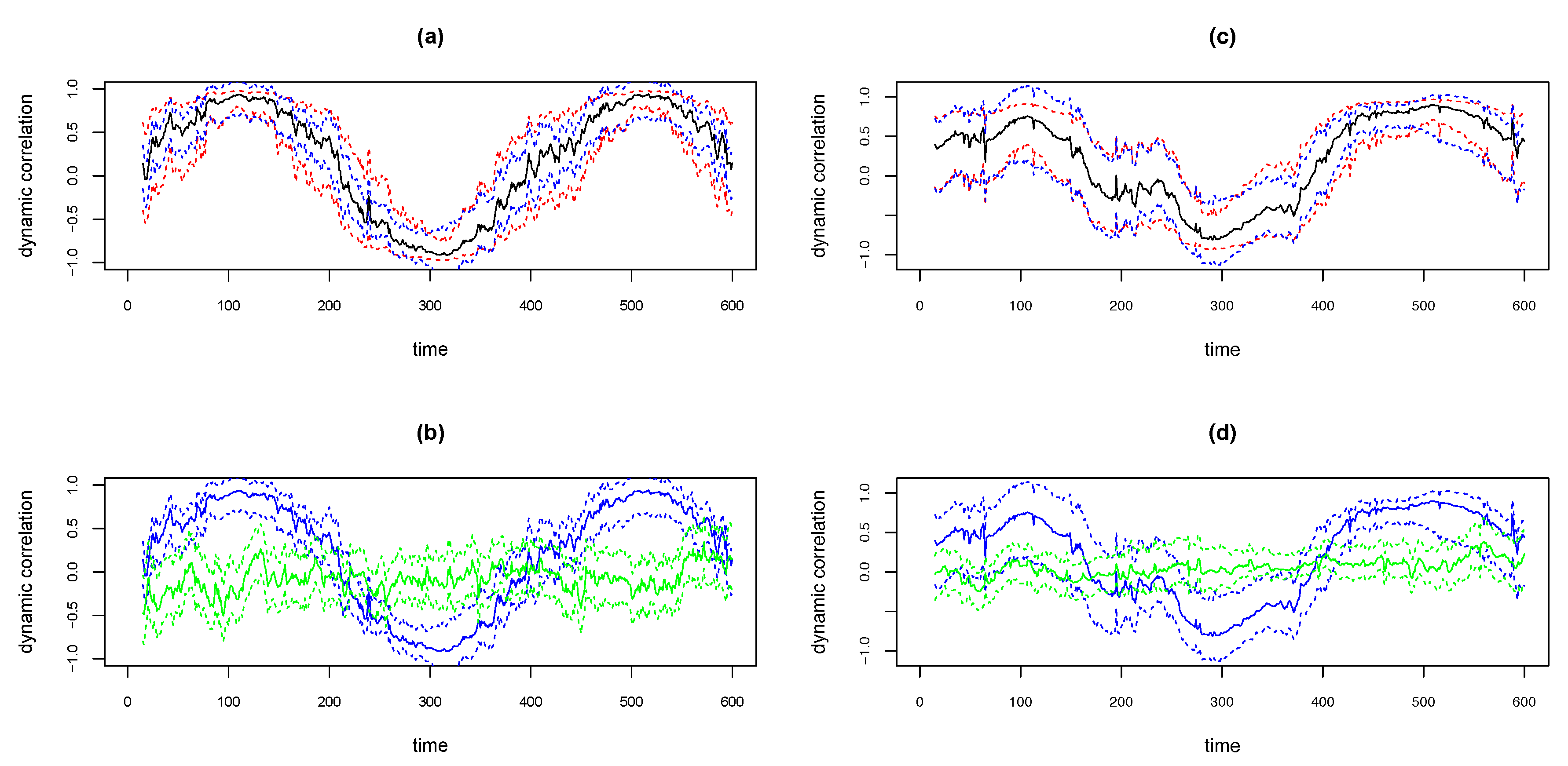
| Mean of Absolute Value of Correlations Across Time | ||||
|---|---|---|---|---|
| T = 150 | T = 300 | T = 600 | T = 1000 | |
| SW | ||||
| WGA | ||||
| DCC | ||||
| Maximum of Absolute Value of Correlations Across Time | ||||
| T = 150 | T = 300 | T = 600 | T = 1000 | |
| SW | ||||
| WGA | ||||
| DCC | ||||
| Mean of Absolute Value of Correlations Across Time | ||||
|---|---|---|---|---|
| T = 150 | T = 300 | T = 600 | T = 1000 | |
| SW | ||||
| WGA | ||||
| DCC | ||||
| Maximum of Absolute Value of Correlations Across Time | ||||
| T = 150 | T = 300 | T = 600 | T = 1000 | |
| SW | ||||
| WGA | ||||
| DCC | ||||
| Mean Value of Correlations Across Time | |||
|---|---|---|---|
| SW | WGA | DCC | |
| Amygdala vs. Caudate Head | |||
| Amygdala vs. Frontal Medial Cortex | |||
| Amygdala vs. Heschel’s Gyrus | |||
| Amygdala vs. Insula | |||
| Amygdala vs. Subcallosal Cortex | |||
| Caudate Head vs. Frontal Medial Cortex | |||
| Caudate Head vs. Heschel’s Gyrus | |||
| Caudate Head vs. Insula | |||
| Caudate Head vs Subcallosal Cortex | |||
| Frontal Medial Cortex vs. Heschel’s Gyrus | |||
| Frontal Medial Cortex vs. Insula | |||
| Frontal Medial Cortex vs. Subcallosal Cortex | |||
| Heschel’s Gyrus vs. Insula | |||
| Heschel’s Gyrus vs. Subcallosal Cortex | |||
| Insula versus Subcallosal Cortex | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
John, M.; Wu, Y.; Narayan, M.; John, A.; Ikuta, T.; Ferbinteanu, J. Estimation of Dynamic Bivariate Correlation Using a Weighted Graph Algorithm. Entropy 2020, 22, 617. https://doi.org/10.3390/e22060617
John M, Wu Y, Narayan M, John A, Ikuta T, Ferbinteanu J. Estimation of Dynamic Bivariate Correlation Using a Weighted Graph Algorithm. Entropy. 2020; 22(6):617. https://doi.org/10.3390/e22060617
Chicago/Turabian StyleJohn, Majnu, Yihren Wu, Manjari Narayan, Aparna John, Toshikazu Ikuta, and Janina Ferbinteanu. 2020. "Estimation of Dynamic Bivariate Correlation Using a Weighted Graph Algorithm" Entropy 22, no. 6: 617. https://doi.org/10.3390/e22060617
APA StyleJohn, M., Wu, Y., Narayan, M., John, A., Ikuta, T., & Ferbinteanu, J. (2020). Estimation of Dynamic Bivariate Correlation Using a Weighted Graph Algorithm. Entropy, 22(6), 617. https://doi.org/10.3390/e22060617






