Path Integral Approach to Nondispersive Optical Fiber Communication Channel
Abstract
1. Introduction
2. Channel Models
2.1. Per-Sample Model
2.2. Extended Model
3. Channel Capacity and Its Bound
3.1. Per-Sample Model
3.1.1. Conditional Probability Density Function
3.1.2. Probability Density Function
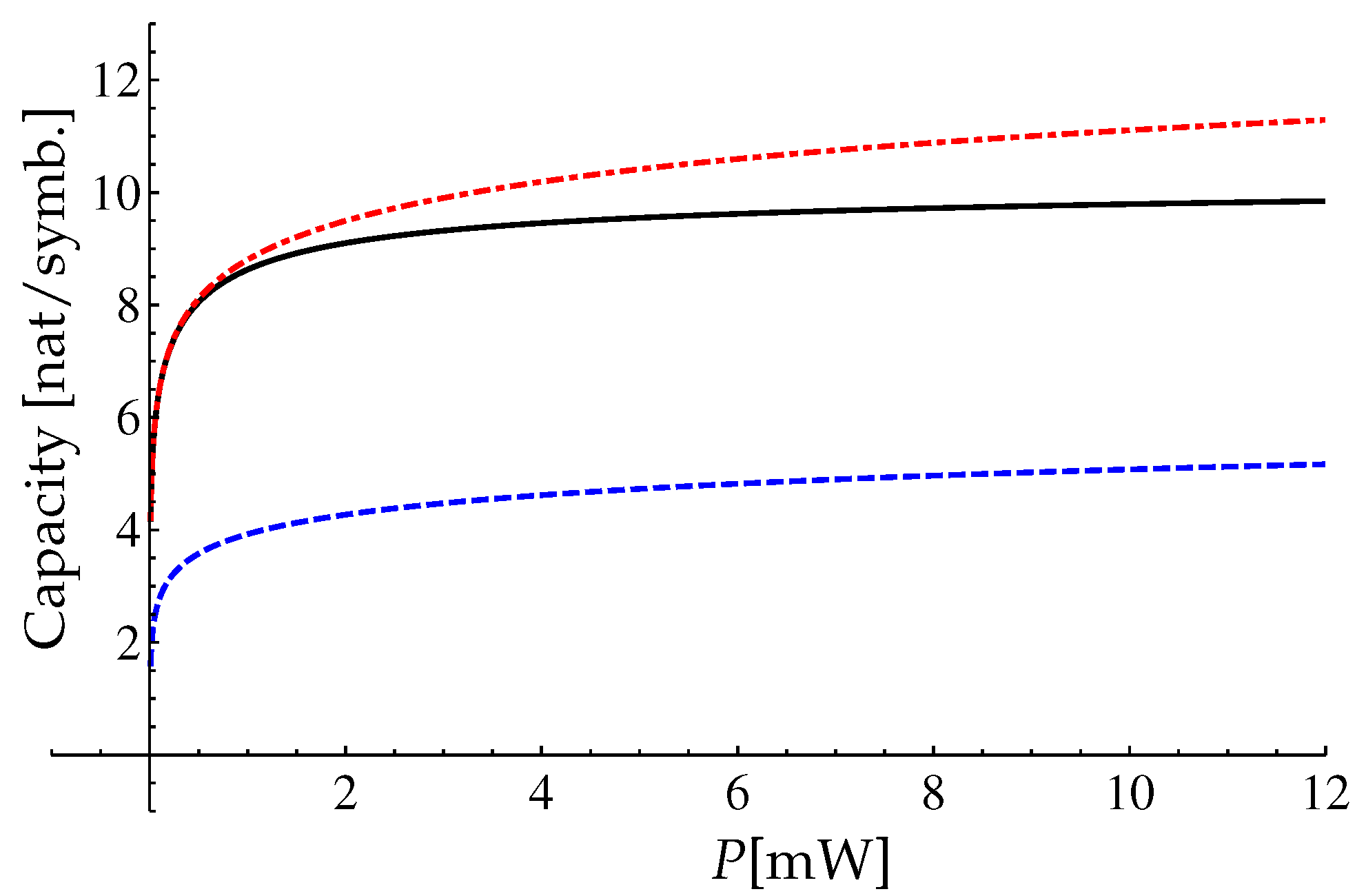
3.1.3. Lower Bound for the Channel Capacity
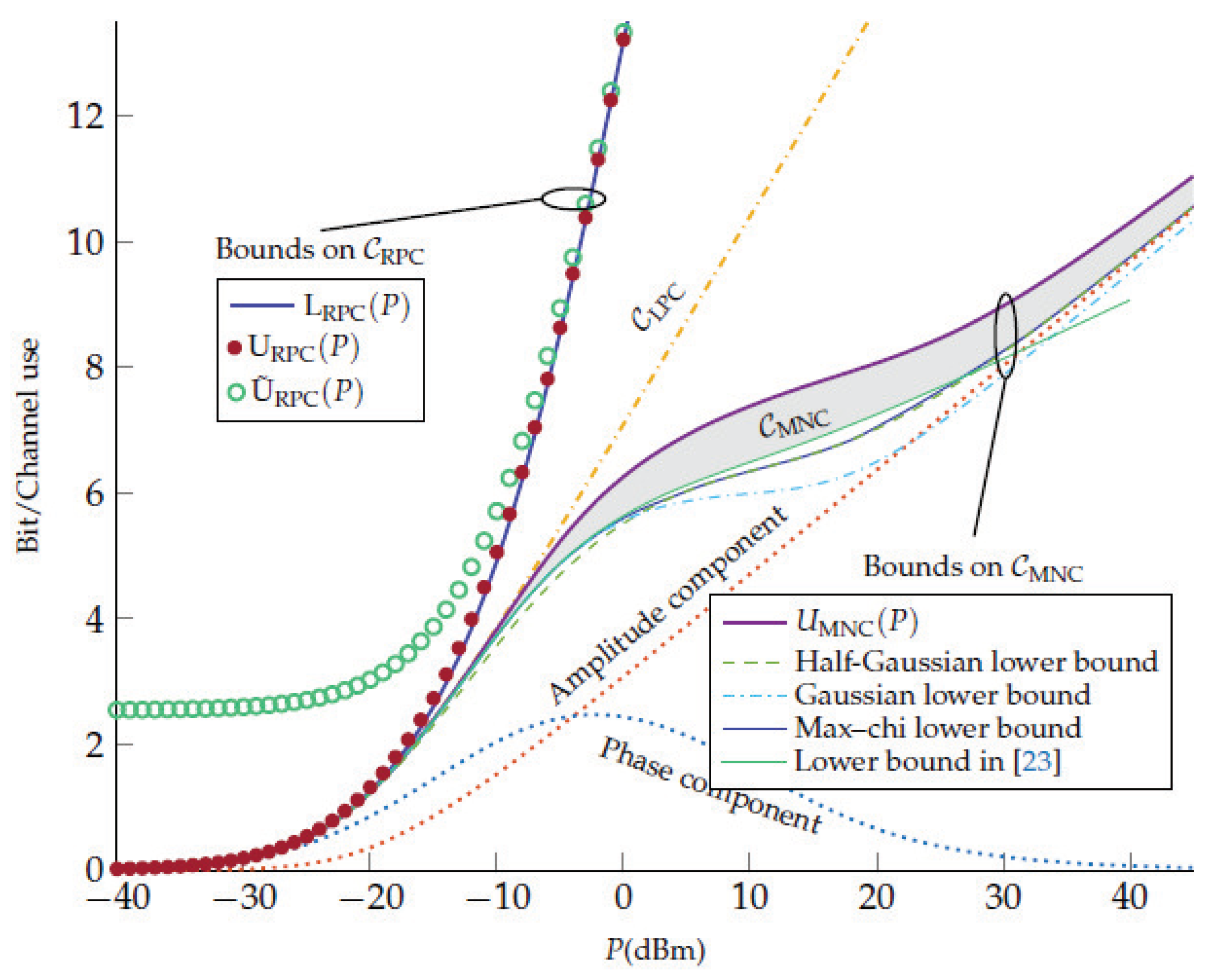
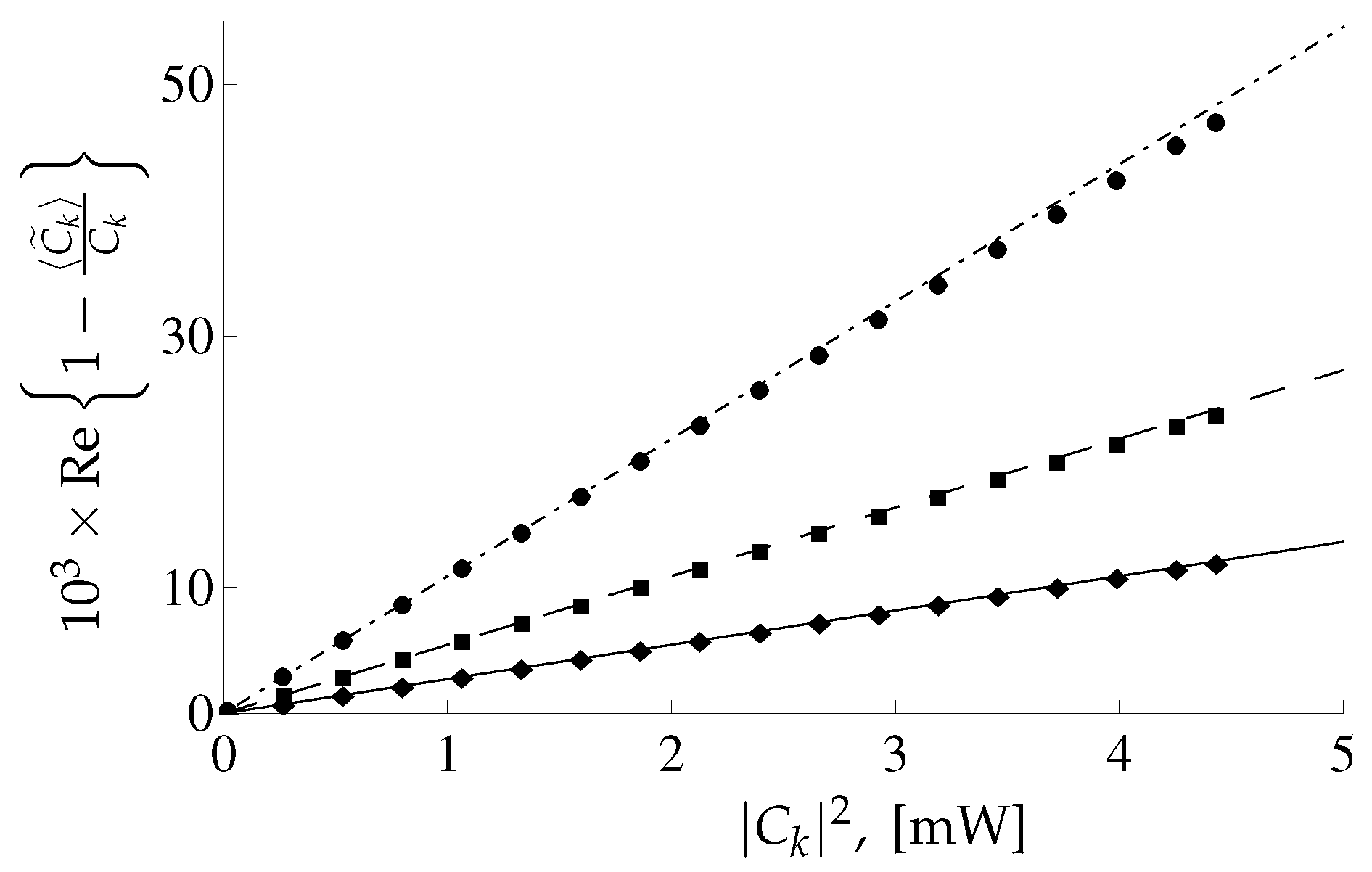
3.2. Extended Model: Considerations of the Time Dependent Input Signals
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Probability density function | |
| NLSE | Nonlinear Schrödinger equation |
| SNR | Signal-to-noise power ratio |
| MNC | Memoryless nonlinear Schrödinger channel |
| RPC | Regular perturbative channel |
| LPC | Logarithmic perturbative channel |
References
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423; 623–656. [Google Scholar] [CrossRef]
- Ilyas, M.; Mouftah, H.T. The Handbook of Optical Communication Networks; CRC Press LLC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Haus, H.A. Quantum noise in a solitonlike repeater system. J. Opt. Soc. Am. B 1991, 8, 1122–1126. [Google Scholar] [CrossRef]
- Mecozzi, A. Limits to long-haul coherent transmission set by the Kerr nonlinearity and noise of the in-line amplifiers. J. Light. Technol. 1994, 12, 1993–2000. [Google Scholar] [CrossRef]
- Iannoe, E.; Matera, F.; Mecozzi, A.; Settembre, M. Nonlinear Optical Communication Networks; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Soviet J. Exp. Theory Phys. 1972, 34, 62–69. [Google Scholar]
- Novikov, S.; Manakov, S.V.; Pitaevskii, L.P.; Zakharov, V.E. Theory of Solitons: The Inverse Scattering Method (Monographs in Contemporary Mathematics); Springer: Rumford, ME, USA, 1984. [Google Scholar]
- Essiambre, R.-J.; Foschini, G.J.; Kramer, G.; Winzer, P.J. Capacity Limits of Information Transport in Fiber-Optic Networks. Phys. Rev. Lett. 2008, 101, 163901. [Google Scholar] [CrossRef]
- Essiambre, R.-J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. J. Light. Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Sorokina, M.A.; Turitsyn, S.K. Regeneration limit of classical Shannon capacity. Nat. Commun. 2014, 5, 3861. [Google Scholar] [CrossRef]
- Terekhov, I.S.; Vergeles, S.S.; Turitsyn, S.K. Conditional Probability Calculations for the Nonlinear Schrödinger Equation with Additive Noise. Phys. Rev. Lett. 2014, 113, 230602. [Google Scholar] [CrossRef]
- Liga, G.; Xu, T.; Alvarado, A.; Killey, R.I.; Bayvel, P. On the performance of multichannel digital backpropagation in high-capacity long-haul optical transmission. Opt. Express 2014, 22, 30053–30062. [Google Scholar] [CrossRef]
- Semrau, D.; Xu, T.; Shevchenko, N.; Paskov, M.; Alvarado, A.; Killey, R.; Bayvel, P. Achievable information rates estimates in optically amplified transmission systems using nonlinearity compensation and probabilistic shaping. Opt. Lett. 2017, 42, 121–124. [Google Scholar] [CrossRef]
- Kramer, G. Autocorrelation Function for Dispersion-Free Fiber Channels with Distributed Amplification. IEEE Tran. Inf. Theory 2018, 64, 5131–5155. [Google Scholar] [CrossRef]
- Tang, J. The Shannon channel capacity of dispersion-free nonlinear optical fiber transmission. J. Light. Technol. 2001, 19, 1104–1109. [Google Scholar] [CrossRef]
- Tang, J. The multispan effects of Kerr nonlinearity and amplifier noises on Shannon channel capacity of a dispersion-free nonlinear optical fiber. J. Light. Technol. 2001, 19, 1110–1115. [Google Scholar] [CrossRef]
- Turitsyn, K.S.; Derevyanko, S.A.; Yurkevich, I.V.; Turitsyn, S.K. Information Capacity of Optical Fiber Channels with Zero Average Dispersion. Phys. Rev. Lett. 2003, 91, 203901. [Google Scholar] [CrossRef]
- Yousefi, M.I.; Kschischang, F.R. On the Per-Sample Capacity of Nondispersive Optical Fibers. IEEE Trans. Inf. Theory 2011, 57, 7522–7541. [Google Scholar] [CrossRef]
- Terekhov, I.S.; Reznichenko, A.V.; Kharkov, Y.A.; Turitsyn, S.K. The loglog growth of channel capacity for nondispersive nonlinear optical fiber channel in intermediate power range. Phys. Rev. E 2017, 95, 062133. [Google Scholar] [CrossRef]
- Panarin, A.A.; Reznichenko, A.V.; Terekhov, I.S. Next-to-leading order corrections to capacity for nondispersive nonlinear optical fiber channel in intermediate power region. Phys. Rev. E 2016, 95, 012127. [Google Scholar] [CrossRef]
- Reznichenko, A.V.; Smirnov, S.V.; Chernykh, A.I.; Terekhov, I.S. The loglog growth of channel capacity for nondispersive nonlinear optical fiber channel in intermediate power range. Extension of the model. Phys. Rev. E 2019, 99, 012133. [Google Scholar] [CrossRef]
- Keykhosravi, K.; Durisi, G.; Agrell, E. Accuracy Assessment of Nondispersive Optical Perturbative Models Through Capacity Analysis. Entropy 2019, 21, 760. [Google Scholar] [CrossRef]
- Mitra, P.; Stark, J.B. Nonlinear limits to the information capacity of optical fibre communications. Nature 2001, 411, 1027–1030. [Google Scholar] [CrossRef]
- Hochberg, D.; Molina-Paris, C.; Perez-Mercader, J.; Visser, M. Effective action for stochastic partial differential equations. Phys. Rev. E 1999, 60, 6343–6360. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences; Springer: New York, NY, USA, 1985. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Lavrentiev, M.A.; Shabat, B.V. Method of Complex Function Theory; Nauka: Moscow, Russisa, 1987. [Google Scholar]
- Gradshtein, I.S.; Ryzik, I.M. Table of Integrals and Series, and Products; Academic Press: Orlando, FL, USA, 2014. [Google Scholar]
- Terekhov, I.S.; Reznichenko, A.V.; Turitsyn, S.K. Calculation of mutual information for nonlinear communication channel at large SNR. Phys. Rev. E 2016, 94, 042203. [Google Scholar] [CrossRef]
- Reznichenko, A.V.; Terekhov, I.S. Channel Capacity and Simple Correlators for Nonlinear Communication Channel at Large SNR and Small Dispersion. IEEE Int. Symp. Inf. Theory Proc. 2018, 2018, 186–190. [Google Scholar]
- Reznichenko, A.V.; Terekhov, I.S.; Turitsyn, S.K. Calculation of mutual information for nonlinear optical-fiber communication channel at large SNR within path-integral formalism. J. Phys. Conf. Ser. 2017, 826, 012026. [Google Scholar] [CrossRef]
- Reznichenko, A.V.; Terekhov, I.S. Channel Capacity Calculation at Large SNR and Small Dispersion within Path-Integral Approach. J. Phys. Conf. Ser. 2018, 999, 012016. [Google Scholar] [CrossRef]
- Reznichenko, A.V.; Terekhov, I.S. Investigation of Nonlinear Communication Channel with Small Dispersion via Stochastic Correlator Approach. J. Phys. Conf. Ser. 2019, 1206, 012013. [Google Scholar] [CrossRef]
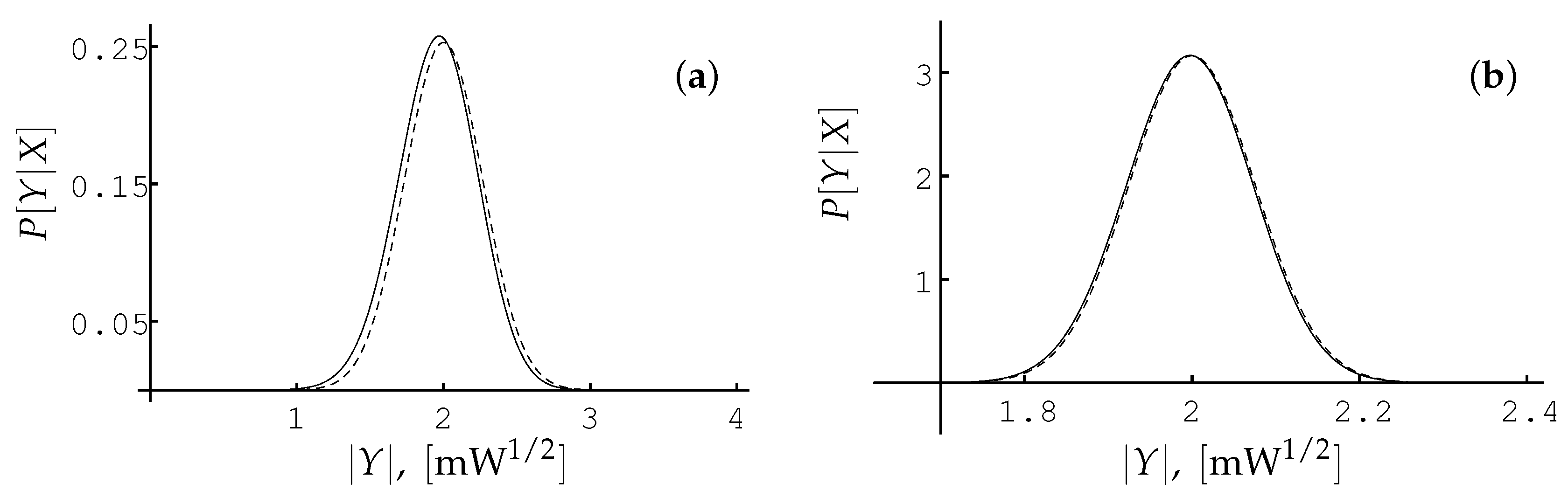
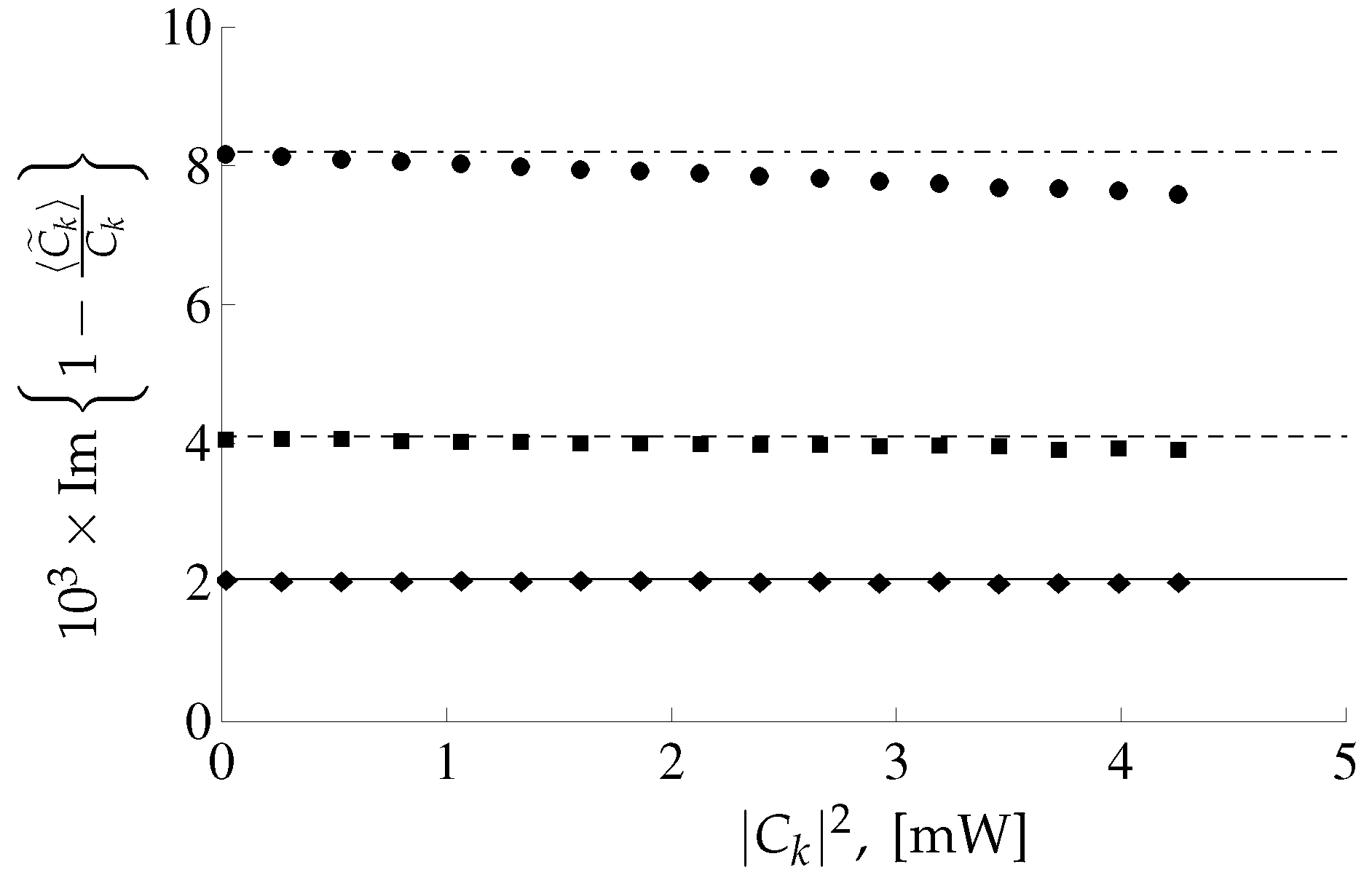
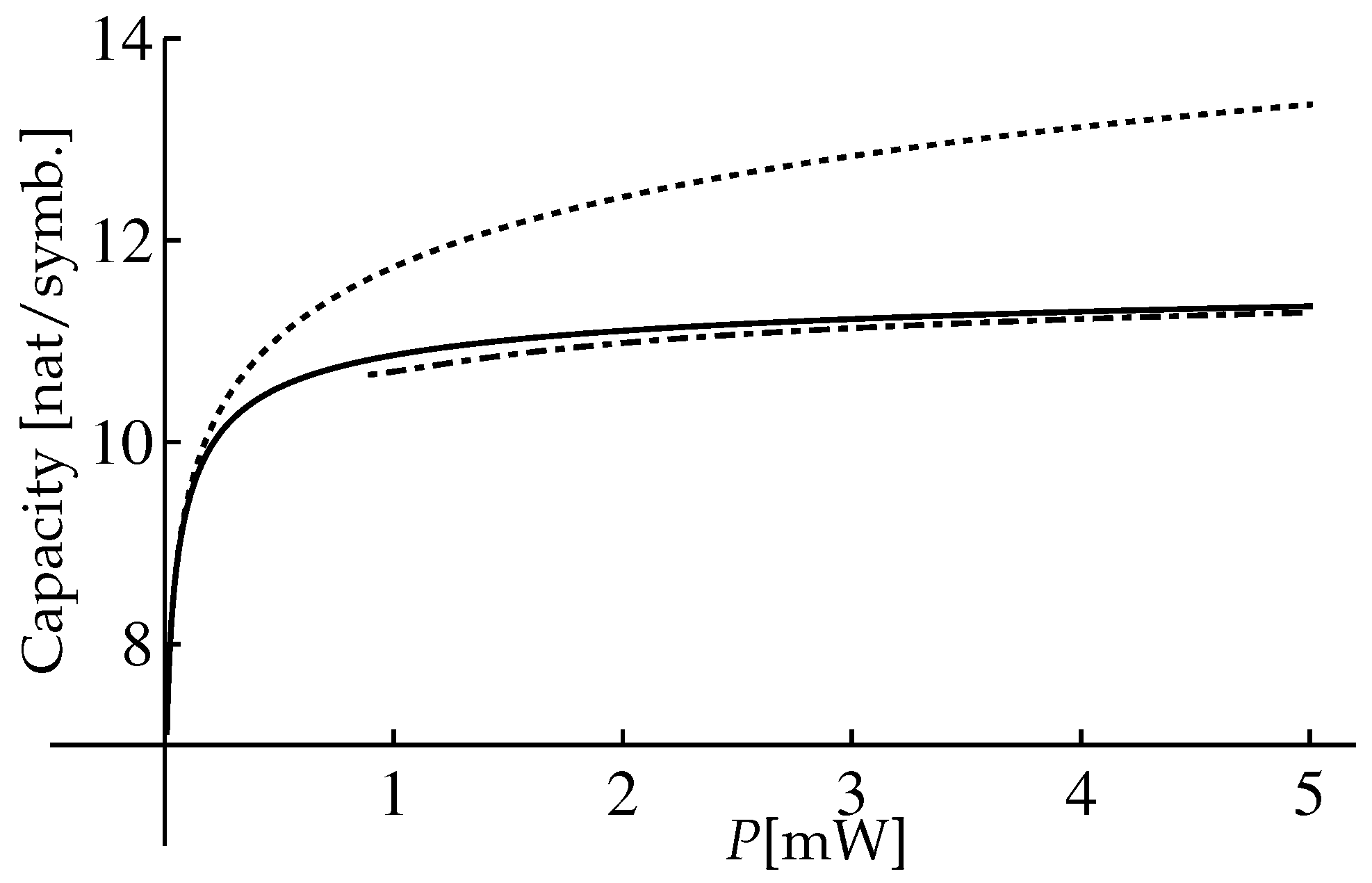
| [(km×mW)] | Q [mW/(km)] | L [km] |
|---|---|---|
| [(km×W)] | [W/(km×Hz)] | L [km] |
|---|---|---|
| 800 |
| [s] | [s] | [s] |
|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reznichenko, A.V.; Terekhov, I.S. Path Integral Approach to Nondispersive Optical Fiber Communication Channel. Entropy 2020, 22, 607. https://doi.org/10.3390/e22060607
Reznichenko AV, Terekhov IS. Path Integral Approach to Nondispersive Optical Fiber Communication Channel. Entropy. 2020; 22(6):607. https://doi.org/10.3390/e22060607
Chicago/Turabian StyleReznichenko, Aleksei V., and Ivan S. Terekhov. 2020. "Path Integral Approach to Nondispersive Optical Fiber Communication Channel" Entropy 22, no. 6: 607. https://doi.org/10.3390/e22060607
APA StyleReznichenko, A. V., & Terekhov, I. S. (2020). Path Integral Approach to Nondispersive Optical Fiber Communication Channel. Entropy, 22(6), 607. https://doi.org/10.3390/e22060607




