Weighted Quantile Regression Forests for Bimodal Distribution Modeling: A Loss Given Default Case
Abstract
1. Introduction
- To what extent is it possible to model and predict future values of the loss given default?
- Does the proposed weighting method introduce improvements to the standard quantile Regression Forest algorithm?
- Which modeling method best determines the loss given default in terms of the performance on a new unseen dataset?
2. Preliminaries
2.1. Loss Given Default Modeling
2.2. Machine Learning and Random Forests
3. Bimodal Distribution
4. Weighted Quantile Regression Forests
- Ranking the pre-defined criterion ();
- Weighting the criteria from their ranks using some rank order weighting approach.
| Algorithm 1. Weighted quantile Regression Forest algorithm pseudocode. |
| input: Number of Trees (), random subset of the features (), training dataset (), probability for quantile estimation |
| output: weighted quantile Regression Forests () |
| 1: is empty |
| 2: for each = 1 to do |
| 3: = Bootstrap Sample () |
| 4: = Random Decision Tree (, ) |
| 5: = |
| 6: end |
| 7: for each = 1 to do |
| 8: Compute using Formula (13) |
| 9: end |
| 10: for each = 1 to do |
| 11: Compute using Formula (12) |
| 12: end |
| 13: for each = 1 to do |
| 14: Compute using Formula (14) |
| 15: end |
| 16: Compute final prediction using Formula (11) |
| 17: return |
5. Empirical Analysis
5.1. Benchmarking Methods
5.2. Numerical Implementation
5.3. Data Characteristics
| Algorithm 2. Variable selection pseudocode. |
| input: List of all explanatory variables , distance function , correlation matrix (), target variable () |
| output: List of the best explanatory variables () |
| 1: create empty cluster list |
| 2: for each = 1 to do |
| 3: create a cluster for each variable |
| 4: end |
| 5: calculate distance matrix as |
| 6: repeat |
| 7: = find smallest element in for all |
| 8: if then |
| 9: break repeat |
| 10: end |
| 11: merge cluster and cluster |
| 12: update distance matrix |
| 13: end |
| 14: create empty |
| 15: for each = 1 to do |
| 16: = estimate mean square error of -th variable for prediction of |
| 17: update based on |
| 18: end |
| 19: for each do |
| 20: select variable based on the and add to |
| 21: end |
| 22: return |
5.4. Model Comparison
6. Conclusions
- Systematization of the knowledge regarding bimodal distribution, loss given default modeling and attempts to improve the Regression Forest algorithm;
- Application of the various modeling methods for loss given default problem;
- Incorporating of the weighting procedure in quantile Regression Forests.
Author Contributions
Funding
Conflicts of Interest
References
- Basel Committee on Banking Supervision. An Explanatory Note on the Basel Iiirb Risk Weight Functions; Basel Committee on Banking Supervision: Basel, Switzerland, 2005. [Google Scholar]
- Basel Committee on Banking Supervision. Basel III Counterparty Credit Risk Frequently Asked Questions; Basel Committee on Banking Supervision: Basel, Switzerland, 2011. [Google Scholar]
- Krüger, S.; Rösch, D. Downturn LGD modeling using quantile regression. J. Bank. Financ. 2017, 79, 42–56. [Google Scholar] [CrossRef]
- Qi, M.; Zhao, X. Comparison of modeling methods for Loss Given Default. J. Bank. Financ. 2011, 35, 2842–2855. [Google Scholar] [CrossRef]
- Gupton, G.M.; Stein, R.M. LossCalc v2: Dynamic prediction of LGD. Moodys KMV Invest. Serv. 2005. Available online: http://www.defaultrisk.com/_pdf6j4/LCv2_DynamicPredictionOfLGD_fixed.pdf (accessed on 1 February 2020).
- Siao, J.S.; Hwang, R.C.; Chu, C.K. Predicting recovery rates using logistic quantile regression with bounded outcomes. Quant. Financ. 2015, 16, 777–792. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Grzegorczyk, I.; Ząbkowski, T.; Bajaj, C. Weighted Random Forests to Improve Arrhythmia Classification. Electronics 2020, 9, 99. [Google Scholar] [CrossRef] [PubMed]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Karwański, M.; Gostkowski, M.; Jałowiecki, P. Loss given default modeling: An application to data from a Polish bank. J. Risk Model Valid. 2015, 9, 23–40. [Google Scholar] [CrossRef]
- Grzybowska, U.; Karwański, M. Application of mixed models and families of classifiers to estimation of financial risk parameters. Quant. Methods Econ. 2015, 16, 108–115. [Google Scholar]
- Frontczak, R.; Rostek, S. Modeling loss given default with stochastic collateral. Econ. Model. 2015, 44, 162–170. [Google Scholar] [CrossRef]
- Hamerle, A.; Knapp, M.; Wildenauer, N. Modelling Loss Given Default: A “Point in Time”-Approach. Basel II Risk Parameters 2006, 127–142. [Google Scholar] [CrossRef]
- Schuermann, T. What do We Know about Loss Given Default? SSRN Electron. J. 2004. [Google Scholar] [CrossRef]
- Calabrese, R. Estimating bank loans loss given default by generalized additive models. In UCD Geary Institute Discussion Paper Series; University College Dublin: Dublin, Ireland, 2012; WP2012/24. [Google Scholar]
- Chalupka, R.; Kopecsni, J. Modelling bank loan LGD of corporate and SME segments: A case study (No. 27/2008). In IES Working Paper; Charles University: Prague, Czech Republic, 2008. [Google Scholar]
- Yashkir, O.; Yashkir, Y. Loss given default modeling: A comparative analysis. J. Risk Model Valid. 2013, 7, 25–59. [Google Scholar] [CrossRef][Green Version]
- Dermine, J.; de Carvalho, C.N. Bank loan losses-given-default: A case study. J. Bank. Financ. 2006, 30, 1219–1243. [Google Scholar] [CrossRef]
- Huang, X.; Oosterlee, C. Generalized beta regression models for random loss-given-default. J. Credit Risk 2011, 7, 45–70. [Google Scholar] [CrossRef][Green Version]
- Bellotti, T.; Crook, J. Loss given default models incorporating macroeconomic variables for credit cards. Int. J. Forecast. 2012, 28, 171–182. [Google Scholar] [CrossRef]
- Hurlin, C.; Leymarie, J.; Patin, A. Loss functions for Loss Given Default model comparison. Eur. J. Oper. Res. 2018, 268, 348–360. [Google Scholar] [CrossRef]
- Bastos, J.A. Forecasting bank loans loss-given-default. J. Bank. Financ. 2010, 34, 2510–2517. [Google Scholar] [CrossRef]
- Hartmann-Wendels, T.; Miller, P.; Töws, E. Loss given default for leasing: Parametric and nonparametric estimations. J. Bank. Financ. 2014, 40, 364–375. [Google Scholar] [CrossRef]
- Yao, X.; Crook, J.; Andreeva, G. Support vector regression for loss given default modelling. Eur. J. Oper. Res. 2015, 240, 528–538. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 261–277. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995. [Google Scholar] [CrossRef]
- Tanaka, K.; Kinkyo, T.; Hamori, S. Financial Hazard Map: Financial Vulnerability Predicted by a Random Forests Classification Model. Sustainability 2018, 10, 1530. [Google Scholar] [CrossRef]
- Nafkha, R.; Gajowniczek, K.; Ząbkowski, T. Do Customers Choose Proper Tariff? Empirical Analysis Based on Polish Data Using Unsupervised Techniques. Energies 2018, 11, 514. [Google Scholar] [CrossRef]
- Ząbkowski, T.; Gajowniczek, K.; Szupiluk, R. Grade analysis for energy usage patterns segmentation based on smart meter data. In Proceedings of the 2015 IEEE 2nd International Conference on Cybernetics (CYBCONF), Gdynia, Poland, 24–26 June 2015. [Google Scholar] [CrossRef]
- Sorzano, C.O.S.; Vargas, J.; Montano, A.P. A survey of dimensionality reduction techniques. arXiv 2014, arXiv:1403.2877. [Google Scholar]
- Yazgana, P.; Kusakci, A.O. A Literature Survey on Association Rule Mining Algorithms. Southeast Eur. J. Soft Comput. 2016, 5. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Ząbkowski, T. Short term electricity forecasting based on user behavior from individual smart meter data. J. Intell. Fuzzy Syst. 2015, 30, 223–234. [Google Scholar] [CrossRef]
- Fabris, F.; de Magalhães, J.P.; Freitas, A.A. A review of supervised machine learning applied to ageing research. Biogerontology 2017, 18, 171–188. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Nafkha, R.; Ząbkowski, T. Electricity peak demand classification with artificial neural networks. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems, Prague, Czech Republic, 3–6 September 2017. [Google Scholar] [CrossRef]
- Bakir, G.; Hofmann, T.; Schölkopf, B.; Smola, A.J.; Taskar, B.; Vishwanathan, S.V.N. Predicting Structured Data; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Gajowniczek, K.; Ząbkowski, T.; Sodenkamp, M. Revealing Household Characteristics from Electricity Meter Data with Grade Analysis and Machine Learning Algorithms. Appl. Sci. 2018, 8, 1654. [Google Scholar] [CrossRef]
- Tripoliti, E.E.; Fotiadis, D.I.; Manis, G. Dynamic construction of Random Forests: Evaluation using biomedical engineering problems. In Proceedings of the 10th IEEE International Conference on Information Technology and Applications in Biomedicine, Corfu, Greece, 2–5 November 2010. [Google Scholar] [CrossRef]
- Tanaka, K.; Kinkyo, T.; Hamori, S. Random forests-based early warning system for bank failures. Econ. Lett. 2016, 148, 118–121. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the ICML’96 Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Beutel, J.; List, S.; von Schweinitz, G. Does machine learning help us predict banking crises? J. Financ. Stab. 2019, 45, 100693. [Google Scholar] [CrossRef]
- Goel, E.; Abhilasha, E. Random forest: A review. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2017, 7, 251–257. [Google Scholar] [CrossRef]
- Xuan, S.; Liu, G.; Li, Z. Refined Weighted Random Forest and Its Application to Credit Card Fraud Detection. Lect. Notes Comput. Sci. 2018, 11280, 343–355. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Rodríguez, J.J. A weighted voting framework for classifiers ensembles. Knowl. Inf. Syst. 2012, 38, 259–275. [Google Scholar] [CrossRef]
- Pham, H.; Olafsson, S. On Cesaro averages for weighted trees in the random forest. J. Classif. 2019, 1–14. [Google Scholar] [CrossRef]
- Byeon, H.; Cha, S.; Lim, K. Exploring Factors Associated with Voucher Program for Speech Language Therapy for the Preschoolers of Parents with Communication Disorder using Weighted Random Forests. Int. J. Adv. Comput. Sci. Appl. 2019, 10. [Google Scholar] [CrossRef]
- Booth, A.; Gerding, E.; McGroarty, F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014, 41, 3651–3661. [Google Scholar] [CrossRef]
- Utkin, L.V.; Konstantinov, A.V.; Chukanov, V.S.; Kots, M.V.; Ryabinin, M.A.; Meldo, A.A. A weighted random survival forest. Knowl. Based Syst. 2019, 177, 136–144. [Google Scholar] [CrossRef]
- Rao, B. Estimation of a Unimodal Density. Sankhyā Indian J. Stat. 1969, 31, 23–36. [Google Scholar]
- Gómez, Y.M.; Gómez-Déniz, E.; Venegas, O.; Gallardo, D.I.; Gómez, H.W. An Asymmetric Bimodal Distribution with Application to Quantile Regression. Symmetry 2019, 11, 899. [Google Scholar] [CrossRef]
- Rindskopf, D.; Shiyko, M. Measures of Dispersion, Skewness and Kurtosis. Int. Encycl. Educ. 2010, 267–273. [Google Scholar] [CrossRef]
- Chatterjee, S.; Handcock, M.S.; Simonoff, J.S. A Casebook for a First Course in Statistics and Data Analysis; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Famoye, F.; Lee, C.; Eugene, N. Beta-Normal Distribution: Bimodality Properties and Application. J. Mod. Appl. Stat. Methods 2004, 3, 85–103. [Google Scholar] [CrossRef]
- Bansal, B.; Gokhale, M.R.; Bhattacharya, A.; Arora, B.M. InAs/InP quantum dots with bimodal size distribution: Two evolution pathways. J. Appl. Phys. 2007, 101, 094303. [Google Scholar] [CrossRef]
- Hassan, M.Y.; Hijazi, R.H. A bimodal exponential power distribution. Pak. J. Statist 2010, 26, 379–396. [Google Scholar]
- Sitek, G. The modes of a mixture of two normal distributions. Sil. J. Pure Appl. Math. 2016, 6, 59–67. [Google Scholar]
- Lin, T.I. Maximum likelihood estimation for multivariate skew normal mixture models. J. Multivar Anal. 2009, 100, 257–265. [Google Scholar] [CrossRef]
- Borkowski, B.; Dudek, H.; Szczesny, W. Wybrane Zagadnienia Ekonometrii; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2003. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Routledge: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning. In Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machinelearning. arXiv 2019, arXiv:1908.09635. [Google Scholar]
- Roszkowska, E. Rank ordering criteria weighting methods—A comparative overview. Optimum. Studia Ekon. 2013, 5. [Google Scholar] [CrossRef]
- R: A Language and Environment for Statistical Computing. Available online: https://www.gbif.org/tool/81287/r-a-language-and-environment-for-statistical-computing (accessed on 29 July 2019).
- Williams, M.L. Bank overdraft pricing and myopic consumers. Econ. Lett. 2016, 139, 84–87. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Buhlmann, P. MissForest--non-parametric missing value imputation for mixed-type data. Bioinformatics 2011, 28, 112–118. [Google Scholar] [CrossRef]
- Chavent, M.; Genuer, R.; Saracco, J. Combining clustering of variables and feature selection using random forests. Commun. Stat. Simul. Comput. 2019, 1–20. [Google Scholar] [CrossRef]
- Hinloopen, J.; van Marrewijk, C. Comparing Distributions: The Harmonic Mass Index. SSRN Electron. J. 2005. [Google Scholar] [CrossRef]



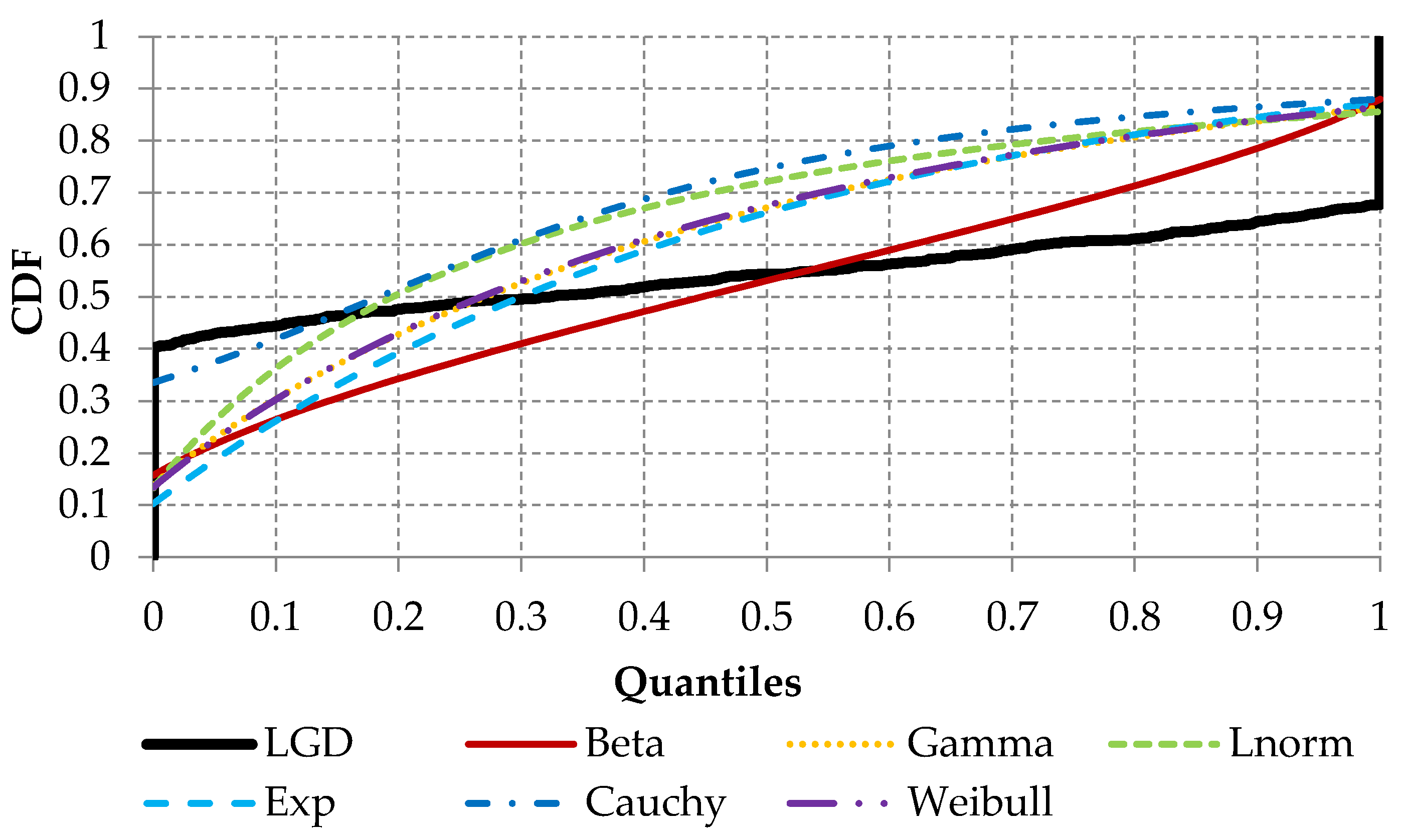
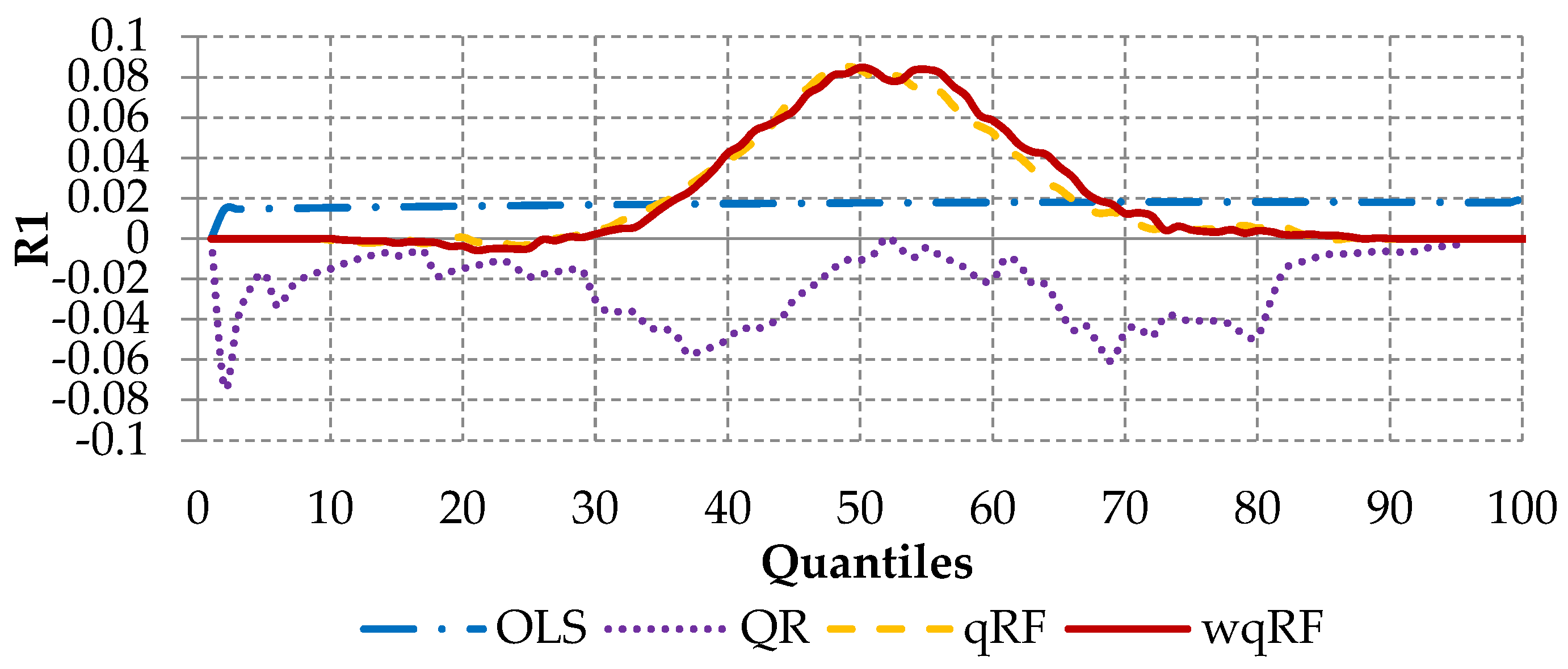
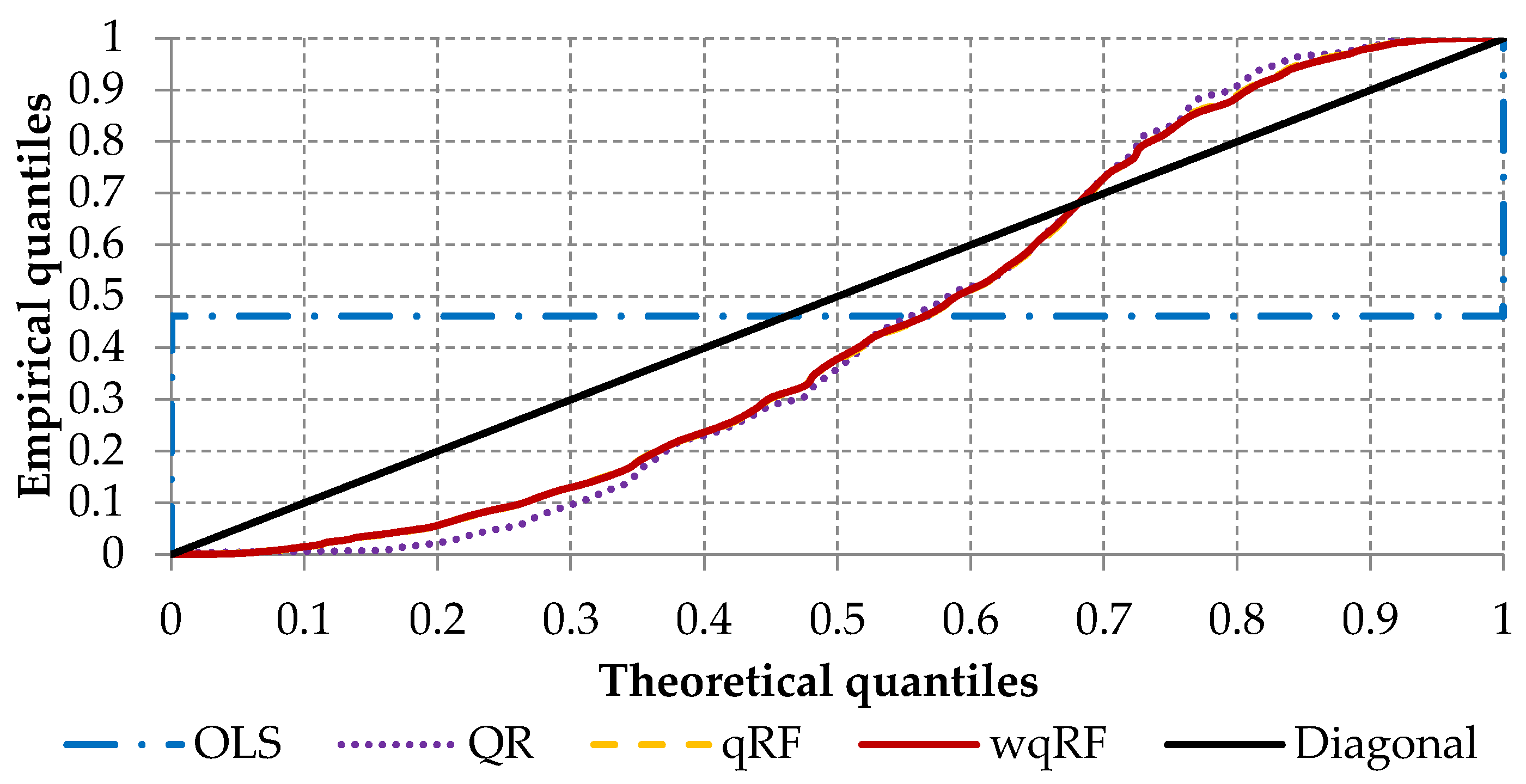
| Characteristics | Min | P25 | P50 | Mean | P75 | Max | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| Value | 0.0000 | 0.0000 | 0.3413 | 0.4570 | 1.0000 | 1.0000 | 0.1699 | −1.8048 |
| Measure | Beta | Gamma | Log-Norm | Exponential | Cauchy | Weibull |
|---|---|---|---|---|---|---|
| Kolmogorov-Smirnov statistic | 0.25 | 0.26 | 0.27 | 0.30 | 0.34 | 0.27 |
| Cramer-von Mises statistic | 16.50 | 19.54 | 20.84 | 23.82 | 28.05 | 20.15 |
| Anderson-Darling statistic | 110.57 | 128.27 | 135.54 | 165.02 | 170.07 | 132.79 |
| Akaike’s Information Criterion | −504.92 | 493.61 | 539.62 | 521.19 | 2049.24 | 501.45 |
| Bayesian Information Criterion | −494.82 | 503.71 | 549.72 | 526.24 | 2059.34 | 511.55 |
| Group | 0% Missing | 0–2% Missing | 2–5% Missing | 5–10% Missing | 10–16% Missing | 16–20% Missing | 20–30% Missing | 30–90% Missing |
|---|---|---|---|---|---|---|---|---|
| Number of missing variables | 142 | 57 | 27 | 5 | 16 | 17 | 14 | 14 |
| Measure | OLS | QR | qRF | wqRF |
|---|---|---|---|---|
| HMI | 0.645 | 0.169 | 0.153 | 0.151 |
| HWMI | 0.256 | 0.022 | 0.017 | 0.017 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gostkowski, M.; Gajowniczek, K. Weighted Quantile Regression Forests for Bimodal Distribution Modeling: A Loss Given Default Case. Entropy 2020, 22, 545. https://doi.org/10.3390/e22050545
Gostkowski M, Gajowniczek K. Weighted Quantile Regression Forests for Bimodal Distribution Modeling: A Loss Given Default Case. Entropy. 2020; 22(5):545. https://doi.org/10.3390/e22050545
Chicago/Turabian StyleGostkowski, Michał, and Krzysztof Gajowniczek. 2020. "Weighted Quantile Regression Forests for Bimodal Distribution Modeling: A Loss Given Default Case" Entropy 22, no. 5: 545. https://doi.org/10.3390/e22050545
APA StyleGostkowski, M., & Gajowniczek, K. (2020). Weighted Quantile Regression Forests for Bimodal Distribution Modeling: A Loss Given Default Case. Entropy, 22(5), 545. https://doi.org/10.3390/e22050545






