Cooperation on Interdependent Networks by Means of Migration and Stochastic Imitation
Abstract
1. Introduction
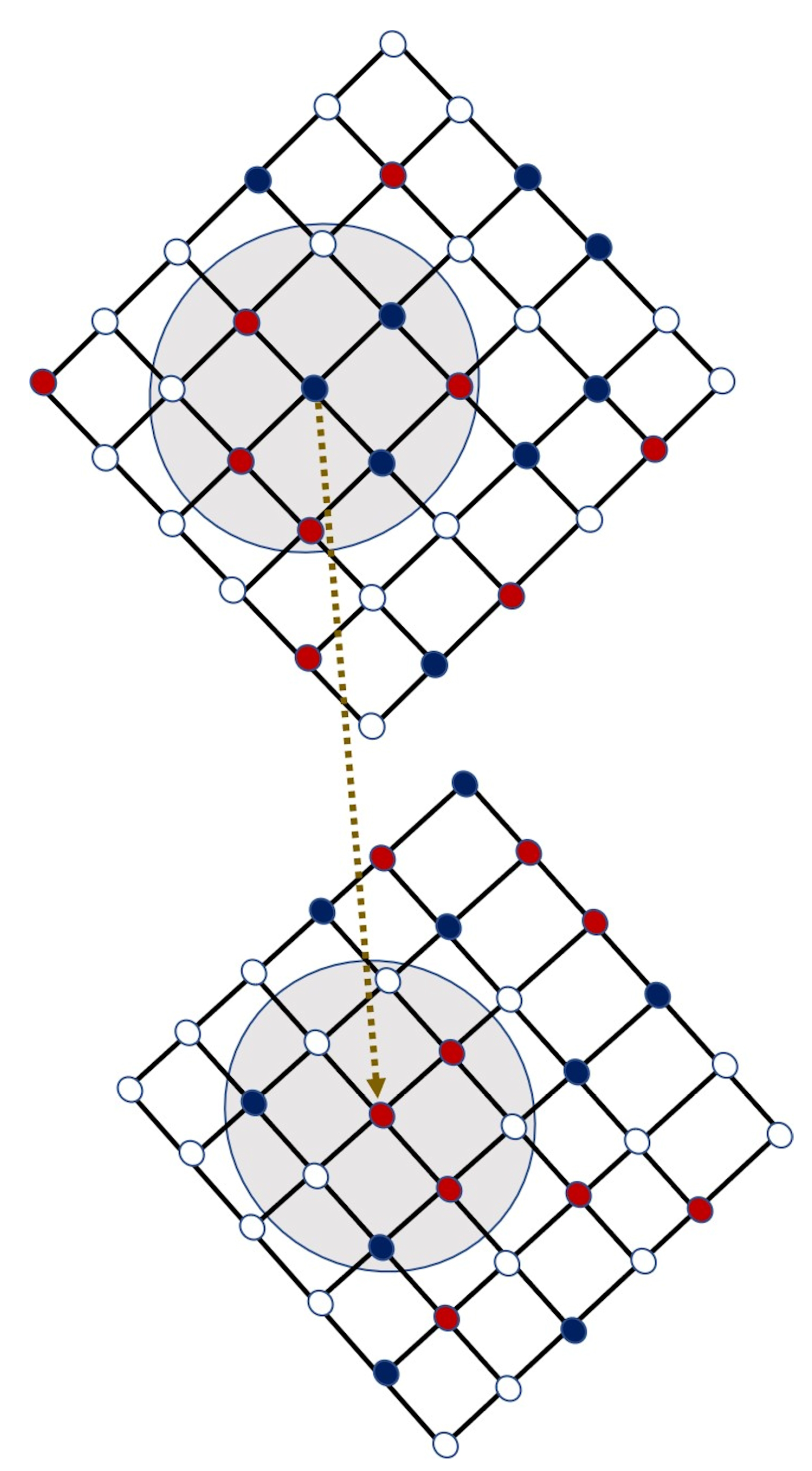
2. Methods
2.1. Algorithm for the Strategy Updating
2.2. Network and Game-Theoretical Model
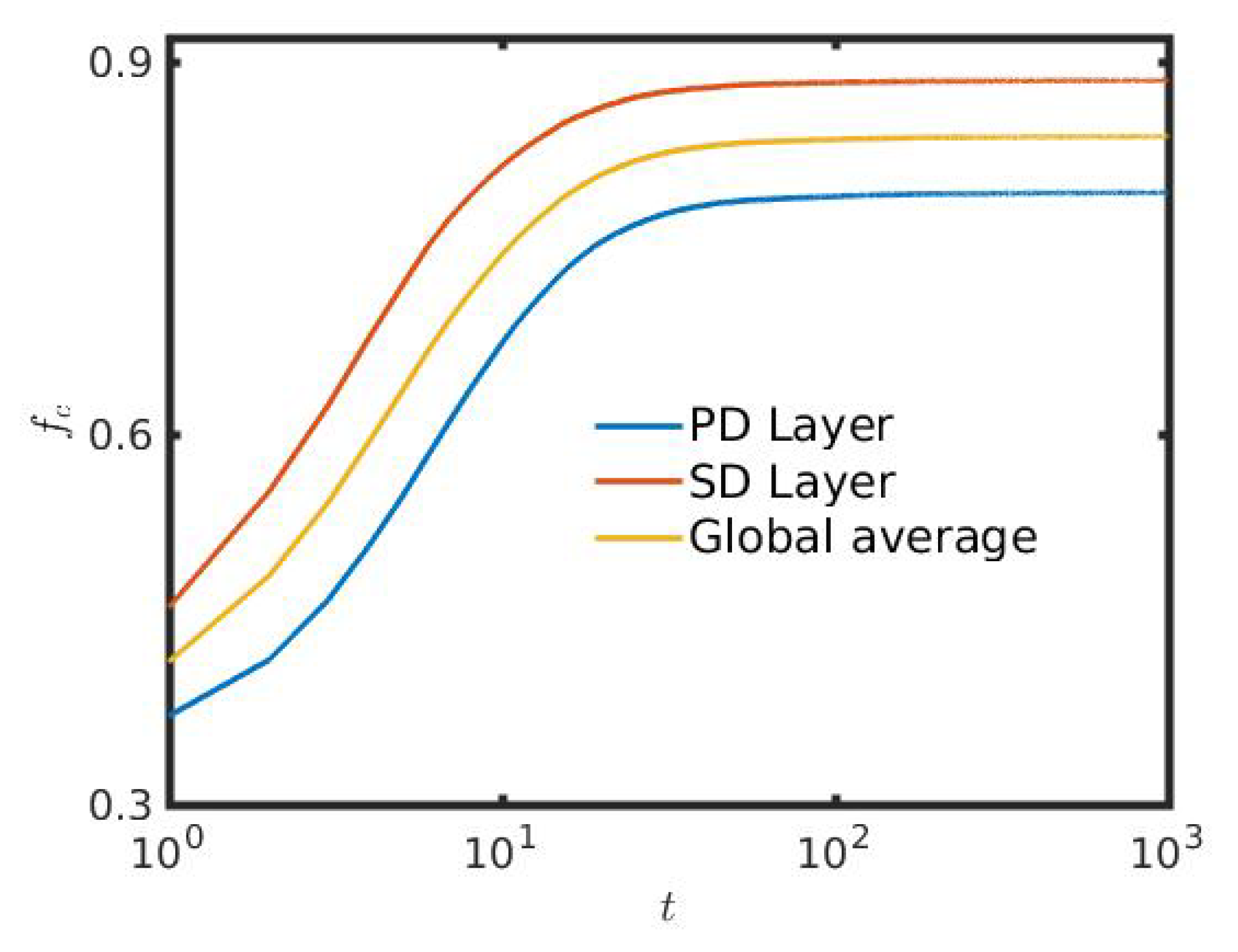
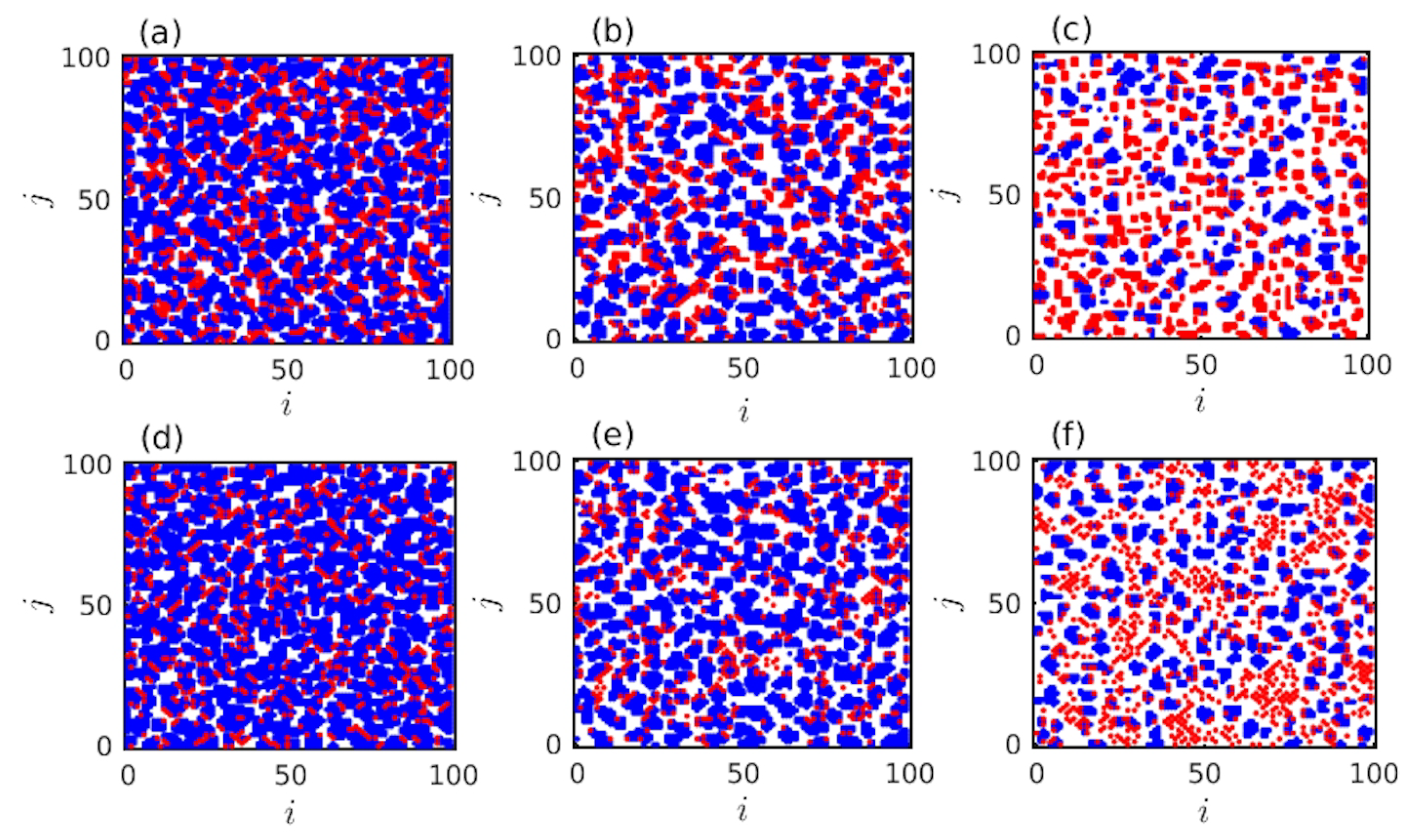
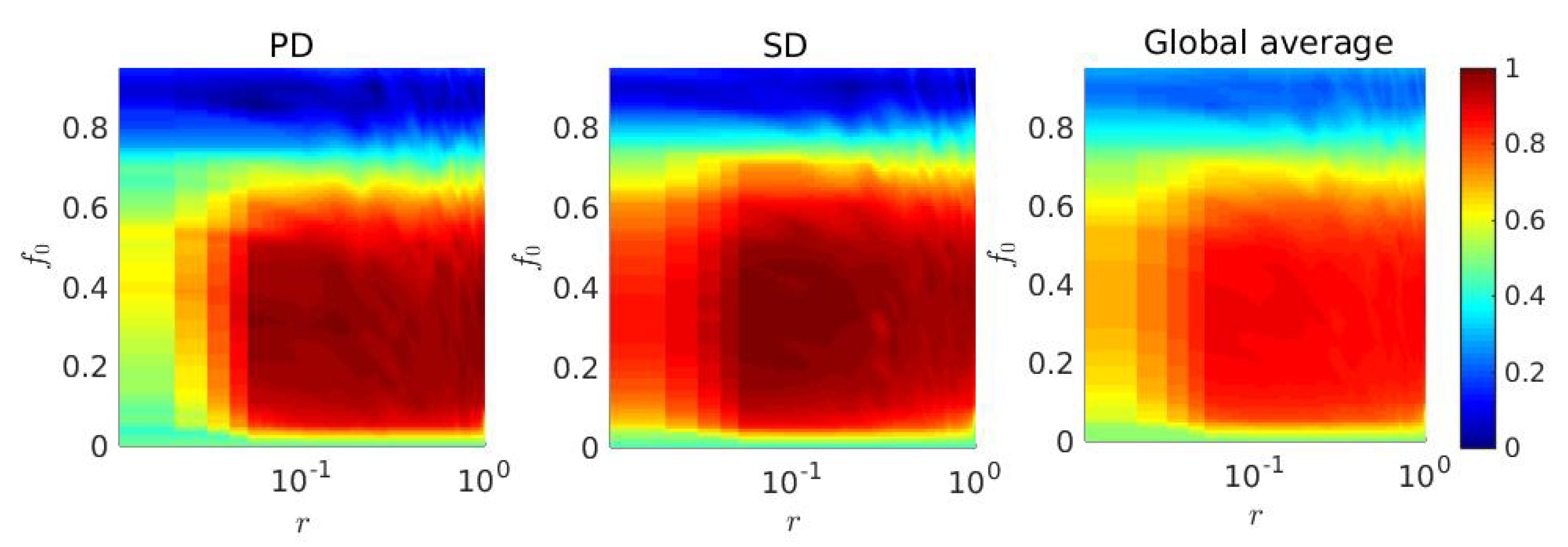
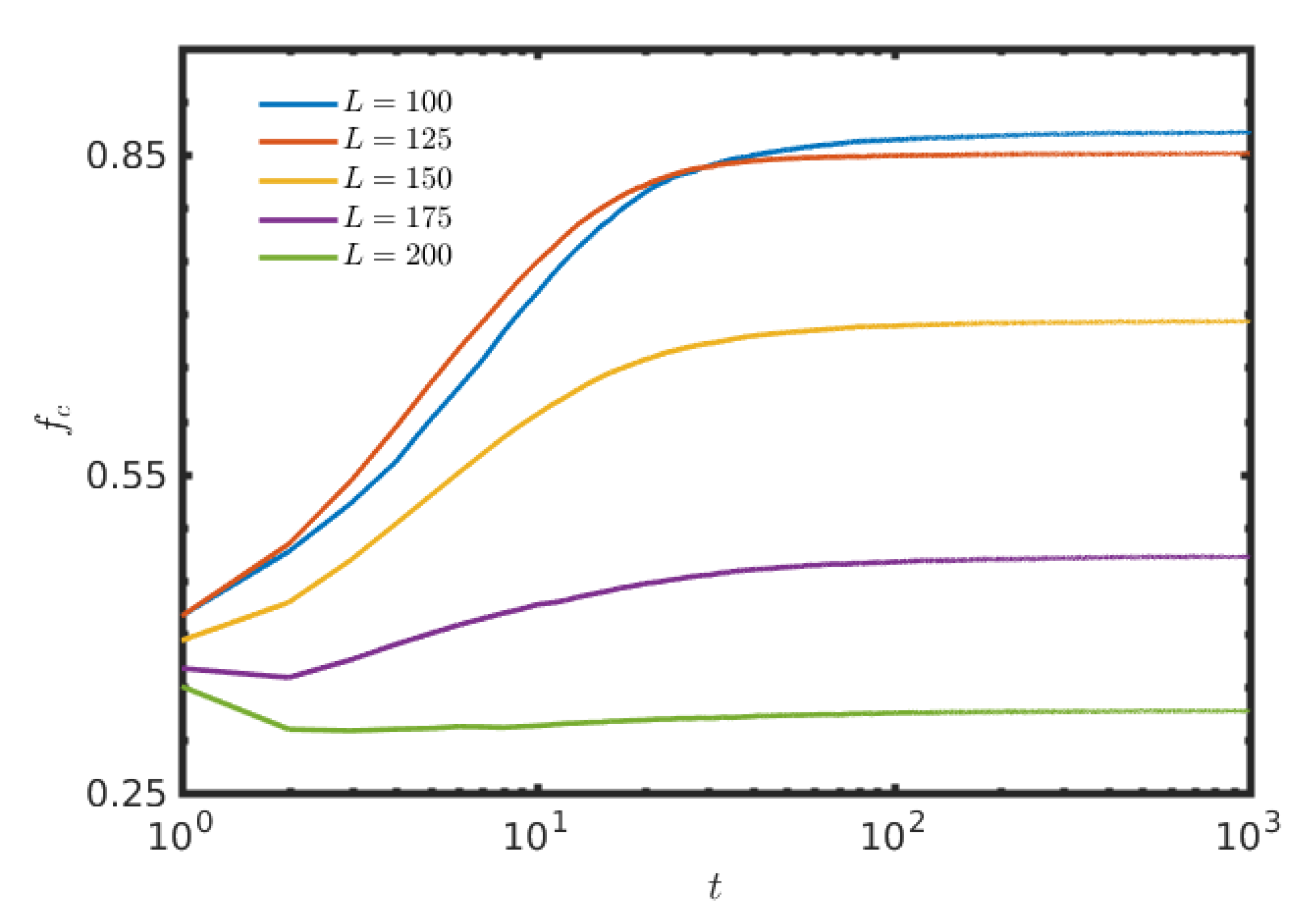
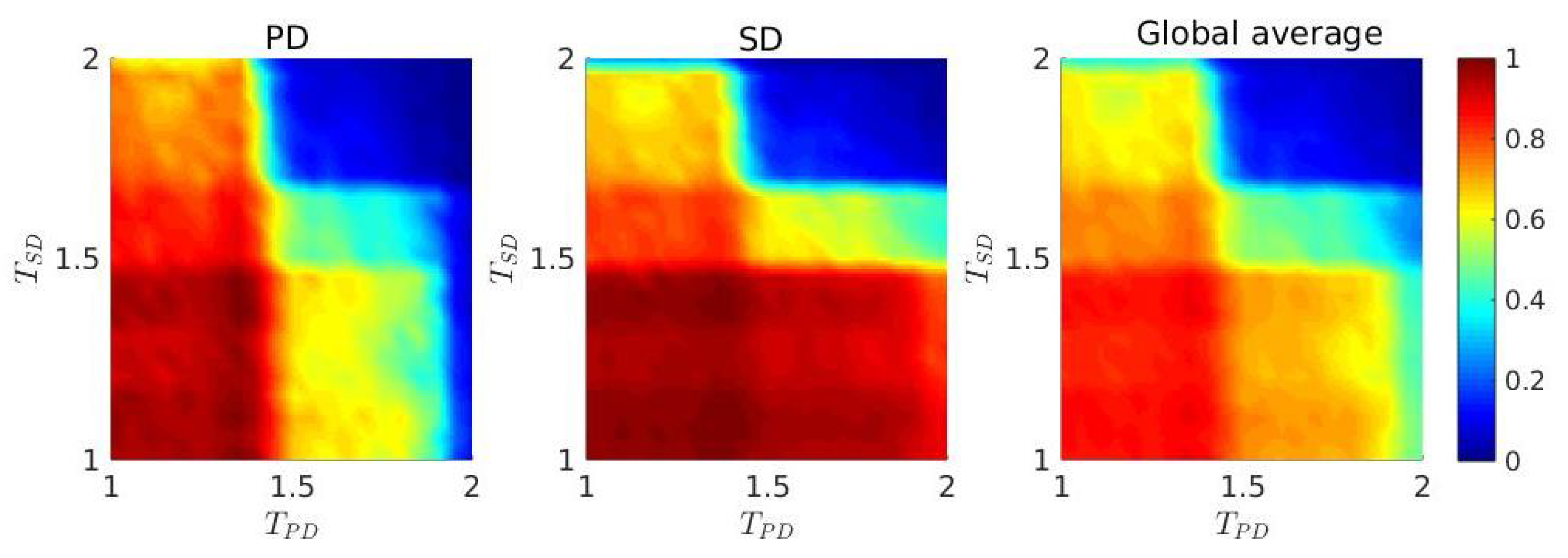
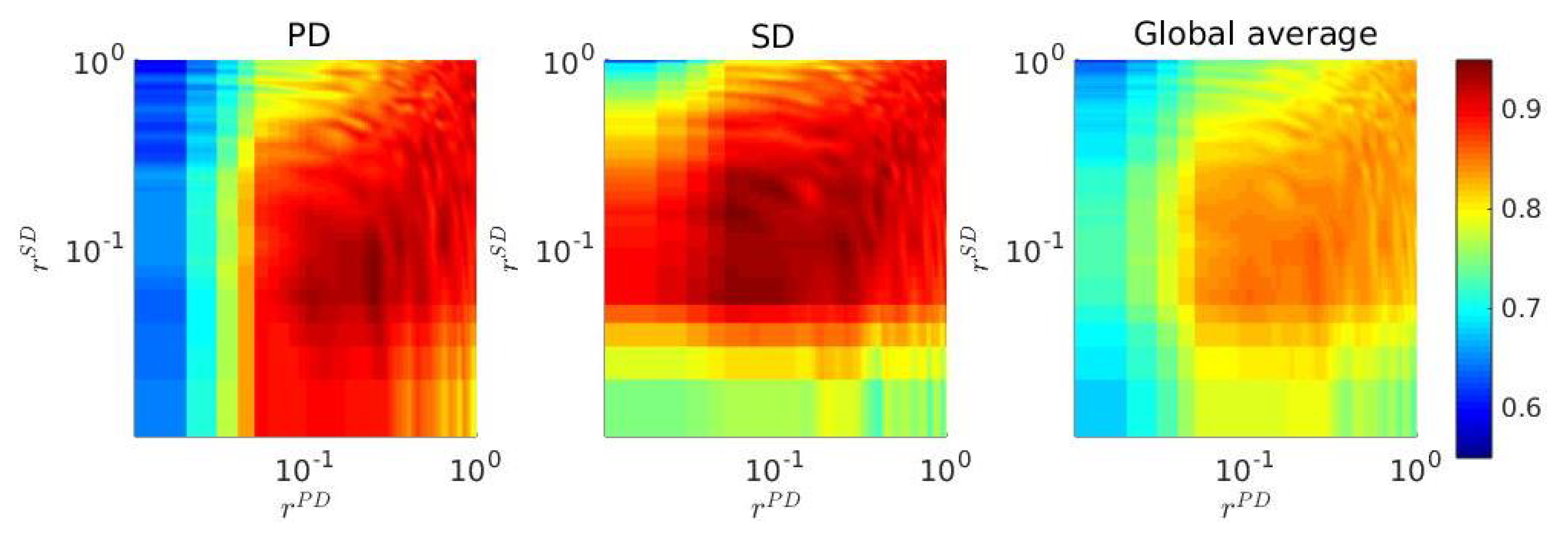
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010; Volume 6. [Google Scholar]
- Perc, M.; Grigolini, P. Collective behavior and evolutionary games-an introduction. Chaos Solitons Fract 2013, 56, 1–5. [Google Scholar] [CrossRef]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Szolnoki, A.; Mobilia, M.; Jiang, L.L.; Szczesny, B.; Rucklidge, A.M.; Perc, M. Cyclic dominance in evolutionary games: A review. J. R. Soc. Interface 2014, 11, 20140735. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Perc, M.; Szolnoki, A. Coevolutionary games–A mini review. BioSystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Capraro, V.; Perc, M. Grand challenges in social physics: In pursuit of moral behavior. Front. Phys. 2018, 6, 107. [Google Scholar] [CrossRef]
- Chowdhury, S.N.; Majhi, S.; Ozer, M.; Ghosh, D.; Perc, M. Synchronization to extreme events in moving agents. New. J. Phys. 2019, 21, 073048. [Google Scholar] [CrossRef]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Skutch, A.F. Helpers among birds. Condor 1961, 63, 198–226. [Google Scholar] [CrossRef]
- Wang, R.W.; Shi, L.; Ai, S.M.; Zheng, Q. Trade-off between reciprocal mutualists: Local resource availability-oriented interaction in fig/fig wasp mutualism. J. Anim. Ecol. 2008, 77, 616–623. [Google Scholar] [CrossRef]
- Wilson, E.O. The Insect Societies; Harvard University Press [Distributed by Oxford University Press]: Cambridge, MA, USA, 1971. [Google Scholar]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef]
- Smith, J.M.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 2005, 95, 098104. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.C.; Pacheco, J.M.; Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef] [PubMed]
- Poncela, J.; Gómez-Gardeñes, J.; Floría, L.M.; Moreno, Y. Robustness of cooperation in the evolutionary prisoner’s dilemma on complex systems. New J. Phys. 2007, 9, 184. [Google Scholar] [CrossRef]
- Gómez-Gardenes, J.; Campillo, M.; Floría, L.M.; Moreno, Y. Dynamical organization of cooperation in complex topologies. Phys. Rev. Lett. 2007, 98, 108103. [Google Scholar] [CrossRef]
- Antonioni, A.; Tomassini, M. Network Fluctuations Hinder Cooperation in Evolutionary Games. PLoS ONE 2011, 6, e25555. [Google Scholar] [CrossRef]
- Tanimoto, J.; Brede, M.; Yamauchi, A. Network reciprocity by coexisting learning and teaching strategies. Phys. Rev. E 2012, 85, 032101. [Google Scholar] [CrossRef]
- Antonioni, A.; Cacault, M.P.; Lalive, R.; Tomassini, M. Know Thy Neighbor: Costly Information Can Hurt Cooperation in Dynamic Networks. PLoS ONE 2014, 9, e110788. [Google Scholar] [CrossRef]
- Wang, Z.; Kokubo, S.; Jusup, M.; Tanimoto, J. Universal scaling for the dilemma strength in evolutionary games. Phys. Life Rev. 2015, 14, 1–30. [Google Scholar] [CrossRef]
- Javarone, M.A. Statistical physics of the spatial Prisoner’s Dilemma with memory-aware agents. Eur. Phys. J. B 2016, 89, 42. [Google Scholar] [CrossRef]
- Amaral, M.A.; Javarone, M.A. Heterogeneous update mechanisms in evolutionary games: Mixing innovative and imitative dynamics. Phys. Rev. E 2018, 97, 042305. [Google Scholar] [CrossRef]
- Vilone, D.; Capraro, V.; Ramasco, J.J. Hierarchical invasion of cooperation in complex networks. J. Phys. Commun. 2018, 2, 025019. [Google Scholar] [CrossRef]
- Fotouhi, B.; Momeni, N.; Allen, B.; Nowak, M.A. Evolution of cooperation on large networks with community structure. J. R. Soc. Interface 2019, 16, 20180677. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Barrat, A.; Barthélemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Nowak, M.A.; May, R.M. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Szabó, G.; Fath, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Majhi, S.; Perc, M.; Ghosh, D. Chimera states in a multilayer network of coupled and uncoupled neurons. Chaos 2017, 27, 073109. [Google Scholar] [CrossRef]
- Kundu, S.; Majhi, S.; Ghosh, D. From asynchronous to synchronous chimeras in ecological multiplex network. Eur. Phys. J. Spec. Top. 2019, 228, 2429–2439. [Google Scholar] [CrossRef]
- Majhi, S.; Perc, M.; Ghosh, D. Chimera states in uncoupled neurons induced by a multilayer structure. Sci. Rep. 2016, 6, 39033. [Google Scholar] [CrossRef]
- Rakshit, S.; Majhi, S.; Bera, B.K.; Sinha, S.; Ghosh, D. Time-varying multiplex network: Intralayer and interlayer synchronization. Phys. Rev. E 2017, 96, 062308. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.; Majhi, S.; Ghosh, D. Chemical synaptic multiplexing enhances rhythmicity in neuronal networks. Nonlinear Dyn. 2019, 98, 1659–1668. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Szolnoki, A.; Perc, M. Evolutionary games on multilayer networks: A colloquium. Eur. Phys. J. B 2015, 88, 124. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, L.; Perc, M. Degree mixing in multilayer networks impedes the evolution of cooperation. Phys. Rev. E 2014, 89, 052813. [Google Scholar] [CrossRef] [PubMed]
- Szolnoki, A.; Perc, M. Emergence of multilevel selection in the prisoner’s dilemma game on coevolving random networks. New. J. Phys. 2009, 11, 093033. [Google Scholar] [CrossRef]
- Duh, M.; Gosak, M.; Slavinec, M.; Perc, M. Assortativity provides a narrow margin for enhanced cooperation on multilayer networks. New. J. Phys. 2019, 21, 123016. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Promoting cooperation in social dilemmas via simple coevolutionary rules. Eur. Phys. J. B 2009, 67, 337–344. [Google Scholar] [CrossRef]
- Szolnoki, A.; Szabó, G. Cooperation enhanced by inhomogeneous activity of teaching for evolutionary Prisoner’s Dilemma games. EPL Europhys. Lett. 2007, 77, 30004. [Google Scholar] [CrossRef]
- Perc, M.; Wang, Z. Heterogeneous aspirations promote cooperation in the prisoner’s dilemma game. PLoS ONE 2010, 5, e15117. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M.; Szabó, G. Diversity of reproduction rate supports cooperation in the prisoner’s dilemma game on complex networks. Eur. Phys. J. B 2008, 61, 505–509. [Google Scholar] [CrossRef]
- Wang, Z.; Perc, M. Aspiring to the fittest and promotion of cooperation in the prisoner’s dilemma game. Phys. Rev. E 2010, 82, 021115. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Szolnoki, A. Cooperation in spatial prisoner’s dilemma with two types of players for increasing number of neighbors. Phys. Rev. E 2009, 79, 016106. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.J.; Sun, S.W.; Wang, L.; Ding, S.; Wang, J.; Xia, C.Y. Promotion of cooperation due to diversity of players in the spatial public goods game with increasing neighborhood size. Phys. A Stat. Mech. Appl. 2014, 406, 145–154. [Google Scholar] [CrossRef]
- Helbing, D.; Yu, W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc. Natl. Acad. Sci. USA 2009, 106, 3680–3685. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.L.; Wang, W.X.; Lai, Y.C.; Wang, B.H. Role of adaptive migration in promoting cooperation in spatial games. Phys. Rev. E 2010, 81, 036108. [Google Scholar] [CrossRef]
- Meloni, S.; Buscarino, A.; Fortuna, L.; Frasca, M.; Gómez-Gardeñes, J.; Latora, V.; Moreno, Y. Effects of mobility in a population of prisoner’s dilemma players. Phys. Rev. E 2009, 79, 067101. [Google Scholar] [CrossRef]
- Noh, J.D.; Rieger, H. Random walks on complex networks. Phys. Rev. Lett. 2004, 92, 118701. [Google Scholar] [CrossRef]
- Aktipis, C.A. Know when to walk away: Contingent movement and the evolution of cooperation. J. Theor. Biol. 2004, 231, 249–260. [Google Scholar] [CrossRef]
- Vainstein, M.H.; Silva, A.T.; Arenzon, J.J. Does mobility decrease cooperation? J. Theor. Biol. 2007, 244, 722–728. [Google Scholar] [CrossRef]
- Smaldino, P.E.; Schank, J.C. Movement patterns, social dynamics, and the evolution of cooperation. Theor. Popul. Biol. 2012, 82, 48–58. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tanimoto, J.; Sagara, H. Relationship between dilemma occurrence and the existence of a weakly dominant strategy in a two-player symmetric game. BioSystems 2007, 90, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Sugden, R. The Economics of Rights, Cooperation and Welfare; Basic Blackwell: Oxford, UK, 1986. [Google Scholar]
- Tayer, M. Possibility of Cooperation: Studies in Rationality and Social Change; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Scheuring, I. The iterated continuous prisoner’s dilemma game cannot explain the evolution of interspecific mutualism in unstructured populations. J. Theor. Biol. 2005, 232, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Tanimoto, J. A simple scaling of the effectiveness of supporting mutual cooperation in donor-recipient games by various reciprocity mechanisms. BioSystems 2009, 96, 29–34. [Google Scholar] [CrossRef]
- Berger, U. Simple scaling of cooperation in donor-recipient games. BioSystems 2009, 97, 165–167. [Google Scholar] [CrossRef] [PubMed]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef]
- Santos, M.D.; Dorogovtsev, S.N.; Mendes, J.F. Biased imitation in coupled evolutionary games in interdependent networks. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef]
- Wang, B.; Pei, Z.; Wang, L. Evolutionary dynamics of cooperation on interdependent networks with the Prisoner’s Dilemma and Snowdrift Game. EPL Europhys. Lett. 2014, 107, 58006. [Google Scholar] [CrossRef]
- Wang, Z.; Szolnoki, A.; Perc, M. Optimal interdependence between networks for the evolution of cooperation. Sci. Rep. 2013, 3, 2470. [Google Scholar] [CrossRef]
- Gómez-Gardenes, J.; Reinares, I.; Arenas, A.; Floría, L.M. Evolution of cooperation in multiplex networks. Sci. Rep. 2012, 2, 620. [Google Scholar] [CrossRef]
- Banerjee, J.; Layek, R.K.; Sasmal, S.K.; Ghosh, D. Delayed evolutionary model for public goods competition with policing in phenotypically variant bacterial biofilms. EPL Europhys. Lett. 2019, 126, 18002. [Google Scholar] [CrossRef]
- Helbing, D. Traffic and related self-driven many-particle systems. Rev. Mod. Phys. 2001, 73, 1067. [Google Scholar] [CrossRef]
- D’Orsogna, M.R.; Perc, M. Statistical physics of crime: A review. Phys. Life Rev. 2015, 12, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Vasconcelos, V.V.; Santos, F.C. Climate change governance, cooperation and self-organization. Phys. Life Rev. 2014, 11, 573–586. [Google Scholar] [CrossRef]
- Chen, X.; Fu, F. Social learning of prescribing behavior can promote population optimum of antibiotic use. Front. Phys. 2018, 6, 193. [Google Scholar] [CrossRef]
- Fu, F.; Rosenbloom, D.I.; Wang, L.; Nowak, M.A. Imitation dynamics of vaccination behaviour on social networks. Proc. R. Soc. B 2011, 278, 42–49. [Google Scholar] [CrossRef]
- Wang, Z.; Bauch, C.T.; Bhattacharyya, S.; d’Onofrio, A.; Manfredi, P.; Perc, M.; Perra, N.; Salathé, M.; Zhao, D. Statistical physics of vaccination. Phys. Rep. 2016, 664, 1–113. [Google Scholar] [CrossRef]
- Perc, M. The social physics collective. Sci. Rep. 2019, 9, 16549. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nag Chowdhury, S.; Kundu, S.; Duh, M.; Perc, M.; Ghosh, D. Cooperation on Interdependent Networks by Means of Migration and Stochastic Imitation. Entropy 2020, 22, 485. https://doi.org/10.3390/e22040485
Nag Chowdhury S, Kundu S, Duh M, Perc M, Ghosh D. Cooperation on Interdependent Networks by Means of Migration and Stochastic Imitation. Entropy. 2020; 22(4):485. https://doi.org/10.3390/e22040485
Chicago/Turabian StyleNag Chowdhury, Sayantan, Srilena Kundu, Maja Duh, Matjaž Perc, and Dibakar Ghosh. 2020. "Cooperation on Interdependent Networks by Means of Migration and Stochastic Imitation" Entropy 22, no. 4: 485. https://doi.org/10.3390/e22040485
APA StyleNag Chowdhury, S., Kundu, S., Duh, M., Perc, M., & Ghosh, D. (2020). Cooperation on Interdependent Networks by Means of Migration and Stochastic Imitation. Entropy, 22(4), 485. https://doi.org/10.3390/e22040485





