Statistical Inference of the Half-Logistic Inverse Rayleigh Distribution
Abstract
1. Introduction
2. The HLIR Distribution
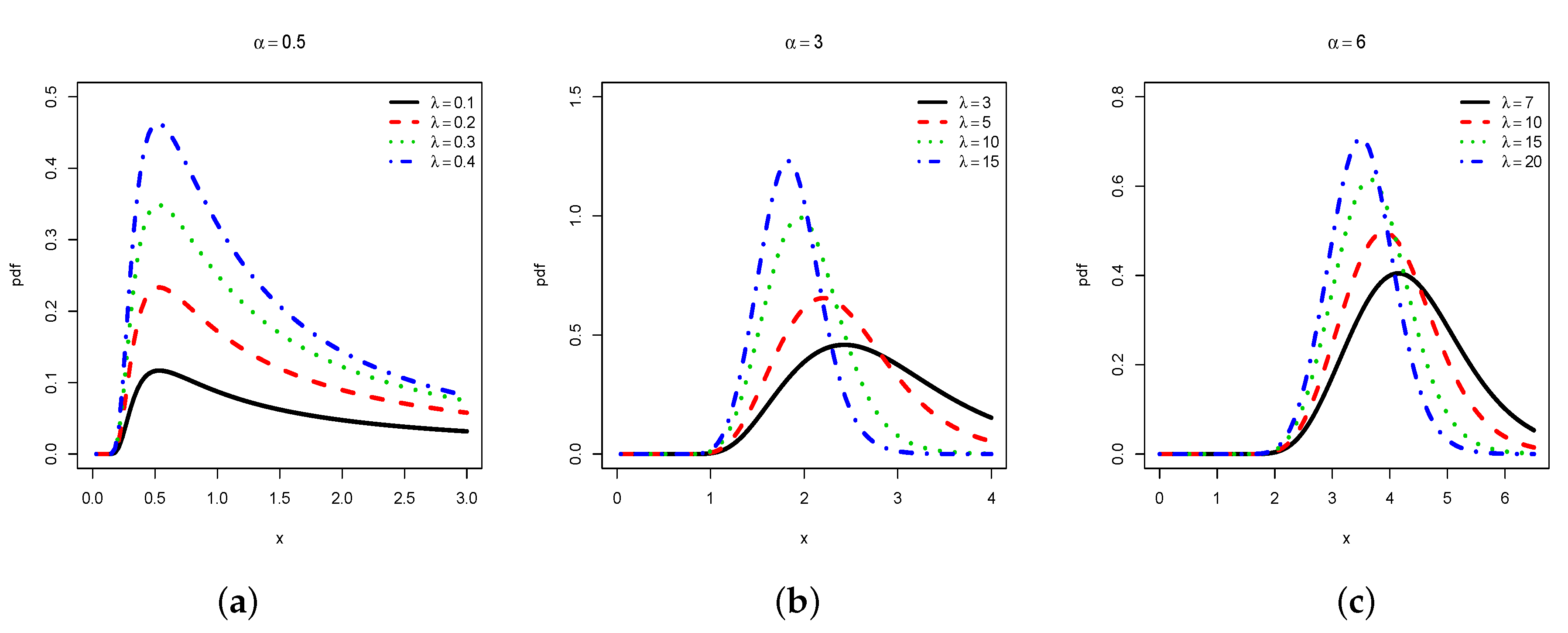
2.1. Probability Functions
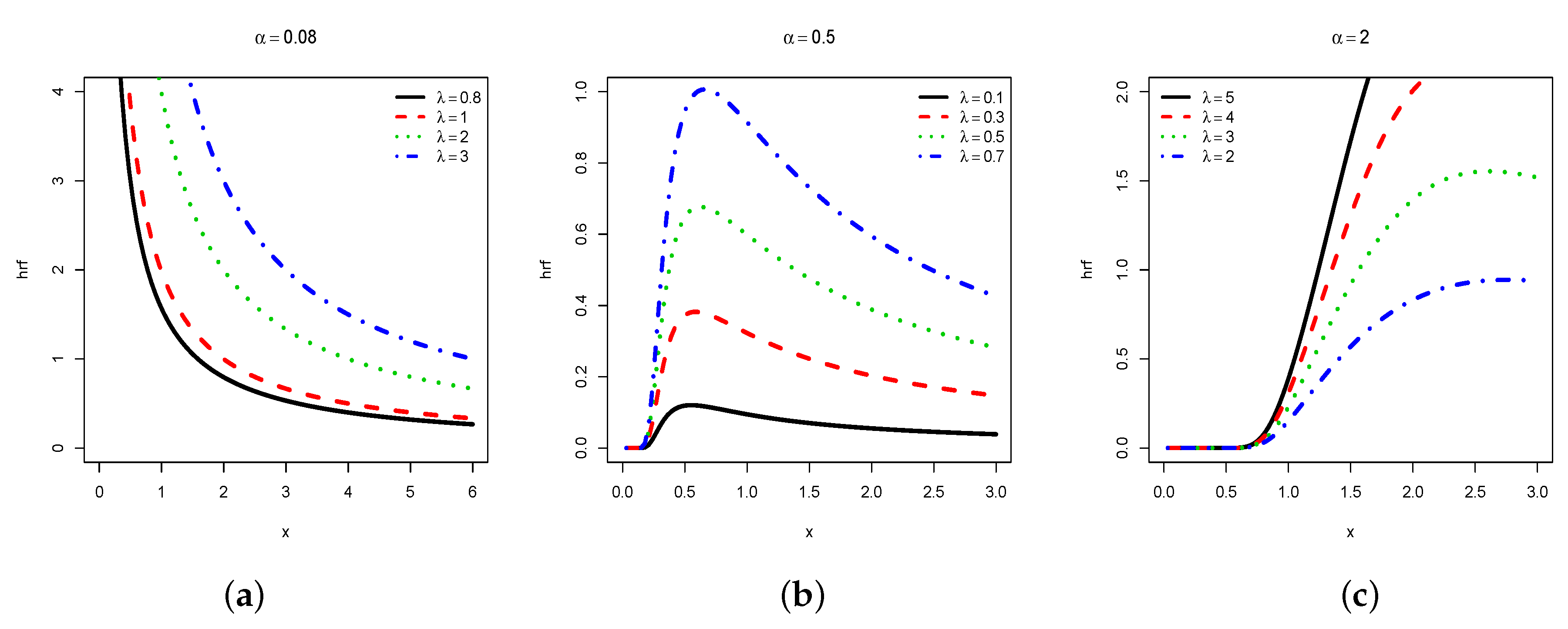
2.2. Functions Analysis
2.3. Quantile Function
3. Mathematical Properties
3.1. Some Stochastic Ordering Results
- For any and , we have .
- For any and , we have .
- After some algebraic manipulations, we getimplying that is strictly decreasing with respect to . Therefore, for any and , we have .
- With the same methodology, we haveimplying that is strictly increasing with respect to . Therefore, for any and , we have .
3.2. Linear Representation
3.3. Raw/Inverted Moments
3.4. Incomplete Moments
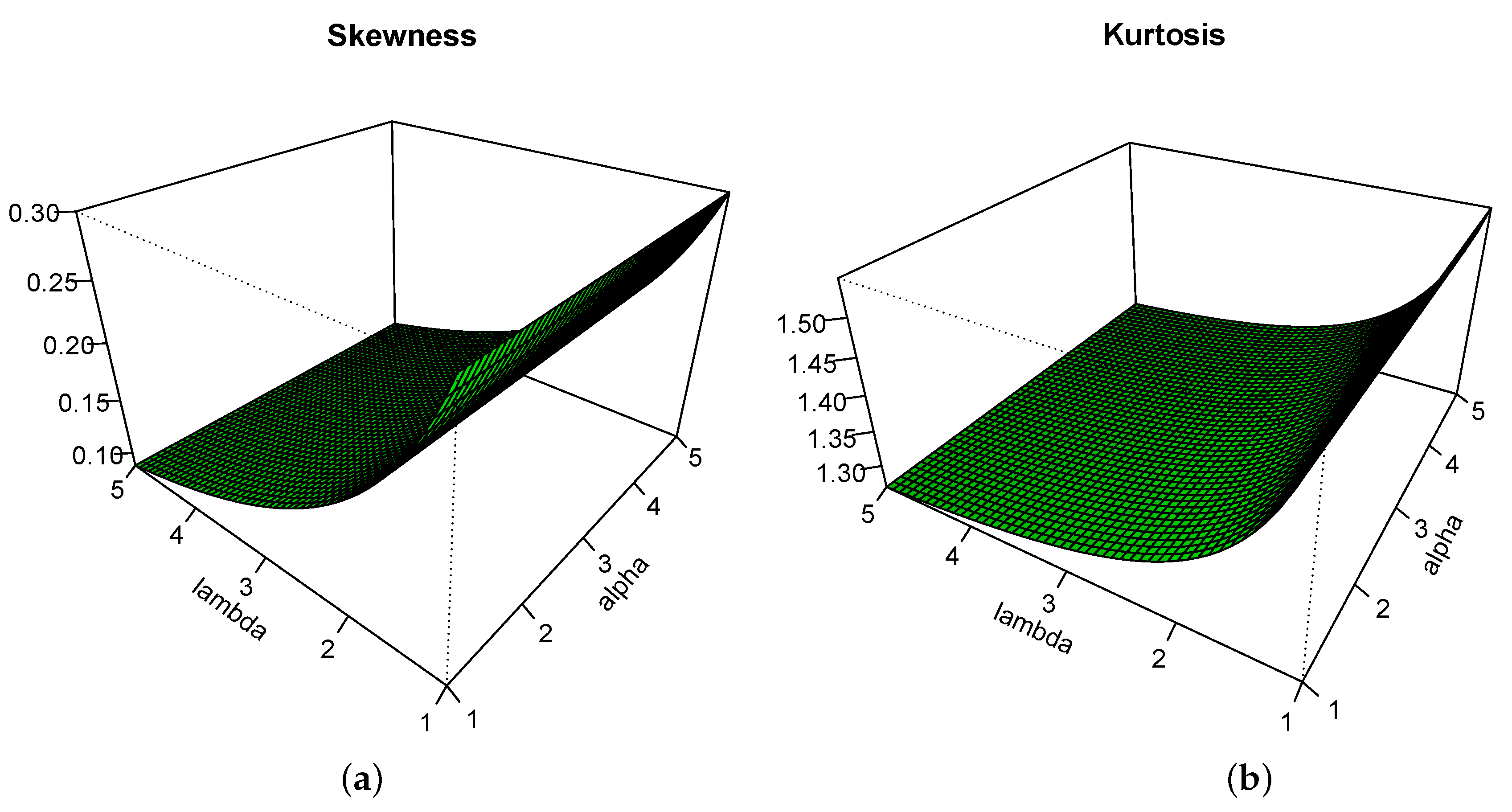
3.5. Skewness and Kurtosis Based on the qf
3.6. Measures Of Entropy
4. Estimation
4.1. Estimation of The Parameters
4.1.1. ML Method
4.1.2. Ordinary and Weighted LS Methods
4.1.3. PC Method
4.1.4. CV Method
4.1.5. Numerical Results
4.2. Estimation of The Entropy
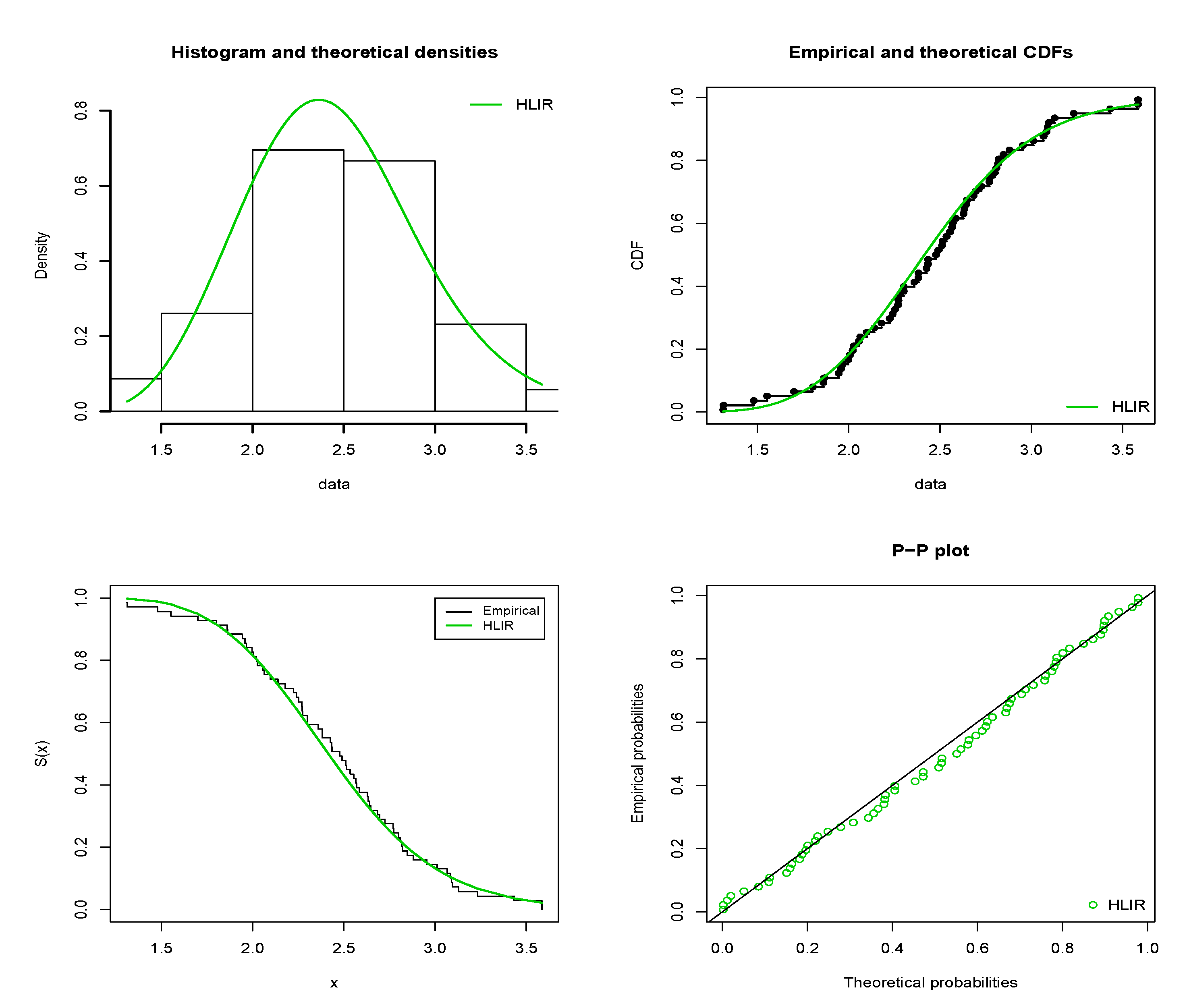
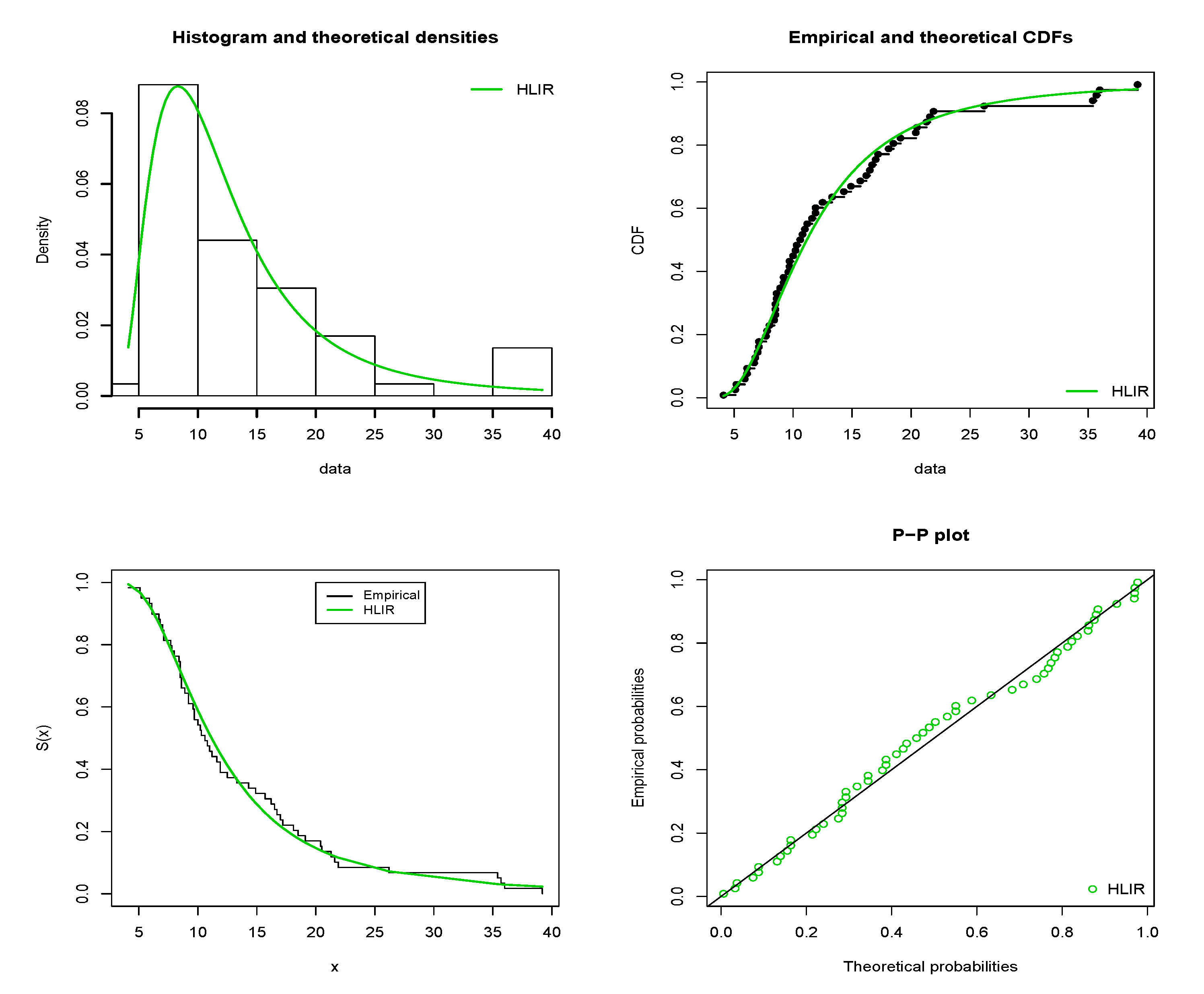
5. Applications to Real Data
- D1.
- The first data set is extracted from ([48], Table 3). For the sake of transparency, the data are: 1.312, 1.314, 1.479, 1.552, 1.700, 1.803, 1.861, 1.865, 1.944, 1.958, 1.966, 1.997, 2.006, 2.021, 2.027, 2.055, 2.063, 2.098, 2.14, 2.179, 2.224, 2.240, 2.253, 2.270, 2.272, 2.274, 2.301, 2.301, 2.359, 2.382, 2.382, 2.426, 2.434, 2.435, 2.478, 2.490, 2.511, 2.514, 2.535, 2.554, 2.566, 2.57, 2.586, 2.629, 2.633, 2.642, 2.648, 2.684, 2.697, 2.726, 2.770, 2.773, 2.800, 2.809, 2.818, 2.821, 2.848, 2.88, 2.954, 3.012, 3.067, 3.084, 3.090, 3.096, 3.128, 3.233, 3.433, 3.585, 3.585.
- D2.
- The second data set coming from [49]. The data consists of the monthly actual taxes revenue in Egypt from January 2006 to November 2010. The data (in 1000 million Egyptian pounds) are: 5.9, 20.4, 14.9, 16.2, 17.2, 7.8, 6.1, 9.2, 10.2, 9.6, 13.3, 8.5, 21.6, 18.5, 5.1, 6.7, 17, 8.6, 9.7, 39.2, 35.7, 15.7, 9.7, 10, 4.1, 36, 8.5, 8, 9.2, 26.2, 21.9, 16.7, 21.3, 35.4, 14.3, 8.5, 10.6, 19.1, 20.5, 7.1, 7.7, 18.1, 16.5, 11.9, 7, 8.6, 12.5, 10.3, 11.2, 6.1, 8.4, 11, 11.6, 11.9, 5.2, 6.8, 8.9, 7.1, 10.8. The corresponding histogram shows that the distribution of the data is highly right-skewed, motivating the use of the HLIR model for suitable fits.
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trayer, V.N. Proceedings of the Academy of Science Belarus; Doklady Akademii Nauk: Minsk, Belarus, 1964. [Google Scholar]
- Voda, V.G. On the inverse Rayleigh distributed random variable. Rep. Stat. Appl. Res. 1972, 19, 13–21. [Google Scholar]
- Gharraph, M.K. Comparison of estimators of location measures of an inverse Rayleigh distribution. Egypt Stat. J. 1993, 37, 295–309. [Google Scholar]
- El-Helbawy, A.A. Bayesian estimation and prediction for the inverse Rayleigh lifetime distribution. In Proceeding of the 40st Annual Conference of Statistics, Computer Sciences and Operation Research; Cairo University: Giza, Egypt, 2005; pp. 45–59. [Google Scholar]
- Mohsin, M.; Shahbaz, M.Q. Comparison of negative moment estimator with maximum likelihood estimator of inverse Rayleigh distribution. Pak. J. Stat. Oper. Res. 2005, 1, 45–48. [Google Scholar] [CrossRef]
- Soliman, A.; Amin, E.A.; Abd-EI Aziz, A.A. Estimation and prediction from inverse Rayleigh distribution based on lower record values. Appl. Math. Sci. 2010, 4, 3057–3066. [Google Scholar]
- Dey, S. Bayesian estimation of the parameter and reliability function of an inverse Rayleigh distribution. Malays. J. Math. Sci. 2012, 6, 113–124. [Google Scholar]
- Sindhu, T.N.; Aslam, M.; Feroze, N. Bayes estimation of the parameters of the inverse Rayleigh distribution for left censored data. Prob. Stat. Forum 2013, 6, 42–59. [Google Scholar]
- Fan, G. Bayes estimation for inverse Rayleigh model under different loss functions. Res. J. Appl. Sci. Eng. Technol. 2015, 9, 1115–1118. [Google Scholar] [CrossRef]
- Rasheed, H.A.; Ismail, S.Z.; Jabir, A.G. A comparison of the classical estimators with the Bayes estimators of one parameter inverse Rayleigh distribution. Int. J. Adv. Res. 2015, 3, 738–749. [Google Scholar]
- Panwar, M.S.; Sudhir, B.A.; Bundel, R.; Tomer, S.K. Parameter estimation of Inverse Rayleigh distribution under competing risk model for masked data. J. Inst. Sci. Technol. 2015, 20, 122–127. [Google Scholar] [CrossRef][Green Version]
- Rasheed, H.A.; Aref, R.K.H. Reliability estimation in inverse Rayleigh distribution using precautionary loss function. Math. Stat. J. 2016, 2, 9–15. [Google Scholar]
- Leao, J.; Saulo, H.; Bourguignon, M.; Cintra, J.; Rego, L.; Cordeiro, G.M. On some properties of the beta Inverse Rayleigh distribution. Chil. J. Stat. 2013, 4, 111–131. [Google Scholar]
- Ahmad, A.; Ahmad, S.P.; Ahmed, A. Transmuted inverse Rayleigh distribution: A generalization of the inverse Rayleigh distribution. Math. Theory Model. 2014, 4, 90–98. [Google Scholar]
- Khan, M.S. Modified inverse Rayleigh distribution. Int. J. Comput. Appl. 2014, 87, 28–33. [Google Scholar]
- Khan, M.S.; King, R. Transmuted modified inverse Rayleigh distribution. Austrian J. Stat. 2015, 44, 17–29. [Google Scholar] [CrossRef]
- Haq, M.A. Transmuted exponentiated inverse Rayleigh distribution. J. Stat. Appl. Prob. 2015, 5, 337–343. [Google Scholar] [CrossRef]
- Haq, M.A. Kumaraswamy exponentiated inverse Rayleigh distribution. Math. Theory Model. 2016, 6, 93–104. [Google Scholar]
- Fatima, K.; Ahmad, S.P. Weighted inverse Rayleigh distribution. Int. J. Stat. Syst. 2017, 12, 119–137. [Google Scholar]
- Elgarhy, M.; Alrajhi, S. The odd Fréchet inverse Rayleigh distribution: Statistical properties and applications. J. Nonlinear Sci. Appl. 2019, 12, 291–299. [Google Scholar] [CrossRef]
- Mohammed, H.F.; Yahia, N. On type II Topp-Leone inverse Rayleigh distribution. Appl. Math. Sci. 2019, 13, 607–615. [Google Scholar] [CrossRef]
- Yahia, N.; Mohammed, H.F. The type II Topp-Leone generalized inverse Rayleigh distribution. Int. J. Contemp. Math. Sci. 2019, 14, 113–122. [Google Scholar] [CrossRef]
- Rao, G.S.; Mbwambo, S. Exponentiated inverse Rayleigh distribution and an application to coating weights of iron sheets data. J. Probab. Stat. 2019, 2019, 7519429. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Marinho, E.P.R.D. The type I half-logistic family of distributions. J. Stat. Comput. Simul. 2016, 86, 707–728. [Google Scholar] [CrossRef]
- Anwar, M.; Zahoor, J. The half-logistic Lomax distribution for lifetime modeling. J. Probab. Stat. 2018, 2018, 3152807. [Google Scholar] [CrossRef]
- Aldahlan, M.A. Different methods of estimation for the parameters of half logistic Lomax distribution. Appl. Math. Sci. 2019, 13, 201–208. [Google Scholar] [CrossRef]
- Elbatal, I.; Almarashi, A.M.; Elgarhy, M.; Haq, M.A. Type I half-logistic power Lindley distribution with applications. Far East J. Math. Sci. (FJMS) 2019, 111, 37–54. [Google Scholar] [CrossRef]
- Anwar, M.; Bibi, A. The Half-Logistic generalized Weibull distribution. J. Probab. Stat. 2018, 2018, 8767826. [Google Scholar] [CrossRef]
- Shrahili, M.; Elbatal, M.; Muhammad, M. The type I half-logistic Burr X distribution: Theory and practice. J. Nonlinear Sci. Appl. 2019, 12, 262–277. [Google Scholar] [CrossRef][Green Version]
- ZeinEldin, R.A.; Chesneau, C.; Jamal, F.; Elgarhy, M. Different estimation methods for Type I half-logistic Topp-Leone distribution. Mathematics 2019, 7, 985. [Google Scholar] [CrossRef]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data, 2nd ed.Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Rady, E.A.; Hassanein, W.A.; Elhaddad, T.A. The Power Lomax Distribution with an Application to Bladder Cancer Data; Springer Plus: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Butler, R.; McDonald, J. Using incomplete moments to measure inequality. J. Econom. 1989, 42, 109–119. [Google Scholar] [CrossRef]
- Cowell, F.A. Measuring Inequality, 2nd ed.; Harvester Wheatsheaf: Hamel Hempstead, UK, 1995. [Google Scholar]
- Kenney, J.F.; Keeping, E.S. Mathematics of Statistics, 3rd ed.; Van Nostrand: Princeton, NJ, USA, 1962. [Google Scholar]
- Moors, J.J.A. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; pp. 47–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Amigo, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Ahsanullah, M.; Kibria, B.M.G.; Shakil, M. Normal and Student’s T Distributions and Their Applications; Atlantis Press: Paris, France, 2014. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury Advanced Series Thomson Learning: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Swain, J.; Venkatraman, S.; Wilson, J. Least squares estimation of distribution function in Johnson’s translation system. J. Stat. Comput. Simul. 1988, 29, 271–297. [Google Scholar] [CrossRef]
- Kao, J.H. Computer methods for estimating Weibull parameters in reliability studies. IRE Trans. Reliab. Qual. Control. 1958, 13, 15–22. [Google Scholar] [CrossRef]
- Kao, J.H. A graphical estimation of mixed Weibull parameters in life-testing of electron tubes. Technometrics 1959, 1, 389–407. [Google Scholar] [CrossRef]
- D’Agostino, R.; Stephens, M. Goodness-of-Fit Techniques; Marcel Dekker: New York, NY, USA, 1986. [Google Scholar]
- Luceno, A. Fitting the generalized Pareto distribution to data using maximum goodness-of-fit estimators. Comput. Stat. Data Anal. 2006, 51, 904–917. [Google Scholar] [CrossRef]
- Macdonald, P.D.M. Comment on an estimation procedure for mixtures of distributions by Choi and Bulgren. J. R. Stat. Soc. B 1971, 33, 326–329. [Google Scholar]
- Kundu, D.; Raqab, M.Z. Estimation of R = P(X < Y) for three parameter Weibull distribution. Statist. Probab. Lett. 2009, 79, 1839–1846. [Google Scholar]
- Mead, M.E. On five- parameter Lomax distribution: Properties and applications. Pak. J. Stat. Oper. Res. 2016, 1, 185–199. [Google Scholar]
- Claeskens, G.; Hjort, N.L. Model Selection and Model Averaging; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Marinho, P.R.D.; Silva, R.B.; Bourguignon, M.; Cordeiro, G.M.; Nadarajah, S. AdequacyModel: An R package for probability distributions and general purpose optimization. PLoS ONE 2019, 14, e0221487. [Google Scholar] [CrossRef]
| n | MLEs | LSEs | WLSEs | PCEs | CVEs | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Es | MSE | Es | MSE | Es | MSE | Es | MSE | Es | MSE | |
| 10 | 1.713 | 0.302 | 1.478 | 0.374 | 1.471 | 0.287 | 1.378 | 0.319 | 1.744 | 1.379 |
| 0.991 | 0.287 | 0.855 | 0.447 | 0.841 | 0.395 | 1.005 | 7.810 | 1.109 | 1.215 | |
| 20 | 1.627 | 0.130 | 1.496 | 0.142 | 1.511 | 0.126 | 1.402 | 0.142 | 1.623 | 0.843 |
| 0.904 | 0.079 | 0.828 | 0.078 | 0.835 | 0.071 | 0.798 | 0.145 | 0.928 | 0.130 | |
| 30 | 1.567 | 0.065 | 1.492 | 0.090 | 1.510 | 0.082 | 1.373 | 0.098 | 1.575 | 0.699 |
| 0.856 | 0.034 | 0.808 | 0.043 | 0.818 | 0.040 | 0.745 | 0.075 | 0.866 | 0.059 | |
| 50 | 1.545 | 0.037 | 1.502 | 0.054 | 1.514 | 0.045 | 1.408 | 0.057 | 1.553 | 0.623 |
| 0.838 | 0.020 | 0.814 | 0.026 | 0.819 | 0.022 | 0.752 | 0.045 | 0.849 | 0.032 | |
| 100 | 1.523 | 0.018 | 1.503 | 0.026 | 1.513 | 0.022 | 1.424 | 0.031 | 1.527 | 0.555 |
| 0.817 | 8.129 * | 0.805 | 0.012 | 0.810 | 9.531 * | 0.747 | 0.024 | 0.821 | 0.013 | |
| 200 | 1.507 | 8.193 * | 1.497 | 8.467 * | 1.500 | 9.781 * | 1.446 | 0.017 | 1.506 | 0.511 |
| 0.807 | 4.213 * | 0.800 | 3.667 * | 0.803 | 4.774 * | 0.761 | 0.014 | 0.808 | 5.512 * | |
| n | MLEs | LSEs | WLSEs | PCEs | CVEs | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Es | MSE | Es | MSE | Es | MSE | Es | MSE | Es | MSE | |
| 10 | 1.822 | 0.613 | 1.521 | 0.617 | 1.510 | 0.542 | 1.398 | 0.455 | 1.868 | 2.750 |
| 0.615 | 0.088 | 0.532 | 0.087 | 0.534 | 0.117 | 0.555 | 0.275 | 0.661 | 0.199 | |
| 20 | 1.682 | 0.211 | 1.508 | 0.235 | 1.559 | 0.243 | 1.407 | 0.196 | 1.673 | 1.673 |
| 0.554 | 0.021 | 0.508 | 0.023 | 0.525 | 0.030 | 0.498 | 0.044 | 0.560 | 0.035 | |
| 30 | 1.590 | 0.104 | 1.486 | 0.151 | 1.511 | 0.121 | 1.378 | 0.131 | 1.591 | 1.360 |
| 0.536 | 0.014 | 0.506 | 0.014 | 0.514 | 0.014 | 0.485 | 0.032 | 0.539 | 0.019 | |
| 50 | 1.557 | 0.057 | 1.485 | 0.074 | 1.511 | 0.070 | 1.395 | 0.074 | 1.547 | 1.176 |
| 0.517 | 6.076 * | 0.499 | 7.249 * | 0.504 | 6.665 * | 0.473 | 0.014 | 0.517 | 8.380 * | |
| 100 | 1.522 | 0.025 | 1.504 | 0.038 | 1.500 | 0.030 | 1.420 | 0.041 | 1.534 | 1.109 |
| 0.507 | 2.733 * | 0.501 | 3.607 * | 0.502 | 2.987 * | 0.476 | 7.316 * | 0.510 | 3.905 * | |
| 200 | 1.516 | 0.011 | 1.503 | 0.021 | 1.508 | 0.014 | 1.445 | 0.020 | 1.518 | 1.058 |
| 0.504 | 1.175 * | 0.500 | 1.744 * | 0.502 | 1.370 * | 0.479 | 4.204 * | 0.505 | 1.811 * | |
| n | MLEs | LSEs | WLSEs | PCEs | CVEs | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Es | MSE | Es | MSE | Es | MSE | Es | MSE | Es | MSE | |
| 10 | 1.696 | 0.263 | 1.466 | 0.270 | 1.477 | 0.248 | 1.383 | 0.272 | 1.706 | 0.842 |
| 1.314 | 0.705 | 1.128 | 1.309 | 1.132 | 1.397 | 1.233 | 5.499 | 1.496 | 3.430 | |
| 20 | 1.616 | 0.102 | 1.513 | 0.131 | 1.526 | 0.114 | 1.408 | 0.129 | 1.630 | 0.545 |
| 1.137 | 0.124 | 1.082 | 0.606 | 1.07 | 0.217 | 1.003 | 0.345 | 1.233 | 1.352 | |
| 30 | 1.556 | 0.055 | 1.485 | 0.072 | 1.499 | 0.062 | 1.388 | 0.092 | 1.56 | 0.391 |
| 1.086 | 0.074 | 1.025 | 0.085 | 1.033 | 0.073 | 0.965 | 0.295 | 1.107 | 0.119 | |
| 50 | 1.537 | 0.032 | 1.489 | 0.045 | 1.502 | 0.037 | 1.406 | 0.054 | 1.533 | 0.332 |
| 1.043 | 0.033 | 1.002 | 0.043 | 1.012 | 0.036 | 0.929 | 0.079 | 1.047 | 0.052 | |
| 100 | 1.513 | 0.014 | 1.490 | 0.020 | 1.498 | 0.016 | 1.429 | 0.030 | 1.522 | 0.295 |
| 1.017 | 0.014 | 0.999 | 0.019 | 1.005 | 0.016 | 0.938 | 0.044 | 1.027 | 0.022 | |
| 200 | 1.511 | 6.475 * | 1.500 | 0.010 | 1.505 | 7.969 * | 1.452 | 0.014 | 1.511 | 0.271 |
| 1.009 | 5.961 * | 1.000 | 8.878 * | 1.005 | 7.127 * | 0.947 | 0.024 | 1.011 | 9.286 * | |
| n | MLEs | LSEs | WLSEs | PCEs | CVEs | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Es | MSE | Es | MSE | Es | MSE | Es | MSE | Es | MSE | |
| 10 | 0.606 | 0.069 | 0.502 | 0.069 | 0.506 | 0.063 | 0.466 | 0.051 | 0.621 | 0.126 |
| 0.615 | 0.088 | 0.538 | 0.145 | 0.541 | 0.143 | 0.557 | 0.284 | 0.664 | 0.213 | |
| 20 | 0.561 | 0.023 | 0.515 | 0.031 | 0.520 | 0.027 | 0.469 | 0.022 | 0.554 | 0.032 |
| 0.554 | 0.021 | 0.526 | 0.052 | 0.525 | 0.030 | 0.498 | 0.044 | 0.553 | 0.035 | |
| 30 | 0.530 | 0.012 | 0.498 | 0.016 | 0.504 | 0.013 | 0.459 | 0.015 | 0.542 | 0.020 |
| 0.536 | 0.014 | 0.510 | 0.015 | 0.514 | 0.014 | 0.485 | 0.032 | 0.540 | 0.017 | |
| 50 | 0.519 | 6.332 * | 0.498 | 9.623 * | 0.504 | 7.787 * | 0.465 | 8.251 * | 0.521 | 0.011 |
| 0.517 | 6.076 * | 0.499 | 7.766 * | 0.504 | 6.665 * | 0.473 | 0.014 | 0.523 | 9.412 * | |
| 100 | 0.507 | 2.773 * | 0.497 | 4.192 * | 0.500 | 3.278 * | 0.473 | 4.530 * | 0.511 | 4.964 * |
| 0.507 | 2.733 * | 0.499 | 3.481 * | 0.502 | 2.987 * | 0.476 | 7.316 * | 0.512 | 4.168 * | |
| 200 | 0.505 | 1.222 * | 0.501 | 2.110 * | 0.503 | 1.600 * | 0.482 | 2.182 * | 0.504 | 1.996 * |
| 0.504 | 1.175 * | 0.500 | 1.665 * | 0.502 | 1.371 * | 0.479 | 4.204 * | 0.504 | 1.788 * | |
| n | 90% | 95% | ||||
|---|---|---|---|---|---|---|
| LB | UB | AL | LB | UB | AL | |
| 10 | 0.9812 | 2.3595 | 1.3783 | 0.8493 | 2.4915 | 1.6422 |
| 0.4155 | 1.8072 | 1.3916 | 0.2823 | 1.9404 | 1.6581 | |
| 20 | 1.0237 | 1.9731 | 0.9494 | 0.9328 | 2.0640 | 1.1311 |
| 0.4570 | 1.0406 | 0.5835 | 0.4012 | 1.0964 | 0.6953 | |
| 30 | 1.1899 | 1.9927 | 0.8028 | 1.1131 | 2.0696 | 0.9565 |
| 0.5637 | 1.1046 | 0.5409 | 0.5119 | 1.1564 | 0.6445 | |
| 50 | 1.3385 | 1.9514 | 0.6130 | 1.2798 | 2.0101 | 0.7303 |
| 0.7090 | 1.2018 | 0.4928 | 0.6618 | 1.2490 | 0.5872 | |
| 100 | 1.2681 | 1.6878 | 0.4197 | 1.2280 | 1.7280 | 0.5000 |
| 0.6276 | 0.8917 | 0.2641 | 0.6023 | 0.9170 | 0.3147 | |
| 200 | 1.3499 | 1.6483 | 0.2983 | 1.3214 | 1.6768 | 0.3554 |
| 0.6857 | 0.8793 | 0.1936 | 0.6671 | 0.8978 | 0.2307 | |
| n | 90% | 95% | ||||
|---|---|---|---|---|---|---|
| LB | UB | AL | LB | UB | AL | |
| 10 | 0.8230 | 2.4433 | 1.6203 | 0.6679 | 2.5984 | 1.9305 |
| 0.2930 | 0.9958 | 0.7028 | 0.2257 | 1.0631 | 0.8374 | |
| 20 | 1.1324 | 2.4175 | 1.2851 | 1.0093 | 2.5405 | 1.5312 |
| 0.3437 | 0.7453 | 0.4016 | 0.3053 | 0.7838 | 0.4785 | |
| 30 | 1.2235 | 2.2379 | 1.0144 | 1.1264 | 2.3351 | 1.2086 |
| 0.3834 | 0.7141 | 0.3307 | 0.3517 | 0.7458 | 0.3941 | |
| 50 | 1.1789 | 1.8935 | 0.7146 | 1.1105 | 1.9619 | 0.8515 |
| 0.3984 | 0.6401 | 0.2416 | 0.3753 | 0.6632 | 0.2879 | |
| 100 | 1.2926 | 1.8030 | 0.5104 | 1.2437 | 1.8519 | 0.6082 |
| 0.4320 | 0.6013 | 0.1693 | 0.4158 | 0.6175 | 0.2017 | |
| 200 | 1.3099 | 1.6611 | 0.3511 | 1.2763 | 1.6947 | 0.4184 |
| 0.4385 | 0.5523 | 0.1138 | 0.4276 | 0.5632 | 0.1356 | |
| n | 90% | 95% | ||||
|---|---|---|---|---|---|---|
| LB | UB | AL | LB | UB | AL | |
| 10 | 1.0988 | 2.3947 | 1.2959 | 0.9747 | 2.5187 | 1.5440 |
| 0.5174 | 2.3797 | 1.8624 | 0.3390 | 2.5580 | 2.2190 | |
| 20 | 1.2117 | 2.1173 | 0.9057 | 1.1249 | 2.2040 | 1.0791 |
| 0.7164 | 1.8340 | 1.1176 | 0.6094 | 1.9410 | 1.3316 | |
| 30 | 1.3016 | 2.0438 | 0.7422 | 1.2305 | 2.1149 | 0.8844 |
| 0.7916 | 1.6449 | 0.8533 | 0.7099 | 1.7265 | 1.0167 | |
| 50 | 1.3957 | 1.9756 | 0.5800 | 1.3401 | 2.0312 | 0.6910 |
| 0.9009 | 1.5806 | 0.6797 | 0.8358 | 1.6457 | 0.8099 | |
| 100 | 1.3614 | 1.7592 | 0.3978 | 1.3233 | 1.7973 | 0.4740 |
| 0.8509 | 1.2381 | 0.3872 | 0.8138 | 1.2752 | 0.4614 | |
| 200 | 1.3840 | 1.6621 | 0.2780 | 1.3574 | 1.6887 | 0.3313 |
| 0.8758 | 1.1375 | 0.2618 | 0.8507 | 1.1626 | 0.3119 | |
| n | 90% | 95% | ||||
|---|---|---|---|---|---|---|
| LB | UB | AL | LB | UB | AL | |
| 10 | 0.3509 | 0.9691 | 0.6182 | 0.2917 | 1.0283 | 0.7365 |
| 0.3310 | 1.1897 | 0.8587 | 0.2488 | 1.2719 | 1.0232 | |
| 20 | 0.3634 | 0.7614 | 0.3980 | 0.3253 | 0.7995 | 0.4742 |
| 0.3625 | 0.7954 | 0.4329 | 0.3211 | 0.8368 | 0.5157 | |
| 30 | 0.4275 | 0.7659 | 0.3384 | 0.3951 | 0.7983 | 0.4032 |
| 0.4320 | 0.8254 | 0.3935 | 0.3943 | 0.8631 | 0.4688 | |
| 50 | 0.3565 | 0.5830 | 0.2264 | 0.3349 | 0.6046 | 0.2698 |
| 0.3658 | 0.5833 | 0.2174 | 0.3450 | 0.6041 | 0.2591 | |
| 100 | 0.4149 | 0.5828 | 0.1680 | 0.3988 | 0.5989 | 0.2001 |
| 0.4147 | 0.5764 | 0.1617 | 0.3993 | 0.5919 | 0.1926 | |
| 200 | 0.4638 | 0.5858 | 0.1220 | 0.4521 | 0.5974 | 0.1454 |
| 0.4591 | 0.5795 | 0.1204 | 0.4475 | 0.5911 | 0.1435 | |
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 0.929 | 0.836 | 0.100 | 0.858 | 0.743 | 0.134 | 0.787 | 0.708 | 0.101 |
| 20 | 0.908 | 0.023 | 0.829 | 0.034 | 0.770 | 0.022 | |||
| 30 | 0.910 | 0.020 | 0.832 | 0.031 | 0.779 | 0.011 | |||
| 50 | 0.917 | 0.013 | 0.842 | 0.018 | 0.782 | 6.454 * | |||
| 100 | 0.937 | 8.576 * | 0.854 | 4.477 * | 0.786 | 1.323 * | |||
| 200 | 0.929 | 0.252 * | 0.858 | 0.004 * | 0.788 | 0.968 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 1.279 | 1.213 | 0.052 | 1.167 | 1.077 | 0.077 | 1.062 | 1.001 | 0.058 |
| 20 | 1.223 | 0.044 | 1.144 | 0.020 | 1.036 | 0.024 | |||
| 30 | 1.265 | 0.011 | 1.149 | 0.015 | 1.038 | 0.022 | |||
| 50 | 1.265 | 0.011 | 1.160 | 6.064 * | 1.055 | 6.444 * | |||
| 100 | 1.267 | 9.558 * | 1.161 | 5.065 * | 1.058 | 3.544 * | |||
| 200 | 1.273 | 5.068 * | 1.164 | 2.707 * | 1.059 | 2.975 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 0.789 | 0.668 | 0.153 | 0.73 | 0.640 | 0.123 | 0.671 | 0.610 | 0.091 |
| 20 | 0.714 | 0.095 | 0.705 | 0.035 | 0.637 | 0.050 | |||
| 30 | 0.761 | 0.035 | 0.712 | 0.026 | 0.659 | 0.017 | |||
| 50 | 0.776 | 0.016 | 0.713 | 0.025 | 0.663 | 0.012 | |||
| 100 | 0.779 | 0.012 | 0.722 | 0.011 | 0.669 | 3.100 * | |||
| 200 | 0.788 | 1.497 * | 0.725 | 6.639 * | 0.671 | 0.357 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 0.802 | 0.730 | 0.089 | 0.69 | 0.604 | 0.125 | 0.585 | 0.522 | 0.108 |
| 20 | 0.778 | 0.030 | 0.661 | 0.042 | 0.568 | 0.029 | |||
| 30 | 0.791 | 0.014 | 0.669 | 0.031 | 0.576 | 0.016 | |||
| 50 | 0.796 | 7.181 * | 0.679 | 0.015 | 0.577 | 0.014 | |||
| 100 | 0.797 | 5.891 * | 0.688 | 2.132 * | 0.589 | 7.532 * | |||
| 200 | 0.800 | 2.364 * | 0.689 | 0.606 * | 0.585 | 0.511 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 1.74 | 1.584 | 0.090 | 1.255 | 1.184 | 0.057 | 0.837 | 0.812 | 0.030 |
| 20 | 1.665 | 0.043 | 1.240 | 0.012 | 0.817 | 0.024 | |||
| 30 | 1.714 | 0.015 | 1.242 | 0.011 | 0.827 | 0.012 | |||
| 50 | 1.722 | 0.010 | 1.247 | 6.763 * | 0.834 | 3.921 * | |||
| 100 | 1.733 | 4.096 * | 1.262 | 5.454 * | 0.838 | 0.951 * | |||
| 200 | 1.738 | 1.241 * | 1.255 | 0.119 * | 0.837 | 0.192 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 2.226 | 2.141 | 0.038 | 1.478 | 1.447 | 0.021 | 0.913 | 0.904 | 0.010 |
| 20 | 2.166 | 0.027 | 1.456 | 0.015 | 0.906 | 8.183 * | |||
| 30 | 2.175 | 0.023 | 1.471 | 4.813 * | 0.913 | 0.362 * | |||
| 50 | 2.204 | 9.500 * | 1.472 | 4.358 * | 0.913 | 0.171 * | |||
| 100 | 2.217 | 3.877 * | 1.473 | 3.469 * | 0.913 | 0.131 * | |||
| 200 | 2.218 | 3.458 * | 1.475 | 2.095 * | 0.913 | 0.111 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 1.523 | 1.374 | 0.098 | 1.137 | 1.024 | 0.099 | 0.787 | 0.754 | 0.041 |
| 20 | 1.465 | 0.038 | 1.068 | 0.061 | 0.761 | 0.033 | |||
| 30 | 1.484 | 0.026 | 1.113 | 0.021 | 0.779 | 9.278 * | |||
| 50 | 1.499 | 0.016 | 1.126 | 9.813 * | 0.784 | 3.558 * | |||
| 100 | 1.512 | 7.609 * | 1.129 | 7.297 * | 0.788 | 1.975 * | |||
| 200 | 1.521 | 1.275 * | 1.136 | 0.757 * | 0.786 | 0.939 * | |||
| n | Exact Value | Exact Value | Exact Value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | RB | Estimate | RB | Estimate | RB | ||||
| 10 | 1.544 | 1.472 | 0.047 | 1.096 | 1.039 | 0.053 | 0.74 | 0.728 | 0.016 |
| 20 | 1.476 | 0.044 | 1.082 | 0.013 | 0.730 | 0.014 | |||
| 30 | 1.518 | 0.017 | 1.090 | 5.887 * | 0.735 | 7.336 * | |||
| 50 | 1.524 | 0.013 | 1.092 | 3.371 * | 0.736 | 5.129 * | |||
| 100 | 1.529 | 9.527 * | 1.095 | 0.878 * | 0.743 | 4.069 * | |||
| 200 | 1.536 | 5.298 * | 1.096 | 0.048 * | 0.742 | 3.075 * | |||
| Model | CVM | AD | KS | KS p-Value | MLEs and (SEs) | |
|---|---|---|---|---|---|---|
| HLIR | 0.0513 | 0.3895 | 0.0596 | 0.9668 | 3.6538 | 10.2773 |
| () | (0.2197) | (2.5587) | ||||
| TIITLIR | 0.0908 | 0.6421 | 0.0776 | 0.7993 | 2.7966 | 10.2992 |
| () | (0.1574) | (2.8538) | ||||
| TIR | 0.1767 | 1.2000 | 0.2540 | 0.0002 | 7.5093 | 0.8891 |
| () | (19.4108) | (0.0182) | ||||
| OFIR | 0.5913 | 3.7026 | 0.1801 | 0.0227 | 2.9540 | 1.3910 |
| () | (0.1862) | (0.1231) | ||||
| IR | 0.1875 | 1.2706 | 0.3549 | 0.0000 | 2.2827 | - |
| () | (0.1374) | - | ||||
| Model | CVM | AD | KS | KS p-Value | MLEs and (SEs) | |
|---|---|---|---|---|---|---|
| HLIR | 0.0476 | 0.2821 | 0.0626 | 0.9745 | 9.0540 | 1.5057 |
| () | (0.8159) | (0.2381) | ||||
| TIITLIR | 0.0487 | 0.2904 | 0.0726 | 0.9142 | 7.1702 | 1.2912 |
| () | (0.5758) | (0.2319) | ||||
| TIR | 0.0496 | 0.2885 | 0.0659 | 0.9598 | 105.9762 | 0.4105 |
| () | (19.4108) | (0.3493) | ||||
| OFIR | 0.0964 | 0.7205 | 0.1458 | 0.1623 | 47.0580 | 0.7820 |
| () | (5.1027) | (0.0838) | ||||
| IR | 0.0488 | 0.2934 | 0.0821 | 0.8203 | 9.3593 | - |
| () | (0.6092) | - | ||||
| Distribution | AIC | CAIC | BIC | HQIC | |
|---|---|---|---|---|---|
| HLIR | 50.5018 | 105.0030 | 105.1856 | 109.4720 | 106.7764 |
| TIITLIR | 52.0685 | 108.1371 | 108.3189 | 112.6053 | 109.9098 |
| TIR | 71.9390 | 145.8787 | 145.9384 | 148.1128 | 146.7651 |
| OFIR | 71.7113 | 147.4228 | 147.6046 | 151.8910 | 149.1955 |
| IR | 88.4130 | 178.8262 | 178.8859 | 181.0603 | 179.7125 |
| Distribution | AIC | CAIC | BIC | HQIC | |
|---|---|---|---|---|---|
| HLIR | 188.4997 | 380.9994 | 381.2137 | 385.1545 | 382.6213 |
| TIITLIR | 188.6142 | 381.2283 | 381.4426 | 385.3834 | 382.8503 |
| TIR | 189.1310 | 382.2620 | 382.4762 | 386.4170 | 383.8839 |
| OFIR | 193.7239 | 391.4479 | 391.6621 | 395.6029 | 393.0698 |
| IR | 190.5877 | 383.1754 | 382.2455 | 385.2529 | 382.9863 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almarashi, A.M.; Badr, M.M.; Elgarhy, M.; Jamal, F.; Chesneau, C. Statistical Inference of the Half-Logistic Inverse Rayleigh Distribution. Entropy 2020, 22, 449. https://doi.org/10.3390/e22040449
Almarashi AM, Badr MM, Elgarhy M, Jamal F, Chesneau C. Statistical Inference of the Half-Logistic Inverse Rayleigh Distribution. Entropy. 2020; 22(4):449. https://doi.org/10.3390/e22040449
Chicago/Turabian StyleAlmarashi, Abdullah M., Majdah M. Badr, Mohammed Elgarhy, Farrukh Jamal, and Christophe Chesneau. 2020. "Statistical Inference of the Half-Logistic Inverse Rayleigh Distribution" Entropy 22, no. 4: 449. https://doi.org/10.3390/e22040449
APA StyleAlmarashi, A. M., Badr, M. M., Elgarhy, M., Jamal, F., & Chesneau, C. (2020). Statistical Inference of the Half-Logistic Inverse Rayleigh Distribution. Entropy, 22(4), 449. https://doi.org/10.3390/e22040449








