Measuring the Tangle of Three-Qubit States
Abstract
1. Introduction
2. Tangle in Three-Qubit States
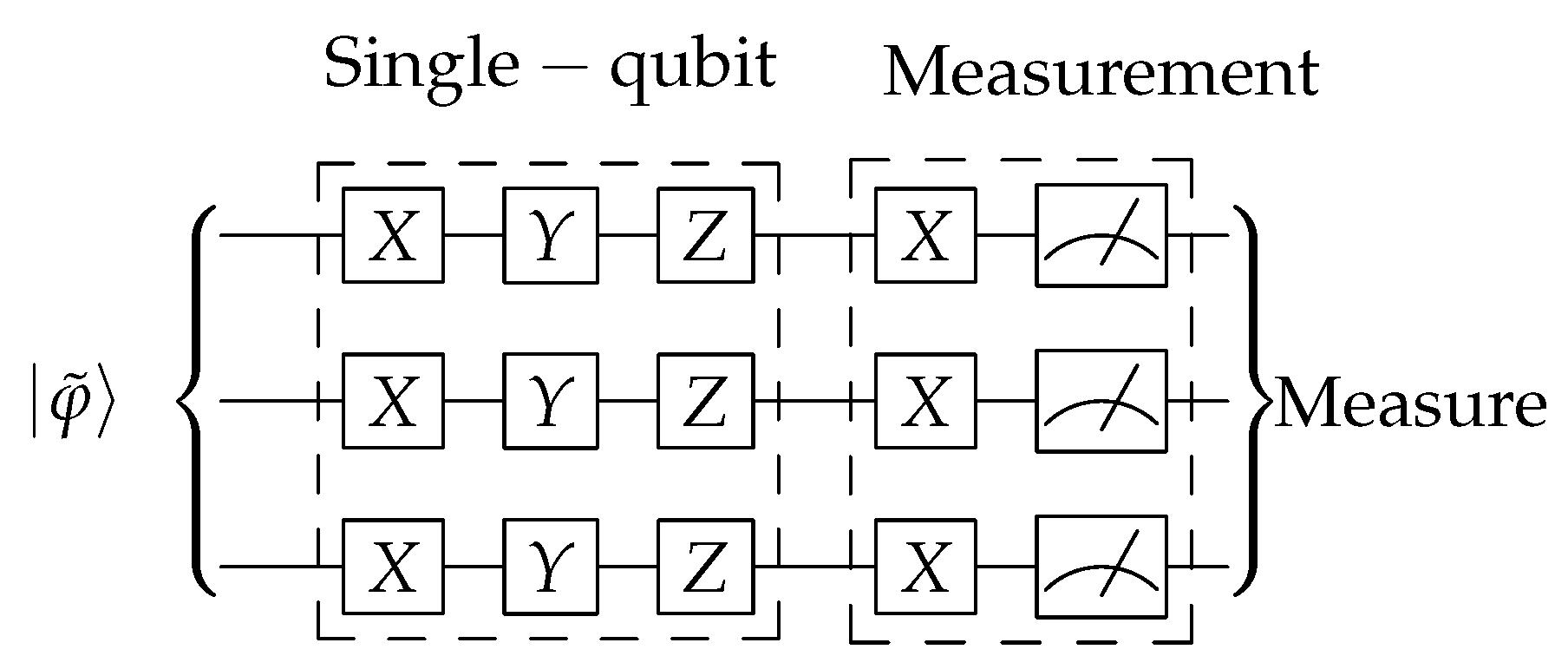
3. Quantum Algorithm for Measuring the Tangle
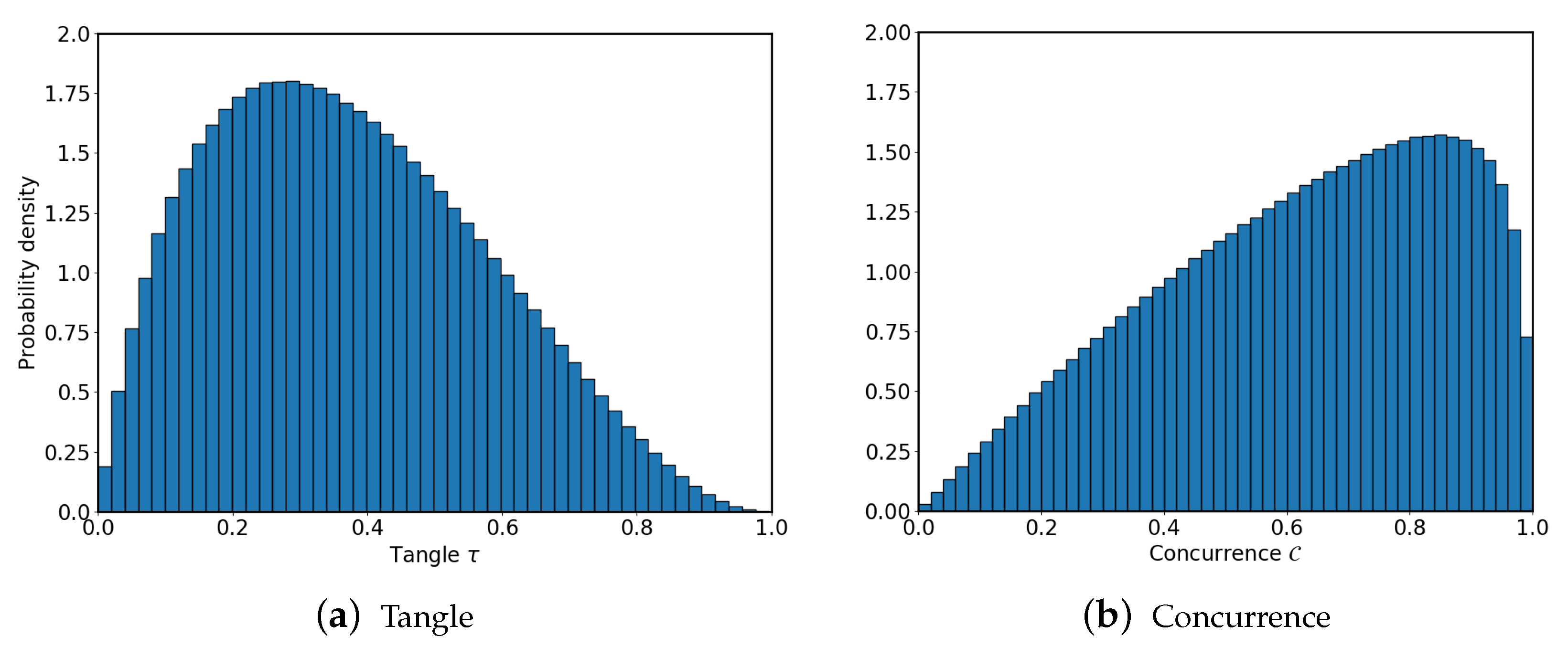
4. Simulations
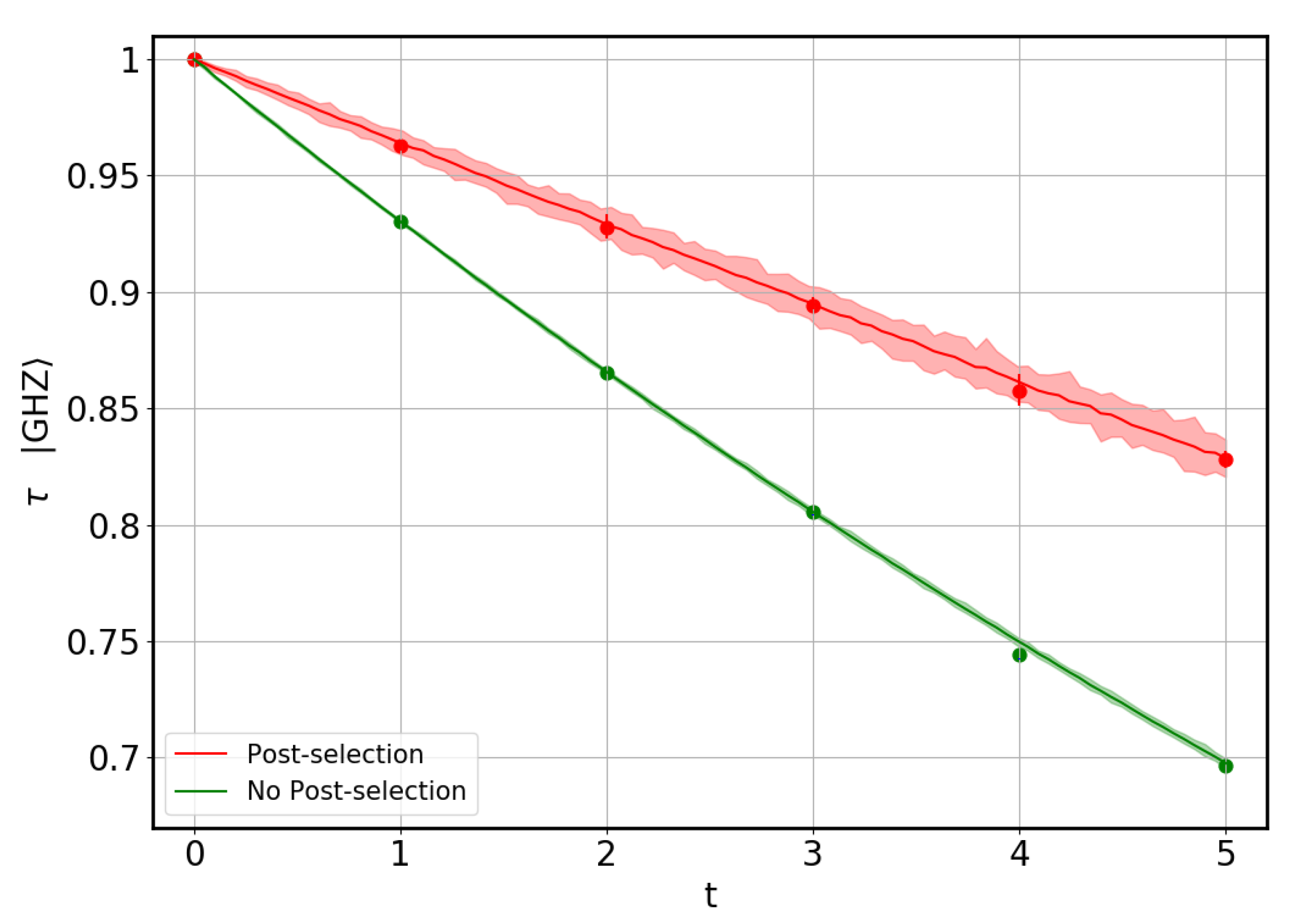
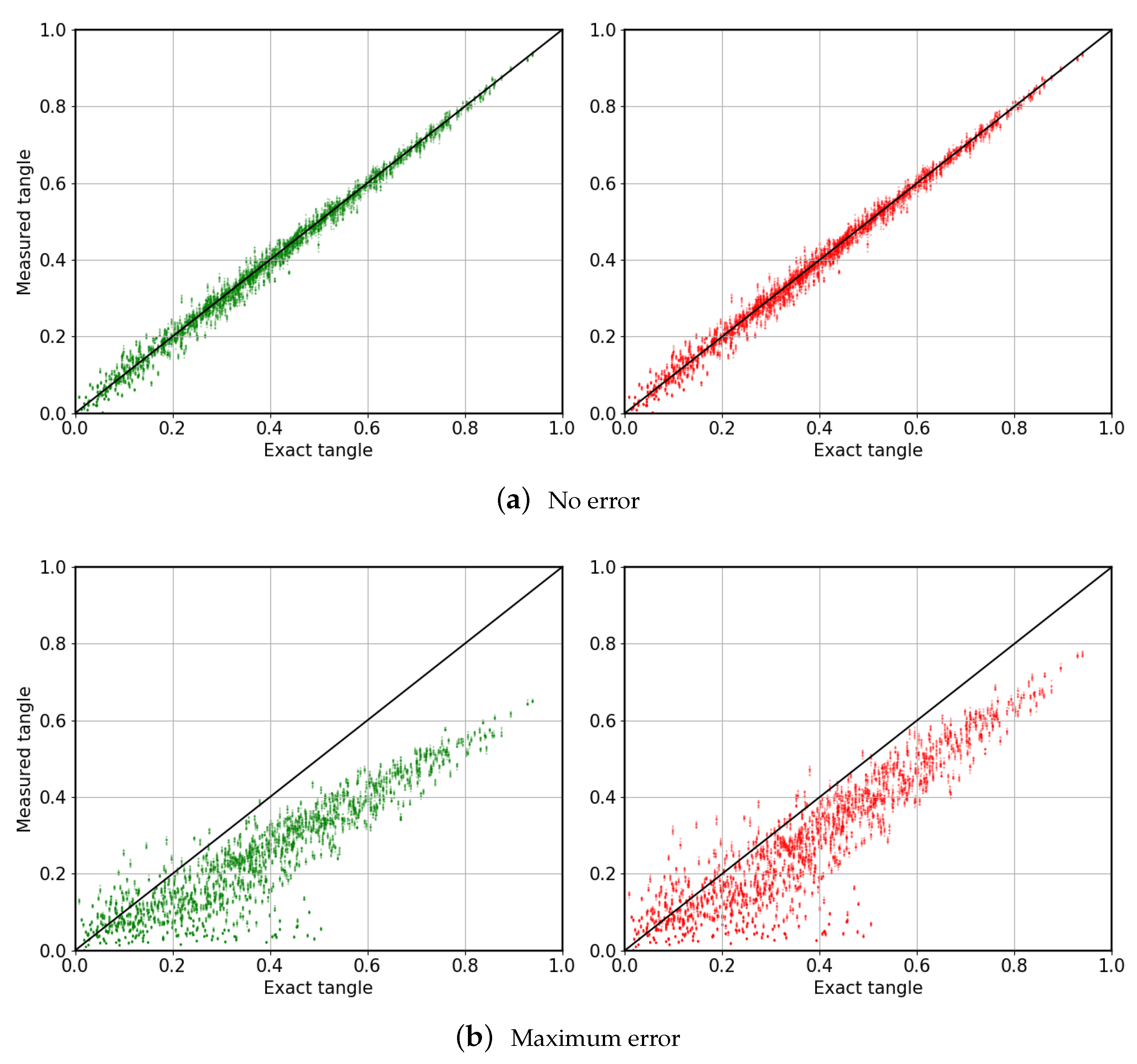
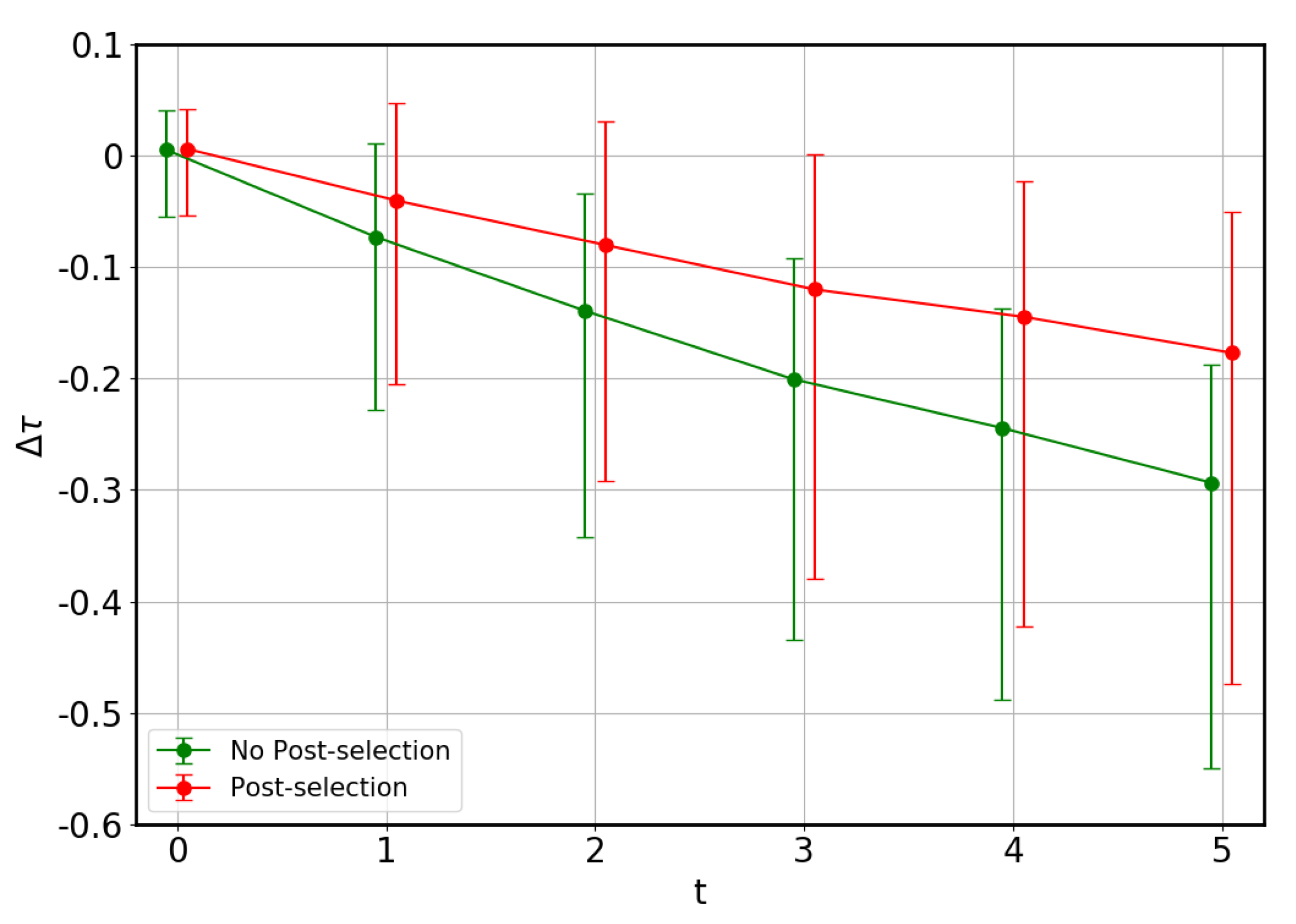
4.1. Error Model
4.2. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Laflorencie, N. Quantum entanglement in condensed matter systems. Phys. Rep. 2016, 646, 1–59. [Google Scholar] [CrossRef]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Verstraete, F.; Dehaene, J.; De Moor, B.; Verschelde, H. Four qubits can be entangled in nine different ways. Phys. Rev. A 2002, 65, 052112. [Google Scholar] [CrossRef]
- Datta, C.; Adhikari, S.; Das, A.; Agrawal, P. Distinguishing different classes of entanglement of three-qubit pure states. Eur. Phys. J. D 2018, 72, 157. [Google Scholar] [CrossRef]
- Leifer, M.S.; Linden, N.; Winter, A. Measuring polynomial invariants of multiparty quantum states. Phys. Rev. A 2004, 69, 052304. [Google Scholar] [CrossRef]
- Ekert, A.; Knight, P.L. Entangled quantum systems and the Schmidt decomposition. Am. J. Phys. 1995, 63, 415–423. [Google Scholar] [CrossRef]
- Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Latorre, J.I.; Riera, A. A short review on entanglement in quantum spin systems. J. Phys. A. Math. Theor. 2009, 42, 504002. [Google Scholar] [CrossRef]
- Peres, A. Higher order Schmidt decompositions. Phys. Lett. A 1995, 202, 16–17. [Google Scholar] [CrossRef]
- Pati, A.K. Existence of the Schmidt decomposition for tripartite systems. Phys. Lett. A 2000, 278, 118–122. [Google Scholar] [CrossRef][Green Version]
- Acín, A.; Andrianov, A.; Costa, L.; Jané, E.; Latorre, J.I.; Tarrach, R. Generalized Schmidt Decomposition and Classification of Three-Quantum-Bit States. Phys. Rev. Lett. 2000, 85, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- LaRose, R.; Tikku, A.; O’Neel-Judy, e.; Cincio, L.; Coles, P.J. Variational quantum state diagonalization. npj Quantum Inf. 2019, 5, 77. [Google Scholar] [CrossRef]
- Bravo-Prieto, C.; García-Martín, D.; Latorre, J.I. Quantum Singular Value Decomposer. arXiv 2019, arXiv:1905.01353. [Google Scholar]
- Mohseni, M.; Rezakhani, A.T.; Lidar, D.A. Quantum-Process Tomography: Resource Analysis of Different Strategies. Phys. Rev. A 2008, 77, 032322. [Google Scholar] [CrossRef]
- Enríquez, M.; Delgado, F.; Zyczkowski, K. Entanglement of Three-Qubit Random Pure States. Entropy 2018, 20, 745. [Google Scholar] [CrossRef]
- Coffman, V.; Kundu, J.; Wootters, W.K. Distributed entanglement. Phys. Rev. A 2000, 61, 052306. [Google Scholar] [CrossRef]
- Cayley, A. The Collected Mathematical Papers of Arthur Cayley; The Cambridge University Press: Cambridge, UK, 1894; Volume 1. [Google Scholar]
- Gelfand, I.M.; Kapranov, M.M.; Zelevinsky, A.V. Discriminants, Resultants, and Multidimensional Determinants; Birkhäuser Boston: Cambridge, MA, USA, 1994. [Google Scholar]
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kraus, B. Local Unitary Equivalence of Multipartite Pure States. Phys. Rev. Lett. 2010, 104, 020504. [Google Scholar] [CrossRef] [PubMed]
- Sudbery, A. On local invariants of pure three-qubit states. J. Phys. A Math. Gen. 2001, 34, 643–652. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.D.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Method. 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Powell, M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
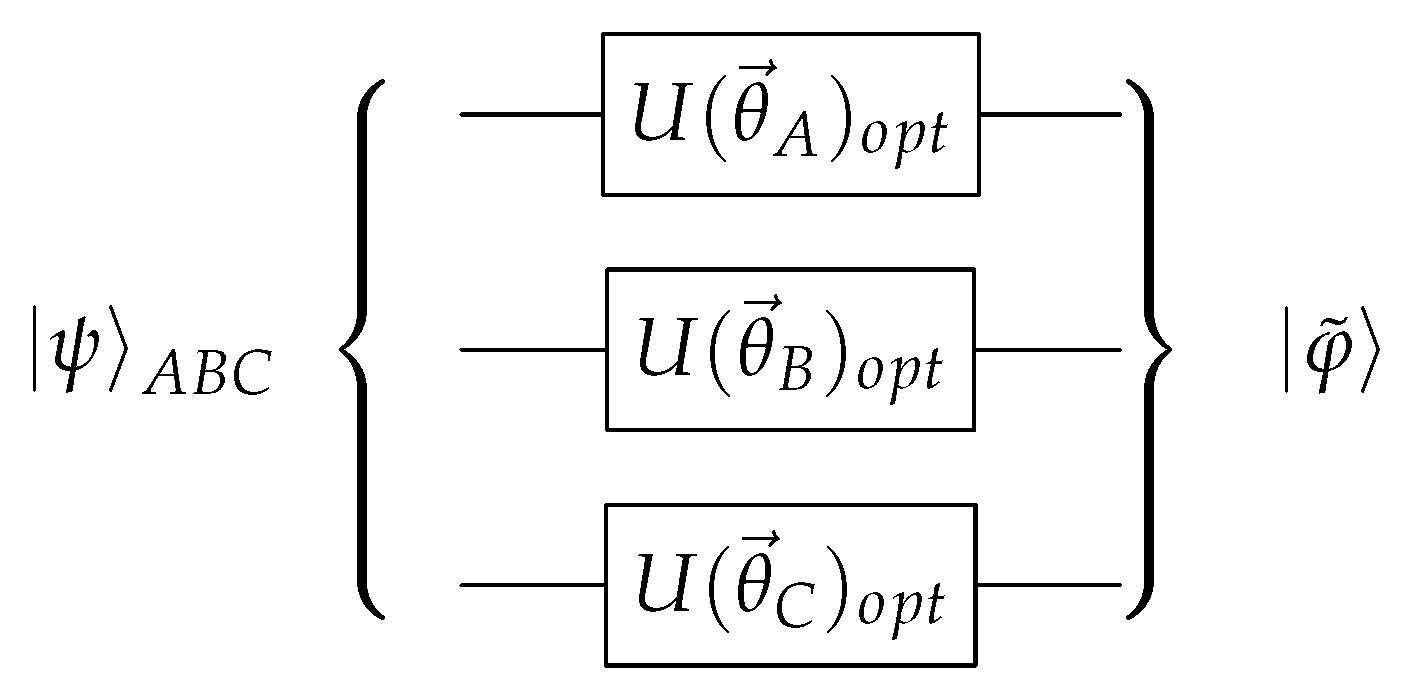
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Salinas, A.; García-Martín, D.; Bravo-Prieto, C.; Latorre, J.I. Measuring the Tangle of Three-Qubit States. Entropy 2020, 22, 436. https://doi.org/10.3390/e22040436
Pérez-Salinas A, García-Martín D, Bravo-Prieto C, Latorre JI. Measuring the Tangle of Three-Qubit States. Entropy. 2020; 22(4):436. https://doi.org/10.3390/e22040436
Chicago/Turabian StylePérez-Salinas, Adrián, Diego García-Martín, Carlos Bravo-Prieto, and José I. Latorre. 2020. "Measuring the Tangle of Three-Qubit States" Entropy 22, no. 4: 436. https://doi.org/10.3390/e22040436
APA StylePérez-Salinas, A., García-Martín, D., Bravo-Prieto, C., & Latorre, J. I. (2020). Measuring the Tangle of Three-Qubit States. Entropy, 22(4), 436. https://doi.org/10.3390/e22040436




