Sensitivity Analysis of Selected Parameters in the Order Picking Process Simulation Model, with Randomly Generated Orders
Abstract
1. Introduction
1.1. Significance of Order Picking Process
1.2. Prior Research on Order Picking Process
1.3. Objectives of the Research
2. Conceptual and Simulation Models
- mean value of lift-truck acceleration or stop, A;
- length of a rack in warehouse, L;
- mean time of lift-truck driving forward or backward (with lowered cabin and forks), ;
- mean time of lift-truck driving forward or backward (with lifted cabin and forks), ;
- rack height (from the ground to the bottom of the highest rack storey), ;
- free lift of forks, ;
- medium value of load unit lifting up time, ;
- medium value of load unit lowering time, ;
- mean time of lift-truck fork ejection or rotation, N;
- time of picking list reading by employee, ;
- time of reading the next row in a picking list, ;
- time of single item picking, .
- mean value of lift-truck acceleration or stop, A = 0.0475 [min] (value based on [31]);
- length of a rack in warehouse, L = 150 [m];
- mean time of lift-truck driving forward or backward (with lowered cabin and forks), F1 = 0.0079 [min/m] (the value of mean of transport velocity, i.e., v = 10.5 km/h, given in [105] has been converted to the F1 parameter, which is used in the analytical calculations; in turn, the velocity of the modeled mean of transport has been noted as vsym = 0.8547 [m/s], which is related to the simultaneous considerations on the mean of transport forward or backward movement with the lifted cabin and forks);
- rack height (from the ground to the bottom of the highest rack storey), H = 14.5 [m] (the adoption of this value is dictated by the fact that the lifting height in the catalog [105] is 14 570 [mm]);
- free lift of forks, h2 = 0.8 [m] (value based on [105]);
- medium value of load unit lifting up time, U = 0.0833 [min/m] (the lifting velocity vU = 0.2 [m/s] given in [105] is used to determine this value);
- medium value of load unit lowering time, D = 0.0417 [min/m] (the lowering velocity vD = 0.4 [m/s] given in [105] is used to determine this value);
- mean time of lift-truck fork ejection or rotation, N = 0.13 [min] (value based on [31]);
- time of picking list reading by employee, = 0.0852 [min] (value based on [31]);
- time of reading the next row in a picking list, = 0.118 [min] (value based on [31]);
- time of single item picking, = 0.118 [min] (value based on [31]).
3. Verification and Validation of Simulation Model
4. Discussion on Sensitivity Analysis of Selected Parameters in the Simulation Model
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Alicke, K.; Arnold, D.; Knöss, A.; Töpfer, F. Optimierung von manuellen Kommissionierbereichen. Logistik für Unternehmen 2001, 15, 54–57. [Google Scholar]
- Ulbrich, A.; Galka, S.; Günthner, W.A. Simulation of Multi-Level Order Picking Systems Within Rough Planning for Decision Making. Available online: https://bit.ly/2GGGebA (accessed on 21 March 2016).
- Lu, W.; McFarlane, D.; Giannikas, V.; Zhang, Q. An algorithm for dynamic order picking in warehouse operations. Eur. J. Oper. Res. 2016, 248, 107–122. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; de Koster, R.M.B.M. Routing order pickers in a warehouse with a middle aisle. Eur. J. Oper. Res. 2001, 133, 32–43. [Google Scholar] [CrossRef]
- Chiang, D.M.-H.; Lin, C.-P.; Chen, M.-C. The adaptive approach for storage assignment by mining data of warehouse management system for distribution centres. Enterp. Inf. Syst. 2011, 5, 219–234. [Google Scholar] [CrossRef]
- Kostrzewski, M. Mathematical Models of Time Computing in Two-Dimensional Order Picking Process in High-Bay Warehouses; Sas, J., Ed.; Quantitative Methods in Logistics Management; AGH University of Science and Technology Press: Kraków, Poland, 2014; pp. 55–69. [Google Scholar]
- Drury, J. Towards More Efficient Order Picking; IMM Monograph No. 1, Report; The Institute of Materials Management: Cranfield, Great Britain, UK, 1988; pp. 1–69. [Google Scholar]
- Gałązka, M.; Jakubiak, M. Simulation as a method of choosing the order picking concept. Logist. Transp. 2010, 11, 81–88. [Google Scholar]
- Tompkins, J.A.; White, J.A.; Bozer, Y.A.; Tanchoco, J.M.A. Facilities Planning, 4th ed.; Wiley: New York, NY, USA, 2010; pp. 1–864. [Google Scholar]
- Frazelle, E.H. World-Class Warehousing; Logistics Resources International: Atlanta, GA, USA, 1996; pp. 1–256. [Google Scholar]
- Bartholdi, J.J.; Hackman, S.T. Warehouse & Distribution Science, 0.98th ed.; The Supply Chain & Logistics Institute, H. Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology: Atlanta, GA, USA, 2016; Available online: https://www.warehouse-science.com/book/index.html (accessed on 20 December 2016).
- de Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Coyle, J.J.; Bardi, E.J.; Langley, C.J. The Management of Business Logistics, 6th ed.; West Publishing: Minneapolis, MN, USA, 1996; pp. 1–631. [Google Scholar]
- Chen, T.-L.; Cheng, C.-Y.; Chen, Y.-Y.; Chan, L.-K. An efficient hybrid algorithm for integrated order batching, sequencing and routing problem. Int. J. Prod. Econ. 2015, 159, 158–167. [Google Scholar] [CrossRef]
- Daly, F. Warehousing: The strategic weapon for customer service. Ind. Eng. J. 1993, 25, 61–62. [Google Scholar]
- Marchet, G.; Melacini, M.; Perotti, S. Investigating order picking system adoption: A case-study-based approach. Int. J. Logist. Res. App. 2015, 18, 82–98. [Google Scholar] [CrossRef]
- Wruck, S.; Vis, I.F.A.; Boter, J. Risk control for staff planning in ecommerce warehouses. Int. J. Prod. Res. 2017, 55, 6453–6469. [Google Scholar] [CrossRef][Green Version]
- van Gils, T.; Ramaekers, K.; Caris, A.; de Koster, R.B.M. Designing efficient order picking systems by combining planning problems: State-of-the-art classification and review. Eur. J. Oper. Res. 2018, 267, 1–15. [Google Scholar] [CrossRef]
- Quader, S.; Castillo-Villar, K.K. Design of an enhanced multi-aisle order picking system considering storage assignments and routing heuristics. Robot. Comput. Integr. Manuf. 2018, 50, 13–29. [Google Scholar] [CrossRef]
- Venkitasubramony, R.; Adil, G.K. Design of an order picking warehouse factoring vertical travel and space sharing. Int. J. Adv. Manuf. Technol. 2017, 91, 1921–1934. [Google Scholar] [CrossRef]
- Zhang, Y. Correlated Storage Assignment Strategy to reduce Travel Distance in Order Picking. IFAC-PapersOnLine 2016, 49, 30–35. [Google Scholar] [CrossRef]
- Pan, J.Ch.-H.; Shih, P.-H.; Wu, M.-H. Storage assignment problem with travel distance and blocking considerations for a picker-to-part order picking system. Comput. Ind. Eng. 2012, 62, 527–535. [Google Scholar] [CrossRef]
- Chew, E.P.; Tang, L.Ch. Travel time analysis for general item location assignment in a rectangular warehouse. Eur. J. Oper. Res. 1999, 112, 582–597. [Google Scholar] [CrossRef]
- Le-Duc, T.; de Koster, R.M.B.M. Travel time estimation and order batching in a 2-block warehouse. Eur. J. Oper. Res. 2007, 176, 374–388. [Google Scholar] [CrossRef]
- Öztürkog, Ö.; Hoser, D. A discrete cross aisle design model for order-picking warehouses. Eur. J. Oper. Res. 2019, 275, 411–430. [Google Scholar] [CrossRef]
- Gibson, D.R.; Sharp, G.P. Order batching procedures. Eur. J. Oper. Res. 1992, 58, 57–67. [Google Scholar] [CrossRef]
- Davarzani, H.; Norrman, A. Toward a relevant agenda for warehousing research: Literature review and practitioners’ input. Logist. Res. 2015, 8, 1–18. [Google Scholar] [CrossRef]
- Chow, H.K.H.; Choy, K.L.; Lee, W.B.; Lau, K.C. Design of a RFID case-based resource management system for warehouse operations. Expert. Syst. Appl. 2006, 30, 561–576. [Google Scholar] [CrossRef]
- House, R.G.; Karrenbauer, J.J. Logistics system modelling. Int. J. Phys. Distrib. Logist. Manag. 1978, 8, 189–199. [Google Scholar] [CrossRef]
- Staudt, F.H.; Alpan, G.; Mascolo, M.D.; Rodriguez, C.M.T. Warehouse performance measurement: A literature review. Int. J. Prod. Res. 2015, 53, 5524–5544. [Google Scholar] [CrossRef]
- Fijałkowski, J. Technologia Magazynowania, Wybrane Zagadnienia; Oficyna Wydawnicza Politechniki Warszawskiej: Warsaw, Poland, 1995; pp. 1–327. [Google Scholar]
- Kostrzewski, M. Modelowanie i Badanie Wybranych Elementów i Obiektów Logistycznych z Wykorzystaniem Metod Symulacyjnych, 1st ed.; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2018; pp. 1–212. [Google Scholar]
- Karkula, M. Modelowanie i Symulacja Procesów Logistycznych, 1st ed.; Wydawnictwa Akademii Górniczo-Hutniczej: Kraków, Poland, 2013; pp. 1–281. [Google Scholar]
- Ardjmand, E.; Bajgiran, O.S.; Youssef, E. Using list-based simulated annealing and genetic algorithm for order batching and picker routing in put wall based picking systems. Appl. Soft Comput. 2019, 75, 106–119. [Google Scholar] [CrossRef]
- Boysen, N.; Stephan, K. The deterministic product location problem under a pick-by-order policy. Discrete Appl. Math. 2013, 161, 2862–2875. [Google Scholar] [CrossRef]
- Fumi, A.; Scarabotti, L.; Schiraldi, M.M. The effect of slot-code optimization in warehouse order picking. Int. J. Eng. Bus. Manag. 2013, 5, 1–10. [Google Scholar] [CrossRef]
- Le-Duc, T. Design and Control of Efficient Order Picking Processes. Ph.D. Thesis, ERIM Ph.D. Series Research in Management, Rotterdam, The Netherlands, 2005; pp. 1–174. [Google Scholar]
- Lorenc, A. Method of effectiveness evaluation of products picking process for pick by order type in warehouse on basis of a picking list. In Proceedings of the International Conference on Industrial Logistics, Zakopane, Poland, 28 September–1 October 2016; pp. 156–167. [Google Scholar]
- Hsu, C.-M.; Chen, K.-Y.; Chen, M.-C. Batching orders in warehouses by minimizing travel distance with genetic algorithms. Comput. Ind. 2005, 56, 169–178. [Google Scholar] [CrossRef]
- Pansart, L.; Catusse, N.; Cambazard, H. Exact algorithms for the order picking problem. Comput. Oper. Res. 2018, 100, 117–127. [Google Scholar] [CrossRef]
- Pawlewski, P. Simulation model to optimize picking operations in a distribution center. Prz. Organ. 2015, 10, 37–43. [Google Scholar] [CrossRef]
- Petersen, C.G.; Aase, G. A comparison of picking, storage, and routing policies in manual order picking. Int. J. Prod. Econ. 2004, 92, 11–19. [Google Scholar] [CrossRef]
- Rojanapitoon, T.; Teeravaraprug, J. A computer simulation for economical order picker routing when considering travel distance and vehicle energy consumption. Int. J. Eng. Technol. 2018, 7, 33–37. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Order picking along a crane-supplied pick face: The SKU switching problem. Eur. J. Oper. Res. 2017, 260, 534–545. [Google Scholar] [CrossRef]
- Tarczyński, G. Warehouse real-time simulator—How to optimize order picking time (Working Paper). SSRN Electron. J. 2013, 1–18. [Google Scholar] [CrossRef]
- Urzúa, M.; Mendoza, A.; González, A.O. Evaluating the impact of order picking strategies on the order fulfilment time: A simulation study. Acta Logist. Int. Sci. J. Logist. 2019, 6, 103–114. [Google Scholar] [CrossRef]
- van Gils, T.; Caris, A.; Ramaekers, K.; Braekers, K.; de Koster, R.B.M. Designing efficient order picking systems: The effect of real-life features on the relationship among planning problems. Transp. Res. E Logist. 2019, 125, 47–73. [Google Scholar] [CrossRef]
- van Gils, T.; Caris, A.; Ramaekers, K.; Braekers, K. Formulating and solving the integrated batching, routing, and picker scheduling problem in a real-life spare parts warehouse. Eur. J. Oper. Res. 277, 814–830. [CrossRef]
- van Gils, T.; Ramaekers, K.; Braekers, K.; Depaire, B.; Caris, A. Increasing order picking efficiency by integrating storage, batching, zone picking, and routing policy decisions. Int. J. Prod. Econ. 2018, 197, 243–261. [Google Scholar] [CrossRef]
- van Nieuwenhuyse, I.; de Koster, R.B.M. Evaluating order throughput time in 2-block warehouses with time window batching. Int. J. Prod. Econ. 2009, 121, 654–664. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, R.-Q.; Fan, K. Improving order-picking operation through efficient storage location assignment: A new approach. Comput. Ind. Eng. 2020, 139, 106186. [Google Scholar] [CrossRef]
- Weidinger, F.; Boysen, N.; Schneider, M. Picker routing in the mixed-shelves warehouses of e-commerce retailers. Eur. J. Oper. Res. 2019, 274, 501–515. [Google Scholar] [CrossRef]
- Bahrami, B.; Aghezzaf, E.; Limere, V. Using simulation to analyze picker blocking in manual order picking systems. Procedia Manuf. 2017, 11, 1798–1808. [Google Scholar] [CrossRef]
- Bòdis, T.; Botzheim, J.; Földesi, P. Necessity and complexity of order picking routing optimisation based on pallet loading features. Acta Univ. Sapientiae Inform. 2017, 9, 162–194. [Google Scholar] [CrossRef]
- Choe, K.; Sharp, G.P. Small Parts Order Picking: Design and Operation. Available online: http://www.isye.gatech.edu/logisticstutorial/order/article.htm (accessed on 21 January 2019).
- Dąbrowska, A.; Giel, R.; Plewa, M. The picking process model in e-commerce industry. In Engineering in Dependability of Computer Systems and Networks. DepCoS-RELCOMEX 2019. Advances in Intelligent Systems and Computing, 1st ed.; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2020; Volume 987, pp. 123–131. [Google Scholar] [CrossRef]
- Füßler, D.; Boysen, N. Efficient order processing in an inverse order picking system. Comput. Oper. Res. 2017, 88, 150–160. [Google Scholar] [CrossRef]
- Giannikas, V.; Lu, W.; Robertson, B.; McFarlane, D. An interventionist strategy for warehouse order picking: Evidence from two case studies. Int. J. Prod. Econ. 2017, 189, 63–76. [Google Scholar] [CrossRef]
- Guan, M.; Li, Z. Genetic Algorithm for scattered storage assignment in Kiva mobile fulfillment system. Am. J. Oper. Res. 2018, 8, 474–485. [Google Scholar] [CrossRef]
- Güller, M.; Hegmanns, T. Simulation-based performance analysis of a miniload multishuttle order picking system. Procedia CIRP 2014, 17, 475–480. [Google Scholar] [CrossRef][Green Version]
- Henn, S. Algorithms for on-line order batching in an order picking warehouse. Comput. Oper. Res. 2012, 39, 2549–2563. [Google Scholar] [CrossRef]
- Henn, S.; Schmid, V. Metaheuristics for order batching and sequencing in manual order picking systems. Comput. Ind. Eng. 2013, 66, 338–351. [Google Scholar] [CrossRef]
- Henn, S.; Wäscher, G. Tabu search heuristics for the order batching problem in manual order picking systems. Eur. J. Oper. Res. 2012, 222, 484–494. [Google Scholar] [CrossRef]
- Hong, S.; Kim, Y. A route-selecting order batching model with the S-shape routes in a parallel-aisle order picking system. Eur. J. Oper. Res. 2017, 257, 185–196. [Google Scholar] [CrossRef]
- Lee, I.G.; Chung, S.H.; Yoon, S.W. Two-stage storage assignment to minimize travel time and congestion for warehouse order picking operations. Comput. Ind. Eng. 2020, 139, 106129. [Google Scholar] [CrossRef]
- Lin, C.-C.; Kang, J.-R.; Hou, C.-C.; Cheng, C.-Y. Joint order batching and picker Manhattan routing problem. Comput. Ind. Eng. 2016, 95, 164–174. [Google Scholar] [CrossRef]
- Onal, S.; Zhang, J.; Das, S. Modelling and performance evaluation of explosive storage policies in internet fulfilment warehouses. Int. J. Prod. Res. 2017, 55, 5902–5915. [Google Scholar] [CrossRef]
- Öncan, T. MILP formulations and an iterated local search algorithm. Eur. J. Oper. Res. 2015, 243, 142–155. [Google Scholar] [CrossRef]
- Öncan, T.; Cağirici, M. MILP formulations for the order batching problem in low-level picker-to-part warehouse systems. IFAC Proc. Vol. 2013, 46, 471–476. [Google Scholar] [CrossRef]
- Pan, J.C.-H.; Shih, P.-H.; Wu, M.-H.; Lin, J.-H. A storage assignment heuristic method based on genetic algorithm for a pick-and-pass warehousing system. Comput. Ind. Eng. 2015, 81, 1–13. [Google Scholar] [CrossRef]
- Parikh, P.J.; Meller, R.D. A travel-time model for a person-onboard order picking system. Eur. J. Oper. Res. 2010, 200, 385–394. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; Vis, I.F.A. A model for warehouse layout. IIE Trans. 2006, 38, 799–812. [Google Scholar] [CrossRef]
- Rubrico, J.I.U.; Higashi, T.; Tamura, H.; Ota, J. Online rescheduling of multiple picking agents for warehouse management. Robot. Comput. Int. Manuf. 2011, 27, 62–71. [Google Scholar] [CrossRef]
- Scholz, A.; Schubert, D.; Wäscher, G. Order picking with multiple pickers and due dates—Simultaneous solution of order batching, batch assignment and sequencing, and picker routing problems. Eur. J. Oper. Res. 2017, 263, 461–478. [Google Scholar] [CrossRef]
- Tarczyński, G. Estimating order-picking times for return heuristic - equations and simulations. LogForum. 2015, 11, 295–303. [Google Scholar] [CrossRef]
- Yu, M. Enhancing Warehouse Performance by Efficient Order Picking. Ph.D. Thesis, ERIM Ph.D. Series Research in Management, Rotterdam, The Netherlands, 2008; pp. 1–191. [Google Scholar]
- Žulj, I.; Kramer, S.; Schneider, M. A hybrid of adaptive large neighborhood search and tabu search for the order-batching problem. Eur. J. Oper. Res. 2018, 264, 653–664. [Google Scholar] [CrossRef]
- Ashayeri, J.; Strijbosch, L.W.G.; Jacobs, E.; van Asten, L. Redesigning storage assignment and order-picking policies of a miniload AS/RS system: A case study. In Progress in Material Handling Research, 1st ed.; Graves, R.J., McGinnis, L.F., Medeiros, D.J., Ward, R.E., Wilhelm, M.R., Eds.; Braun-Brumfield Inc.: Ann Arbor, MI, USA, 1998; pp. 61–85. [Google Scholar]
- Battini, D.; Calzavara, M.; Persona, A.; Roncari, M.; Sgarbossa, F. Dual-tray vertical lift module for order picking: A performance and storage assignment preliminary study. In Proceedings of the XX Summer School "Francesco Turco"—Industrial Systems Engineering, Naples, Italy, 16–18 September 2015; pp. 85–90. Available online: https://pdfs.semanticscholar:3c95/661ea92d0c6f13c647c98c0d8a53f2ae14a1.pdf (accessed on 6 February 2019).
- Battini, D.; Calzavara, M.; Persona, A.; Sgarbossa, F. Dual-tray vertical lift modules for fast order picking. In Proceedings of the 14th IMHRC Proceedings, Karlsruhe, Germany, 12–16 June 2016; Available online: https://digitalcommons.georgiasouthern.edu/pmhr_2016/6 (accessed on 6 February 2019).
- Bottani, E.; Volpi, A.; Montanari, R. Design and optimization of order picking systems: An integrated procedure and two case studies. Comput. Ind. Eng. 2019, 137, 106035. [Google Scholar] [CrossRef]
- Burinskienė, A. Order picking process at warehouses. Int. J. Logist. Syst. Manag. 2010, 6, 162–178. [Google Scholar] [CrossRef]
- Burinskienė, A.; Davidavičienė, V.; Raudelinienė, I.; Meidutė-Kavaliauskienė, I. Simulation and order picking in a very-narrow- aisle warehouse. Ekon. Istraz. 2018, 31, 1574–1589. [Google Scholar] [CrossRef]
- Gómez-Montoya, R.A.; Correa-Espinal, A.A.; Hernñndez-Vahos, J.D. Picking routing problem with k homogenous material handling equipment for a refrigerated warehouse. Rev. Fac. Ing. Univ. Ant. 2016, 80, 9–20. [Google Scholar] [CrossRef]
- Huang, M.; Guo, Q.; Liu, J.; Huang, X. Mixed model assembly line scheduling approach to order picking problem in online supermarkets. Sustainability 2018, 10, 3931. [Google Scholar] [CrossRef]
- Masood, T.; Weston, R.; Rahimifard, A. A computer integrated unified modelling approach to responsive manufacturing. Int. J. Ind. Syst. Eng. 2010, 5, 287–312. [Google Scholar] [CrossRef]
- Renaud, J.; Ruiz, A. Improving product location and order picking activities in a distribution centre. J. Oper. Res. Soc. 2008, 59, 1603–1613. Available online: www.jstor:stable/20202246 (accessed on 6 February 2020). [CrossRef]
- Santini, B.; de Moura Filho, J.P. A tool for analyzing picking operations within a distribution center. In Proceedings of the 2012 Winter Simulation Conference, Berlin, Germany, 9–12 December 2012; Laroque, C., Himmelspach, J., Pasupathy, R., Rose, O., Uhrmacher, A.M., Eds.; [Google Scholar]
- Takakuwa, S.; Takizawa, H.; Ito, K.; Hiraoka, S. Simulation and analysis of non-automated distribution warehouses. In Proceedings of the 2000 Winter Simulation Conference, Orlando, FL, USA, 10–13 December 2000; Joines, J.A., Barton, R.R., Kang, K., Fishwick, P.A., Eds.; pp. 1177–1184. [Google Scholar]
- Fosso Wamba, S.; Chatfield, A.T. RFID-enabled Warehouse Process Optimization in the TPL Industry. In Proceedings of the 43rd Hawaii International Conference on System Sciences, Kolua, Kauai, HI, USA, 5–8 January 2010; pp. 1–10. [Google Scholar] [CrossRef]
- Wasusri, T.; Theerawongsathon, P. An application of discrete event simulation on order picking strategies: A case study of footwear warehouses. In Proceedings of the 30th European Conference on Modelling and Simulation, Regensburg, Germany, 31 May–3 June 2016; Claus, T., Herrmann, F., Manitz, M., Rose, O., Eds.; pp. 1–7. [Google Scholar]
- Zuñiga, J.B.; Martínez, J.A.S.; Salais Fierro, T.E.; Marmolejo Saucedo, J.A. Optimization of the Storage Location Assignment and the Picker-Routing Problem by Using Mathematical Programming. Appl. Sci. 2020, 10, 534. [Google Scholar] [CrossRef]
- Cano, J.A.; Correa-Espinal, A.A.; Gómez-Montoya, R.A. An evaluation of picking routing policies to improve warehouse efficiency. Int. J. Ind. Eng. Manag. 2017, 8, 229–238. [Google Scholar]
- Charu, T.; Panagiotopoulos, T.; Kotipalli, P.; Haynes, M.; Starner, T. RF-Pick: Comparing Order Picking Using a HUD with Wearable RFID Verification to Traditional Pick Methods. West Point Res. Pap. 2018, 69, 168–175. Available online: https://digitalcommons.usmalibrary:usma_research_papers/69 (accessed on 6 February 2020).
- Chen, M.; Wu, H. An association-based clustering approach to order batching considering customer demand patterns. Omega 2005, 33, 333–343. [Google Scholar] [CrossRef]
- Furmans, K.; Huber, C.; Wisser, J. Queueing Models for manual order picking systems with blocking. Logist. J. 2009, 1, 1–16. [Google Scholar] [CrossRef]
- Kawczyński, Ł.; Aguilar-Sommar, R. Comprehensive design of an order picking line by simulation. IFAC Proc. 2006, 39, 365–370. [Google Scholar] [CrossRef]
- Tappia, E.; Roy, D.; Melacini, M.; de Koster, R.B.M. Integrated Storage-order Picking Systems: Technology, Performance Models, and Design Insights. Eur. J. Oper. Res. 2018, 274, 947–965. [Google Scholar] [CrossRef]
- Yu, M.; de Koster, R.B.M. The impact of order batching and picking area zoning on order picking system performance. Eur. J. Oper. Res. 2009, 198, 480–490. [Google Scholar] [CrossRef]
- Banks, J.; Carson, J.S.; Nelson, B.L.; Nicol, D.M. Discrete Event System Simulation, 3rd ed.; Prentice-Hall: Upper Saddle River, NY, USA, 2000; pp. 1–600. [Google Scholar]
- Zeigler, B.P. Theory of Modeling and Simulation, 1st ed.; Wiley Interscience: New York, NY, USA, 1976; pp. 1–510. [Google Scholar]
- Kostrzewski, M. Comparison of the order picking processes duration based on data obtained from the use of pseudorandom number generator. Transp. Res. Procedia 2019, 40, 317–324. [Google Scholar] [CrossRef]
- Kostrzewski, M. Zastosowanie metod symulacyjnych w badaniu wybranych procesów magazynowych w magazynie wysokoregałowym. Prace Nauk. Politech. Warsz. Transp. 2016, 111, 301–312. [Google Scholar]
- Kostrzewski, M. Zastosowanie wybranego generatora liczb pseudolosowych w analizie procesu komisjonowania. Prace Nauk. Politech. Warsz. Transp. 2017, 117, 129–138. [Google Scholar]
- Jungheinrich, Electric Order Picker/ Tri-Lateral Stacker (1250–1500 kg). Available online: http://www.centralgroup.co.nz/site/centralfor/files/EKX513.pdf (accessed on 14 March 2017).
- Gutenbaum, J. Modelowanie Matematyczne Systemów, 3rd ed.; Akademicka Oficyna Wydawnicza EXIT: Warsaw, Poland, 2003; pp. 1–420. [Google Scholar]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–148. [Google Scholar] [CrossRef]
- Schuster, H.G. Chaos Deterministyczny; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1993. [Google Scholar]
- L’Ecuyer, P. Efficient and Portable Combined Random Number Generators. Commun. ACM 1988, 31, 742–750. [Google Scholar] [CrossRef]
- Facchini, F.; De Pascale, G.; Faccilongo, N. Pallet Picking Strategy in Food Collecting Center. Appl. Sci. 2018, 8, 1503. [Google Scholar] [CrossRef]
- United Nations. International Standard Industrial Classification of All Economic Activities, Revision 4, 1st ed.; United Nations (Department of Economic and Social Affairs, Statistics Division): New York, NY, USA, 2008; pp. 1–291. Available online: https://unstats.un:unsd/publication/seriesM/seriesm_4rev4e.pdf (accessed on 4 April 2020).
- S&P Global Market Intelligence. GICS® Global Industry Classification Standard, 1st ed.; S&P Global Market Intelligence: New York, NY, USA, 2018; pp. 1–48. Available online: https://www.spglobal.com/marketintelligence/en/documents/112727-gics-mapbook_2018_v3_letter_digitalspreads.pdf (accessed on 4 April 2020).
- Lee, C.K.; Zhang, S.; Ng, K.K. In-Plant Logistics Simulation Model for the Catering Service Industry Towards Sustainable Development: A Case Study. Sustainability 2019, 11, 3655. [Google Scholar] [CrossRef]
- Kostrzewski, M.; Gnap, J.; Varjan, P.; Likos, M. Application of simulation methods for study on availability of one-aisle machine order picking process. Communications 2020, 22, 107–114. [Google Scholar] [CrossRef]
- Li, Z.P.; Zhang, J.L.; Zhang, H.J.; Hua, G.W. Optimal Selection of Movable Shelves under Cargo-to-Person Picking Mode. Int. J. Simul. Model. 2017, 16, 145–156. [Google Scholar] [CrossRef]
- Dinu, O.M.; Rosca, E.; Popa, M.; Rosca, M.A.; Rusca, A. Assessing materials handling and storage capacities in port terminals, MODTECH International Conference–Modern Technologies in Industrial Engineering V, Book Series: IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012039. [Google Scholar] [CrossRef]
- Filina-Dawidowicz, L. Rationalization of servicing reefer containers in sea port area with taking into account risk influence. Pol. Marit. Res. 2014, 21, 76–85. [Google Scholar] [CrossRef]
| Way of Picking List Application | References that Mention Particular Way | Necessary Comments |
|---|---|---|
| generalized random picking lists | [19,24,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] | Fumi et al. (2013) [36] mentioned the variable picking list. Le-Duc and de Koster (2007) [24] applied random picking lists which consisted of only one line. Pawlewski (2015) [41] defined the methodology of the simulation model building, while implementing the design step of creating examples of picking lists (random or historical). Quader et al. (2016) [19] used a fixed and random picking list. Urzuà et al. (2019) [46] applied a random picking list based on historical data. |
| uniform distribution picking lists | [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77] | Giannikas et al. (2017) [58] mentioned the uniform demand for the stock keeping unit. Lee et al. (2020) [65] applied uniform distribution picking list indirectly by implementation of uniform pick-up time. In the case of Žulj et al. (2018) [77], picking lists were indirectly connected to uniform distribution. |
| picking lists based on historic data | [41,46,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92] | Battini et al. (2016) and Battini et al. (2015) [79,80] suggested that the actual time needed to pick an item from a vertical lift tray was the average value. Burinskienė (2010) [82] mentioned the picking list data base. Gómez-Montoya et al. (2016) [84] mentioned a variable picking list connected to empirical data. Urzêa et al. (2019) [46] applied a random picking list based on historical data. |
| other | [93,94,95,96,97,98,99] | Cano et al. (2017) [93] applied ad hoc picking lists. Charu et al. (2018) [94] mentioned non-uniform distribution. Chen and Wu (2005) [95] applied normal distribution picking lists. Furmans et al. (2009) [96] applied lognormal distribution and suggested pick times that follow exponential distribution. In the case of Kawczyński and Aguilar-Sommar (2006) [97], the number of products per order is variable, and it is assumed to be described by exponential distribution. Tappia et al. (2019) [98] applied pick times that follow an exponential distribution. Yu and de Koster (2009) [99] applied a random picking list with Poisson order arrivals. |
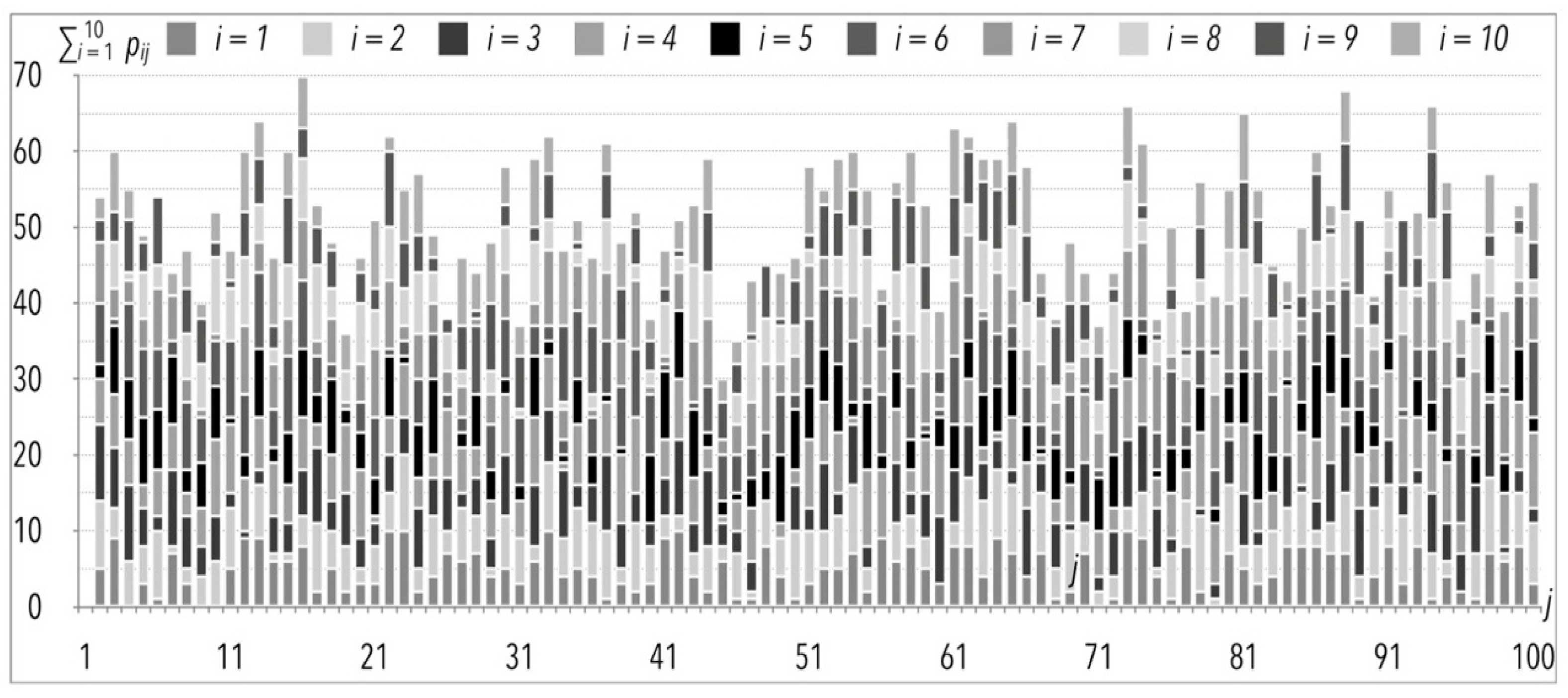
| j | {pj1, pj2, pj3, pj4, pj5, pj6, pj7, pj8, pj9, pj10} | j | {pj1, pj2, pj3, pj4, pj5, pj6, pj7, pj8, pj9, pj10} | j | {pj1, pj2, pj3, pj4, pj5, pj6, pj7, pj8, pj9, pj10} |
|---|---|---|---|---|---|
| 1 | {5,9,10,6,2,8,8,0,3,3} | 35 | {4,7,5,0,4,5,1,2,9,9} | 69 | {7,4,8,9,0,1,4,2,5,4} |
| 2 | {9,4,8,7,9,1,4,6,4,8} | 36 | {1,9,10,7,1,7,9,7,6,4} | 70 | {0,2,2,6,7,1,5,4,6,4} |
| 3 | {0,6,10,6,8,10,3,1,7,4} | 37 | {3,2,6,9,1,8,6,0,7,6} | 71 | {1,3,6,3,7,9,2,9,2,2} |
| 4 | {3,5,5,3,9,9,4,6,4,1} | 38 | {2,9,4,10,0,9,9,2,5,2} | 72 | {10,3,9,8,8,0,9,9,2,8} |
| 5 | {1,9,2,6,8,8,8,3,9,0} | 39 | {3,5,3,0,9,8,1,2,4,3} | 73 | {9,6,9,9,3,2,10,3,2,8} |
| 6 | {7,1,10,6,9,2,6,0,0,3} | 40 | {9,3,5,5,9,1,1,7,2,5} | 74 | {4,1,8,4,1,5,9,3,1,2} |
| 7 | {3,2,7,3,3,9,3,6,6,5} | 41 | {10,2,10,8,9,0,5,2,1,4} | 75 | {1,6,2,6,6,10,2,6,3,8} |
| 8 | {0,4,4,5,6,6,1,6,6,2} | 42 | {4,3,4,6,9,1,8,10,0,8} | 76 | {8,6,0,4,3,3,6,3,1,5} |
| 9 | {0,6,6,10,7,6,1,10,2,4} | 43 | {2,6,10,3,2,6,9,6,8,7} | 77 | {2,10,1,10,6,5,6,3,7,6} |
| 10 | {5,8,2,9,1,10,0,7,1,4} | 44 | {6,2,3,1,2,6,2,0,5,3} | 78 | {0,1,2,8,2,5,10,5,1,7} |
| 11 | {9,0,1,7,3,8,9,9,6,8} | 45 | {1,6,3,4,1,5,4,4,4,3} | 79 | {7,9,6,2,5,2,9,7,0,8} |
| 12 | {9,7,2,7,9,10,4,5,6,5} | 46 | {1,1,4,7,4,4,6,8,1,7} | 80 | {5,3,7,9,7,3,7,6,9,9} |
| 13 | {6,1,5,7,2,5,6,2,3,9} | 47 | {8,6,0,0,4,5,9,6,7,0} | 81 | {3,5,2,4,9,8,7,7,6,4} |
| 14 | {6,1,4,5,7,10,5,7,9,6} | 48 | {4,5,0,2,9,8,4,5,1,6} | 82 | {4,6,0,5,5,8,6,4,6,1} |
| 15 | {8,4,6,7,9,9,8,8,4,7} | 49 | {1,9,6,2,8,2,5,4,6,3} | 83 | {8,5,7,9,1,0,4,5,1,3} |
| 16 | {2,9,10,3,4,5,2,10,5,3} | 50 | {3,7,3,9,7,9,7,2,2,9} | 84 | {8,7,1,7,4,9,2,0,3,9} |
| 17 | {5,5,4,6,10,2,6,4,5,1} | 51 | {5,5,9,8,7,8,4,0,7,2} | 85 | {8,2,4,8,10,7,3,6,9,3} |
| 18 | {2,6,7,9,2,0,1,4,0,5} | 52 | {5,7,3,8,9,9,1,4,6,7} | 86 | {7,4,8,9,8,4,2,7,1,3} |
| 19 | {3,2,4,9,5,4,5,8,4,2} | 53 | {7,9,8,1,2,8,6,9,5,5} | 87 | {7,8,9,2,7,9,1,9,9,7} |
| 20 | {3,5,3,1,5,8,9,5,3,9} | 54 | {2,3,3,10,9,2,8,9,4,5} | 88 | {1,3,9,7,6,4,7,4,10,0} |
| 21 | {10,5,5,5,8,1,9,7,10,2} | 55 | {9,0,0,9,2,8,6,0,6,2} | 89 | {4,9,3,5,3,5,5,3,3,1} |
| 22 | {10,10,5,7,1,2,2,5,6,7} | 56 | {6,5,8,7,5,5,2,6,10,2} | 90 | {8,8,6,9,4,9,3,4,0,4} |
| 23 | {2,3,8,4,7,6,6,8,5,8} | 57 | {8,4,3,3,4,7,7,9,8,7} | 91 | {3,9,4,9,0,1,10,6,9,0} |
| 24 | {4,8,5,3,10,6,4,4,2,3} | 58 | {5,4,6,7,1,1,7,8,6,8} | 92 | {8,8,2,7,5,4,7,1,4,6} |
| 25 | {7,3,7,9,0,2,3,5,2,0} | 59 | {3,0,9,9,4,1,2,0,3,8} | 93 | {1,6,8,8,4,7,9,8,9,6} |
| 26 | {6,7,2,6,2,2,4,2,6,9} | 60 | {8,3,7,0,6,9,10,3,8,9} | 94 | {4,2,5,8,2,8,6,8,9,4} |
| 27 | {7,5,5,4,7,9,1,0,1,5} | 61 | {8,9,7,6,5,6,8,4,7,2} | 95 | {2,0,5,4,0,10,2,7,3,5} |
| 28 | {4,1,4,5,4,6,4,3,9,8} | 62 | {4,10,5,2,7,10,1,9,8,3} | 96 | {1,6,9,0,4,1,10,6,2,5} |
| 29 | {5,7,8,8,2,8,6,6,3,5} | 63 | {9,9,4,1,6,7,8,3,8,4} | 97 | {7,10,10,1,8,2,3,5,3,8} |
| 30 | {3,6,0,5,2,9,0,1,7,4} | 64 | {7,9,2,7,9,3,5,8,7,7} | 98 | {6,1,1,7,4,1,8,0,1,10} |
| 31 | {6,2,8,9,8,4,3,8,2,9} | 65 | {4,0,9,6,5,5,5,6,9,9} | 99 | {8,7,3,9,7,7,2,6,2,2} |
| 32 | {10,9,7,7,2,2,10,4,6,5} | 66 | {7,8,4,1,1,3,8,6,3,3} | 100 | {3,8,2,10,2,10,6,2,5,8} |
| 33 | {4,5,9,1,1,2,4,1,10,10} | 67 | {1,4,6,3,7,2,4,2,8,1} | - | - |
| 34 | {5,8,3,8,6,9,6,2,1,3} | 68 | {2,8,1,5,2,10,3,1,8,8} | - | - |
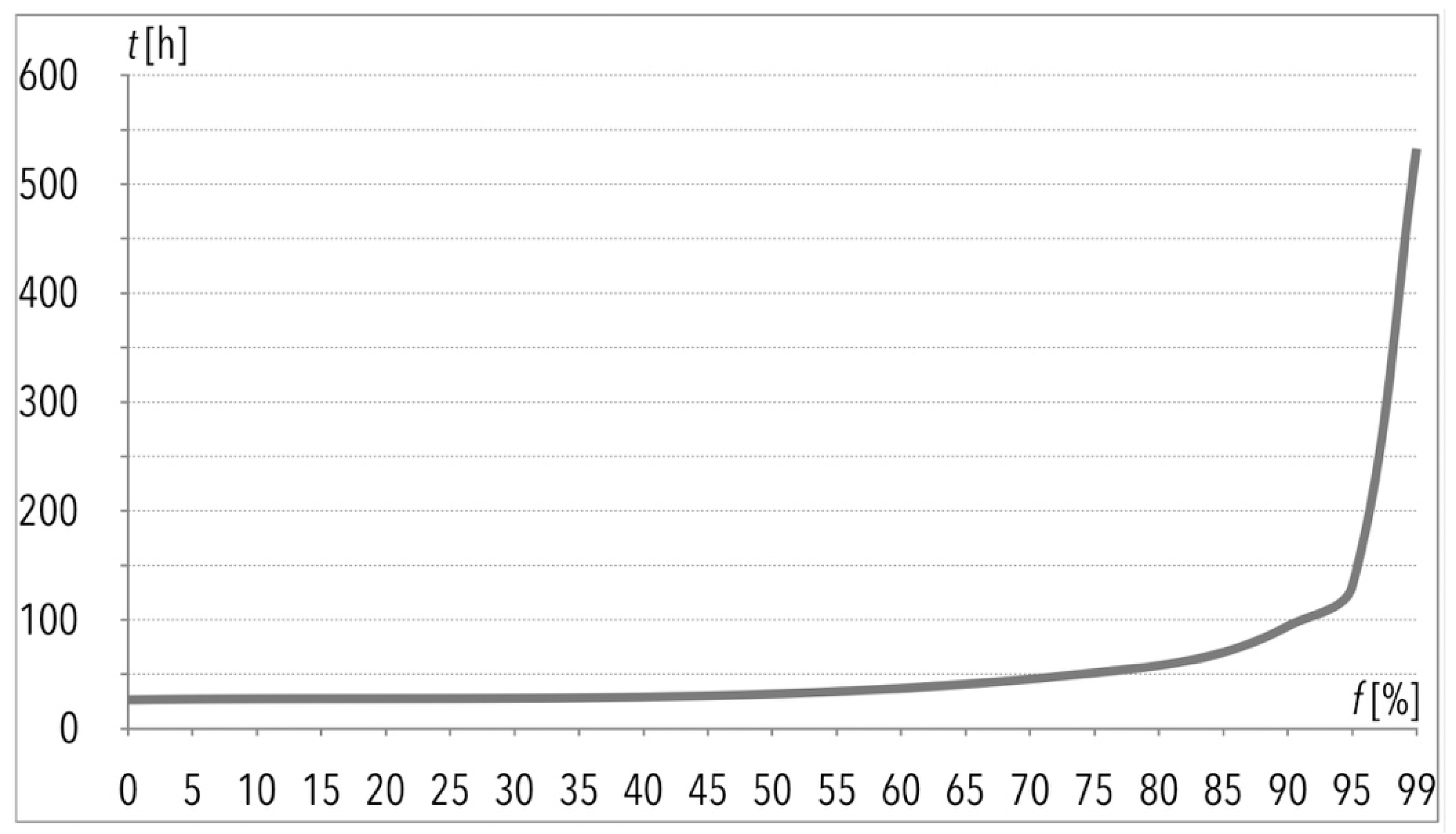
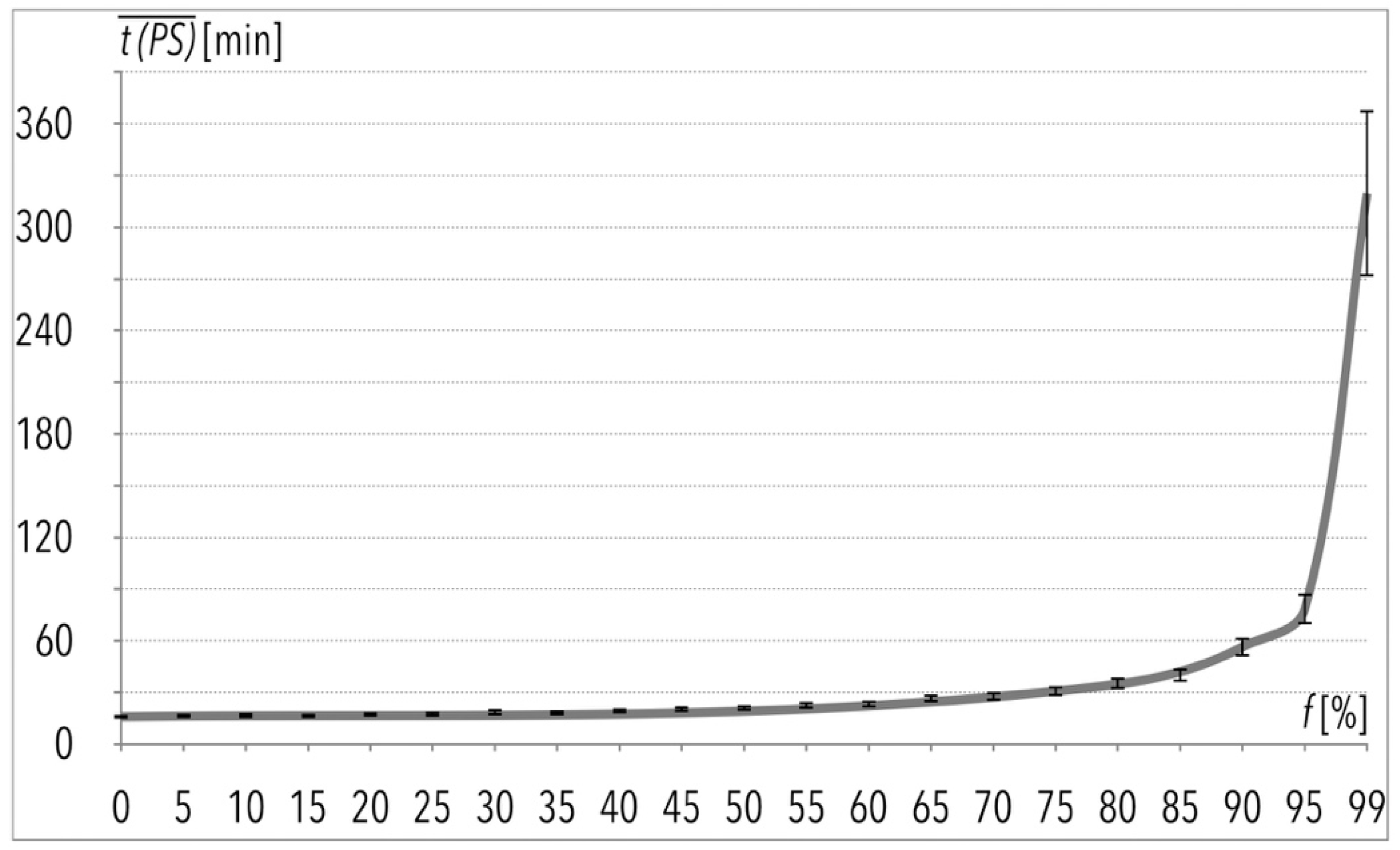
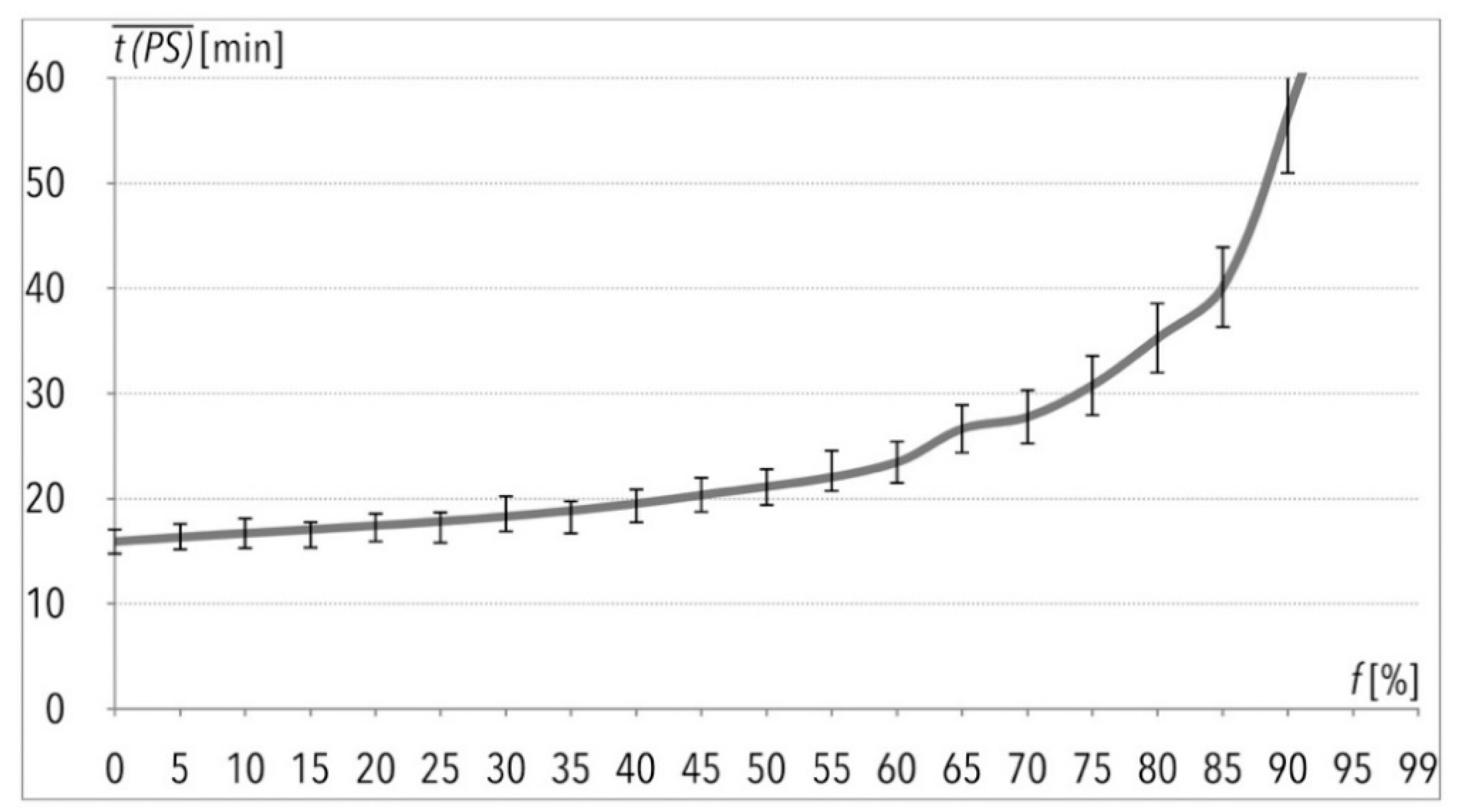
| k | [%] | Total Order Picking Process Time for Sample (t) | [min] | [min] | [min] | [min] | |
|---|---|---|---|---|---|---|---|
| [min] | [h] | ||||||
| 1 | 0 | 1591.68 | 26.53 | 15.92 | 1.28 | 0.13 | 0.00 |
| 2 | 5 | 1635.85 | 27.26 | 16.36 | 1.32 | 0.13 | 0.44 |
| 3 | 10 | 1668.71 | 27.81 | 16.68 | 1.51 | 0.15 | 0.33 |
| 4 | 15 | 1656.41 | 27.61 | 16.56 | 1.33 | 0.13 | 0.12 |
| 5 | 20 | 1727.45 | 28.79 | 17.27 | 1.44 | 0.14 | 0.71 |
| 6 | 25 | 1727.52 | 28.79 | 17.28 | 1.56 | 0.16 | 0.00 |
| 7 | 30 | 1854.48 | 30.91 | 18.54 | 1.80 | 0.18 | 1.27 |
| 8 | 35 | 1824.97 | 30.42 | 18.25 | 1.64 | 0.16 | 0.30 |
| 9 | 40 | 1931.22 | 32.19 | 19.31 | 1.67 | 0.17 | 1.06 |
| 10 | 45 | 2033.89 | 33.90 | 20.34 | 1.73 | 0.17 | 1.03 |
| 11 | 50 | 2108.16 | 35.14 | 21.08 | 1.80 | 0.18 | 0.74 |
| 12 | 55 | 2265.92 | 37.77 | 22.66 | 2.03 | 0.20 | 1.58 |
| 13 | 60 | 2345.79 | 39.10 | 23.46 | 2.08 | 0.21 | 0.80 |
| 14 | 65 | 2663.12 | 44.39 | 26.63 | 2.39 | 0.24 | 3.17 |
| 15 | 70 | 2775.42 | 46.26 | 27.75 | 2.63 | 0.26 | 1.12 |
| 16 | 75 | 3077.35 | 51.29 | 30.77 | 2.93 | 0.29 | 3.02 |
| 17 | 80 | 3525.15 | 58.75 | 35.25 | 3.40 | 0.34 | 4.48 |
| 18 | 85 | 4011.17 | 66.85 | 40.11 | 3.88 | 0.39 | 4.86 |
| 19 | 90 | 5649.00 | 94.15 | 56.49 | 5.65 | 0.57 | 16.38 |
| 20 | 95 | 7849.27 | 130.82 | 78.49 | 8.90 | 0.89 | 22.00 |
| 21 | 99 | 31966.38 | 532.77 | 319.66 | 48.38 | 4.84 | 241.17 |
| k | [%] | MTTR [min] | Operational [%] | Failed [%] | [min] | [min] | [min] | |
|---|---|---|---|---|---|---|---|---|
| Working | Working | |||||||
| 22 | 10 | 1 | 77.54 | 12.42 | 10.04 | 16.84 | 0.94 | 0.09 |
| 23 | 10 | 3 | 78.75 | 11.06 | 10.19 | 17.37 | 1.07 | 0.11 |
| 24 | 10 | 9 | 80.19 | 10.61 | 9.20 | 18.01 | 1.01 | 0.10 |
| 25 | 10 | 27 | 76.25 | 14.47 | 9.28 | 18.09 | 0.77 | 0.08 |
| 26 | 10 | 81 | 81.96 | 9.29 | 8.75 | 16.82 | 0.95 | 0.10 |
| 27 | 10 | 243 | 67.74 | 17.48 | 14.78 | 16.66 | 0.98 | 0.10 |
| 28 | 20 | 1 | 62.38 | 17.45 | 20.17 | 17.50 | 0.79 | 0.08 |
| 29 | 20 | 3 | 60.51 | 19.26 | 20.23 | 17.93 | 0.77 | 0.08 |
| 30 | 20 | 9 | 60.60 | 18.34 | 21.06 | 19.14 | 1.57 | 0.16 |
| 31 | 20 | 27 | 63.28 | 18.02 | 18.70 | 19.73 | 1.16 | 0.12 |
| 32 | 20 | 81 | 65.00 | 16.94 | 18.06 | 19.30 | 1.73 | 0.17 |
| 33 | 20 | 243 | 58.13 | 21.02 | 20.85 | 16.66 | 0.98 | 0.10 |
| 34 | 30 | 1 | 47.12 | 22.65 | 30.23 | 18.65 | 0.53 | 0.05 |
| 35 | 30 | 3 | 46.33 | 22.80 | 30.87 | 18.92 | 1.47 | 0.15 |
| 36 | 30 | 9 | 45.63 | 23.28 | 31.09 | 20.27 | 2.15 | 0.22 |
| 37 | 30 | 27 | 51.07 | 22.30 | 26.63 | 20.54 | 1.80 | 0.18 |
| 38 | 30 | 81 | 52.40 | 21.68 | 25.92 | 22.15 | 2.48 | 0.25 |
| 39 | 30 | 243 | 55.40 | 21.41 | 23.19 | 18.61 | 2.49 | 0.25 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostrzewski, M. Sensitivity Analysis of Selected Parameters in the Order Picking Process Simulation Model, with Randomly Generated Orders. Entropy 2020, 22, 423. https://doi.org/10.3390/e22040423
Kostrzewski M. Sensitivity Analysis of Selected Parameters in the Order Picking Process Simulation Model, with Randomly Generated Orders. Entropy. 2020; 22(4):423. https://doi.org/10.3390/e22040423
Chicago/Turabian StyleKostrzewski, Mariusz. 2020. "Sensitivity Analysis of Selected Parameters in the Order Picking Process Simulation Model, with Randomly Generated Orders" Entropy 22, no. 4: 423. https://doi.org/10.3390/e22040423
APA StyleKostrzewski, M. (2020). Sensitivity Analysis of Selected Parameters in the Order Picking Process Simulation Model, with Randomly Generated Orders. Entropy, 22(4), 423. https://doi.org/10.3390/e22040423






