Representational Rényi Heterogeneity
Abstract
:1. Introduction
2. Existing Heterogeneity Indices
2.1. Rényi Heterogeneity in Categorical Systems
2.1.1. Properties of the Rényi Heterogeneity
- Event spaces are disjoint: for all where
- All systems have equal heterogeneity:
2.1.2. Decomposition of Categorical Rényi Heterogeneity
2.1.3. Limitations of Categorical Rényi Heterogeneity
2.2. Non-Categorical Heterogeneity Indices
2.2.1. Numbers Equivalent Quadratic Entropy
2.2.2. Functional Hill Numbers
2.2.3. Leinster–Cobbold Index
2.2.4. Limitations of Existing Non-Categorical Heterogeneity Indices
- 1
- Non-negativity:
- 2
- Identity of indiscernibles:
- 3
- Symmetry:
- 4
- Triangle inequality:
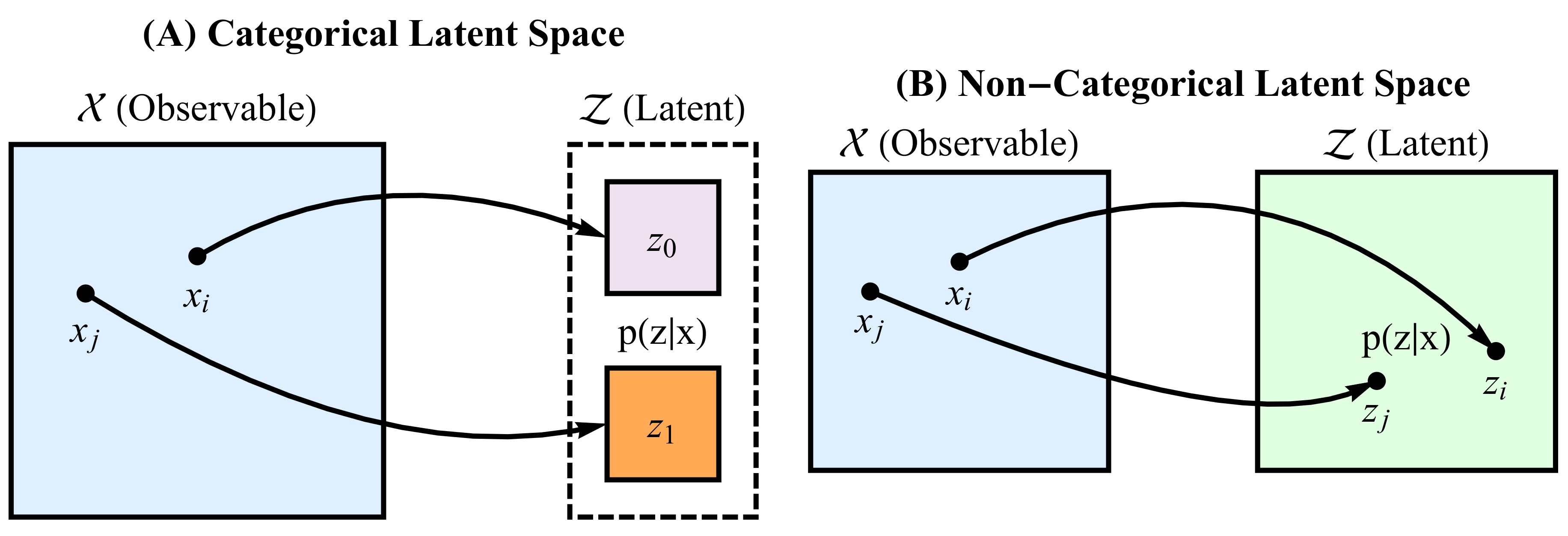
3. Representational Rényi Heterogeneity
- The representation Z captures the semantically relevant variation in X
- Rényi heterogeneity can be directly computed on Z
- A.
- Application of standard Rényi heterogeneity (Section 2.1) when Z is a categorical representation
- B.
- Deriving parametric forms for Rényi heterogeneity when Z is a non-categorical representation
3.1. Rényi Heterogeneity on Categorical Representations
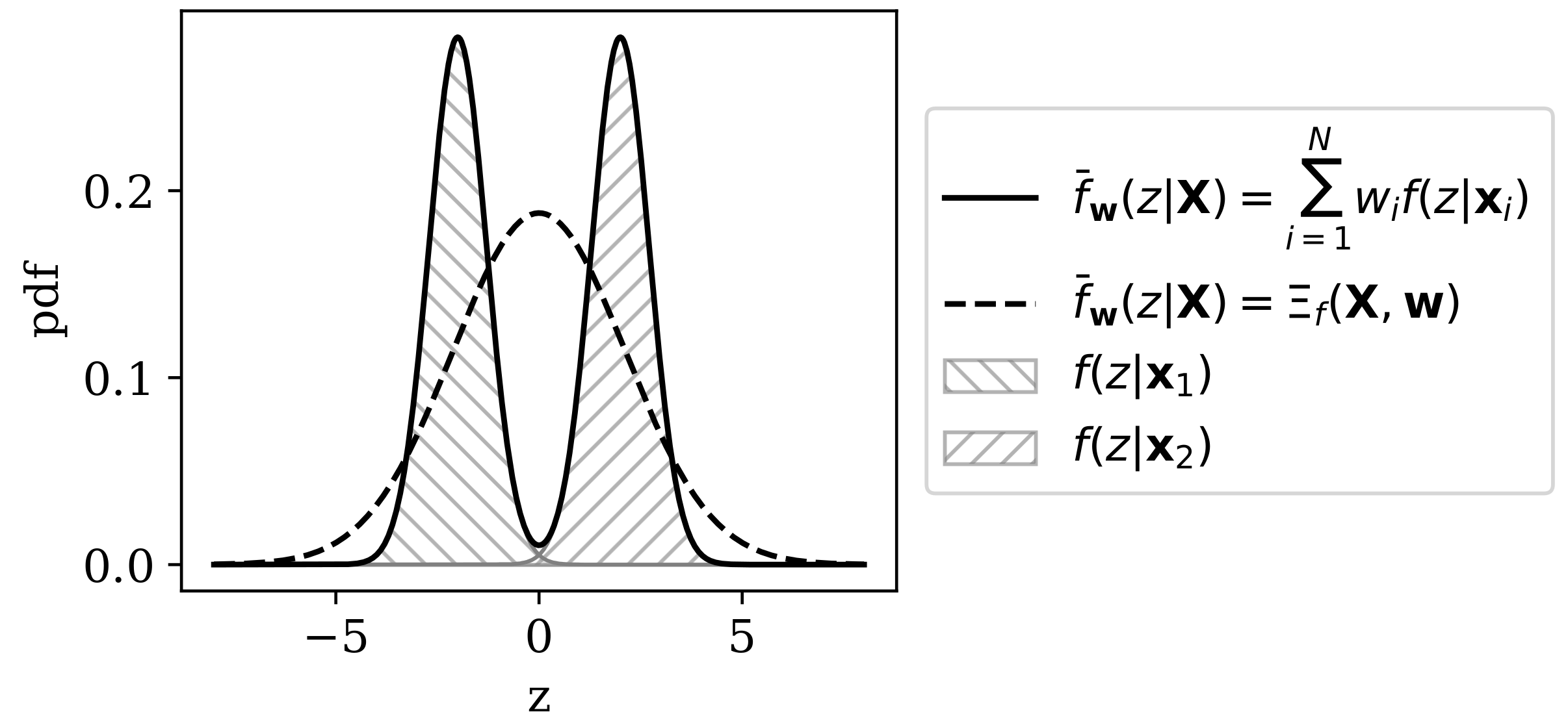
3.2. Rényi Heterogeneity on Non-Categorical Representations
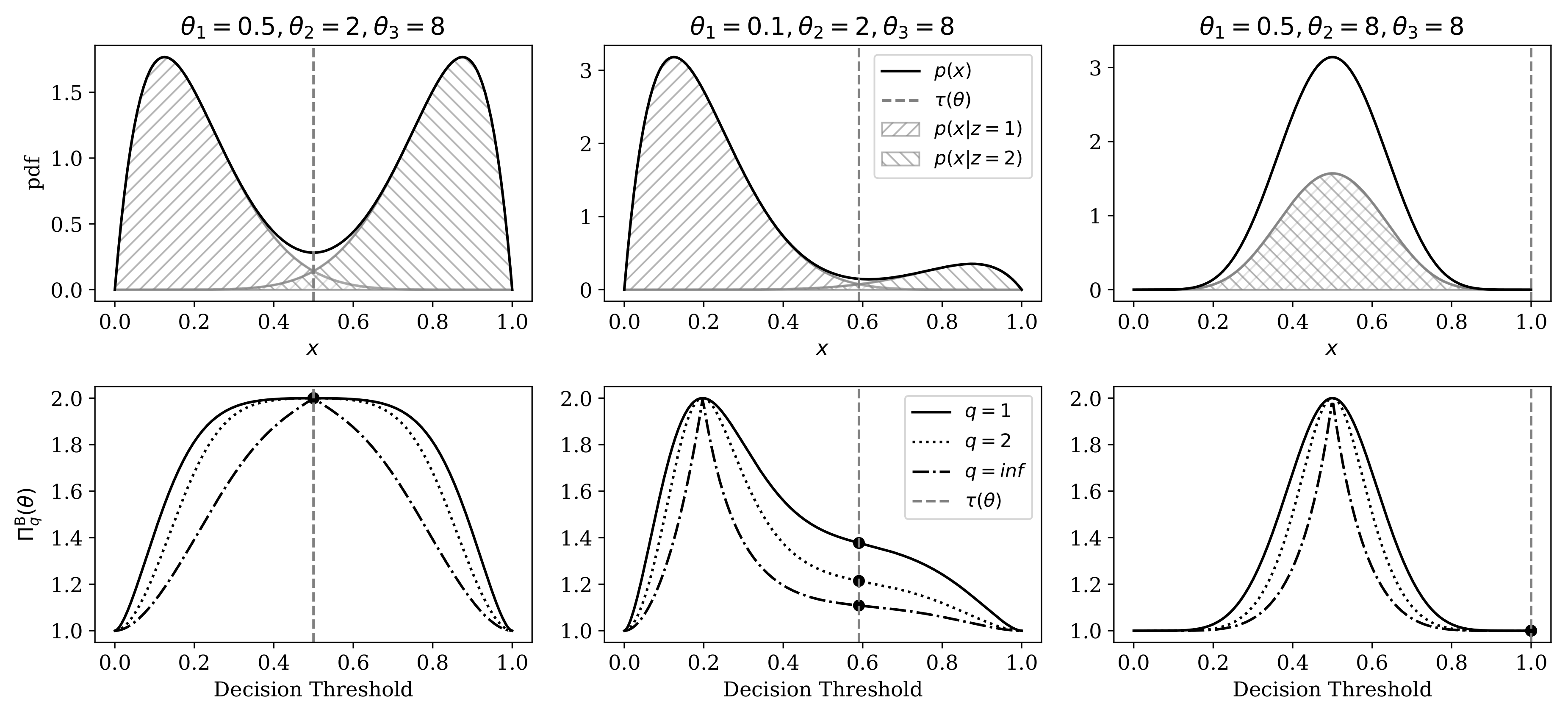
4. Empirical Applications of Representational Rényi Heterogeneity
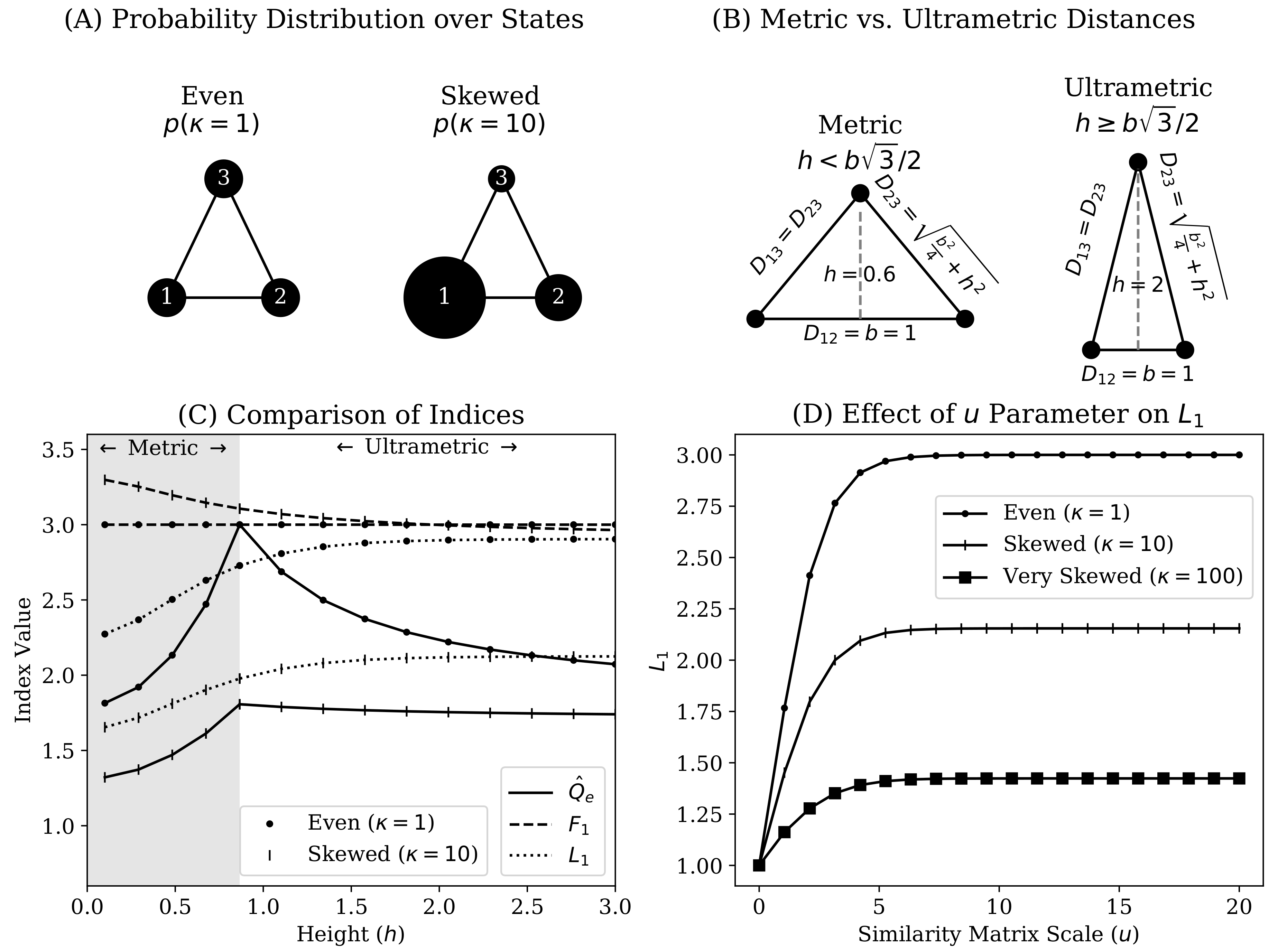
4.1. Comparison of Heterogeneity Indices Under a Mixture of Beta Distributions
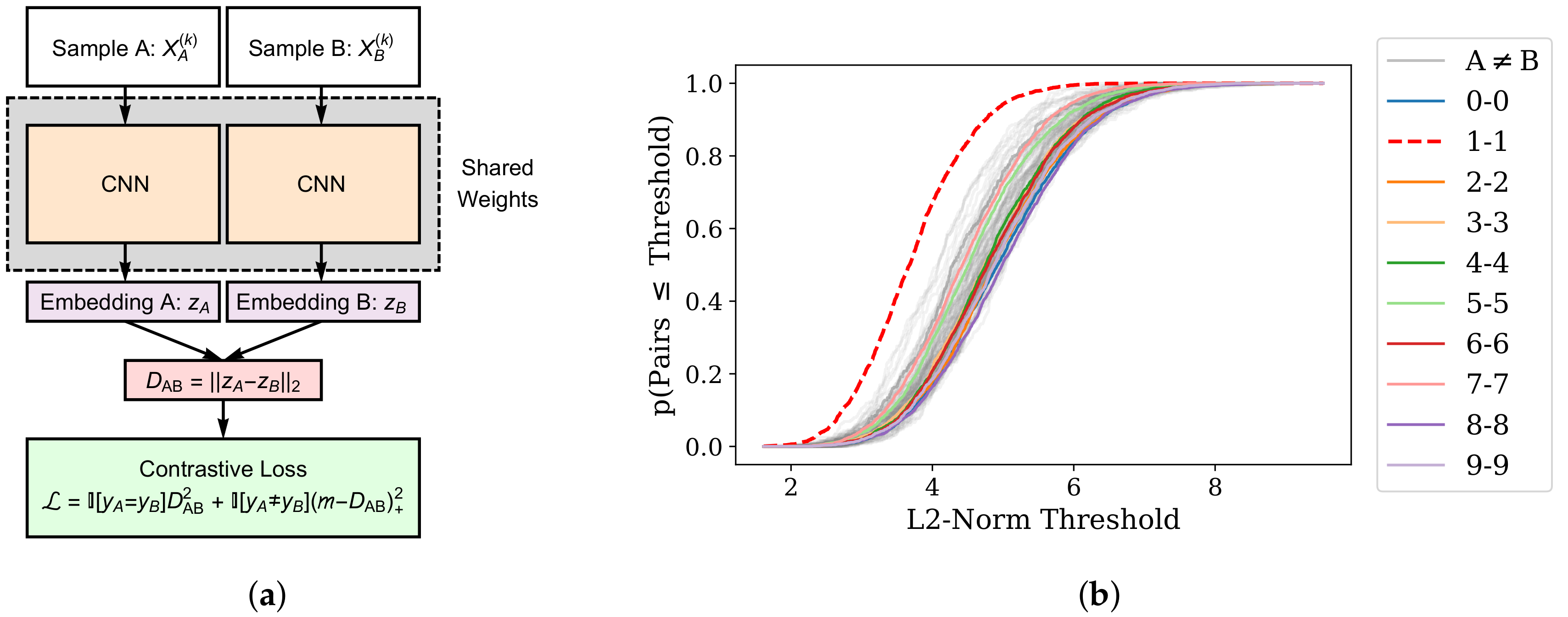
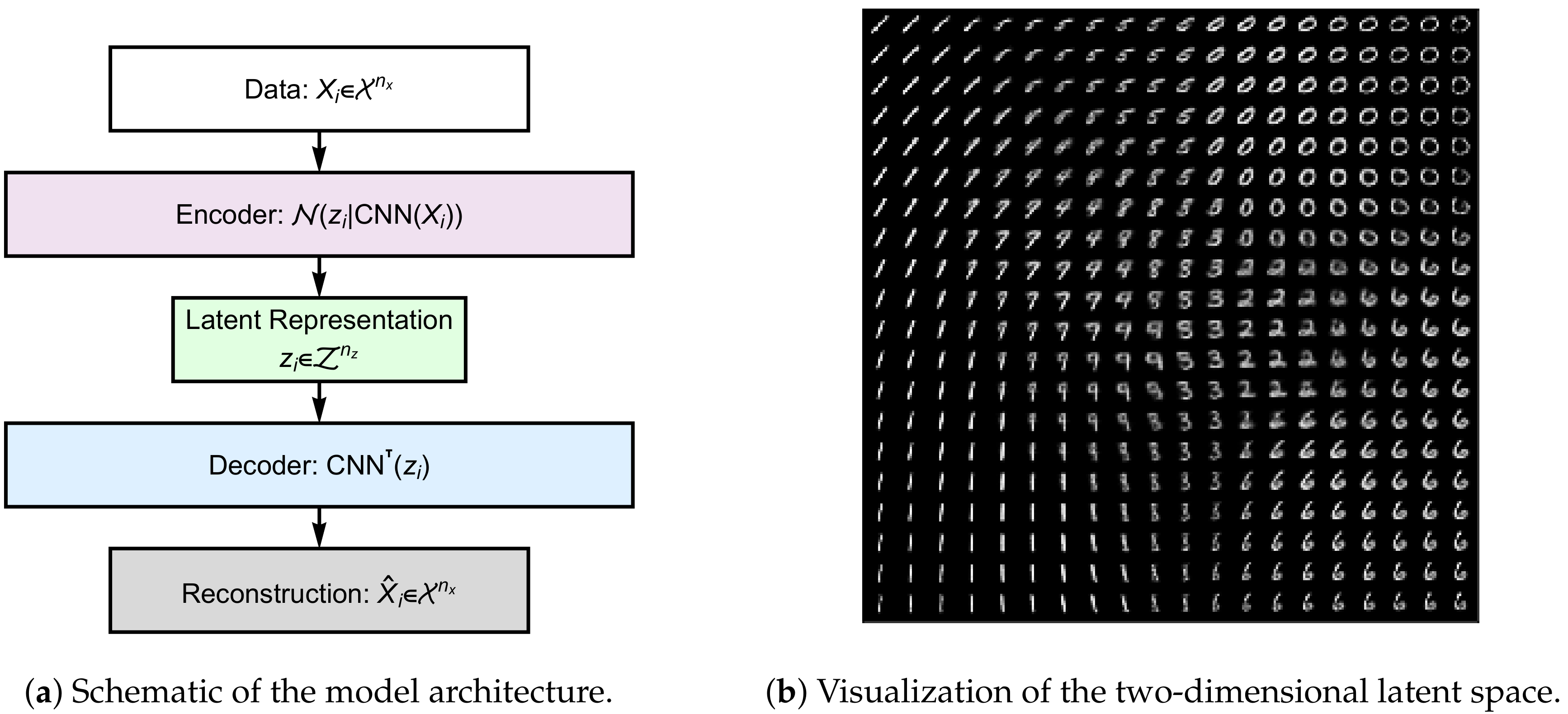
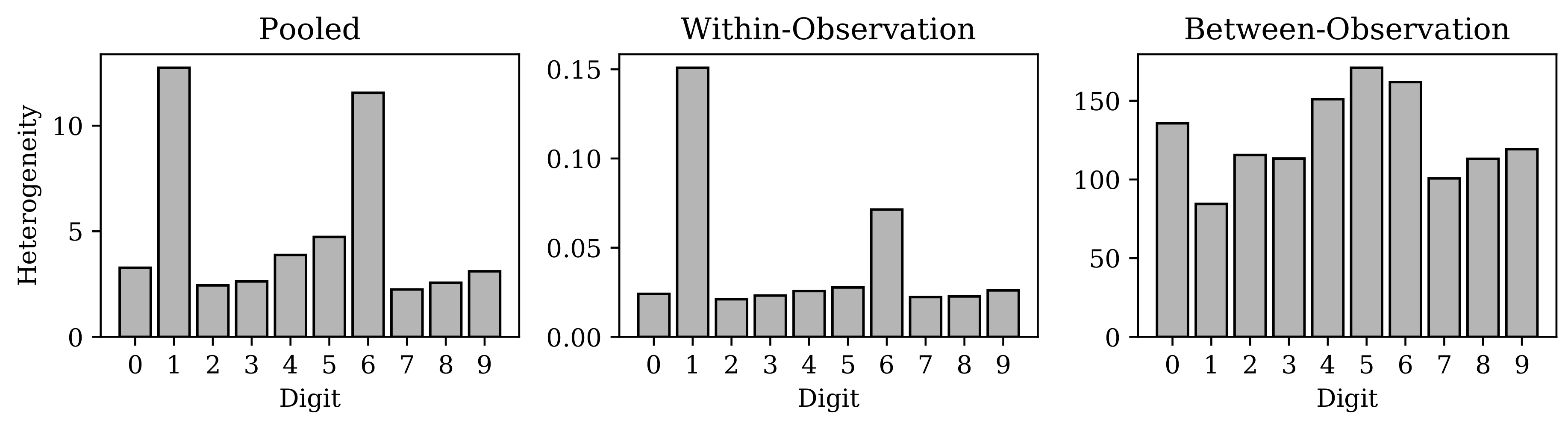
4.2. Representational Rényi Heterogeneity is Scalable to Deep Learning Models
5. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Mathematical Appendix
Appendix B. Expected Distance Between two Beta-Distributed Random Variables
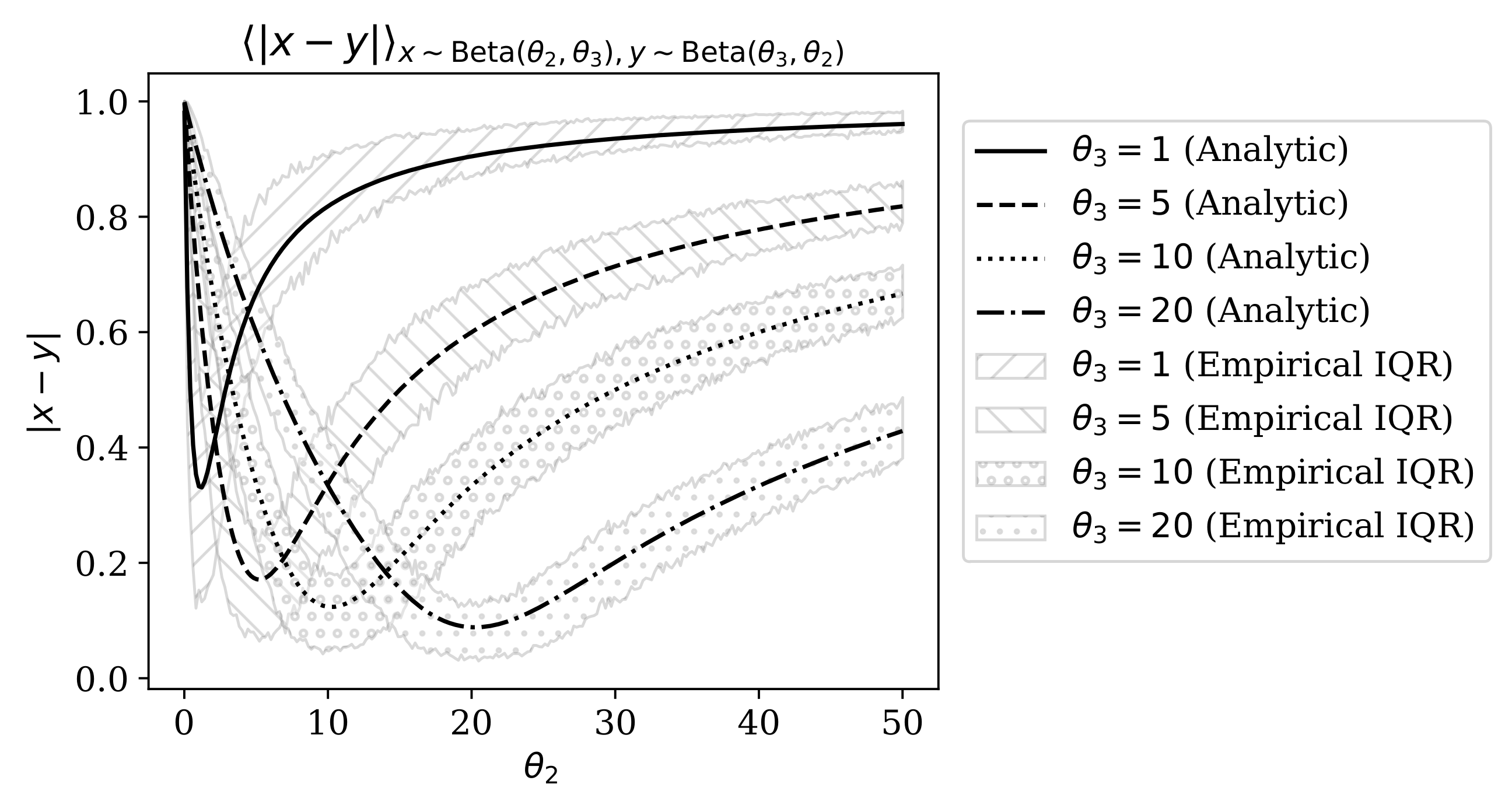
Appendix C. Evidence Supporting Relative Homogeneity of MNIST “Ones”
References
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Prehn-Kristensen, A.; Zimmermann, A.; Tittmann, L.; Lieb, W.; Schreiber, S.; Baving, L.; Fischer, A. Reduced microbiome alpha diversity in young patients with ADHD. PLoS ONE 2018, 13, e0200728. [Google Scholar] [CrossRef] [PubMed]
- Cowell, F. Measuring Inequality, 2nd ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Higgins, J.P.T.; Thompson, S.G.; Deeks, J.J.; Altman, D.G. Measuring inconsistency in meta-analyses. BMJ Br. Med. J. 2003, 327, 557–560. [Google Scholar] [CrossRef] [Green Version]
- Hooper, D.U.; Chapin, F.S.; Ewel, J.J.; Hector, A.; Inchausti, P.; Lavorel, S.; Lawton, J.H.; Lodge, D.M.; Loreau, M.; Naeem, S.; et al. Effects of biodiversity on ecosystem functioning: A consensus of current knowledge. Ecol. Monogr. 2005, 75, 3–35. [Google Scholar] [CrossRef]
- Botta-Dukát, Z. The generalized replication principle and the partitioning of functional diversity into independent alpha and beta components. Ecography 2018, 41, 40–50. [Google Scholar] [CrossRef] [Green Version]
- Mouchet, M.A.; Villéger, S.; Mason, N.W.; Mouillot, D. Functional diversity measures: An overview of their redundancy and their ability to discriminate community assembly rules. Funct. Ecol. 2010, 24, 867–876. [Google Scholar] [CrossRef]
- Chiu, C.H.; Chao, A. Distance-based functional diversity measures and their decomposition: A framework based on hill numbers. PLoS ONE 2014, 9, e113561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petchey, O.L.; Gaston, K.J. Functional diversity (FD), species richness and community composition. Ecol. Lett. 2002. [Google Scholar] [CrossRef]
- Leinster, T.; Cobbold, C.A. Measuring diversity: The importance of species similarity. Ecology 2012, 93, 477–489. [Google Scholar] [CrossRef] [Green Version]
- Chao, A.; Chiu, C.H.; Jost, L. Unifying Species Diversity, Phylogenetic Diversity, Functional Diversity, and Related Similarity and Differentiation Measures Through Hill Numbers. Annu. Rev. Ecol. Evol. Syst. 2014, 45, 297–324. [Google Scholar] [CrossRef] [Green Version]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Publishing: Washington, DC, USA, 2013. [Google Scholar]
- Regier, D.A.; Narrow, W.E.; Clarke, D.E.; Kraemer, H.C.; Kuramoto, S.J.; Kuhl, E.A.; Kupfer, D.J. DSM-5 field trials in the United States and Canada, part II: Test-retest reliability of selected categorical diagnoses. Am. J. Psychiatr. 2013, 170, 59–70. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Arvanitidis, G.; Hansen, L.K.; Hauberg, S. Latent Space Oddity: On the Curvature of Deep Generative Models. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–15. [Google Scholar]
- Shao, H.; Kumar, A.; Thomas Fletcher, P. The Riemannian geometry of deep generative models. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Nickel, M.; Kiela, D. Poincaré embeddings for learning hierarchical representations. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6339–6348. [Google Scholar]
- Rényi, A. On measures of information and entropy. Proc. Fourth Berkeley Symp. Math. Stat. Probab. 1961, 114, 547–561. [Google Scholar]
- Hill, M.O. Diversity and Evenness: A Unifying Notation and Its Consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef] [Green Version]
- Hannah, L.; Kay, J.A. Concentration in Modern Industry: Theory, Measurement and The U.K. Experience; The MacMillan Press, Ltd.: London, UK, 1977. [Google Scholar]
- Ricotta, C.; Szeidl, L. Diversity partitioning of Rao’s quadratic entropy. Theor. Popul. Biol. 2009, 76, 299–302. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. ICLR 2014 2014, arXiv:1312.6114v10. [Google Scholar]
- Kingma, D.P.; Welling, M. An Introduction to Variational Autoencoders. Found. Trend. Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Eliazar, I.I.; Sokolov, I.M. Measuring statistical evenness: A panoramic overview. Phys. A Stat. Mech. Its Appl. 2012, 391, 1323–1353. [Google Scholar] [CrossRef]
- Patil, A.G.P.; Taillie, C. Diversity as a Concept and its Measurement. J. Am. Stat. Assoc. 1982, 77, 548–561. [Google Scholar] [CrossRef]
- Adelman, M.A. Comment on the “H” Concentration Measure as a Numbers-Equivalent. Rev. Econ. Stat. 1969, 51, 99–101. [Google Scholar] [CrossRef]
- Jost, L. Partitioning Diversity into Independent Alpha and Beta Components. Ecology 2007, 88, 2427–2439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Eliazar, I. How random is a random vector? Ann. Phys. 2015, 363, 164–184. [Google Scholar] [CrossRef]
- Gotelli, N.J.; Chao, A. Measuring and Estimating Species Richness, Species Diversity, and Biotic Similarity from Sampling Data. In Encyclopedia of Biodiversity, 2nd ed.; Levin, S.A., Ed.; Academic Press: Waltham, MA, USA, 2013; pp. 195–211. [Google Scholar]
- Berger, W.H.; Parker, F.L. Diversity of planktonic foraminifera in deep-sea sediments. Science 1970, 168, 1345–1347. [Google Scholar] [CrossRef] [PubMed]
- Daly, A.; Baetens, J.; De Baets, B. Ecological Diversity: Measuring the Unmeasurable. Mathematics 2018, 6, 119. [Google Scholar] [CrossRef] [Green Version]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Simpson, E.H. Measurement of Diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Gini, C. Variabilità e mutabilità. Contributo allo Studio delle Distribuzioni e delle Relazioni Statistiche; C. Cuppini: Bologna, Italy, 1912. [Google Scholar]
- Shorrocks, A.F. The Class of Additively Decomposable Inequality Measures. Econometrica 1980, 48, 613–625. [Google Scholar] [CrossRef] [Green Version]
- Jost, L. Mismeasuring biological diversity: Response to Hoffmann and Hoffmann (2008). Ecol. Econ. 2009, 68, 925–928. [Google Scholar] [CrossRef]
- Pigou, A.C. Wealth and Welfare; MacMillan and Co., Ltd: London, England, 1912. [Google Scholar]
- Dalton, H. The Measurement of the Inequality of Incomes. Econ. J. 1920, 30, 348. [Google Scholar] [CrossRef]
- Macarthur, R.H. Patterns of species diversity. Biol. Rev. 1965, 40, 510–533. [Google Scholar] [CrossRef]
- Lande, R. Statistics and partitioning of species diversity and similarity among multiple communities. Oikos 1996, 76, 5–13. [Google Scholar] [CrossRef]
- Rao, C.R. Diversity and dissimilarity coefficients: A unified approach. Theor. Popul. Biol. 1982, 21, 24–43. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Distributed representations of words and hrases and their compositionality. In Proceedings of the NIPS 2013, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1–9. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C. Glove: Global Vectors for Word Representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar] [CrossRef]
- Nunes, A.; Alda, M.; Trappenberg, T. On the Multiplicative Decomposition of Heterogeneity in Continuous Assemblages. arXiv 2020, arXiv:2002.09734. [Google Scholar]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. In Proceedings of the Advances in Neural Information Processing Systems 6, Denver, CO, USA, 29 November–2 December 1993; pp. 737–744. [Google Scholar]
- Hadsell, R.; Chopra, S.; LeCun, Y. Dimensionality Reduction by Learning an Invariant Mapping. In Proceedings of the CVPR 2006, New York, NY, USA, 17–22 June 2006; pp. 1735–1742. [Google Scholar]



| Index | Expression |
|---|---|
| Observed richness [31] | |
| Perplexity [30] | |
| Inverse Simpson concentration [1] | |
| Berger-Parker Diversity Index [32,33] | |
| Rényi entropy [18] | |
| Shannon entropy [29] | |
| Tsallis entropy [34] | |
| Simpson concentration [35] | |
| Gini-Simpson index [36] | |
| Generalized entropy index [3,37] |
| Analytical Context | ||
|---|---|---|
| Symbol | Biodiversity | Economic Equality |
| X | Ecosystem, whose observation yields an organism denoted by vector | A system of resources, whose observation yields an asset denoted by vector |
| -dimensional feature space of organisms in the ecosystem | -dimensional feature space of assets in the economy, whose topology is such that the “economic” or monetary value is equal at each coordinate | |
| -dimensional space of one-hot species labels | -dimensional space of one-hot labels over wealth-owning agents | |
| A model that performs the mapping of organisms to discrete probability distributions over | A model that performs the mapping of assets to discrete probability distributions over | |
| The number of organisms observed belonging to species | The number of equal valued assets belonging to agent | |
| The total number of organisms observed | The total quantity of assets observed | |
| A sample of N organisms | A sample of N assets | |
| Sample weights, such that and | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, A.; Alda, M.; Bardouille, T.; Trappenberg, T. Representational Rényi Heterogeneity. Entropy 2020, 22, 417. https://doi.org/10.3390/e22040417
Nunes A, Alda M, Bardouille T, Trappenberg T. Representational Rényi Heterogeneity. Entropy. 2020; 22(4):417. https://doi.org/10.3390/e22040417
Chicago/Turabian StyleNunes, Abraham, Martin Alda, Timothy Bardouille, and Thomas Trappenberg. 2020. "Representational Rényi Heterogeneity" Entropy 22, no. 4: 417. https://doi.org/10.3390/e22040417
APA StyleNunes, A., Alda, M., Bardouille, T., & Trappenberg, T. (2020). Representational Rényi Heterogeneity. Entropy, 22(4), 417. https://doi.org/10.3390/e22040417





