Constraining LQG Graph with Light Surfaces: Properties of BH Thermodynamics for Mini-Super-Space, Semi-Classical Polymeric BH
Abstract
1. Introduction
2. On LBHs and the Metric Bundles
2.1. The Metric
2.1.1. On the MBs, Horizons, and Observers
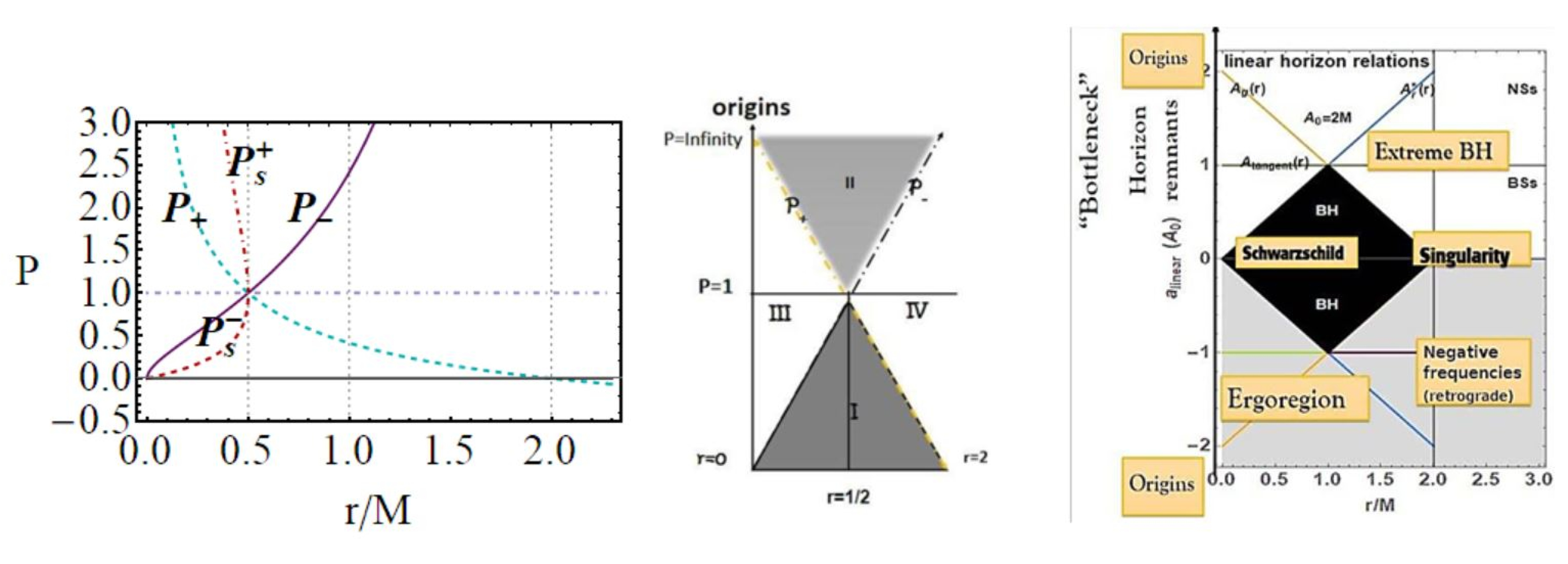
- Definitions of horizon’s replicas and confinementConsidering a generic property of the horizon as distinguished in the extended plane, as the horizon frequency for the spinning BH horizons, there is a replica of the horizon, in the same spacetime when there is an orbit (radius) such that , where is a point of the horizon curve in the extended plane. From MB definition, there are horizons replicas in different geometries, i.e., there are a and a , where p and are values of the extended plane parameter , corresponding to two different geometries (distinguished with two horizontal lines of the extended plane) such that: . In both points, , there is equal light-like orbital frequency. Vice versa, the (MBs’) horizon confinement is interpreted as the presence of a “local causal ball” in the extended plane, which is a region of the extended plane , where MBs are entirely confined, this means that there are no horizons replicas in any other region of the extended plane, in any other geometry, although we can be interested in specifying this definition to confinement of the ℘ property in the same geometry. Typically, for the Kerr spacetime, the causal ball is a region upper bounded in the extended plane by the a portion of the horizon curve corresponding to the a set of the inner horizon BHs—[6,9,10,11]. The analysis of self-intersections of the bundles curves on the extended plane, in the same geometry (horizon confinement) or intersection of bundles curves in different geometries is therefore an important point of the MBs analysis. (It is obvious that, in the spherically symmetric spacetime, the definition of replica is adapted to the frame of the MBs approximation to the horizon curve in the extended pane, i.e., ). We precise the definition of the MBs by considering explicitly the definition for the Kerr spacetimes; in this discussion, it is easier to consider explicitly the definition for the metric bundles adapted to the more general axially symmetric case as in [6,7,8,9,10,11]). Therefore, the Kerr horizons are null surfaces, , whose null generators coincide with the orbits of a one-parameter group of isometries; thus, there exists a Killing field that is normal to . MBs satisfy the condition , where is a Killing field of the geometry . In BH spacetimes, this Killing vector defines also the thermodynamic variables and the Killing horizons. Therefore, metric bundles are solutions of the zero-norm condition ( for the outer horizon ). The condition is related to the definition of stationary observers, characterized by a four-velocity of the form . The spacetime causal structure of the Kerr geometry can be then studied by considering also stationary observers [30]: timelike stationary observers have orbital frequencies (from now on simply called frequencies) in the interval having limiting orbital frequencies, which are the photon orbital frequencies , which, evaluated on the Kerr horizons , provide the frequencies of the Killing horizons. In general, a Killing horizon is a light-like hypersurface (generated by the flow of a Killing vector), where the norm of a Killing vector is null. The event horizons of a spinning BH are therefore Killing horizons with respect to the Killing field , where is in general angular velocity of the horizons. (The event horizon of a stationary asymptotically flat solution with matter satisfying suitable hyperbolic equations is a Killing horizon). Conditions on constant represent the BH rigid rotation. For static (and spherically symmetric) BH spacetimes, the event, apparent, and Killing horizons with respect to the Killing field coincide. In the limiting case of the static Schwarzschild spacetime or the Reissner Nordström spacetime, the event horizons are Killing horizons with respect to the Killing vector .
- MBs and thermodynamics: In this work, we also investigate some BHs thermodynamics properties of the LBHs in the extended plane through the analysis of MBs. The BH Killing horizons of stationary solutions have constant surface gravity (zeroth BH law-area theorem): the norm of is constant on the BH horizon. Moreover, the BH surface gravity, which is a conformal invariant of the metric, may be defined as the rate at which the norm of the Killing vector vanishes from outside (). For a Kerr spacetime, the surface gravity re-scales with the conformal Killing vector, i.e., it is not the same on all generators, but, because of the symmetries, it is constant along one specific generator. More precisely: the constant , evaluated on the outer horizon , defines the BH surface gravity, i.e., constant on the orbits of (equivalently, we can write and , where is the Lie derivative—therefore defining a non-affine geodesic equation). The BH surface area is non-decreasing (second BH law); consequently, the impossibility to achieve by a physical process a BH state with zero surface gravity. More precisely, non-extremal BH cannot reach an extremal case in a finite number of steps—third BH law: at the extreme case for the Kerr geometry , the maximum of the horizon curve in the extended plane, where , the surface gravity is zero and, consequently, the temperature is , but not its entropy (and therefore the BH area).(This fact poses constraints also with respect to the stability against Hawking radiation) The mass variation, the surface gravity, and the horizons frequencies are related by the first law of BH thermodynamics, which can be written as , where there is the variation of the BH mass, the horizon area and angular momentum J, for the Kerr (BH), representing the “work term”, is the BH area.
2.1.2. The Extended Plane
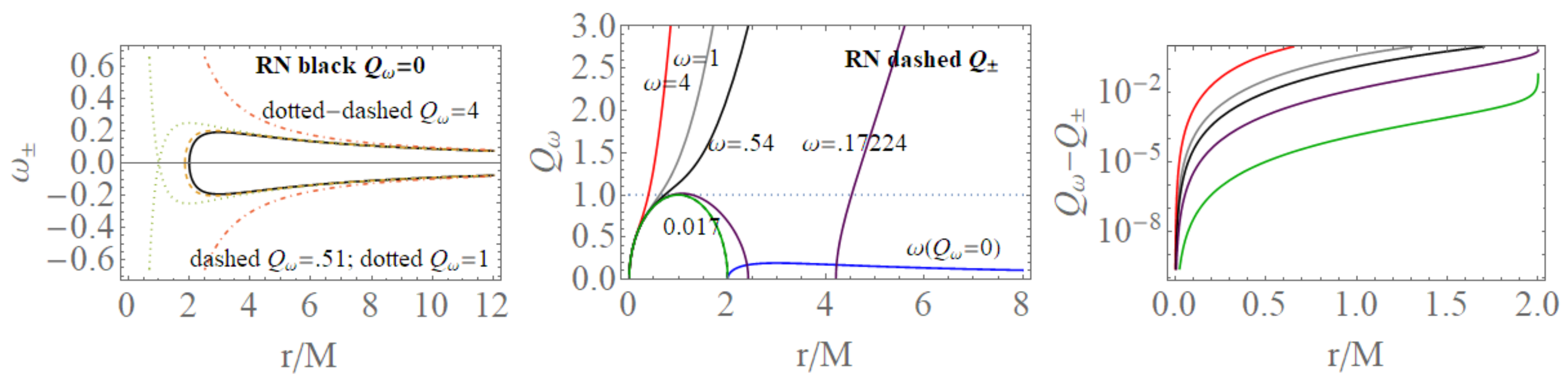
2.2. Comparison with the Reissner–Norström Geometry
3. Metric Killing Bundles of the LBHs
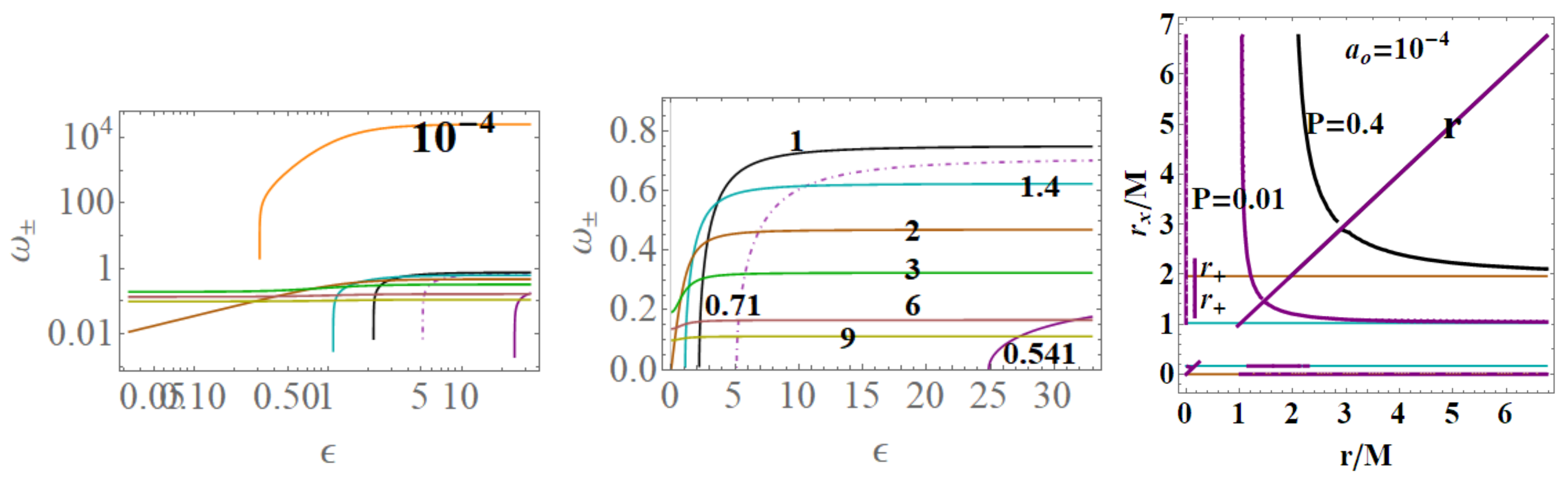
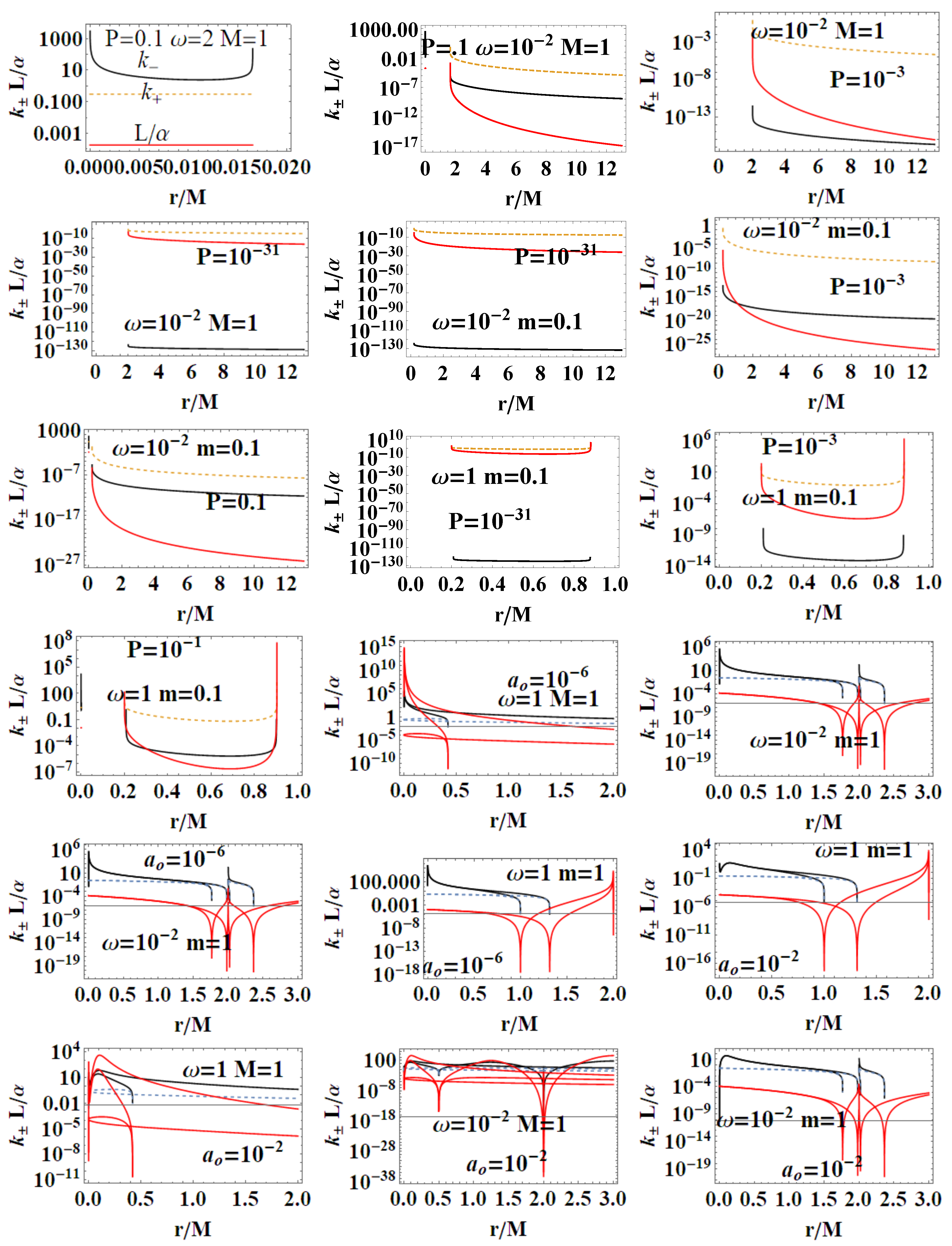
3.1. Light Surfaces (LS) Frequencies
3.2. Metric Bundles Parametrization
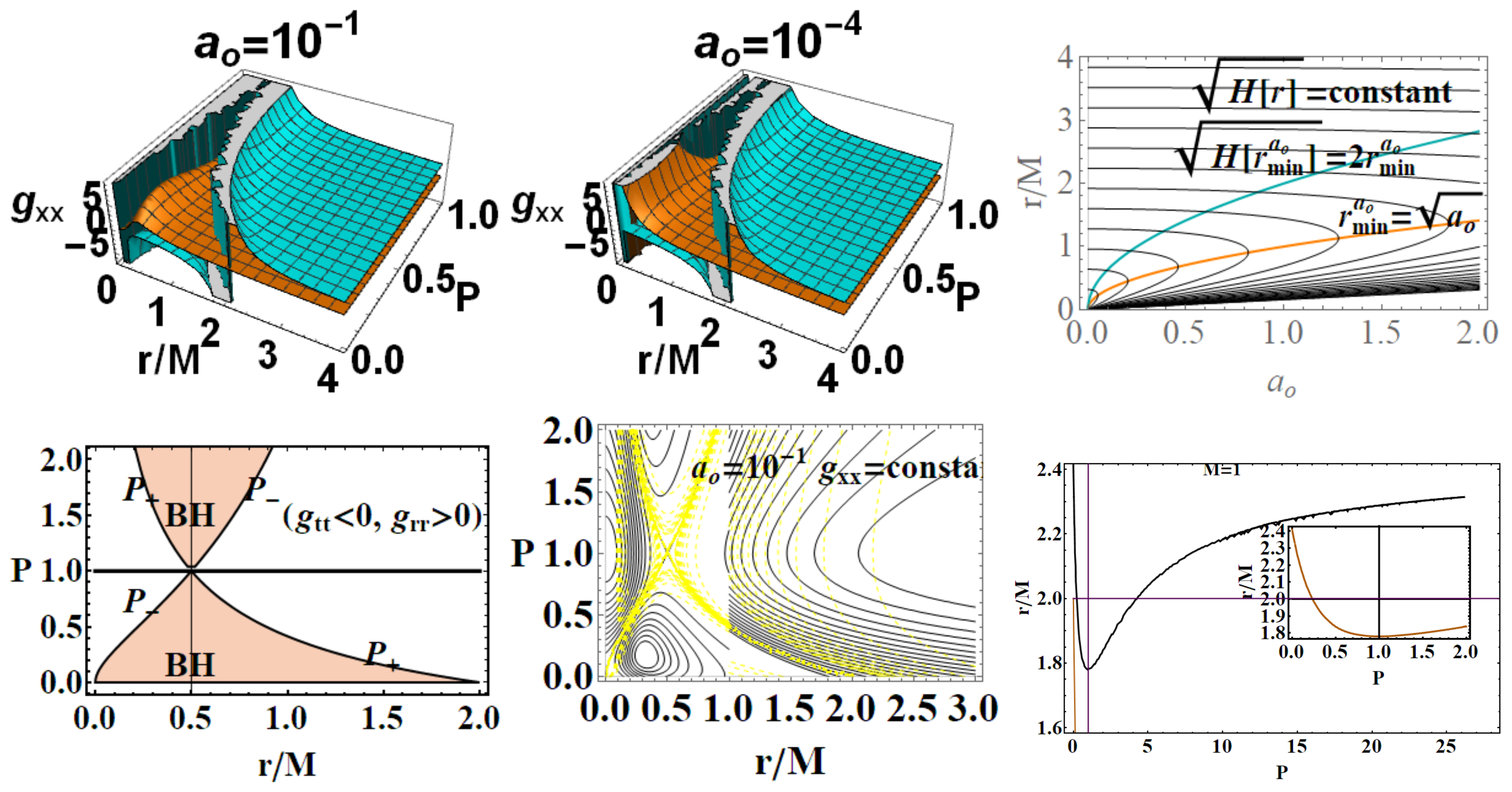
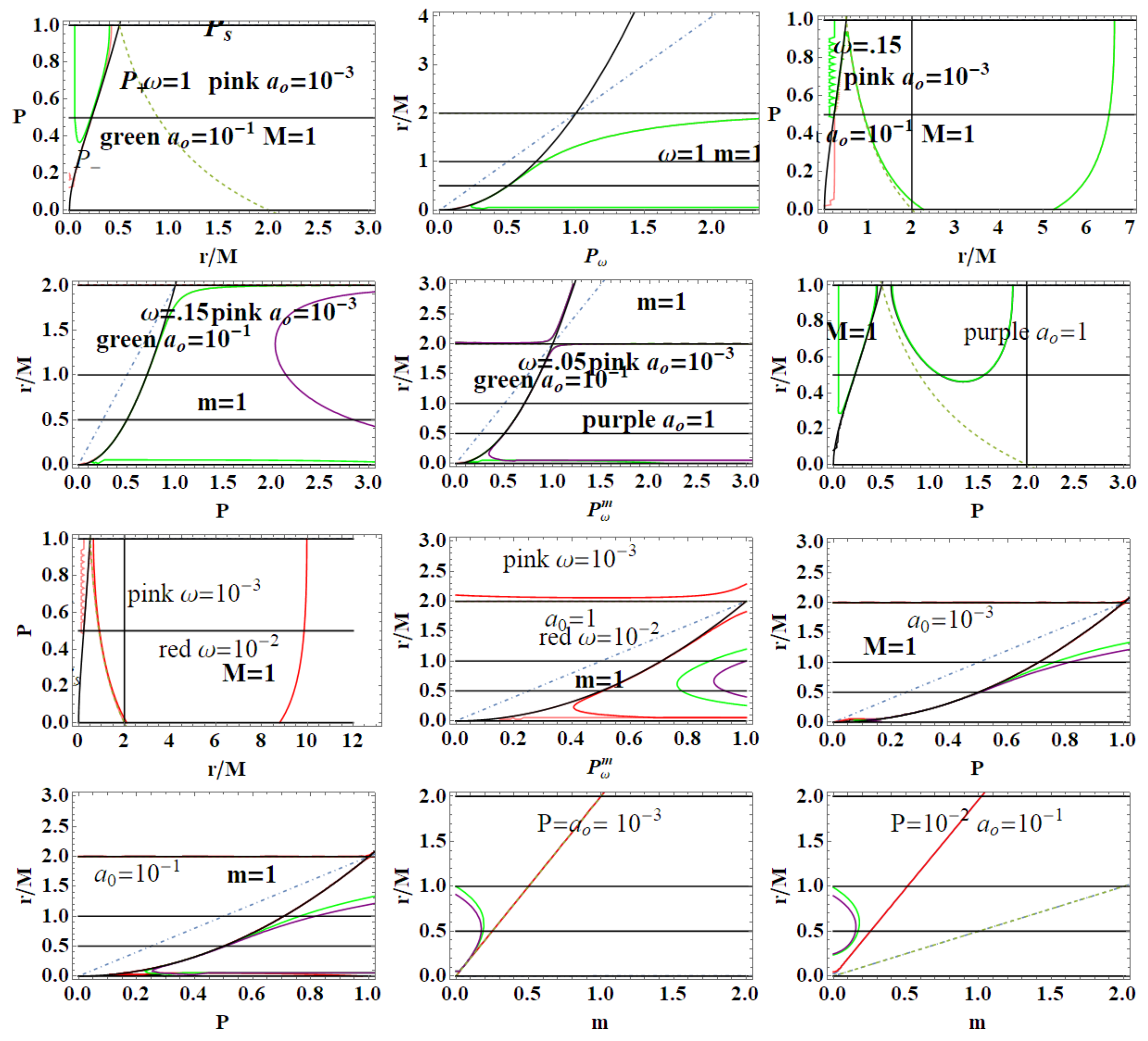
- Metric bundles: parametrization according to As the metric is spherically symmetric, we can consider, without loss of generality, , i.e., a fixed (Schwarzschild BH) equatorial plane. Nevertheless, we could consider explicitly a parametrization according to the “poloidal” angle , obtaining the curves:In here, metric bundles with constant are on the hyperplane . Clearly, this choice is relevant for the parametrization . Note that there is for . Figure 10 represent special and limiting cases of metric bundles.
- Metric bundles: -parametrizationIt is relevant to study a -parametrization to consider the families of metrics for different minimum areas parameter . Implementing therefore the notion of metric bundles with the area parameter, we obtain explicitlyrepresented in Figure 11. Providing constraints on the loop minimal areas, functions are not well defined on the horizons in the extended plane, and limits to is null.
- Metric bundles: P-parametrizationHere, we consider the leading parameter P. Metric bundles in the extended plane and are shown in Figure 6, where there is also a focus on the vertical and horizontal lines of the extended planes and horizons’ replicas at different values of the parameter.The equation for the metric bundles according to the P-parametrization is polynomial function of degree 8, , where
4. The LBHs Thermodynamical Properties
4.1. BHs Thermodynamics and LQG Parameters
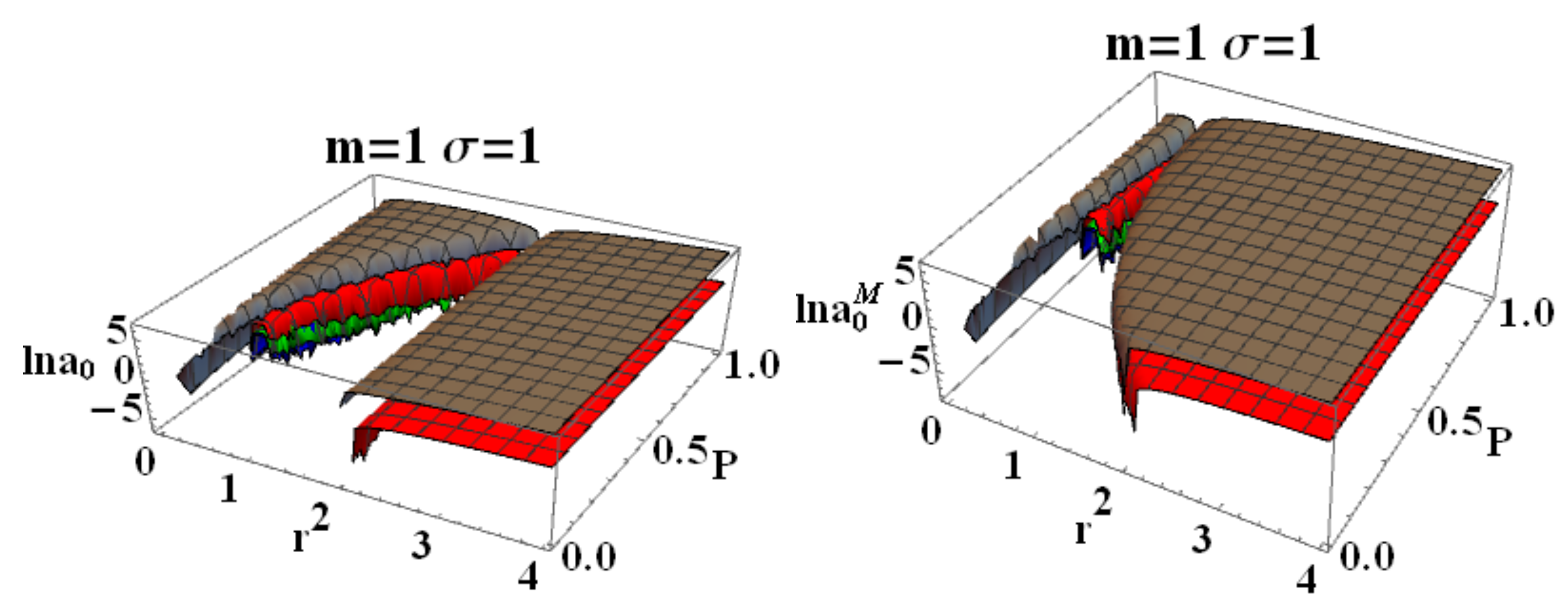
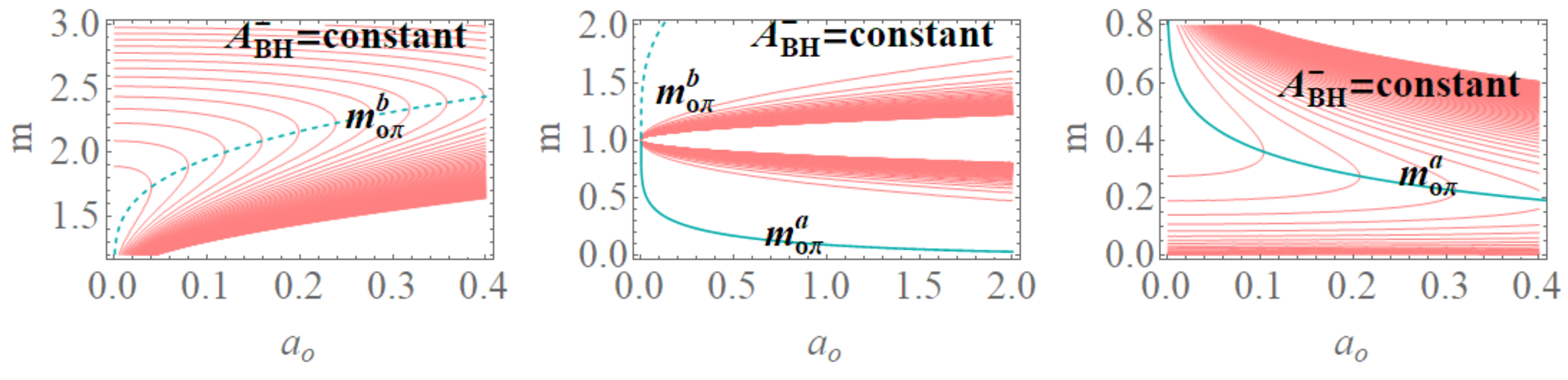
- BH areas We can evaluate the BH areas as follows:In , we used the quantity , where is related to the surface bounded by the outer and the inner BH horizon. (In the extended plane, it is necessary to consider horizons ). Note that does not depend explicitly on P. When considered in the extended plane, there are some special values of the parameters for which there is a coincidence of the areas , for the equal values of . There is (within the assumption ) for or , while for , or , wheresee Figure 12. Interestingly, however, the LBHs areas have extreme points: for and for ; finally, for , wherefor (, ( for ), where() see Figure 13, where the role of and is clear. Note, interestingly, the presence of an extreme of the BHs areas related to the graph loop parameters.
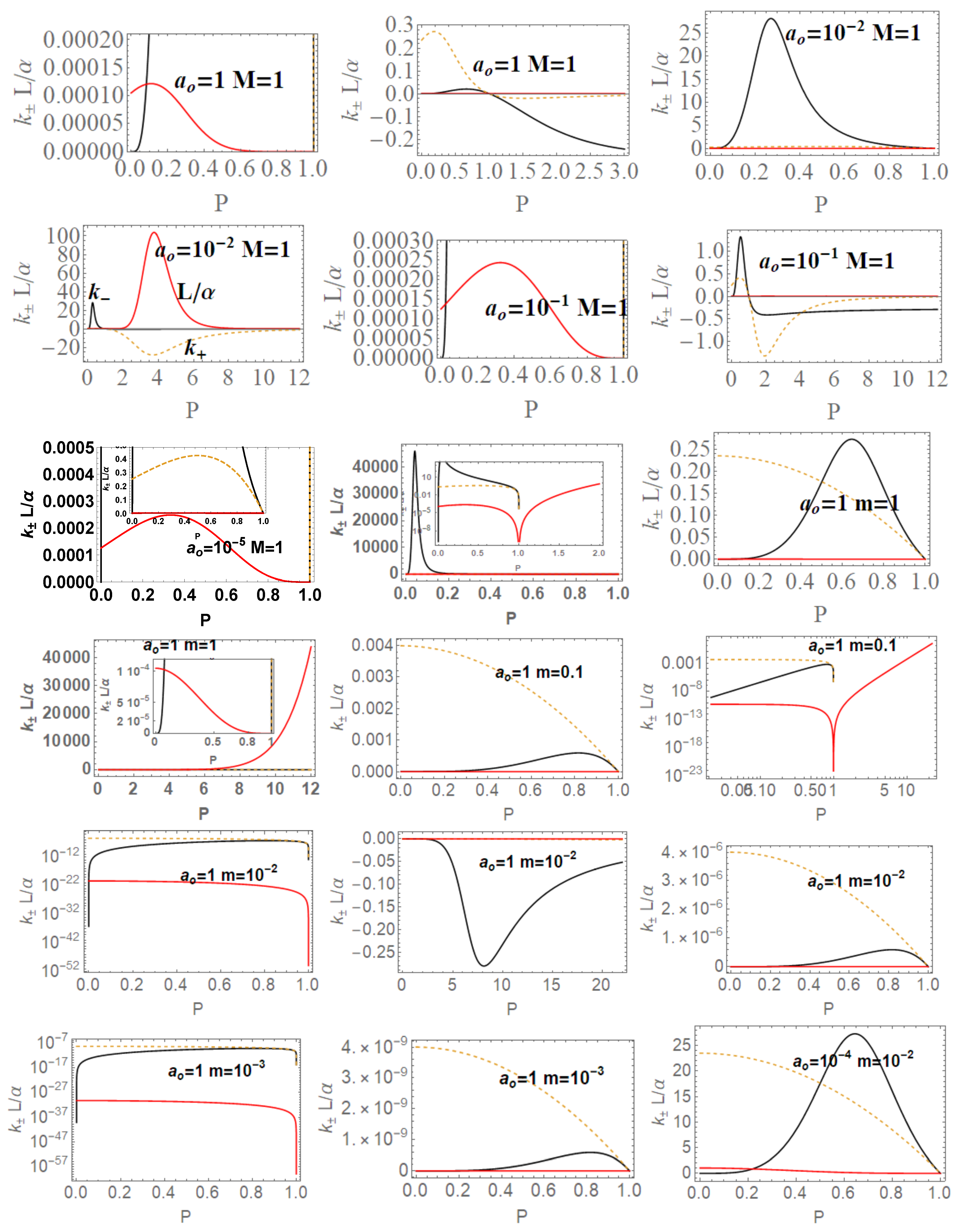
- Surfaces gravity: We can evaluate a LBH “surface gravity” correspondent to the outer and inner horizons , respectively, as :Comparing the extended planes of Kerr geometries and the regular LBH geometries of Figure 2, we expect surface gravities to vanish in some extreme conditions on the loop graph parameters. It is then clear that for and for , which is the region of the polymeric function values we explore here. Thus, there isThe limiting , occurring in the extended plane of Figure 2 at , is also an extreme for the . Extremes are for limiting conditions , , , relating the limiting values on and the ADM mass. A further extreme is for minimal area (or ) for and for . For convenience, we report in Table 2 all the relevant minimal areas for , introduced in this discussion and represented in Figure 14. Similarly, there is for and , and also for with for and for .There is an extreme for at for the limiting condition –([1]). There is then for , for and for and . On the other hand, , for the limiting cases (including ) and for . Analogously, there is , an extreme condition having the special solution , notably independent from the polymeric parameter.In Figure 14, we also considered an extended region of the parameters.
- The temperatures: The evaluation of the temperature associated with the (regular) LBH proceeds directly in terms of surface gravity :We actually evaluate the temperatures in terms of , respectively, for the outer and inner horizons . The interpretation and the evaluation of the temperature is debated in literature. In this analysis, while we intend clearly as the BH temperature, when we intend the BH in the extended plane, as in Figure 15, then we need to consider . On the other hand, considering the extended plane or , we expect the occurrence of an “extreme” case, where the temperature is null (similarly to the case of extreme Kerr BH) as made evident from the study of the surface gravity . Temperature is vanishing for , in the case :
- The luminosity: In the analysis of luminosity, we consider [1]. The luminosity can be estimated by considering the Stefan–Boltzmann law as , where is the area (on horizon ), and is a factor depending on the evaluation model adapted for the luminosity. However, in this work, we mainly consider the quantity . By assuming constant, we focus on the analysis of luminosity with the variation of the parameters of the LQG graph and on the metric bundles. Studying (or ), we investigate the regular BH mass evaporation process (the energy flux particularly where BH evaporation occurs through the Hawking emission in the proximity of the BH outer horizon , with a temperature evaluated according to the Bekenstein–Hawking law and connected therefore to the surface gravity ). We perform our investigation considering different values of and on the geometries connected by the metric bundles. The luminosity is, therefore, in terms of m:In the Schwarzschild limit, (correspondent to ), there isWe should note that: for or (in this special analysis, we consider m and P independent—for the limiting condition for the approximate geometry; see, for example, discussion in [1]). It is, however, relevant to consider the extremes of luminosity function L (related to the BH evaporation process for mass loss). Therefore, conveniently, we introduce here the following special values of the minimal length parameter :represented in Figure 14. Therefore, there is for and for some limiting cases on (for example, vertices of the LBHs triangle in Figure 2, i.e., limiting geometries for parameters values as studied in Section 2). Considering explicitly dependence on P, there is and for the limiting cases on the parameters . We now focus on the situations when . In this case, there is an extreme for the minimal area. (We include also the extremes in the limiting cases and for ). Then, there is in the limiting cases and for , where only for the limiting cases. In Figure 15, we consider different limiting cases on the LBH model parameters on the BHs quantities , , and the temperature , making evident the presence of extreme points and even negative values of temperature in extended regions of parameters.
- LBHs thermodynamical properties and MBs: We now consider the quantities of the regular LBHs geometries, (surface gravity) and (luminosity) evaluated on the metric bundles of the geometry. This analysis will connect different geometries of the same metric bundle through their thermodynamical properties. This treatment of the thermodynamical properties and LQG-BH will also characterize the role of the graph parameters in shaping different solutions. Eventually, this analysis connects the extended plane parameter variation with the transition from a LBH solution to another solution. In Figure 16, we note the presence of singularities and the behaviors at increasing distance from the (the bundles’ origins). A transformation from one solution of the bundle to another follows transformations of on the curves evaluated on the bundles. This analysis explores the possibility of a transition from one solution of a metric family to another geometry of the same family, which, for example, can occur after interaction of the attractor with the surrounding matter environment in non-isolated BH systems, which is the general case in the most common astrophysical environments. This process would lead a BH from a point to another point of its extended plane representation. (This transition could also involve, of course, for some other diverse processes, a transition of the graph parameters). The relevant aspect of this analysis is that this transition must carry the system from one point to another in the extended plane along an MB curve. This means that the observer from the initial state will see a transition of the fixed frequency from a point to (in general, there are no fixed point along constant), where and are two points along the bundle uniquely identified by the detection of the fixed photon frequency. Vice versa, the observer will be able to recognize at the fixed point through the photon orbital frequency variation in the external region any geometry transition in the extended plane (regulated by thermodynamic laws). At fixed frequency, there is always one and only one bundle; furthermore, a bundle curve does not in general self-cross– there is an absence of knots. Therefore, we also test the hypothesis that the bundles, connecting the solutions uniquely through their characteristic frequencies and defining the associated light surfaces, could have a role in such transitions. Obviously, the thermodynamic onset provides in the new points of the plane a series of quantities as surface of gravity luminosity or temperature that have evolved on the bundles as shown in these analyses. Therefore, these results have to be compared with the correspondent analysis of MB curves. It should be also noted that, in Figure 16, we have fixed, depending on the parametrization of the bundles, different parameters and the frequency. (The functions associated with these quantities are generally well defined far from the horizons. In the analysis, we have taken advantage of this property to evaluate in the extended plane these quantities also on the horizon curves as clear from the analysis in Figure 16. Whatever the parameterizations adopted and the fixed parameters set, the horizon points of the extended plane clearly highlighted by the vertices of the correspondent triangle in the representation of the Figure 2 indicate signs of singularity for these quantities).
5. Discussion and Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Alesci, E.; Modesto, L. Hawking radiation from Loop Black Holes. J. Phys. Conf. Ser. 2012, 360, 012036. [Google Scholar] [CrossRef]
- Modesto, L. Semiclassical loop quantum black hole. Int. J. Theor. Phys. 2010, 49, 1649. [Google Scholar] [CrossRef]
- Modesto, L.; Premont-Schwarz, I. Self-dual Black Holes in LQG: Theory and Phenomenology. Phys. Rev. D 2009, 80, 064041. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and Evaporation of Nonsingular Black Holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Modesto, L.; Premont-Schwarz, I. Model for nonsingular black hole collapse and evaporation. Phys. Rev. D 2010, 81, 044036. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H. Disclosing connections between black holes and naked singularities: Horizon remnants, Killing throats and bottlenecks. Eur. Phys. J. C 2019, 79, 209. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H. Observers in Kerr spacetimes: The ergoregion on the equatorial plane. Eur. Phys. J. C 2018, 78, 69. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H. The ergoregion in the Kerr spacetime: Properties of the equatorial circular motion. Eur. Phys. J. C 2015, 75, 234. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H. On the metric bundles of axially symmetric spacetimes. arXiv 2019, arXiv:1910.04996. [Google Scholar]
- Pugliese, D.; Quevedo, H. Killing horizons, throats and bottlenecks in the ergoregion of the Kerr spacetime. arXiv 2019, arXiv:1910.02808. [Google Scholar]
- Pugliese, D.; Quevedo, H. Kerr metric Killing bundles.Killing horizons confinement, light-surfaces and horizons replicas. 2020. submitted. [Google Scholar]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular orbits of neutral test particles in the Kerr-Newman spacetime. Phys. Rev. D 2013, 88, 024042. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular motion in Kerr spacetime. Phys. Rev. D 2011, 84, 044030. [Google Scholar] [CrossRef]
- De Felice, F. Rotating frames and measurements of forces in general relativity. Mon. Not. R. Astron. Soc. 1991, 252, 197–202. [Google Scholar] [CrossRef][Green Version]
- De Felice, F.; Usseglio-Tomasset, S. On the pre-horizon regime in the Kerr metric. Class. Quantum Gravity 1991, 8, 1871–1880. [Google Scholar] [CrossRef]
- De Felice, F.; Usseglio-Tomasset, S. Circular orbits and relative strains in Schwarzschild space-time. Gen. Relativ. Gravit. 1992, 24, 10. [Google Scholar] [CrossRef]
- De Felice, F.; Sigalotti, L.; Di, G. Rotating Stars: The Angular Momentum Constraints. Astrophys. J. 1992, 389, 386–391. [Google Scholar] [CrossRef]
- De Felice, F.; Yunqiang, Y. Schwarzschild spacetime: Measurements in orbiting space stations. Class. Quantm Gravity 1993, 10, 353–364. [Google Scholar] [CrossRef]
- De Felice, F. Kerr metric: The permitted angular velocity pattern and the pre-horizon regime. Class. Quantum Gravity 1994, 11, 1283–1292. [Google Scholar] [CrossRef]
- De Felice, F.; Usseglio-Tomasset, S. Strains and rigidity in black-hole fields. Gen. Relativ. Gravit. 1996, 28, 2. [Google Scholar] [CrossRef]
- Chakraborty, C.; Patil, M.; Kocherlakota, P.; Bhattacharyya, S.; Joshi, P.S.; Królak, A. Distinguishing Kerr naked singularities and black holes using the spin precession of a test gyro in strong gravitational fields. Phys. Rev. D 2017, 95, 084024. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Super-Penrose process and rotating wormholes. Phys. Rev. D 2018, 98, 104030. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Center of mass energy of colliding electrically neutral particles and super-Penrose process. Phys. Rev. D 2019, 100, 024050. [Google Scholar] [CrossRef]
- Tanatarov, I.V.; Zaslavskii, O.B. Collisional super-Penrose process and Wald inequalities. Gen. Relativ. Gravit. 2017, 49, 119. [Google Scholar] [CrossRef][Green Version]
- Perez, A. Black Holes in Loop Quantum Gravity. Rep. Prog. Phys. 2017, 80, 126901. [Google Scholar] [CrossRef]
- Barrau, A.; Martineau, K.; Moulin, F. A status report on the phenomenology of black holes in loop quantum gravity: Evaporation, tunneling to white holes, dark matter and gravitational waves. Universe 2018, 4, 102. [Google Scholar] [CrossRef]
- Barrau, A.; Martineau, K.; Martinon, J.; Moulin, F. Quasinormal modes of black holes in a toy-model for cumulative quantum gravity. Phys. Lett. B 2019, 795, 346. [Google Scholar] [CrossRef]
- Haggard, H.M.; Rovelli, C. Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef]
- Alesci, E.; Modesto, L. Particle Creation by Loop Black Holes. Gen. Relativ. Gravity 2014, 46, 1656. [Google Scholar] [CrossRef]
- Malament, D.B. The class of continuous timelike curves determines the topology of spacetime. J. Math. Phys. 1977, 18, 1399. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.W.; Park, Y.J. Thermodynamics of regular black hole. Gen. Relativ. Gravit. 2009, 41, 1051. [Google Scholar] [CrossRef]







| Killing fields of the geometry | Equation (12)–Section 2.1 and Section 3 | |
| , | the area parameter | Equation (2)–Section 2.1 |
| minimum area gap of LQG | Equation (2)–Section 2.1 | |
| P | metric polymeric parameter | Equation (2)–Figures 1 and 2–Section 2.1 |
| = metric polymeric parameter, = Barbero–Immirzi parameter | Equation (2)–Figures 1 and 2–Section 2.1 | |
| M | ADM mass in the Schwarzschild limit | Equation (2)–Section 2.1 |
| m | mass polymeric parameter function | Equation (2)–Figures 1 and 2–Section 2.1 |
| horizons | Equation (3)–Figures 1 and 2–Section 2.1 | |
| horizons in -loop parameter | Equation (6)–Figure 2 | |
| horizons in P-loop parameter in extended plane | Equation (4) | |
| null Killing vector (generators of Killing event horizons) | Section 2.1.1 | |
| Killing vector norm | Equation (12)–Section 2.1.1 and Section 3 | |
| light-like () limiting frequencies for stationary observers | Equation (9) | |
| limiting frequencies for the Schwarzschild geometry | Equations (9) and (23) | |
| RN spacetime “total charge” | Equation (8)–Section 2.2 | |
| Kerr Killing horizon curve in the extended plane | Section 2.2 | |
| RN horizon in the extended plane | Section 2.2–Figure 2 | |
| RN metric bundles | Equation (9) | |
| a minimum curve for the as function of r () | Figure 4–Section 2.1 | |
| metric bundles: parametrization | Equation (27) | |
| metric bundles: -parametrization | Equation (28)–Figure 11 | |
| solution of | Equation (26)–Figure 9 | |
| solution of | Equation (24) | |
| (acceleration) on , define BH surface gravity | Equation (36)–Section 2.1.1 and Section 4.1 | |
| BH temperature | Section 2.1.1 and Section 4.1 | |
| BH areas | Equation (31)–Figure 12–Section 2.1 and Section 4.1 | |
| Luminosity | Equation (42)–Figure 15–Section 4.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pugliese, D.; Montani, G. Constraining LQG Graph with Light Surfaces: Properties of BH Thermodynamics for Mini-Super-Space, Semi-Classical Polymeric BH. Entropy 2020, 22, 402. https://doi.org/10.3390/e22040402
Pugliese D, Montani G. Constraining LQG Graph with Light Surfaces: Properties of BH Thermodynamics for Mini-Super-Space, Semi-Classical Polymeric BH. Entropy. 2020; 22(4):402. https://doi.org/10.3390/e22040402
Chicago/Turabian StylePugliese, Daniela, and Giovanni Montani. 2020. "Constraining LQG Graph with Light Surfaces: Properties of BH Thermodynamics for Mini-Super-Space, Semi-Classical Polymeric BH" Entropy 22, no. 4: 402. https://doi.org/10.3390/e22040402
APA StylePugliese, D., & Montani, G. (2020). Constraining LQG Graph with Light Surfaces: Properties of BH Thermodynamics for Mini-Super-Space, Semi-Classical Polymeric BH. Entropy, 22(4), 402. https://doi.org/10.3390/e22040402





