Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 2): Correlations for Limiting Cases
Abstract
:1. Introduction
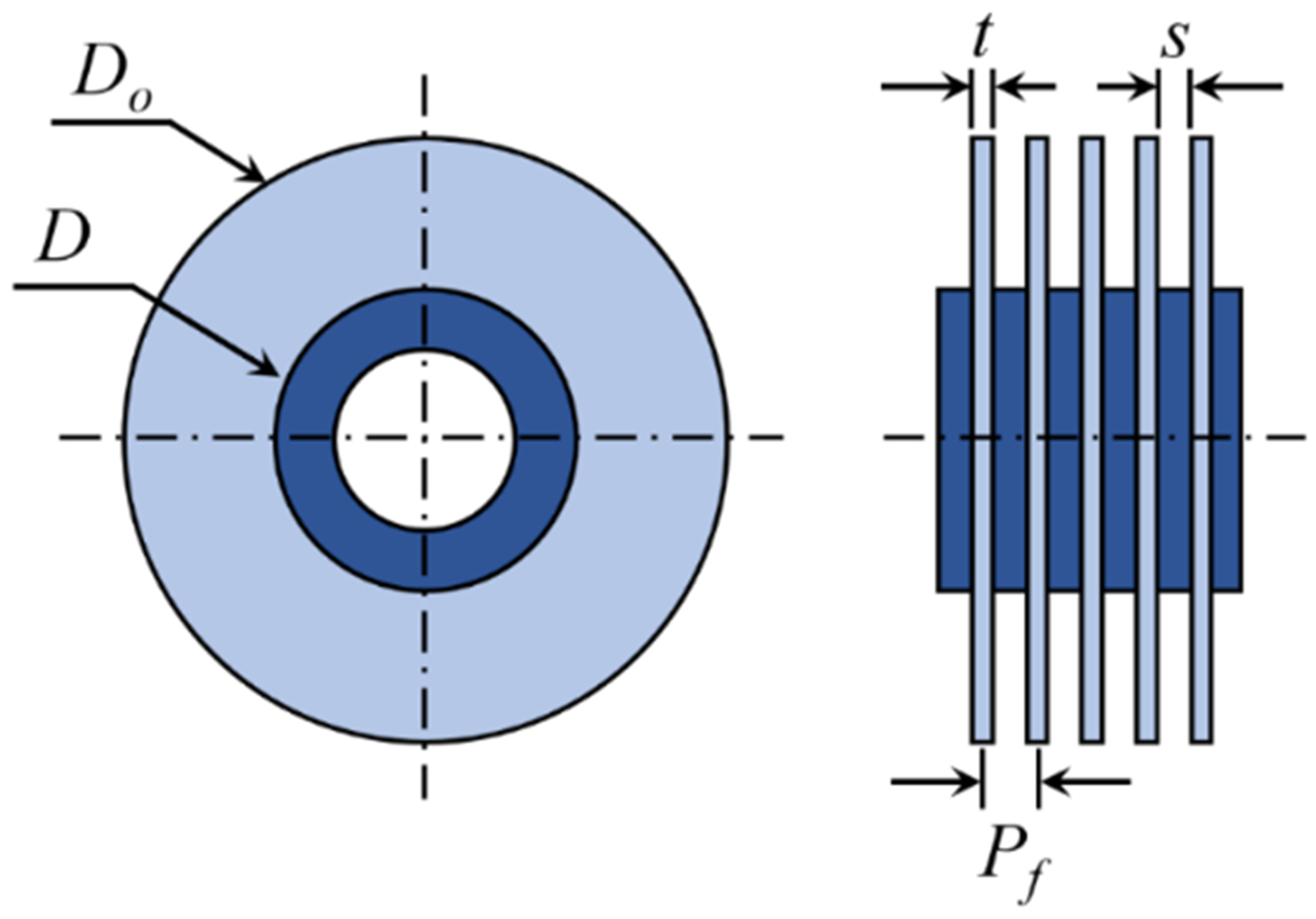
2. Heat Exchanger Model
3. Limiting Cases
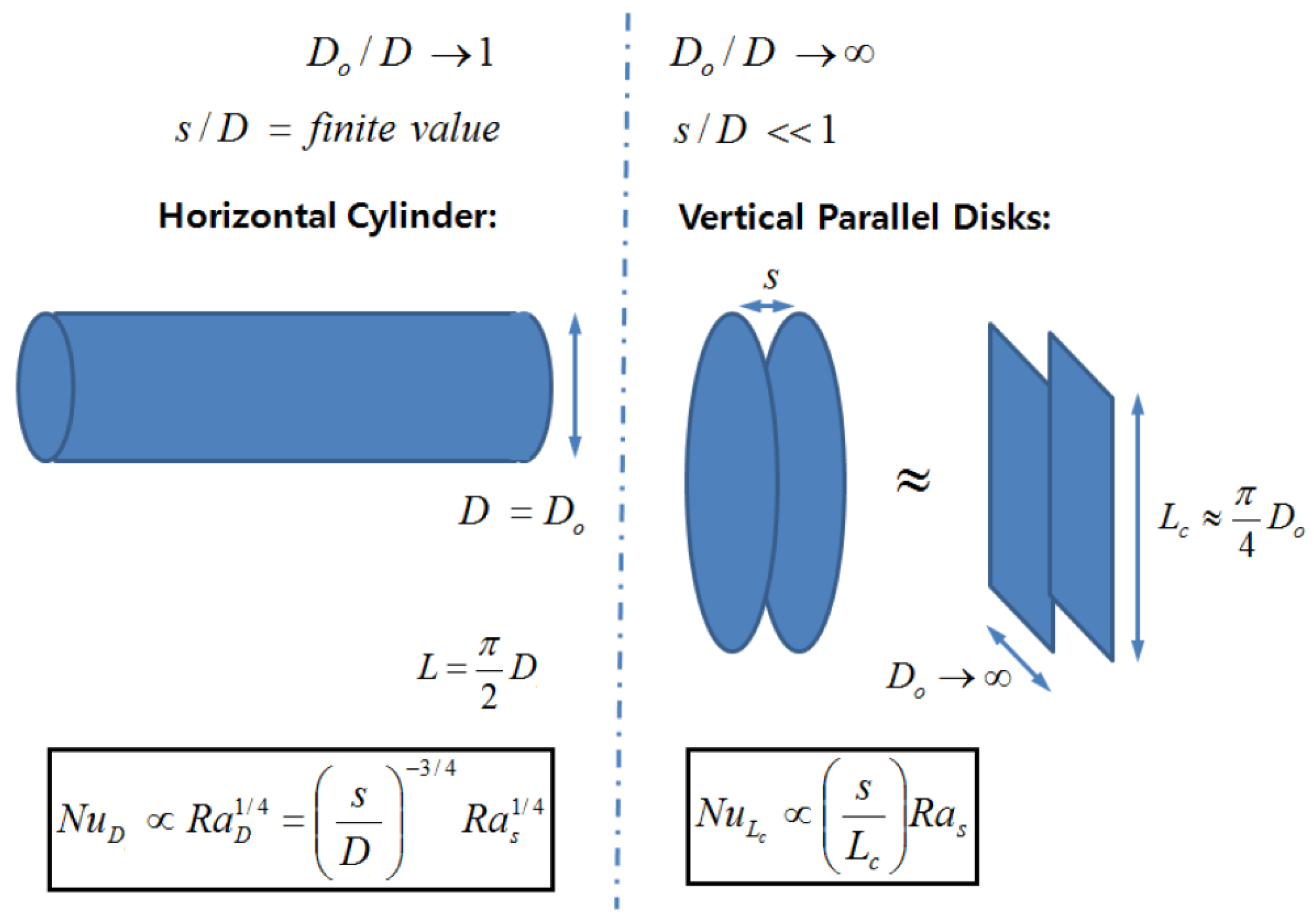
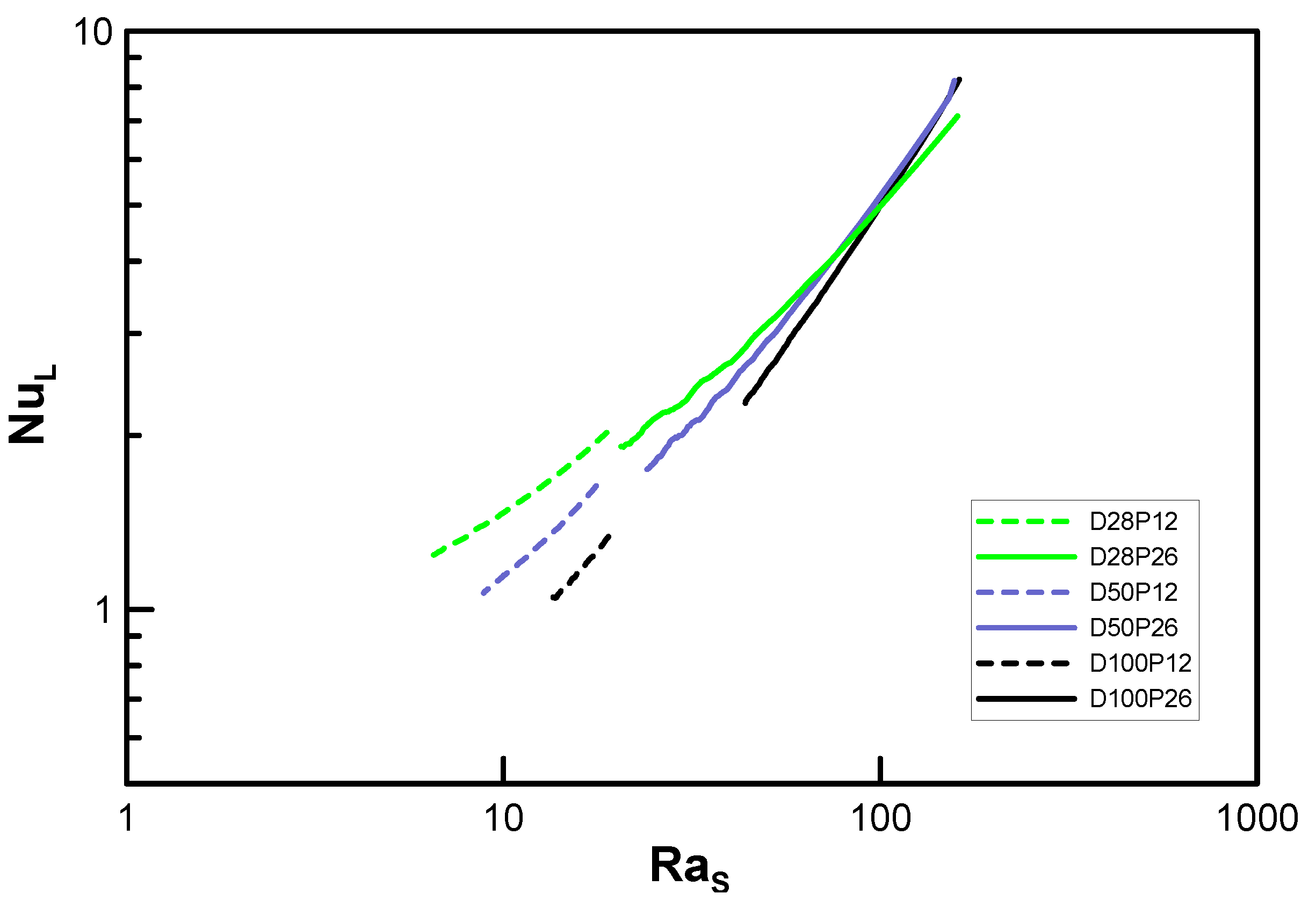
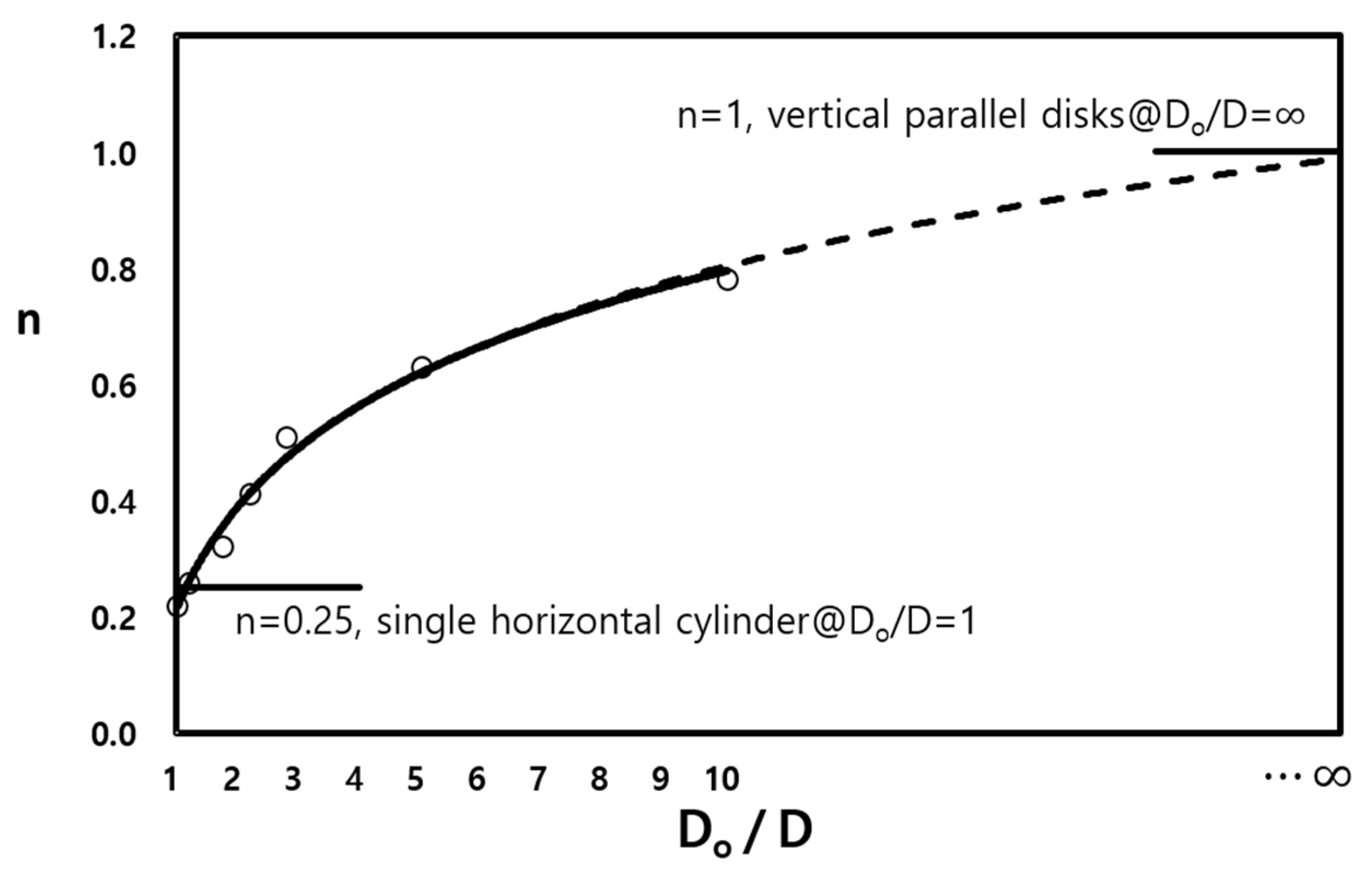
3.1. Lowest Case: Do/D → 1, s/D = Finite Value (Single Horizontal Cylinder)
3.2. Hightest Case: Do/D → ∞, s/D << 1 (Vertical Parallel Disks)
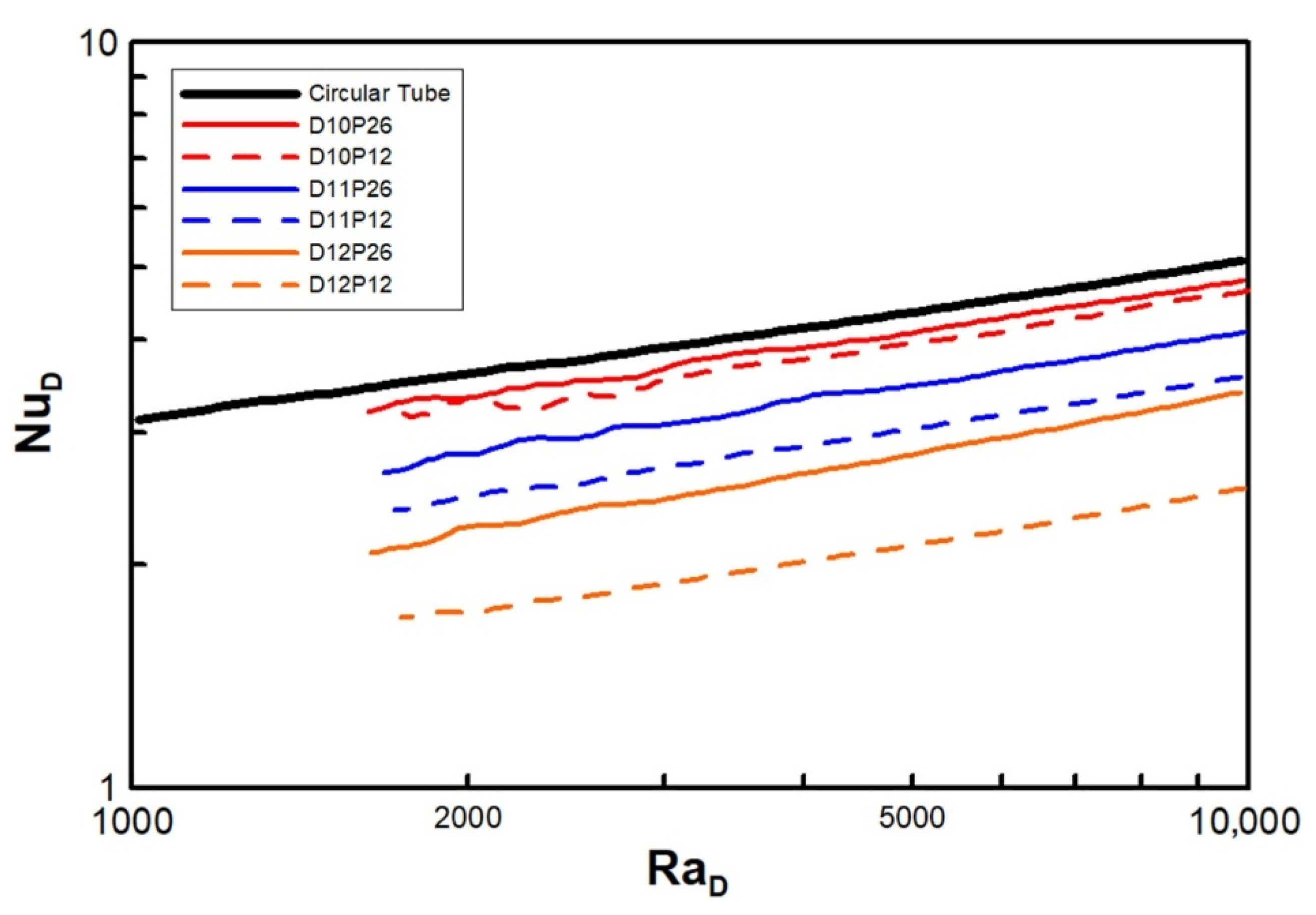
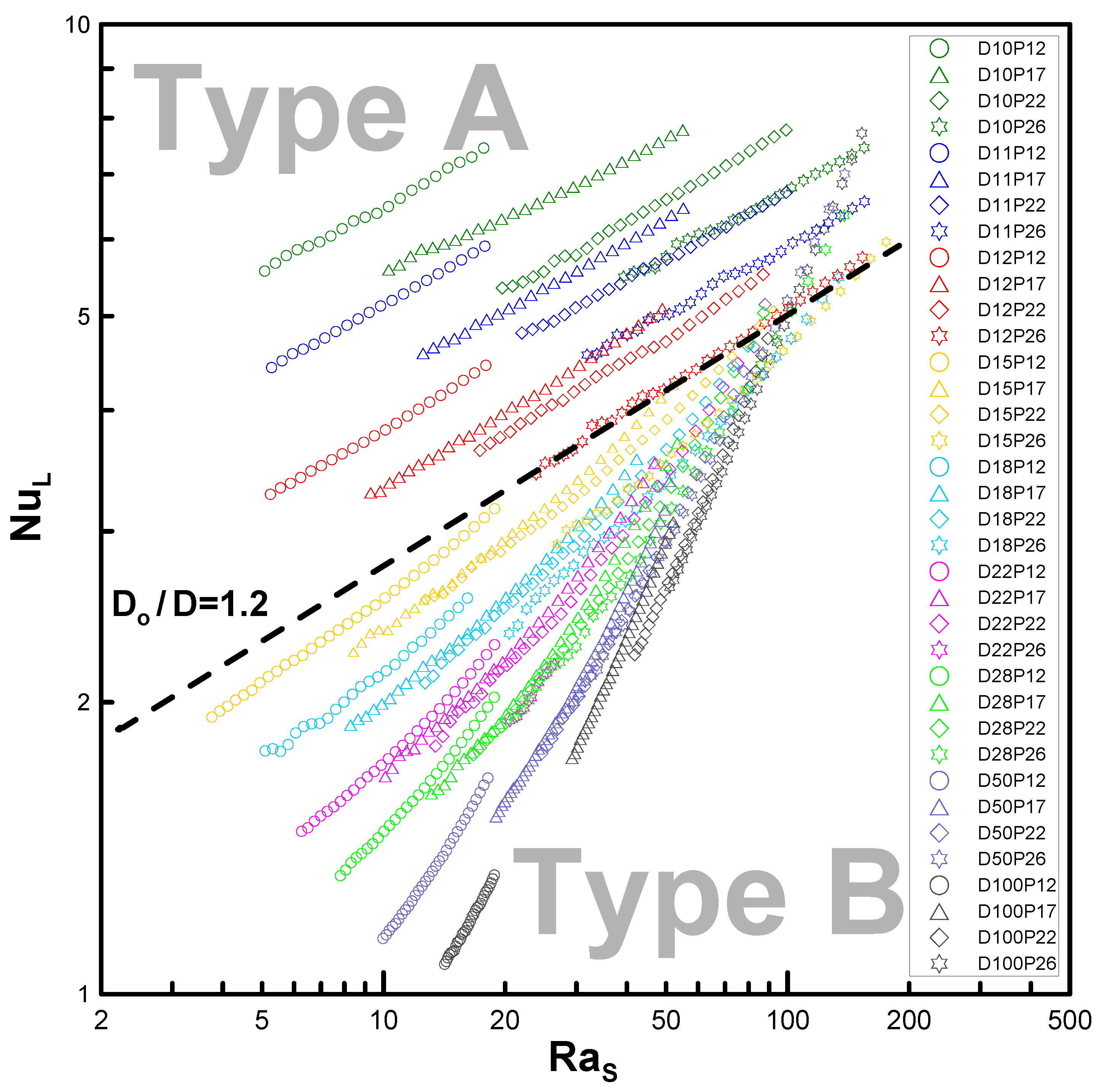
4. Classification Criteria for Types A and B
5. Correlation Expansion and Validity
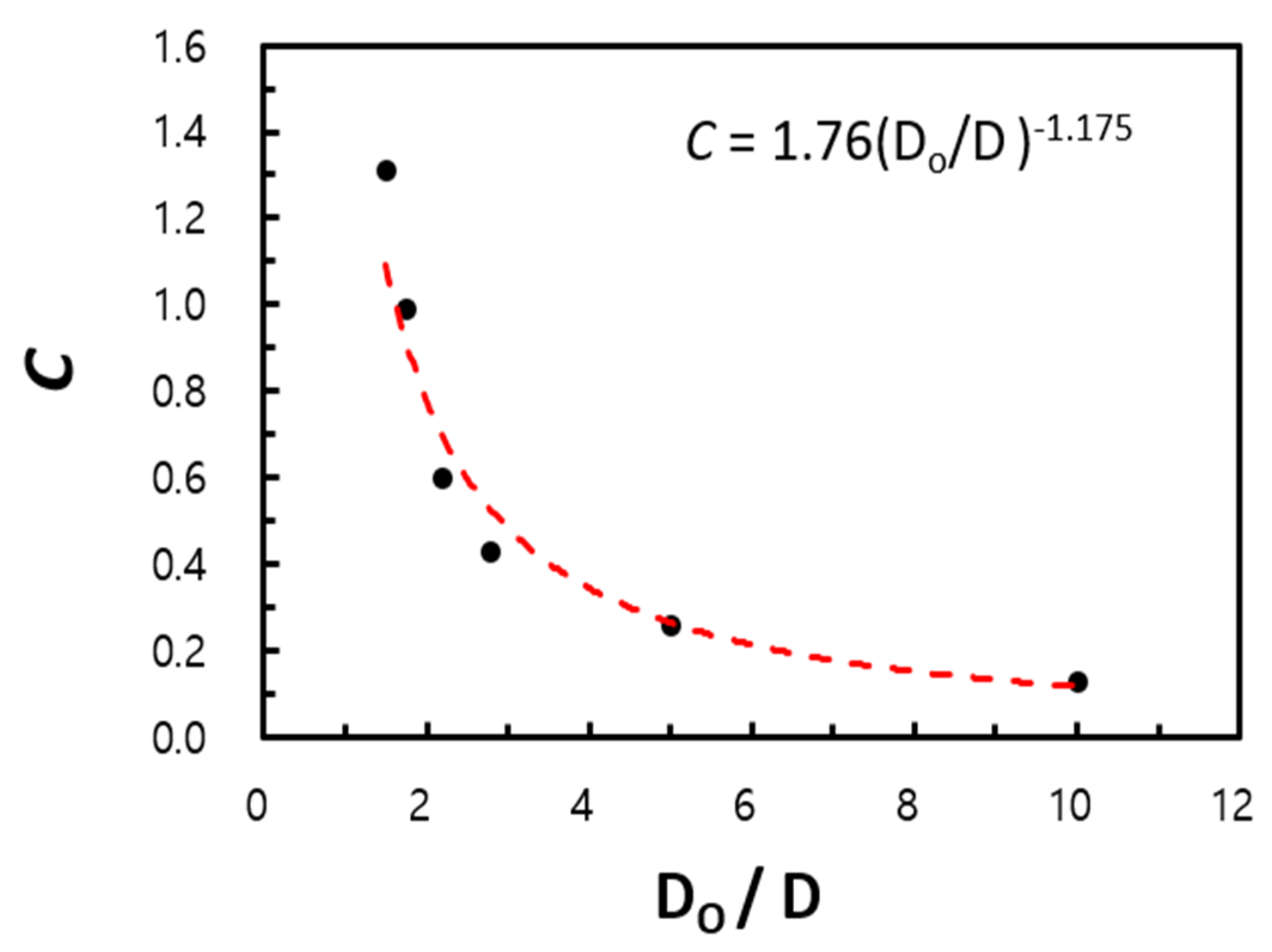
5.1. Expansion of Correlation
5.2. Validity of Correlation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| proportional coefficient, is a function of the | |
| specific heat capacity [J/kg·K] | |
| circular tube diameter [m] | |
| circular fin diameter [m] | |
| Grashof number based on tube diameter | |
| correction factor | |
| thermal conductivity of air [Wm−1K−1] | |
| characteristic length [m] | |
| Nusselt number based on tube diameter | |
| Nusselt number based on characteristic length | |
| Nusselt number based on fin spacing | |
| power, is the logarithmic function of | |
| fin pitch [m] | |
| Prandtl number | |
| Rayleigh number based on tube diameter | |
| Rayleigh number based on fin spacing | |
| fin spacing [m] | |
| fin thickness [m] | |
| dynamic viscosity [kg/m·s] | |
| ratio of the circumference of a circle to its diameter |
References
- Lee, J.H.; Shin, J.-H.; Chang, S.M.; Min, T. Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 1): Numerical Method. J. Entropy 2020, 22, 1–11. [Google Scholar]
- Merk, H.J.; Prins, J.A. Thermal Convection Laminar Boundary Layer III. Appl. Sci. Res. 1954, A4, 207–221. [Google Scholar] [CrossRef]
- Morgan, V.T. The Overall Convective Heat Transfer from Smooth Circular Cylinders. Adv. Heat Transf. 1975, 11, 199–264. [Google Scholar]
- Churchill, S.W.; Chu, H.H. Correlating Equations for Laminar and Turbulent Free Convection from a Horizontal Cylinder. Int. J. Heat Mass Transf. 1975, 18, 1049–1053. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H. Correlating Equations for Laminar and Turbulent Free Convection from a Vertical Plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Fujii, T.; Fujii, M.; Matsunaga, T. A numerical analysis of laminar free convection around an isothermal horizontal circular cylinder. Numer. Heat Transf. Part A Appl. 1979, 2, 329–344. [Google Scholar] [CrossRef]
- Kang, H.C.; Jang, H.S. Natural Convection Correlations of Circular Finned Tube Heat Exchanger. In Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference. American Society of Mechanical Engineers Digital Collection, Hamamatsu, Japan, 24–29 July 2011; pp. 4023–4027. [Google Scholar]
- Chen, H.T.; Lin, Y.S.; Chen, P.C.; Chang, J.R. Numerical and Experimental Study of Natural Convection Heat Transfer Characteristics for Vertical Plate Fin and Tube Heat Exchangers with Various Tube Diameters. Int. J. Heat Mass Transf. 2016, 100, 320–331. [Google Scholar] [CrossRef]
- Kang, H.C.; Chang, S.M. The Correlation of Heat Transfer Coefficients for the Laminar Natural Convection in a Circular Finned-Tube Heat Exchanger. J. Heat Transf. 2018, 140, 031801. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX Training Manual, Version 11.0; ANSYS: San Diego, CA, USA, 2006. [Google Scholar]



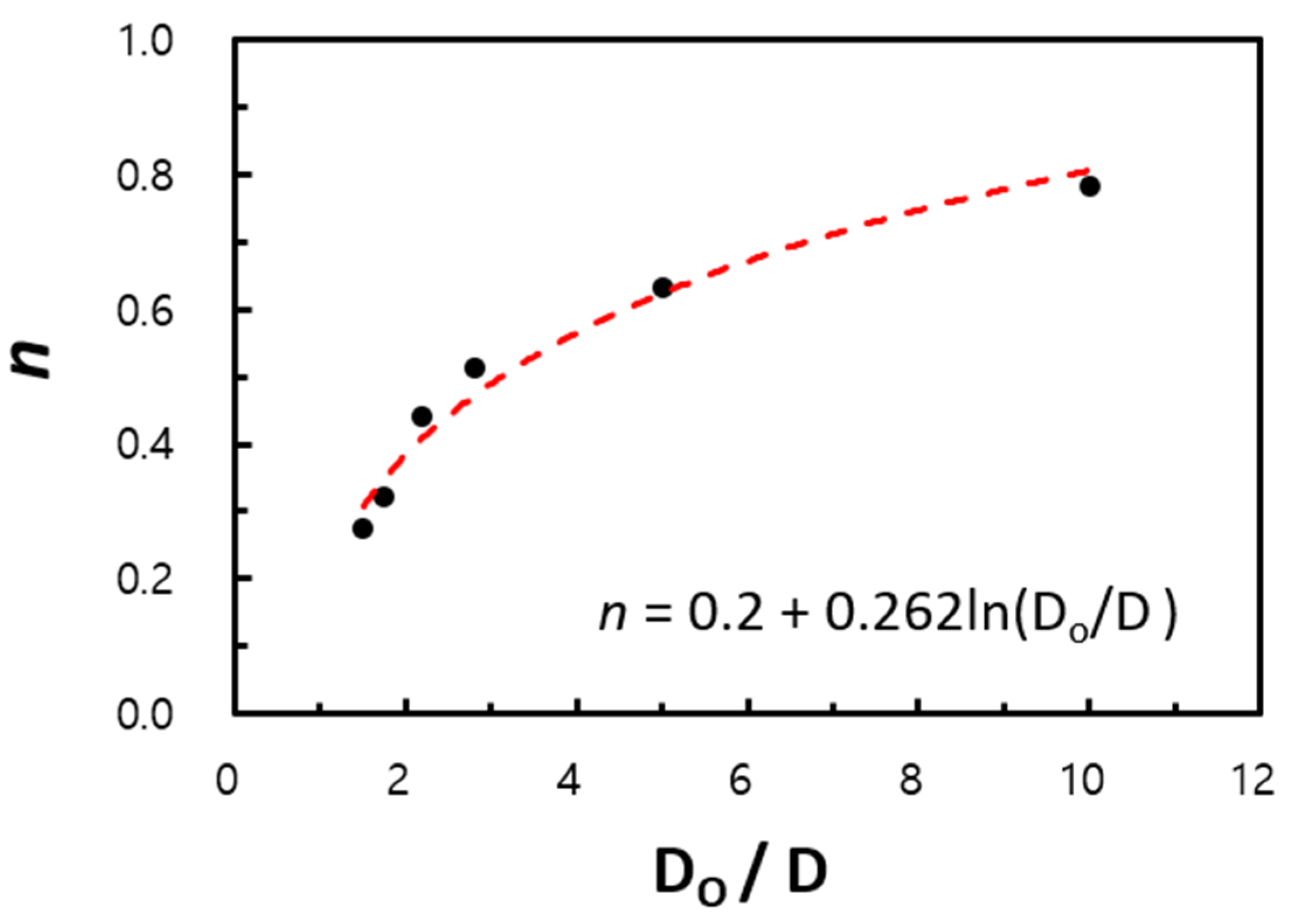
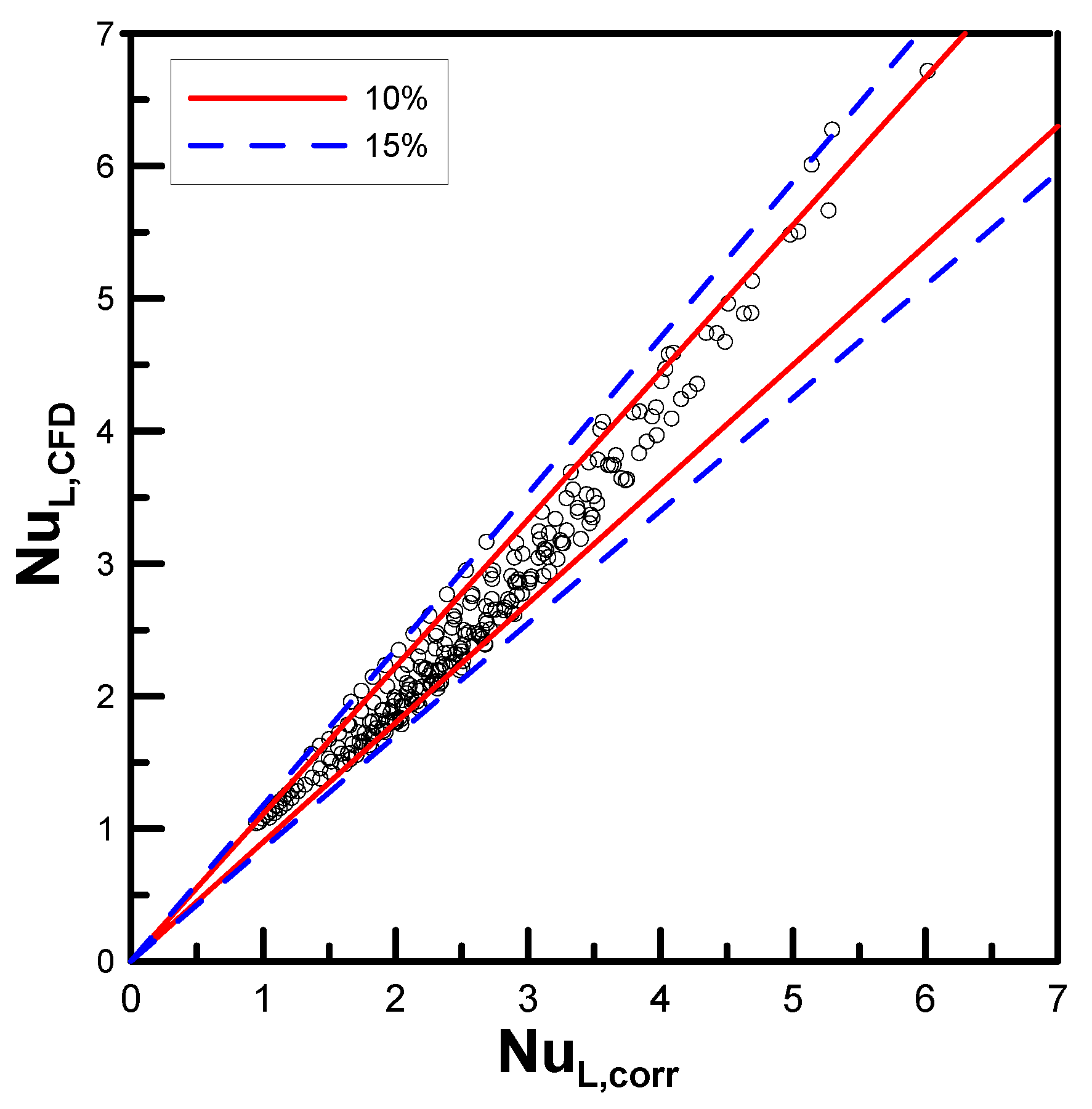
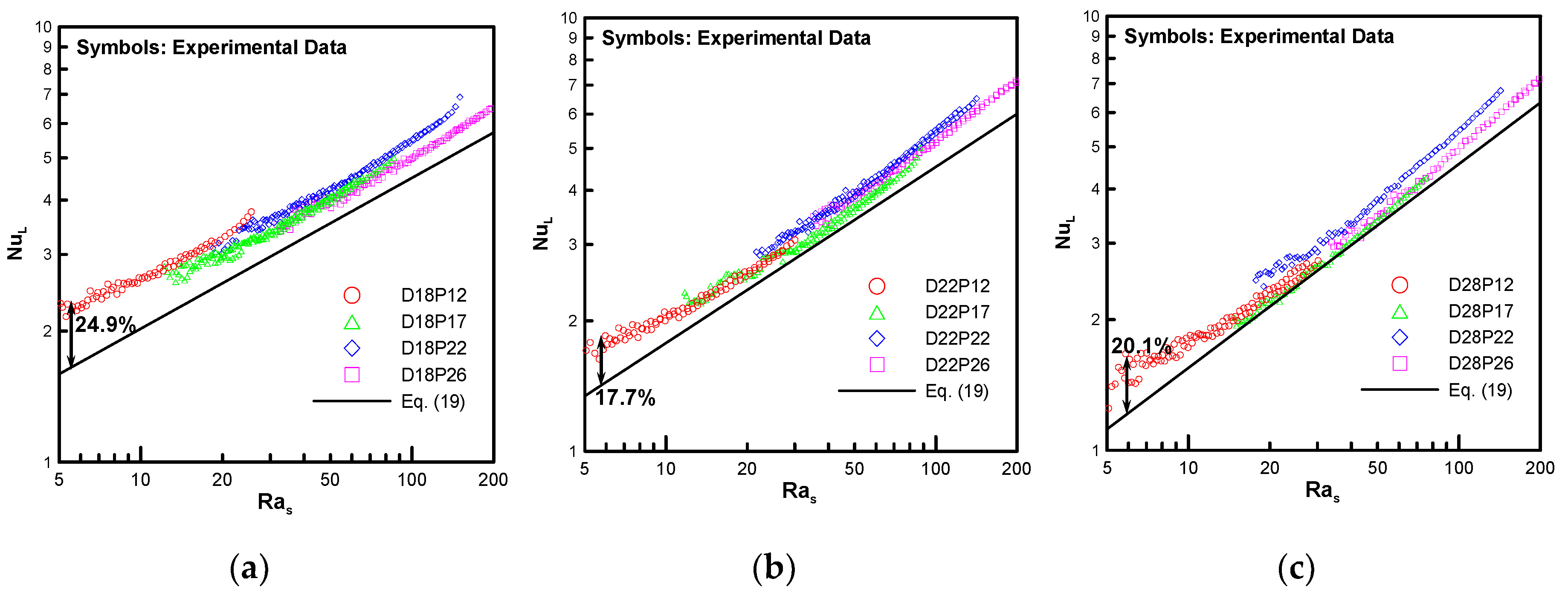
| 0.675 | 0.058 | |
| 1.020 | 0.148 | |
| 0.850 | 0.188 | |
| 0.480 | 0.250 | |
| 0.125 | 0.333 |
| Case | D | Do | Pf | t | Do/D | s/D | Case | D | Do | Pf | t | Do/D | s/D | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D10 | P12 | 15.88 | 16.1 | 2.89 | 1.0 | 1.01 | 0.119 | D22 | P12 | 15.88 | 34.9 | 2.89 | 1.0 | 2.20 | 0.119 |
| P17 | 3.68 | 0.169 | P17 | 3.68 | 0.169 | ||||||||||
| P21 | 4.26 | 0.205 | P21 | 4.26 | 0.205 | ||||||||||
| P26 | 5.06 | 0.256 | P26 | 5.06 | 0.256 | ||||||||||
| D11 | P12 | 17.1 | 2.89 | 1.07 | 0.119 | D28 | P12 | 44.5 | 2.89 | 2.80 | 0.119 | ||||
| P17 | 3.68 | 0.169 | P17 | 3.68 | 0.169 | ||||||||||
| P21 | 4.26 | 0.205 | P21 | 4.26 | 0.205 | ||||||||||
| P26 | 5.06 | 0.256 | P26 | 5.06 | 0.256 | ||||||||||
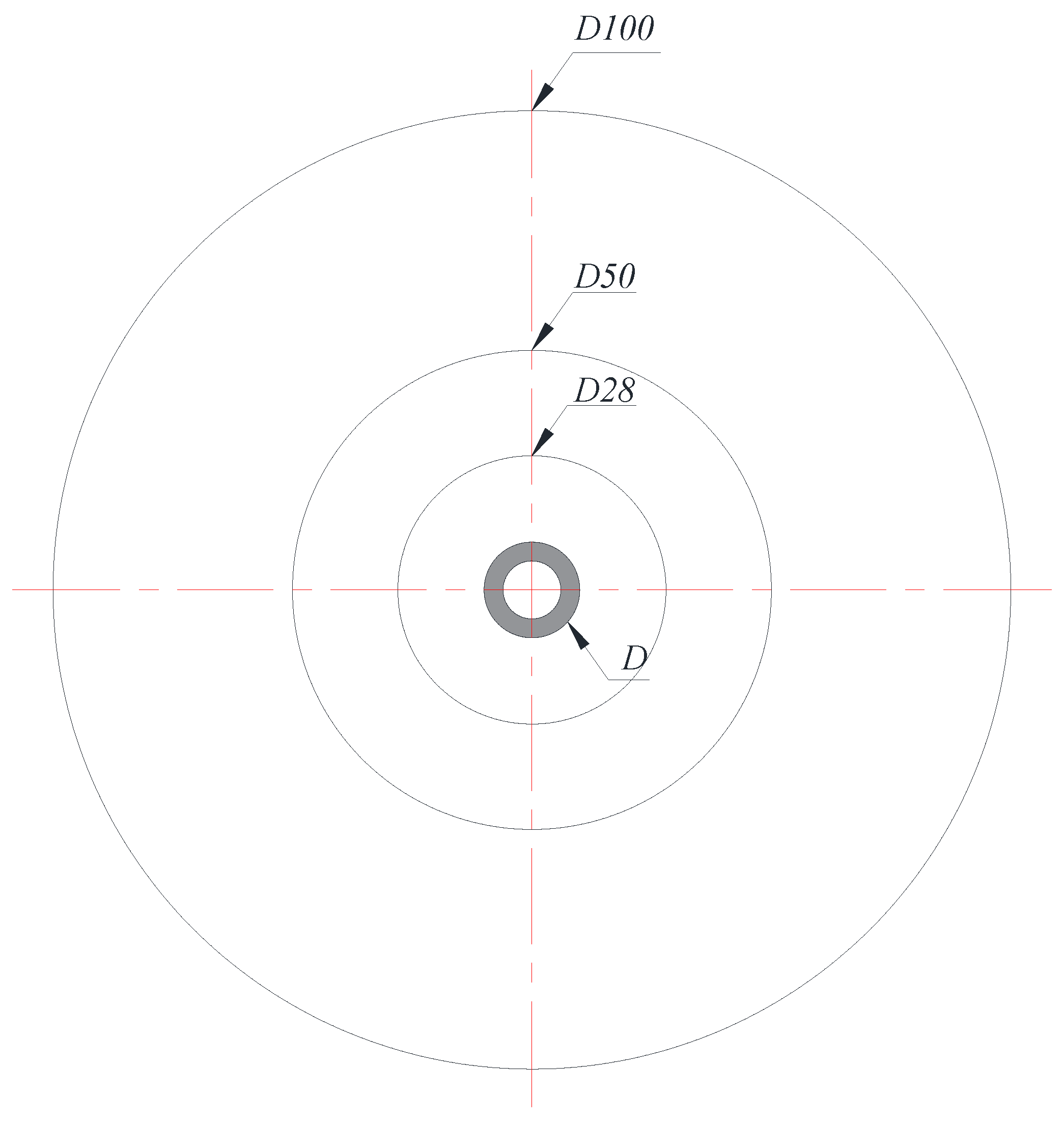
| D12 | P12 | 19.1 | 2.89 | 1.20 | 0.119 | D50 | P12 | 79.4 | 2.89 | 5.00 | 0.119 | ||||
| P17 | 3.68 | 0.169 | P17 | 3.68 | 0.169 | ||||||||||
| P21 | 4.26 | 0.205 | P21 | 4.26 | 0.205 | ||||||||||
| P26 | 5.06 | 0.256 | P26 | 5.06 | 0.256 | ||||||||||
| D18 | P12 | 27.8 | 2.89 | 1.75 | 0.119 | D100 | P12 | 158.8 | 2.89 | 10.0 | 0.119 | ||||
| P17 | 3.68 | 0.169 | P17 | 3.68 | 0.169 | ||||||||||
| P21 | 4.26 | 0.205 | P21 | 4.26 | 0.205 | ||||||||||
| P26 | 5.06 | 0.256 | P26 | 5.06 | 0.256 | ||||||||||
| Case | D | Do | Pf | t | Do/D | s/D | |
|---|---|---|---|---|---|---|---|
| D15 | P12 | 15.88 | 23.8 | 2.89 | 1.0 | 1.50 | 0.119 |
| P17 | 3.68 | 0.169 | |||||
| P21 | 4.26 | 0.205 | |||||
| P26 | 5.06 | 0.256 | |||||
| Case | Case | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Ave. | Min. | Max. | Ave. | ||||
| D15 | P12 | 15.2 | 20.8 | 18.3 | D28 | P12 | 0.0 | 22.3 | 12.7 |
| P17 | 6.3 | 13.9 | 11.6 | P17 | 0.2 | 17.0 | 6.5 | ||
| P21 | 3.4 | 9.7 | 8.1 | P21 | 0.2 | 17.2 | 7.1 | ||
| P26 | 7.7 | 14.2 | 12.4 | P26 | 0.3 | 21.2 | 14.4 | ||
| D18 | P12 | 0.0 | 6.6 | 1.1 | D50 | P12 | 136.7 | 154.1 | 143.0 |
| P17 | 2.9 | 16.0 | 12.0 | P17 | 143.7 | 165.0 | 150.8 | ||
| P21 | 0.0 | 13.0 | 9.0 | P21 | 142.8 | 165.4 | 149.5 | ||
| P26 | 4.6 | 15.1 | 11.6 | P26 | 138.3 | 156.6 | 143.2 | ||
| D22 | P12 | 6.3 | 21.7 | 16.5 | D100 | P12 | 101.7 | 102.2 | 101.9 |
| P17 | 0.0 | 17.3 | 11.4 | P17 | 102.6 | 103.7 | 103.1 | ||
| P21 | 0.0 | 17.6 | 11.1 | P21 | 102.6 | 103.7 | 103.0 | ||
| P26 | 0.0 | 19.4 | 13.9 | P26 | 102.1 | 103.2 | 102.5 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.H.; Son, Y.W.; Chang, S.-M. Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 2): Correlations for Limiting Cases. Entropy 2020, 22, 358. https://doi.org/10.3390/e22030358
Lee JH, Son YW, Chang S-M. Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 2): Correlations for Limiting Cases. Entropy. 2020; 22(3):358. https://doi.org/10.3390/e22030358
Chicago/Turabian StyleLee, Jong Hwi, Young Woo Son, and Se-Myong Chang. 2020. "Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 2): Correlations for Limiting Cases" Entropy 22, no. 3: 358. https://doi.org/10.3390/e22030358
APA StyleLee, J. H., Son, Y. W., & Chang, S.-M. (2020). Numerical Analysis on Natural Convection Heat Transfer in a Single Circular Fin-Tube Heat Exchanger (Part 2): Correlations for Limiting Cases. Entropy, 22(3), 358. https://doi.org/10.3390/e22030358





