Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues
Abstract
1. Introduction
2. The Proposed Chaotic System and Its Properties
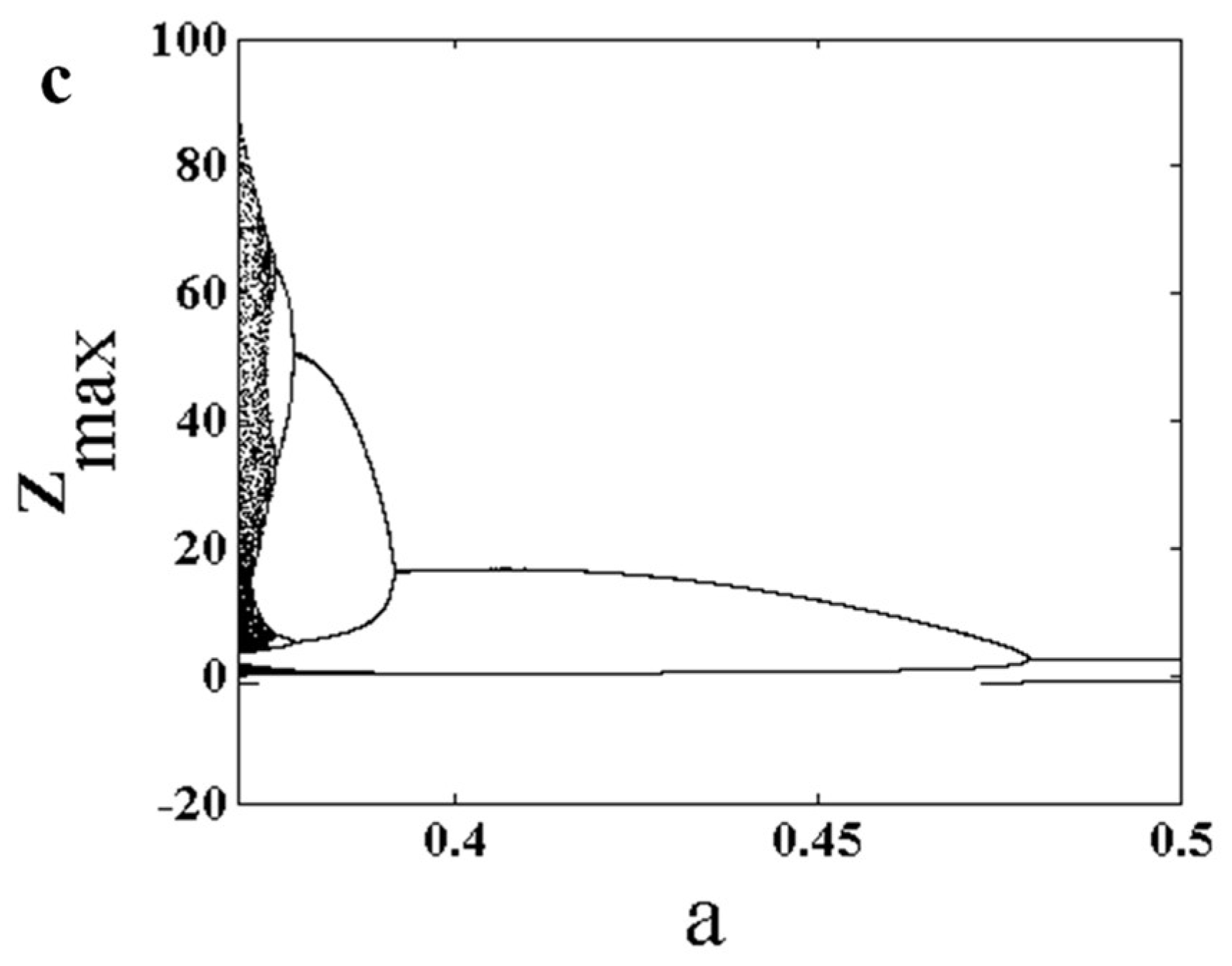
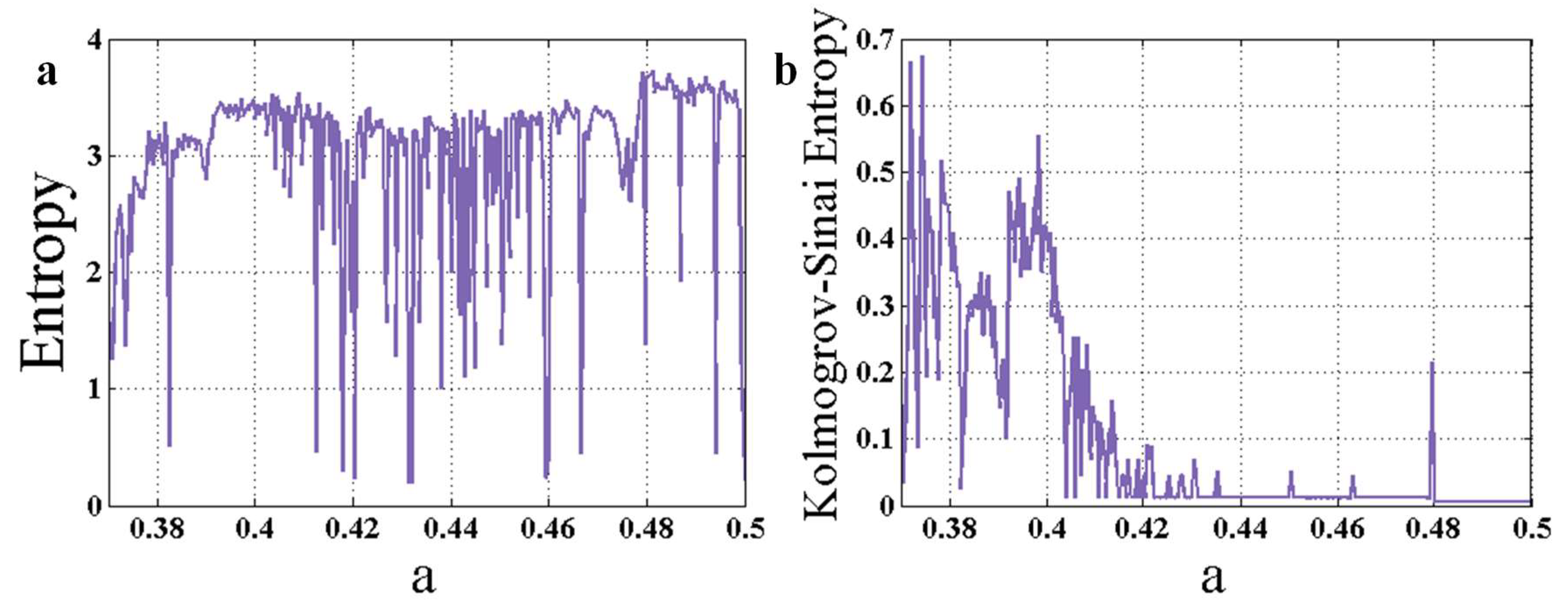
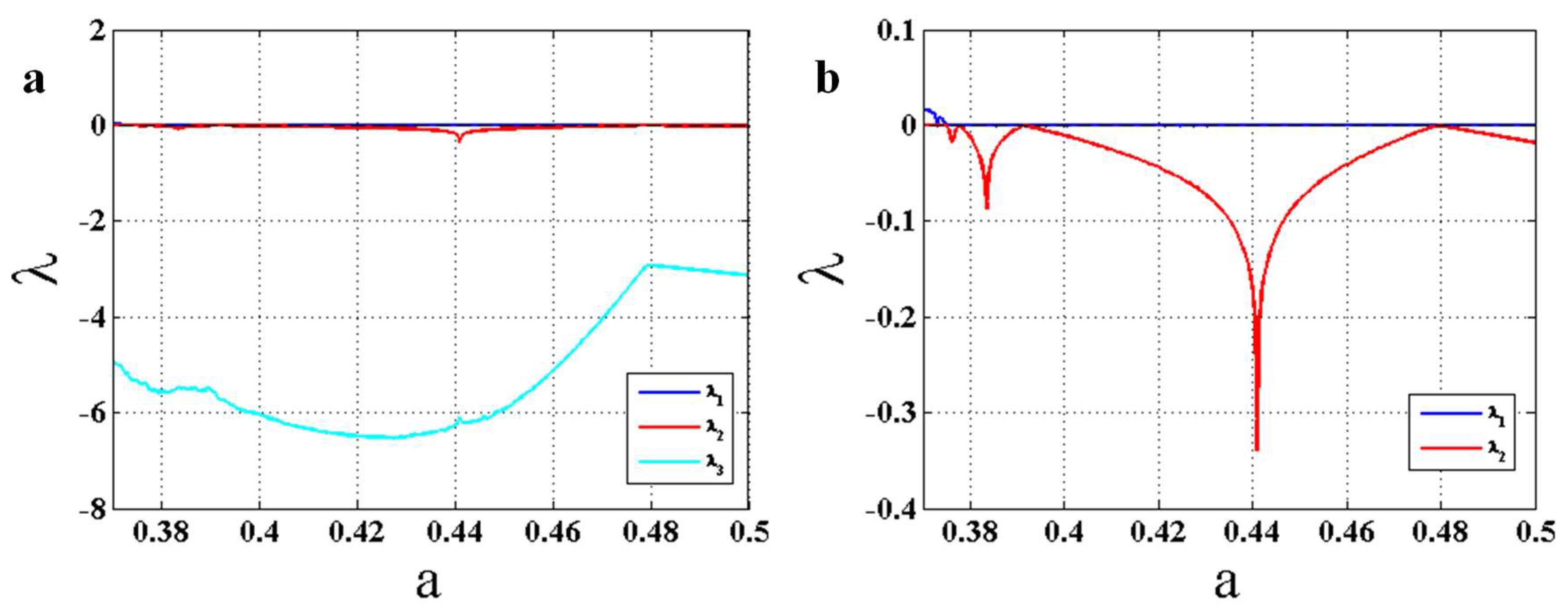
3. Entropy Analysis as an Early Warning Signal
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, H.; Bao, B.; Liu, Z.; Xu, Q.; Jiang, P. Chaotic and periodic bursting phenomena in a memristive Wien-bridge oscillator. Nonlinear Dyn. 2016, 83, 893–903. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Ruan, J.; Sun, K.; Mou, J.; He, S.; Zhang, L. Fractional-order simplest memristor-based chaotic circuit with new derivative. Eur. Phys. J. Plus 2018, 133, 3. [Google Scholar] [CrossRef]
- Alamodi, A.O.; Sun, K.; Ai, W.; Chen, C.; Peng, D. Design new chaotic maps based on dimension expansion. Chin. Phys. B 2019, 28, 020503. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Hashemi Golpayegani, S.M.R. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Gotthans, T.; Sprott, J.C.; Petrzela, J. Simple chaotic flow with circle and square equilibrium. Int. J. Bifurc. Chaos 2016, 26, 1650137. [Google Scholar] [CrossRef]
- Ai, W.; Sun, K.; Fu, Y. Design of multiwing-multiscroll grid compound chaotic system and its circuit implementation. Int. J. Mod. Phys. C 2018, 29, 1850049. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Molaie, M. A simple chaotic flow with a plane of equilibria. Int. J. Bifurc. Chaos 2016, 26, 1650098. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Gotthans, T.; Petržela, J. New class of chaotic systems with circular equilibrium. Nonlinear Dyn. 2015, 81, 1143–1149. [Google Scholar] [CrossRef]
- Sambas, A.; Mamat, M.; Arafa, A.A.; Mahmoud, G.M.; Mohamed, M.A.; Sanjaya, W. A new chaotic system with line of equilibria: Dynamics, passive control and circuit design. Int. J. Electr. Comput. Eng. 2019, 9. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Abed-Elhameed, T.M.; Ahmed, M.E. Generalization of combination–combination synchronization of chaotic n-dimensional fractional-order dynamical systems. Nonlinear Dyn. 2016, 83, 1885–1893. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; He, S.; Wang, H.; Xu, Y. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. Eur. Phys. J. Plus 2017, 132, 31. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Arafa, A.A.; Abed-Elhameed, T.M.; Mahmoud, E.E. Chaos control of integer and fractional orders of chaotic Burke–Shaw system using time delayed feedback control. Chaos Solitons Fractals 2017, 104, 680–692. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Farghaly, A.A.; Abed-Elhameed, T.M.; Aly, S.A.; Arafa, A.A. Dynamics of distributed-order hyperchaotic complex van der Pol oscillators and their synchronization and control. Eur. Phys. J. Plus 2020, 135, 32. [Google Scholar] [CrossRef]
- Dina, Q.; Elabbasyb, E.; Elsadanyc, A.; Ibrahimd, S. Bifurcation analysis and chaos control of a second-order exponential difference equation. Filomat 2019, 33, 5003–5022. [Google Scholar] [CrossRef]
- Din, Q.; Elsadany, A.; Ibrahim, S. Bifurcation analysis and chaos control in a second-order rational difference equation. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 53–68. [Google Scholar] [CrossRef]
- Hilborn, R.C. Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Sprott, J.C. Elegant Chaos: Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Khajanchi, S.; Perc, M.; Ghosh, D. The influence of time delay in a chaotic cancer model. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 103101. [Google Scholar] [CrossRef]
- Ginoux, J.-M.; Ruskeepää, H.; Perc, M.; Naeck, R.; Di Costanzo, V.; Bouchouicha, M.; Fnaiech, F.; Sayadi, M.; Hamdi, T. Is type 1 diabetes a chaotic phenomenon? Chaos Solitons Fractals 2018, 111, 198–205. [Google Scholar] [CrossRef]
- Elsonbaty, A.; Elsadany, A. Bifurcation analysis of chaotic geomagnetic field model. Chaos Solitons Fractals 2017, 103, 325–335. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Jafari, S.; Hashemi Golpayegani, S.M.R.; Perc, M.; Sprott, J.C. Predicting tipping points of dynamical systems during a period-doubling route to chaos. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 073102. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Golpayegani, S.M.R.H.; Hatef, B. Does the onset of epileptic seizure start from a bifurcation point? Eur. Phys. J. Spec. Top. 2018, 227, 697–705. [Google Scholar] [CrossRef]
- Dakos, V.; Carpenter, S.R.; Brock, W.A.; Ellison, A.M.; Guttal, V.; Ives, A.R.; Kefi, S.; Livina, V.; Seekell, D.A.; van Nes, E.H. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 2012, 7, 41010. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Ghaffari, A.; Jafari, S.; Golpayegani, S.M.R.H. Sparse Recovery and Dictionary Learning to Identify the Nonlinear Dynamical Systems: One Step Toward Finding Bifurcation Points in Real Systems. Int. J. Bifurc. Chaos 2019, 29, 1950030. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Jafari, S.; Golpayegani, S.M.R.H.; Sprott, J. Can Lyapunov exponent predict critical transitions in biological systems? Nonlinear Dyn. 2017, 88, 1493–1500. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; Van de Koppel, J.; Van de Leemput, I.A.; Levin, S.A.; Van Nes, E.H. Anticipating critical transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef]
- Blahut, R.E.; Blahut, R.E. Principles and Practice of Information Theory; Addison-Wesley: Reading, MA, USA, 1987; Volume 1. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois press: Champaign, IL, USA, 1998. [Google Scholar]
- Baptista, M.; Ngamga, E.; Pinto, P.R.; Brito, M.; Kurths, J. Kolmogorov–Sinai entropy from recurrence times. Phys. Lett. A 2010, 374, 1135–1140. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Nazarimehr, F.; Jafari, S.; Tlelo-Cuautle, E.; Hussain, I. Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues. Entropy 2020, 22, 341. https://doi.org/10.3390/e22030341
Chen L, Nazarimehr F, Jafari S, Tlelo-Cuautle E, Hussain I. Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues. Entropy. 2020; 22(3):341. https://doi.org/10.3390/e22030341
Chicago/Turabian StyleChen, Lianyu, Fahimeh Nazarimehr, Sajad Jafari, Esteban Tlelo-Cuautle, and Iqtadar Hussain. 2020. "Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues" Entropy 22, no. 3: 341. https://doi.org/10.3390/e22030341
APA StyleChen, L., Nazarimehr, F., Jafari, S., Tlelo-Cuautle, E., & Hussain, I. (2020). Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues. Entropy, 22(3), 341. https://doi.org/10.3390/e22030341





