Weighted Mean Squared Deviation Feature Screening for Binary Features
Abstract
:1. Introduction
2. Methodology
2.1. Weighted Mean Squared Deviation
- (1)
- ;
- (2)
- there exists , such that .
2.2. Feature Selection Via Pearson Correlation Coefficient
2.3. The Relationships between Chi-Square Statistic, Mutual Information and WMSD
3. Numerical Studies
3.1. Simulation Study
3.2. An Application in Chinese Text Classification
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Some Necessary Derivations
Appendix B.1. Derivation of the Relationship between Chi-Square Statistic and WMSD
Appendix B.2. Derivation of the Relationship between Mutual Information and WMSD
References
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. B 2008, 70, 849–911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, L.; Li, L.; Li, R.; Zhu, L. Model-free feature screening for ultrahigh dimensional data. J. Am. Stat. Assoc. 2011, 106, 1464–1475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, R.; Zhong, W.; Zhu, L. Feature screening via distance correlation learning. J. Am. Stat. Assoc. 2012, 107, 1129–1139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, H.; Li, R.; Zhong, W. Model-free feature screening for ultrahigh dimensional discriminant analysis. J. Am. Stat. Assoc. 2015, 110, 630–641. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Dong, Y.; Zhu, L. Trace Pursuit: A general framework for model-free variable selection. J. Am. Stat. Assoc. 2016, 111, 813–821. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, X.; Hao, M. Model-free feature screening for high-dimensional survival data. Sci. China Math. 2018, 61, 1617–1636. [Google Scholar] [CrossRef]
- Pan, W.; Wang, X.; Xiao, W.; Zhu, H. A generic sure independence screening procedure. J. Am. Stat. Assoc. 2019, 114, 928–937. [Google Scholar] [CrossRef]
- An, B.; Wang, H.; Guo, J. Testing the statistical significance of an ultra-high-dimensional naive Bayes classifier. Stat. Interface 2013, 6, 223–229. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Li, R.; Wang, H. Feature screening for ultrahigh dimensional categorical data with applications. J. Bus. Econ. Stat. 2014, 32, 237–244. [Google Scholar] [CrossRef]
- Lee, C.; Lee, G.G. Information gain and divergence-based feature selection for machine learning-based text categorization. Inform. Process. Manag. 2006, 42, 155–165. [Google Scholar] [CrossRef]
- Pascoal, C.; Oliveira, M.R.; Pacheco, A.; Valadas, R. Theoretical evaluation of feature selection methods based on mutual information. Neurocomputing 2017, 226, 168–181. [Google Scholar] [CrossRef] [Green Version]
- Guan, G.; Shan, N.; Guo, J. Feature screening for ultrahigh dimensional binary data. Stat. Interface 2018, 11, 41–50. [Google Scholar] [CrossRef]
- Dai, W.; Guo, D. Beta Distribution-Based Cross-Entropy for Feature Selection. Entropy 2019, 21, 769. [Google Scholar] [CrossRef] [Green Version]
- Feng, G.; Guo, J.; Jing, B.; Hao, L. A Bayesian feature selection paradigm for text classification. Inform. Process. Manag. 2012, 48, 283–302. [Google Scholar] [CrossRef]
- Feng, G.; Guo, J.; Jing, B.; Sun, T. Feature subset selection using naive Bayes for text classification. Pattern Recogn. Lett. 2015, 65, 109–115. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
- Stumpf, M.P.; Porter, M.A. Critical Truths About Power Laws. Science 2012, 335, 665–666. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Mccallum, A.; Nigam, K. A comparison of event models for naive Bayes text classification. In Proceedings of the AAAI-98 Workshop on Learning for Text Categorization, Madison, WI, USA, 26–31 July 1998; pp. 41–48. [Google Scholar]
- Galambos, J.; Simonelli, I. Bonferroni-Type Inequalities with Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
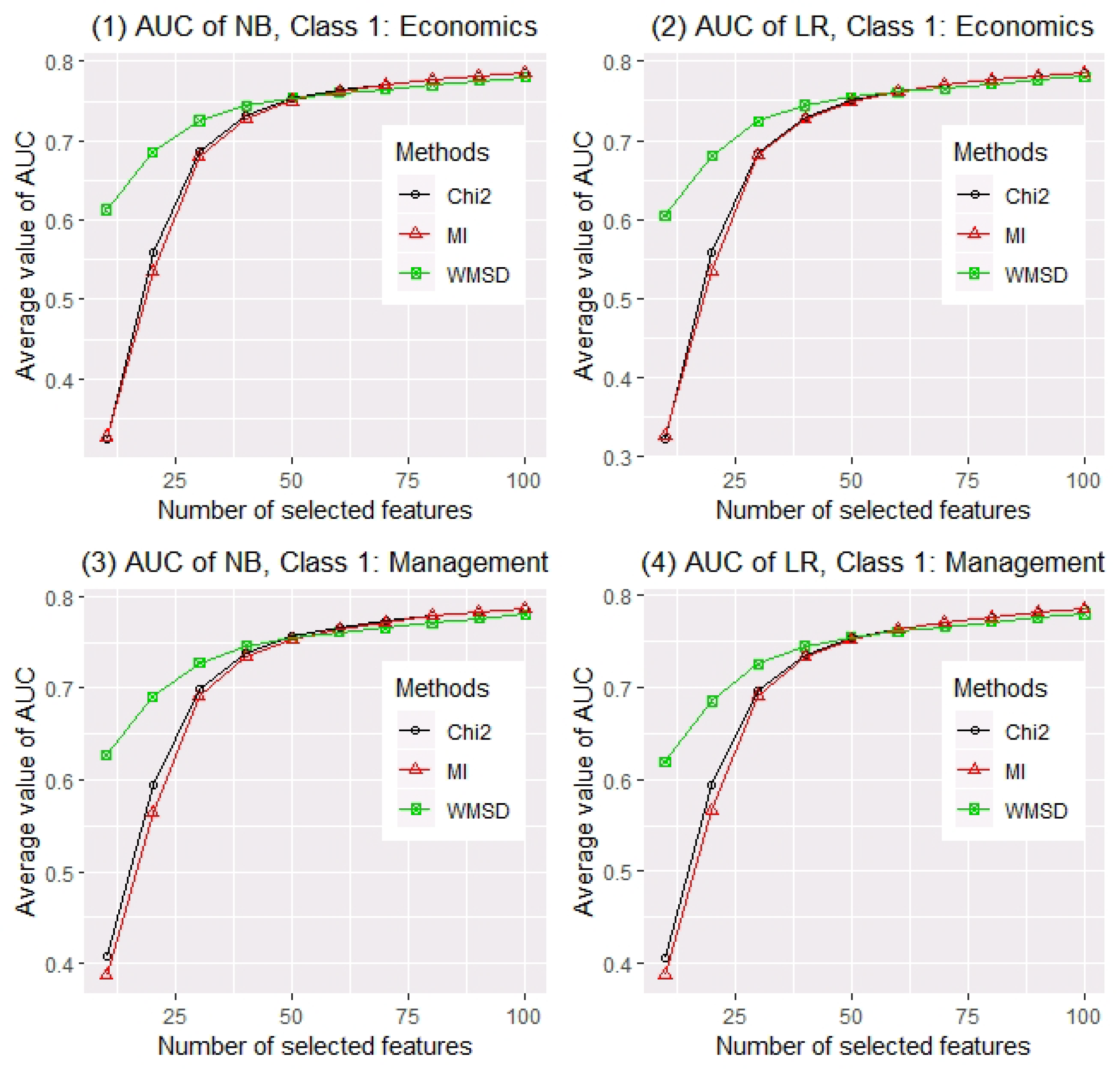
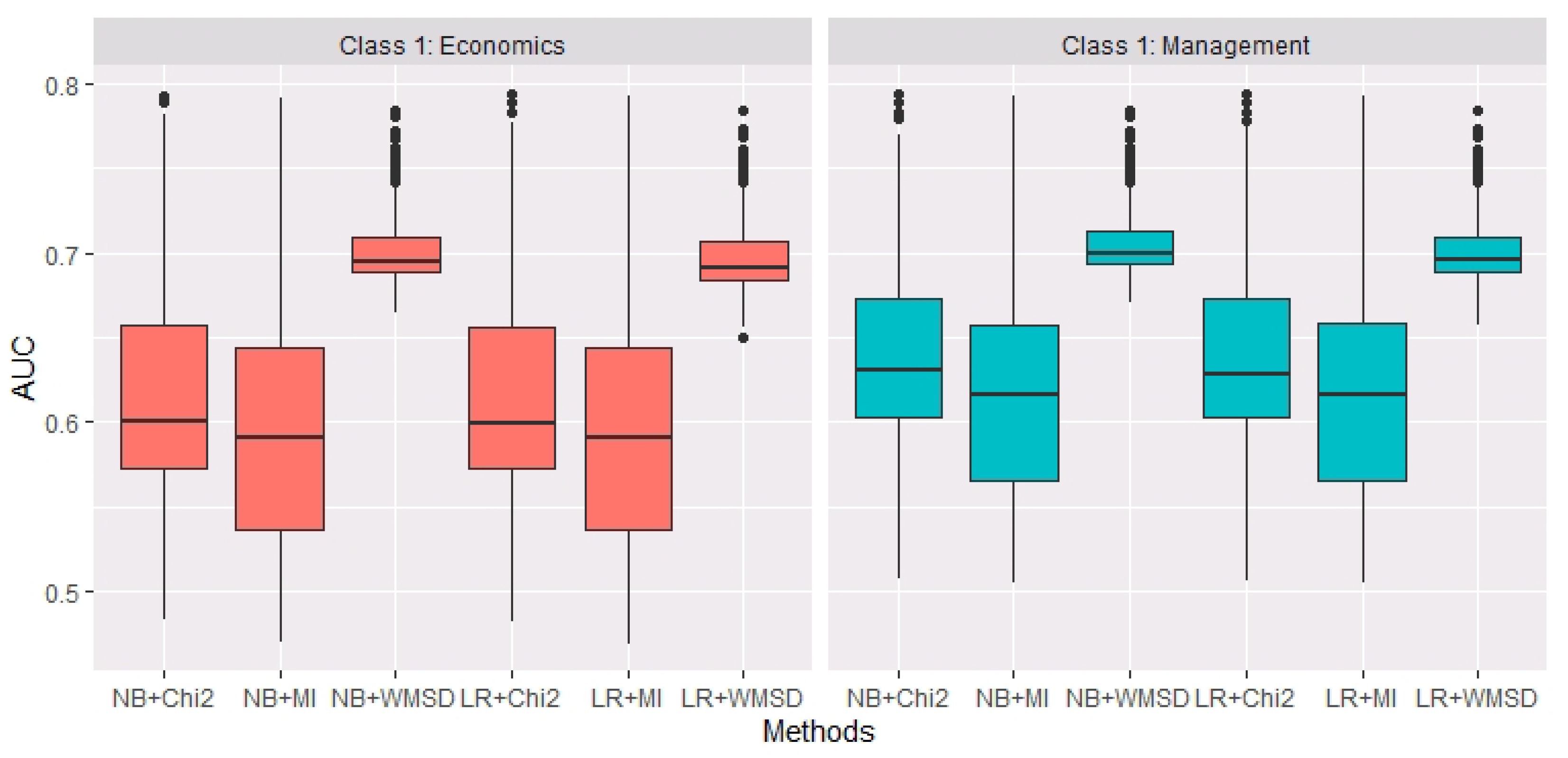
| AUC of NB | AUC of LR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p | n | Chi2 | MI | WMSD | Chi2 | MI | WMSD | FPR | FNR | |
| 20 | 500 | 1000 | 0.7238 | 0.7233 | 0.7318 | 0.6966 | 0.6960 | 0.7033 | 0.4188 | 0.0001 |
| 2000 | 0.7610 | 0.7609 | 0.7625 | 0.7411 | 0.7411 | 0.7428 | 0.1930 | 0.0000 | ||
| 5000 | 0.7778 | 0.7778 | 0.7779 | 0.7673 | 0.7673 | 0.7676 | 0.0108 | 0.0013 | ||
| 1000 | 1000 | 0.7145 | 0.7135 | 0.7303 | 0.6849 | 0.6839 | 0.7007 | 0.4014 | 0.0001 | |
| 2000 | 0.7545 | 0.7543 | 0.7591 | 0.7335 | 0.7332 | 0.7399 | 0.1599 | 0.0001 | ||
| 5000 | 0.7693 | 0.7693 | 0.7697 | 0.7584 | 0.7584 | 0.7592 | 0.0024 | 0.0010 | ||
| 50 | 500 | 1000 | 0.8936 | 0.8935 | 0.8973 | 0.8463 | 0.8460 | 0.8499 | 0.2976 | 0.0008 |
| 2000 | 0.9102 | 0.9102 | 0.9110 | 0.8837 | 0.8837 | 0.8850 | 0.1058 | 0.0001 | ||
| 5000 | 0.9165 | 0.9165 | 0.9165 | 0.8998 | 0.8998 | 0.8998 | 0.0096 | 0.0005 | ||
| 1000 | 1000 | 0.8789 | 0.8787 | 0.8851 | 0.8239 | 0.8233 | 0.8313 | 0.3408 | 0.0004 | |
| 2000 | 0.9014 | 0.9013 | 0.9031 | 0.8717 | 0.8716 | 0.8748 | 0.1106 | 0.0001 | ||
| 5000 | 0.9097 | 0.9097 | 0.9098 | 0.8921 | 0.8921 | 0.8923 | 0.0017 | 0.0007 | ||
| 20 | 500 | 1000 | 0.6372 | 0.6502 | 0.6883 | 0.6422 | 0.6545 | 0.6905 | 0.4796 | 0.0007 |
| 2000 | 0.7206 | 0.7237 | 0.7303 | 0.7203 | 0.7239 | 0.7307 | 0.3413 | 0.0001 | ||
| 5000 | 0.7692 | 0.7692 | 0.7696 | 0.7658 | 0.7659 | 0.7664 | 0.0706 | 0.0001 | ||
| 1000 | 1000 | 0.6171 | 0.6329 | 0.6908 | 0.6268 | 0.6405 | 0.6936 | 0.4833 | 0.0007 | |
| 2000 | 0.7183 | 0.7210 | 0.7328 | 0.7190 | 0.7216 | 0.7330 | 0.3214 | 0.0001 | ||
| 5000 | 0.7642 | 0.7640 | 0.7658 | 0.7614 | 0.7613 | 0.7627 | 0.0406 | 0.0002 | ||
| 50 | 500 | 1000 | 0.8636 | 0.8665 | 0.8746 | 0.8537 | 0.8542 | 0.8594 | 0.4739 | 0.0017 |
| 2000 | 0.9018 | 0.9022 | 0.9043 | 0.8930 | 0.8923 | 0.8935 | 0.2115 | 0.0005 | ||
| 5000 | 0.9149 | 0.9149 | 0.9150 | 0.9107 | 0.9107 | 0.9107 | 0.0442 | 0.0000 | ||
| 1000 | 1000 | 0.8428 | 0.8468 | 0.8583 | 0.8326 | 0.8337 | 0.8425 | 0.5433 | 0.0008 | |
| 2000 | 0.8894 | 0.8899 | 0.8943 | 0.8790 | 0.8783 | 0.8821 | 0.2291 | 0.0004 | ||
| 5000 | 0.9075 | 0.9074 | 0.9079 | 0.9028 | 0.9027 | 0.9034 | 0.0295 | 0.0001 | ||
| Methods | Probabilities of Top 10 Words | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Chi2 | 0.285 | 0.034 | 0.133 | 0.029 | 0.043 | 0.047 | 0.012 | 0.014 | 0.022 | 0.017 |
| MI | 0.285 | 0.133 | 0.034 | 0.029 | 0.022 | 0.043 | 0.026 | 0.019 | 0.012 | 0.047 |
| WMSD | 0.285 | 0.133 | 0.541 | 0.211 | 0.223 | 0.203 | 0.034 | 0.235 | 0.047 | 0.043 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Guan, G. Weighted Mean Squared Deviation Feature Screening for Binary Features. Entropy 2020, 22, 335. https://doi.org/10.3390/e22030335
Wang G, Guan G. Weighted Mean Squared Deviation Feature Screening for Binary Features. Entropy. 2020; 22(3):335. https://doi.org/10.3390/e22030335
Chicago/Turabian StyleWang, Gaizhen, and Guoyu Guan. 2020. "Weighted Mean Squared Deviation Feature Screening for Binary Features" Entropy 22, no. 3: 335. https://doi.org/10.3390/e22030335
APA StyleWang, G., & Guan, G. (2020). Weighted Mean Squared Deviation Feature Screening for Binary Features. Entropy, 22(3), 335. https://doi.org/10.3390/e22030335





