Semantic and Generalized Entropy Loss Functions for Semi-Supervised Deep Learning
Abstract
1. Introduction
- If the two analyzed regularization terms prove to be effective in semi-supervised classification tasks, which loss function provides the best results?
- What is the relation between semantic loss function and generalized entropy loss function?
- What is the impact of the input and tuning parameter values on both proposed approaches on the final results?
2. Preliminaries
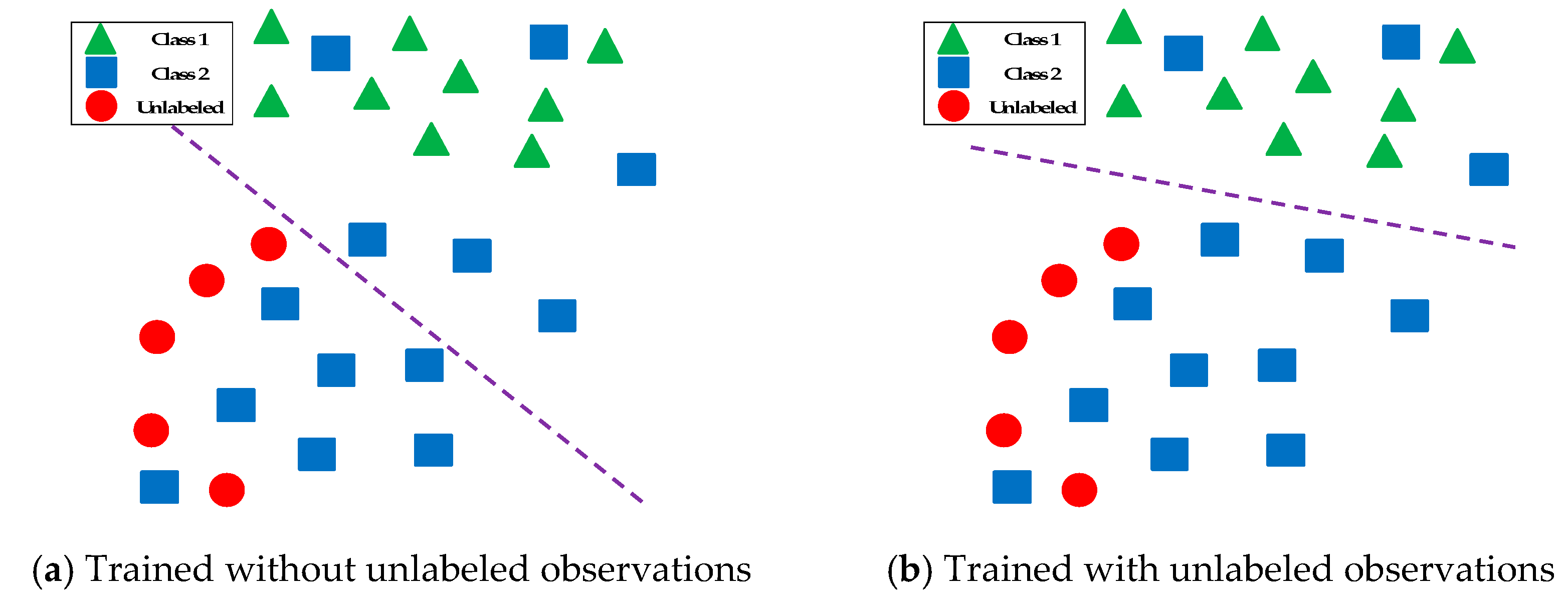
2.1. Semi-Supervised Learning
- Manifold assumption, the data lie approximately on a manifold of much lower dimension than the input space. This assumption allows the use of distances and densities which are defined on a manifold;
- Continuity assumption, the algorithm assumes that (after transformed to a lower dimension) the points which are closer to each other are more likely to have the same output label;
- Cluster assumption, (after transformed to a lower dimension) the data is divided into discrete clusters and points in the same cluster are more likely to share an output label.
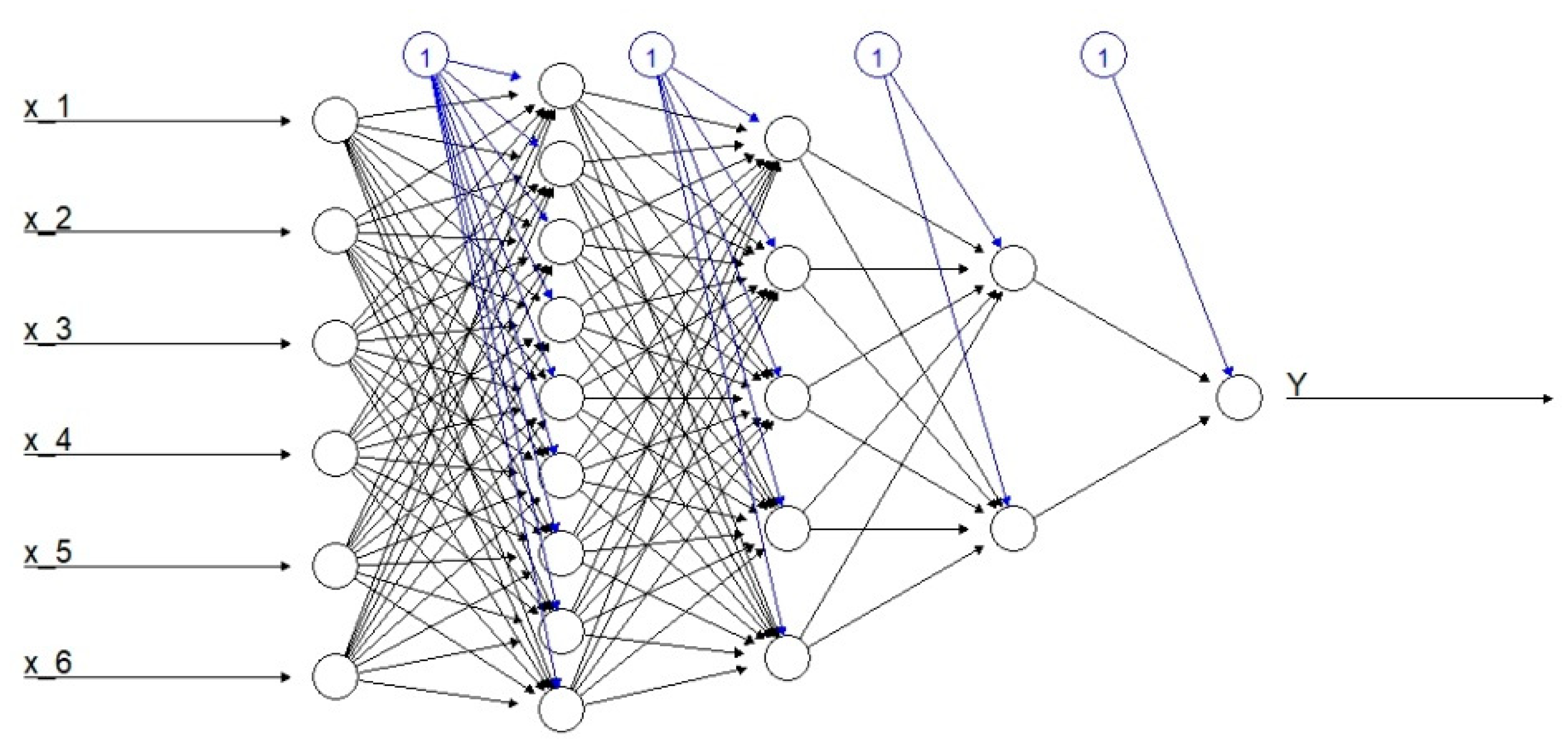
2.2. Deep Neural Networks
2.3. Propositional Logic
3. Theoretical Framework of the Semantic and the Generalized Entropy Loss Functions
3.1. Semantic Loss Function
3.2. Generalized Entropy Loss function
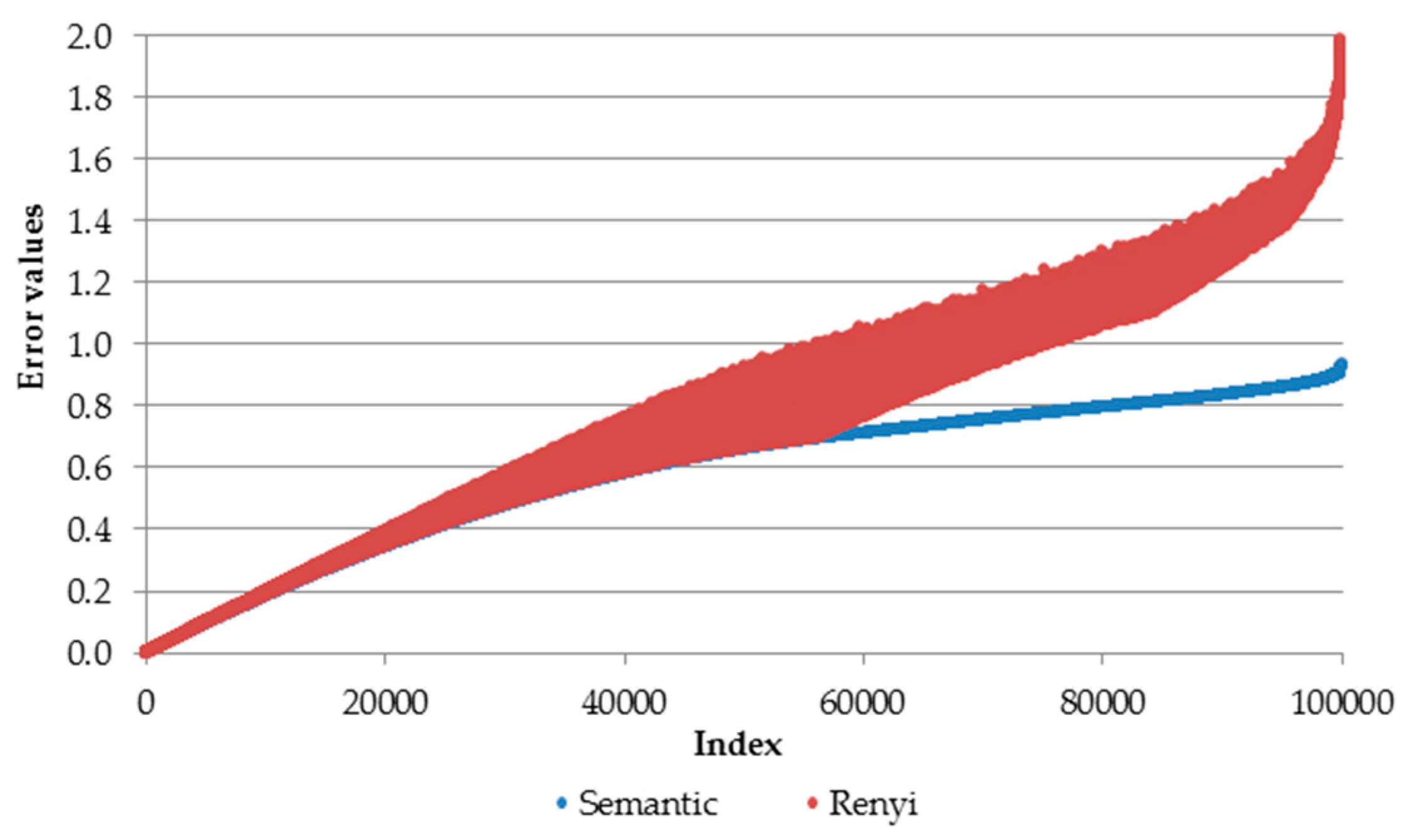
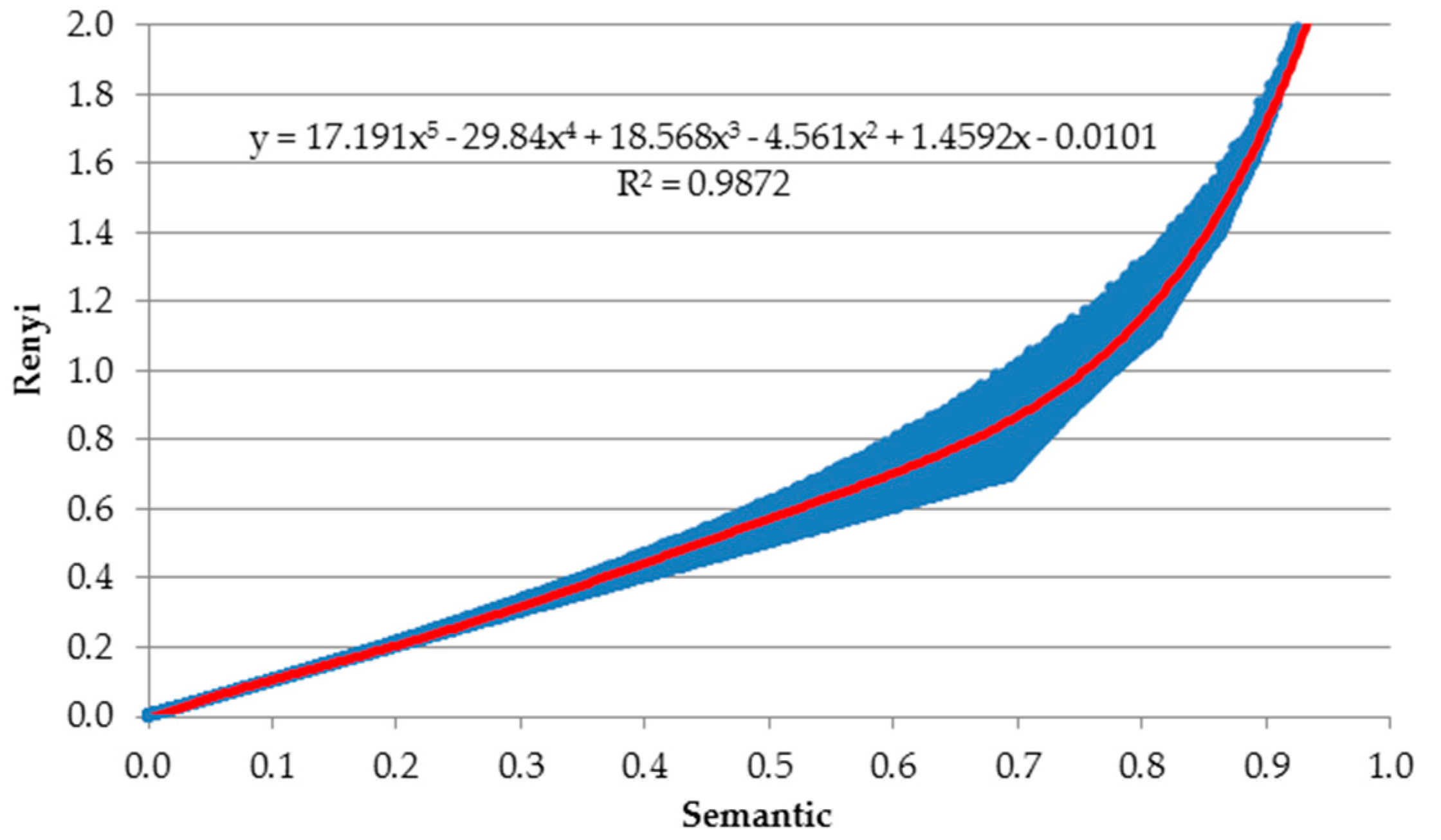
3.3. Relation between Generalized Entropy and Semantic Loss Functions
4. Research Framework and Settings
4.1. Datasets Characteristics
4.2. Performance Measure
4.3. Numerical Implementation
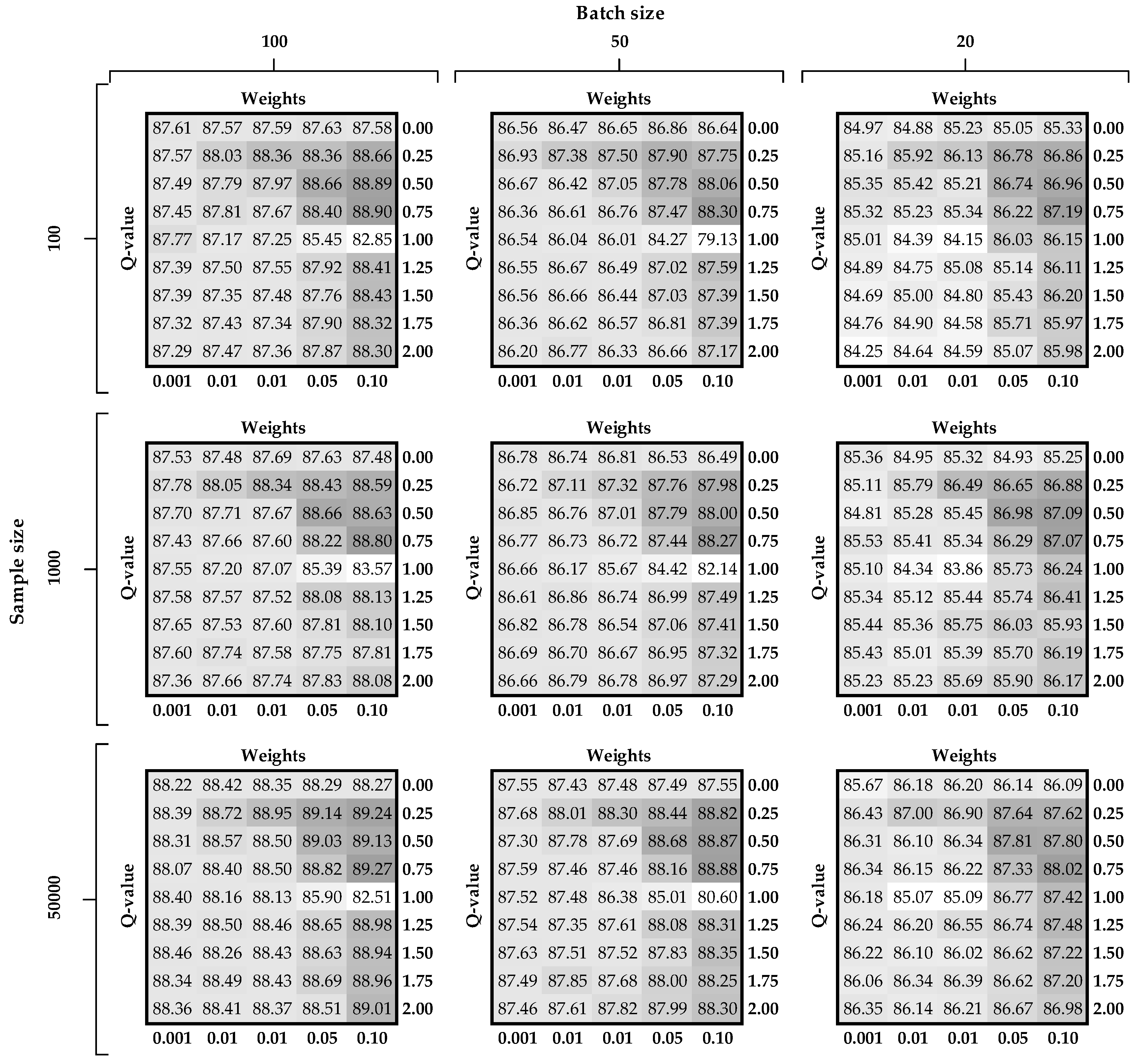
4.4. Tuning of the Parameters
- -value —from the Equation (6);
- Weights , which is the hyper-parameter associated with the Rényi or semantic regularization term in Equation (2);
- Batch size ,which is the mini-batch size needed for adaptive stochastic gradient descent optimization algorithm;
- Number of labeled examples , which is the number of randomly chosen labeled examples from the training set with the assumption that the final set is balanced, i.e., no particular class is overrepresented.
4.5. Benchmarking Models
5. Empirical Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gajowniczek, K.; Orłowski, A.; Ząbkowski, T. Simulation Study on the Application of the Generalized Entropy Concept in Artificial Neural Networks. Entropy 2018, 20, 249. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Ząbkowski, T.; Sodenkamp, M. Revealing Household Characteristics from Electricity Meter Data with Grade Analysis and Machine Learning Algorithms. Appl. Sci. 2018, 8, 1654. [Google Scholar] [CrossRef]
- Sadarangani, A.; Jivani, A. A survey of semi-Supervised learning. Int. J. Eng. Sci. Res. Technol. 2016, 5. [Google Scholar] [CrossRef]
- Nafkha, R.; Gajowniczek, K.; Ząbkowski, T. Do Customers Choose Proper Tariff? Empirical Analysis Based on Polish Data Using Unsupervised Techniques. Energies 2018, 11, 514. [Google Scholar] [CrossRef]
- Prakash, V.J.; Nithya, D.L. A survey on semi-supervised learning techniques. arXiv 2014, arXiv:1402.4645. [Google Scholar]
- Xu, J.; Zhang, Z.; Friedman, T.; Liang, Y.; Van den Broeck, G. A semantic loss function for deep learning with symbolic knowledge. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Xu, J.; Zhang, Z.; Friedman, T.; Liang, Y.; Van den Broeck, G. A Semantic Loss Function for Deep Learning Under Weak Supervision. In Proceedings of the NIPS 2017 Workshop on Learning with Limited Labeled Data: Weak Supervision and Beyond, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef]
- Miyato, T.; Maeda, S.-I.; Koyama, M.; Ishii, S. Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1979–1993. [Google Scholar] [CrossRef]
- Alaya, M.Z.; Bussy, S.; Gaıffas, S.; Guilloux, A. Binarsity: A penalization for one-Hot encoded features in linear supervised learning. J. Mach. Learn. Res. 2019, 20, 1–34. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. In the fourth Berkeley Symposium on Mathematics, Statistics and Probability; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Amigó, J.; Balogh, S.; Hernández, S. A Brief Review of Generalized Entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Karpio, K.; Łukasiewicz, P.; Orłowski, A.; Ząbkowski, T. Q-Entropy Approach to Selecting High Income Households. Acta Phys. Pol. A 2015, 127, A:38–A:44. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Orłowski, A.; Ząbkowski, T. Entropy Based Trees to Support Decision Making for Customer Churn Management. Acta Phys. Pol. A 2016, 129, 971–979. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-Mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Schwenker, F.; Trentin, E. Pattern classification and clustering: A review of partially supervised learning approaches. Pattern Recognit. Lett. 2014, 37, 4–14. [Google Scholar] [CrossRef]
- van Engelen, J.E.; Hoos, H.H. A survey on semi-Supervised learning. Mach. Learn. 2019, 1–68. [Google Scholar] [CrossRef]
- Bengio, Y.; Lee, D.H.; Bornschein, J.; Mesnard, T.; Lin, Z. Towards biologically plausible deep learning. arXiv 2015, arXiv:1502.04156. [Google Scholar]
- Marblestone, A.H.; Wayne, G.; Kording, K.P. Toward an Integration of Deep Learning and Neuroscience. Front. Comput. Neurosci. 2016, 10, 94. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Villanustre, F.; Khoshgoftaar, T.M.; Seliya, N.; Wald, R.; Muharemagic, E. Deep learning applications and challenges in big data analytics. J. Big Data 2015, 2. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML), Haifa, Israel, 21–25 June 2010; pp. 807–814. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015. [Google Scholar]
- Darwiche, A. SDD: A new canonical representation of propositional knowledge bases. In Proceedings of the 22nd International Joint Conference on Artificial Intelligence (IJCAI), Barcelona, Spain, 16–22 July 2011. [Google Scholar]
- Tomamichel, M.; Berta, M.; Hayashi, M. Relating different quantum generalizations of the conditional Rényi entropy. J. Math. Phys. 2014, 55, 082206. [Google Scholar] [CrossRef]
- Fehr, S.; Berens, S. On the Conditional Rényi Entropy. IEEE Trans. Inf. Theory 2014, 60, 6801–6810. [Google Scholar] [CrossRef]
- The R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Ghemawat, S. Tensorflow: Large-Scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-Supervised learning with ladder networks. In Proceedings of the Neural Information Processing Systems 2015 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 3546–3554. [Google Scholar]
- Pitelis, N.; Russell, C.; Agapito, L. Semi-Supervised learning using an unsupervised atlas. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2014; pp. 565–580. [Google Scholar]
- Kingma, D.P.; Mohamed, S.; Rezende, D.J.; Welling, M. Semi-Supervised learning with deep generative models. In Proceedings of the Neural Information Processing Systems 2014 (NIPS 2014), Montreal, QC, Canada, 8–11 December 2014; pp. 3581–3589. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]


| Predicted Value | |||||
|---|---|---|---|---|---|
| Class 1 | Class 2 | Class k | |||
| Real value | Class 1 | True1 | False1 | False1 | |
| Class 2 | False2 | True2 | False2 | ||
| Class k | Falsek | Falsek | Truek | ||
| Sample Size | Loss | -Value | Weight | Batch Size | Mean Validation Accuracy | Mean Test Accuracy |
|---|---|---|---|---|---|---|
| 100 | Semantic | 0.005 | 100 | 98.02 (∓0.04) | 97.98 (∓0.04) | |
| Rényi | 0.75 | 0.100 | 100 | 98.20 (∓0.02) | 98.21 (∓0.03) | |
| MLP | 100 | 78.46 (∓1.94) | ||||
| AtlasRBF | 91.9 (∓0.95) | |||||
| Deep Generative | 96.67 (∓0.14) | |||||
| Virtual Adversarial | 97.67 | |||||
| Ladder Net | 98.94 (∓0.37) | |||||
| 1000 | Semantic | 0.100 | 100 | 97.95 (∓0.05) | 98.02 (∓0.03) | |
| Rényi | 0.50 | 0.100 | 100 | 98.27 (∓0.03) | 98.25 (∓0.03) | |
| MLP | 100 | 94.26 (∓0.31) | ||||
| AtlasRBF | 96.32 (∓0.12) | |||||
| Deep Generative | 97.60 (∓0.02) | |||||
| Virtual Adversarial | 98.64 | |||||
| Ladder Net | 99.16 (∓0.08) | |||||
| 50,000 | Semantic | 0.100 | 100 | 98.13 (∓0.03) | 98.15 (∓0.04) | |
| Rényi | 0.50 | 0.100 | 100 | 98.29 (∓0.02) | 98.29 (∓0.03) | |
| MLP | 100 | 98.13 (∓0.04) | ||||
| AtlasRBF | 98.69 | |||||
| Deep Generative | 99.04 | |||||
| Virtual Adversarial | 99.36 | |||||
| Ladder Net | 99.43 (∓0.02) | |||||
| ResNet | 99.40 |
| Sample Size | Loss | -Value | Weight | Batch Size | Mean Validation Accuracy | Mean Test Accuracy |
|---|---|---|---|---|---|---|
| 100 | Semantic | 0.005 | 100 | 88.65 (∓0.11) | 87.65 (∓0.07) | |
| Rényi | 0.50 | 0.100 | 100 | 89.62 (∓0.07) | 88.89 (∓0.10) | |
| MLP | 100 | 69.45 (∓2.03) | ||||
| Ladder Net | 81.46 (∓0.64) | |||||
| 1000 | Semantic | 0.100 | 100 | 88.71 (∓0.06) | 87.83 (∓0.07) | |
| Rényi | 0.75 | 0.100 | 100 | 89.54 (∓0.35) | 88.80 (∓0.08) | |
| MLP | 100 | 78.12 (∓1.41) | ||||
| Ladder Net | 86.48 (∓0.15) | |||||
| 50,000 | Semantic | 0.100 | 100 | 89.26 (∓0.08) | 88.49 (∓0.10) | |
| Rényi | 0.50 | 0.100 | 100 | 89.90 (∓0.06) | 89.03 (∓0.06) | |
| MLP | 100 | 88.26 (∓0.18) | ||||
| Ladder Net | 90.46 | |||||
| ResNet | 92.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajowniczek, K.; Liang, Y.; Friedman, T.; Ząbkowski, T.; Van den Broeck, G. Semantic and Generalized Entropy Loss Functions for Semi-Supervised Deep Learning. Entropy 2020, 22, 334. https://doi.org/10.3390/e22030334
Gajowniczek K, Liang Y, Friedman T, Ząbkowski T, Van den Broeck G. Semantic and Generalized Entropy Loss Functions for Semi-Supervised Deep Learning. Entropy. 2020; 22(3):334. https://doi.org/10.3390/e22030334
Chicago/Turabian StyleGajowniczek, Krzysztof, Yitao Liang, Tal Friedman, Tomasz Ząbkowski, and Guy Van den Broeck. 2020. "Semantic and Generalized Entropy Loss Functions for Semi-Supervised Deep Learning" Entropy 22, no. 3: 334. https://doi.org/10.3390/e22030334
APA StyleGajowniczek, K., Liang, Y., Friedman, T., Ząbkowski, T., & Van den Broeck, G. (2020). Semantic and Generalized Entropy Loss Functions for Semi-Supervised Deep Learning. Entropy, 22(3), 334. https://doi.org/10.3390/e22030334






