Averaging Is Probably Not the Optimum Way of Aggregating Parameters in Federated Learning
Abstract
1. Introduction
- (1)
- All participating clients download the latest global model parameter vector .
- (2)
- Each client improves downloaded model based on their local data using, e.g., stochastic gradient descent (SGD) [13] with a fixed learning rate : , where , and is the local objective function for the qth device.
- (3)
- Each improved model parameter is sent from the client to the server.
- (4)
- The server aggregates all updated parameters to construct an enhanced global model .
2. Related Work
3. Estimating the Mutual Information
3.1. MI Derivative Formula under Multi-D Gaussian
3.2. KNN Discretization Estimator
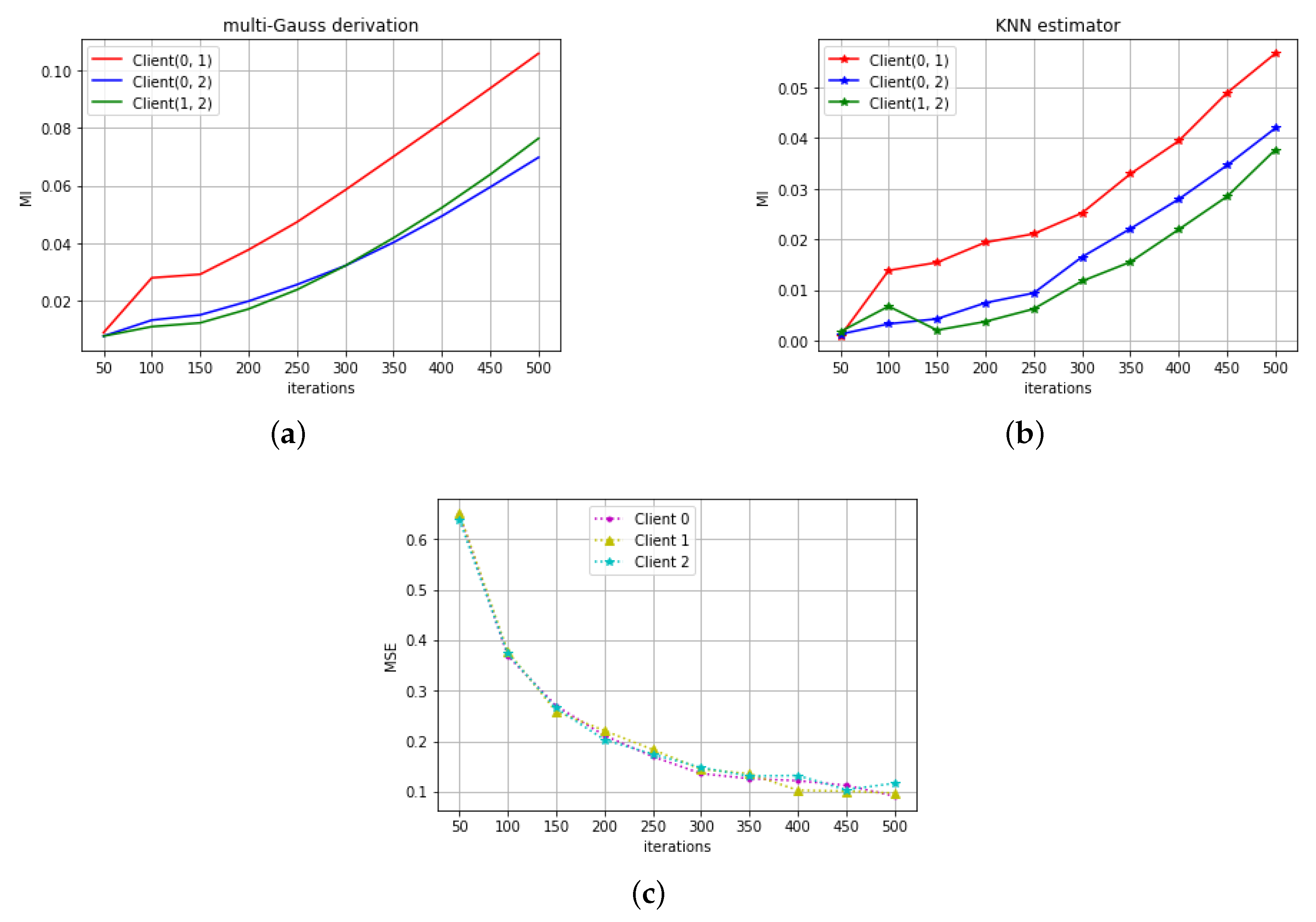
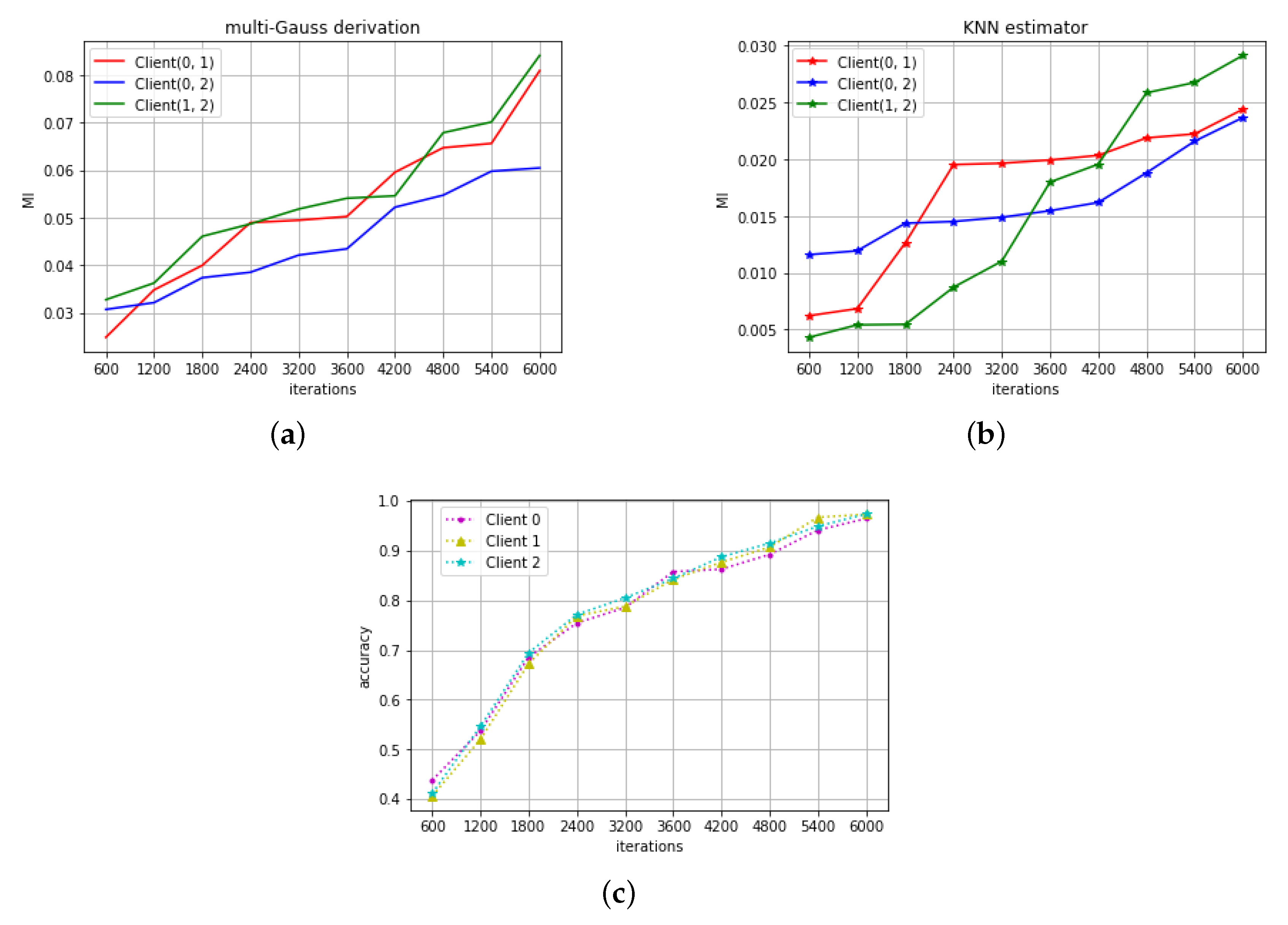
4. Simulation Results
4.1. RNN on Signal Variation Prediction
4.2. CNN on Digit Recognition
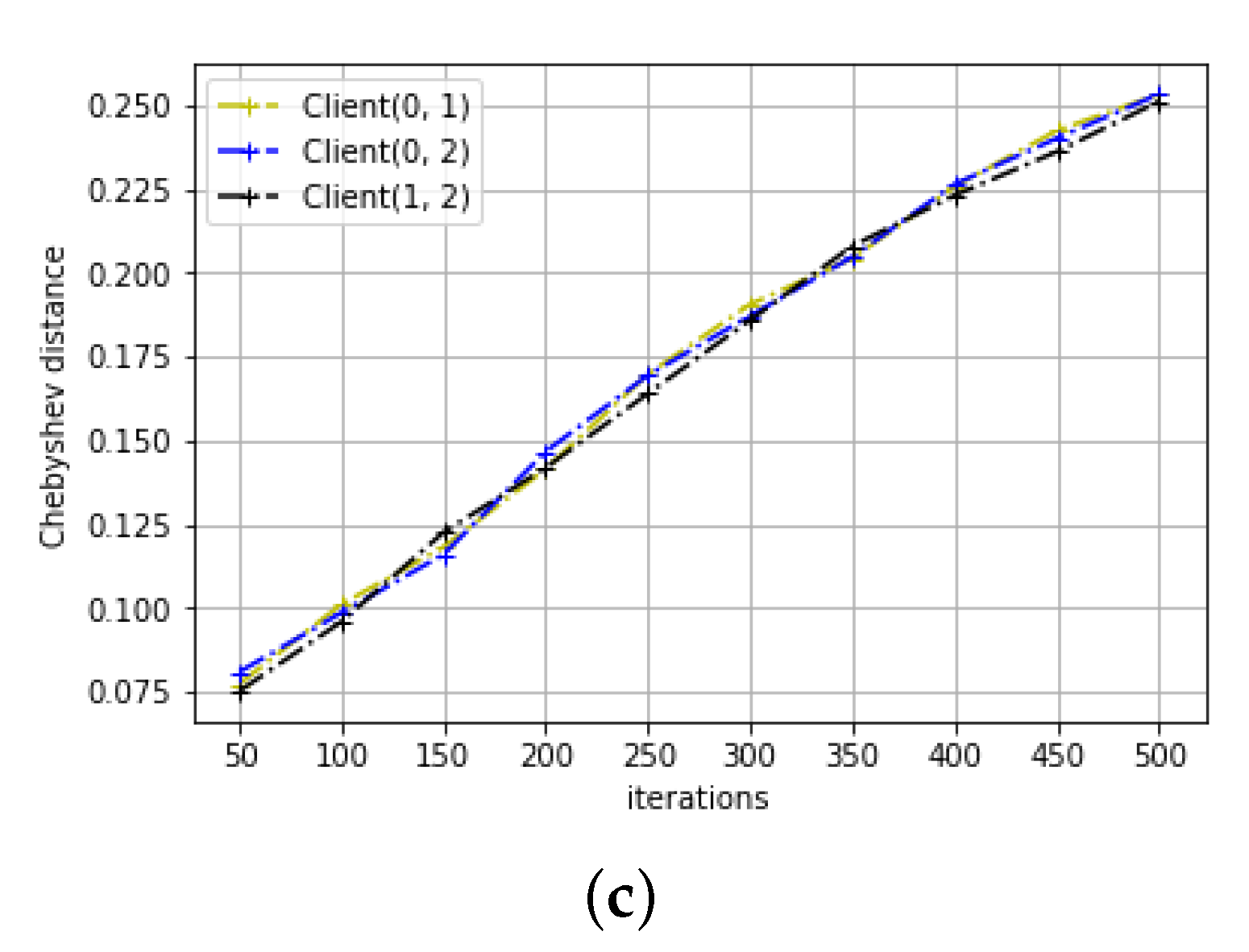
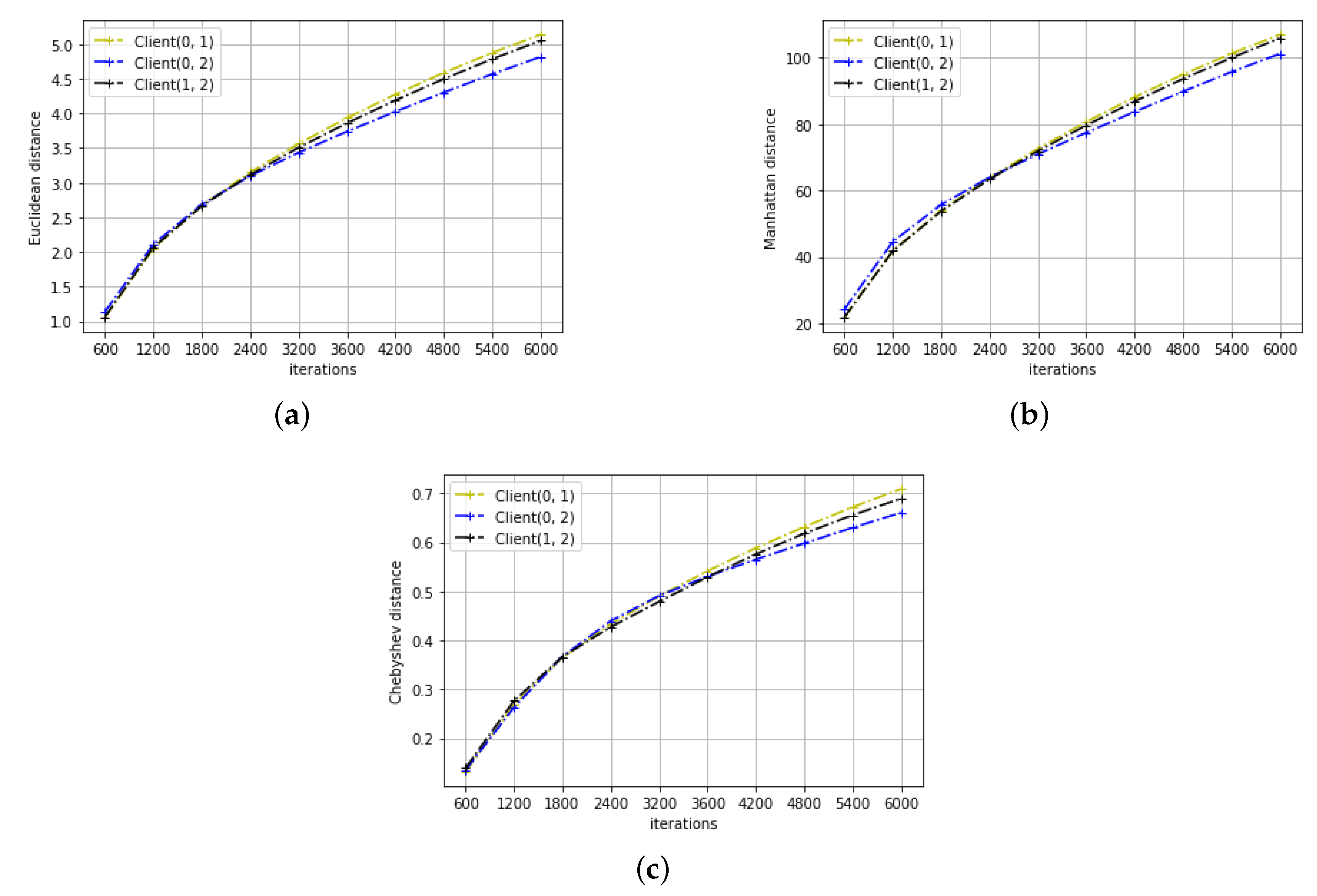
4.3. Distance Metrics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Poushter, J. Smartphone ownership and internet usage continues to climb in emerging economies. Pew Res. Center 2016, 22, 1–44. [Google Scholar]
- Haghi, M.; Thurow, K.; Stoll, R. Wearable devices in medical internet of things: Scientific research and commercially available devices. Healthc. Inform. Res. 2017, 23, 4–15. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.; Baron, D.; Schmidt, D. The world in 2025-predictions for the next ten years. In Proceedings of the 2015 10th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 21–23 October 2015; pp. 192–195. [Google Scholar]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog computing and its role in the internet of things. In Proceedings of the First Edition of the MCC Workshop on Mobile Cloud Computing, Helsinki, Finland, 17 August 2012; pp. 13–16. [Google Scholar]
- Garcia Lopez, P.; Montresor, A.; Epema, D.; Datta, A.; Higashino, T.; Iamnitchi, A.; Barcellos, M.; Felber, P.; Riviere, E. Edge-centric computing: Vision and challenges. ACM SIGCOMM Comput. Commun. Rev. 2015, 45, 37–42. [Google Scholar] [CrossRef]
- House, W. Consumer Data Privacy in a Networked World: A Framework for Protecting Privacy and Promoting Innovation in the Global Digital Economy; White House: Washington, DC, USA, 2012; pp. 1–62. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S. Communication-efficient learning of deep networks from decentralized data. arXiv 2016, arXiv:1602.05629. [Google Scholar]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.; Senior, A.; Tucker, P.; Yang, K. Large scale distributed deep networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1223–1231. [Google Scholar]
- Hard, A.; Rao, K.; Mathews, R.; Ramaswamy, S.; Beaufays, F.; Augenstein, S.; Eichner, H.; Kiddon, C.; Ramage, D. Federated learning for mobile keyboard prediction. arXiv 2018, arXiv:1811.03604. [Google Scholar]
- Ramaswamy, S.; Mathews, R.; Rao, K.; Beaufays, F. Federated learning for emoji prediction in a mobile keyboard. arXiv 2019, arXiv:1906.04329. [Google Scholar]
- Huang, L.; Yin, Y.; Fu, Z.; Zhang, S.; Deng, H.; Liu, D. LoAdaBoost: Loss-Based AdaBoost Federated Machine Learning on medical Data. arXiv 2018, arXiv:1811.12629. [Google Scholar]
- Samarakoon, S.; Bennis, M.; Saad, W.; Debbah, M. Federated learning for ultra-reliable low-latency V2V communications. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Sattler, F.; Wiedemann, S.; Müller, K.R.; Samek, W. Robust and communication-efficient federated learning from non-iid data. IEEE Trans. Neural Netw. Learn. Syst. 2019. [Google Scholar] [CrossRef] [PubMed]
- McMahan, H.B.; Ramage, D.; Talwar, K.; Zhang, L. Learning differentially private recurrent language models. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Agarwal, N.; Suresh, A.T.; Yu, F.X.X.; Kumar, S.; McMahan, B. cpSGD: Communication-efficient and differentially- private distributed SGD. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 7564–7575. [Google Scholar]
- He, L.; Bian, A.; Jaggi, M. Cola: Decentralized linear learning. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 4536–4546. [Google Scholar]
- Woodworth, B.E.; Wang, J.; Smith, A.; McMahan, B.; Srebro, N. Graph oracle models, lower bounds, and gaps for parallel stochastic optimization. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 8496–8506. [Google Scholar]
- Eichner, H.; Koren, T.; Mcmahan, B.; Srebro, N.; Talwar, K. Semi-Cyclic Stochastic Gradient Descent. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 1764–1773. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Ross, B.C. Mutual information between discrete and continuous data sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Mikolov, T.; Karafiát, M.; Burget, L.; Černockỳ, J.; Khudanpur, S. Recurrent neural network based language model. In Proceedings of the Eleventh Annual Conference of the International Speech Communication Association, Chiba, Japan, 26–30 September 2010. [Google Scholar]
- Danielsson, P.E. Euclidean distance mapping. Comput. Gr. Image Process. 1980, 14, 227–248. [Google Scholar] [CrossRef]
- Krause, E.F. Taxicab Geometry: An Adventure in Non-Euclidean Geometry; Courier Corporation: Chelmsford, MA, USA, 1986. [Google Scholar]
- Cantrell, C.D. Modern Mathematical Methods for Physicists and Engineers; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the black box of deep neural networks via information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Noshad, M.; Zeng, Y.; Hero, A.O. Scalable mutual information estimation using dependence graphs. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 2962–2966. [Google Scholar]
- Kolchinsky, A.; Tracey, B.D.; Wolpert, D.H. Nonlinear information bottleneck. Entropy 2019, 21, 1181. [Google Scholar] [CrossRef]
- Wickstrøm, K.; Løkse, S.; Kampffmeyer, M.; Yu, S.; Principe, J.; Jenssen, R. Information Plane Analysis of Deep Neural Networks via Matrix-Based Renyi’s Entropy and Tensor Kernels. arXiv 2019, arXiv:1909.11396. [Google Scholar]
- Adilova, L.; Rosenzweig, J.; Kamp, M. Information-Theoretic Perspective of Federated Learning. arXiv 2019, arXiv:1911.07652. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Deng, L. The MNIST database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. Proceedings of The International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Cheng, S.; Stankovic, V.; Vukobratovic, D. Averaging Is Probably Not the Optimum Way of Aggregating Parameters in Federated Learning. Entropy 2020, 22, 314. https://doi.org/10.3390/e22030314
Xiao P, Cheng S, Stankovic V, Vukobratovic D. Averaging Is Probably Not the Optimum Way of Aggregating Parameters in Federated Learning. Entropy. 2020; 22(3):314. https://doi.org/10.3390/e22030314
Chicago/Turabian StyleXiao, Peng, Samuel Cheng, Vladimir Stankovic, and Dejan Vukobratovic. 2020. "Averaging Is Probably Not the Optimum Way of Aggregating Parameters in Federated Learning" Entropy 22, no. 3: 314. https://doi.org/10.3390/e22030314
APA StyleXiao, P., Cheng, S., Stankovic, V., & Vukobratovic, D. (2020). Averaging Is Probably Not the Optimum Way of Aggregating Parameters in Federated Learning. Entropy, 22(3), 314. https://doi.org/10.3390/e22030314





