Traveling-Wave Convection with Periodic Source Defects in Binary Fluid Mixtures with Strong Soret Effect
Abstract
1. Introduction
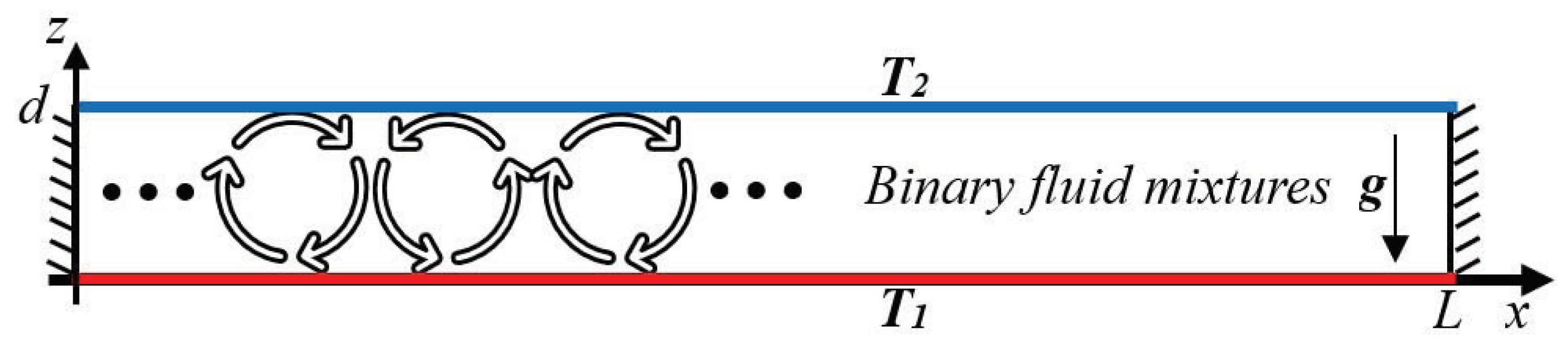
2. Mathematical Physical Model
2.1. Governing Equations
2.2. Boundary and Initial Conditions
2.3. Order Parameters
2.4. Numerical Method
3. Results and Discussion
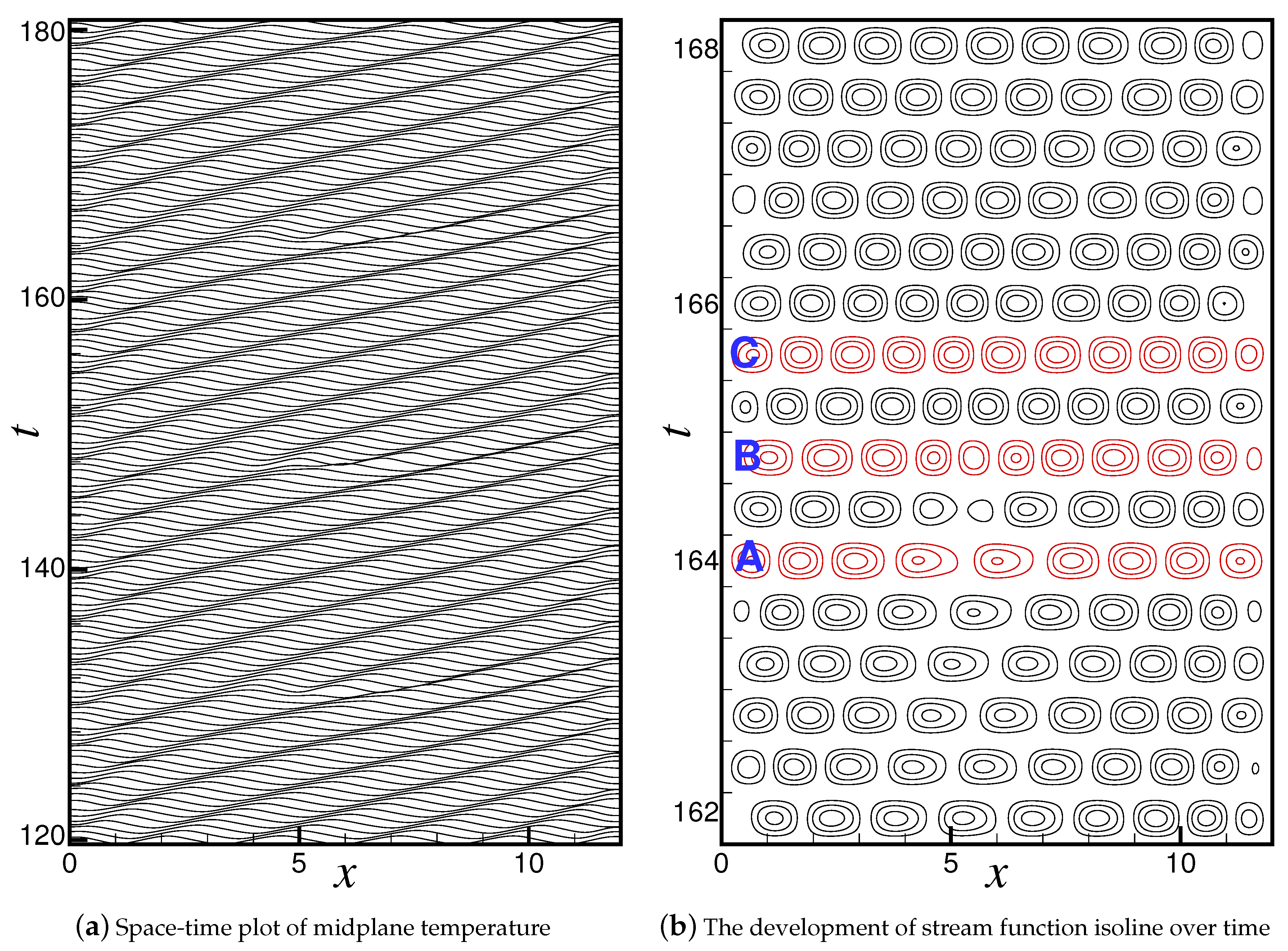
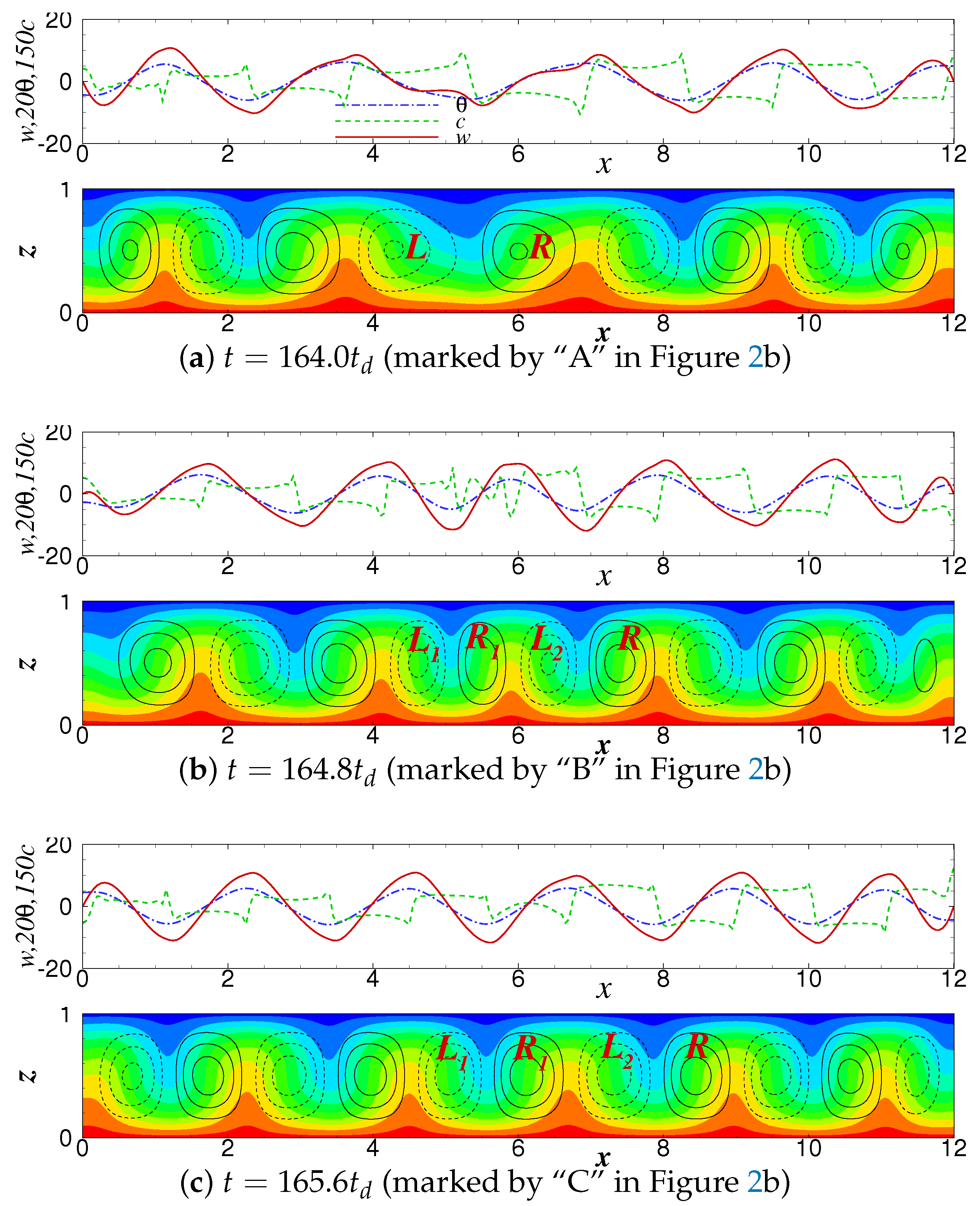
3.1. Spatiotemporal Evolution of the PSD-TW State
3.2. Causes of Formation and Survival for the PSD-TW State
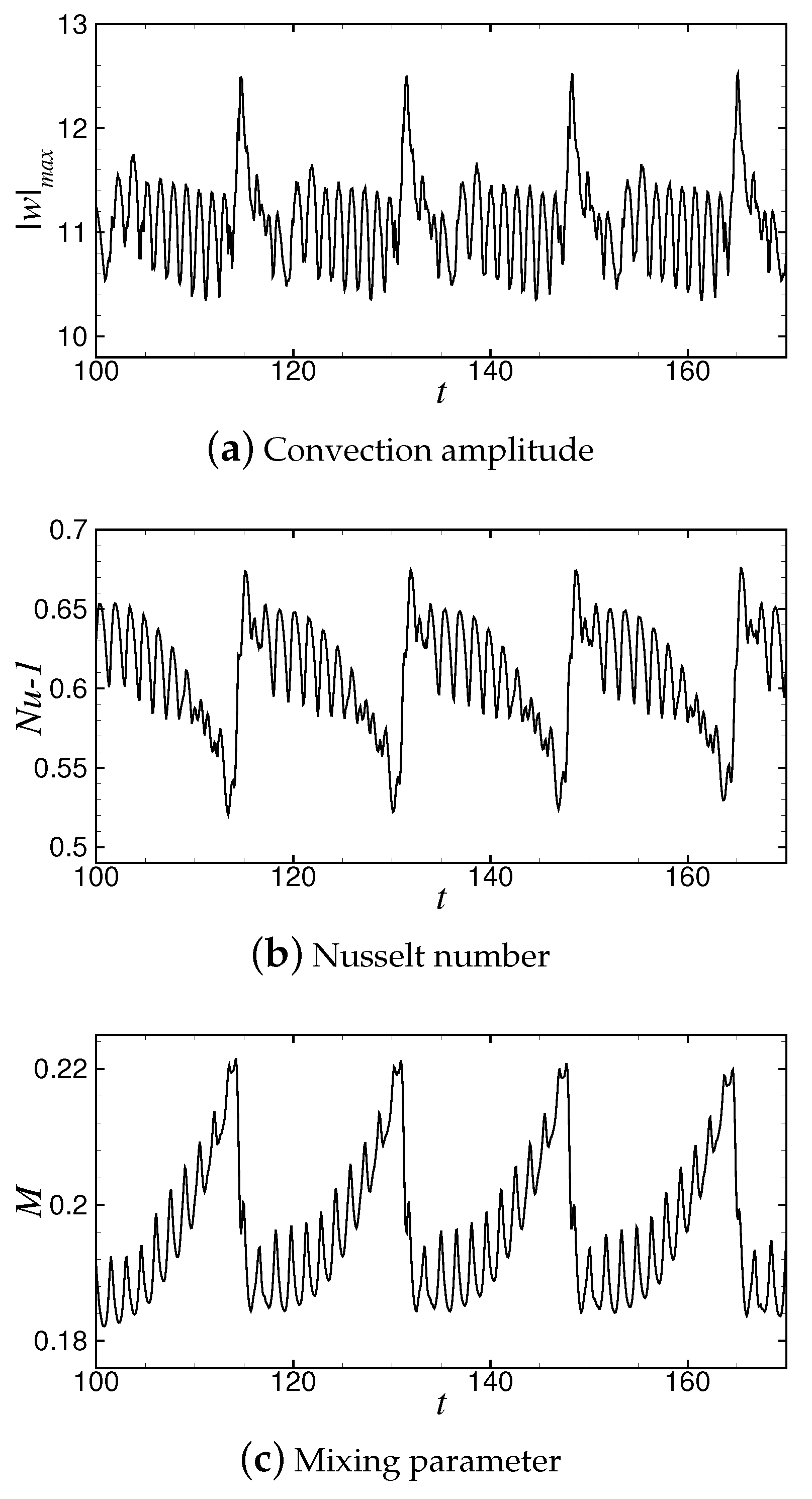
3.3. Variation of the Order Parameters
3.4. Influences of and
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Walden, R.W.; Kolodner, P.; Passner, A.; Surko, C.M. Traveling waves and chaos in convection in binary fluid mixtures. Phys. Rev. Lett. 1985, 55, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Moses, E.; Fineberg, J.; Steinberg, V. Multistability and confined traveling-wave patterns in a convecting binary mixture. Phys. Rev. A 1987, 35, 2757–2760. [Google Scholar] [CrossRef] [PubMed]
- Heinrichs, R.; Ahlers, G.; Cannell, D.S. Traveling waves and spatial variation in the convection of a binary mixture. Phys. Rev. A 1987, 35, 2761–2764. [Google Scholar] [CrossRef] [PubMed]
- Fineberg, J.; Moses, E.; Steinberg, V. Spatially and temporally modulated traveling-wave pattern in convecting binary mixtures. Phys. Rev. Lett. 1988, 61, 838–841. [Google Scholar] [CrossRef]
- Kolodner, P.; Surko, C.M. Weakly nonlinear traveling-wave convection. Phys. Rev. Lett. 1988, 61, 842–845. [Google Scholar] [CrossRef]
- Steinberg, V.; Fineberg, J.; Moses, E.; Rehberg, I. Pattern selection and transition to turbulence in propagating waves. Physica D 1989, 37, 359–383. [Google Scholar] [CrossRef]
- Kolodner, P.; Surko, C.M.; Williams, H. Dynamics of traveling waves near the onset of convection in binary fluid mixtures. Physica D 1989, 37, 319–333. [Google Scholar] [CrossRef]
- Kolodner, P.; Glazier, J.A.; Williams, H. Dispersive chaos in one-dimensional traveling-wave convection. Phys. Rev. Lett. 1990, 65, 1579–1582. [Google Scholar] [CrossRef]
- Barten, W.; Lücke, M.; Hort, W.; Kamps, M. Fully developed traveling-wave convection in binary fluid mixtures. Phys. Rev. Lett. 1989, 63, 376–379. [Google Scholar] [CrossRef]
- Barten, W.; Lücke, M.; Kamps, M.; Schmitz, R. Convection in binary-fluid mixtures I. Extended traveling-wave and stationary states. Phys. Rev. E 1995, 51, 5636–5661. [Google Scholar] [CrossRef] [PubMed]
- Barten, W.; Lücke, M.; Kamps, M.; Schmitz, R. Convection in binary-fluid mixtures II. Localized traveling waves. Phys. Rev. E 1995, 51, 5662–5680. [Google Scholar] [CrossRef] [PubMed]
- Jung, D.; Lücke, M. Localized waves without the existence of extended waves: Oscillatory convection of binary mixtures with strong Soret effect. Phys. Rev. Lett. 2002, 89, 054502. [Google Scholar] [CrossRef] [PubMed]
- Ning, L.Z.; Harada, Y.; Yahata, H. Modulated traveling waves in binary fluid convection in an intermediate-aspect-ratio rectangular cell. Prog. Theor. Phys. 1997, 97, 831–848. [Google Scholar] [CrossRef][Green Version]
- Batiste, O.; Knobloch, E.; Alonso, A.; Mercader, I. Spatially localized binary-fluid convection. J. Fluid Mech. 2006, 560, 149–158. [Google Scholar] [CrossRef]
- Mercader, I.; Batiste, O.; Alonso, A.; Knobloch, E. Convectons, anticonvectons and multiconvectons in binary fluid convection. J. Fluid Mech. 2011, 667, 586–606. [Google Scholar] [CrossRef]
- Mercader, I.; Batiste, O.; Alonso, A.; Knobloch, E. Travelling convectons in binary fluid convection. J. Fluid Mech. 2013, 722, 240–266. [Google Scholar] [CrossRef]
- Taraut, A.V.; Smorodin, B.L.; Lücke, M. Collisions of localized convection structures in binary fluid mixtures. New J. Phys 2012, 14, 093055. [Google Scholar] [CrossRef]
- Watanabe, T.; Iima, M.; Nishiura, Y. Spontaneous formation of travelling localized structures and their asymptotic behaviour in binary fluid convection. J. Fluid Mech. 2012, 712, 219–243. [Google Scholar] [CrossRef]
- Smorodin, B.L.; Myznikova, B.I.; Ishutov, S.M. Traveling-wave convection in a binary fluid mixture under high-frequency vertical vibrations. Phys. Rev. E 2014, 89, 053004. [Google Scholar] [CrossRef]
- Zhao, B.; Tian, Z. Numerical investigation of binary fluid convection with a weak negative separation ratio in finite containers. Phys. Fluids 2015, 27, 074102. [Google Scholar] [CrossRef]
- Mercader, I.; Batiste, O.; Alonso, A.; Knobloch, E. Effect of small inclination on binary convection in elongated rectangular cells. Phys. Rev. E 2019, 99, 023113. [Google Scholar] [CrossRef] [PubMed]
- Mercader, I.; Alonso, A.; Batiste, O. Numerical analysis of the Eckhaus instability in travelling-wave convection in binary mixtures. Eur. Phys. J. E 2004, 15, 311–318. [Google Scholar] [CrossRef]
- Alonso, A.; Batiste, O.; Mercader, I. Numerical simulations of binary fluid convection in large aspect ratio annular containers. Eur. Phys. J. Spec. Top. 2007, 146, 261–277. [Google Scholar] [CrossRef]
- Büchel, P.; Lücke, M. Sidewall induced Eckhaus instability of propagating wave convection in binary fluid mixtures. Entropy 1999, 218, 22–26. [Google Scholar]
- Li, G.D.; Huang, Y.N. Traveling-wave convection with Eckhaus instability modulation in a binary fluid mixture. Acta Phys. Sin.-Ch. Ed. 2007, 56, 4742–4748. [Google Scholar]
- Ning, L.Z.; Qi, X.; Zhou, Y.; Yu, L. Defect structures of Rayleigh-Bénard travelling wave convection in binary fluid mixtures. Acta Phys. Sin.-Ch. Ed. 2009, 58, 2528–2534. [Google Scholar]
- Van der Poel, E.P.; Ostilla-Mónico, R.; Verzicco, R.; Grossmann, S.; Lohse, D. Logarithmic mean temperature profiles and their connection to plume emissions in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett. 2015, 115, 154501. [Google Scholar] [CrossRef]
- Zhu, X.; Mathai, V.; Stevens, R.J.A.M.; Verzicco, R.; Lohse, D. Transition to the ultimate regime in two-dimensional Rayleigh-Bénard convection. Phys. Rev. Lett. 2018, 120, 144502. [Google Scholar] [CrossRef]
- Schmalzl, J.; Breuer, M.; Hansen, U. On the validity of two-dimensional numerical approaches to time-dependent thermal convection. EPL 2004, 67, 390–396. [Google Scholar] [CrossRef]
- Van der Poel, E.P.; Stevens, R.J.A.M.; Lohse, D. Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 2013, 736, 177–194. [Google Scholar] [CrossRef]
- Huang, Y.-X.; Zhou, Q. Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 2013, 737, R3. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.-X.; Jiang, N.; Liu, Y.-L.; Lu, Z.-M.; Qiu, X.; Zhou, Q. Statistics of velocity and temperature fluctuations in two-dimensional Rayleigh-Bénard convection. Phys. Rev. E 2017, 96, 023105. [Google Scholar] [CrossRef] [PubMed]
- Batiste, O.; Knobloch, E. Simulations of localized states of stationary convection in 3He-4He mixtures. Phys. Rev. Lett. 2005, 95, 244501. [Google Scholar] [CrossRef]
- Kolodner, P.; Bensimon, D.; Surko, C.M. Traveling-wave convection in an annulus. Phys. Rev. Lett. 1988, 60, 1723–1726. [Google Scholar] [CrossRef]
- Baxter, G.W.; Eaton, K.D.; Surko, C.M. Eckhaus instability for traveling waves. Phys. Rev. A 1992, 46, 1735–1738. [Google Scholar] [CrossRef]
- Kolodner, P. Observations of the Eckhaus instability in one-dimensional traveling-wave convection. Phys. Rev. A 1992, 46, R1739–R1742. [Google Scholar] [CrossRef]
- Kolodner, P. Extended states of nonlinear traveling-wave convection. I. The Eckhaus instability. Phys. Rev. A 1992, 46, 6431–6451. [Google Scholar] [CrossRef]
- Kolodner, P. Extended states of nonlinear traveling-wave convection. II. Fronts and spatiotemporal defects. Phys. Rev. A 1992, 46, 6452–6468. [Google Scholar] [CrossRef]
- Qin, Q.; Xia, Z.A.; Tian, Z.F. High accuracy numerical investigation of double-diffusive convection in a rectangular enclosure with horizontal temperature and concentration gradients. Int. J. Heat Mass Tran. 2014, 71, 405–423. [Google Scholar] [CrossRef]
- Tian, Z.; Liang, X.; Yu, P. A higher order compact finite difference algorithm for solving the incompressible Navier-Stokes equations. Int. J. Numer. Meth. Eng. 2011, 88, 511–532. [Google Scholar] [CrossRef]
- Kolodner, P.; Williams, H.; Moe, C. Optical measurement of the Soret coefficient of ethanolwater solutions. J. Chem. Phys. 1988, 88, 6512–6524. [Google Scholar] [CrossRef]
- Knobloch, E.; Moore, D.R. Linear stability of experimental Soret convection. Phys. Rev. A 1988, 37, 860–870. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Zhao, B.; Yang, J.; Tian, Z.; Ye, M. Traveling-Wave Convection with Periodic Source Defects in Binary Fluid Mixtures with Strong Soret Effect. Entropy 2020, 22, 283. https://doi.org/10.3390/e22030283
Zheng L, Zhao B, Yang J, Tian Z, Ye M. Traveling-Wave Convection with Periodic Source Defects in Binary Fluid Mixtures with Strong Soret Effect. Entropy. 2020; 22(3):283. https://doi.org/10.3390/e22030283
Chicago/Turabian StyleZheng, Laiyun, Bingxin Zhao, Jianqing Yang, Zhenfu Tian, and Ming Ye. 2020. "Traveling-Wave Convection with Periodic Source Defects in Binary Fluid Mixtures with Strong Soret Effect" Entropy 22, no. 3: 283. https://doi.org/10.3390/e22030283
APA StyleZheng, L., Zhao, B., Yang, J., Tian, Z., & Ye, M. (2020). Traveling-Wave Convection with Periodic Source Defects in Binary Fluid Mixtures with Strong Soret Effect. Entropy, 22(3), 283. https://doi.org/10.3390/e22030283




