Synchronization of a Non-Equilibrium Four-Dimensional Chaotic System Using a Disturbance-Observer-Based Adaptive Terminal Sliding Mode Control Method
Abstract
1. Introduction
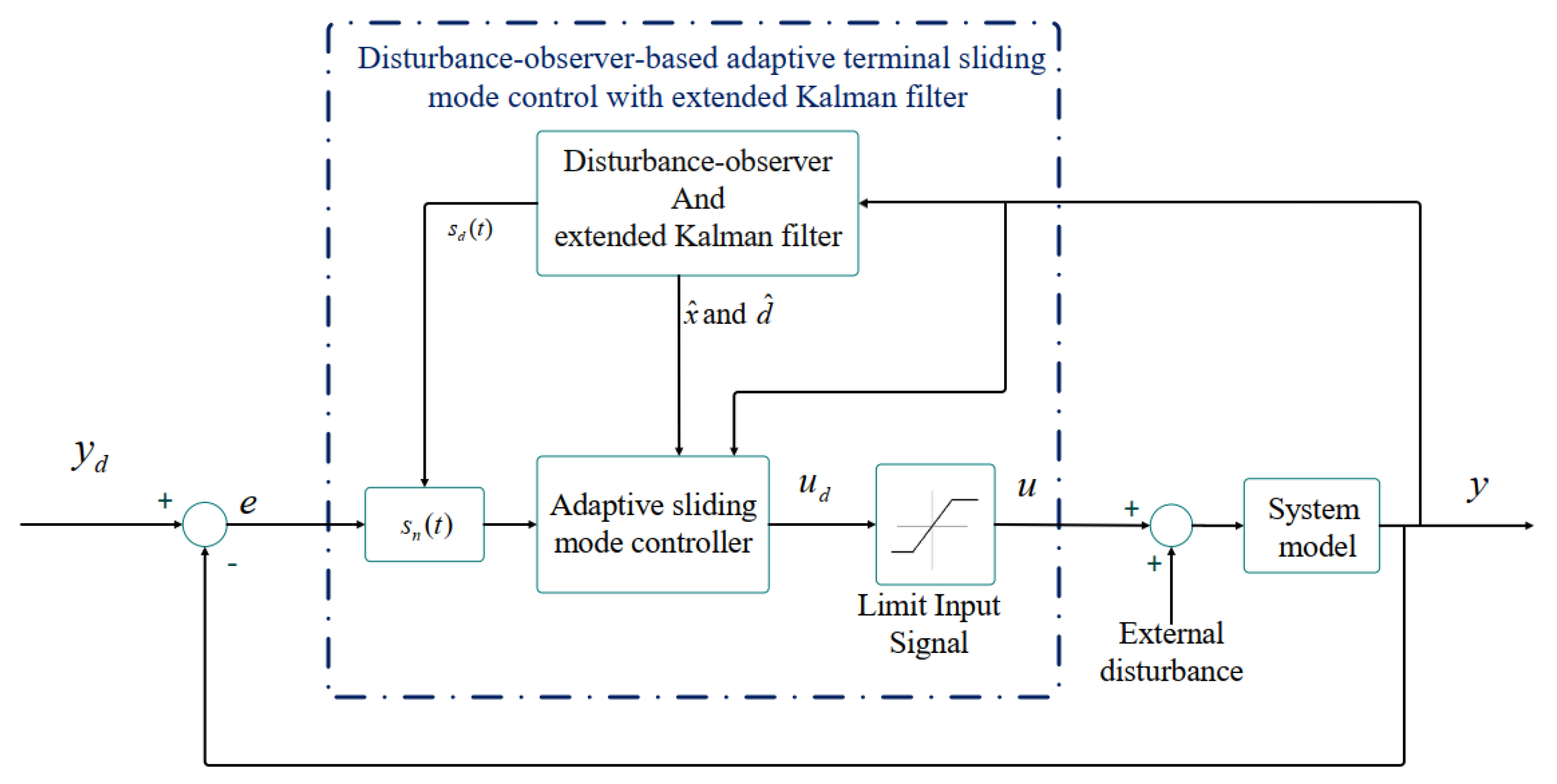
- The combination of disturbance-observer-based adaptive terminal sliding mode control (ATSMC) with a disturbance observer was developed for control and synchronization of an uncertain chaotic system in the presence of disturbances.
- The control input saturation was considered.
- An extended Kalman filter (EKF) approach was implemented with the controller for condition monitoring purposes. Indeed, this algorithm was used to estimate the actual amounts of the states of the system.
- A genetic algorithm (GA) optimization was used to reduce the chattering phenomena.
- Finally, numerical simulations illustrated the main characteristics and dynamical behaviors of the analyzed four-dimensional chaotic system, as well as the proposed controller for its synchronization.
2. Methods
2.1. System Description and Dynamical Analysis
2.2. Controller Design
2.2.1. Fast Disturbance Observer
2.2.2. Adaptive Sliding Mode Control
2.2.3. Extended Kalman Filter
3. Results and Discussion
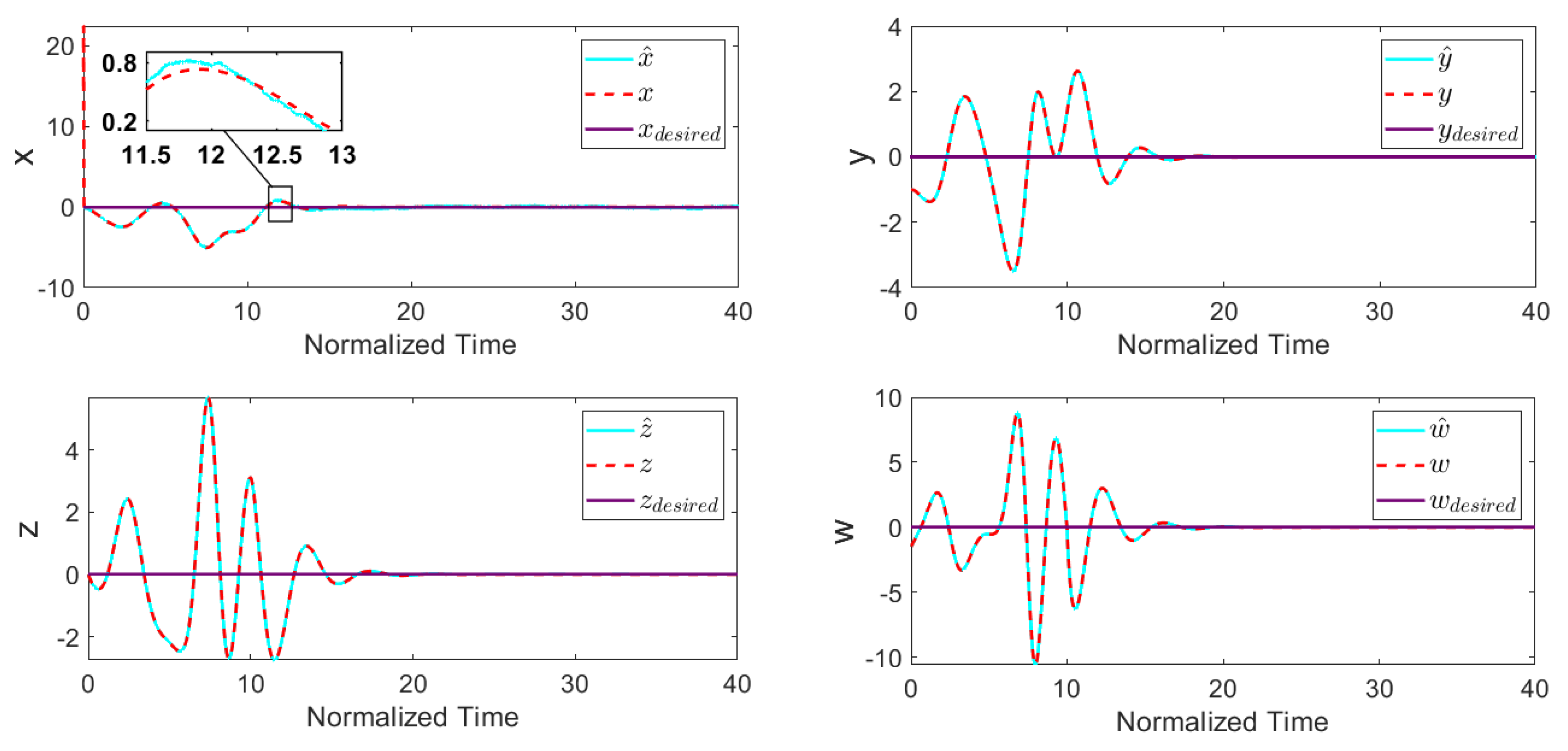
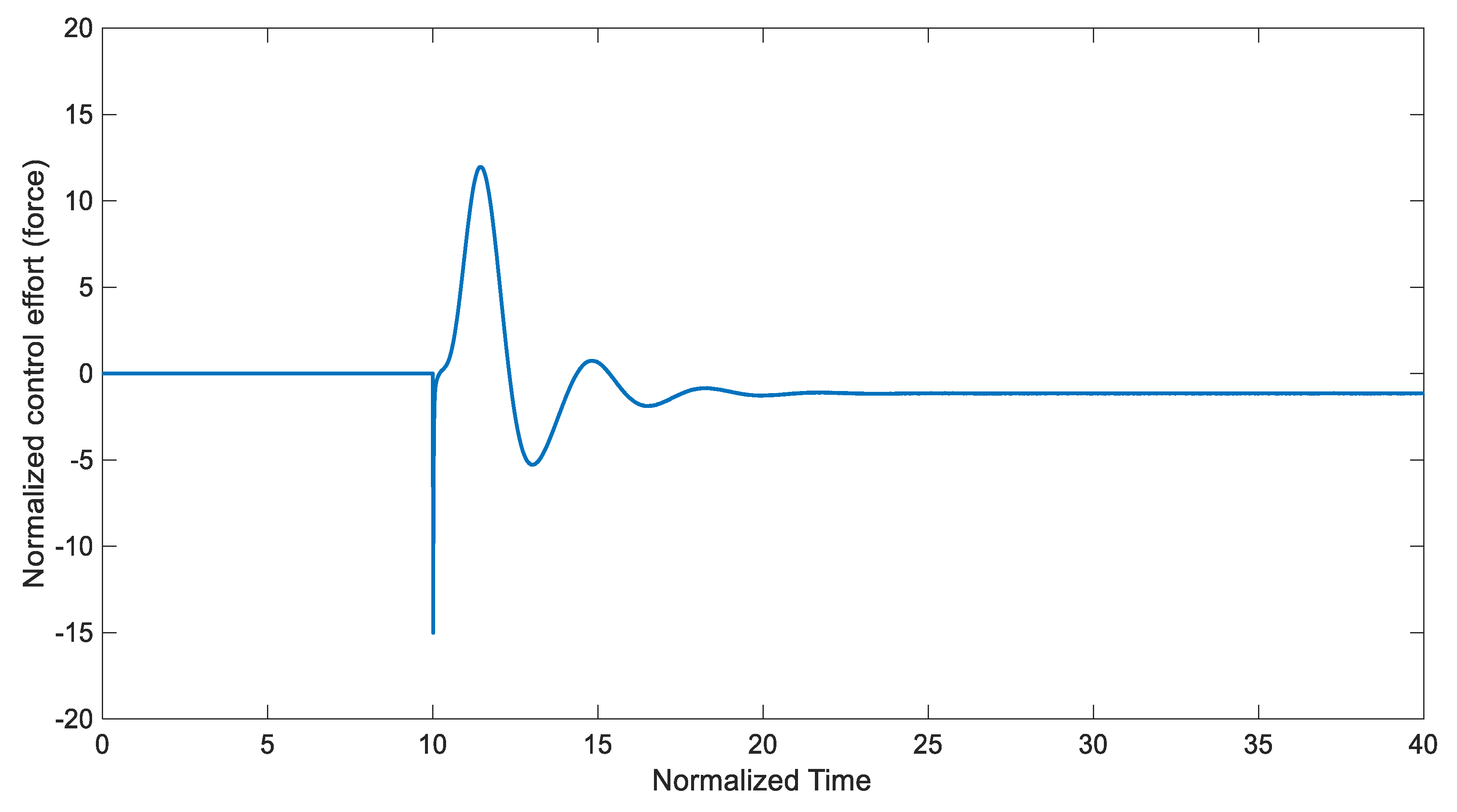
3.1. Chaos Control with Incomplete State Measurement
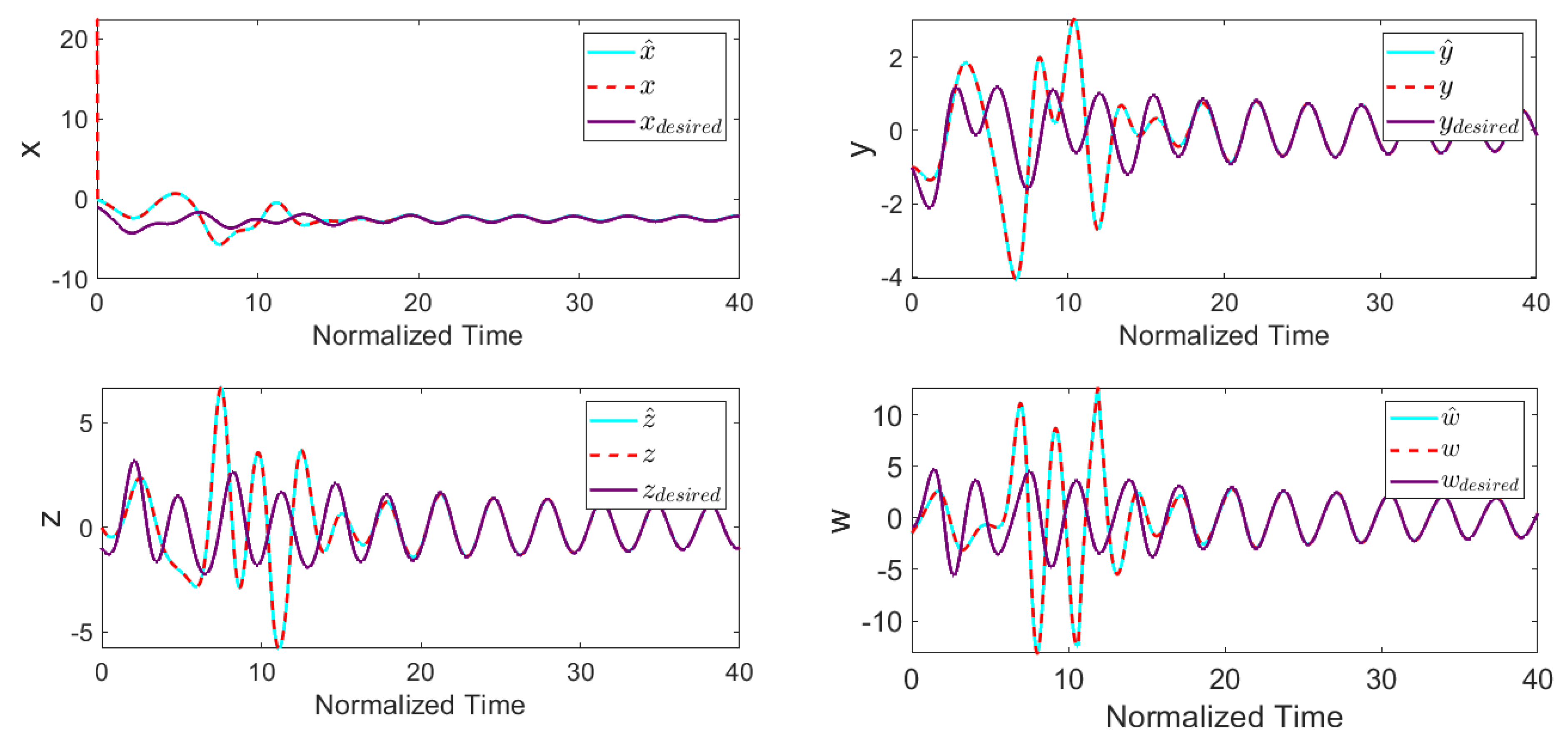
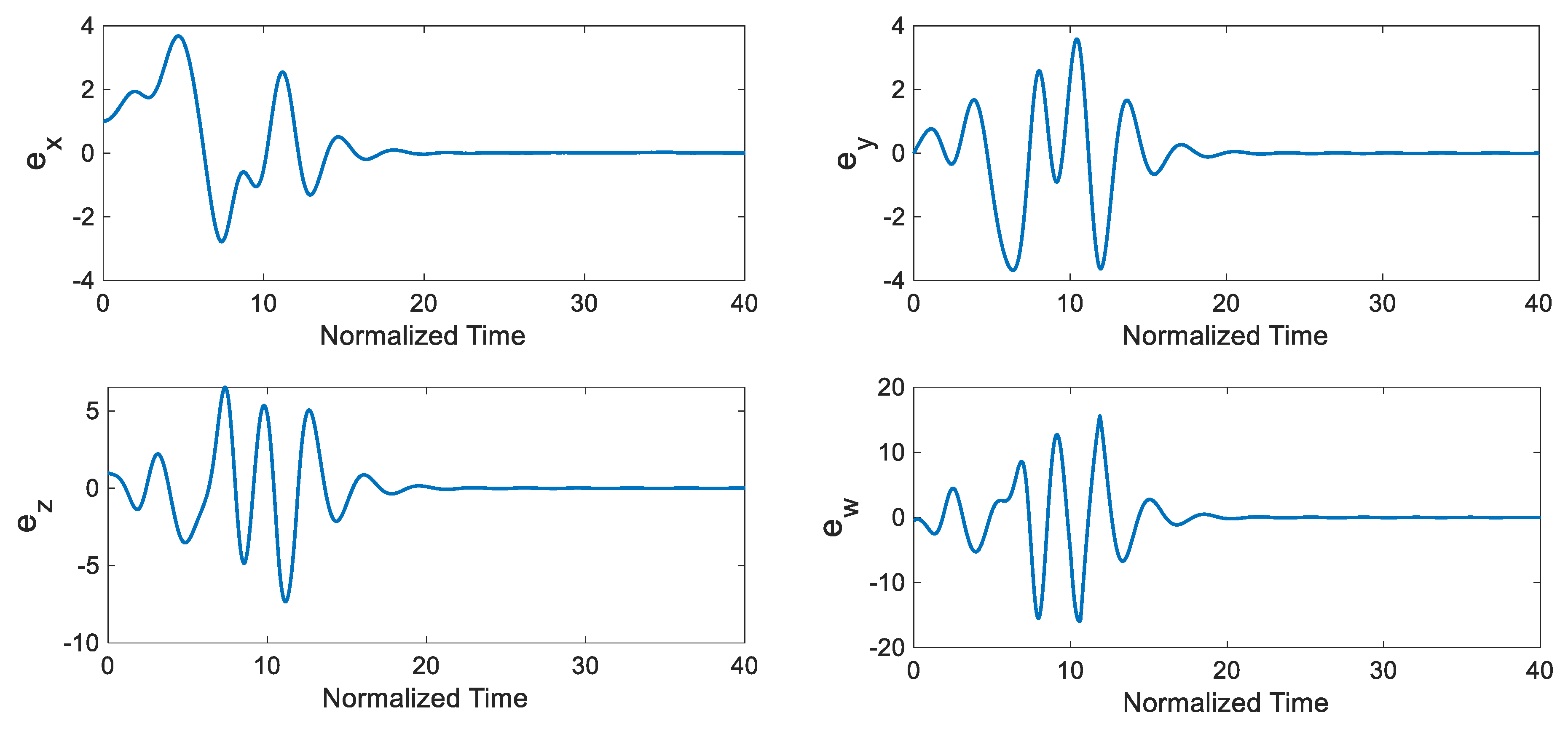
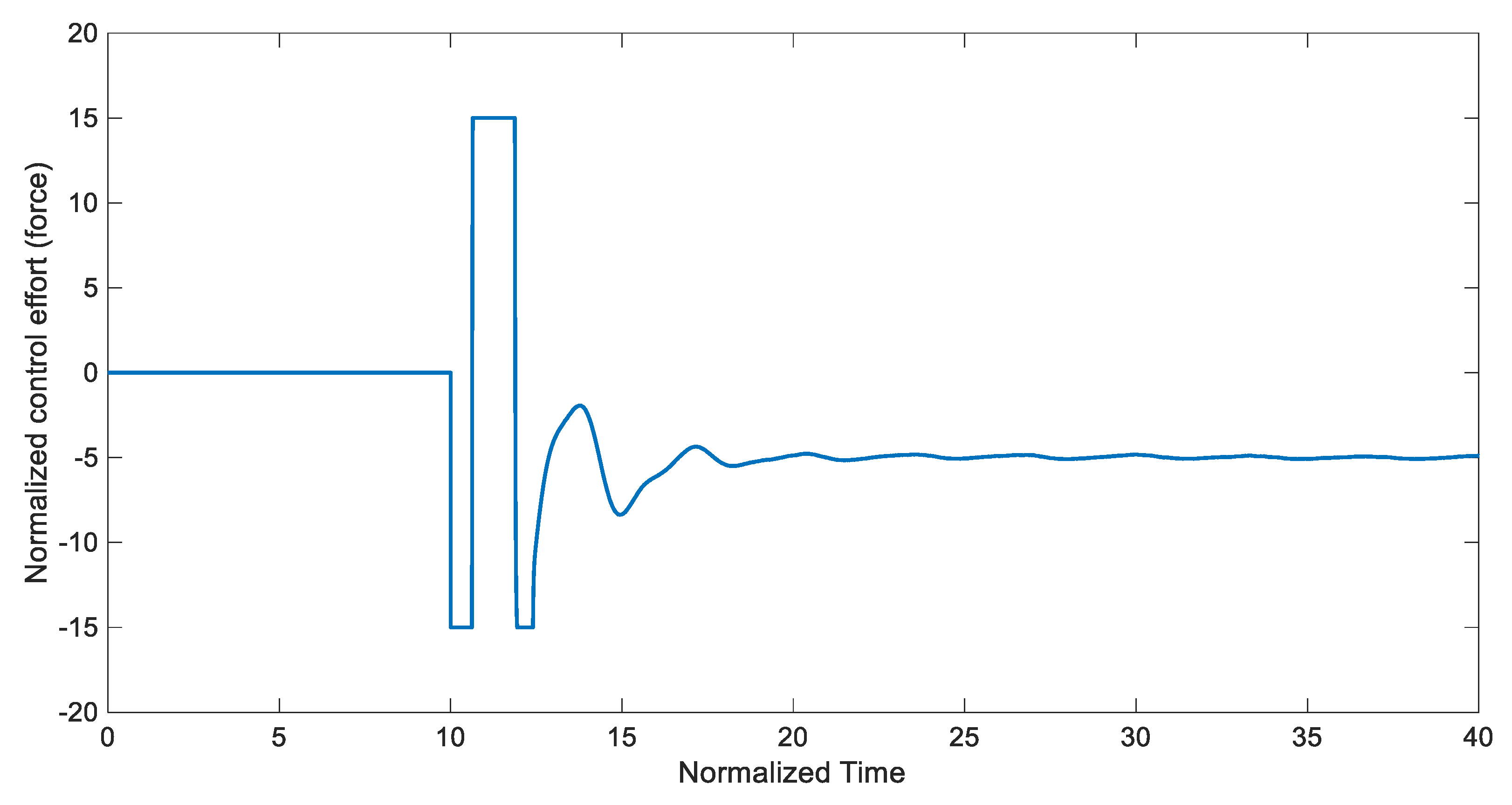
3.2. Adaptive Synchronization of the Uncertain Chaotic System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Pham, V.-T.; Volos, C.; Fortuna, L. Memristor-Based Systems: Nonlinearity, Dynamics and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Boubaker, O.; Jafari, S. Recent Advances in Chaotic Systems and Synchronization: From Theory to Real World Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Yousefpour, A.; Bahrami, A.; Haeri Yazdi, M.R. Multi-frequency piezomagnetoelastic energy harvesting in the monostable mode. J. Theor. Appl. Vib. Acoust. 2018, 4, 1–18. [Google Scholar]
- Jahanshahi, H.; Rajagopal, K.; Akgul, A.; Sari, N.N.; Namazi, H.; Jafari, S. Complete analysis and engineering applications of a megastable nonlinear oscillator. Int. J. Non-Linear Mech. 2018, 107, 126–136. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Shahriari-Kahkeshi, M.; Alcaraz, R.; Wang, X.; Singh, V.P.; Pham, V.-T. Entropy analysis and neural network-based adaptive control of a non-equilibrium four-dimensional chaotic system with hidden attractors. Entropy 2019, 21, 156. [Google Scholar] [CrossRef]
- Bao, B.-C.; Xu, Q.; Bao, H.; Chen, M. Extreme multistability in a memristive circuit. Electron. Lett. 2016, 52, 1008–1010. [Google Scholar] [CrossRef]
- Bao, B.; Jiang, T.; Xu, Q.; Chen, M.; Wu, H.; Hu, Y. Coexisting infinitely many attractors in active band-pass filter-based memristive circuit. Nonlinear Dyn. 2016, 86, 1711–1723. [Google Scholar] [CrossRef]
- Sharma, P.R.; Shrimali, M.D.; Prasad, A.; Kuznetsov, N.V.; Leonov, G.A. Control of multistability in hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1485–1491. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, S. Generating multiple chaotic attractors from sprott B system. Int. J. Bifurc. Chaos 2016, 26, 1650177. [Google Scholar] [CrossRef]
- Sprott, J.C.; Jafari, S.; Khalaf, A.J.M.; Kapitaniak, T. Megastability: Coexistence of a countable infinity of nested attractors in a periodically-forced oscillator with spatially-periodic damping. Eur. Phys. J. Spec. Top. 2017, 226, 1979–1985. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.J.; Pano-Azucena, A.D.; Obeso-Rodelo, P.J.; Nuñez-Perez, J.C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Tlelo-Cuautle, E.; Toxqui-Toxqui, I.; Sanchez-Lopez, C.; Trejo-Guerra, R. Frequency limitations in generating multi-scroll chaotic attractors using CFOAs. Int. J. Electron. 2014, 101, 1559–1569. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.-T.; Volos, C.; Jafari, S.; Kapitaniak, T. Coexistence of hidden chaotic attractors in a novel no-equilibrium system. Nonlinear Dyn. 2017, 87, 2001–2010. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Volos, C.; Gotthans, T.; Wang, X.; Hoang, D.V. A chaotic system with rounded square equilibrium and with no-equilibrium. Opt. Int. J. Light Electron Opt. 2017, 130, 365–371. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Golpayegani, S.M.R.H. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Pham, V.-T.; Akgul, A.; Volos, C.; Jafari, S.; Kapitaniak, T. Dynamics and circuit realization of a no-equilibrium chaotic system with a boostable variable. AEU Int. J. Electron. Commun. 2017, 78, 134–140. [Google Scholar] [CrossRef]
- Ren, S.; Panahi, S.; Rajagopal, K.; Akgul, A.; Pham, V.-T.; Jafari, S. A new chaotic flow with hidden attractor: The first hyperjerk system with no equilibrium. J. Phys. Sci. 2018, 73, 239–249. [Google Scholar] [CrossRef]
- Rossler, O.E. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.; Jafari, S.; Kingni, S.T. A no-equilibrium hyperchaotic system with a cubic nonlinear term. Opt. Int. J. Light Electron Opt. 2016, 127, 3259–3265. [Google Scholar] [CrossRef]
- Bao, B.C.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z.; Wang, M.; Xiong, L. Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability. Chaos Interdiscipl. J. Nonlinear Sci. 2018, 28, 013113. [Google Scholar] [CrossRef] [PubMed]
- Jahanshahi, H.; Jafarzadeh, M.; Sari, N.N.; Pham, V.-T.; Huynh, V.V.; Nguyen, X.Q. Robot motion planning in an unknown environment with danger space. Electronics 2019, 8, 201. [Google Scholar] [CrossRef]
- Sari, N.N.; Jahanshahi, H.; Fakoor, M. Adaptive fuzzy PID control strategy for spacecraft attitude control. Int. J. Fuzzy Syst. 2019, 21, 769–781. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jahanshahi, H.; Jafari, S.; Weldegiorgis, R.; Karthikeyan, A.; Duraisamy, P. Coexisting attractors in a fractional order hydro turbine governing system and fuzzy PID based chaos control. Asian J. Control 2020. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. An optimal fuzzy PID control approach for docking maneuver of two spacecraft: Orientational motion. Eng. Sci. Technol. Int. J. 2017, 20, 293–309. [Google Scholar] [CrossRef]
- Jahanshahi, H. Smooth control of HIV/AIDS infection using a robust adaptive scheme with decoupled sliding mode supervision. Eur. Phys. J. Spec. Top. 2018, 227, 707–718. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. Optimal FPID control approach for a docking maneuver of two spacecraft: Translational motion. J. Aerosp. Eng. 2017, 30, 04017011. [Google Scholar] [CrossRef]
- Yousefpour, A.; Vahidi-Moghaddam, A.; Rajaei, A.; Ayati, M. Stabilization of nonlinear vibrations of carbon nanotubes using observer-based terminal sliding mode control. Trans. Inst. Meas. Control 2019. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sari, N.N.; Pham, V.-T.; Alsaadi, F.E.; Hayat, T. Optimal adaptive higher order controllers subject to sliding modes for a carrier system. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Rajaei, A.; Vahidi-Moghaddam, A.; Chizfahm, A.; Sharifi, M. Control of malaria outbreak using a non-linear robust strategy with adaptive gains. IET Control Theory Appl. 2019, 13, 2308–2317. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.J.; Jahanshahi, H. Multi-objective optimized fuzzy-PID controllers for fourth order nonlinear systems. Eng. Sci. Technol. Int. J. 2016, 19, 1084–1098. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H. Fast disturbance-observer-based robust integral terminal sliding mode control of a hyperchaotic memristor oscillator. Eur. Phys. J. Spec. Top. 2019, 228, 2247–2268. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jahanshahi, H.; Varan, M.; Bayır, I.; Pham, V.-T.; Jafari, S.; Karthikeyan, A. A hyperchaotic memristor oscillator with fuzzy based chaos control and LQR based chaos synchronization. AEU Int. J. Electron. Commun. 2018, 94, 55–68. [Google Scholar] [CrossRef]
- Pérez-Cruz, J.H.; Tamayo-Meza, P.A.; Figueroa, M.; Silva-Ortigoza, R.; Ponce-Silva, M.; Rivera-Blas, R.; Aldape-Pérez, M. Exponential synchronization of chaotic xian system using linear feedback control. Complexity 2019. [Google Scholar] [CrossRef]
- Pérez-Cruz, J.H. Stabilization and synchronization of uncertain zhang system by means of robust adaptive control. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Akgul, A.; Iu, H.H.C.; Zhao, Y. A new chaotic oscillator with free control. Chaos Interdiscipl. J. Nonlinear Sci. 2017, 27, 083101. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Variable-boostable chaotic flows. Optik 2016, 127, 10389–10398. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Chen, G. Diagnosing multistability by offset boosting. Nonlinear Dyn. 2017, 90, 1335–1341. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Xing, H. Constructing chaotic systems with conditional symmetry. Nonlinear Dyn. 2017, 87, 1351–1358. [Google Scholar] [CrossRef]
- Mobayen, S.; Javadi, S. Disturbance observer and finite-time tracker design of disturbed third-order nonholonomic systems using terminal sliding mode. J. Vib. Control 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]

| 212.5013 | 15 | 17.7775 | 17.0458 | 16.2175 | 16.7562 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yousefpour, A.; Yusuf, A.; Jahanshahi, H.; Alcaraz, R.; He, S.; Munoz-Pacheco, J.M. Synchronization of a Non-Equilibrium Four-Dimensional Chaotic System Using a Disturbance-Observer-Based Adaptive Terminal Sliding Mode Control Method. Entropy 2020, 22, 271. https://doi.org/10.3390/e22030271
Wang S, Yousefpour A, Yusuf A, Jahanshahi H, Alcaraz R, He S, Munoz-Pacheco JM. Synchronization of a Non-Equilibrium Four-Dimensional Chaotic System Using a Disturbance-Observer-Based Adaptive Terminal Sliding Mode Control Method. Entropy. 2020; 22(3):271. https://doi.org/10.3390/e22030271
Chicago/Turabian StyleWang, Shaojie, Amin Yousefpour, Abdullahi Yusuf, Hadi Jahanshahi, Raúl Alcaraz, Shaobo He, and Jesus M. Munoz-Pacheco. 2020. "Synchronization of a Non-Equilibrium Four-Dimensional Chaotic System Using a Disturbance-Observer-Based Adaptive Terminal Sliding Mode Control Method" Entropy 22, no. 3: 271. https://doi.org/10.3390/e22030271
APA StyleWang, S., Yousefpour, A., Yusuf, A., Jahanshahi, H., Alcaraz, R., He, S., & Munoz-Pacheco, J. M. (2020). Synchronization of a Non-Equilibrium Four-Dimensional Chaotic System Using a Disturbance-Observer-Based Adaptive Terminal Sliding Mode Control Method. Entropy, 22(3), 271. https://doi.org/10.3390/e22030271








