Characteristics of Nonthermal Dupree Diffusion on Space-Charge Wave in a Kappa Distribution Plasma Column with Turbulent Diffusion
Abstract
:1. Introduction
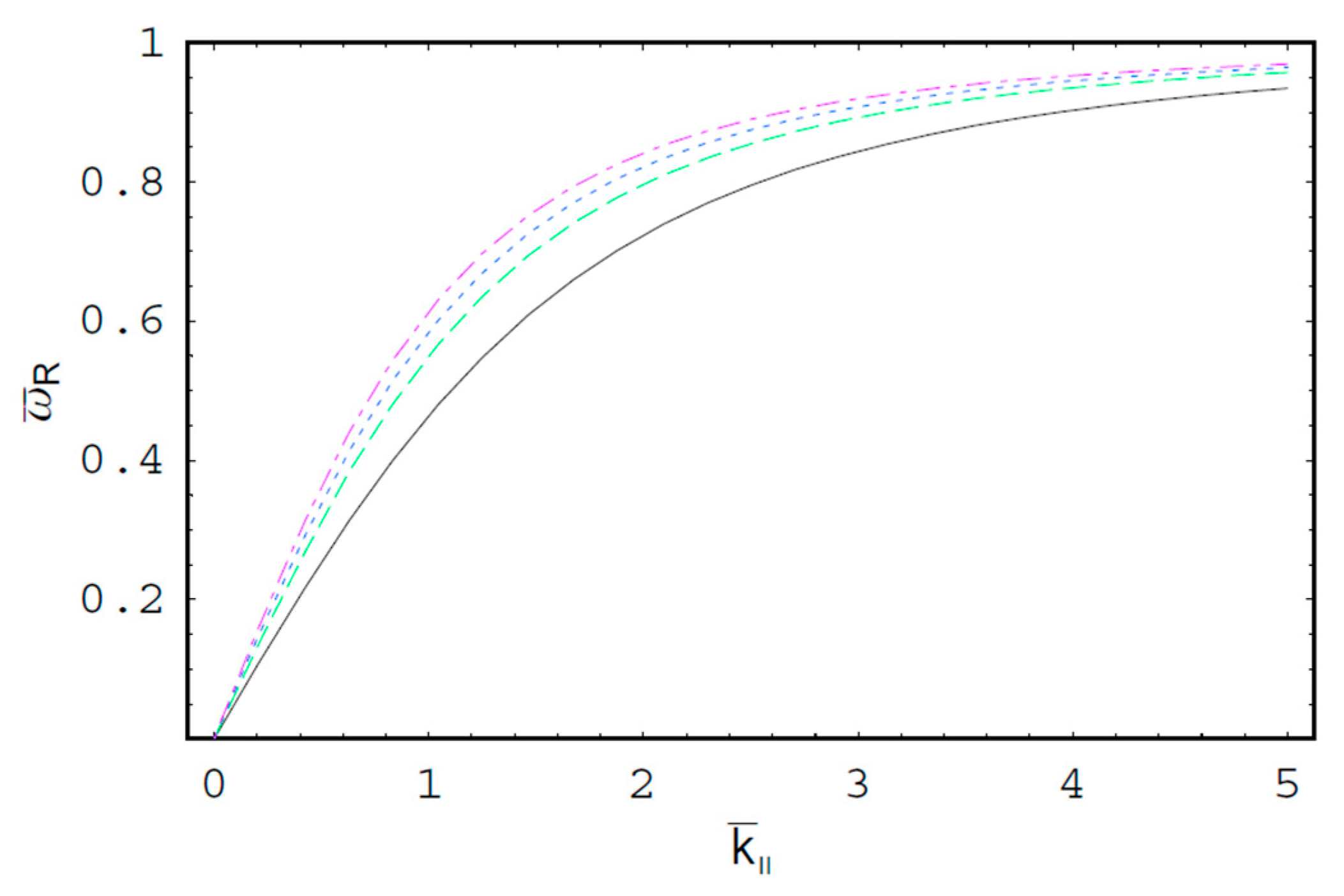
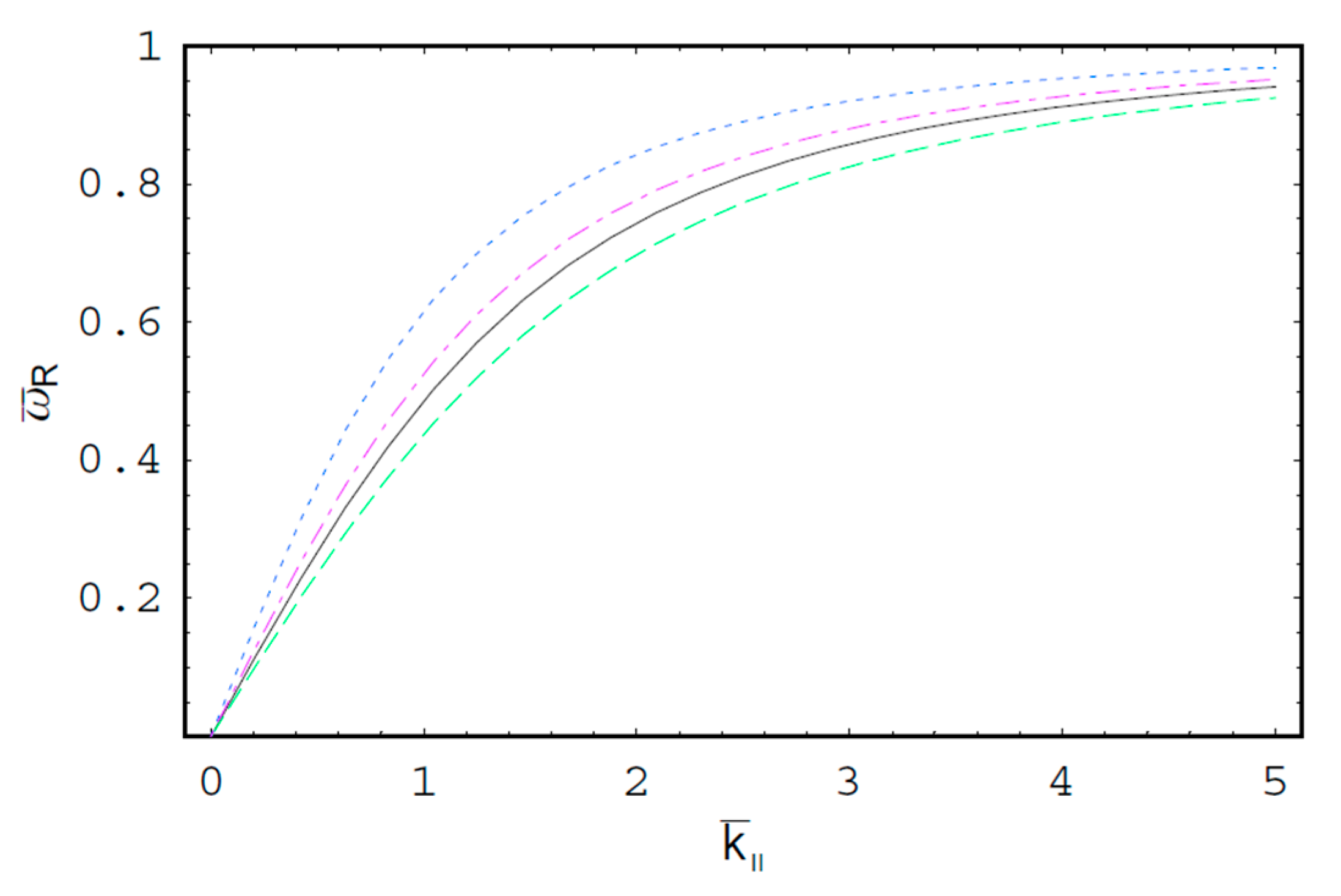
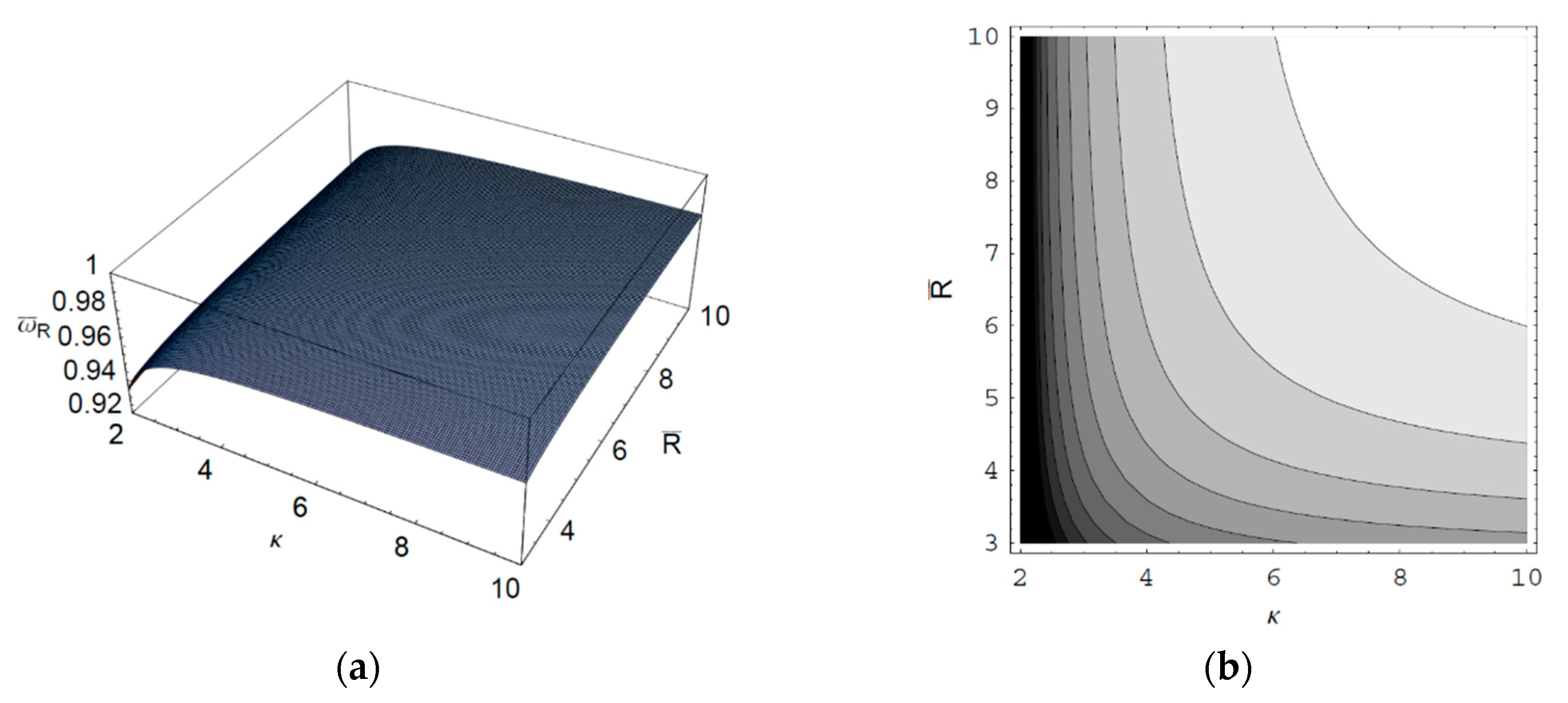
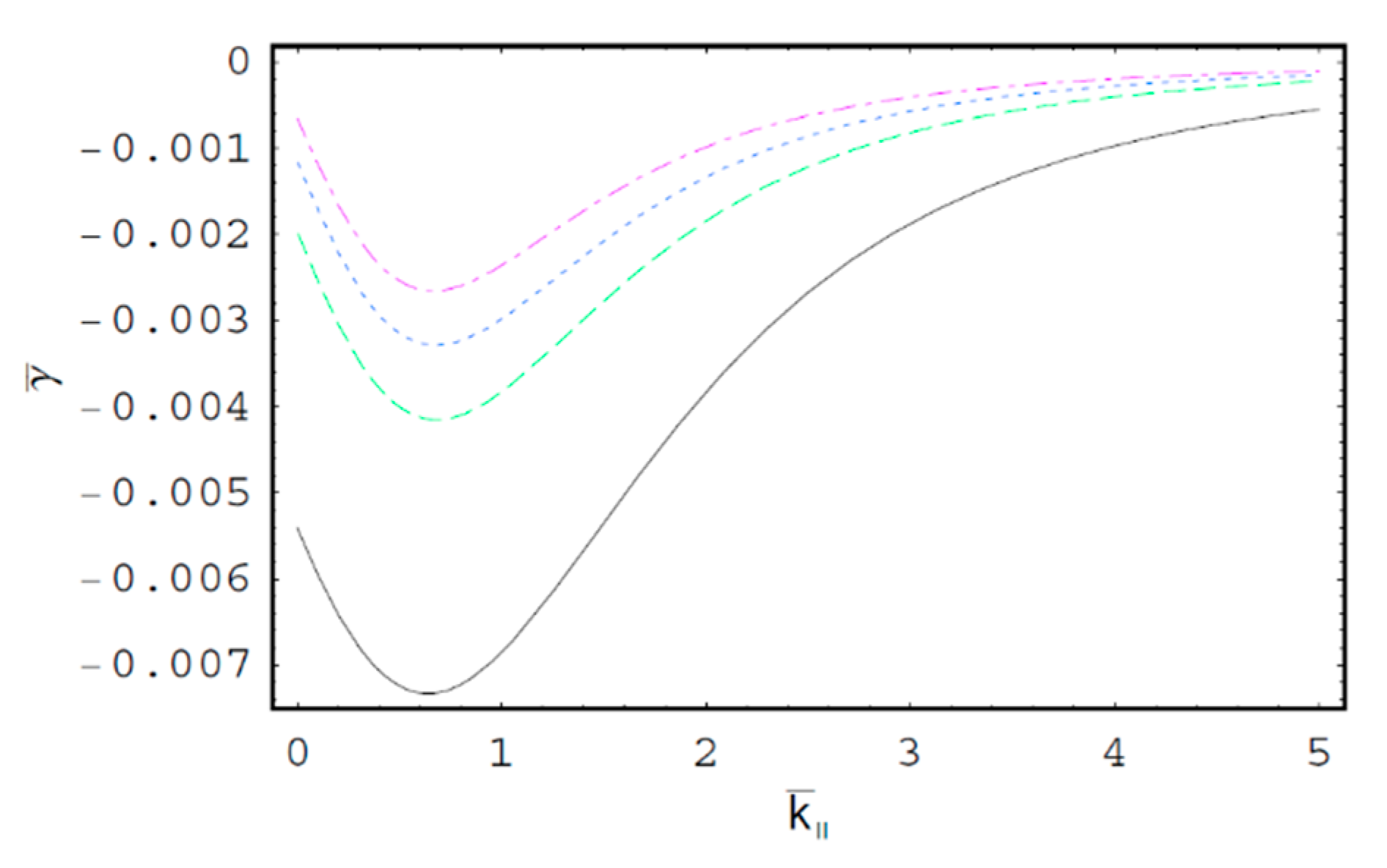
2. Theory and Calculations
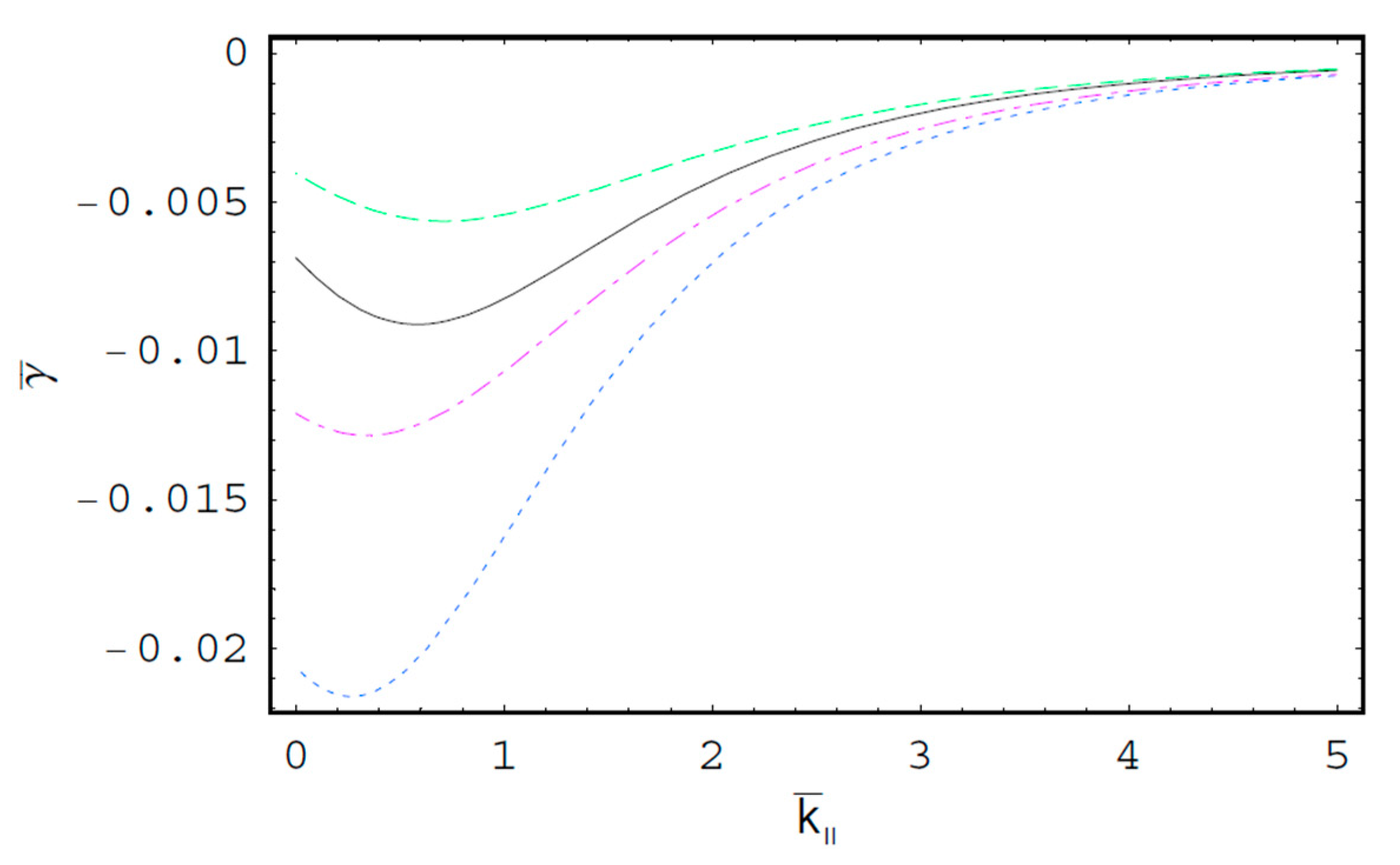
3. Discussions
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Dispersion Relation
Appendix B. Bessel Functions
References
- Gradov, O.M.; Stenflo, L. Magnetic-field generation by a finite-radius electromagnetic beam. Phys. Lett. A 1983, 95, 233–234. [Google Scholar] [CrossRef]
- Gradov, O.M.; Stenflo, L. Multisolitary plasma surface waves in the presence of an external pump field. Phys. Fluids B 1991, 3, 3201–3202. [Google Scholar] [CrossRef]
- Stenflo, L.; Gradov, O.M. Acceleration of solitary ion-acoustic surface waves. Phys. Rev. A 1991, 44, 5320–5321. [Google Scholar] [CrossRef] [PubMed]
- Gradov, O.M.; Stenflo, L. Solitary electrostatic waves in a thin plasma slab. Phys. Rev. E 1994, 50, 1695–1696. [Google Scholar] [CrossRef] [PubMed]
- Stenflo, L.; Gradov, O.M. Electron oscillations in a plasma slab. Phys. Rev. E 1998, 68, 8044–8045. [Google Scholar] [CrossRef]
- Stenflo, L.; Shukla, P.K. Dust acoustic waves in thin dusty layers. Phys. Plasmas 2000, 7, 3472–3473. [Google Scholar] [CrossRef]
- Stenflo, L.; Yu, M.Y. Oscillons at a plasma surface. Phys. Plasmas 2003, 10, 912–913. [Google Scholar] [CrossRef]
- Lee, H.J. Comment on “Kinetic theory of surface waves in plasma jets”. Phys. Plasmas 2005, 12, 094701. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.J.; Lim, Y.K. Kinetic theory of surface waves in a plasma slab. J. Korean Phys. Soc. 2007, 50, 1056–1061. [Google Scholar] [CrossRef]
- Lee, M.-J.; Jung, Y.-D. Whimsicality of multi-mode Hasegawa space-charge waves in a complex plasma containing collision-dominated electrons and streaming ions. Plasma Phys. Control. Fusion 2017, 59, 095007. [Google Scholar] [CrossRef]
- Alexandrov, A.F.; Bogdankevich, L.S.; Rukhadze, A.A. Principles of Plasma Electrodynamics; Springer: Berlin/Heidelberg, Germany, 1984; pp. 308–309. [Google Scholar]
- Aliev, Y.M.; Schlüter, H.; Shivarova, A. Guided-Wave-Produced Plasmas; Springer: Berlin/Heidelberg, Germany, 2000; pp. 49–50. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. i. small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Tsytovich, V.N. An Introduction to the Theory of Plasma Turbulence; Pergamon: Oxford, UK, 1972; pp. 14–26. [Google Scholar]
- Shukla, P.K.; Spatschek, K.-H. Shielding of a moving test charge in a turbulent plasma. Phys. Lett. A 1973, 44, 398–400. [Google Scholar] [CrossRef]
- Tegeback, R.; Stenflo, L. Test charge potentials in turbulent plasmas. Plasma Phys. 1975, 17, 991–993. [Google Scholar] [CrossRef]
- Hasegawa, A.; Mima, K.; Duong-van, M. Plasma distribution function in a superthermal radiation field. Phys. Rev. Lett. 1985, 54, 2608–2610. [Google Scholar] [CrossRef] [PubMed]
- Rubab, N.; Murtaza, G. Debye length in non-Maxwellian plasmas. Phys. Scr. 2006, 74, 145–148. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G.; Wicks, R.T. On the calculation of the effective polytropic index in space plasmas. Entropy 2020, 21, 997. [Google Scholar] [CrossRef] [Green Version]
- Nicolaou, G.; Livadiotis, G.; Wicks, R.T. On the determination of kappa distribution functions from space plasma observations. Entropy 2020, 22, 212. [Google Scholar] [CrossRef] [Green Version]
- Stix, T.H. Waves in Plasmas; Springer-Verlag: New York, NY, USA, 1992; pp. 126–128. [Google Scholar]
- Krall, N.A.; Trivelpiece, A.W. Principles of Plasma Physics; McGraw-Hill: New York, NY, USA, 1973; pp. 173–175. [Google Scholar]
- Zhang, K.-Z.; Xue, J.-K. Streaming instability in bounded three-component quantum plasmas. Phys. Plasmas 2010, 17, 032113. [Google Scholar] [CrossRef]
- Bers, A. Plasma Physics and Fusion Plasma Electrodynamics; Oxford University Press: Oxford, UK, 2016; Volume 1, pp. 1504–1512. [Google Scholar]
- Woods, L.C. Physics of Plasma; WILEY-VCH: Weinheim, Germany, 2004; pp. 106–107. [Google Scholar]
- Lee, M.-J.; Jung, Y.-D. Effect of turbulence on the dissipation of the space-charge wave in a bounded turbulent plasma column. Phys. Plasmas 2016, 23, 072107. [Google Scholar] [CrossRef]
- Swanson, D.G. Plasma Waves, 2nd ed.; Institute of Physics Publishing: Bristol, UK, 2003; pp. 216–219. [Google Scholar]
- Lee, M.-J.; Jung, Y.-D. Non-thermal Dupree diffusivity and shielding effects on atomic collisions in astrophysical turbulent plasmas. Astroparticle Phys. 2016, 74, 58–63. [Google Scholar] [CrossRef]
- Qureshi, M.N.S.; Shah, H.A.; Murtaza, G.; Schwartz, S.J.; Mahmood, F. Parallel propagating electromagnetic modes with the generalized (r, q) distribution function. Phys. Plasmas 2004, 11, 3819–3829. [Google Scholar] [CrossRef]
- Mahmoodi, J.; Shukla, P.K.; Tsintsadze, N.L.; Tskhakaya, D.D. Dispersion properties of a dusty plasma containing nonspherical rotating dust grains. Phys. Rev. Lett. 2000, 84, 2626–2629. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Kodanova, S.K.; Dzhumagulova, K.N.; Bastykova, N.K. The new method for measuring of dust particles charge in glow discharge plasma. EPL 2011, 96, 45004. [Google Scholar] [CrossRef]
- Ussenov, Y.A.; Ramazanov, T.S.; Dzhumagulova, K.N.; Dosbolayev, M.K. Application of dust grains and Langmuir probe for plasma diagnostics. EPL 2014, 105, 15002. [Google Scholar] [CrossRef]
- Akbari-Moghanjoughi, M. Generalized model screening potentials for Fermi-Dirac plasmas. Phys. Plasmas. 2016, 23, 042706. [Google Scholar] [CrossRef]
- Eliasson, B.; Akbari-Moghanjoughi, M. Finite temperature static charge screening in quantum plasmas. Phys. Lett. A 2016, 380, 2518. [Google Scholar] [CrossRef] [Green Version]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 675–739. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.-J.; Jung, Y.-D. Characteristics of Nonthermal Dupree Diffusion on Space-Charge Wave in a Kappa Distribution Plasma Column with Turbulent Diffusion. Entropy 2020, 22, 257. https://doi.org/10.3390/e22020257
Lee M-J, Jung Y-D. Characteristics of Nonthermal Dupree Diffusion on Space-Charge Wave in a Kappa Distribution Plasma Column with Turbulent Diffusion. Entropy. 2020; 22(2):257. https://doi.org/10.3390/e22020257
Chicago/Turabian StyleLee, Myoung-Jae, and Young-Dae Jung. 2020. "Characteristics of Nonthermal Dupree Diffusion on Space-Charge Wave in a Kappa Distribution Plasma Column with Turbulent Diffusion" Entropy 22, no. 2: 257. https://doi.org/10.3390/e22020257
APA StyleLee, M.-J., & Jung, Y.-D. (2020). Characteristics of Nonthermal Dupree Diffusion on Space-Charge Wave in a Kappa Distribution Plasma Column with Turbulent Diffusion. Entropy, 22(2), 257. https://doi.org/10.3390/e22020257




