Theory of Quantum Path Entanglement and Interference with Multiplane Diffraction of Classical Light Sources
Abstract
1. Introduction
- introduction and operator theory modeling of two novel quantum resources, i.e., QPE and QPI, denoting temporal correlations and the interference among quantum trajectories, respectively, in MPD while utilizing the tensor product structure for future quantum computing and communication architectures and foundational QM studies;
- theoretical modeling and numerical analysis of MPD setup for the violation of LGI, with the ambiguous and no-signaling forms recently proposed by Emary in Reference [16], reaching of correlation amplitude numerically obtained for three-time formulation while leaving the maximization of the violation to the boundary levels as an open issue;
- a novel setup, i.e., MPD, violating the ambiguous form of LGI with classical light sources complementing the recent experiment utilizing linear polarization degree of freedom of the classical light [19] while MPD setup with remarkably low complexity design utilizing classical light sources and photon-counting intensity detection;
- theoretical modeling and numerical analysis of counterintuitive properties and examples of the interference among MPD-based Feynman paths denoted as QPI promising to be easily verified experimentally in future studies;
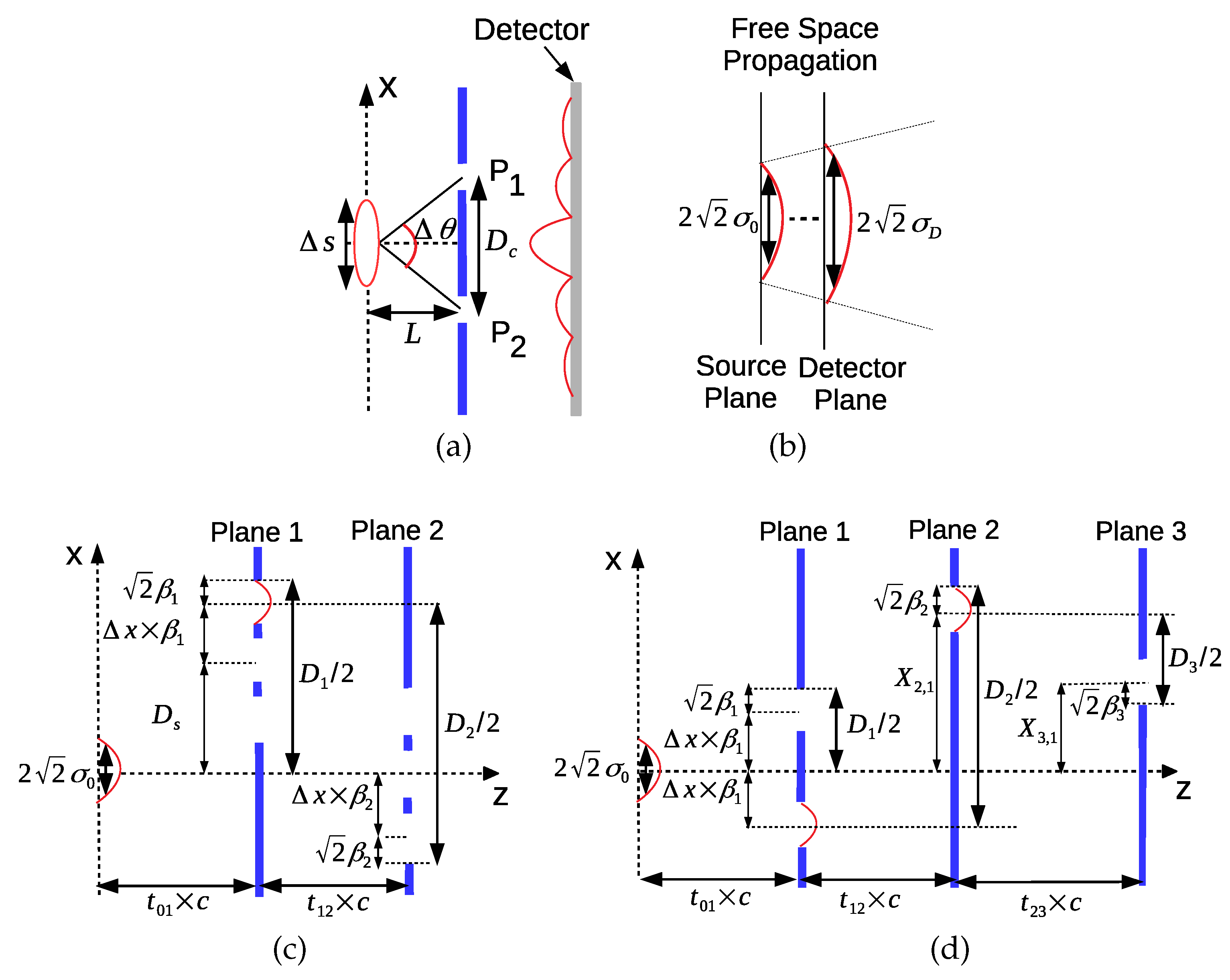
- the modeling and numerical analysis of the coherence properties of the light sources in terms of spatial and temporal dimensions while discussing design issues for MPD setup with coherent light sources; and
- discussion for future applications of QPE and QPI as quantum resources and experimental implementations.
2. Results
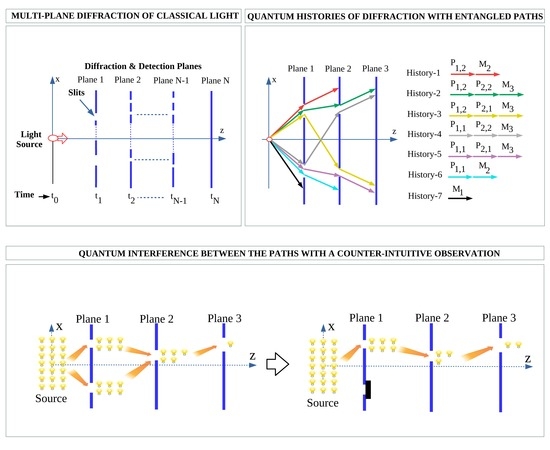
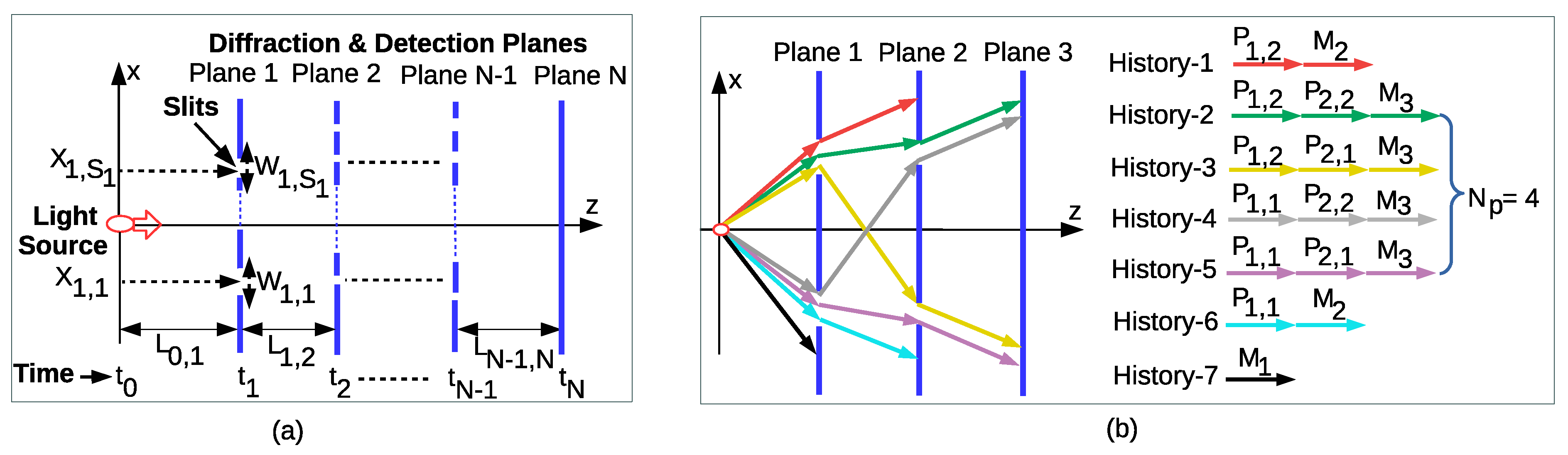
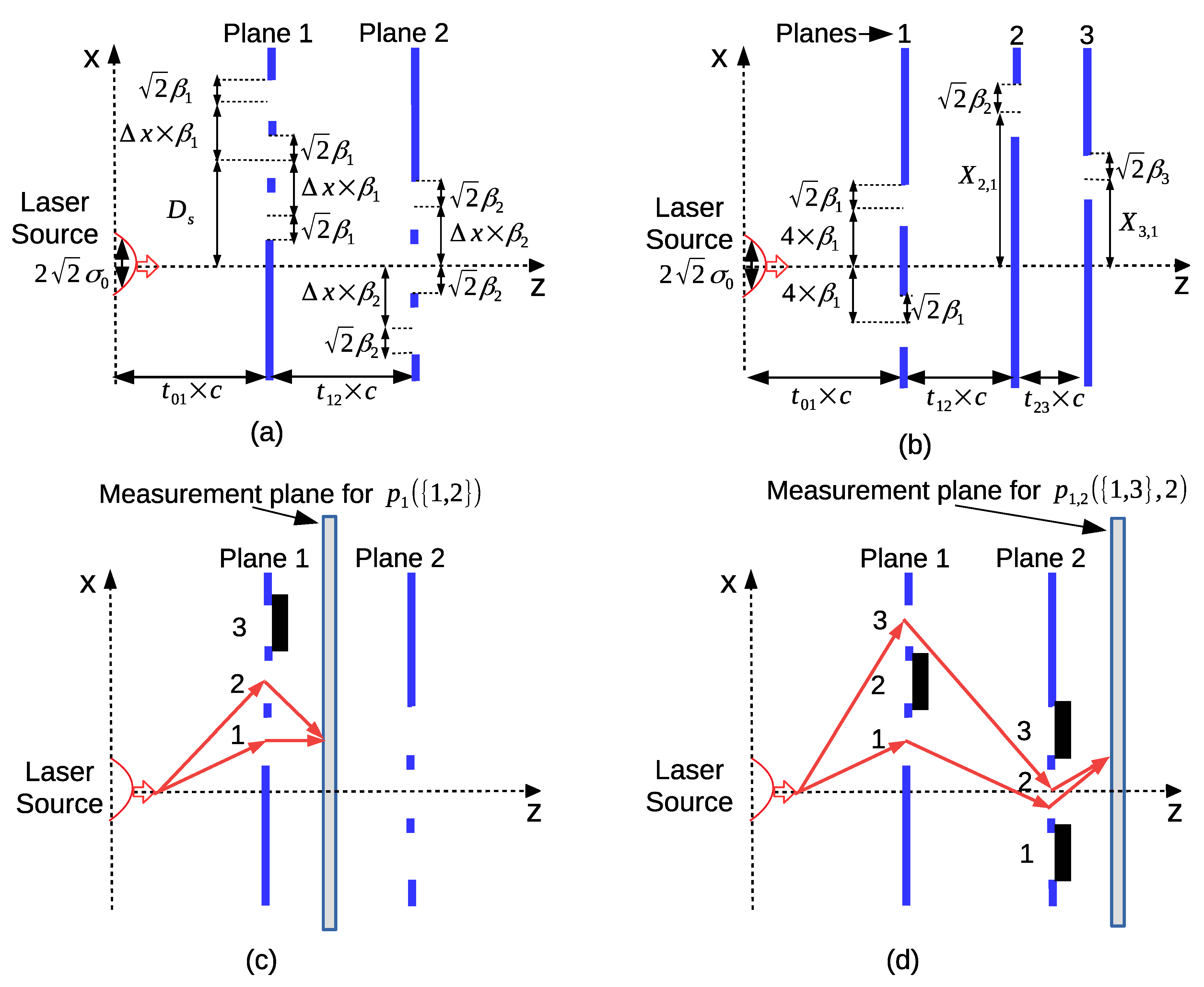
2.1. MPD Setup for Quantum Temporal Correlations
2.2. Diffractive Projection and Measurement Operators
2.3. History State Modeling of QPE
Event Probabilities
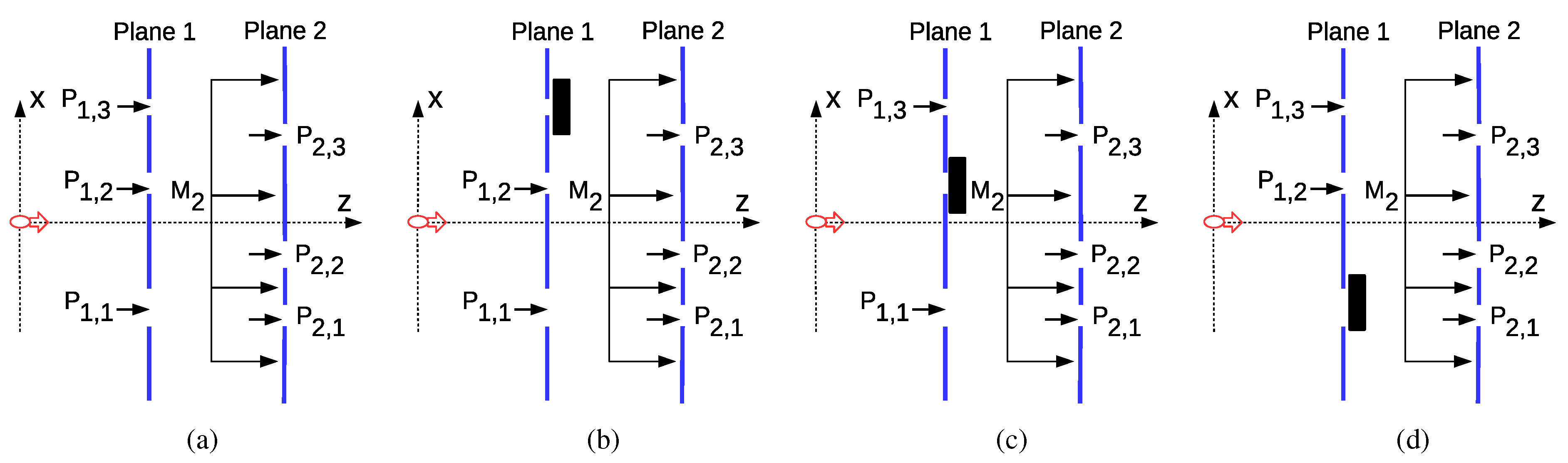
2.4. Modeling of the Violation of LGI in MPD
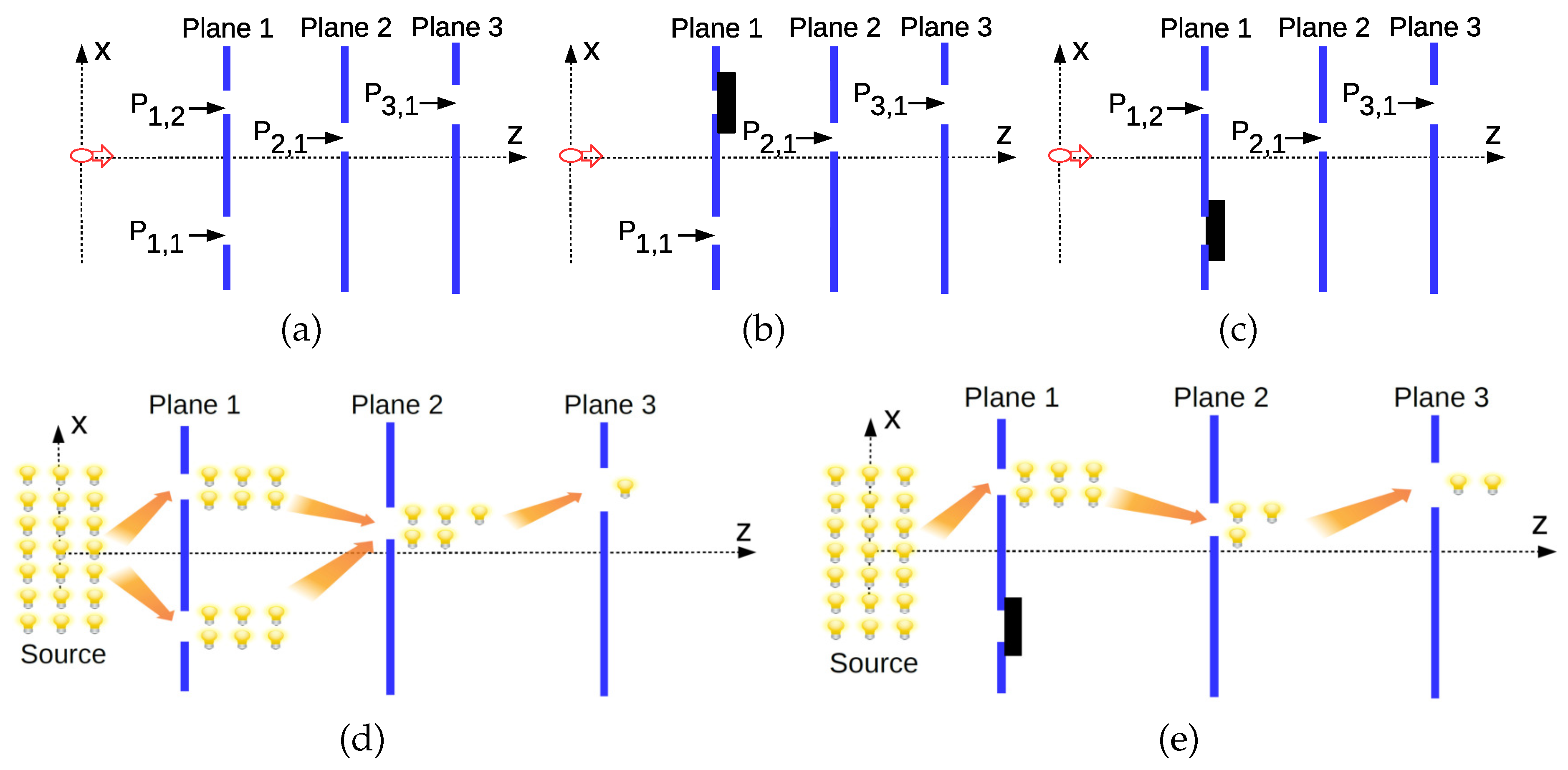
2.5. Modeling of QPI
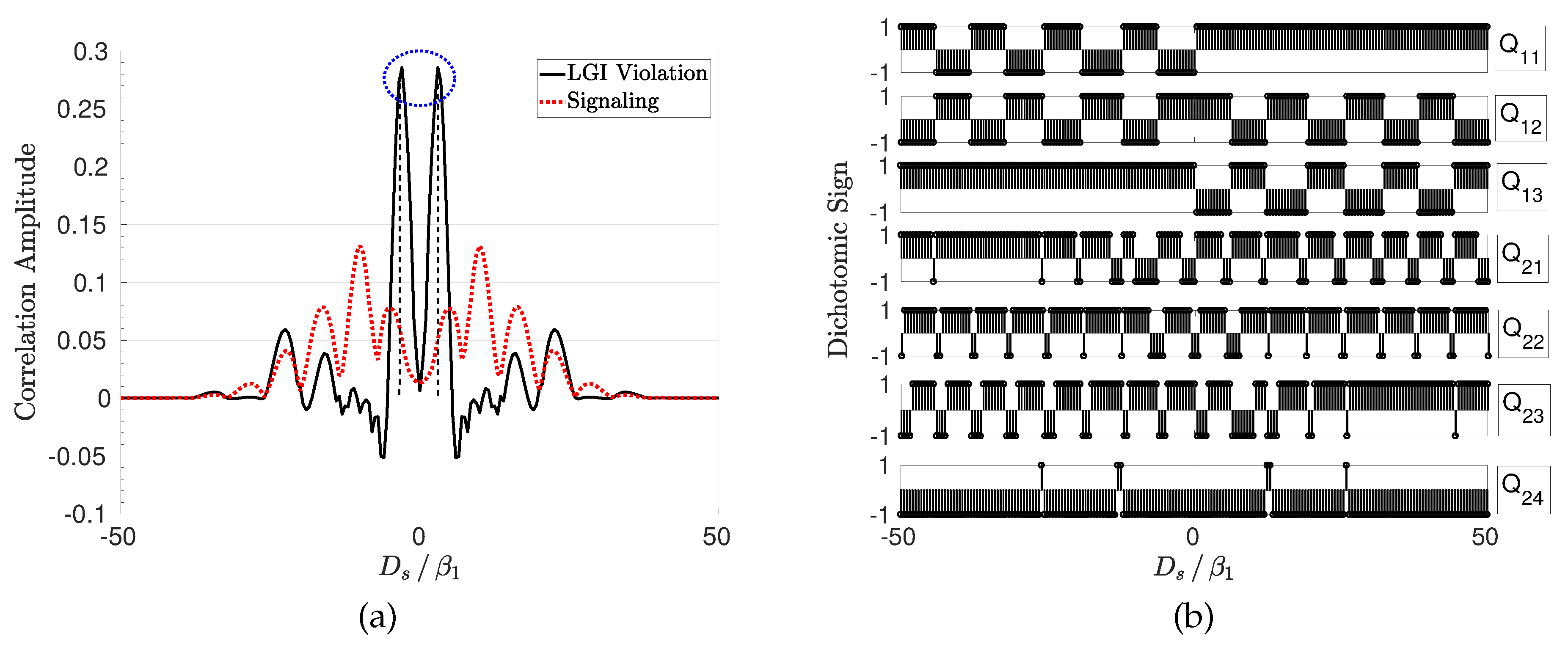
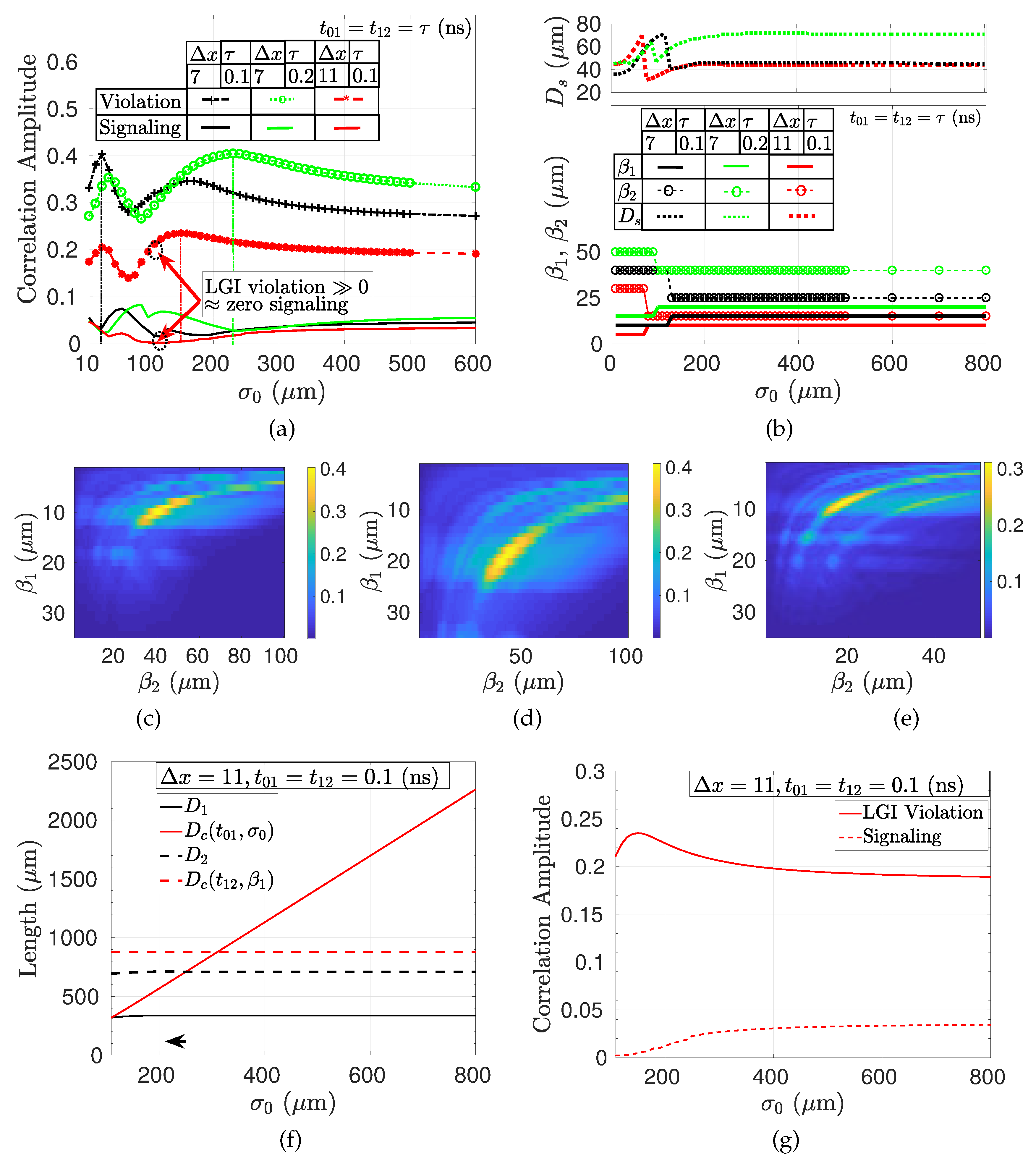
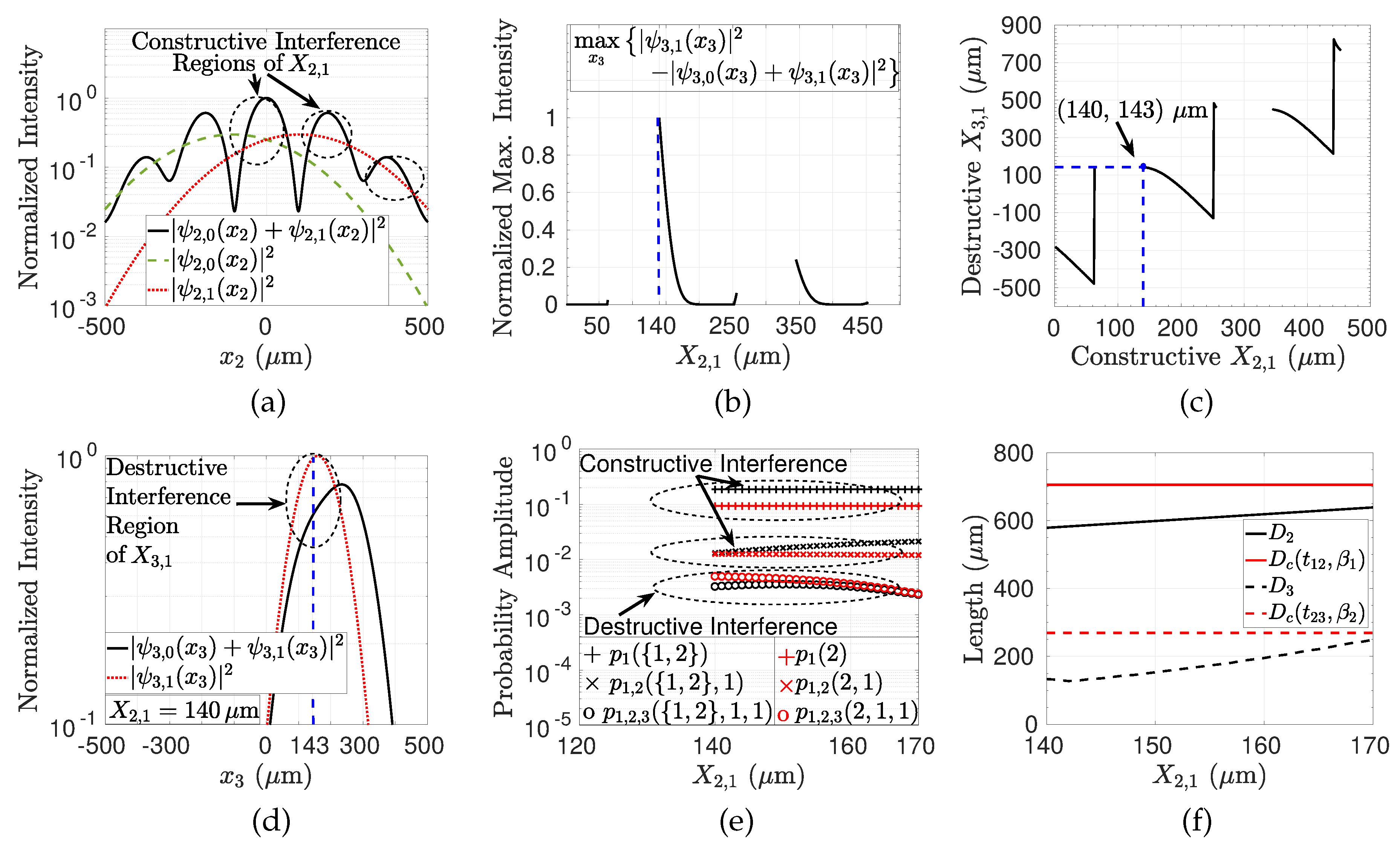
2.6. Numerical Results
2.6.1. Violation of LGI
2.6.2. QPI Analysis
3. Discussion and Conclusions
4. Methods
4.1. Parameters for FPI Modeling of the Violation of LGI
4.2. Temporal and Spatial Coherence of the Light Sources
Funding
Conflicts of Interest
Abbreviations
| MPD | Multiplane diffraction |
| QC | Quantum computing |
| QM | Quantum mechanical |
| QPE | Quantum path entanglement |
| QPI | Quantum path interference |
| FPI | Feynman’s path integral |
| LGI | Leggett-Garg Inequality |
| MR | Macroscopic realism |
| NIM | Non-invasive measurability |
| SIT | Signaling-in-time |
| GHZ | Greenberger-Horne-Zeilinger |
| FWHM | Full width half maximum |
References
- Cotler, J.; Wilczek, F. Entangled histories. Phys. Scr. 2016, 2016, 014004. [Google Scholar] [CrossRef][Green Version]
- Feynman, R.P.; Hibbs, A.R.; Styer, D.F. Quantum Mechanics and Path Integrals; Dover: Mineola, NY, USA, 2010. [Google Scholar]
- Griffiths, R.B. Consistent histories and the interpretation of quantum mechanics. J. Stat. Phys. 1984, 36, 219–272. [Google Scholar] [CrossRef]
- Griffiths, R.B. Consistent interpretation of quantum mechanics using quantum trajectories. Phys. Rev. Lett. 1993, 70, 2201. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, R.B. Consistent Quantum Theory; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Aharonov, Y.; Vaidman, L. The two-state vector formalism: An updated review. In Time in Quantum Mechanics, 2nd ed.; Muga, G., Sala Mayato, R., Egusquiza, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1, pp. 399–447. [Google Scholar]
- Nowakowski, M.; Cohen, E.; Horodecki, P. Entangled histories vs. the two-state-vector formalism-towards a better understanding of quantum temporal correlations. arXiv 2018, arXiv:1803.11267. [Google Scholar]
- Gulbahar, B. Quantum path computing: Computing architecture with propagation paths in multiple plane diffraction of classical sources of fermion and boson particles. Quantum Inf. Process. 2019, 18, 167. [Google Scholar] [CrossRef]
- Gulbahar, B. Quantum path computing and communications with Fourier optics. arXiv 2019, arXiv:1908.02274. [Google Scholar]
- Gulbahar, B.; Memisoglu, G. Quantum spatial modulation of optical channels: Quantum boosting in spectral efficiency. IEEE Comm. Lett. 2019, 23, 2026–2030. [Google Scholar] [CrossRef]
- Cotler, J.; Duan, L.M.; Hou, P.Y.; Wilczek, F.; Xu, D.; Yin, Z.Q.; Zu, C. Experimental test of entangled histories. Ann. Phys. 2017, 387, 334–347. [Google Scholar] [CrossRef]
- Leggett, A.J.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857. [Google Scholar] [CrossRef]
- Emary, C.; Lambert, N.; Nori, F. Leggett–Garg inequalities. Rep. Prog. Phys. 2013, 77, 016001. [Google Scholar] [CrossRef]
- Emary, C.; Lambert, N.; Nori, F. Leggett-Garg inequality in electron interferometers. Phys. Rev. B 2012, 86, 235447. [Google Scholar] [CrossRef]
- Wilde, M.M.; Mizel, A. Addressing the clumsiness loophole in a Leggett-Garg test of macrorealism. Found. Phys. 2012, 42, 256–265. [Google Scholar] [CrossRef]
- Emary, C. Ambiguous measurements, signaling, and violations of Leggett-Garg inequalities. Phys. Rev. A 2017, 96, 042102. [Google Scholar] [CrossRef]
- Katiyar, H.; Brodutch, A.; Lu, D.; Laflamme, R. Experimental violation of the Leggett–Garg inequality in a three-level system. New J. Phys. 2017, 19, 023033. [Google Scholar] [CrossRef]
- Morikoshi, F. Information-theoretic temporal Bell inequality and quantum computation. Phys. Rev. A 2006, 73, 052308. [Google Scholar] [CrossRef]
- Zhang, X.; Li, T.; Yang, Z.; Zhang, X. Experimental observation of the Leggett-Garg inequality violation in classical light. J. Opt. 2018, 21, 015605. [Google Scholar] [CrossRef]
- Wang, K.; Emary, C.; Zhan, X.; Bian, Z.; Li, J.; Xue, P. Enhanced violations of Leggett-Garg inequalities in an experimental three-level system. Opt. Express 2017, 25, 31462–31470. [Google Scholar] [CrossRef]
- Xu, J.-S.; Li, C.F.; Zou, X.B.; Guo, G.C. Experimental violation of the Leggett-Garg inequality under decoherence. Sci. Rep. 2011, 1, 101. [Google Scholar] [CrossRef]
- Asano, M.; Hashimoto, T.; Khrennikov, A.; Ohya, M.; Tanaka, Y. Violation of contextual generalization of the Leggett-Garg inequality for recognition of ambiguous figures. Phys. Scr. 2014, T163, 014006. [Google Scholar] [CrossRef]
- Losada, M.; Laura, R. Generalized contexts and consistent histories in quantum mechanics. Ann. Phys. 2014, 344, 263–274. [Google Scholar] [CrossRef]
- Howard, M.; Wallman, J.; Veitch, V.; Emerson, J. Contextuality supplies the ‘magic’ for quantum computation. Nature 2014, 510, 351–355. [Google Scholar] [CrossRef]
- Zavatta, A.; Viciani, S.; Bellini, M. Quantum-to-classical transition with single-photon-added coherent states of light. Science 2004, 306, 660–662. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J. Quantum Theory of Optical Coherence: Selected Papers and Lectures; John Wiley & Sons: Weinhaim, Germany, 2007. [Google Scholar]
- Chen, Z.; Beierle, P.; Batelaan, H. Spatial correlation in matter-wave interference as a measure of decoherence, dephasing, and entropy. Phys. Rev. A 2018, 97, 043608. [Google Scholar] [CrossRef]
- DiVincenzo, D.; Terhal, B. Decoherence: The obstacle to quantum computation. Phys. World 1998, 11, 53. [Google Scholar] [CrossRef]
- da Paz, I.; Vieira, C.H.S.; Ducharme, R.; Cabral, L.A.; Alexander, H.; Sampaio, M.D.R. Gouy phase in nonclassical paths in a triple-slit interference experiment. Phys. Rev. A 2016, 93, 033621. [Google Scholar] [CrossRef]
- Santos, E.A.; Castro, F.; Torres, R. Huygens-Fresnel principle: Analyzing consistency at the photon level. Phys. Rev. A 2018, 97, 043853. [Google Scholar] [CrossRef]
- Sawant, R.; Samuel, J.; Sinha, A.; Sinha, S.; Sinha, U. Nonclassical paths in quantum interference experiments. Phys. Rev. Lett. 2014, 113, 120406. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform with Applications in Optics and Signal Processing; John Wiley and Sons: Chichester, UK, 2001. [Google Scholar]
- Dowker, H.; Halliwell, J.J. Quantum mechanics of history: The decoherence functional in quantum mechanics. Phys. Rev. D 1992, 46, 1580. [Google Scholar] [CrossRef]
- Meng, Z.; Stewart, G.; Whitenett, G. Stable single-mode operation of a narrow-linewidth, linearly polarized, erbium-fiber ring laser using a saturable absorber. J. Lightw. Technol. 2006, 24, 2179. [Google Scholar] [CrossRef]
- Sinha, A.; Vijay, A.H.; Sinha, U. On the superposition principle in interference experiments. Sci. Rep. 2015, 5, 10304. [Google Scholar] [CrossRef]
- Magana-Loaiza, O.S.; De Leon, I.; Mirhosseini, M.; Fickler, R.; Safari, A.; Mick, U.; McIntyre, B.; Banzer, P.; Rodenburg, B.; Leuchs, G.; et al. Exotic looped trajectories of photons in three-slit interference. Nat. Commun. 2016, 7, 13987. [Google Scholar] [CrossRef]
- Gagnon, E.; Brown, C.D.; Lytle, A.L. Effects of detector size and position on a test of Born’s rule using a three-slit experiment. Phys. Rev. A 2014, 90, 013832. [Google Scholar] [CrossRef]
- Brukner, C.; Taylor, S.; Cheung, S.; Vedral, V. Quantum entanglement in time. arXiv 2004, arXiv:1701.08116. [Google Scholar]
- Aharonov, Y.; Popescu, S.; Tollaksen, J.; Vaidman, L. Multiple-time states and multiple-time measurements in quantum mechanics. Phys. Rev. A 2009, 79, 052110. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Hartle, J.B. Alternative decohering histories in quantum mechanics. In Proceedings of the 25th International Conference on High Energy Physics, Singapore, 2–8 August 1990. [Google Scholar]
- Omnès, R. Interpretation of quantum mechanics. Phys. Lett. A 1987, 125, 169–172. [Google Scholar] [CrossRef]
- Isham, C.J. Quantum logic and the histories approach to quantum theory. J. Math. Phys. 1994, 35, 2157–2185. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Coherence properties of optical fields. Rev. Mod. Phys. 1965, 37, 231. [Google Scholar] [CrossRef]
- Akcay, C.; Parrein, P.; Rolland, J.P. Estimation of longitudinal resolution in optical coherence imaging. Appl. Opt. 2002, 41, 5256–5262. [Google Scholar] [CrossRef] [PubMed]
- Latychevskaia, T. Spatial coherence of electron beams from field emitters and its effect on the resolution of imaged objects. Ultramicroscopy 2017, 175, 121–129. [Google Scholar] [CrossRef]
- Zernike, F. The concept of degree of coherence and its application to optical problems. Physica 1938, 5, 785–795. [Google Scholar] [CrossRef]
| ID | Property | Value | ID | Property | Value |
|---|---|---|---|---|---|
| (m) | |||||
| ; | ; (m) | (m) | |||
| (ns) | (ns) | , , | |||
| , (m) | , | , , (m) | 25, 35, 45 | ||
| (m) | (m) | 200 |
| Formula | Formula | Formula | |||
|---|---|---|---|---|---|
| Formula | Formula | Formula | |||
|---|---|---|---|---|---|
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulbahar, B. Theory of Quantum Path Entanglement and Interference with Multiplane Diffraction of Classical Light Sources. Entropy 2020, 22, 246. https://doi.org/10.3390/e22020246
Gulbahar B. Theory of Quantum Path Entanglement and Interference with Multiplane Diffraction of Classical Light Sources. Entropy. 2020; 22(2):246. https://doi.org/10.3390/e22020246
Chicago/Turabian StyleGulbahar, Burhan. 2020. "Theory of Quantum Path Entanglement and Interference with Multiplane Diffraction of Classical Light Sources" Entropy 22, no. 2: 246. https://doi.org/10.3390/e22020246
APA StyleGulbahar, B. (2020). Theory of Quantum Path Entanglement and Interference with Multiplane Diffraction of Classical Light Sources. Entropy, 22(2), 246. https://doi.org/10.3390/e22020246