Musical Collaboration in Rhythmic Improvisation
Abstract
1. Introduction
2. Materials and Methods
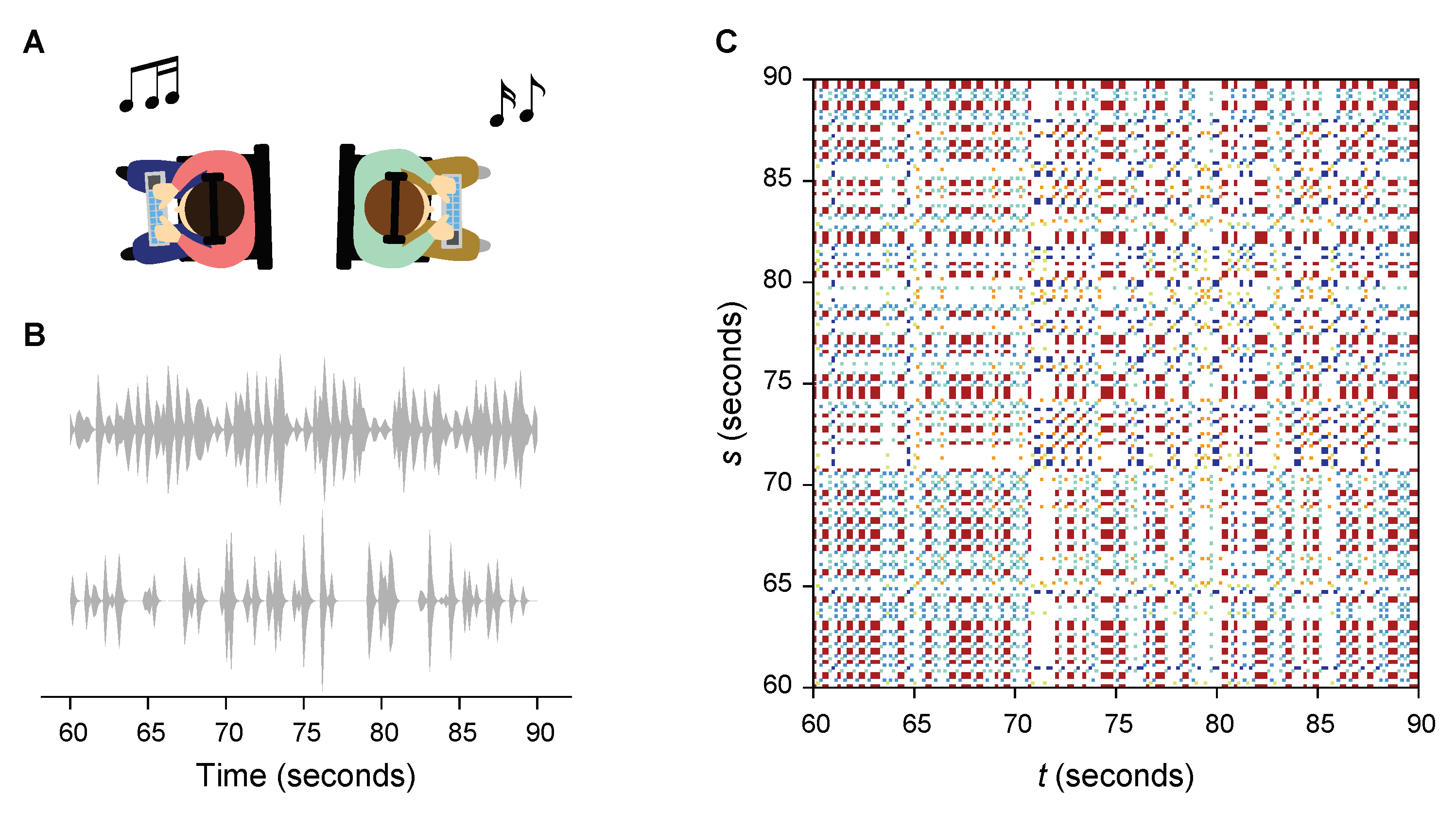
2.1. Experiment Setup
2.2. Data Collection
2.3. Symbolic-Recurrence Quantification
2.4. Analysis
3. Results and Discussion
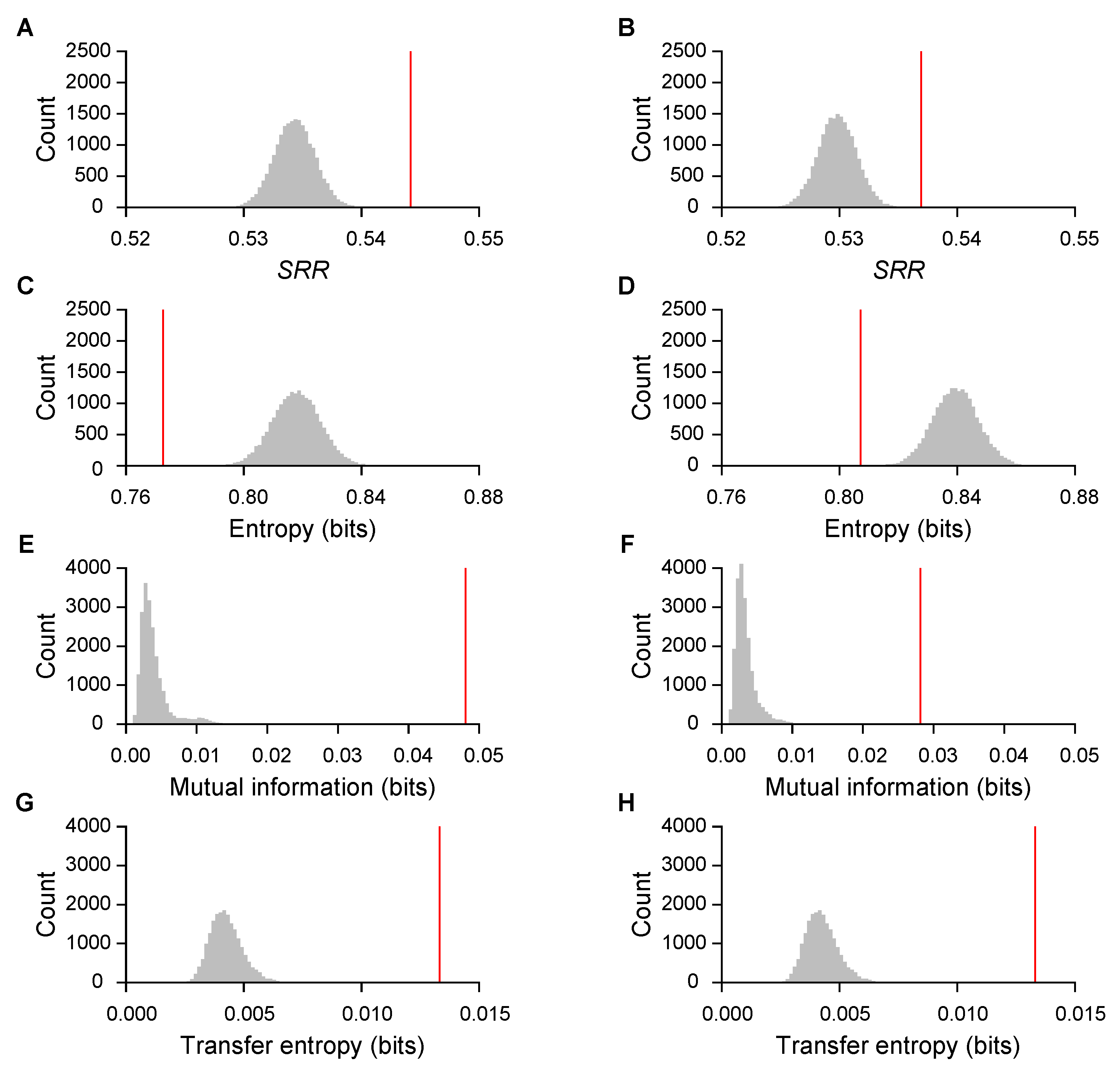
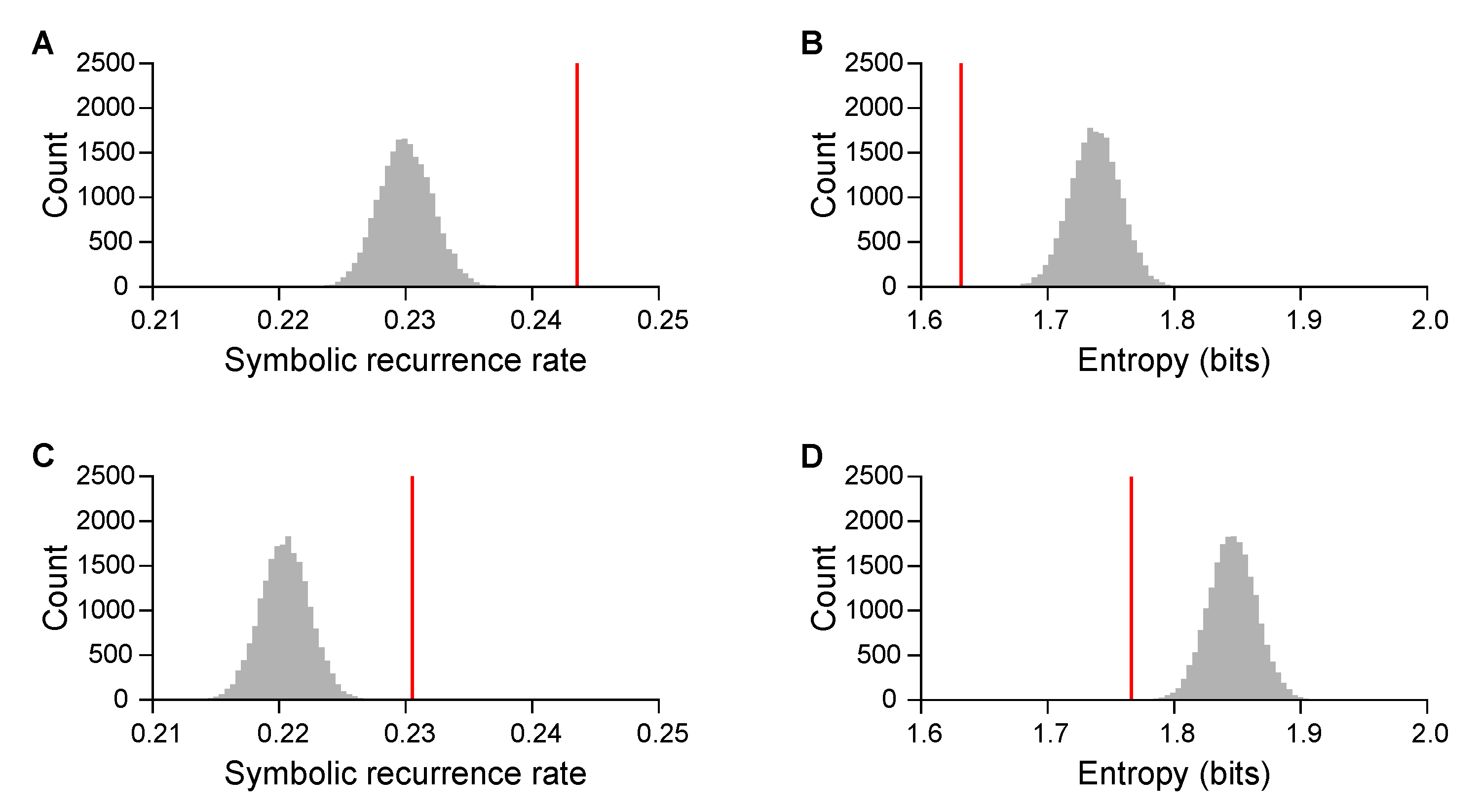
3.1. Symbolic-Recurrence Quantification of Music
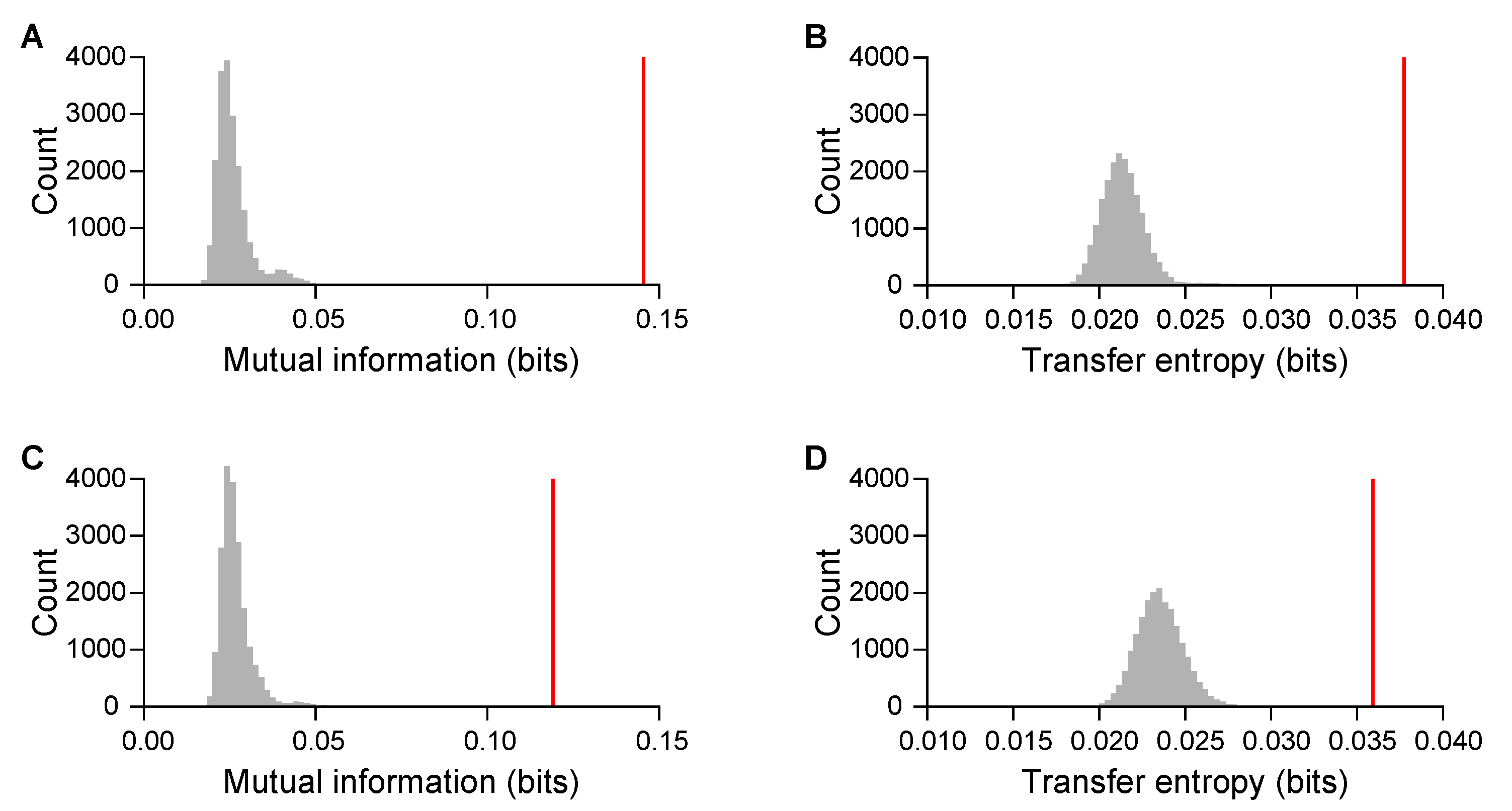
3.2. Information Sharing and Transfer on Symbolic Recurrence
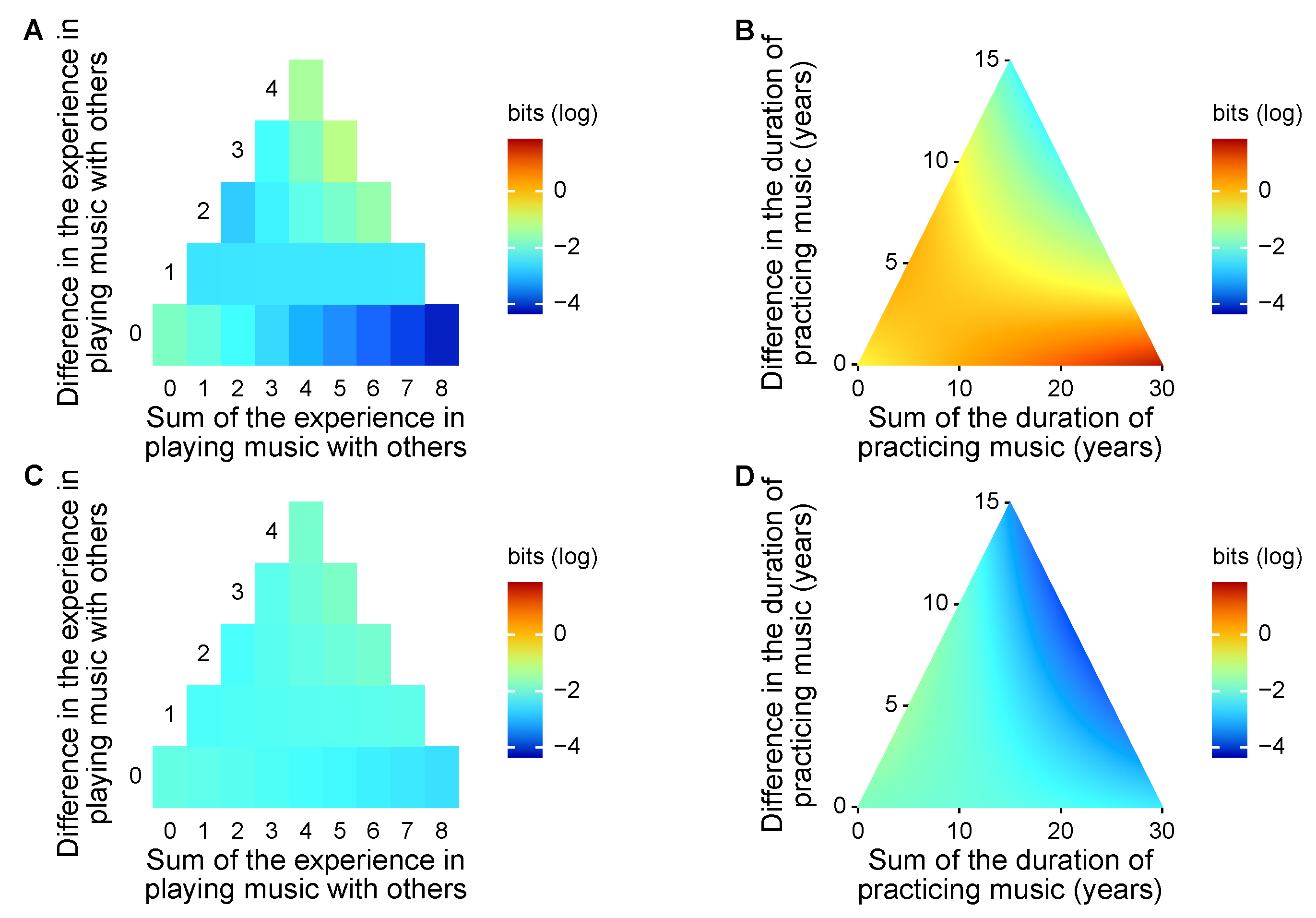
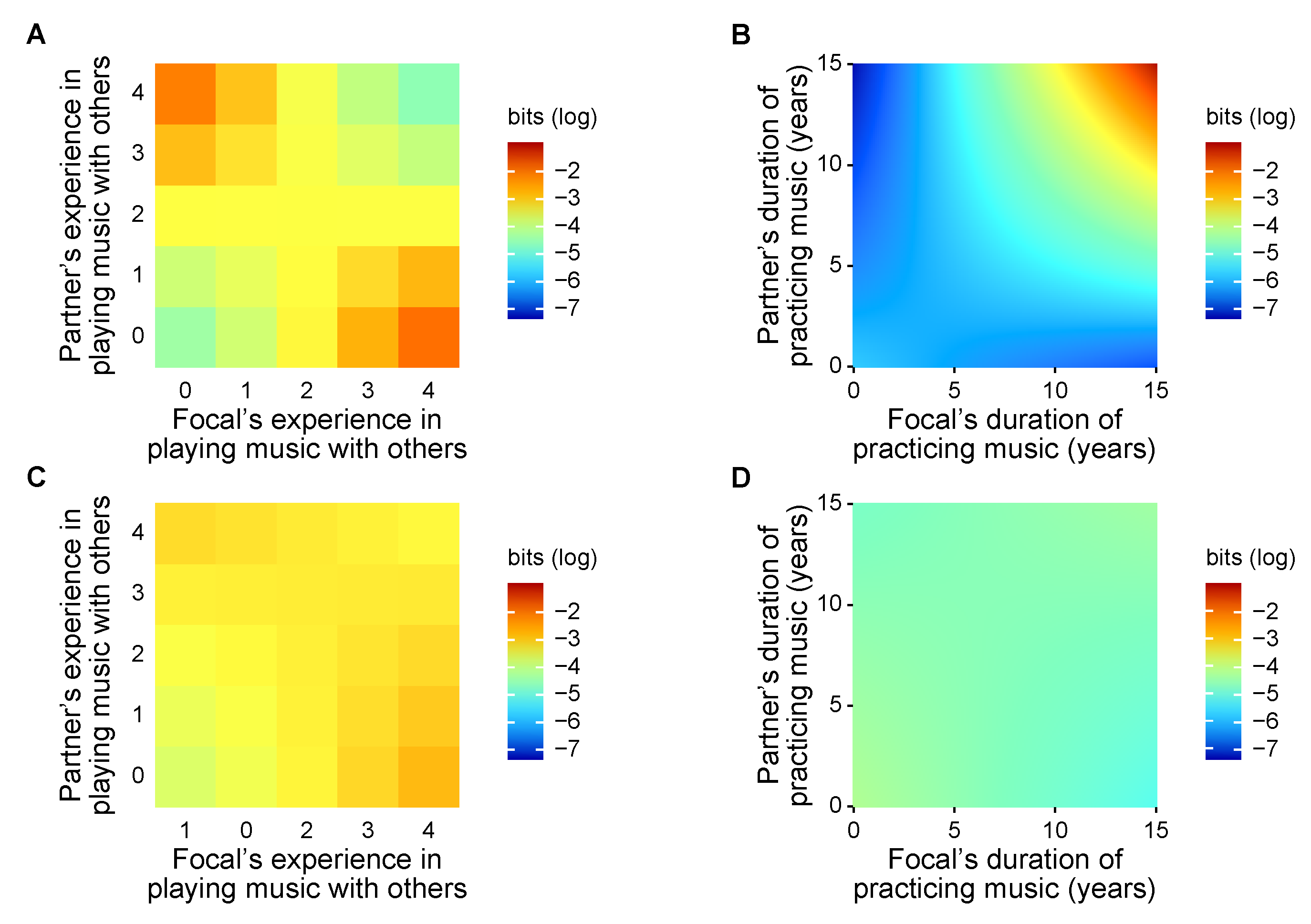
3.3. Effects of Pair and Individual Traits on Information Sharing and Transfer
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
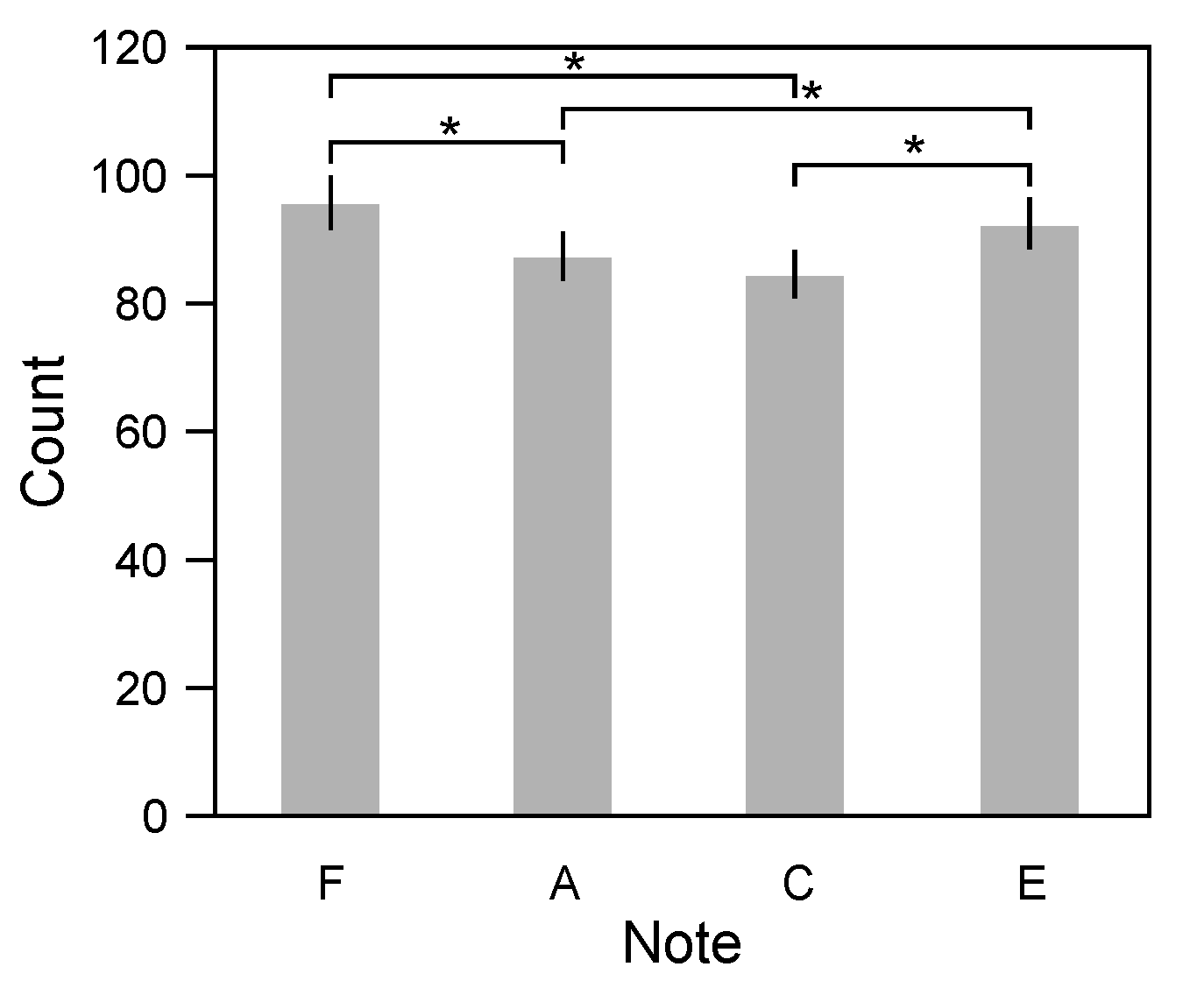
Appendix A.1. Preference of Notes Played by Participants
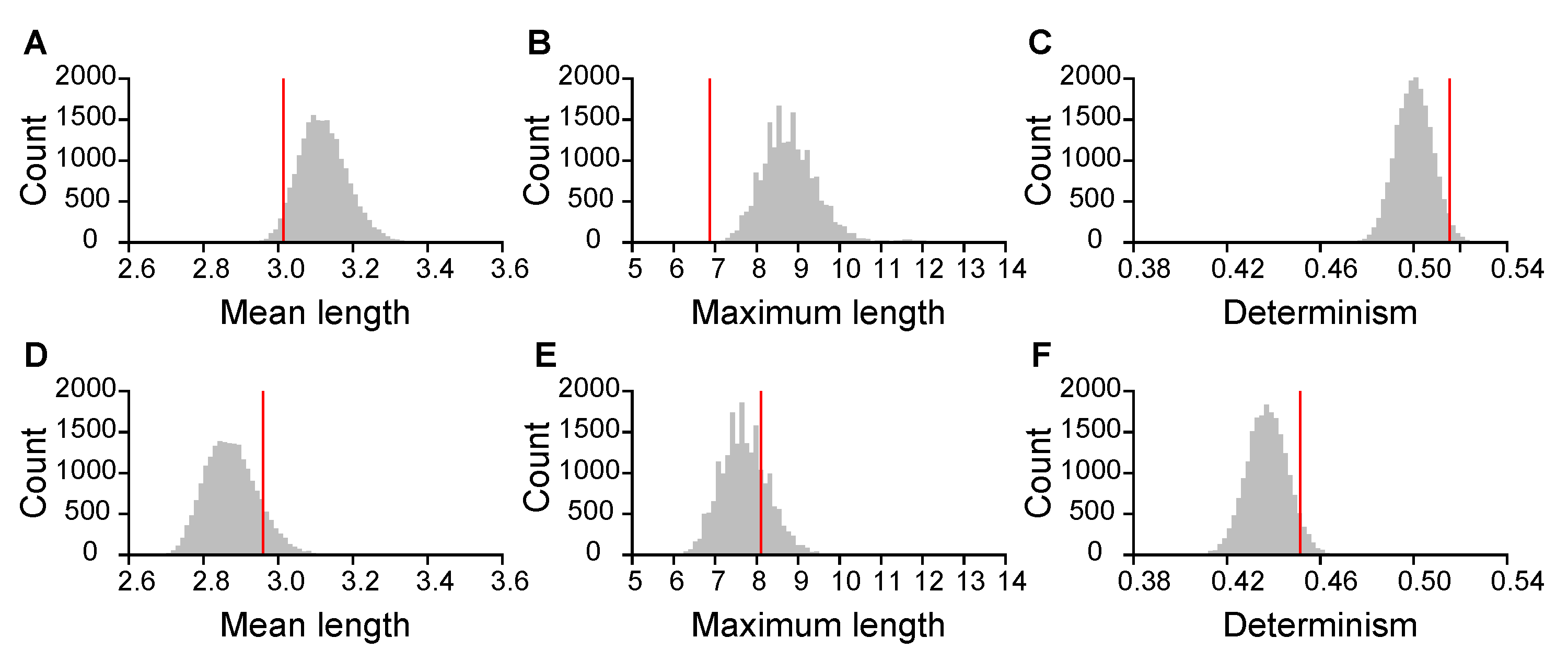
Appendix A.2. Other Recurrence Metrics on Music
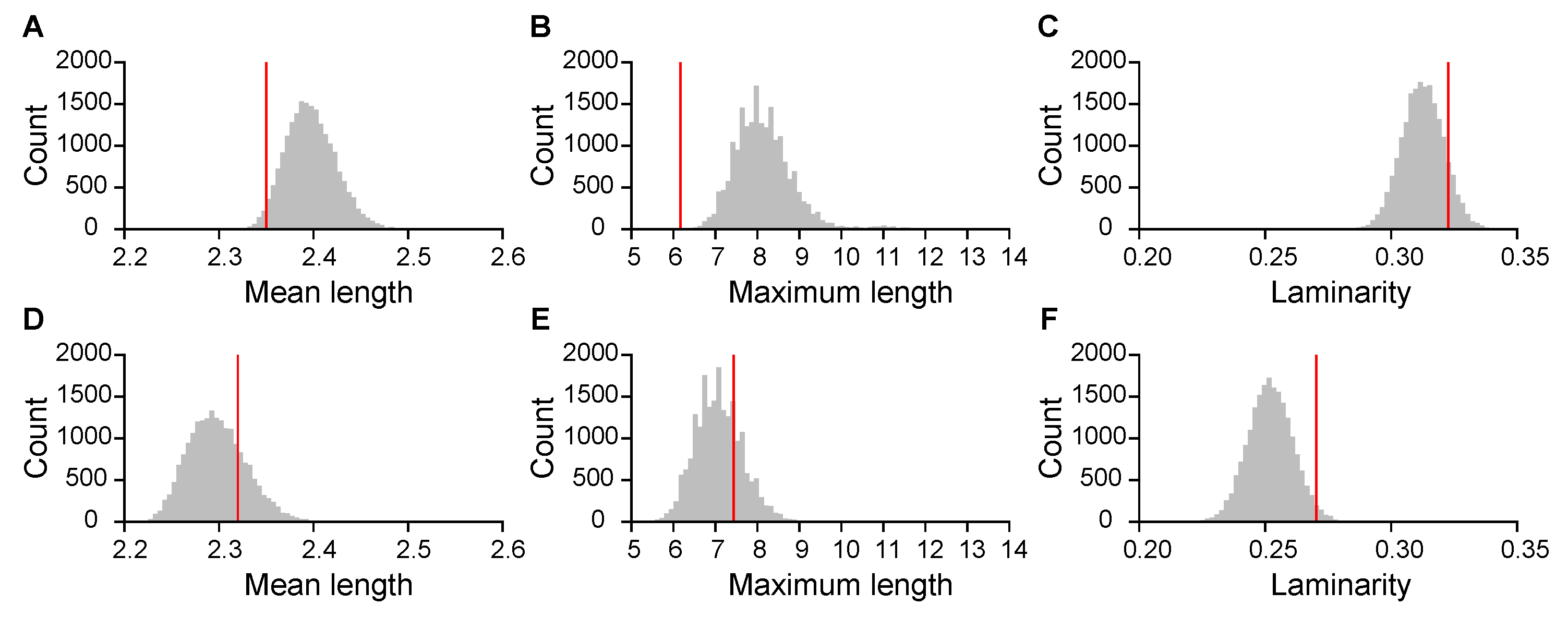
Appendix A.3. Effect of Downsampling Rate on Recurrence Metrics
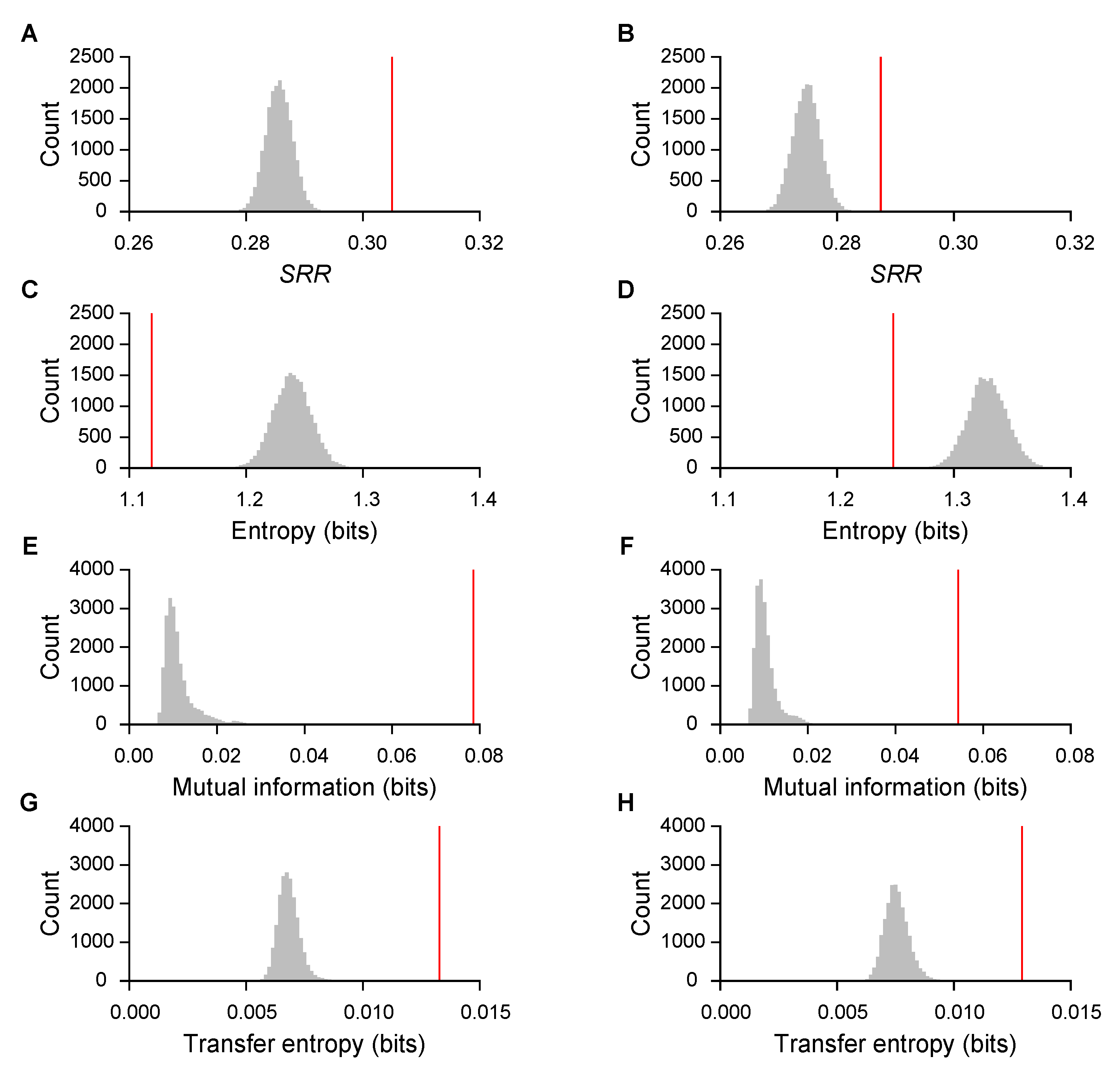
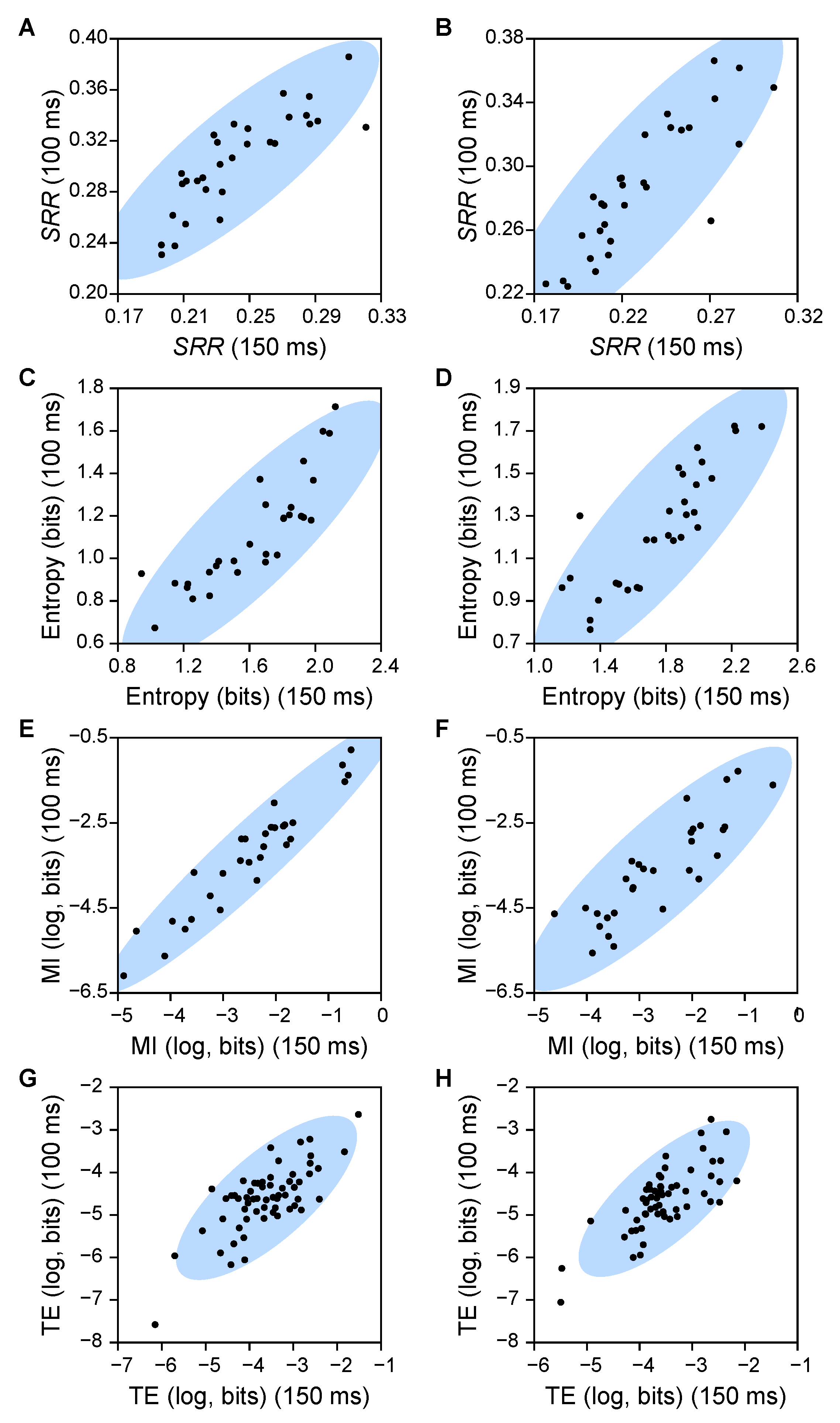
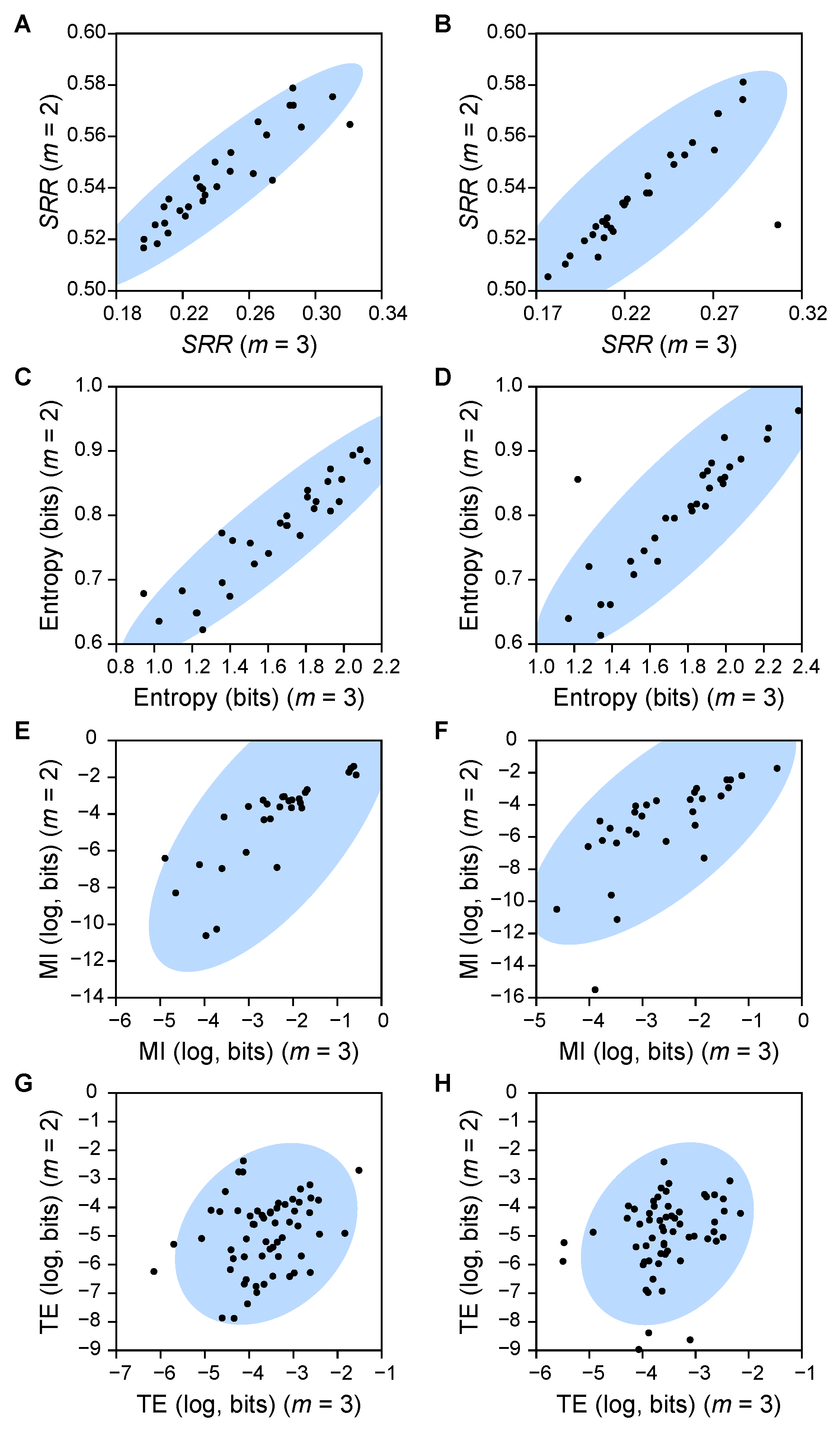
Appendix A.4. Effect of m on Recurrence Metrics
References
- Wallin, N.L.; Merker, B.; Brown, S. The Origins of Music; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Bowman, W.D. Philosophical Perspectives on Music; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Craft, R. Conversations with Igor Stravinsky; Faber & Faber: London, UK, 2013. [Google Scholar]
- Lendvai, E. Béla Bartók: An Analysis of His Music; Stanmore Press: London, UK, 1971. [Google Scholar]
- Foote, J. Visualizing music and audio using self-similarity. In Proceedings of the Seventh ACM International Conference on Multimedia, Orlando, FL, USA, 30 October–5 November 1999; ACM Multimedia: New York, NY, USA, 1999; pp. 77–80. [Google Scholar]
- Serrà, J.; Carlos, A.; Andrzejak, R.G. Nonlinear audio recurrence analysis with application to genre classification. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 169–172. [Google Scholar]
- Fukino, M.; Hirata, Y.; Aihara, K. Coarse-graining time series data: Recurrence plot of recurrence plots and its application for music. Chaos 2016, 26, 023116. [Google Scholar] [CrossRef]
- Liu, X.F.; Chi, K.T.; Small, M. Complex network structure of musical compositions: Algorithmic generation of appealing music. Phys. A 2010, 389, 126–132. [Google Scholar] [CrossRef]
- Moore, J.M.; Corrêa, D.C.; Small, M. Is Bach’s brain a Markov chain? Recurrence quantification to assess Markov order for short, symbolic, musical compositions. Chaos 2018, 28, 085715. [Google Scholar] [CrossRef] [PubMed]
- Eck, D.; Schmidhuber, J. Finding temporal structure in music: Blues improvisation with LSTM recurrent networks. In Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing, Martigny, Switzerland, 6 September 2002; pp. 747–756. [Google Scholar]
- Dubnov, S.; Assayag, G.; Lartillot, O.; Bejerano, G. Using machine-learning methods for musical style modeling. Computer 2003, 36, 73–80. [Google Scholar] [CrossRef]
- Weinberg, G.; Driscoll, S. Toward robotic musicianship. Comput. Music J. 2006, 30, 28–45. [Google Scholar] [CrossRef]
- Bello, J.P. Measuring structural similarity in music. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2013–2025. [Google Scholar] [CrossRef]
- Walton, A.E.; Washburn, A.; Langland-Hassan, P.; Chemero, A.; Kloos, H.; Richardson, M.J. Creating time: Social collaboration in music improvisation. Top. Cogn. Sci. 2018, 10, 95–119. [Google Scholar] [CrossRef] [PubMed]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137. [Google Scholar] [CrossRef]
- Néda, Z.; Ravasz, E.; Vicsek, T.; Brechet, Y.; Barabási, A.L. Physics of the rhythmic applause. Phys. Rev. E 2000, 61, 6987. [Google Scholar] [CrossRef] [PubMed]
- Canonne, C.; Garnier, N. Individual decisions and perceived form in collective free improvisation. J. New Music Res. 2015, 44, 145–167. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N. How jazz musicians improvise. Music Percept. 2002, 19, 415–442. [Google Scholar] [CrossRef]
- Kenny, B.J.; Gellrich, M. Improvisation. In The Science and Psychology of Music Performance; Parncutt, R., Gary, M., Eds.; Oxford University Press: Oxford, UK, 2002; pp. 117–134. [Google Scholar]
- Winkler, I.; Háden, G.P.; Ladinig, O.; Sziller, I.; Honing, H. Newborn infants detect the beat in music. Proc. Natl. Acad. Sci. USA 2009, 106, 2468–2471. [Google Scholar] [CrossRef] [PubMed]
- Zentner, M.; Eerola, T. Rhythmic engagement with music in infancy. Proc. Natl. Acad. Sci. USA 2010, 107, 5768–5773. [Google Scholar] [CrossRef] [PubMed]
- Williamon, A.; Davidson, J.W. Exploring co-performer communication. Music. Sci. 2002, 6, 53–72. [Google Scholar] [CrossRef]
- Healey, P.G.; Leach, J.; Bryan-Kinns, N. Inter-play: Understanding group music improvisation as a form of everyday interaction. In Proceedings of the Less Is More—Simple Computing in an Age of Complexity, Cambridge, UK, 27–28 April 2005. [Google Scholar]
- Caballero-Pintado, M.V.; Matilla-García, M.; Ruiz Marín, M. Symbolic recurrence plots to analyze dynamical systems. Chaos 2018, 28, 063112. [Google Scholar] [CrossRef]
- Boldini, A.; Karakaya, M.; Ruiz Marín, M.; Porfiri, M. Application of symbolic recurrence to experimental data, from firearm prevalence to fish swimming. Chaos 2019, 29, 113128. [Google Scholar] [CrossRef]
- Ravignani, A.; Delgado, T.; Kirby, S. Musical evolution in the lab exhibits rhythmic universals. Nat. Hum. Behav. 2016, 1, 1–7. [Google Scholar] [CrossRef]
- Porfiri, M.; Ruiz Marín, M. Transfer entropy on symbolic recurrences. Chaos 2019, 29, 063123. [Google Scholar] [CrossRef]
- Badke-Schaub, P.; Neumann, A.; Lauche, K.; Mohammed, S. Mental models in design teams: A valid approach to performance in design collaboration? CoDesign 2007, 3, 5–20. [Google Scholar] [CrossRef]
- Cataldo, C. The art of improvising: The Be-Bop language and the major seventh chords. Art Des. Rev. 2017, 5, 222. [Google Scholar] [CrossRef][Green Version]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.; Colebatch, J.; Brown, P.; Rothwell, J.; Day, B.; Obeso, J.; Marsden, C. Voluntary stimulus-sensitive jerks and jumps mimicking myoclonus or pathological startle syndromes. Mov. Disord. 1992, 7, 257–262. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 17 February 2020).
- Sueur, J.; Aubin, T.; Simonis, C. Seewave: A free modular tool for sound analysis and synthesis. Bioacoustics 2008, 18, 213–226. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Sage Publishing: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Oliphant, T.E. A guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006; Volume 1. [Google Scholar]
- Cross, I. Music, cognition, culture, and evolution. Ann. N. Y. Acad. Sci. 2001, 930, 28–42. [Google Scholar] [CrossRef]
- Honing, H.; ten Cate, C.; Peretz, I.; Trehub, S.E. Without it no music: Cognition, biology and evolution of musicality. Philos. Trans. R. Soc. B 2015, 370. [Google Scholar] [CrossRef]
- Desain, P.; Honing, H. The formation of rhythmic categories and metric priming. Perception 2003, 32, 341–365. [Google Scholar] [CrossRef]
- Savage, P.E.; Brown, S.; Sakai, E.; Currie, T.E. Statistical universals reveal the structures and functions of human music. Proc. Natl. Acad. Sci. USA 2015, 112, 8987–8992. [Google Scholar] [CrossRef]
- Trehub, S.E. Cross-cultural convergence of musical features. Proc. Natl. Acad. Sci. USA 2015, 112, 8809–8810. [Google Scholar] [CrossRef]
- Ng, H.H. Collective free music improvisation as a sociocommunicative endeavor: A literature review. Update Appl. Res. Music Educ. 2019, 37, 15–23. [Google Scholar] [CrossRef]
- Sawyer, R.K. Improvised conversations: Music, collaboration, and development. Psychol. Music 1999, 27, 192–205. [Google Scholar] [CrossRef]
- Krumhansl, C.L.; Toivanen, P.; Eerola, T.; Toiviainen, P.; Järvinen, T.; Louhivuori, J. Cross-cultural music cognition: Cognitive methodology applied to North Sami yoiks. Cognition 2000, 76, 13–58. [Google Scholar] [CrossRef]
- Hannon, E.E.; Soley, G.; Ullal, S. Familiarity overrides complexity in rhythm perception: A cross-cultural comparison of American and Turkish listeners. J. Exp. Psychol. Hum. Percept. Perform. 2012, 38, 543. [Google Scholar] [CrossRef] [PubMed]
- Stevens, C.J. Music perception and cognition: A review of recent cross-cultural research. Top. Cogn. Sci. 2012, 4, 653–667. [Google Scholar] [CrossRef] [PubMed]
- Yates, C.M.; Justus, T.; Atalay, N.B.; Mert, N.; Trehub, S.E. Effects of musical training and culture on meter perception. Psychol. Music 2017, 45, 231–245. [Google Scholar] [CrossRef]
- Kolinski, M. A cross-cultural approach to metro-rhythmic patterns. Ethnomusicology 1973, 17, 494–506. [Google Scholar] [CrossRef]
- LeBlanc, A. An interactive theory of music preference. J. Music Ther. 1982, 19, 28–45. [Google Scholar] [CrossRef]
- Morrison, S.J.; Demorest, S.M. Cultural constraints on music perception and cognition. Prog. Brain Res. 2009, 178, 67–77. [Google Scholar]
- Polak, R.; Jacoby, N.; Fischinger, T.; Goldberg, D.; Holzapfel, A.; London, J. Rhythmic prototypes across cultures: A comparative study of tapping synchronization. Music Percept. 2018, 36, 1–23. [Google Scholar] [CrossRef]
- Soley, G.; Hannon, E.E. Infants prefer the musical meter of their own culture: A cross-cultural comparison. Dev. Psychol. 2010, 46, 286. [Google Scholar] [CrossRef]
- Turek, R.; Schindler, A. The Elements of Music: Concepts and Applications; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Azzara, C.D. An aural approach to improvisation. Music Educ. 1999, 86, 21–25. [Google Scholar] [CrossRef]
- Becker, H.S. The etiquette of improvisation. Mind Cult. Act. 2000, 7, 171–176. [Google Scholar] [CrossRef]
- Biasutti, M.; Frezza, L. Dimensions of music improvisation. Creat. Res. J. 2009, 21, 232–242. [Google Scholar] [CrossRef]
- McDermott, J.; Hauser, M. The origins of music: Innateness, uniqueness, and evolution. Music Percept. 2005, 23, 29–59. [Google Scholar] [CrossRef]
- Patel, A.D. Musical rhythm, linguistic rhythm, and human evolution. Music Percept. 2006, 24, 99–104. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Hothorn, T.; Bretz, F.; Westfall, P. Simultaneous Inference in General Parametric Models. Biom. J. 2008, 50, 346–363. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Mero, A.; Komi, P.V. Reaction time and electromyographic activity during a sprint start. Eur. J. Appl. Physiol. Occup. Physiol. 1990, 61, 73–80. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakayama, S.; Soman, V.R.; Porfiri, M. Musical Collaboration in Rhythmic Improvisation. Entropy 2020, 22, 233. https://doi.org/10.3390/e22020233
Nakayama S, Soman VR, Porfiri M. Musical Collaboration in Rhythmic Improvisation. Entropy. 2020; 22(2):233. https://doi.org/10.3390/e22020233
Chicago/Turabian StyleNakayama, Shinnosuke, Vrishin R. Soman, and Maurizio Porfiri. 2020. "Musical Collaboration in Rhythmic Improvisation" Entropy 22, no. 2: 233. https://doi.org/10.3390/e22020233
APA StyleNakayama, S., Soman, V. R., & Porfiri, M. (2020). Musical Collaboration in Rhythmic Improvisation. Entropy, 22(2), 233. https://doi.org/10.3390/e22020233




