Experimentally Demonstrate the Spin-1 Information Entropic Inequality Based on Simulated Photonic Qutrit States
Abstract
1. Introduction
2. The Theory of Information Entropy Inequality
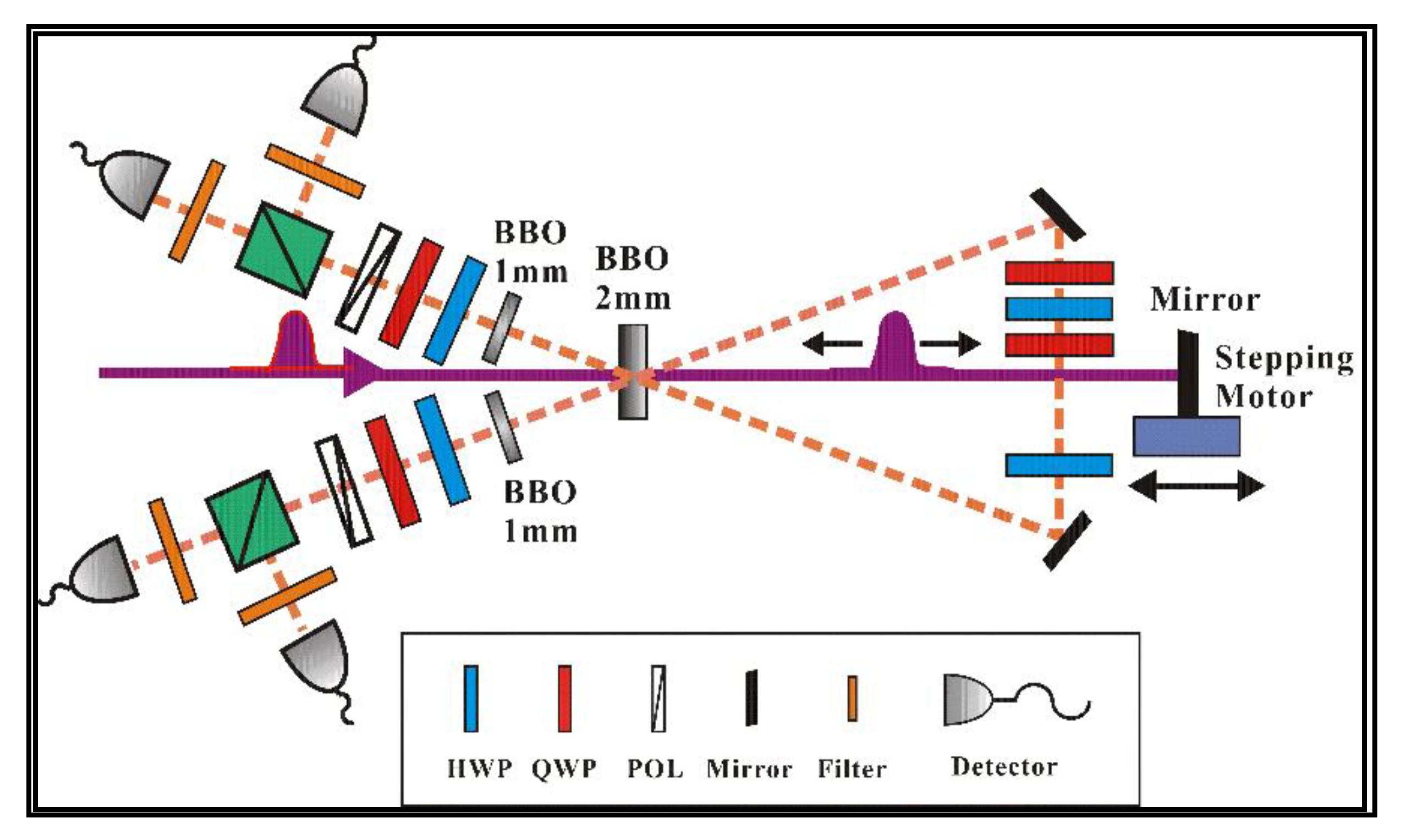
3. Entanglement State Experimental Implementation
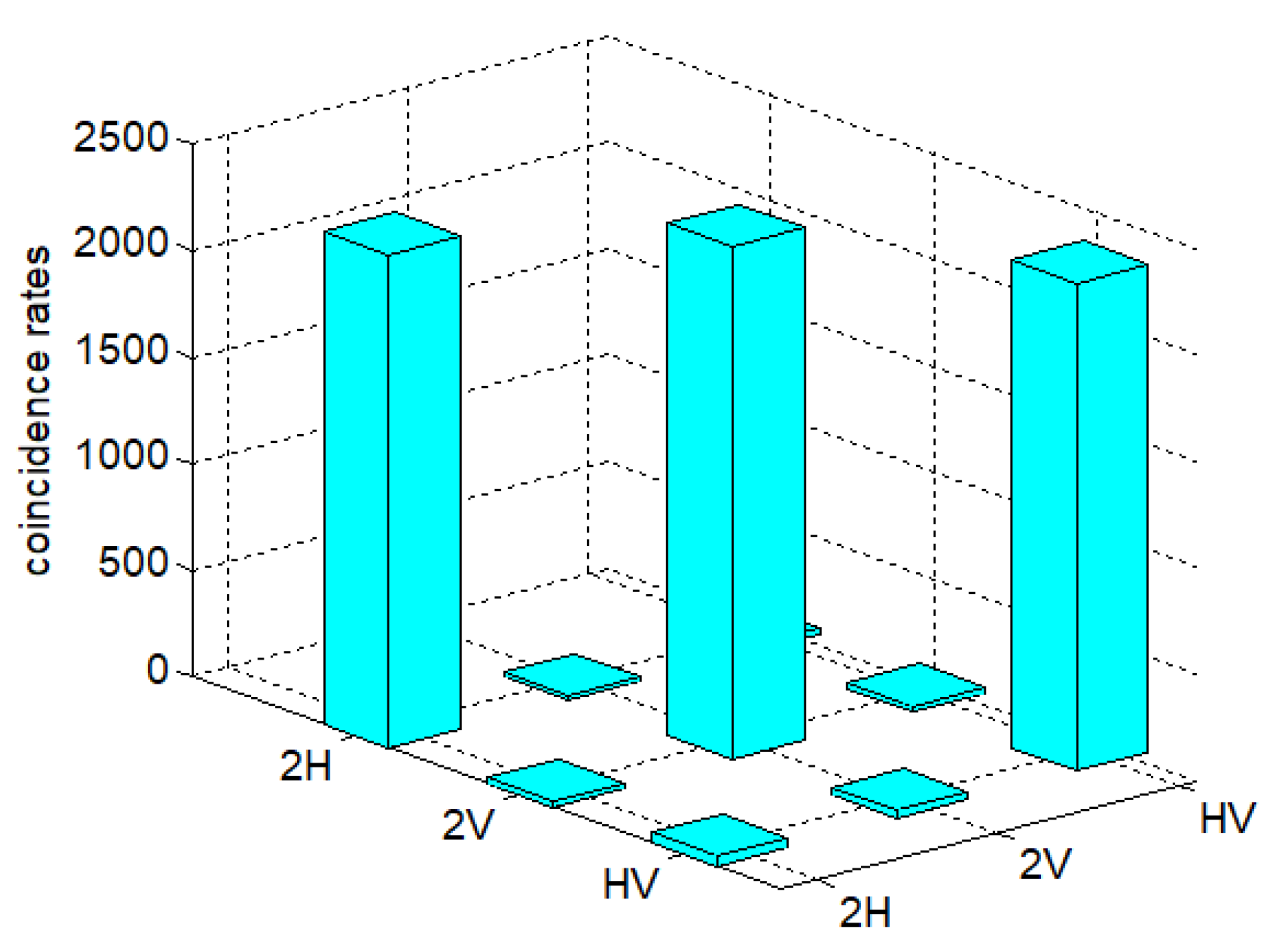
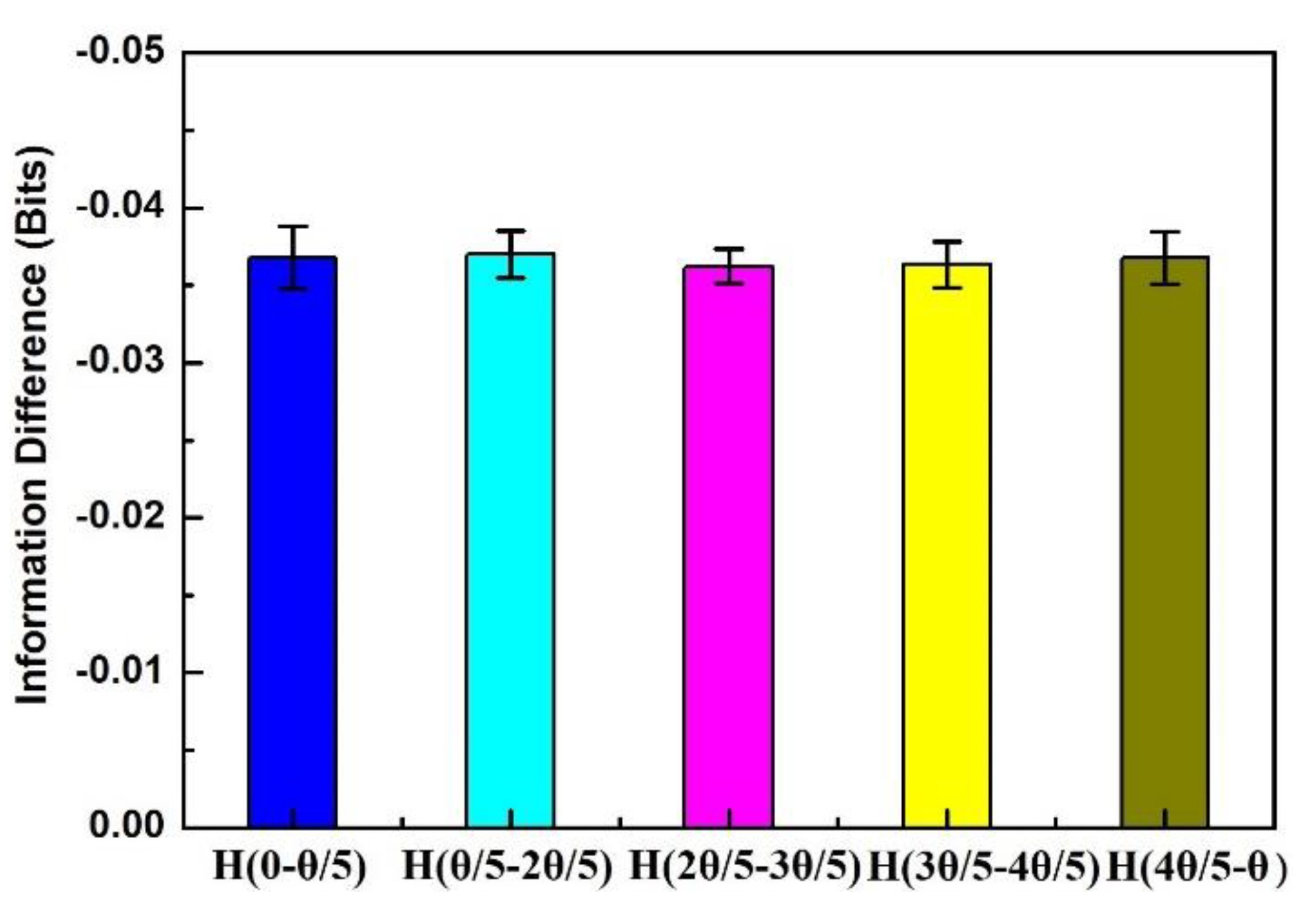
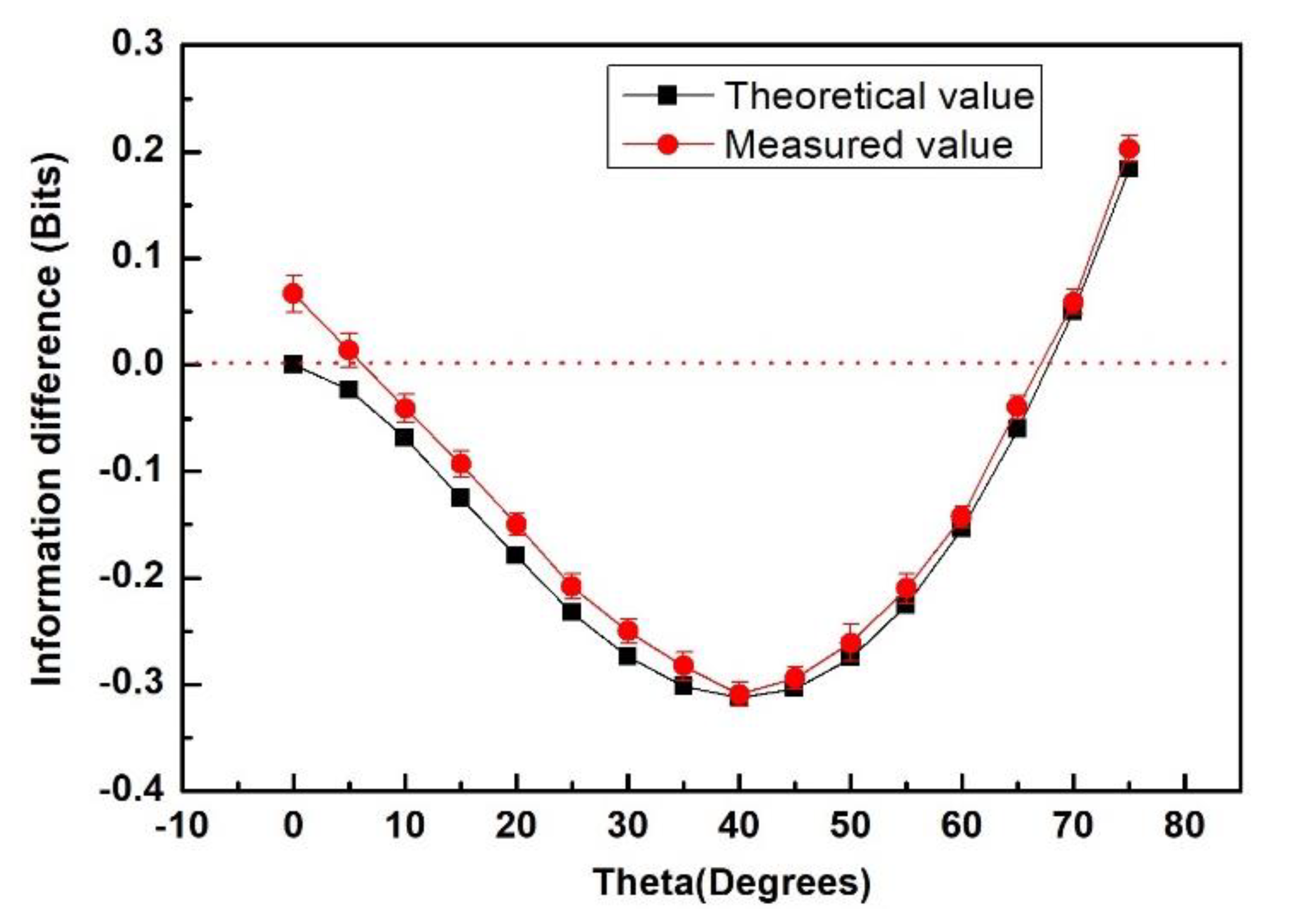
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lukin, A.; Rispoli, M.; Schittko, R.; Tai, M.E.; Kaufman, A.M.; Choi, S.; Khemani, V.; Léonard, J.; Greiner, M. Probing entanglement in a many-body-localized system. Science 2019, 364, 256–260. [Google Scholar] [PubMed]
- Wang, X.L.; Luo, Y.H.; Huang, H.L.; Chen, M.C.; Su, Z.E.; Liu, C.; Chen, C.; Li, W.; Fang, Y.Q.; Jiang, X.; et al. 18-qubit entanglement with six photons’ three degrees of freedom. Phys. Rev. Lett. 2018, 120, 260502. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.H.; Zhong, H.S.; Erhard, M.; Wang, X.L.; Peng, L.C.; Krenn, M.; Jiang, X.; Li, L.; Liu, N.L.; Lu, C.Y.; et al. Quantum teleportation in high dimensions. Phys. Rev. Lett. 2019, 123, 070505. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; Caves, C.M. Information-theoretic Bell inequalities. Phys. Rev. Lett. 1988, 61, 662–665. [Google Scholar] [CrossRef]
- Chaves, R. Entropic inequalities as a necessary and sufficient condition to noncontextuality and locality. Phys. Rev. A 2013, 87, 022102. [Google Scholar] [CrossRef]
- Branciard, C.; Gisin, N.; Pironio, S. Characterizing the nonlocal correlations created via entanglement swapping. Phys. Rev. Lett. 2010, 104, 170401. [Google Scholar] [CrossRef]
- Wood, C.J.; Spekkens, R.W. The lesson of causal discovery algorithms for quantum correlations: Causal explanations of Bell-inequality violations require fine-tuning. New J. Phys. 2015, 17, 033002. [Google Scholar] [CrossRef]
- Bennett, C.H.; Shor, P.W. Quantum Information Theory. IEEE Trans. Inf. Theory 1998, 44, 2724–2742. [Google Scholar] [CrossRef]
- Morikoshi, F. Information-theoretic temporal Bell inequality and quantum computation. Phys. Rev. A 2006, 73, 052308. [Google Scholar] [CrossRef]
- Fritz, T.; Chaves, R. Entropic inequalities and marginal problems. IEEE Trans. Inf. Theory 2012, 59, 803–817. [Google Scholar] [CrossRef]
- Kurzyński, P.; Ramanthan, R.; Kaszlikowski, D. Entropic test of quantum contextuality. Phys. Rev. Lett. 2012, 109, 020404. [Google Scholar] [CrossRef]
- Barrett, J.; Hardy, L.; Kent, A. No signaling and quantum key distribution. Phys. Rev. Lett. 2005, 95, 010503. [Google Scholar] [CrossRef]
- Chaves, R.; Fritz, T. Entropic approach to local realism and noncontextuality. Phys. Rev. A 2012, 85, 032113. [Google Scholar] [CrossRef]
- Conroy, J.M.; Miller, H.G. Determining the Tsallis parameter via maximum entropy. Phys. Rev. E 2015, 91, 052112. [Google Scholar] [CrossRef]
- Rastegin, A.E. On entropic uncertainty relations for measurements of energy and its “complement”. Ann. Phys. 2019, 531, 1800466. [Google Scholar] [CrossRef]
- Paraoanu, G.S. Recent progress in quantum simulation using superconducting circuits. J. Low Temp. Phys. 2014, 175, 633–654. [Google Scholar] [CrossRef]
- Lamas-Linares, A.; Howell, J.C.; Bouwmeester, D. Stimulated emission of polarization-entangled photons. Nature 2001, 412, 887–890. [Google Scholar] [CrossRef]
- Howell, J.C.; Lamas-Linares, A.; Bouwmeester, D. Experimental violation of a spin-1 Bell inequality using maximally entangled four-photon states. Phys. Rev. Lett. 2002, 88, 030401. [Google Scholar] [CrossRef]
- Das, D.; Datta, S.; Goswami, S.; Majumdar, A.S.; Home, D. Bipartite qutrit local realist inequalities and the robustness of their quantum mechanical violation. Phys. Lett. A 2017, 381, 3396–3404. [Google Scholar] [CrossRef][Green Version]
- Cao, L.Z.; Zhao, J.Q.; Liu, X.; Yang, Y.; Wang, X.Q.; Chen, Z.B.; Lu, H.X. Experimental investigation of the information entropic Bell inequality. Sci. Rep. 2016, 6, 23758. [Google Scholar] [CrossRef]
- Liu, X.; Lu, H.X.; Zhao, J.Q.; Yang, Y.; Li, Y.D.; Cao, L.Z. Evolution of quantum correlation undergoing decoherence using the information entropy inequality. Laser Phys. Lett. 2018, 15, 125207. [Google Scholar] [CrossRef]
- Wang, J.W.; Paesani, S.; Ding, Y.H.; Santagati, R.; Skrzypczyk, P.; Salavrakos, A.; Tura, J.; Augusiak, R.; Mancinska, L.; Bacco, D.; et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018, 360, 285–291. [Google Scholar] [CrossRef]
- Erhard, M.; Malik, M.; Krenn, M.; Zeilinger, A. Experimental Greenberger-Horne-Zeilinger entanglement beyond qubits. Nat. Photon. 2018, 12, 759–764. [Google Scholar] [CrossRef]
- Lόpez-Saldívar, J.A.; Castaños, O.; Nahmad-Achar, E.; Lόpez-Peña, R.; Manko, M.A.; Manko, V.I. Geometry and entanglement of two-qubit states in the quantum probabilistic representation. Entropy 2018, 20, 630. [Google Scholar]
- Lόpez-Saldívar, J.A.; Castaños, O.; Manko, M.A.; Manko, V.I. A new mechanism of open system evolution and its entropy using unitary transformations in noncomposite qudit systems. Entropy 2019, 21, 736. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; Liu, X.; Yang, Y.; Zhang, Q.; Zhao, J.; Lu, H. Experimentally Demonstrate the Spin-1 Information Entropic Inequality Based on Simulated Photonic Qutrit States. Entropy 2020, 22, 219. https://doi.org/10.3390/e22020219
Cao L, Liu X, Yang Y, Zhang Q, Zhao J, Lu H. Experimentally Demonstrate the Spin-1 Information Entropic Inequality Based on Simulated Photonic Qutrit States. Entropy. 2020; 22(2):219. https://doi.org/10.3390/e22020219
Chicago/Turabian StyleCao, Lianzhen, Xia Liu, Yang Yang, Qinwei Zhang, Jiaqiang Zhao, and Huaixin Lu. 2020. "Experimentally Demonstrate the Spin-1 Information Entropic Inequality Based on Simulated Photonic Qutrit States" Entropy 22, no. 2: 219. https://doi.org/10.3390/e22020219
APA StyleCao, L., Liu, X., Yang, Y., Zhang, Q., Zhao, J., & Lu, H. (2020). Experimentally Demonstrate the Spin-1 Information Entropic Inequality Based on Simulated Photonic Qutrit States. Entropy, 22(2), 219. https://doi.org/10.3390/e22020219



