Allometric Scaling of Mutual Information in Complex Networks: A Conceptual Framework and Empirical Approach
Abstract
1. Introduction
1.1. The Context
1.2. The Complexity Framework: Allometric Nature of Mutual Information
1.2.1. Structural Mutual Information: SMI
1.2.2. Total Mutual Information, I
1.3. The Economic Dimension
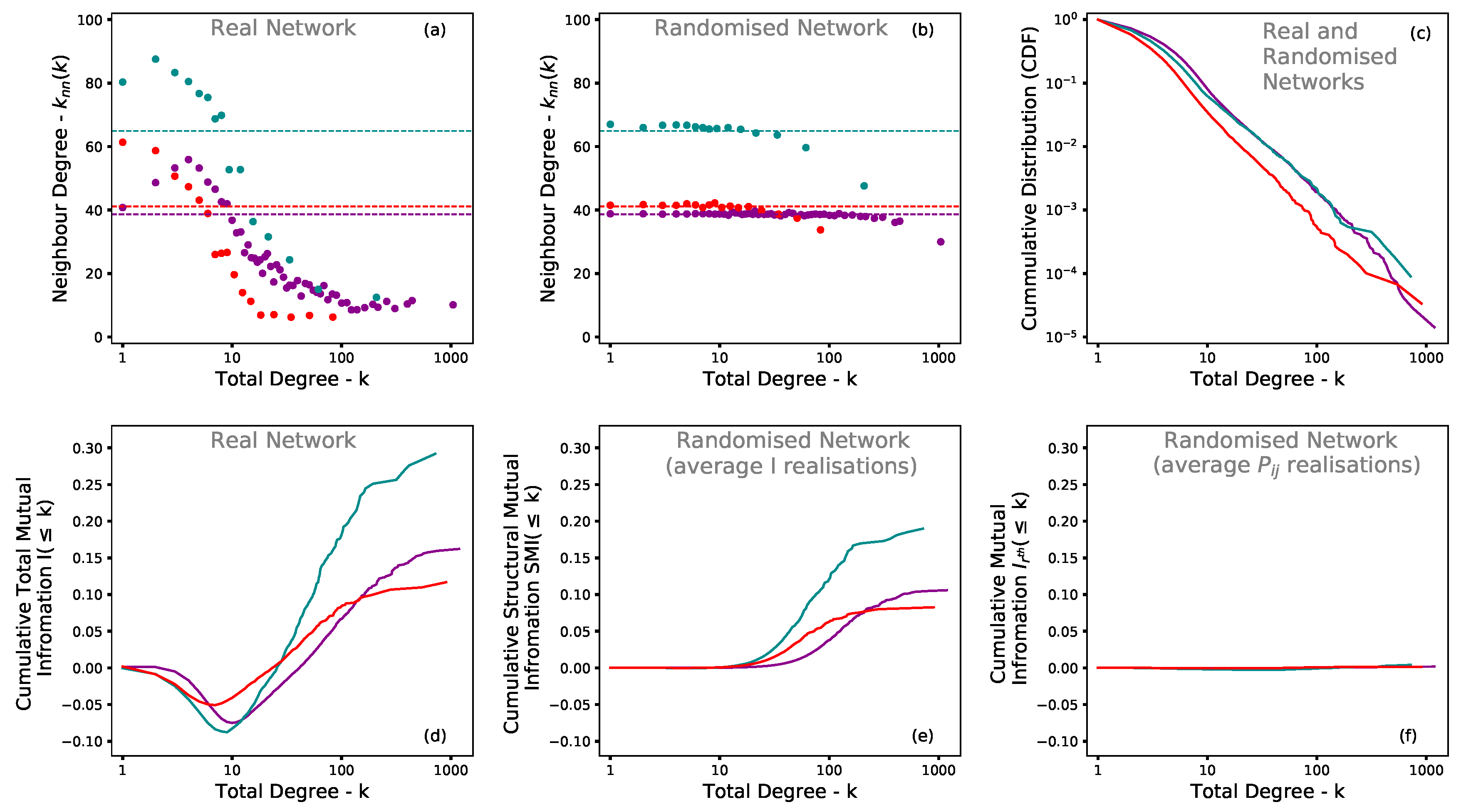
2. Results
2.1. Data Analysis
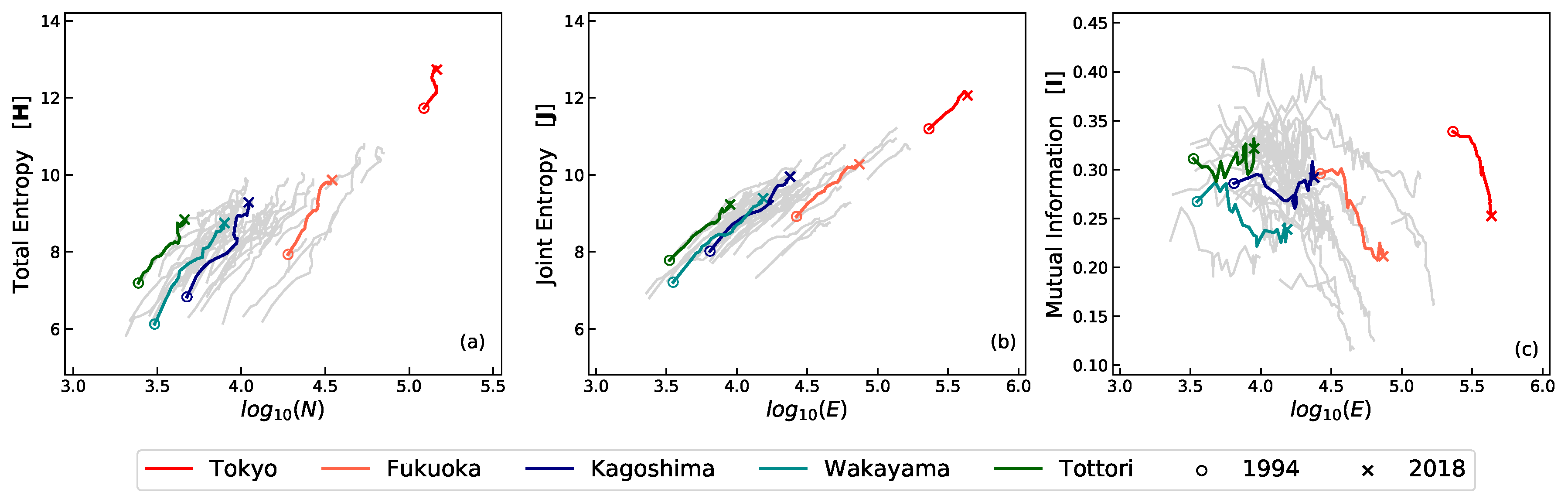
2.1.1. Macro Features of Entropy and Mutual Information
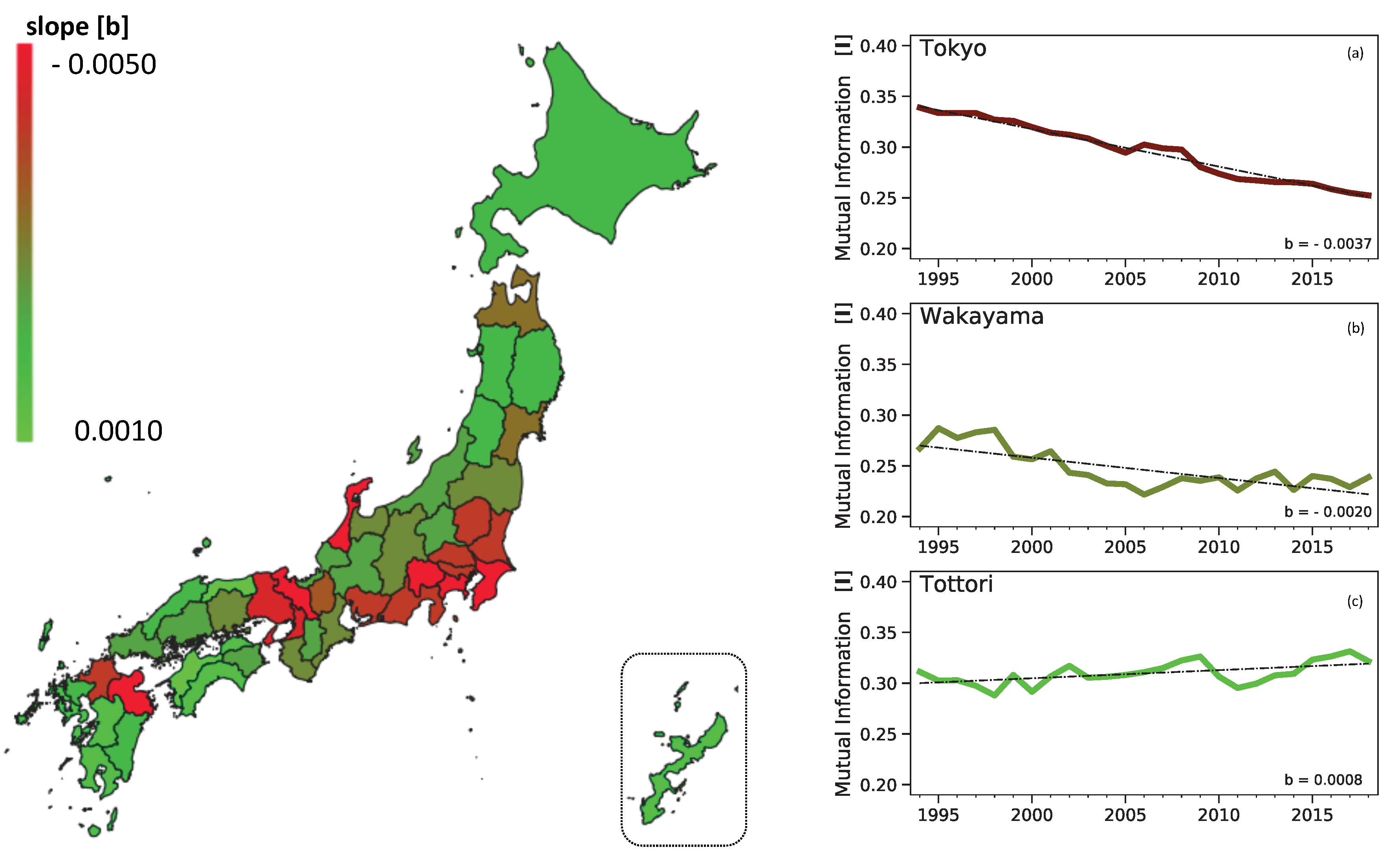
2.1.2. The Geographical Perspective of Mutual Information
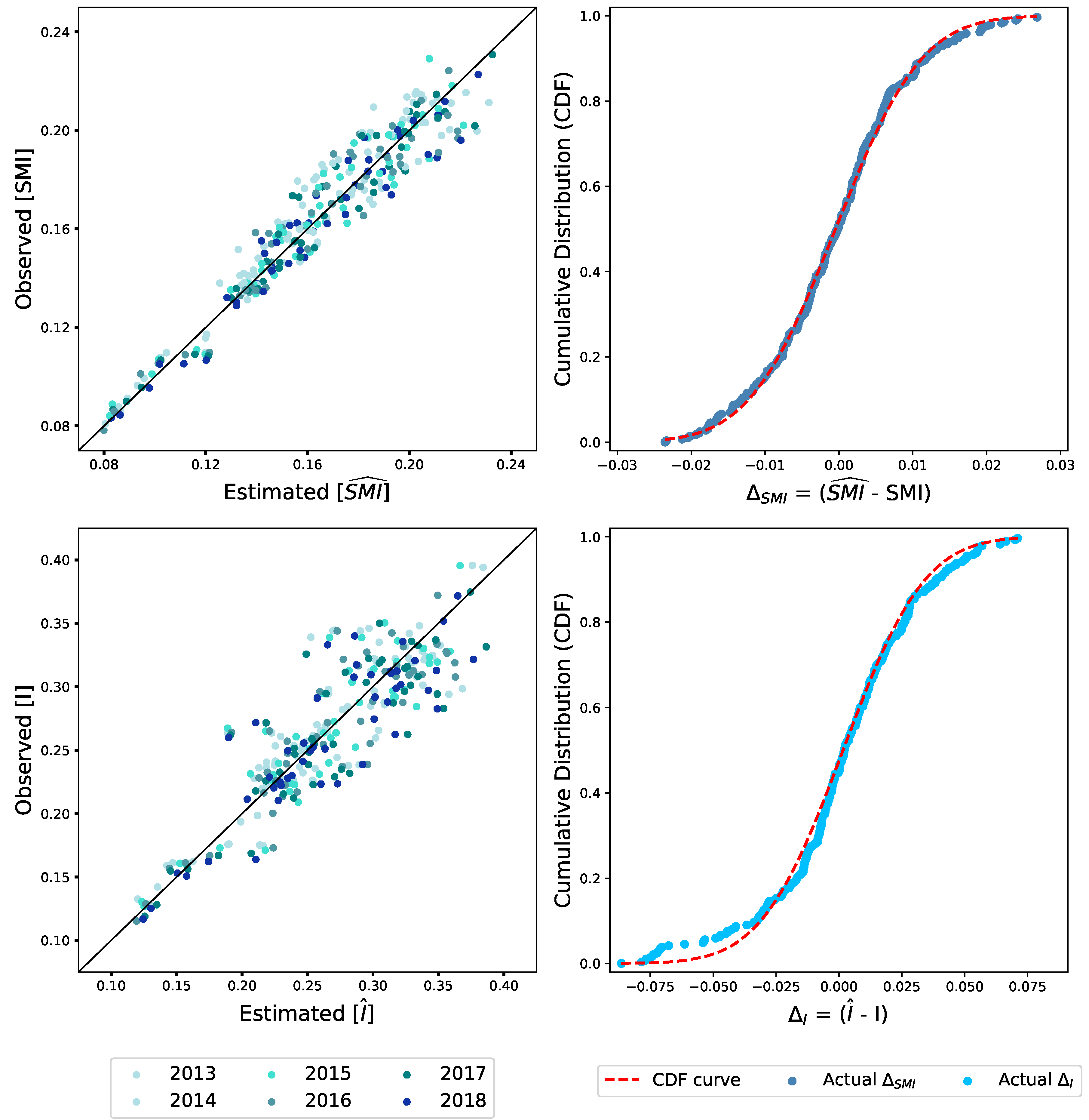
3. The Allometric Nature of Mutual Information
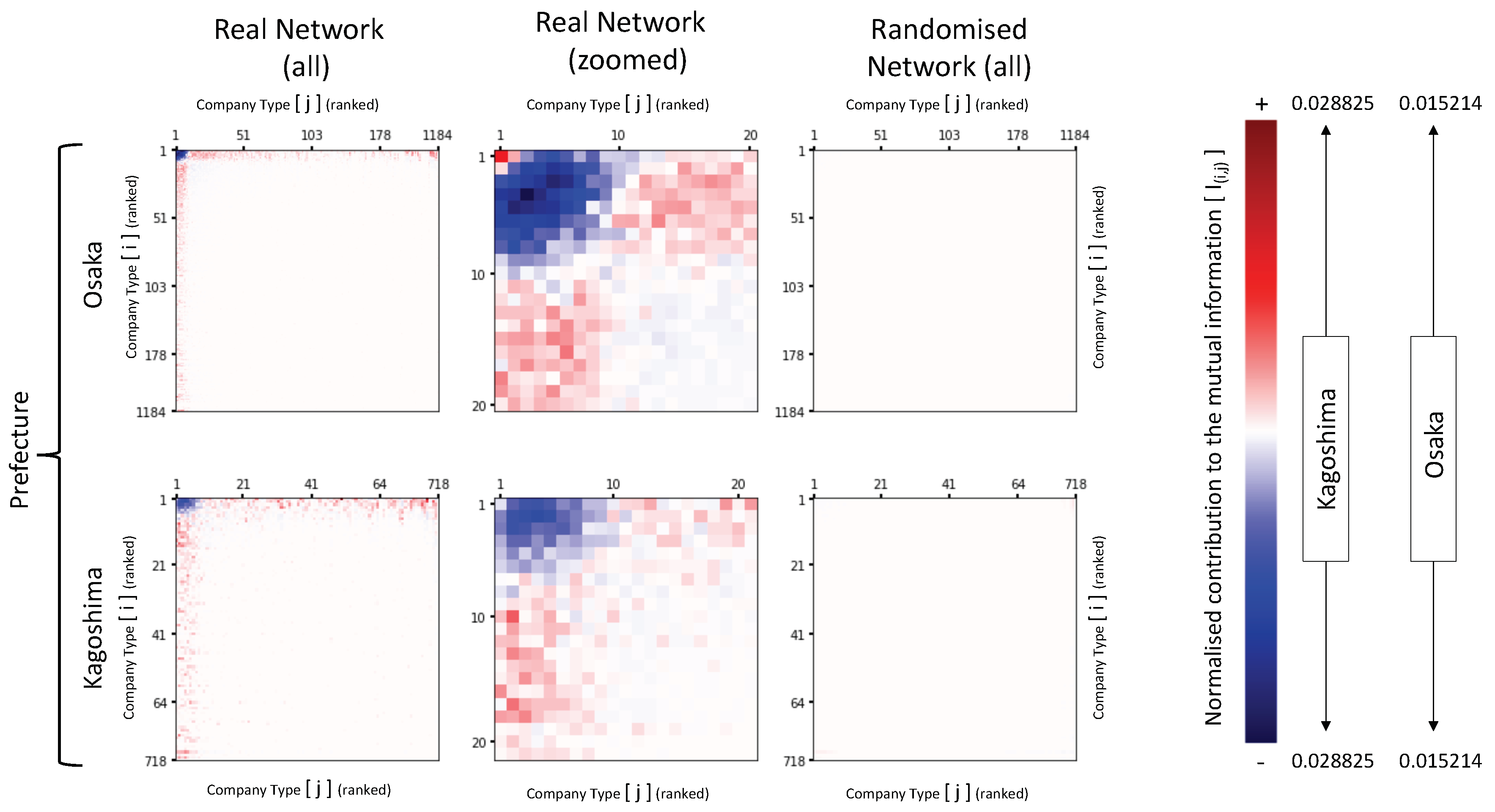
Entropy and Mutual Information Micro Features
4. Conclusions and Discussion
5. Materials and Methods
5.1. Measuring Entropy and Mutual Information
5.2. Network Randomisation and Rewiring Process
5.3. Methods Underpinning the Complexity Framework
5.3.1. Structural Mutual Information, SMI
5.3.2. Total Mutual Information I
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SMI | Structural Mutual Information |
| I | Total Mutual Information |
| H | Entropy |
| J | Total Joint Entropy |
| GDP | Gross Domestic Product |
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Techn. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- von Neumann, J. Papers of John Von Neumann on Computing and Computer Theory; MIT Press: Cambridge, MA, USA, 1987. [Google Scholar]
- von Neumann, J. Collected Works/Vol. V, Design of Computers, Theory of Automata and Numerical Analysis; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Dehmer, M.; Emmert-Streib, F.; Mehler, A. The Central Role of Information Theory in Ecology. In Towards an Information Theory of Complex Networks: Statistical Methods and Applications, 1st ed.; Birkhäuser Boston: Boston, MA, USA, 2011; pp. 153–167. [Google Scholar]
- Ulanowicz, R.E. Reckoning the nonexistent: Putting the science right. Ecol. Model. 2014, 293, 22–30. [Google Scholar] [CrossRef]
- West, G.B. A general model for the origin allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301. [Google Scholar] [CrossRef] [PubMed]
- West, G.B. Santa Fe Institute studies in the sciences of complexity. In Scaling in Biology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Goto, H.; Viegas, E.; Jensen, H.J.; Takayasu, H.; Takayasu, M. Appearance of Unstable Monopoly State Caused by Selective and Concentrative Mergers in Business Networks. Sci. Rep. 2017, 7, 5064. [Google Scholar] [CrossRef] [PubMed]
- Goto, H.; Viegas, E.; Jensen, H.; Takayasu, H.; Takayasu, M. Smoluchowski Equation for Networks: Merger Induced Intermittent Giant Node Formation and Degree Gap. J. Stat. Phys. 2018, 172, 1086–1100. [Google Scholar] [CrossRef]
- Takayasu, M.; Sameshima, S.; Watanabe, H.; Ohnishi, T.; Iyatomi, H.; Iino, T.; Kobayashi, Y.; Kamehama, K.; Ikeda, Y.; Takayasu, H.; et al. Massive Economics Data Analysis by Econophysics Method-The Case of Companies’ Network Structure; Annual Report of the Earth Simulator Center; Earth Simulator Center: Yokohama, Japan, 2008; pp. 237–241. [Google Scholar]
- Viegas, E.; Goto, H.; Takayasu, H.; Takayasu, M.; Jensen, H. Assembling real networks from synthetic and unstructured subsets: The corporate reporting case. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, H.; Takayasu, H.; Takayasu, M. Relations between allometric scalings and fluctuations in complex systems: The case of Japanese firms. Physica A 2013, 392, 741–756. [Google Scholar] [CrossRef]
- Huang, J.; Ulanowicz, R. Ecological Network Analysis for Economic Systems: Growth and Development and Implications for Sustainable Development. PLoS ONE 2014, 9, e100923. [Google Scholar] [CrossRef] [PubMed]
- Arkolakis, C. Market Penetration Costs and the New Consumers Margin in International Trade; Working Paper No. 14214; NBER: Washington, DC, USA, Augest 2008. [Google Scholar]
- Price, D.D.S. A general theory of bibliometric and other cumulative advantage processes. J. Assoc. Inf. Sci. Technol. 1976, 27, 292–306. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Sanchirico, A.; Fiorentino, M. Scale-free networks as entropy competition. Phys. Rev. E 2008, 78, 046114. [Google Scholar] [CrossRef] [PubMed]
- Sutton, J. Sunk Costs and Market Structure: Price Competition, Advertising, and the Evolution of Concentration; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Viegas, E.; Cockburn, S.P.; Jensen, H.J.; West, G.B. The dynamics of mergers and acquisitions: Ancestry as the seminal determinant. Proc. Math. Phys. Eng. Sci. 2014, 470, 20140370. [Google Scholar] [CrossRef] [PubMed]
- Aitsahlia, F.; Yoon, J.H. Information stages in efficient markets. J. Bank. Finance 2016, 69, 84–94. [Google Scholar] [CrossRef]
- Ito, M.; Noda, A.; Wada, T. The evolution of stock market efficiency in the US: A non-Bayesian time-varying model approach. Appl. Econ. 2016, 48, 621–635. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, P.J.; Jeong, H. Statistical properties of sampled networks. Phys. Rev. E 2006, 73, 016102. [Google Scholar] [CrossRef] [PubMed]
- West, G. Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies; Penguin Press: New York, NY. USA, 2017. [Google Scholar]
- Boettke, P.J. What Happened to “Efficient Markets”? Indep. Rev. 2010, 14, 363–375. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viegas, E.; Goto, H.; Kobayashi, Y.; Takayasu, M.; Takayasu, H.; Jensen, H.J. Allometric Scaling of Mutual Information in Complex Networks: A Conceptual Framework and Empirical Approach. Entropy 2020, 22, 206. https://doi.org/10.3390/e22020206
Viegas E, Goto H, Kobayashi Y, Takayasu M, Takayasu H, Jensen HJ. Allometric Scaling of Mutual Information in Complex Networks: A Conceptual Framework and Empirical Approach. Entropy. 2020; 22(2):206. https://doi.org/10.3390/e22020206
Chicago/Turabian StyleViegas, Eduardo, Hayato Goto, Yuh Kobayashi, Misako Takayasu, Hideki Takayasu, and Henrik Jeldtoft Jensen. 2020. "Allometric Scaling of Mutual Information in Complex Networks: A Conceptual Framework and Empirical Approach" Entropy 22, no. 2: 206. https://doi.org/10.3390/e22020206
APA StyleViegas, E., Goto, H., Kobayashi, Y., Takayasu, M., Takayasu, H., & Jensen, H. J. (2020). Allometric Scaling of Mutual Information in Complex Networks: A Conceptual Framework and Empirical Approach. Entropy, 22(2), 206. https://doi.org/10.3390/e22020206





