Mean Shift Cluster Recognition Method Implementation in the Nested Sampling Algorithm
Abstract
1. Introduction
2. Nested Sampling and NestedFit
2.1. The Nested Sampling Algorithm
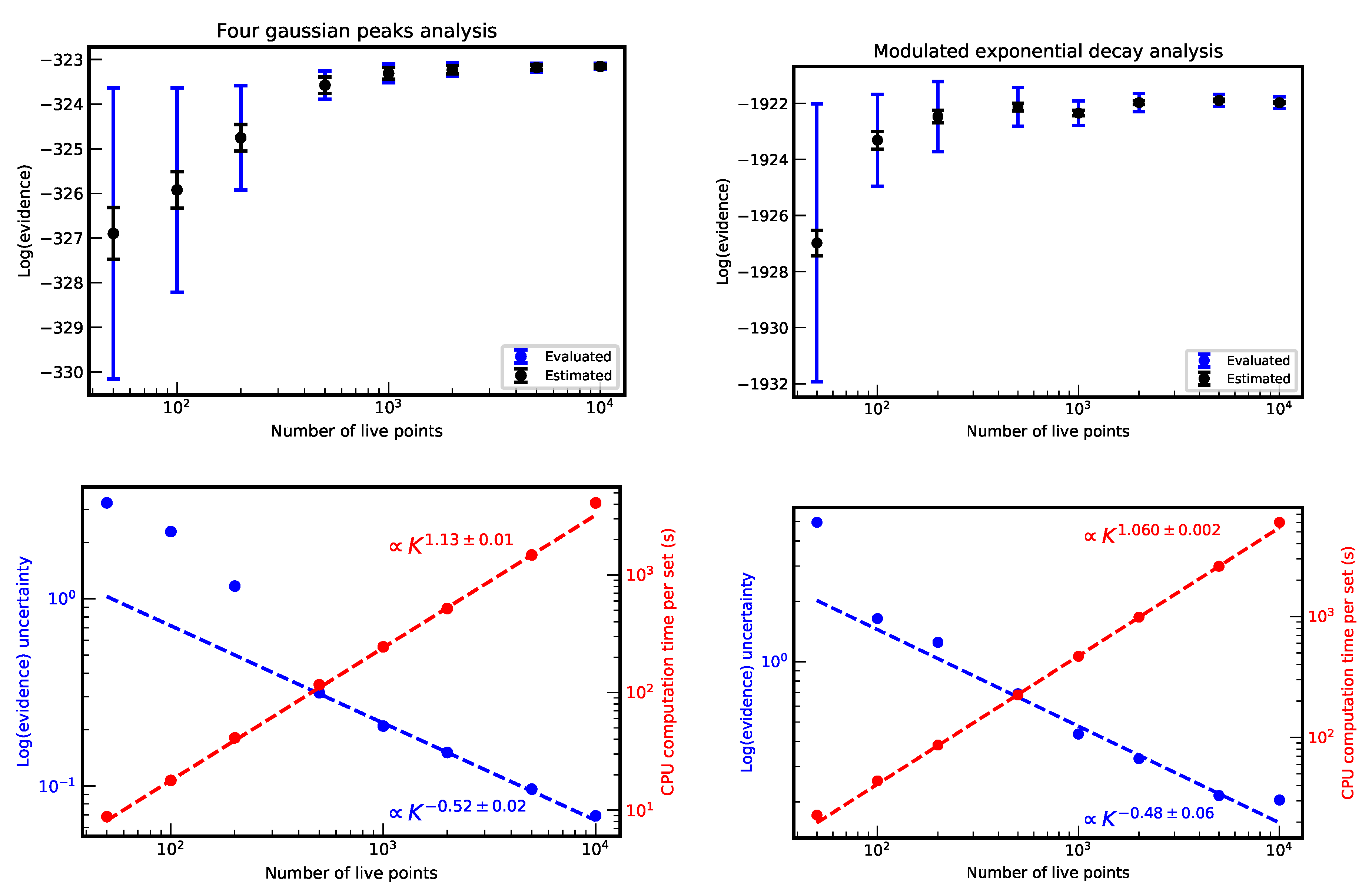
2.2. Bottleneck of Nested Sampling and Proposed Solutions
2.3. The NestedFit Program
2.4. NenstedFit Search Algorithm
3. Mean Shift Clustering Algorithm and Its Implementation
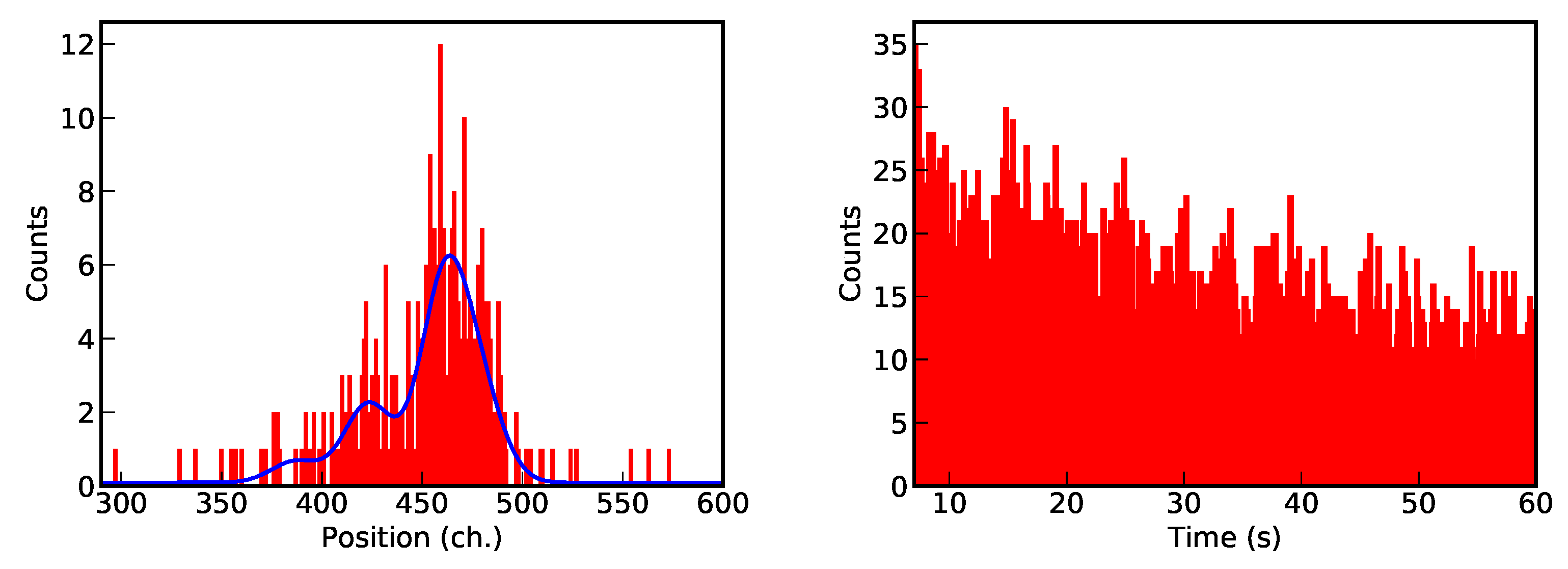
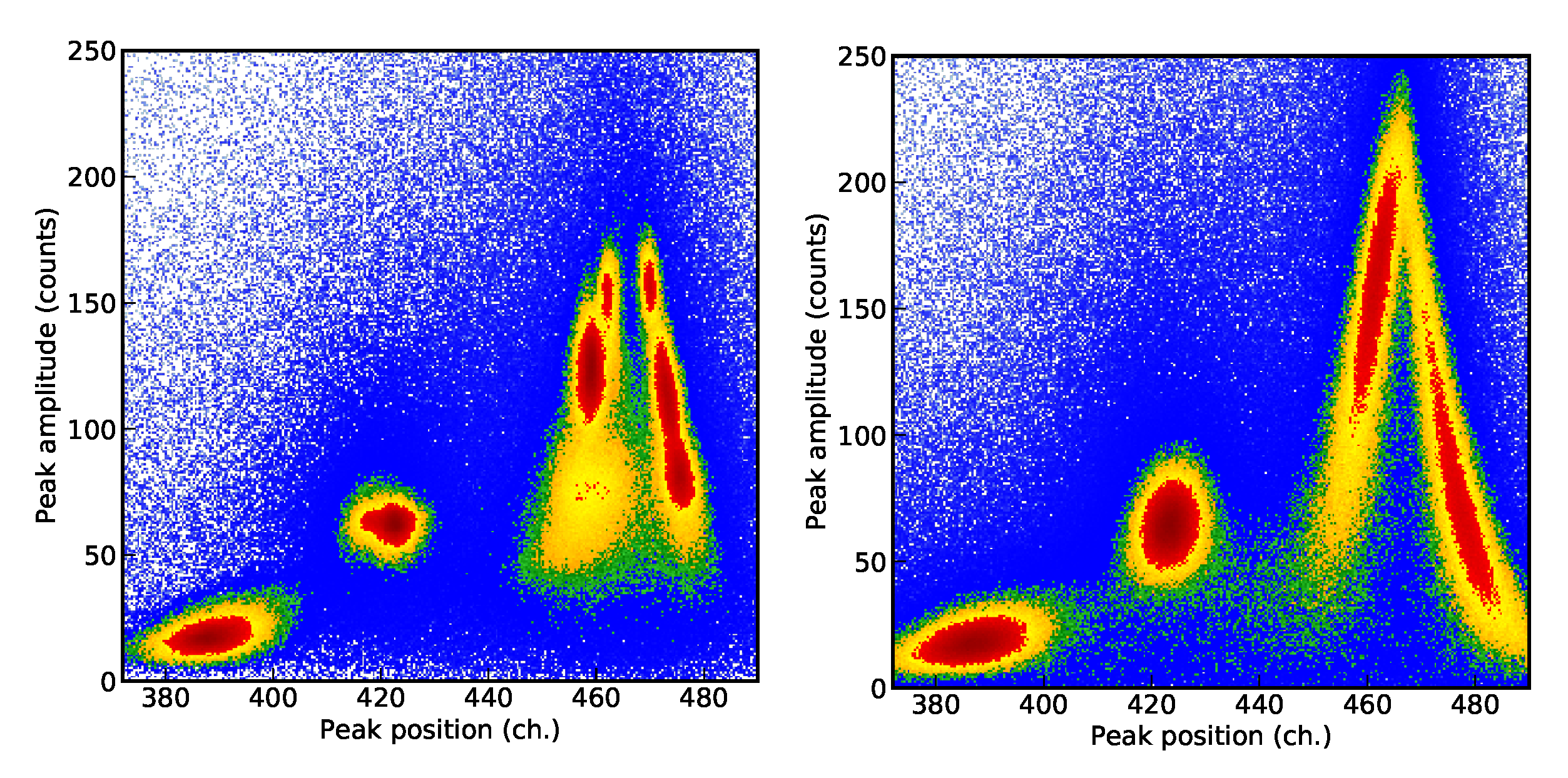
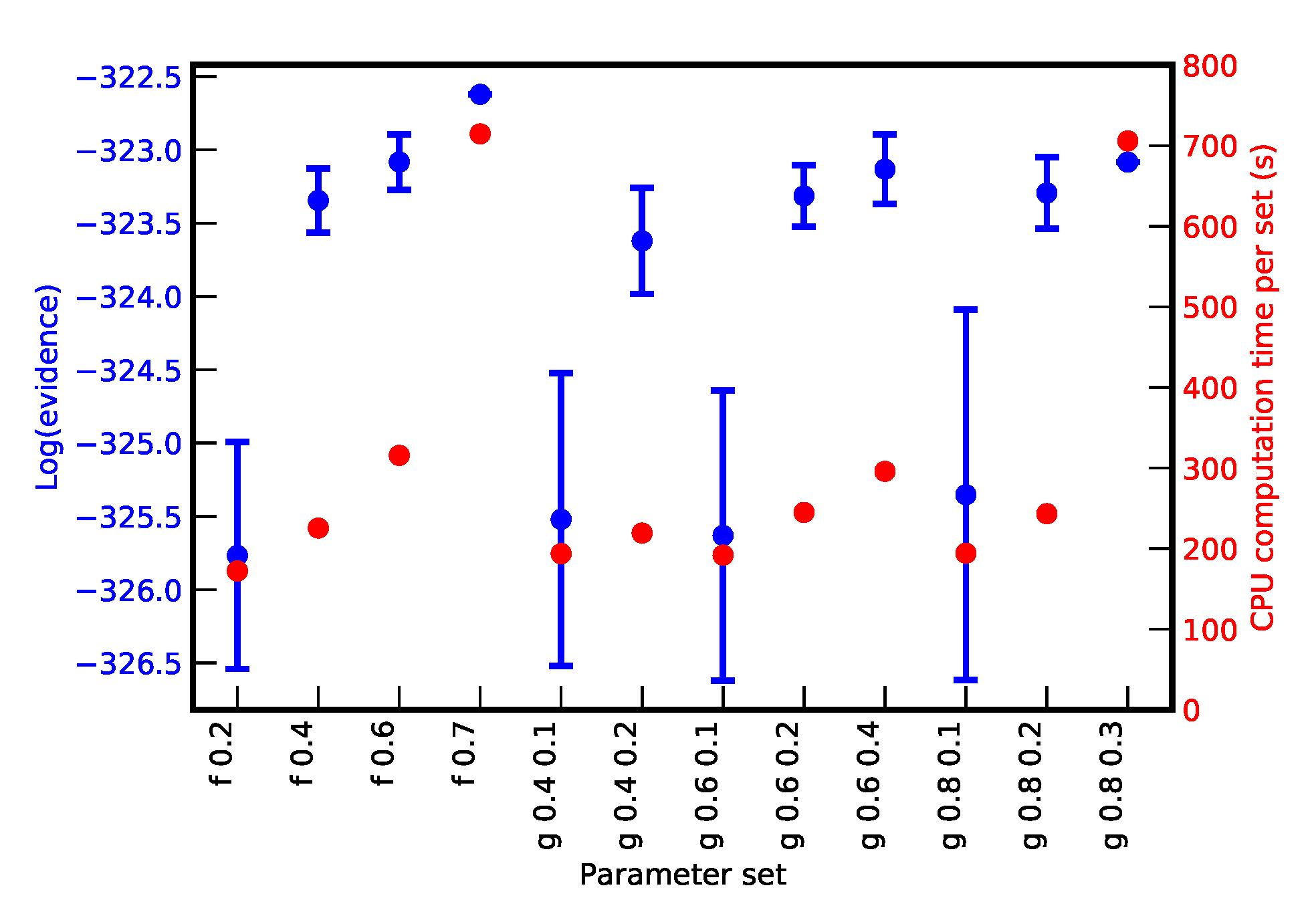
3.1. Preliminary Tests and Considerations on Other Cluster Recognition Algoritms
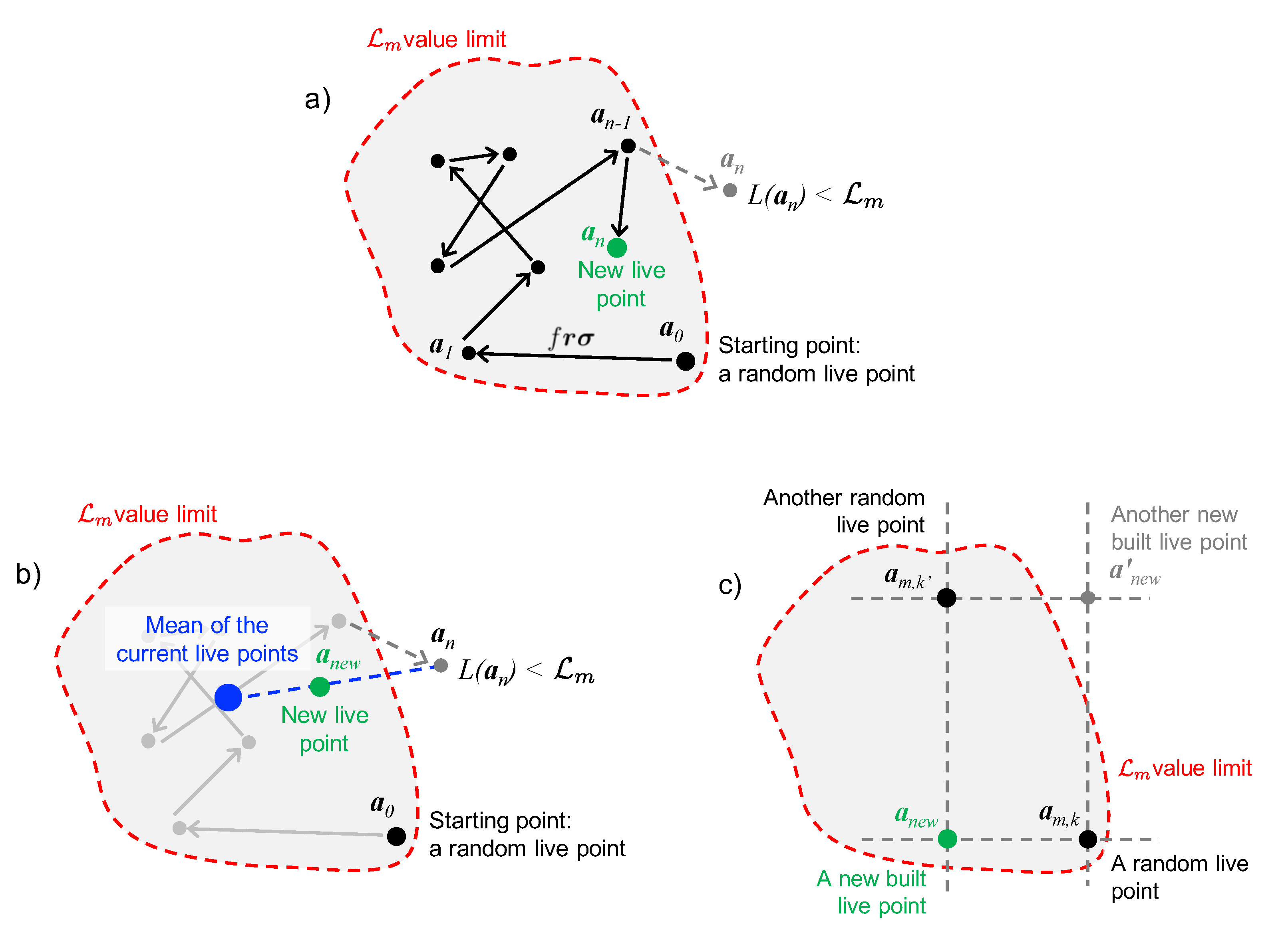
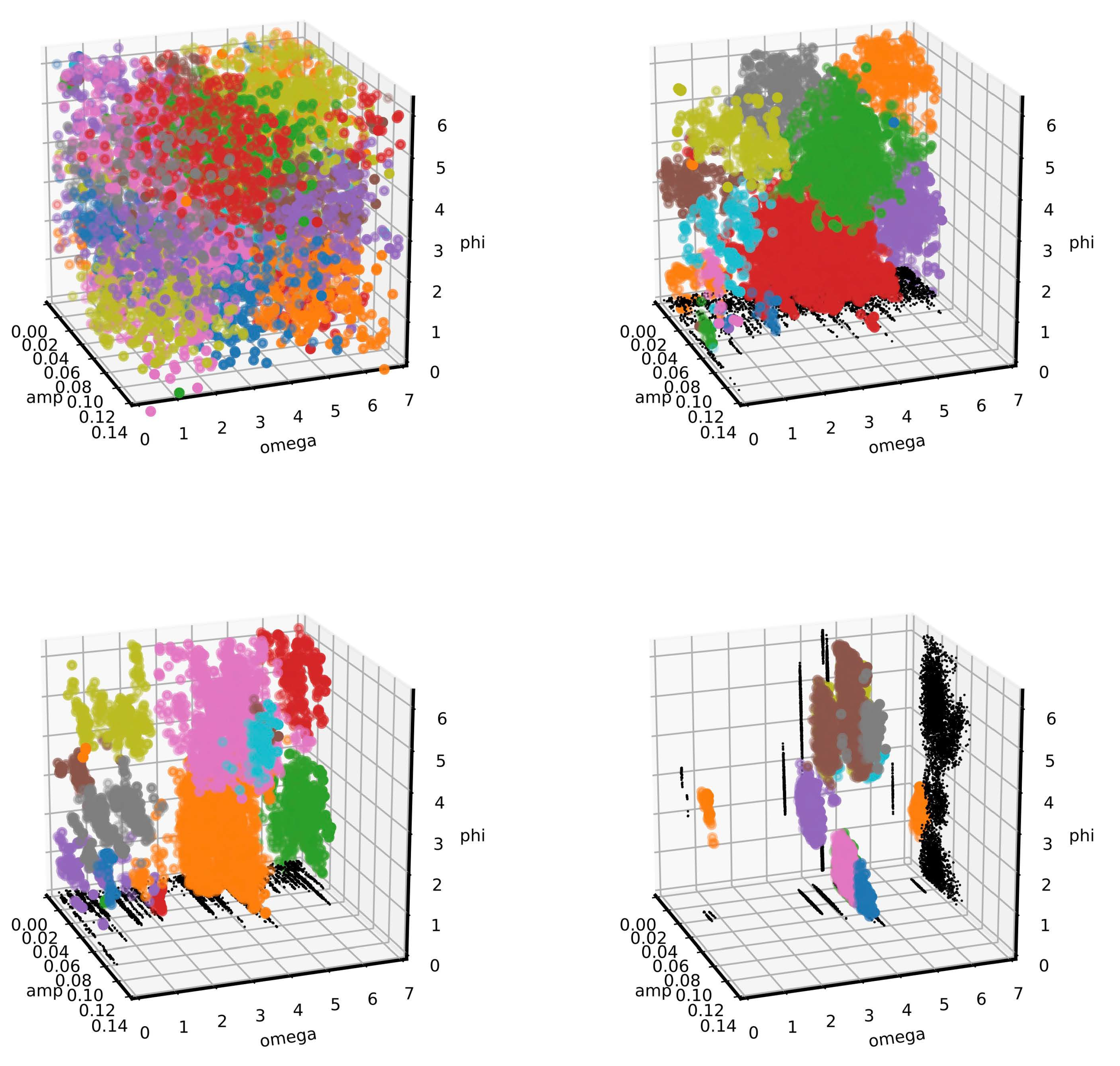
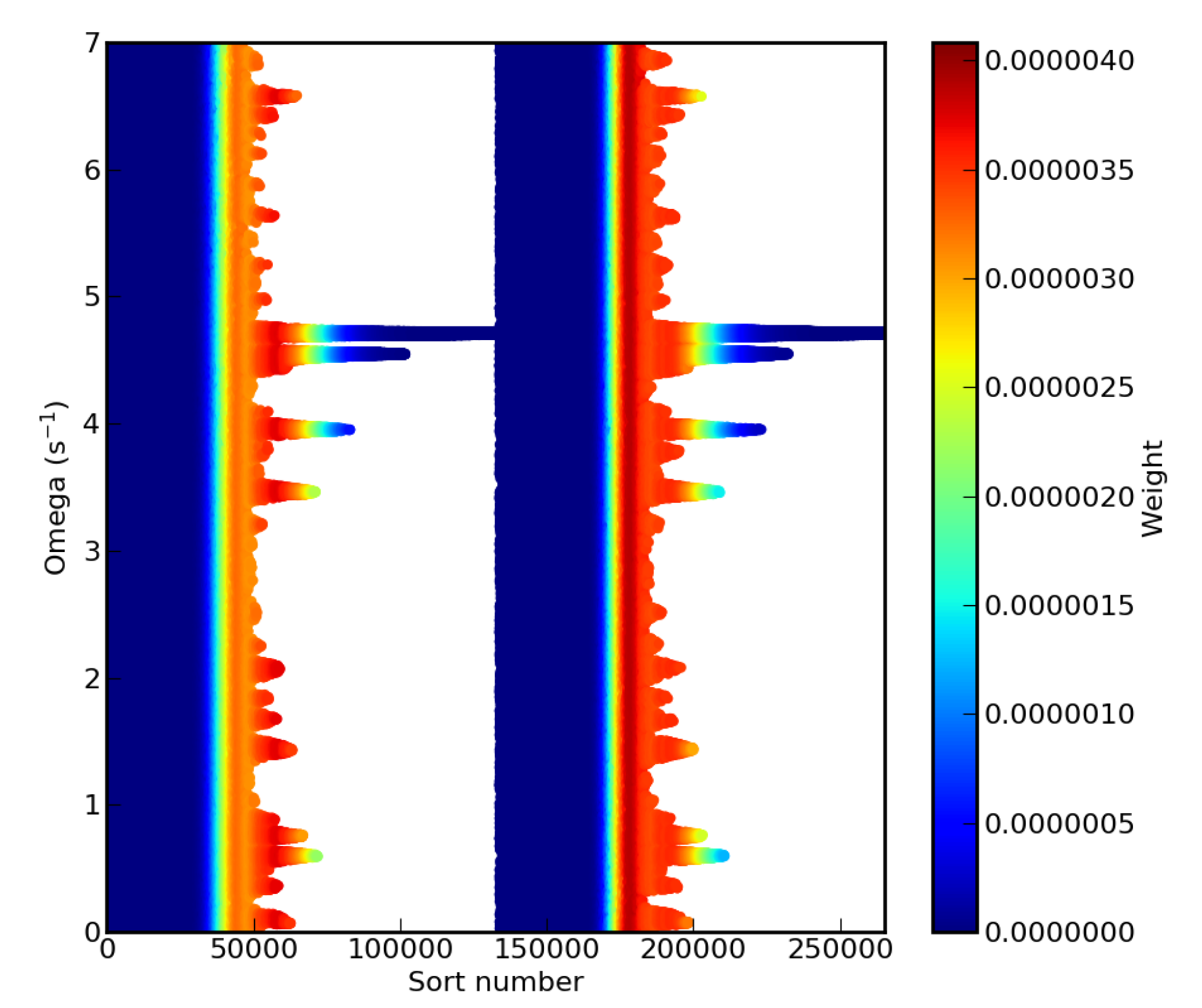
3.2. The Mean Shift Algorithm for Cluster Recognition
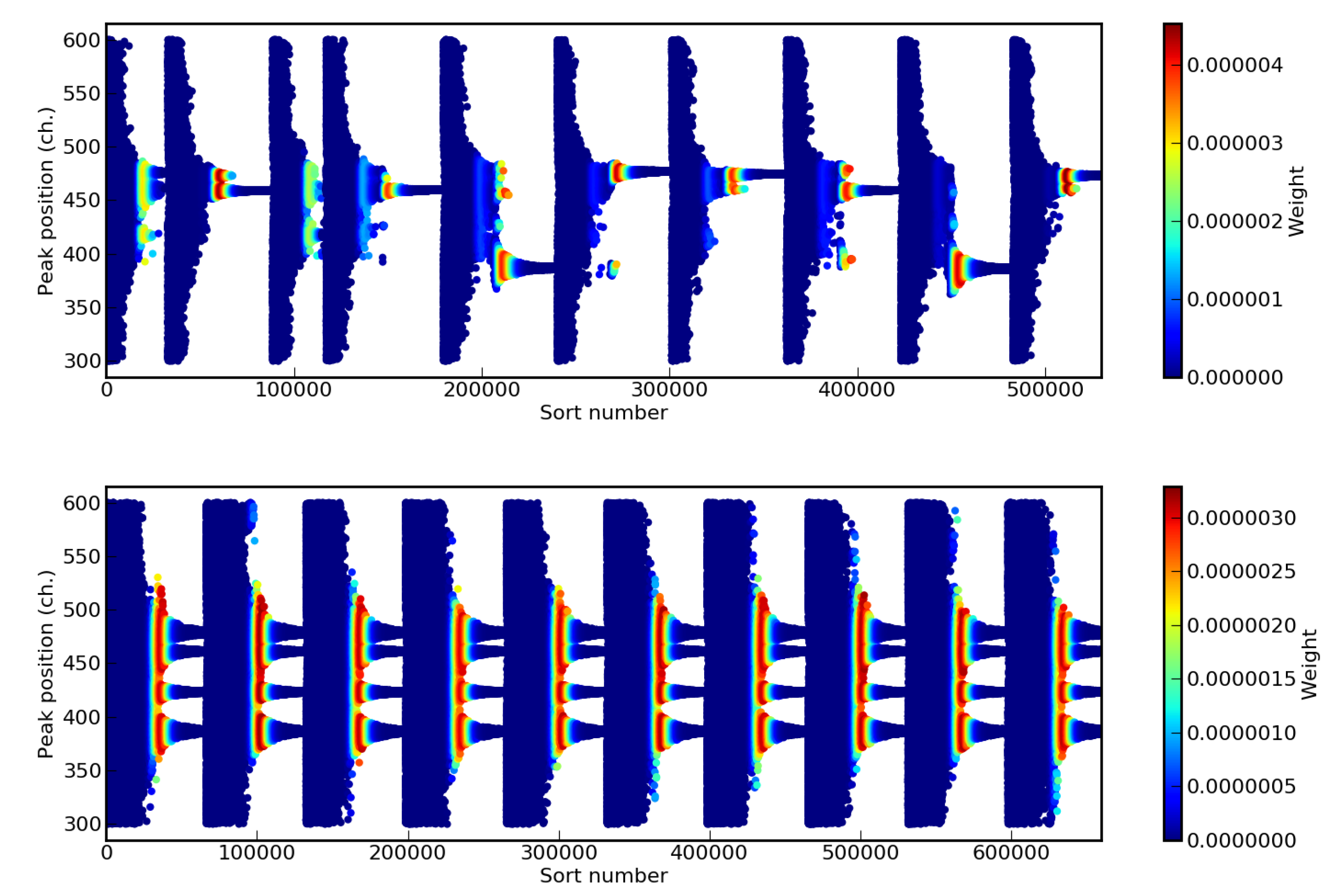
3.3. Mean Shift Implementation in NestedFit
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Trotta, R. Bayes in the sky: Bayesian inference and model selection in cosmology. Contemp. Phys. 2008, 49, 71–104. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P.; Bridges, M. MultiNest: An efficient and robust Bayesian inference tool for cosmology and particle physics. Mon. Not. R. Astron. Soc. 2009, 398, 1601–1614. [Google Scholar] [CrossRef]
- Xu, J.; van Dyk, D.A.; Kashyap, V.L.; Siemiginowska, A.; Connors, A.; Drake, J.; Meng, X.L.; Ratzlaff, P.; Yu, Y. A Fully Bayesian Method for Jointly Fitting Instrumental Calibration and X-ray Spectral Models. Astrophys. J. 2014, 794, 97. [Google Scholar] [CrossRef]
- Yu, X.; Zanna, G.D.; Stenning, D.C.; Cisewski-Kehe, J.; Kashyap, V.L.; Stein, N.; van Dyk, D.A.; Warren, H.P.; Weber, M.A. Incorporating Uncertainties in Atomic Data into the Analysis of Solar and Stellar Observations: A Case Study in Fe xiii. Astrophys. J. 2018, 866, 146. [Google Scholar] [CrossRef]
- Günther, M.N.; Pozuelos, F.J.; Dittmann, J.A.; Dragomir, D.; Kane, S.R.; Daylan, T.; Feinstein, A.D.; Huang, C.X.; Morton, T.D.; Bonfanti, A.; et al. A super-Earth and two sub-Neptunes transiting the nearby and quiet M dwarf TOI-270. Nat. Astron. 2019, 3, 1099–1108. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4M⊙. arXiv 2020, arXiv:2001.01761. [Google Scholar]
- Particle Data Group. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Langenberg, A.; Svensson, J.; Marchuk, O.; Fuchert, G.; Bozhenkov, S.; Damm, H.; Pasch, E.; Pavone, A.; Thomsen, H.; Pablant, N.A.; et al. Inference of temperature and density profiles via forward modeling of an X-ray imaging crystal spectrometer within the Minerva Bayesian analysis framework. Rev. Sci. Instrum. 2019, 90, 063505. [Google Scholar] [CrossRef]
- Milhone, J.; Flanagan, K.; Nornberg, M.D.; Tabbutt, M.; Forest, C.B. A spectrometer for high-precision ion temperature and velocity measurements in low-temperature plasmas. Rev. Sci. Instrum. 2019, 90, 063502. [Google Scholar] [CrossRef]
- Barber, D. Bayesian Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- von Toussaint, U. Bayesian inference in physics. Rev. Mod. Phys. 2011, 83, 943–999. [Google Scholar] [CrossRef]
- von der Linden, W.; Dose, V.; von Toussaint, U. Bayesian Probability Theory: Applications in the Physical Sciences; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- King, G.; Lovell, A.; Neufcourt, L.; Nunes, F. Direct Comparison between Bayesian and Frequentist Uncertainty Quantification for Nuclear Reactions. Phys. Rev. Lett. 2019, 122, 232502. [Google Scholar] [CrossRef]
- Ozturk, F.C.; Akkus, B.; Atanasov, D.; Beyer, H.; Bosch, F.; Boutin, D.; Brandau, C.; Bühler, P.; Cakirli, R.B.; Chen, R.J.; et al. New test of modulated electron capture decay of hydrogen-like 142Pm ions: Precision measurement of purely exponential decay. Phys. Lett. B 2019, 797, 134800. [Google Scholar] [CrossRef]
- Stockton, J.K.; Wu, X.; Kasevich, M.A. Bayesian estimation of differential interferometer phase. Phys. Rev. A 2007, 76, 033613. [Google Scholar] [CrossRef]
- Calonico, D.; Levi, F.; Lorini, L.; Mana, G. Bayesian inference of a negative quantity from positive measurement results. Metrologia 2009, 46, 267. [Google Scholar] [CrossRef]
- Mooser, A.; Kracke, H.; Blaum, K.; Bräuninger, S.A.; Franke, K.; Leiteritz, C.; Quint, W.; Rodegheri, C.C.; Ulmer, S.; Walz, J. Resolution of Single Spin Flips of a Single Proton. Phys. Rev. Lett. 2013, 110, 140405. [Google Scholar] [CrossRef]
- Covita, D.S.; Anagnostopoulos, D.F.; Fuhrmann, H.; Gorke, H.; Gotta, D.; Gruber, A.; Hirtl, A.; Ishiwatari, T.; Indelicato, P.; Jensen, T.S.; et al. Line shape analysis of the Kβ transition in muonic hydrogen. Eur. Phys. J. D 2018, 72, 72. [Google Scholar] [CrossRef]
- Heim, P.; Rumetshofer, M.; Ranftl, S.; Thaler, B.; Ernst, W.E.; Koch, M.; von der Linden, W. Bayesian Analysis of Femtosecond Pump-Probe Photoelectron-Photoion Coincidence Spectra with Fluctuating Laser Intensities. Entropy 2019, 21, 93. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Lawrence, A. Probability in Physics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Skilling, J. Nested Sampling. AIP Conf. Proc. 2004, 735, 395–405. [Google Scholar] [CrossRef]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Sivia, D.S.; Skilling, J. Data Analysis: A Bayesian Tutorial, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Feroz, F.; Hobson, M.P. Multimodal nested sampling: An efficient and robust alternative to Markov Chain Monte Carlo methods for astronomical data analyses. Mon. Not. R. Astron. Soc. 2008, 384, 449–463. [Google Scholar] [CrossRef]
- Corsaro, E.; Ridder, J.D. DIAMONDS: A new Bayesian nested sampling tool. Astron. Astrophys. 2014, 571, A71. [Google Scholar] [CrossRef]
- Handley, W.J.; Hobson, M.P.; Lasenby, A.N. Polychord: Next-generation nested sampling. Mon. Not. R. Astron. Soc. 2015, 453, 4384–4398. [Google Scholar] [CrossRef]
- Brewer, B.J.; Foreman-Mackey, D. DNest4: Diffusive Nested Sampling in C++ and Python. J. Stat. Softw. 2018, 86, 33. [Google Scholar] [CrossRef]
- Speagle, J.S. Dynesty: A Dynamic Nested Sampling Package for Estimating Bayesian Posteriors and Evidences. arXiv 2019, arXiv:1904.02180. [Google Scholar] [CrossRef]
- Murray, I.; MacKay, D.J.C.; Ghahramani, Z.; Skilling, J. Nested Sampling for Potts Models. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2006; Volume 18, pp. 947–954. [Google Scholar]
- Nielsen, S.O. Nested sampling in the canonical ensemble: Direct calculation of the partition function from NVT trajectories. J. Chem. Phys. 2013, 139, 124104. [Google Scholar] [CrossRef] [PubMed]
- Baldock, R.J.N.; Bernstein, N.; Salerno, K.M.; Pártay, L.B.; Csányi, G. Constant-pressure nested sampling with atomistic dynamics. Phys. Rev. E 2017, 96, 043311. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Csányi, G. Nested Transition Path Sampling. Phys. Rev. Lett. 2018, 120, 250601. [Google Scholar] [CrossRef]
- Pártay, L.B.; Bartók, A.P.; Csányi, G. Efficient Sampling of Atomic Configurational Spaces. J. Phys. Chem. B 2010, 114, 10502–10512. [Google Scholar] [CrossRef]
- Burkoff, N.; Várnai, C.; Wells, S.; Wild, D. Exploring the Energy Landscapes of Protein Folding Simulations with Bayesian Computation. Biophys. J. 2012, 102, 878–886. [Google Scholar] [CrossRef]
- Pártay, L.B.; Bartók, A.P.; Csányi, G. Nested sampling for materials: The case of hard spheres. Phys. Rev. E 2014, 89, 022302. [Google Scholar] [CrossRef]
- Trassinelli, M. Bayesian data analysis tools for atomic physics. Nucl. Instrum. Methods B 2017, 408, 301–312. [Google Scholar] [CrossRef]
- Trassinelli, M. The Nested_fit Data Analysis Program. Proceedings 2019, 33, 14. [Google Scholar] [CrossRef]
- Mukherjee, P.; Parkinson, D.; Liddle, A.R. A Nested Sampling Algorithm for Cosmological Model Selection. Astrophys. J. Lett. 2006, 638, L51. [Google Scholar] [CrossRef]
- Veitch, J.; Vecchio, A. Bayesian coherent analysis of in-spiral gravitational wave signals with a detector network. Phys. Rev. D 2010, 81, 062003. [Google Scholar] [CrossRef]
- Brewer, B.J.; Pártay, L.B.; Csányi, G. Diffusive nested sampling. Stat. Comput. 2011, 21, 649–656. [Google Scholar] [CrossRef]
- Skilling, J. Galilean and Hamiltonian Monte Carlo. Proceedings 2019, 33, 19. [Google Scholar] [CrossRef]
- Martiniani, S.; Stevenson, J.D.; Wales, D.J.; Frenkel, D. Superposition Enhanced Nested Sampling. Phys. Rev. X 2014, 4, 031034. [Google Scholar] [CrossRef]
- Bruchner, J. A statistical test for nested sampling algorithms. Stat. Comput. 2016, 26, 383–392. [Google Scholar] [CrossRef]
- Trassinelli, M.; Anagnostopoulos, D.F.; Borchert, G.; Dax, A.; Egger, J.P.; Gotta, D.; Hennebach, M.; Indelicato, P.; Liu, Y.W.; Manil, B.; et al. Measurement of the charged pion mass using X-ray spectroscopy of exotic atoms. Phys. Lett. B 2016, 759, 583–588. [Google Scholar] [CrossRef]
- Trassinelli, M.; Anagnostopoulos, D.; Borchert, G.; Dax, A.; Egger, J.P.; Gotta, D.; Hennebach, M.; Indelicato, P.; Liu, Y.W.; Manil, B.; et al. Measurement of the charged pion mass using a low-density target of light atoms. EPJ Web Conf. 2016, 130, 01022. [Google Scholar] [CrossRef]
- Papagiannouli, I.; Patanen, M.; Blanchet, V.; Bozek, J.D.; de Anda Villa, M.; Huttula, M.; Kokkonen, E.; Lamour, E.; Mevel, E.; Pelimanni, E.; et al. Depth Profiling of the Chemical Composition of Free-Standing Carbon Dots Using X-ray Photoelectron Spectroscopy. J. Phys. Chem. A 2018, 122, 14889–14897. [Google Scholar] [CrossRef]
- Villa, M.D.A.; Gaudin, J.; Amans, D.; Boudjada, F.; Bozek, J.; Grisenti, R.E.; Lamour, E.; Laurens, G.; Macé, S.; Nicolas, C.; et al. Assessing the Surface Oxidation State of Free-Standing Gold Nanoparticles Produced by Laser Ablation. Langmuir 2019, 35, 11859–11871. [Google Scholar] [CrossRef] [PubMed]
- Dierckx, P. Curve and Surface Fitting with Splines; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Skilling, J. Nested Sampling’s Convergence. AIP Conf. Proc. 2009, 1193, 277–291. [Google Scholar] [CrossRef]
- Chopin, N.; Robert, C.P. Properties of nested sampling. Biometrika 2010, 97, 741–755. [Google Scholar] [CrossRef]
- Theisen, M. Analyse der Linienform von Röntgenübergängen Nach der Bayesmethode. Master’s Thesis, Faculty of Mathematics, Computer Science and Natural Sciences, RWTH Aachen University, Aachen, Germany, 2013. [Google Scholar]
- Fukunaga, K.; Hostetler, L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern. Anal. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Trassinelli, M.; Kumar, A.; Beyer, H.F.; Indelicato, P.; Märtin, R.; Reuschl, R.; Kozhedub, Y.S.; Brandau, C.; Bräuning, H.; Geyer, S.; et al. Observation of the 2p3/2→2s1/2 intra-shell transition in He-like uranium. Eur. Phys. Lett. 2009, 87, 63001. [Google Scholar] [CrossRef]
- Gordon, C.; Trotta, R. Bayesian calibrated significance levels applied to the spectral tilt and hemispherical asymmetry. Mon. Not. R. Astron. Soc. 2007, 382, 1859–1863. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trassinelli, M.; Ciccodicola, P. Mean Shift Cluster Recognition Method Implementation in the Nested Sampling Algorithm. Entropy 2020, 22, 185. https://doi.org/10.3390/e22020185
Trassinelli M, Ciccodicola P. Mean Shift Cluster Recognition Method Implementation in the Nested Sampling Algorithm. Entropy. 2020; 22(2):185. https://doi.org/10.3390/e22020185
Chicago/Turabian StyleTrassinelli, Martino, and Pierre Ciccodicola. 2020. "Mean Shift Cluster Recognition Method Implementation in the Nested Sampling Algorithm" Entropy 22, no. 2: 185. https://doi.org/10.3390/e22020185
APA StyleTrassinelli, M., & Ciccodicola, P. (2020). Mean Shift Cluster Recognition Method Implementation in the Nested Sampling Algorithm. Entropy, 22(2), 185. https://doi.org/10.3390/e22020185




