Effect of Prandtl Number on Mixed Convective Heat Transfer from a Porous Cylinder in the Steady Flow Regime
Abstract
1. Introduction
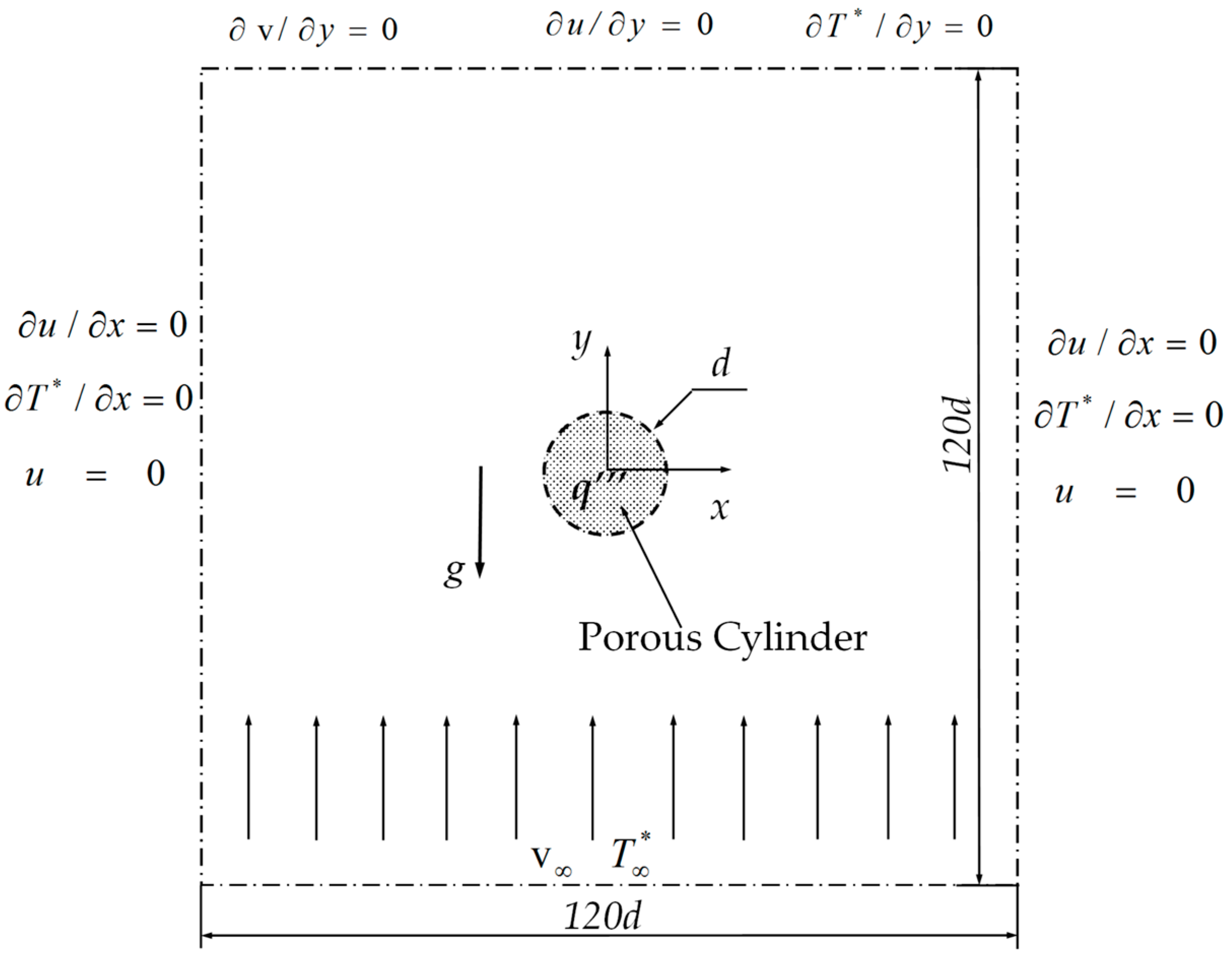
2. Problem Statement and Mathematical Formulation
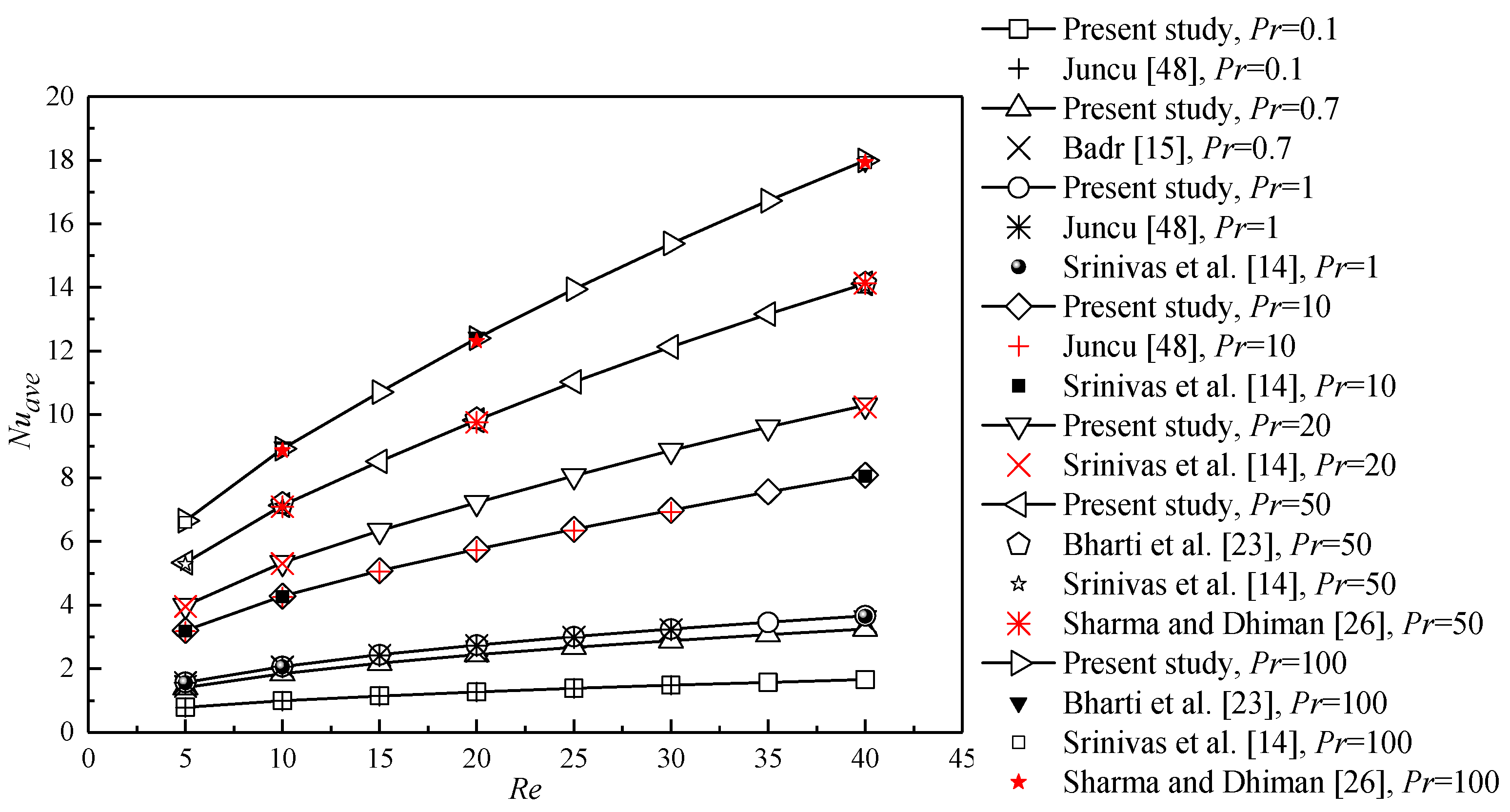
3. Grid-Independence Analysis and Code Validation
4. Results and Discussions
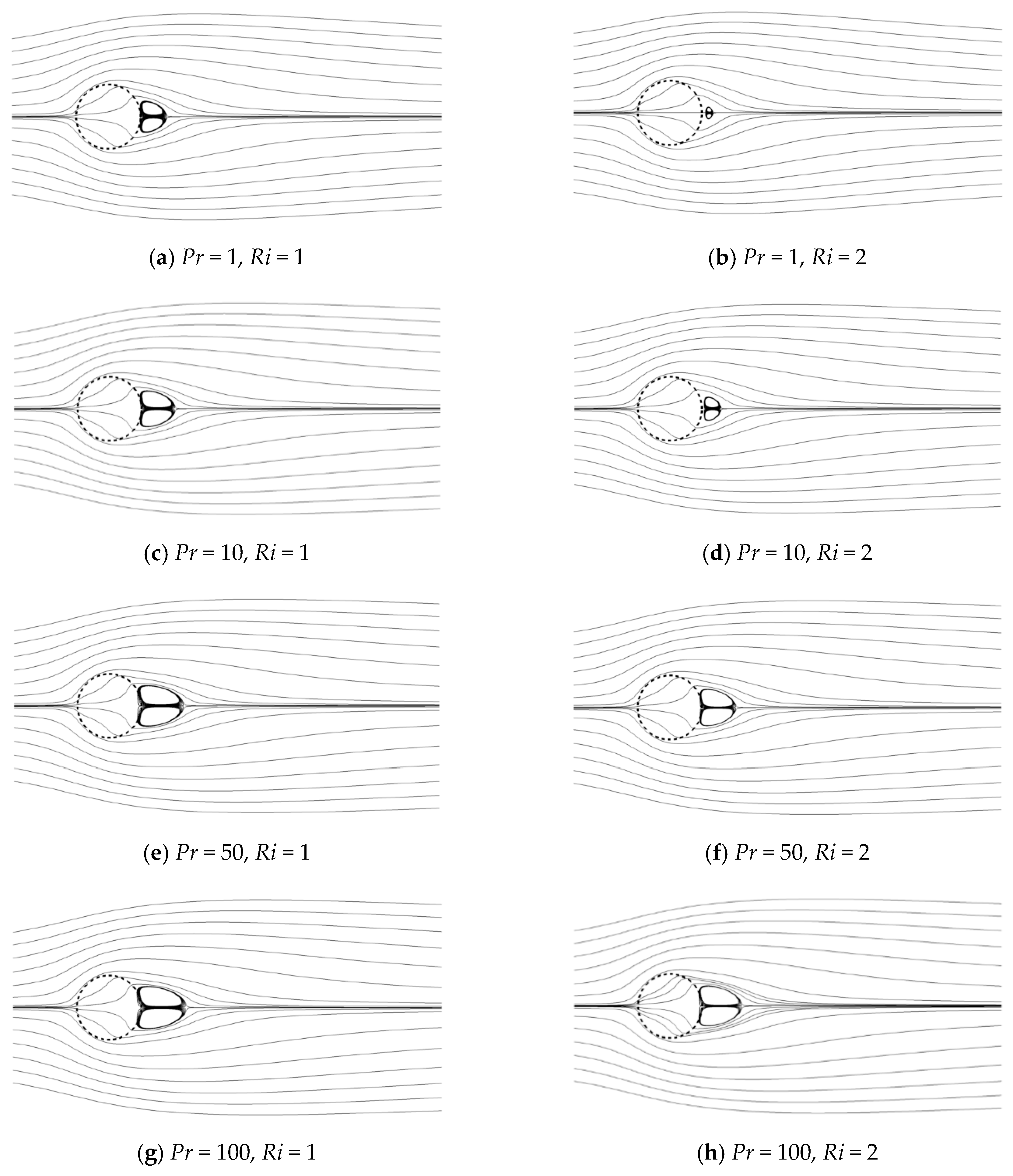
4.1. Flow Pattern
4.2. Temperature Field
4.3. Heat Transfer Rate
4.3.1. Local Nusselt Number
4.3.2. Enhancement Ratio
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| g | gravitational acceleration, [m/s2] |
| q′″ | heat source, [W/m3] |
| d | diameter of cylinder, [m] |
| A | surface area, [m2] |
| K | permeability of cylinder, [m2] |
| kf | thermal conductivity of fluid, [W/(m·°C)] |
| ke | effective thermal conductivity, [W/(m·°C)] |
| Rc | thermal conductivity ratio |
| h | heat transfer coefficient, [W/(m2·°C)] |
| x | dimensional horizontal coordinate, [m] |
| y | dimensional vertical coordinate, [m] |
| u | dimensional x-component velocity, [m/s] |
| v | dimensional y-component velocity, [m/s] |
| p | pressure, [Pa] |
| T* | temperature, [°C] |
| X | dimensionless horizontal coordinate |
| Y | dimensionless vertical coordinate |
| U | dimensionless x-component velocity |
| V | dimensionless y-component velocity |
| P | dimensionless pressure |
| T | dimensionless temperature |
| Lw | the wake length |
| Lp | the penetration depth |
| Re | Reynolds number |
| Pr | Prandtl number |
| Gr | Grashof number |
| Ri | Richardson number |
| Da | Darcy number |
| Nu | Nusselt number |
| Er | enhancement ratio |
| n | the dimensionless normal direction |
| Greek symbols | |
| α | thermal diffusivity, [m2/s] |
| β | thermal expansion coefficient, [°C−1] |
| υ | fluid kinematic viscosity, [m2/s] |
| ε | fluid kinematic viscosity porosity |
| ρ | fluid density, [kg/m3] |
| δ | the thickness of the thermal boundary layer |
| a binary constant | |
| Subscripts | |
| ∞ | free stream |
| ave | average |
References
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Vadász, P. Emerging Topics in Heat and Mass Transfer in Porous Media: From Bioengineering and Microelectronics to Nanotechnology; Springer Science & Business Media: New York, NY, USA, 2008; Volume 22. [Google Scholar]
- Seo, J.-W.; Kim, Y.-H.; Kim, D.; Choi, Y.-D.; Lee, K.-J. Heat transfer and pressure drop characteristics in straight microchannel of printed circuit heat exchangers. Entropy 2015, 17, 3438–3457. [Google Scholar] [CrossRef]
- Ma, H.; Duan, Z.; Su, L.; Ning, X.; Bai, J.; Lv, X. Fluid flow and entropy generation analysis of Al2O3—Water nanofluid in microchannel plate fin heat sinks. Entropy 2019, 21, 739. [Google Scholar] [CrossRef]
- Mahdi, R.A.; Mohammed, H.; Munisamy, K.; Saeid, N. Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew. Sustain. Energy Rev. 2015, 41, 715–734. [Google Scholar] [CrossRef]
- Smakulski, P.; Pietrowicz, S. A review of the capabilities of high heat flux removal by porous materials, microchannels and spray cooling techniques. Appl. Therm. Eng. 2016, 104, 636–646. [Google Scholar] [CrossRef]
- Chen, H.; Zheng, Z.; Chen, Z.; Bi, X. A lattice gas automata model for the coupled heat transfer and chemical reaction of gas flow around and through a porous circular cylinder. Entropy 2016, 18, 2. [Google Scholar] [CrossRef]
- Dhinakaran, S.; Ponmozhi, J. Heat transfer from a permeable square cylinder to a flowing fluid. Energy Convers. Manag. 2011, 52, 2170–2182. [Google Scholar] [CrossRef]
- Rashidi, S.; Hayatdavoodi, M.; Esfahani, J.A. Vortex shedding suppression and wake control: A review. Ocean Eng. 2016, 126, 57–80. [Google Scholar] [CrossRef]
- Al-Sumaily, G.F.; Thompson, M.C. Forced convection from a circular cylinder in pulsating flow with and without the presence of porous media. Int. J. Heat Mass Transf. 2013, 61, 226–244. [Google Scholar] [CrossRef]
- Hu, H.; Koochesfahani, M. Thermal effects on the wake of a heated circular cylinder operating in mixed convection regime. J. Fluid Mech. 2011, 685, 235–270. [Google Scholar] [CrossRef]
- Ahmad, R.; Qureshi, Z. Laminar mixed convection from a uniform heat flux horizontal cylinder in a crossflow. J. Thermophys. Heat Transf. 1992, 6, 277–287. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Salman, Y.K. Experimental investigation of mixed convection heat transfer for thermally developing flow in a horizontal circular cylinder. Appl. Therm. Eng. 2007, 27, 1522–1533. [Google Scholar] [CrossRef]
- Srinivas, A.T.; Bharti, R.P.; Chhabra, R.P. Mixed convection heat transfer from a cylinder in power-law fluids: Effect of aiding buoyancy. Ind. Eng. Chem. Res. 2009, 48, 9735–9754. [Google Scholar] [CrossRef]
- Badr, H. A theoretical study of laminar mixed convection from a horizontal cylinder in a cross stream. Int. J. Heat Mass Transf. 1983, 26, 639–653. [Google Scholar] [CrossRef]
- Sharma, N.; Dhiman, A.K.; Kumar, S. Mixed convection flow and heat transfer across a square cylinder under the influence of aiding buoyancy at low Reynolds numbers. Int. J. Heat Mass Transf. 2012, 55, 2601–2614. [Google Scholar] [CrossRef]
- Wu, H.-W.; Wang, R.-H. Mixed convective heat transfer past a heated square porous cylinder in a horizontal channel with varying channel height. J. Heat Transf. 2011, 133. [Google Scholar] [CrossRef]
- Yu, S.; Yu, P.; Tang, T. Effect of thermal buoyancy on flow and heat transfer around a permeable circular cylinder with internal heat generation. Int. J. Heat Mass Transf. 2018, 126, 1143–1163. [Google Scholar] [CrossRef]
- Dhiman, A.; Chhabra, R.; Sharma, A.; Eswaran, V. Effects of Reynolds and Prandtl numbers on heat transfer across a square cylinder in the steady flow regime. Numer. Heat Transf. 2006, 49, 717–731. [Google Scholar] [CrossRef]
- Ajith Kumar, S.; Mathur, M.; Sameen, A.; Anil Lal, S. Effects of Prandtl number on the laminar cross flow past a heated cylinder. Phys. Fluids 2016, 28, 113603. [Google Scholar] [CrossRef]
- Dennis, S.C.R.; Hudson, J.; Smith, N. Steady laminar forced convection from a circular cylinder at low Reynolds numbers. Phys. Fluids 1968, 11, 933–940. [Google Scholar] [CrossRef]
- Vilimpoq, V.; Cole, R.; Sukanek, P. Heat transfer in Newtonian liquids around a circular cylinder. Int. J. Heat Mass Transf. 1990, 33, 447–456. [Google Scholar] [CrossRef]
- Bharti, R.P.; Chhabra, R.; Eswaran, V. A numerical study of the steady forced convection heat transfer from an unconfined circular cylinder. Heat Mass Transf. 2007, 43, 639–648. [Google Scholar] [CrossRef]
- Dhiman, A.; Chhabra, R.; Eswaran, V. Flow and heat transfer across a confined square cylinder in the steady flow regime: Effect of Peclet number. Int. J. Heat Mass Transf. 2005, 48, 4598–4614. [Google Scholar] [CrossRef]
- Sahu, A.K.; Chhabra, R.; Eswaran, V. Effects of Reynolds and Prandtl numbers on heat transfer from a square cylinder in the unsteady flow regime. Int. J. Heat Mass Transf. 2009, 52, 839–850. [Google Scholar] [CrossRef]
- Sharma, V.; Dhiman, A.K. Heat transfer from a rotating circular cylinder in the steady regime: Effects of Prandtl number. Therm. Sci 2012, 16, 79–91. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, X.; Zhang, J. Effects of Reynolds and Prandtl numbers on heat transfer around a circular cylinder by the simplified thermal lattice Boltzmann model. Commun. Comput. Phys. 2015, 17, 937–959. [Google Scholar] [CrossRef]
- Sufyan, M.; Manzoor, S.; Sheikh, N.A. Free stream flow and forced convection heat transfer across rotating circular cylinder in steady regime: Effects of rotation, Prandtl number and thermal boundary condition. J. Mech. Sci. Technol. 2015, 29, 1781–1797. [Google Scholar] [CrossRef]
- Kim, S.J.; Jang, S.P. Effects of the Darcy number, the Prandtl number, and the Reynolds number on local thermal non-equilibrium. Int. J. Heat Mass Transf. 2002, 45, 3885–3896. [Google Scholar] [CrossRef]
- Anirudh, K.; Dhinakaran, S. Effects of Prandtl number on the forced convection heat transfer from a porous square cylinder. Int. J. Heat Mass Transf. 2018, 126, 1358–1375. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Taj, M.; Ullah, I.; Aldawsari, A.M.; Thounthong, P.; Sooppy Nisar, K. MHD Flow and Heat Transfer in Sodium Alginate Fluid with Thermal Radiation and Porosity Effects: Fractional Model of Atangana–Baleanu Derivative of Non-Local and Non-Singular Kernel. Symmetry 2019, 11, 1295. [Google Scholar] [CrossRef]
- Steinberg, D.S. Cooling Techniques for Electronic Equipment; Wiley-Interscience: New York, NY, USA, 1980; p. 387. [Google Scholar]
- Hardee, H.; Nilson, R. Natural convection in porous media with heat generation. Nucl. Sci. Eng. 1977, 63, 119–132. [Google Scholar] [CrossRef]
- Ismagilov, Z.; Pushkarev, V.; Podyacheva, O.Y.; Koryabkina, N.; Veringa, H. A catalytic heat-exchanging tubular reactor for combining of high temperature exothermic and endothermic reactions. Chem. Eng. J. 2001, 82, 355–360. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Nisar, K.S. Activation energy on MHD flow of titanium alloy (Ti6Al4V) nanoparticle along with a cross flow and streamwise direction with binary chemical reaction and non-linear radiation: Dual Solutions. J. Mater. Res. Technol. 2019. [Google Scholar] [CrossRef]
- Ochoa-Tapia, J.A.; Whitaker, S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid—I. Theoretical development. Int. J. Heat Mass Transf. 1995, 38, 2635–2646. [Google Scholar] [CrossRef]
- Ochoa-Tapia, J.A.; Whitaker, S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid—II. Comparison with experiment. Int. J. Heat Mass Transf. 1995, 38, 2647–2655. [Google Scholar] [CrossRef]
- Alberto, J. Momentum jump condition at the boundary between a porous medium and a homogeneous fluid: Inertial effects. J. Porous Media 1998, 1, 201–217. [Google Scholar]
- Yu, P.; Lee, T.S.; Zeng, Y.; Low, H.T. A numerical method for flows in porous and homogenous fluid domains coupled at the interface by stress jump. Int. J. Numer. Methods Fluids 2007, 53, 1755–1775. [Google Scholar] [CrossRef]
- Chen, X.; Yu, P.; Winoto, S.; Low, H.T. A numerical method for forced convection in porous and homogeneous fluid domains coupled at interface by stress jump. Int. J. Numer. Methods Fluids 2008, 56, 1705–1729. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Roache, P.J. Verification of codes and calculations. AIAA J. 1998, 36, 696–702. [Google Scholar] [CrossRef]
- Yu, P.; Zeng, Y.; Lee, T.; Bai, H.; Low, H. Wake structure for flow past and through a porous square cylinder. Int. J. Heat Fluid Flow 2010, 31, 141–153. [Google Scholar] [CrossRef]
- Yu, P.; Zeng, Y.; Lee, T.S.; Chen, X.B.; Low, H.T. Steady flow around and through a permeable circular cylinder. Comput. Fluids 2011, 42, 1–12. [Google Scholar] [CrossRef]
- Yu, P.; Zeng, Y.; Lee, T.S.; Chen, X.B.; Low, H.T. Numerical simulation on steady flow around and through a porous sphere. Int. J. Heat Fluid Flow 2012, 36, 142–152. [Google Scholar] [CrossRef]
- Chen, X.; Yu, P.; Winoto, S.; Low, H. Numerical analysis for the flow past a porous trapezoidal-cylinder based on the stress-jump interfacial-conditions. Int. J. Numer. Methods Heat Fluid Flow 2009, 19, 223–241. [Google Scholar] [CrossRef]
- Juncu, G. A numerical study of momentum and forced convection heat transfer around two tandem circular cylinders at low Reynolds numbers. Part II: Forced convection heat transfer. Int. J. Heat Mass Transf. 2007, 50, 3799–3808. [Google Scholar] [CrossRef]
- Leal, L.; Acrivos, A. The effect of base bleed on the steady separated flow past bluff objects. J. Fluid Mech. 1969, 39, 735–752. [Google Scholar] [CrossRef]
- Abu-Hijleh, B.A.K. Entropy generation due to cross-flow heat transfer from a cylinder covered with an orthotropic porous layer. Heat Mass Transf. 2002, 39, 27–40. [Google Scholar] [CrossRef]
- Ya, C.; Ghajar, A.; Ma, H. Heat and Mass Transfer: Fundamentals & Applications; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
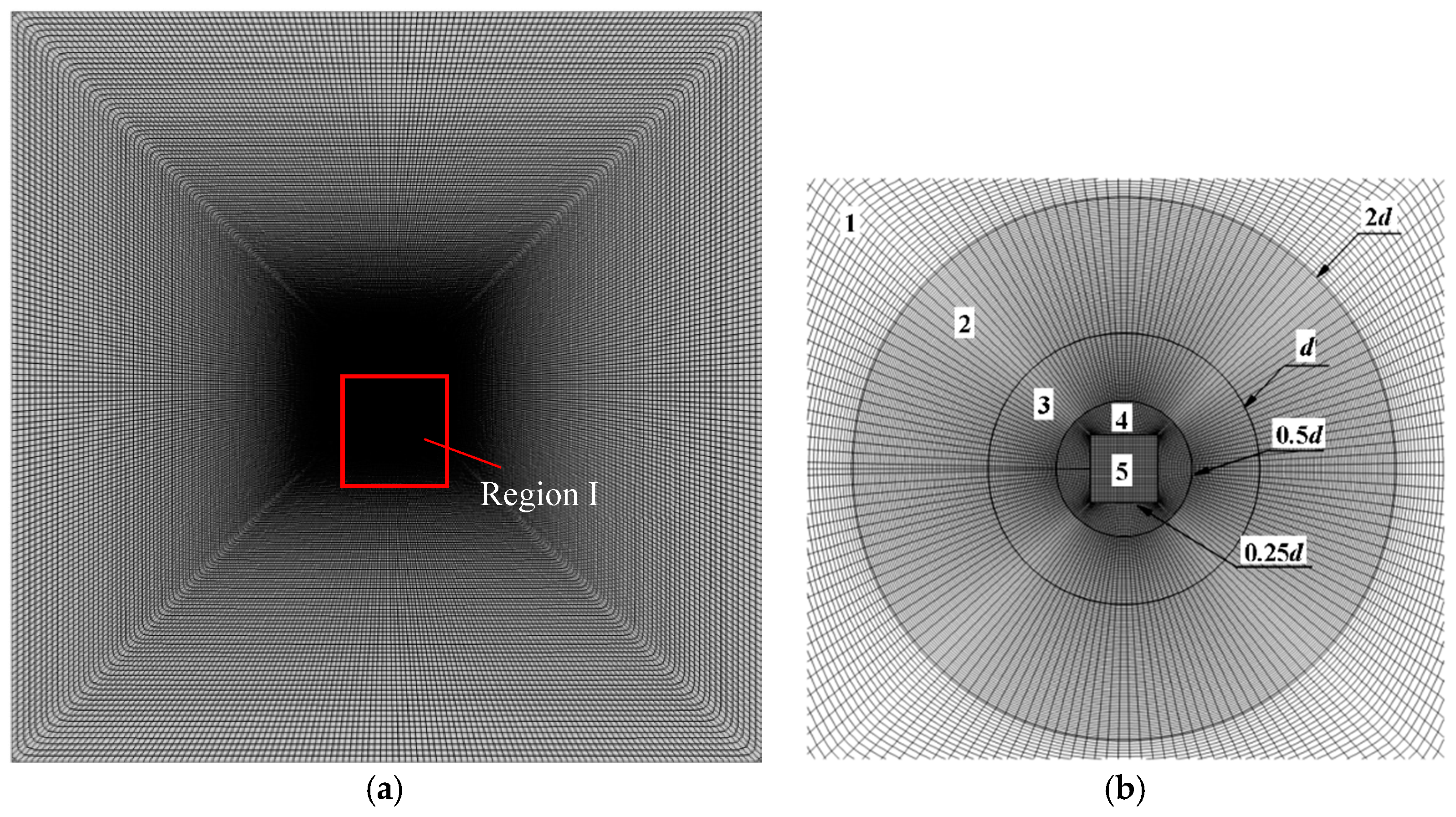
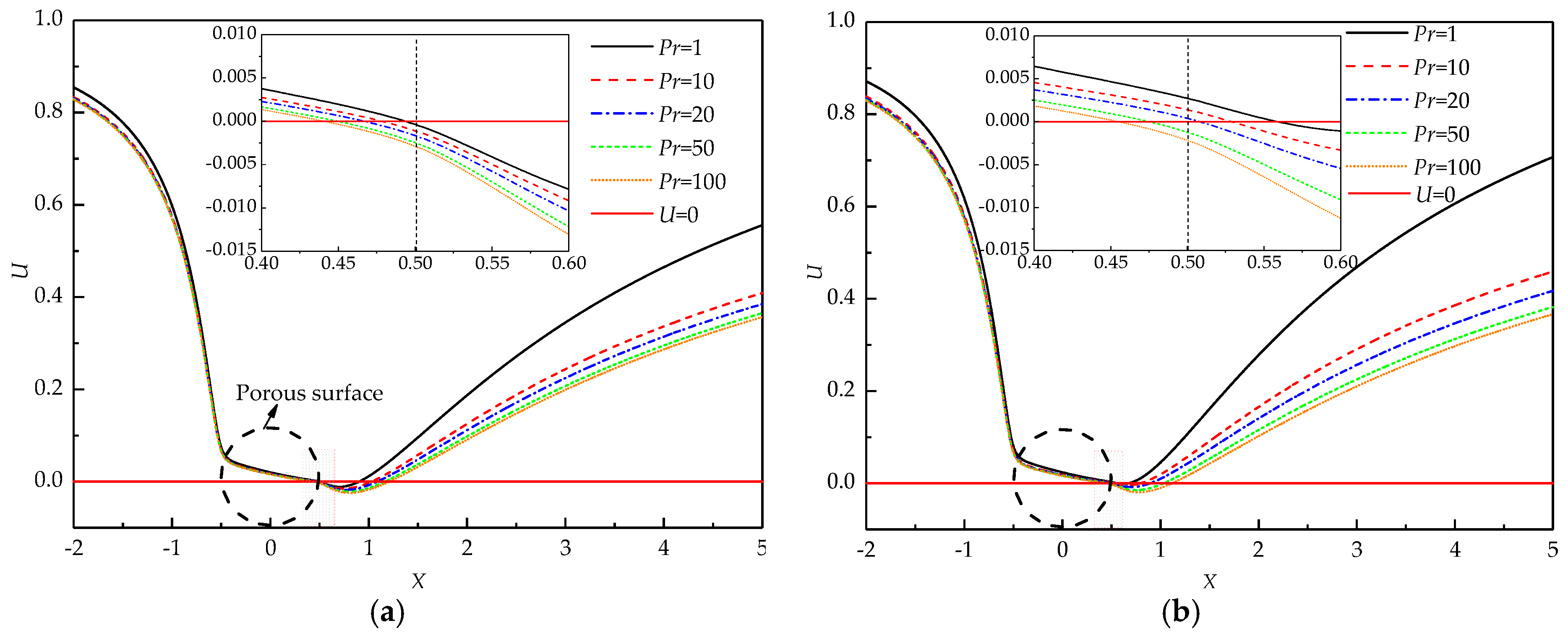
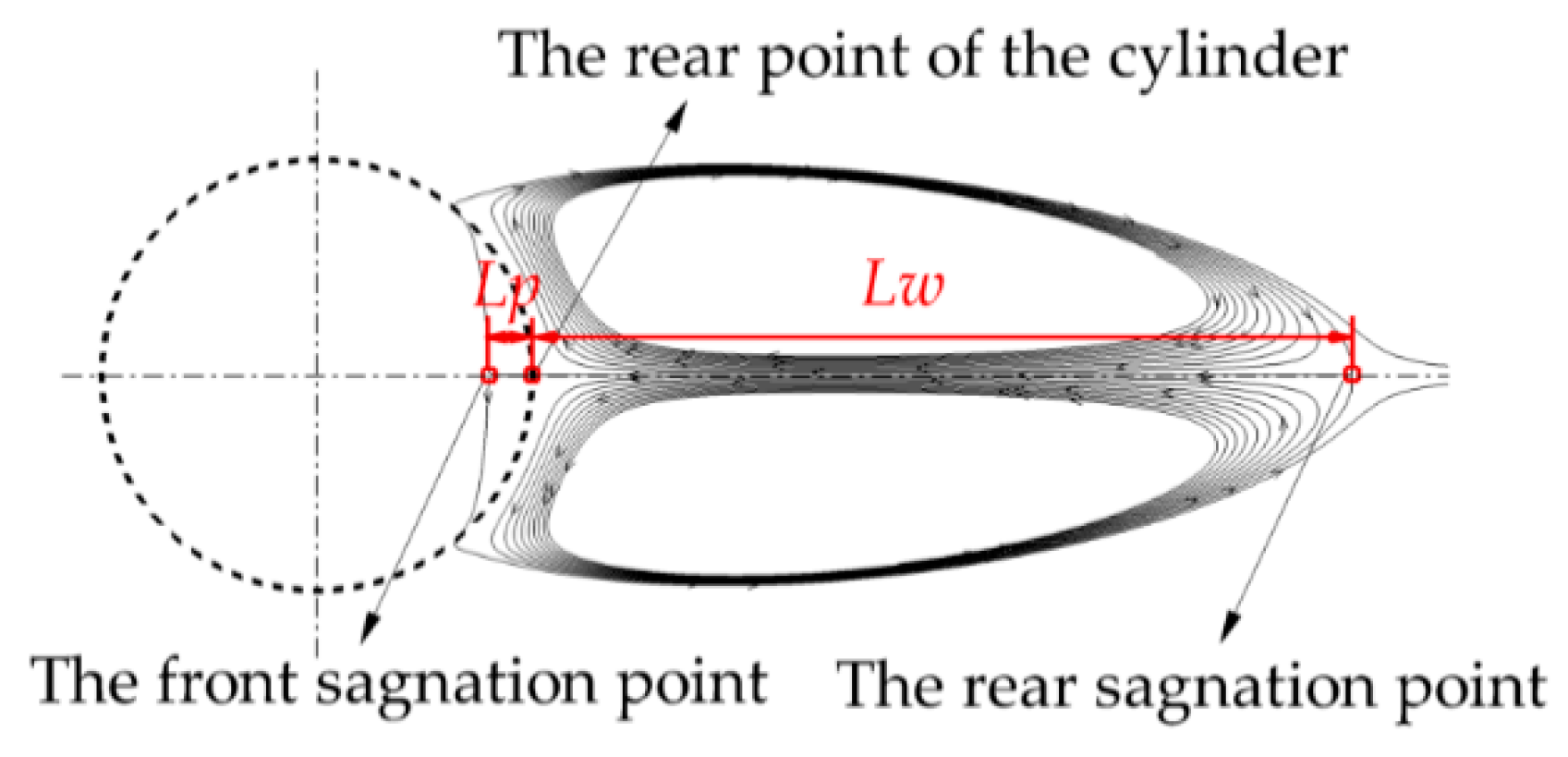

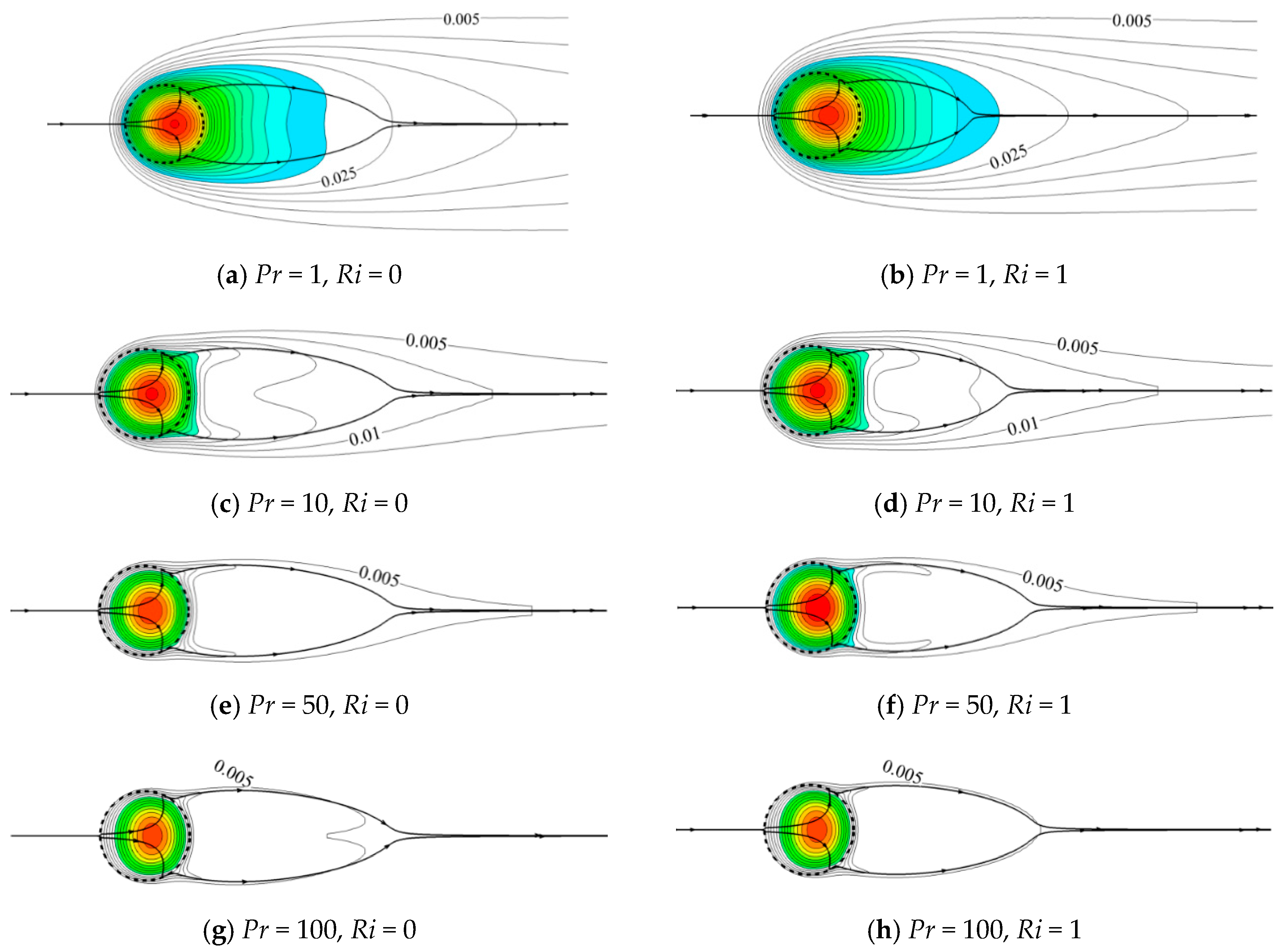

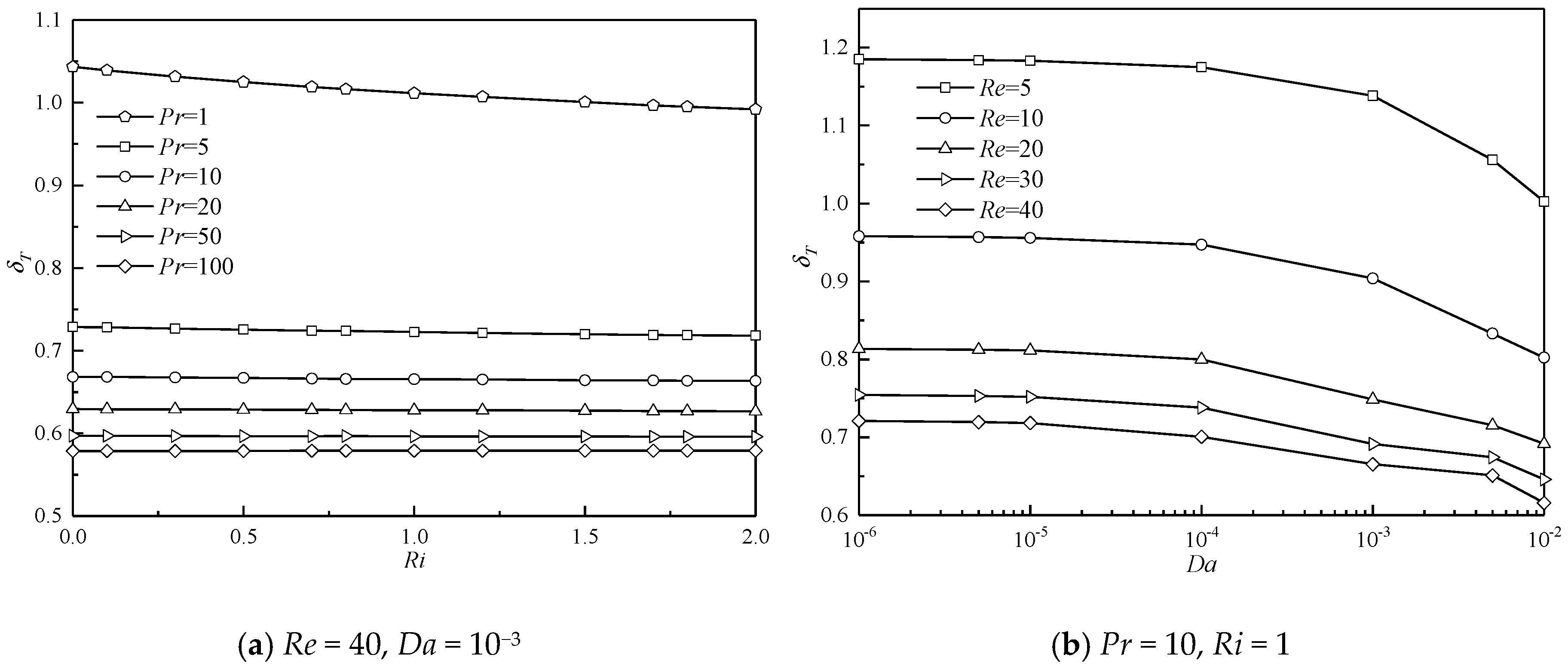
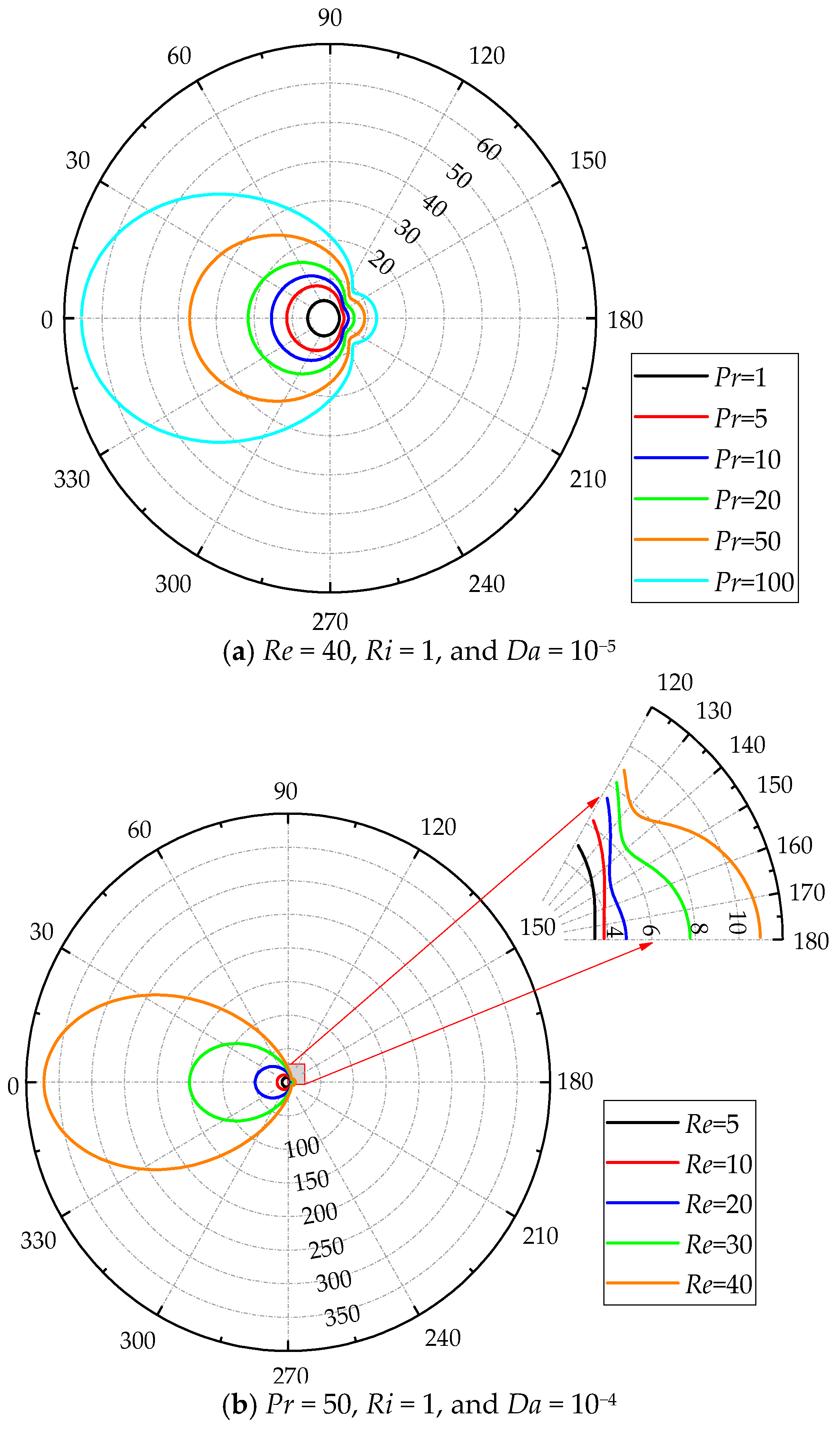
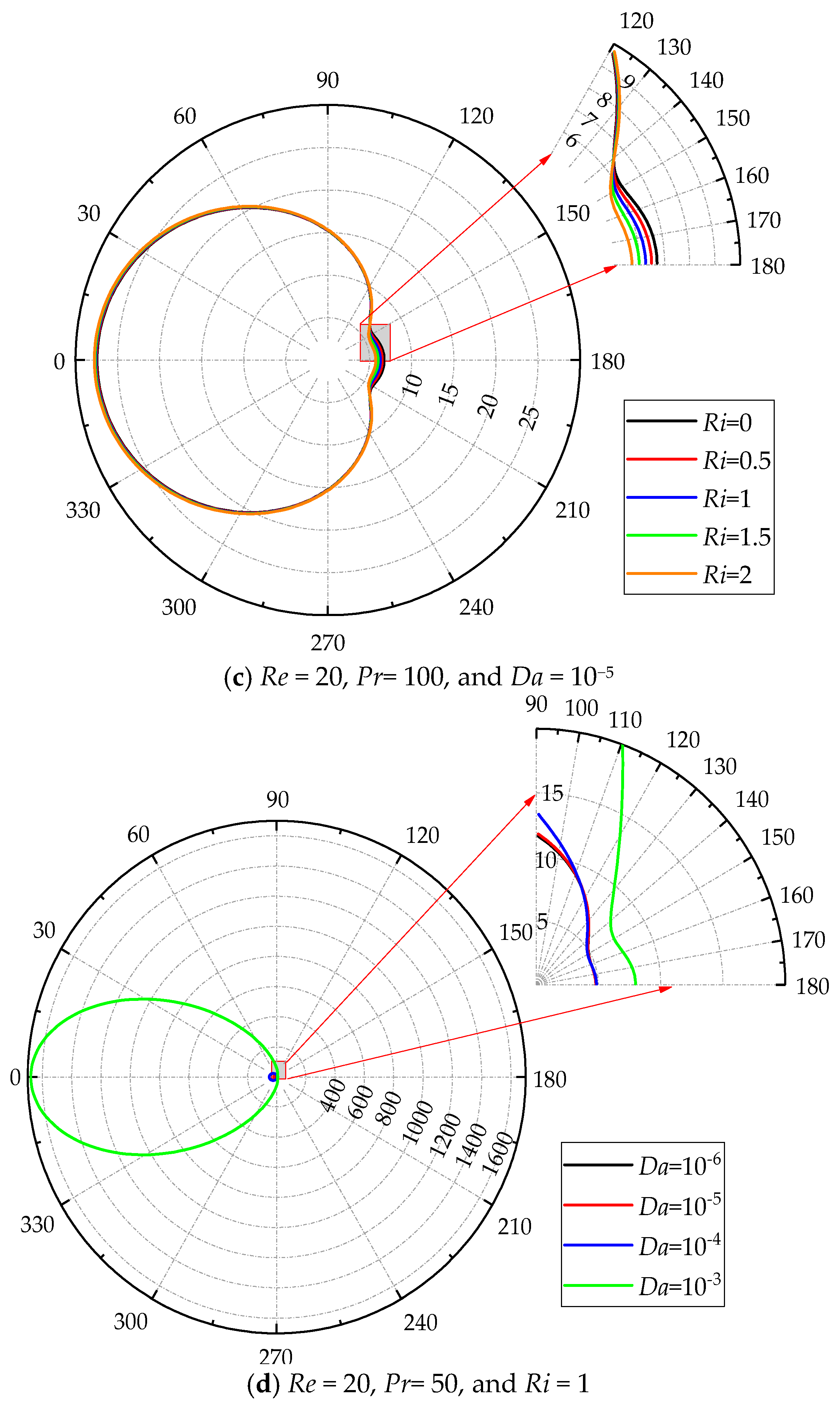

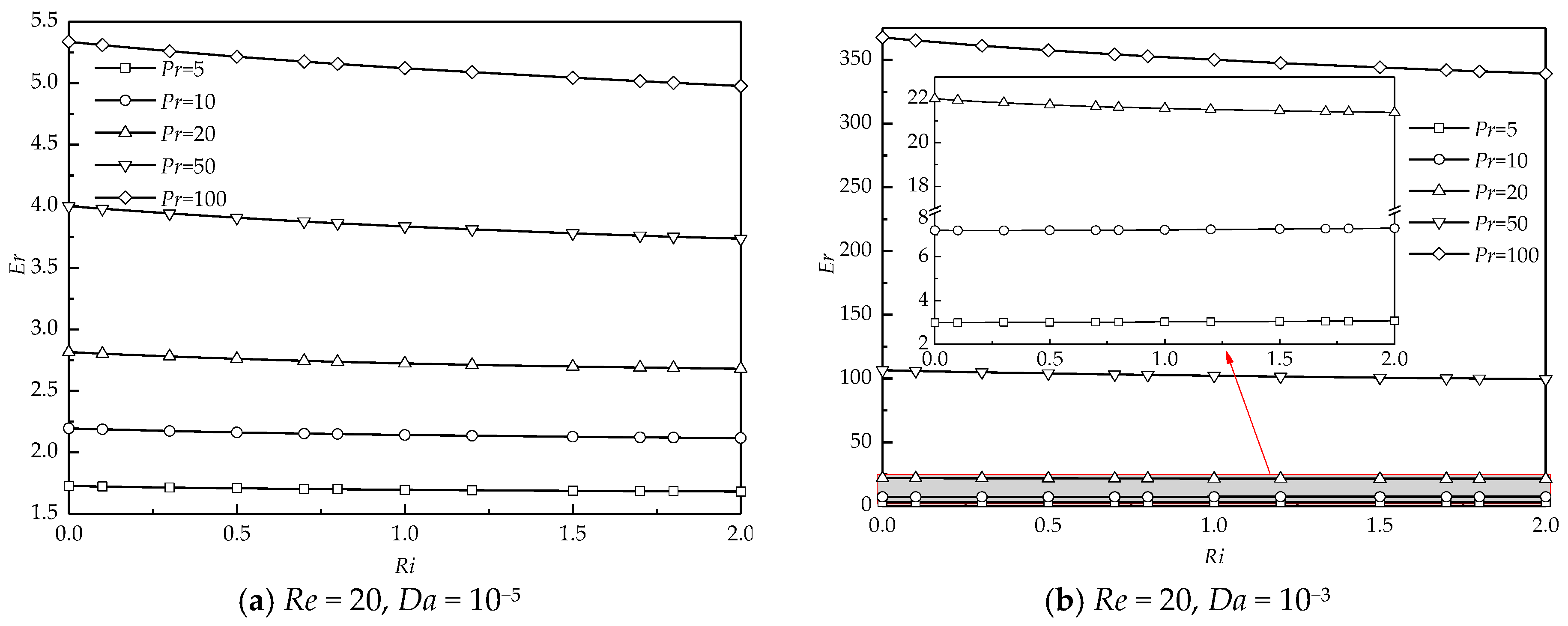
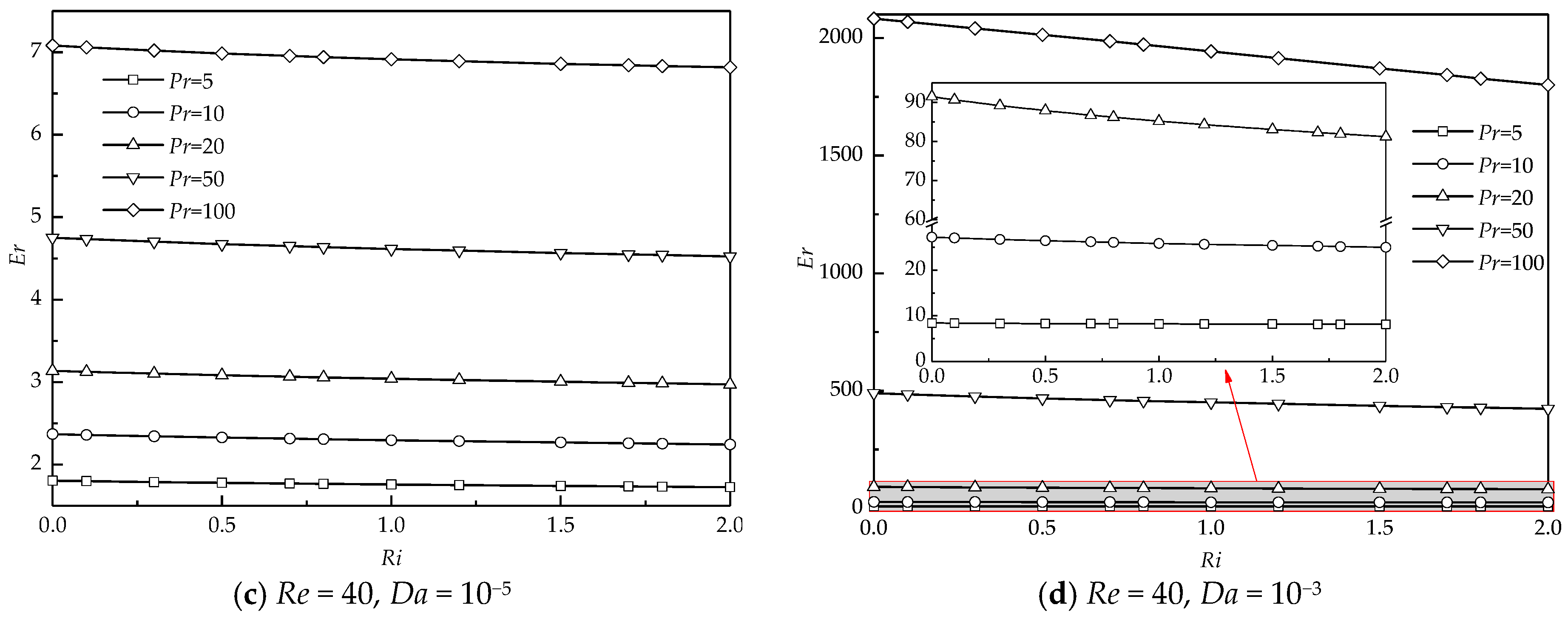
| Case | Total Size | Grid Size | Nuave | ||||
|---|---|---|---|---|---|---|---|
| Block1 | Block2 | Block3 | Block4 | Block5 | |||
| Case 1 | 15,080 | 80 × 60 | 80 × 55 | 80 × 40 | 80 × 15 | 20 × 20 | 4.36899 |
| Case 2 | 48,420 | 160 × 140 | 160 × 70 | 160 × 50 | 160 × 20 | 40 × 40 | 4.35218 (0.7004%) |
| Case 3 | 100,160 | 240 × 220 | 240 × 80 | 240 × 60 | 240 × 30 | 60 × 60 | 4.34866 (0.3520%) |
| Case 4 | 170,300 | 320 × 300 | 320 × 90 | 320 × 70 | 320 × 40 | 80 × 80 | 4.35157 (0.4676%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Tang, T.; Li, J.; Yu, P. Effect of Prandtl Number on Mixed Convective Heat Transfer from a Porous Cylinder in the Steady Flow Regime. Entropy 2020, 22, 184. https://doi.org/10.3390/e22020184
Yu S, Tang T, Li J, Yu P. Effect of Prandtl Number on Mixed Convective Heat Transfer from a Porous Cylinder in the Steady Flow Regime. Entropy. 2020; 22(2):184. https://doi.org/10.3390/e22020184
Chicago/Turabian StyleYu, Shimin, Tingting Tang, Jianhui Li, and Peng Yu. 2020. "Effect of Prandtl Number on Mixed Convective Heat Transfer from a Porous Cylinder in the Steady Flow Regime" Entropy 22, no. 2: 184. https://doi.org/10.3390/e22020184
APA StyleYu, S., Tang, T., Li, J., & Yu, P. (2020). Effect of Prandtl Number on Mixed Convective Heat Transfer from a Porous Cylinder in the Steady Flow Regime. Entropy, 22(2), 184. https://doi.org/10.3390/e22020184





