Fractal-Like Flow-Fields with Minimum Entropy Production for Polymer Electrolyte Membrane Fuel Cells
Abstract
1. Introduction
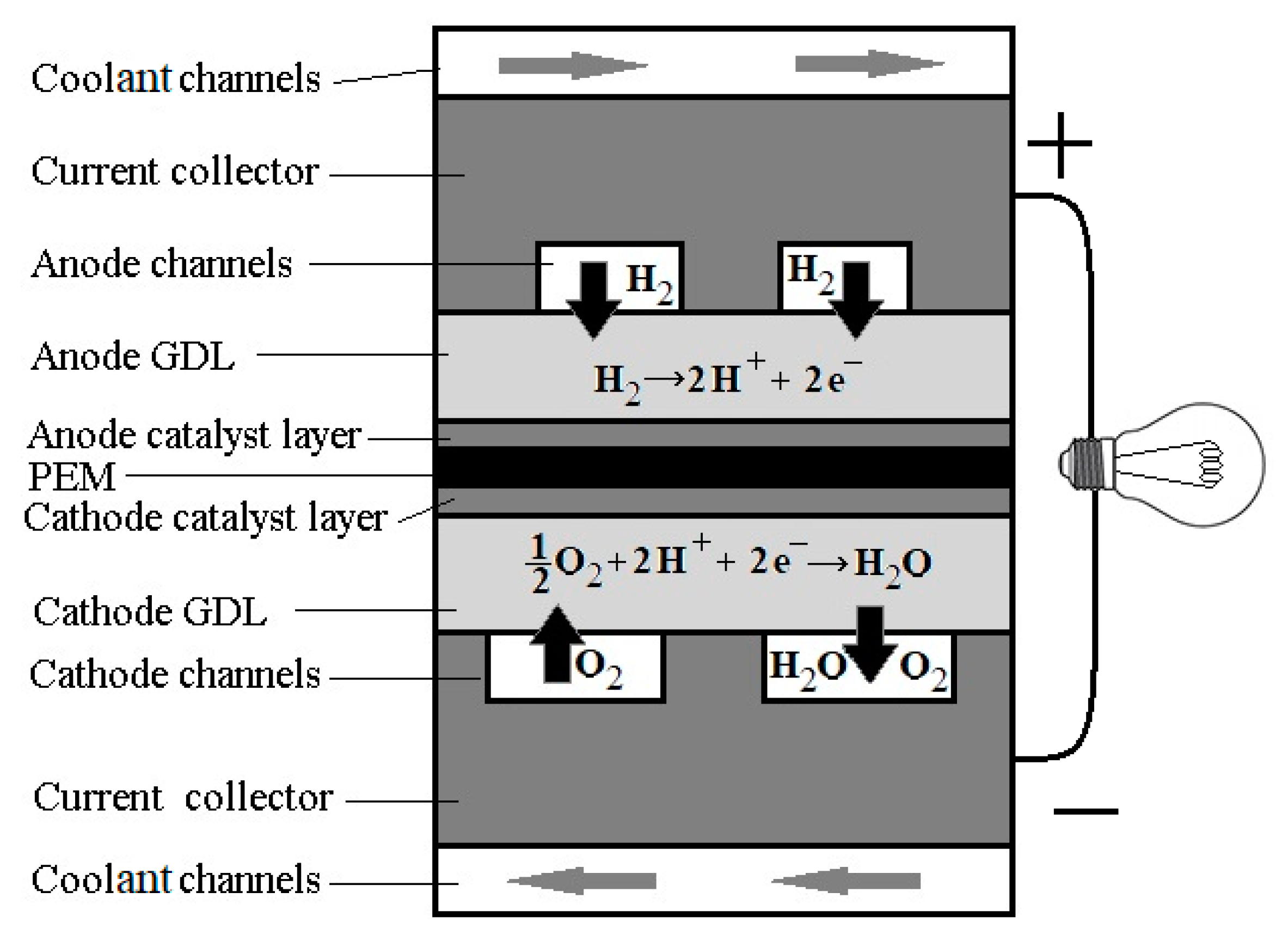
2. Tree-Like Branching Networks for Distribution of Fluids to the Catalytic
2.1. Properties of Natural and Man-Made Distribution Systems
- 1)
- Open-side channels which are in direct contact with a gas distribution layer (GDL);
- 2)
- Closed channels which are in direct contact with GDL via the branches of the last generation only.
2.2. Flow in Fractal-Like Fluid Delivery Systems
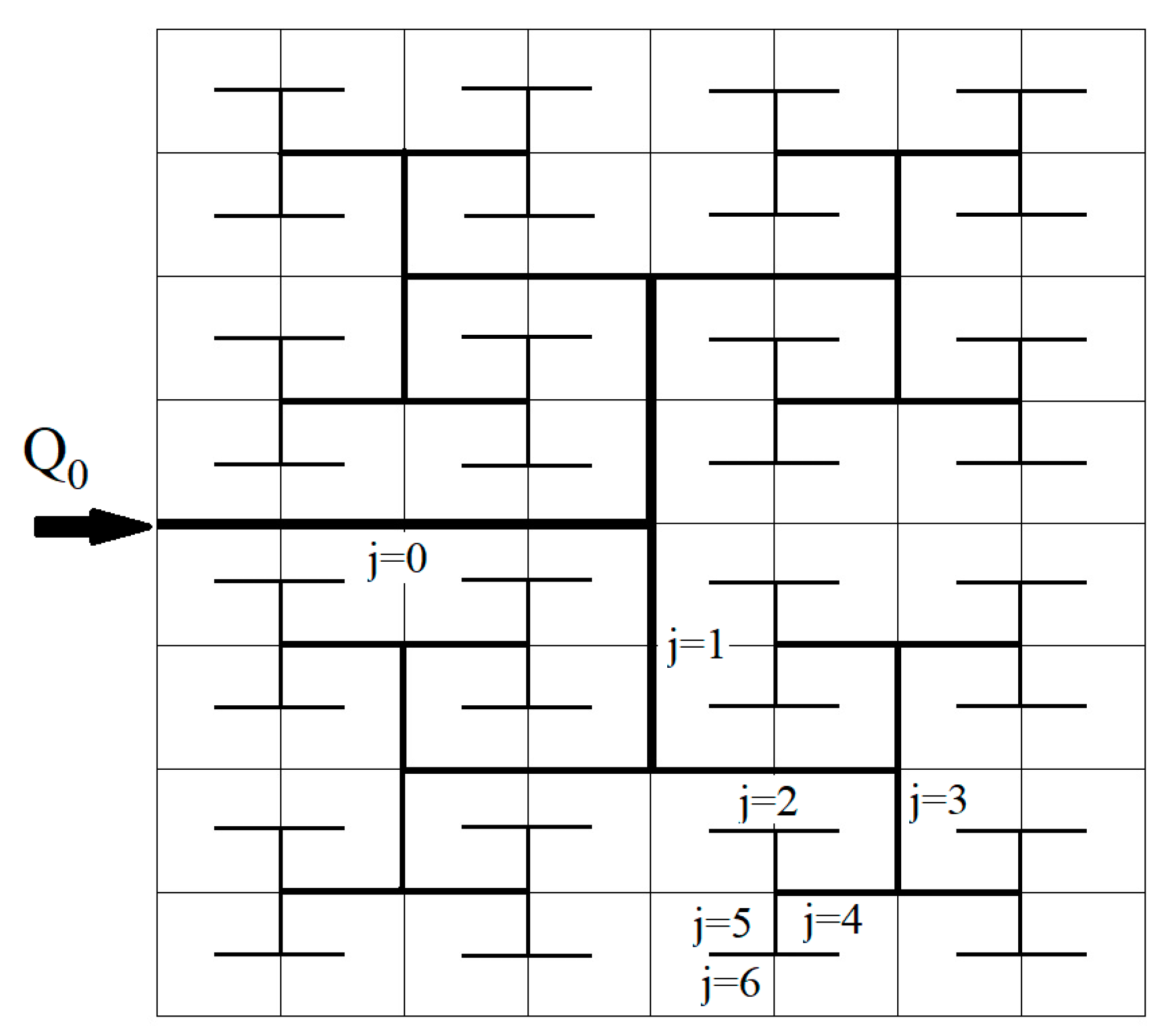
3. System and Case Studies
- (1)
- Flow in rectangular channels computed from (14)–(16);
- (2)
- Flow in cylindrical tubes with equivalent hydraulic diameters determined by (8);
- (3)
- Flow in cylindrical tubes with the same cross-sectional areas as of the rectangular channels, i.e., with diameters
- (4)
- Flow in cylindrical tubes with the same hydraulic resistivity as the rectangular channels, i.e., with diameters
4. The Optimization Problem
4.1. The State of Minimum Entropy Production
- Case 1): The equivalent hydraulic diameters (8)—scaling by (22);
- Case 2): The equivalent cross-sectional area diameters (17)—scaling by (25);
- Case 3): The equivalent hydraulic resistivity diameters (18)—scaling by (26).
4.2. An Approximation to the State of Minimum Entropy Production: Constant Pressure Gradient
- Case 4): the equivalent hydraulic diameters (8)—scaling by (29);
- Case 5): the equivalent cross-sectional area diameters (17)—scaling by (30);
- Case 6): the equivalent hydraulic resistivity diameters (18)—scaling by (31).
5. Method of Calculation
5.1. Transport Properties
5.2. State of Minimum Entropy Production
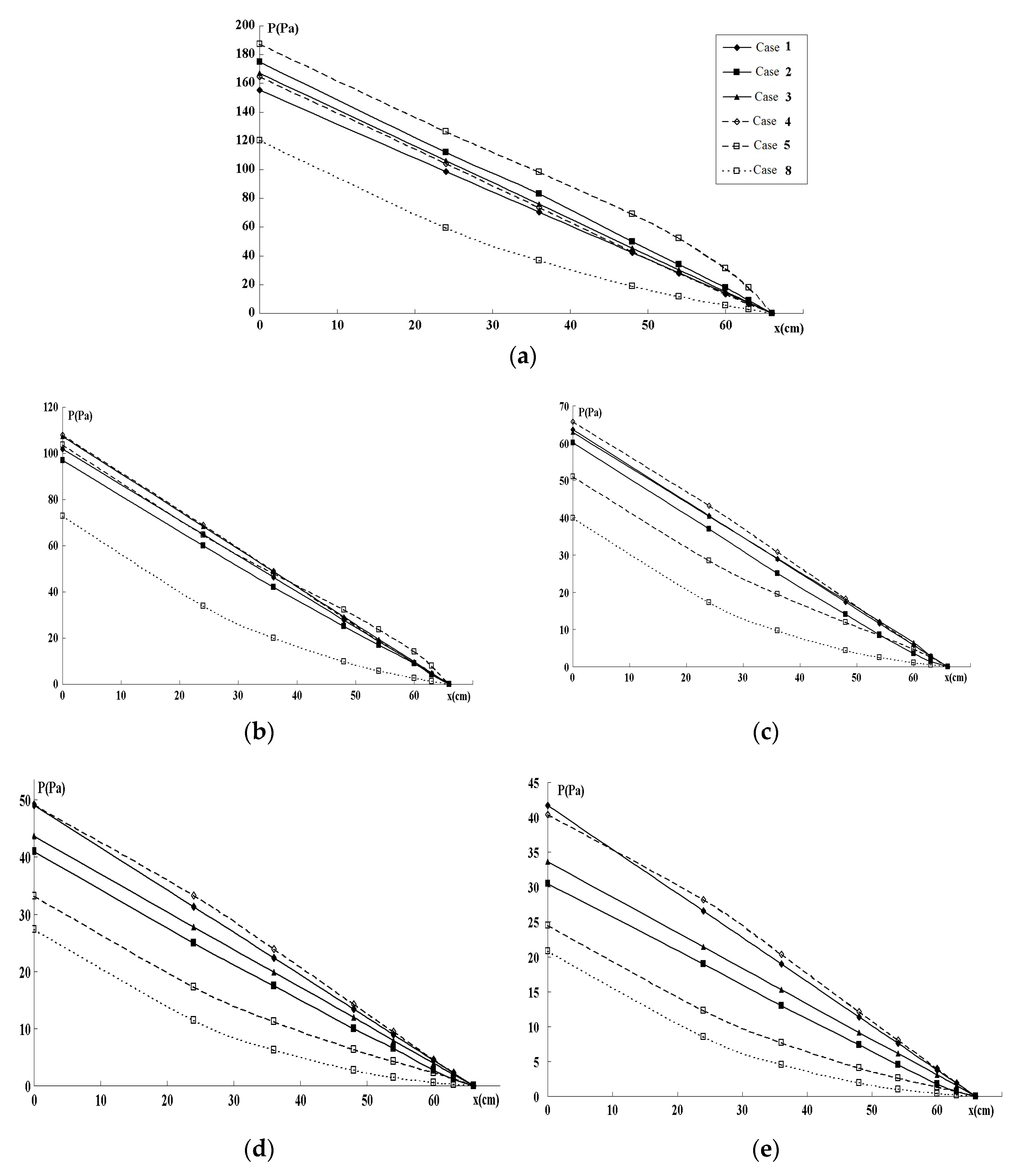
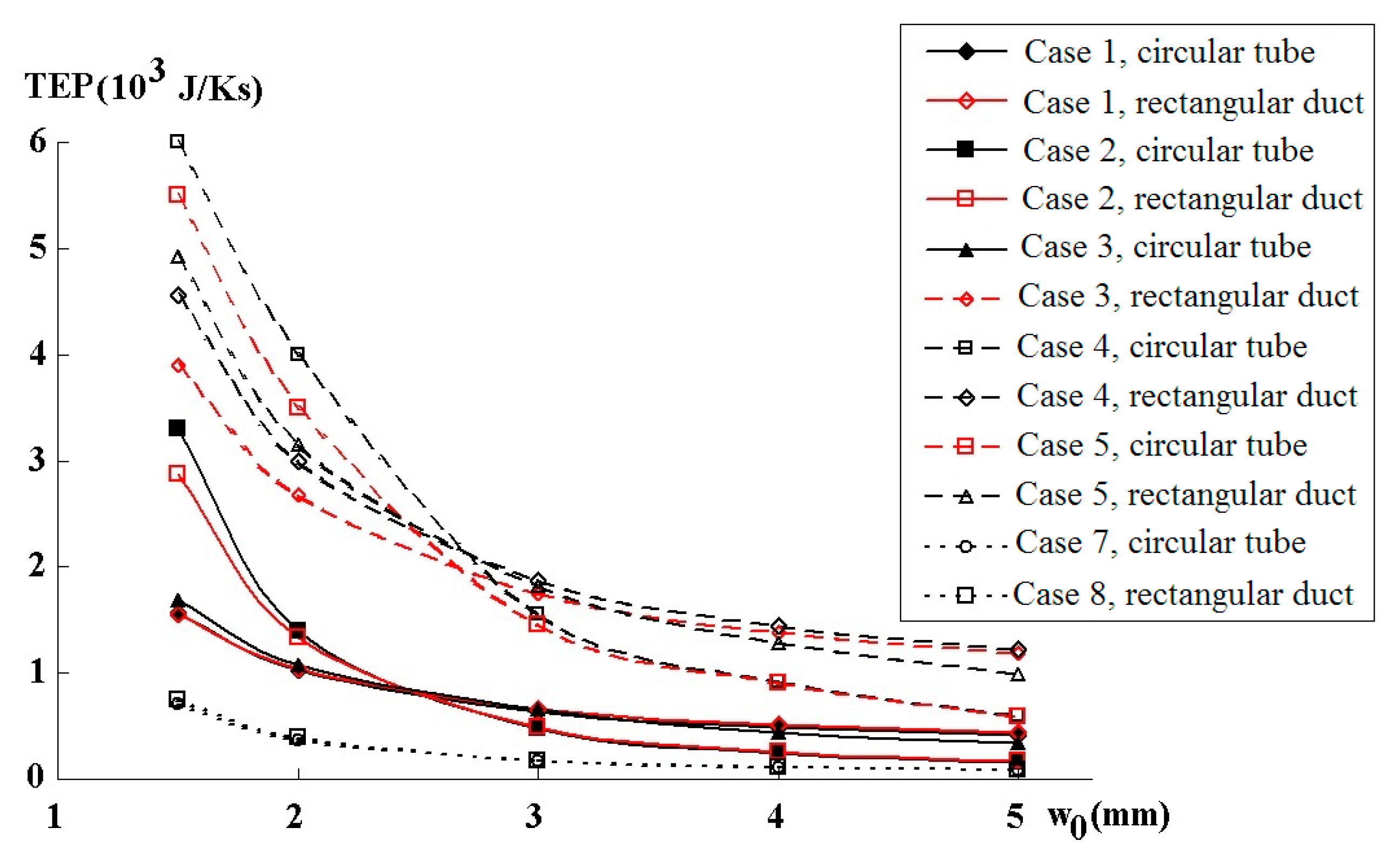
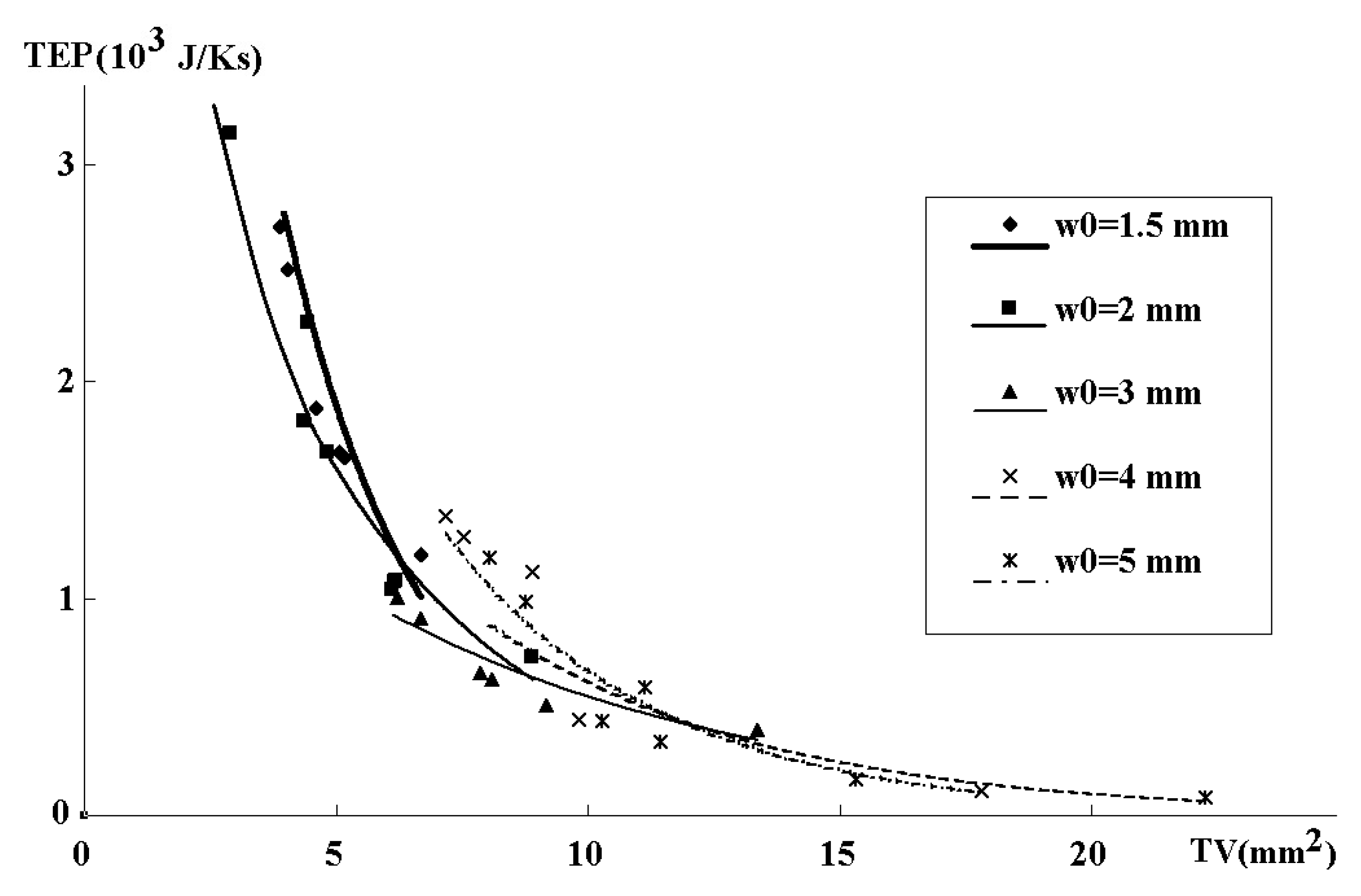
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shell. World Energy Model. A View To 2100. Shell International BV. 2017. Available online: https://www.shell.com/ (accessed on 18 April 2019).
- Fuel Cells and Hydrogen. From Fundamentals to Applied Research, 1st ed.; Hacker, V., Mitsushima, S., Eds.; Elsevier: Amsterdam, Netherlands, 2018. [Google Scholar]
- 2018 Cost Projections of PEM Fuel Cell Systems for Automobiles and Medium-Duty Vehicles. Brian James, Strategic Analysis Inc. Available online: https://www.energy.gov/sites/prod/files/2018/04/f51/fcto_webinarslides_2018_costs_pem_fc_autos_trucks_042518.pdf (accessed on 18 April 2019).
- Sauermoser, M.; Kizilova, N.; Kjelstrup, S.; Pollet, B.G. Flow field patterns for proton exchange membrane (PEM) fuel cells. Front. Phys. (under review).
- Li, X.; Sabir, I. Review of bipolar plates in PEM fuel cells: flow field designs. Int. J. Hydrogen Energy 2005, 30, 359–371. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Genc, O.; Toros, S. Numerical optimization of channel to land width ratio for PEM fuel cell. Intern. J. Hydrogen Energy 2018, 43, 10798–10809. [Google Scholar] [CrossRef]
- Kahraman, H.; Orhan, M.F. Flow field bipolar plates in a proton exchange membrane fuel cell: Analysis & Modeling. Energy Convers. Manag. 2017, 133, 363–384. [Google Scholar] [CrossRef]
- Shabany, Y. Heat Transfer: Thermal Management of Electronics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Tuckerman, D.B.; Pease, R.F. High performance heat sinking for VLSI. IEEE Electron. Dev. Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- La Barbera, M. Principles of design of fluid transport systems in zoology. Science 1990, 249, 992–1000. [Google Scholar] [CrossRef]
- Gheorghiu, S.; Kjelstrup, S.; Pfeifer, P.; Coppens, M.-O. Coppens Is the lung an optimal gas exchanger. In Fractals in Biology and Medicine; Losa, G.A., Merlini, D., Nonnenmacher, T.F., Wiebel, E.R., Eds.; Birkauser: Berlin, Germany, 2005; pp. 31–42. [Google Scholar] [CrossRef]
- Hou, C.; Gheorghiu, S.; Coppens, M.O.; Huxley, V.H.; Pfeifer, P. Gas diffusion through the fractal landscape of the lung: How deep does oxygen enter the alveolar system. In Fractals in Biology and Medicine; Losa, G.A., Merlini, D., Nonnenmacher, T.F., Wiebel, E.R., Eds.; Birkauser: Berlin, Germany, 2005; pp. 17–30. [Google Scholar] [CrossRef]
- Kizilova, N. Long-distance liquid transport in plants. Proc. Estonian Acad. Sci. Ser. Phys. Math. 2008, 57, 179–203. [Google Scholar] [CrossRef]
- Kizilova, N. Computational approach to optimal transport network construction in biomechanics. Lect. Notes Comput. Sci. 2004, 3044, 476–485. [Google Scholar] [CrossRef]
- Roux, W. Uber die Verzweigungen der Blutgefasse. PhD Thesis, University of Jena, Jena, Germany, 1878. [Google Scholar]
- Murray, C.D. The physiological principle of minimum work. I. The vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef]
- Murray, C.D. The physiological principle of minimum work applied to the angle of branching of arteries. J. Gen. Physiol. 1926, 9, 835–841. [Google Scholar] [CrossRef]
- Pries, A.R.; Secomb, T.W.; Gaehtgens, P. Design principles of vascular beds. Circ. Res. 1995, 77, 1017–1023. [Google Scholar] [CrossRef] [PubMed]
- Zamir, M.; Bigelov, D.C. Cost of departure from optimality in arterial branching. J. Theor. Biol. 1984, 109, 401–409. [Google Scholar] [CrossRef]
- Zamir, M. Branching characteristics of human coronary arteries. Canad. J. Physiol. 1986, 64, 661–668. [Google Scholar] [CrossRef] [PubMed]
- Dawson, C.A.; Krenz, G.S.; Karau, K.L.; Haworth, S.T.; Hanger, C.C.; Linehan, J.H. Structure-function relationships in the pulmonary arterial tree. J. Appl. Physiol. 1999, 86, 569–583. [Google Scholar] [CrossRef] [PubMed]
- Singhal, S.; Henderson, R. Morphometry of the human pulmonary arterial tree. Circ. Res. 1973, 33, 190–198. [Google Scholar] [CrossRef]
- Taylor, C.R.; Weibel, E.R. Design of the mammalian respiratory system. Respir Physiol. 1981, 44, 1–10. [Google Scholar] [CrossRef]
- Popescu, A.I. Bionics, biological systems and the principle of optimal design. Acta Biotheor. 1999, 46, 299–310. [Google Scholar] [CrossRef]
- Honda, H. Tree branch angle: maximizing effective leaf area. Science 1978, 199, 888–889. [Google Scholar] [CrossRef]
- Zhi, W.; Zhao, M.; Yu, Q.-X. Modeling of Branching Structures of Plants. J. Theor. Biol. 2001, 209, 383–394. [Google Scholar] [CrossRef][Green Version]
- McCulloh, K.A.; Sperry, J.S.; Adler, F.R. Water transport in plants obeys Murray’s law. Nature 2003, 421, 939–942. [Google Scholar] [CrossRef]
- Uylings, H.B.M. Optimization of diameters and bifurcation angles in lung and vascular tree structures. Bull. Math. Biol. 1977, 39, 509–520. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A. Heterogeneous porous media as multiscale structures for maximum flow access. J. Appl. Phys. 2006, 100, 114909. [Google Scholar] [CrossRef]
- Wattez, T.; Lorente, S. From pore network prediction based on the Constructal law to macroscopic properties of porous media. J. Phys. D Appl. Phys. 2015, 48, 485503. [Google Scholar] [CrossRef]
- Barber, R.; Cieslicki, K.; Emerson, D. Using Murray’s law to design artificial vascular microfluidic networks. In Design and Nature III: Comparing Design in Nature with Science and Engineering; WIT Press: Southampton, UK, 2006; pp. 245–254. [Google Scholar] [CrossRef]
- Trogadas, P.; Cho, J.; Neville, T.; Marquis, J.; Wu, B.; Brett, D.; Coppens, M.-O. A lung-inspired approach to scalable and robust fuel cell design. Energy Environ. Sci. 2018, 11, 136–143. [Google Scholar] [CrossRef]
- Cho, J.; Neville, T.; Trogadas, P.; Meyer, Q.; Wu, Y.; Ziesche, R.; Boillat, P.; Cochet, M.; Manzi-Orezzoli, V.; Shearing, P. Visualization of liquid water in a lung-inspired flow-field based polymer electrolyte membrane fuel cell via neutron radiography. Energy 2019, 170, 14–21. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, C.; Teng, J.; Huang, S.; Jin, S.; Lian, Y.; Cheng, C.; Xu, T.; Chu, J.-C.; Chang, Y.-J. A study on the hydraulic and thermal characteristics in fractal tree-like microchannels by numerical and experimental methods. Int. J. Heat Mass Transf. 2012, 55, 7499–7507. [Google Scholar] [CrossRef]
- Sauermoser, M.; Kjelstrup, S.; Kizilova, N.; Pollet, B.G.; Flekkøy, E.G. Seeking minimum entropy production for a tree-like flow-field in a fuel cell. Phys. Chem. Chem. Phys. 2020. under review. [Google Scholar]
- Wang, X.-Q.; Mujumdar, A.S.; Yap, C. Effect of bifurcation angle in tree-shaped microchannel networks. J. Appl. Phys. 2007, 102, 073530. [Google Scholar] [CrossRef]
- Stephenson, D.; Patronis, A.; Holland, D.M.; Lockerby, D.A. Generalizing Murray’s law: An optimization principle for fluidic networks of arbitrary shape and scale. J. Appl. Phys. 2015, 118, 174302. [Google Scholar] [CrossRef]
- Pence, D.V. Reduced pumping power and wall temperature in microchannel heat sinks with fractal-like branching channel network. Microscale Thermophys. Eng. 2003, 6, 319–330. [Google Scholar] [CrossRef]
- Chen, Y.P.; Cheng, P. Heat transfer and pressure drop in fractal tree-like microchannel nets. Int. J. Heat Mass Transf. 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, P. An experimental investigation on the thermal efficiency of fractal tree-like microchannel nets. Int. J. Heat Mass Transf. 2005, 32, 931–938. [Google Scholar] [CrossRef]
- Tüber, K.; Oedegaard, A.; Hermann, M.; Hebling, C. Investigation of fractal flow-fields in portable proton exchange membrane and direct methanol fuel cells. J. Power Sources 2004, 131, 175–181. [Google Scholar] [CrossRef]
- Alharbi, A.Y.; Pence, D.V.; Cullion, R.N. Thermal characteristics of microscale fractal-like branching channels. ASME J. Heat Transf. 2004, 126, 744–752. [Google Scholar] [CrossRef]
- Senn, S.; Poulikakos, D. Tree network channels as fluid distributors constructing double staircase polymer electrolyte fuel cells. J. Appl. Phys. 2004, 96, 842–852. [Google Scholar] [CrossRef]
- Senn, S.M.; Poulikakos, D. Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Sources 2004, 130, 178–191. [Google Scholar] [CrossRef]
- Ghodoossi, L. Thermal and hydrodynamic analysis of a fractal microchannel network. Energy Convers. Manag. 2005, 46, 771–788. [Google Scholar] [CrossRef]
- Zimparov, V.D.; da Silva, A.K.; Bejan, A. Constructal tree-shaped parallel flow heat exchangers. Int. J. Heat Mass Transfer 2006, 49, 4558–4566. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S.; Yap, C. Thermal characteristics of tree-shaped microchannel nets for cooling of a rectangular heat sink. Int. J. Therm. Sci. 2006, 45, 1103–1112. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S.; Yap, C. Numerical analysis of blockage and optimization of heat transfer performance of fractal-like microchannel nets. J. Electron. Packag. 2006, 128, 38–45. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S.; Yap, C. Laminar heat transfer in constructal microchannel networks with loops. ASME J. Electron. Packag. 2006, 128, 273–280. [Google Scholar] [CrossRef]
- Wang, L.; Fan, Y.; Luo, L. Lattice Boltzmann method for shape optimization of fluid distributor. Comput. Fluids 2014, 94, 49–57. [Google Scholar] [CrossRef]
- Xu, P.; Wang, X.-Q.; Mujumdar, A.S.; Yapa, C.; Yu, B.M. Thermal characteristics of tree-shaped microchannel nets with/without loops. Intern. J. Thermal Sci. 2009, 48, 2139–2147. [Google Scholar] [CrossRef]
- Daniels, B.; Liburdy, J.A.; Pence, D.V. Adiabatic flow boiling in fractal-like microchannels. Heat Transfer Eng. 2007, 28, 817–825. [Google Scholar] [CrossRef]
- Hong, F.J.; Cheng, P.; Ge, H.; Joo, G.T. Conjugate heat transfer in fractal-shaped microchannel network heat sink for integrated microelectronic cooling application. Int. J. Heat Mass Transf. 2007, 50, 4986–4998. [Google Scholar] [CrossRef]
- Escher, W.; Michel, B.; Poulikakos, D. Efficiency of optimized bifurcating treelike and parallel microchannel networks in the cooling of electronics. Int. J. Heat Mass Transf. 2009, 52, 1421–1430. [Google Scholar] [CrossRef]
- Chen, Y.P.; Zhang, C.B.; Shi, M.H.; Yang, Y. Thermal and hydrodynamic characteristics of constructal tree-shaped minichannel heat sink. AIChE J. 2010, 56, 2018–2029. [Google Scholar] [CrossRef]
- Chen, Y.P.; Deng, Z. Gas flow in micro tree-shaped hierarchical network. Int. J. Heat Mass Transf. 2015, 80, 163–169. [Google Scholar] [CrossRef]
- Zhang, C.B.; Chen, Y.P.; Wu, R.; Shi, M.H. Flow boiling in constructal tree-shaped minichannel network. Int. J. Heat Mass Transf. 2011, 54, 202–209. [Google Scholar] [CrossRef]
- Chen, Y.P.; Zhang, C.B.; Wu, R.; Shi, M.H. Methanol steam reforming in microreactor with constructal tree-shaped network. J. Power Sources 2011, 196, 6366–6373. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, F.; Sunden, B.; Zhang, W. Constructal design and thermal analysis of microchannel heat sinks with multistage bifurcations in single-phase liquid flow. Appl. Therm. Eng. 2014, 62, 791–802. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, F.; Sunden, B.; Xie, G. Laminar thermal performance of microchannel heat sinks with constructal vertical y-shaped bifurcation plates. Appl. Therm. Eng. 2014, 73, 185–195. [Google Scholar] [CrossRef]
- Xie, G.; Shen, H.; Wang, C.-C. Parametric study on thermal performance of microchannel heat sinks with internal vertical y-shaped bifurcations. Int. J. Heat Mass Transf. 2015, 90, 948–958. [Google Scholar] [CrossRef]
- Chen, Y.P.; Yao, F.; Huang, X. Mass transfer and reaction in methanol steam reforming reactor with fractal tree-like microchannel network. Int. J. Heat Mass Transf. 2015, 87, 279–283. [Google Scholar] [CrossRef]
- Damian-Ascencio, C.E.; Saldana-Robles, A.; Hernandez-Guerrero, A.; Cano-Andrade, S. Numerical modeling of a proton exchange membrane fuel cell with tree-like flow field channels based on an entropy generation analysis. Energy 2017, 133, 306–316. [Google Scholar] [CrossRef]
- Li, P.; Coopamah, D.; Ki, J.-P. Uniform distribution of species in fuel cells using a multiple flow bifurcation design. In Proceedings of the 6th International Fuel Cell Science, Engineering and Technology Conference, Denver, CO, USA, 16–18 June 2008; pp. 897–902. [Google Scholar] [CrossRef]
- Damian-Ascencio, C.E.; Hernandez-Guerrero, A.; Escobar-Vargas, J.A.; Rubio-Arana, C.; Elizalde-Blancas, F. Three dimensional numerical prediction of the current density for a constructal theory-based flow field pattern. In Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition, Seattle, DC, USA, 11–15 November 2007; pp. 627–635. [Google Scholar] [CrossRef]
- Fan, Z.; Zhou, X.; Luo, L.; Yuan, W. Experimental investigation of the flow distribution of a 2-dimensional constructal distributor. Experim. Thermal Fluid Sci 2008, 33, 77–83. [Google Scholar] [CrossRef]
- Ramos-Alvarado, B.; Hernandez-Guerrero, A.; Elizalde-Blancas, F.; Ellis, M.W. Constructal flow distributor as a bipolar plate for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 12965–12976. [Google Scholar] [CrossRef]
- Haller, D.; PWoias, N. Kockmann, Simulation and experimental investigation of pressure loss and heat transfer in microchannel networks containing bends and T-junctions. Int. J. Heat Mass Transf. 2009, 52, 2678–2689. [Google Scholar] [CrossRef]
- Xia, C.; Fu, J.; Lai, J.; Yao, X.; Chen, Z. Conjugate heat transfer in fractal tree-like channels network heat sink for high-speed motorized spindle cooling. Appl. Thermal Eng. 2015, 90, 1032–1042. [Google Scholar] [CrossRef]
- Gosselin, L. Optimization of tree-shaped fluid networks with size limitations. Int. J. Therm. Sci. 2007, 46, 434–443. [Google Scholar] [CrossRef]
- Alharbi, A.Y.; Pence, D.V.; Cullion, R.N. Fluid flow through microscale fractal-like branching channel networks. ASME J. Fluids Eng. 2003, 125, 1051–1057. [Google Scholar] [CrossRef]
- Xu, G.; Wang, M.; Tao, Z.; Ding, S.; Wu, H.; Guo, J. Numerical analysis of flow and heat transfer characteristics of Y-fractal-link micro channel networks. In Proceedings of the ICHMT International Symposium on Advances in Computational Heat Transfer (CHT-08), Marrakech, Morocco, 11–16 May 2008. [Google Scholar] [CrossRef]
- Hong, F.J.; Cheng, P.; Wu, H.Y. Characterization on the performance of a fractal-shaped microchannel network for microelectronic cooling. J. Micromech. Microeng. 2011, 21, 065018. [Google Scholar] [CrossRef]
- Pence, D.V. Improved thermal efficiency and temperature uniformity using fractal-like branching channel networks. Heat Transfer and Transport Phenomena in Microsystems. In Proceedings of the Engineering. Foundation Conference on Heat Transfer and Transport Phenomena in Microscale, Banff, AB, Canada, 23 May 2000; pp. 142–148. [Google Scholar]
- Wechsatol, W.; Lorente, S.; Bejan, A. Optimal tree-shaped networks for fluid flow in a disc-shaped body. Int. J. Heat Mass Transf. 2002, 45, 4911–4924. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–811. [Google Scholar] [CrossRef]
- Bejan, A.; Errera, M.R. Convective trees of fluid channels for volumetric cooling. Int. J. Heat Mass Transf. 2000, 43, 3105–3118. [Google Scholar] [CrossRef]
- Sauermoser, M.; Kizilova, N.; Kjelstrup, S. Minimum entropy production approach to optimal design of the flow field plates in polymer electrolyte fuel cells. In Proceedings of the Joint European Thermodynamics Conference (JETC2019), Barcelona, Spain, 21–24 May 2019; p. 70. [Google Scholar]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Tang, X.; Dai, W.; Nassar, R.; Bejan, A. Optimal temperature distribution in a 3D triple layered skin structure embedded with artery and vein vasculature. Numer. Heat Transf. A 2006, 50, 809–843. [Google Scholar] [CrossRef]
- Bejan, A. The method of entropy generation minimization. In Energy and the environment. Environmental science and Technology Library; Bejan, A., Vadász, P., Kröger, D.G., Eds.; Springer: Dordrecht, The Netherland, 1999; Volume 15, pp. 11–22. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D. Non-equilibrium Thermodynamics of Heterogeneous Systems; World Scientific: Singapore, 2008. [Google Scholar]
- Tondeur, D.; Kvaalen, E. Equipartition of entropy production. An optimality criterion for transfer and separation processes. Ind. Eng. Chem. Res. 1987, 26, 50–56. [Google Scholar] [CrossRef]

| N | Fuel Cell Pane | FFP Design | Compared to | Verification Method | Heat Effects | Pressure Drop and Pumping Power | Maximum Power Density/Efficiency | Fuel Conversion Rate | FoM* | Wall T, Heat Resistivity | T Uniformity | Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Circular | Fractal (n=4, ), | 1D | + | 60% ↓ | - | - | - | 30 °C ↓ | - | [39] | |
| 2 | Fractal (n=4, ) | 1D+ experiment | + | 54–64% ↓ | - | - | - | - | 2.17–2.78 ↑ | [40,41] | ||
| 3 | Rectangle | Fractal (n=5, , smooth) rectangle cross-sections, combined with parallel | Serpentine, parallel | Experiment PEMFC, DMFC | - | similar performance to parallel designs | - | - | - | - | [42] | |
| 4 | Circular | Fractal (n=4, ), | 3D CFD | + | 10% ↓ | - | - | - | - | 75 ↑ | [43] | |
| 5 | Rectangle | Fractal, rectangle cross-sections | 1D | + | 8.6–15% ↓ | 1.7–26% ↑ | - | - | - | - | [44] | |
| 6 | Rectangle | Fractal, rectangle cross-sections | 2D | + | ↓ | ↑ | - | - | - | - | [45] | |
| 7 | Rectangle | Fractal (n=5, ) | 1D | + | ↓ for turbulent ↑ for laminar | - | - | - | - | - | [46] | |
| 8 | Rectangle, Square, Circular | Fractal + parallel | ↓ | - | - | - | - | - | [47] | |||
| 9 | Rectangle | Fractal (n=2,3, ) | 3D CFD | + | ↓ | - | - | - | ↓ | ↑ | [37,48,49,50,51,52] | |
| 10 | Rectangle | Fractal (n=4, ) | 1D | + | ↑ or ↓ | - | - | - | ↑ or ↓ | - | [53] | |
| 11 | Square | Fractal (n=6, ) | 3D CFD | + | ↓ | - | - | - | ↓ | ↑ | [54] | |
| 12 | Rectangle | Fractal (n=5, ) | 1D | + | ↑ in 5 times | - | - | - | - | ↑ | [55] | |
| 13 | Rectangle | Fractal (n=6, ) | 3D CFD | + | ↓ | - | - | - | ↓ | ↑ | [56,57] | |
| 14 | Rectangle | Fractal (n=6, ) | 1D | + | ↓ | ↑ | - | - | - | ↑ | [58] | |
| 15 | Rectangle | Fractal (n=6, ), h=const | 3D CFD for DMFC | - | - | 10% ↑ | - | - | - | [59] | ||
| 16 | Rectangle | Fractal (n=1,2, ) | 3D CFD | + | ↑ | - | - | - | ↓ | ↑ | [60] | |
| 17 | Rectangle | Fractal (n=1, ) | 3D CFD | + | ↑ | 30–60% ↑ | - | - | ↓ | ↑ | [61,62] | |
| 18 | Rectangle | Fractal (n=4, ), h=const | 3D CFD for DMFC | - | - | ↑ | ↑ | - | - | [63] | ||
| 19 | Rectangle | Fractal (n=2, ) | 3D CFD | - | ↓ | ↓ | - | - | - | - | [64] | |
| 20 | Square | 3D 5-layered lung-inspired fractal (n=4, + ) | Serpentine | 10 cm2 FEMFC | ↓↓ | ↑, max in fractal with n=4, better than in serpentine (at 50% and 75% RH**) | [33] | |||||
| 21 | Square | 3D 5-layered lung-inspired fractal (n=4, + ) | Serpentine | Experiment, PEM FC | + | + | ↓, high water accumulation; less stable performance than the serpentine | - | - | - | + | [34] |
| 22 | Rectangle | Fractal (n=6, ) | - | 1D, 2D, 3D CFD | - | ↓ and close to linear | - | - | - | - | - | [36] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kizilova, N.; Sauermoser, M.; Kjelstrup, S.; Pollet, B.G. Fractal-Like Flow-Fields with Minimum Entropy Production for Polymer Electrolyte Membrane Fuel Cells. Entropy 2020, 22, 176. https://doi.org/10.3390/e22020176
Kizilova N, Sauermoser M, Kjelstrup S, Pollet BG. Fractal-Like Flow-Fields with Minimum Entropy Production for Polymer Electrolyte Membrane Fuel Cells. Entropy. 2020; 22(2):176. https://doi.org/10.3390/e22020176
Chicago/Turabian StyleKizilova, Natalya, Marco Sauermoser, Signe Kjelstrup, and Bruno G. Pollet. 2020. "Fractal-Like Flow-Fields with Minimum Entropy Production for Polymer Electrolyte Membrane Fuel Cells" Entropy 22, no. 2: 176. https://doi.org/10.3390/e22020176
APA StyleKizilova, N., Sauermoser, M., Kjelstrup, S., & Pollet, B. G. (2020). Fractal-Like Flow-Fields with Minimum Entropy Production for Polymer Electrolyte Membrane Fuel Cells. Entropy, 22(2), 176. https://doi.org/10.3390/e22020176







