Ballistic-Diffusive Model for Heat Transport in Superlattices and the Minimum Effective Heat Conductivity
Abstract
1. Introduction
2. Methods
2.1. Two Temperature Ballistic-Diffusive Model
2.2. Effective Medium Theory
3. Results
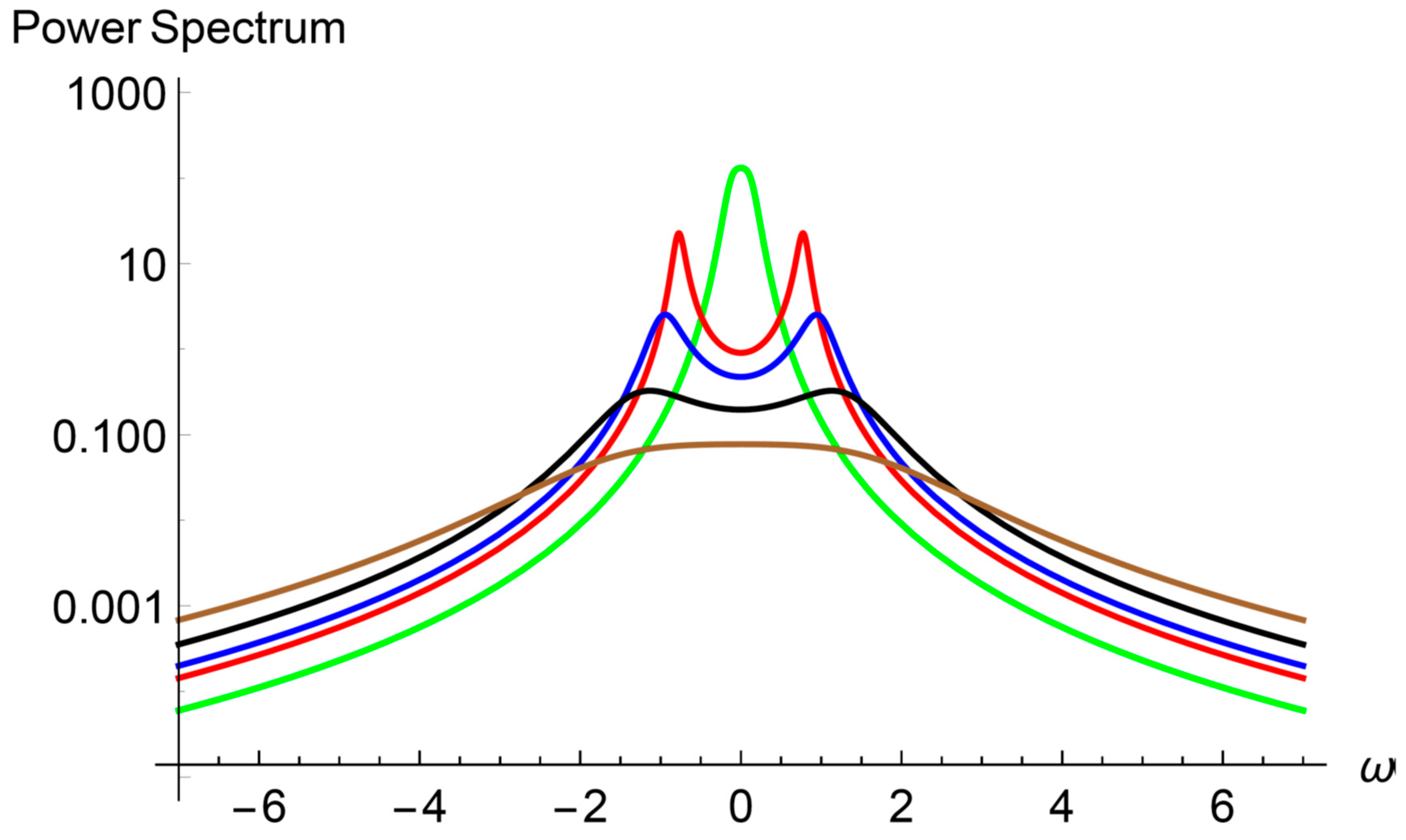
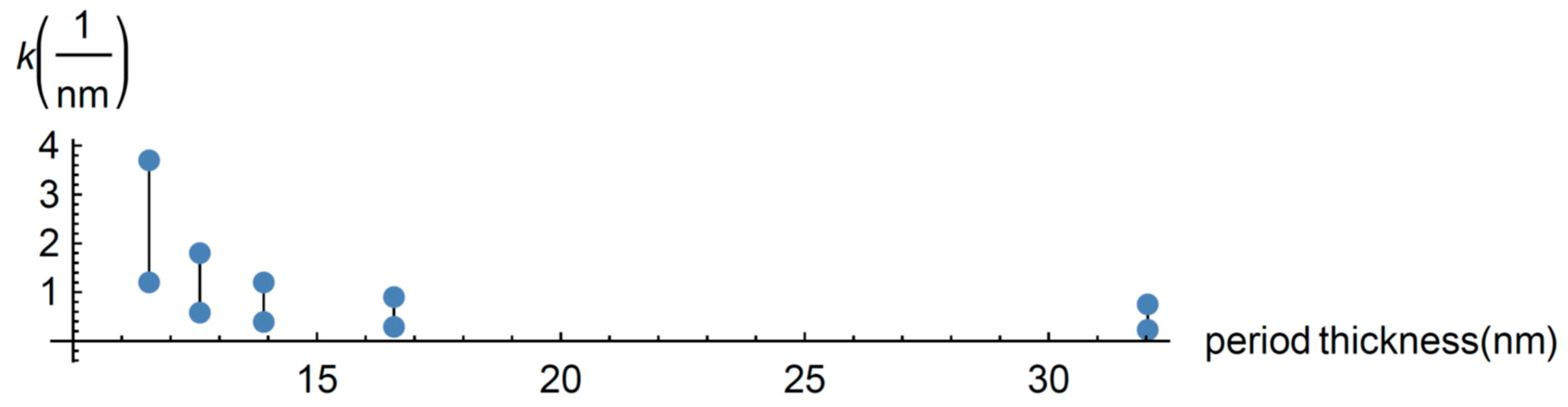
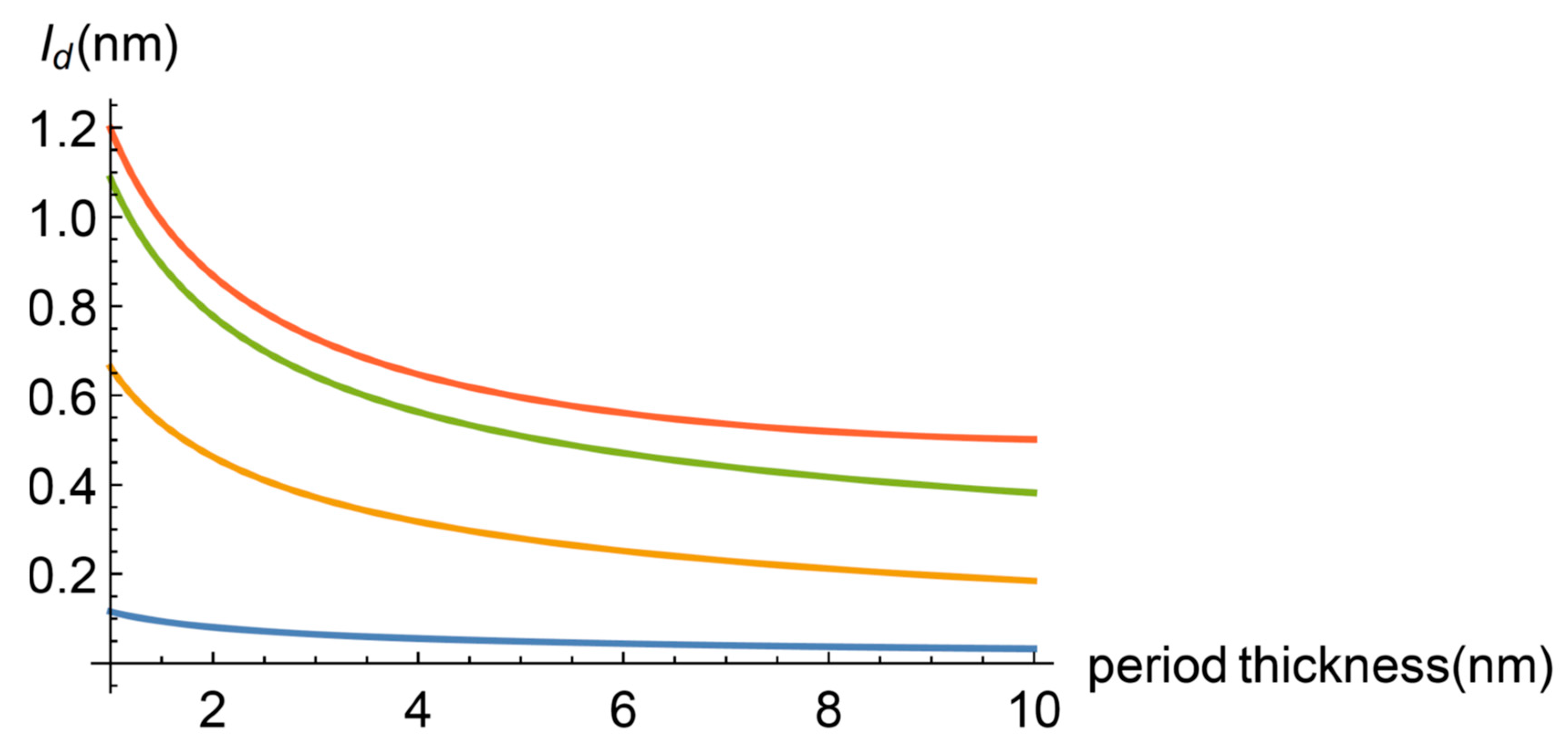
3.1. Heat Carrier Properties
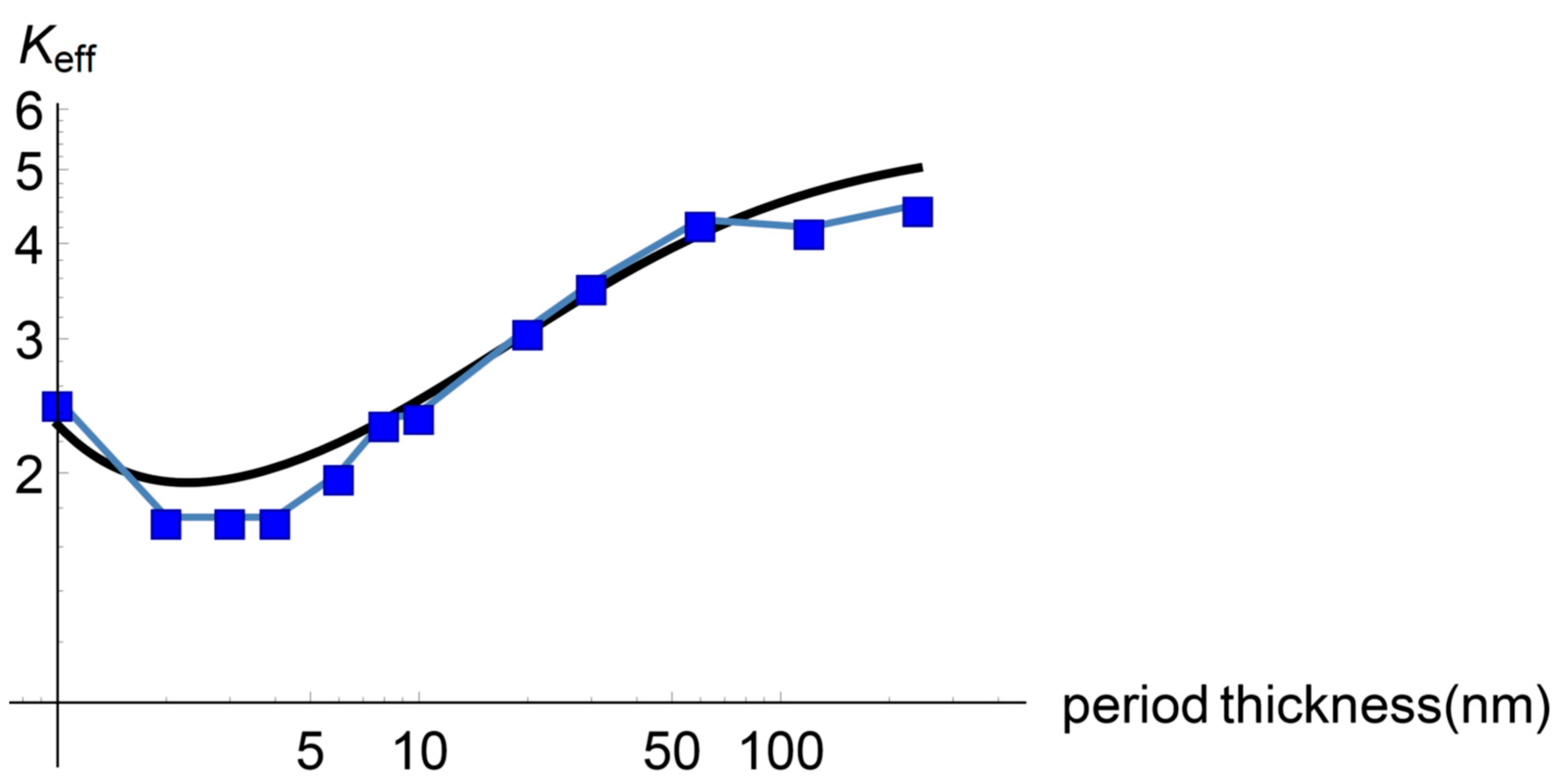
3.2. Minimum Effective Heat Conductivity
4. Discussion
4.1. Preliminar
4.2. On the Transition to Coherent Heat Transport Regime for Small Period Thickness
4.3. Comparison with Lebon, Machrafi and Grmela model [22,23]
4.4. Comparison with High Order Dissipative Fluxes Formalism by Álvarez and Jou [27]
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, L.; Dames, C.; Lukes, J.R.; Reddy, P.; Duda, J.; Cahill, D.G.; Lee, J.; Marconnet, A.; Goodson, K.E.; Bahk, J.-H.; et al. Evaluating Broader Impacts of Nanoscale Thermal Transport Research. Nanoscale Microscale Thermophys. Eng. 2015, 19, 127–165. [Google Scholar] [CrossRef]
- Saha, B.; Koh, Y.R.; Comparan, J.; Sadasivam, S.; Schroeder, J.; Garbrecht, M.; Mohammed, A.; Birch, J.; Fisher, T.; Shakouri, A.; et al. Cross-plane thermal conductivity of (Ti,W)N/(Al,Sc)N metal/semiconductor superlattices. Phys. Rev. B 2016, 93, 045311. [Google Scholar] [CrossRef]
- Saha, B.; Koh, Y.R.; Feser, J.P.; Sadasivam, S.; Fisher, T.; Shakouri, A.; Sands, T.D. Phonon wave effects in the thermal transport of epitaxial TiN/(Al,Sc)N metal/ semiconductor superlattices. J. Appl. Phys. 2017, 121, 015109. [Google Scholar] [CrossRef]
- Ravichandran, J.; Yadav, A.K.; Cheaito, R.; Rossen, P.B.; Soukiassian, A.; Suresha, S.J.; Duda, J.C.; Foley, B.M.; Lee, C.-H.; Zhu, Y.; et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 2013, 13, 168–172. [Google Scholar] [CrossRef] [PubMed]
- Luckyanova, M.N.; Garg, J.; Esfarjani, K.; Jandl, A.; Bulsara, M.T.; Schmidt, A.J.; Minnich, A.J.; Chen, S.; Dresselhaus, M.S.; Ren, Z.; et al. Coherent Phonon Heat Conduction in Superlattices. Science 2012, 338, 936–939. [Google Scholar] [CrossRef] [PubMed]
- Siemens, M.E.; Li, Q.; Yang, R.; Nelson, K.A.; Anderson, E.H.; Murnane, M.M.; Kapteyn, H.C. Quasi-ballistic thermal transport from nanoscale interfaces observed using ultrafast coherent soft X-ray beams. Nat. Mater. 2010, 9, 26–30. [Google Scholar] [CrossRef]
- Ziabari, A.; Álvarez, F.X.; Vermeersch, B.; Xuan, Y. Full-field thermal imaging of quasiballistic crosstalk reduction in nanoscale devices. Nat. Commun. 2018, 9, 255. [Google Scholar] [CrossRef]
- Ván, P.; Fülöp, T. Universality in heat conduction theory: Weakly nonlocal thermodynamics. Ann. Phys. 2012, 524, 470–478. [Google Scholar] [CrossRef]
- Ván, P. Theories and heat pulse experiments of non-Fourier heat conduction. Commun. Appl. Ind. Math. 2016, 7, 150–166. [Google Scholar] [CrossRef]
- Ván, P.; Berezovski, A.; Fülöp, T.; Gróf, G.; Kóvacs, R.; Lovas, Á.; Verhás, J. Guyer-Krumhansl–type heat conduction at room temperature. EPL 2017, 118, 50005. [Google Scholar] [CrossRef]
- Valenti, A.; Torrisi, M.; Lebon, G. Heat pulse propagation by second sound in dielectric crystals. J. Phys. Condens. Matter 1997, 9, 3117–3127. [Google Scholar] [CrossRef]
- Lebon, G.; Torrisi, M.; Valenti, A. A non-local thermodynamic analysis of second sound propagation in crystalline dielectrics. J. Phys. Condens. Matter 1995, 7, 1461–1474. [Google Scholar] [CrossRef]
- Kovács, R.; Ván, P. Generalized heat conduction in heat pulse experiments. Int. J. Heat and Mass Transf. 2015, 83, 613–620. [Google Scholar] [CrossRef]
- Kovács, R.; Ván, P. Models of Ballistic Propagation of Heat at Low Temperatures. Int. J. Thermophys. 2016, 37, 95. [Google Scholar] [CrossRef]
- Kóvacs, R.; Ván, P. Second sound and ballistic heat conduction: NaF experiments revisited. Int. J. Heat Mass Transf. 2018, 117, 682–690. [Google Scholar] [CrossRef]
- Garg, J.; Chen, G. Minimum thermal conductivity in superlattices: A first-principles formalism. Phys. Rev. B 2013, 87, 140302. [Google Scholar] [CrossRef]
- Simkin, M.V.; Mahan, G.D. Minimum Thermal Conductivity of Superlattices. Phys. Rev. Lett. 2000, 84, 927–930. [Google Scholar] [CrossRef]
- Grmela, M.; Lebon, G.; Dubois, C. Multiscale thermodynamics and mechanics of heat. Phys. Rev. E 2011, 83, 061134. [Google Scholar] [CrossRef]
- Kovács, R. On the Rarefied Gas Experiments. Entropy 2019, 21, 718. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M. Phonon hydrodynamics for nanoscale heat transport at ordinary temperatures. Phys. Rev. B 2018, 97, 035421. [Google Scholar] [CrossRef]
- Chen, G. Ballistic-Diffusive Heat-Conduction Equations. Phys. Rev. Lett. 2001, 86, 2297–2300. [Google Scholar] [CrossRef] [PubMed]
- Lebon, G.; Machrafi, H.; Grmela, M.; Dubois, C. An extended thermodynamic model of transient heat conduction at sub-continuum scales. Proc. R. Soc. A 2011, 467, 3241–3256. [Google Scholar] [CrossRef]
- Lebon, G. Heat conduction at micro and nanoscales: A review through the prism of Extended Irreversible Thermodynamics. J. NonEquil. Thermodyn. 2014, 39, 35–59. [Google Scholar] [CrossRef]
- Wang, Y.; Hutter, K. Phenomenological Thermodynamics of Irreversible Processes. Entropy 2018, 20, 479. [Google Scholar] [CrossRef]
- Berezovski, A. Internal variables representation of generalized heat equations. Continuum Mech. Thermodyn. 2019, 31, 1733–1741. [Google Scholar] [CrossRef]
- Berezovski, A. On the influence of microstructure on heat conduction in solids. Int. J. Heat Mass Transf. 2016, 103, 516–520. [Google Scholar] [CrossRef]
- Álvarez, F.X.; Jou, D. Memory and nonlocal effects in heat transport: From diffusive to ballistic regimes. Appl. Phys. Lett. 2007, 90, 083109. [Google Scholar]
- McKane, A.; Vázquez, F. Fluctuation dissipation theorems and irreversible thermodynamics. Phys. Rev. E 2001, 64, 046116. [Google Scholar] [CrossRef]
- Vázquez, F.; del Río, J.A. Thermodynamic characterization of the diffusive transport to wave propagation transition in heat conducting thin films. J. Appl. Phys. 2012, 112, 123707. [Google Scholar] [CrossRef]
- Álvarez, F.X.; Jou, D. Boundary conditions and evolution of ballistic heat transport. J. Heat Transf. 2010, 132, 012404. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez, F.; Ván, P.; Kovács, R. Ballistic-Diffusive Model for Heat Transport in Superlattices and the Minimum Effective Heat Conductivity. Entropy 2020, 22, 167. https://doi.org/10.3390/e22020167
Vázquez F, Ván P, Kovács R. Ballistic-Diffusive Model for Heat Transport in Superlattices and the Minimum Effective Heat Conductivity. Entropy. 2020; 22(2):167. https://doi.org/10.3390/e22020167
Chicago/Turabian StyleVázquez, Federico, Péter Ván, and Róbert Kovács. 2020. "Ballistic-Diffusive Model for Heat Transport in Superlattices and the Minimum Effective Heat Conductivity" Entropy 22, no. 2: 167. https://doi.org/10.3390/e22020167
APA StyleVázquez, F., Ván, P., & Kovács, R. (2020). Ballistic-Diffusive Model for Heat Transport in Superlattices and the Minimum Effective Heat Conductivity. Entropy, 22(2), 167. https://doi.org/10.3390/e22020167





