Nonlinear Fokker–Planck Equation Approach to Systems of Interacting Particles: Thermostatistical Features Related to the Range of the Interactions
Abstract
1. Introduction
2. Entropies, -Exponentials, and -Gaussians
3. Thermostatistics of Overdamped Motion
4. Short-Range versus Long-Range Interactions in Confined Many-Body Systems with Overdamped Motion: A Case Study
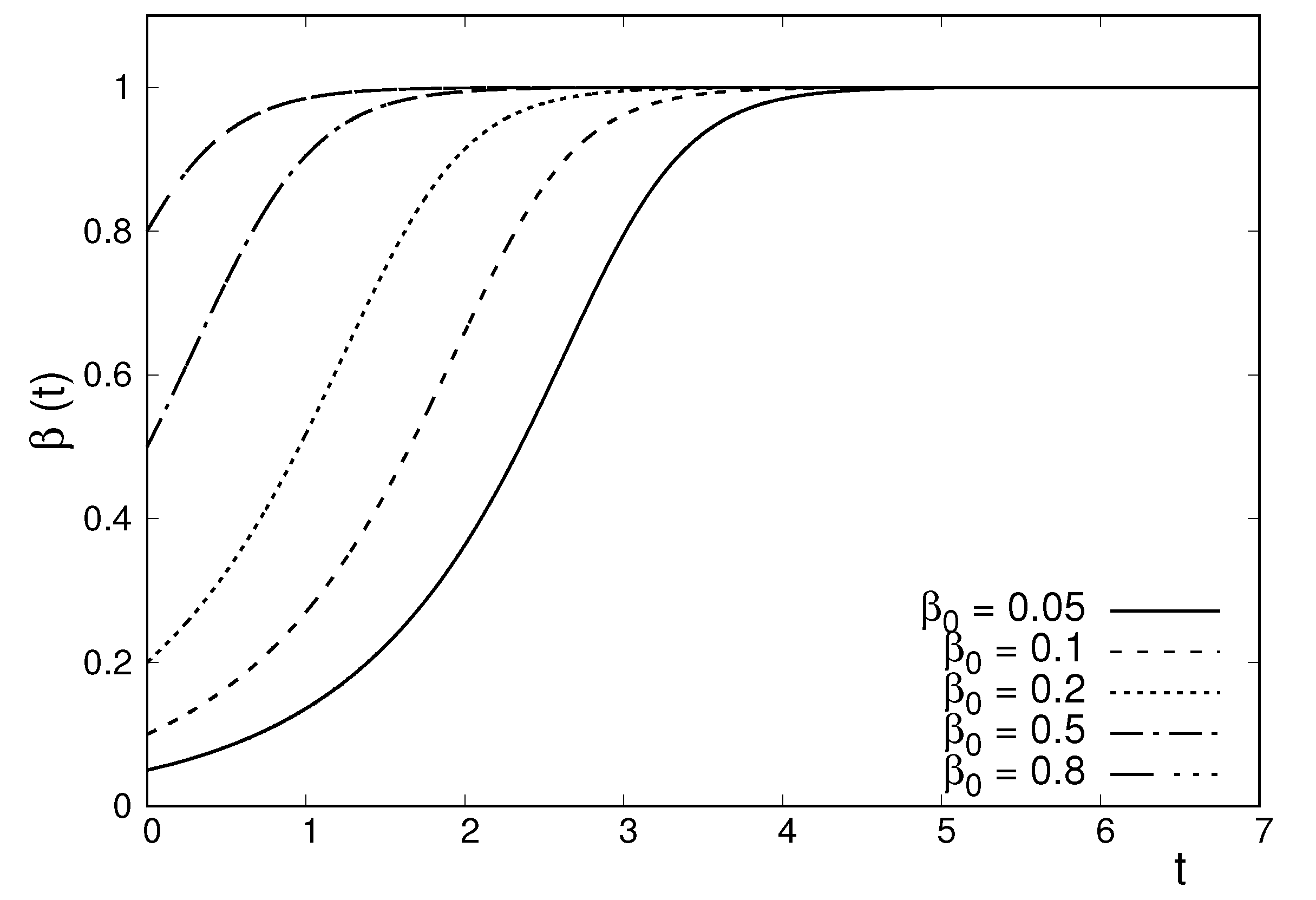
4.1. A Two-Dimensional System Described by a Nonlinear Fokker–Planck Equation
4.2. A Two-Dimensional System with Particles Interacting Through Inverse Square Forces
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tsallis, C. The nonadditive entropy Sq and its applications in physics and elsewhere: Some remarks. Entropy 2011, 13, 1765–1804. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Stellar polytropes and Tsallis’ entropy. Phys. Lett. A 1993, 174, 384–386. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Rodríguez, A.; Nobre, F.D.; Tsallis, C. d-Dimensional classical Heisenberg model with arbitrarily-ranged interactions: Lyapunov exponents and distributions of momenta and energies. Entropy 2019, 21, 31. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Silva, R.; Santos, J. Jeans’ gravitational instability and nonextensive kinetic theory. Astron. Astrophys. 2002, 396, 309–313. [Google Scholar] [CrossRef]
- Taruya, A.; Sakagami, M. Long-term evolution of stellar self-gravitating systems away from thermal equilibrium: Connection with nonextensive statistics. Phys. Rev. Lett. 2003, 90, 181101. [Google Scholar] [CrossRef]
- Chavanis, P.H.; Sire, C. On the interpretations of Tsallis functional in connection with Vlasov–Poisson and related systems: Dynamics vs thermodynamics. Physica A 2005, 356, 419–446. [Google Scholar] [CrossRef]
- Hansen, S.H.; Moore, B. A universal density slope—velocity anisotropy relation for relaxed structures. New Astron. 2006, 11, 333–338. [Google Scholar] [CrossRef]
- Calvo, J.; Florido, E.; Sánchez, O.; Battaner, E.; Soler, J.; Ruiz-Granados, B. On a unified theory of cold dark matter halos based on collisionless Boltzmann-Poisson polytropes. Physica A 2009, 388, 2321–2330. [Google Scholar] [CrossRef]
- Frigerio Martins, C.; Lima, J.A.S.; Chimenti, P. Galaxy rotation curves and nonextensive statistics. Mon. Not. R. Astron. Soc. 1995, 449, 3645–3650. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker-Planck equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker-Planck Equations: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, R2197–R2200. [Google Scholar] [CrossRef] [PubMed]
- Malacarne, L.C.; Mendes, R.S.; Pedron, I.T.; Lenzi, E.K. N-dimensional nonlinear Fokker-Planck equation with time-dependent coefficients. Phys. Rev. E 2002, 65, 052101. [Google Scholar] [CrossRef] [PubMed]
- Schwämmle, V.; Nobre, F.D.; Curado, E.M.F. Consequences of the H theorem from nonlinear Fokker-Planck equations. Phys. Rev. E 2007, 76, 041123. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Classes of N-dimensional nonlinear Fokker-Planck equations associated to Tsallis entropy. Entropy 2011, 13, 1928–1944. [Google Scholar] [CrossRef]
- Conroy, J.M.; Miller, H.G. Determining the Tsallis parameter via maximum entropy. Phys. Rev. E 2015, 91, 052112. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Time evolution of interacting vortices under overdamped motion. Phys. Rev. E 2012, 85, 021146. [Google Scholar] [CrossRef]
- Moreira, A.A.; Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Tsallis, C. Overdamped dynamics of particles with repulsive power-law interactions. Phys. Rev. E 2018, 98, 032138. [Google Scholar] [CrossRef]
- Souza, A.M.C.; Andrade, R.F.S.; Nobre, F.D.; Curado, E.M.F. Thermodynamic framework for compact q-Gaussian distributions. Physica A 2018, 491, 153–166. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D. Repulsive particles under a general external potential: Thermodynamics by neglecting thermal noise. Phys. Rev. E 2016, 94, 022120. [Google Scholar] [CrossRef] [PubMed]
- Curado, E.M.F.; Souza, A.M.C.; Nobre, F.D.; Andrade, R.F.S. Carnot cycle for interacting particles in the absence of thermal noise. Phys. Rev. E 2014, 89, 022117. [Google Scholar] [CrossRef] [PubMed]
- Combe, G.; Richefeu, V.; Stasiak, M.; Atman, A.P.F. Experimental validation of a nonextensive scaling law in confined granular media. Phys. Rev. Lett. 2015, 115, 238301. [Google Scholar] [CrossRef] [PubMed]
- Chavanis, P.H. Generalized thermodynamics and Fokker-Planck equations: applications to stellar dynamics and two-dimensional turbulence. Phys. Rev. E 2003, 68, 036108. [Google Scholar] [CrossRef]
- Mendes, G.A.; Ribeiro, M.S.; Mendes, R.S.; Lenzi, E.K.; Nobre, F.D. Nonlinear Kramers equation associated with nonextensive statistical mechanics. Phys. Rev. E 2015, 91, 052106. [Google Scholar] [CrossRef]
- Frank, T.D.; Friedrich, R. Estimating the nonextensivity of systems from experimental data: A nonlinear diffusion equation approach. Physica A 2005, 347, 65–76. [Google Scholar] [CrossRef]
- Ubriaco, M.R. A simple mathematical model for anomalous diffusion via Fisher’s information theory. Phys. Lett. A 2009, 373, 4017–4021. [Google Scholar] [CrossRef]
- Newman, W.I.; Sagan, C. Galactic civilizations: Population dynamics and interstellar diffusion. Icarus 1981, 46, 293–327. [Google Scholar] [CrossRef]
- Colombo, E.H.; Anteneodo, C. Nonlinear population dynamics in a bounded habitat. J. Theor. Biol. 2018, 446, 11–18. [Google Scholar] [CrossRef]
- Mulansky, M.; Pikovsky, A. Energy spreading in strongly nonlinear disordered lattices. N. Journ. Phys. 2013, 15, 053015. [Google Scholar] [CrossRef]
- Nobre, F.D.; Rego-Monteiro, M.A.; Tsallis, C. Nonlinear relativistic and quantum equations with a common type of solution. Phys. Rev. Lett. 2011, 106, 140601. [Google Scholar] [CrossRef] [PubMed]
- Plastino, A.R.; Wedemann, R.S. Nonlinear wave equations related to nonextensive thermostatistics. Entropy 2017, 19, 60. [Google Scholar] [CrossRef]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann-Gibbs statistics to Tsallis statistics. Nat. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef] [PubMed]
- Sicuro, G.; Tempesta, P.; Rodriguez, A.; Tsallis, C. On the robustness of the q-Gaussian family. Ann. Phys. 2015, 363, 316–336. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Understanding Kappa Distributions: A Toolbox for Space Science and Astrophysics. Space Sci. Rev. 2013, 175, 183–214. [Google Scholar] [CrossRef]
- Pluchino, A.; Rapisarda, A. Metastability in the Hamiltonian mean field model and Kuramoto model. Physica A 2006, 365, 184–189. [Google Scholar] [CrossRef][Green Version]
- Beck, C. Generalised information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Naudts, J. Generalised Thermostatistics; Springer: London, UK, 2011. [Google Scholar]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A Brief Review of Generalized Entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Brito, S.; da Silva, L.R.; Tsallis, C. Role of dimensionality in complex networks. Nat. Sci. Rep. 2016, 6, 27992. [Google Scholar] [CrossRef]
- González, G.A.; Reina, J.I. An infinite family of generalized Kalnajs discs. MNRAS 2006, 371, 1873–1876. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plastino, A.R.; Wedemann, R.S. Nonlinear Fokker–Planck Equation Approach to Systems of Interacting Particles: Thermostatistical Features Related to the Range of the Interactions. Entropy 2020, 22, 163. https://doi.org/10.3390/e22020163
Plastino AR, Wedemann RS. Nonlinear Fokker–Planck Equation Approach to Systems of Interacting Particles: Thermostatistical Features Related to the Range of the Interactions. Entropy. 2020; 22(2):163. https://doi.org/10.3390/e22020163
Chicago/Turabian StylePlastino, Angel R., and Roseli S. Wedemann. 2020. "Nonlinear Fokker–Planck Equation Approach to Systems of Interacting Particles: Thermostatistical Features Related to the Range of the Interactions" Entropy 22, no. 2: 163. https://doi.org/10.3390/e22020163
APA StylePlastino, A. R., & Wedemann, R. S. (2020). Nonlinear Fokker–Planck Equation Approach to Systems of Interacting Particles: Thermostatistical Features Related to the Range of the Interactions. Entropy, 22(2), 163. https://doi.org/10.3390/e22020163




