1. Introduction
Consider a random variable
and a corresponding response function defined as a posteriori probability
. Estimation of the a posteriori probability is of paramount importance in machine learning and statistics since many frequently applied methods, e.g., logistic or tree-based classifiers, rely on it. One of the main estimation methods of
q is a parametric approach for which the response function is assumed to have parametric form
for some fixed
and known
. If Equation (
1) holds, that is the underlying structure is correctly specified, then it is known that
or, equivalently (cf., e.g., [
1])
where
is the expected value of a random variable
and
is Kullback–Leibler distance between the binary distributions with success probabilities
and
:
The equalities in Equations (
2) and (
3) form the theoretical underpinning of (conditional) maximum likelihood (ML) method as the expression under the expected value in Equation (
2) is the conditional log-likelihood of
Y given
X in the parametric model. Moreover, it is a crucial property needed to show that ML estimates of
under appropriate conditions approximate
.
However, more frequently than not, the model in Equation (
1) does not hold, i.e., response
q is misspecified and ML estimators do not approximate
, but the quantity defined by the right-hand side of Equation (
3), namely
Thus, parametric fit using conditional ML method, which is the most popular approach to modeling binary response, also has very intuitive geometric and information-theoretic flavor. Indeed, fitting a parametric model, we try to approximate the
which yields averaged KL projection of unknown
q on set of parametric models
. A typical situation is a semi-parametric framework the true response function satisfies when
for some unknown
and the model in Equation (
1) is fitted where
. An important problem is then how
in Equation (
4) relates to
in Equation (
5). In particular, a frequently asked question is what can be said about a support of
, i.e., the set
, which consists of indices of predictors which truly influence
Y. More specifically, an interplay between supports of
and analogously defined support of
is of importance as the latter is consistently estimated and the support of ML estimator is frequently considered as an approximation of the set of true predictors. Variable selection, or equivalently the support recovery of
in high-dimensional setting, is one of the most intensively studied subjects in contemporary statistics and machine learning. This is related to many applications in bioinformatics, biology, image processing, spatiotemporal analysis, and other research areas (see [
2,
3,
4]). It is usually studied under a correct model specification, i.e., under theassumption that data are generated following a given parametric model (e.g., logistic or, in the case of quantitative
Y, linear model).
Consider the following example: let
, where
is the logistic function. Define regression model by
, where
is
-distributed vector of predictors,
and
. Then, the considered model will obviously be misspecified when the family of logistic models is fitted. However, it turns out in this case that, as
X is elliptically contoured,
and
(see [
5]) and thus supports of
and
coincide. Thus, in this case, despite misspecification variable selection, i.e., finding out that
and
are the only active predictors, it can be solved using the methods described below.
For recent contributions to the study of Kullback–Leibler projections on logistic model (which coincide with Equation (
4) for a logistic loss, see below) and references, we refer to the works of Kubkowski and Mielniczuk [
6], Kubkowski and Mielniczuk [
7] and Kubkowski [
8]. We also refer to the work of Lu et al. [
9], where the asymptotic distribution of adaptive Lasso is studied under misspecification in the case of fixed number of deterministic predictors. Questions of robustness analysis evolve around an interplay between
and
, in particular under what conditions the directions of
and
coincide (cf. the important contribution by Brillinger [
10] and Ruud [
11]).
In the present paper, we discuss this problem in a more general non-parametric setting. Namely, the minus conditional log-likelihood
is replaced by a general loss function of the form
where
is some function,
, and
is the associated risk function for
. Our aim is to determine a support of
, where
Coordinates of
corresponding to non-zero coefficients are called active predictors and vector
the pseudo-true vector.
The most popular loss functions are related to minus log-likelihood of specific parametric models such as logistic loss
related to
, probit loss
related to
, or quadratic loss
related to linear regression and quantitative response. Other losses which do not correspond to any parametric model such as Huber loss (see [
12]) are constructed with a specific aim to induce certain desired properties of corresponding estimators such as robustness to outliers. We show in the following that variable selection problem can be studied for a general loss function imposing certain analytic properties such as its convexity and Lipschitz property.
For fixed number
p of predictors smaller than sample size
n, the statistical consequences of misspecification of a semi-parametric regression model were intensively studied by H. White and his collaborators in the 1980s. The concept of a projection on the fitted parametric model is central to these investigations which show how the distribution of maximum likelihood estimator of
centered by
changes under misspecification (cf. e.g., [
13,
14]). However, for the case when
, the maximum likelihood estimator, which is a natural tool for fixed
case, is ill-defined and a natural question arises: What can be estimated and by what methods?
The aim of the present paper is to study the above problem in high-dimensional setting. To this end, we introduce two-stage approach in which the first stage is based on Lasso estimation (cf., e.g., [
2])
where
and the empirical risk
corresponding to
is
Parameter
is Lasso penalty, which penalizes large
-norms of potential candidates for a solution. Note that the criterion function in Equation (
8) for
can be viewed as penalized empirical risk for the logistic loss. Lasso estimator is thoroughly studied in the case of the linear model when considered loss is square loss (see, e.g., [
2,
4] for references and overview of the subject) and some of the papers treat the case when such model is fitted to
Y, which is not necessarily linearly dependent on regressors (cf. [
15]). In this case, regression model is misspecified with respect to linear fit. However, similar results are scarce for other scenarios such as logistic fit under misspecification in particular. One of the notable exceptions is Negahban et al. [
16], who studied the behavior of Lasso estimate i for a general loss function and possibly misspecified models.
The output of the first stage is Lasso estimate
. The second stage consists in ordering of predictors according to the absolute values of corresponding non-zero coordinates of Lasso estimator and then minimization of Generalized Information Criterion (GIC) on the resulting nested family. This is a variant of SOS (Screening-Ordering-Selection) procedure introduced in [
17]. Let
be the model chosen by GIC procedure.
Our main contributions are as follows:
We prove that under misspecification when the sample size grows support
coincides with support of
with probability tending to 1. In the general framework allowing for misspecification this means that selection rule
is consistent, i.e.,
when
. In particular, when the model in Equation (
1) is correctly specified this means that we recover the support of the true vector
with probability tending to 1.
We also prove approximation result for Lasso estimator when predictors are random and is a convex Lipschitz function (cf. Theorem 1).
A useful corollary of the last result derived in the paper is determination of sufficient conditions under which active predictors can be separated from spurious ones based on the absolute values of corresponding coordinates of Lasso estimator. This makes construction of nested family containing with a large probability possible.
Significant insight has been gained for fitting of parametric model when predictors are elliptically contoured (e.g., multivariate normal). Namely, it is known that in such situation
, i.e., these two vectors are collinear [
5]. Thus, in the case when
we have that support
of
coincides with support
s of
and the selection consistency of two-step procedure proved in the paper entails direction and support recovery of
. This may be considered as a partial justification of a frequent observation that classification methods are robust to misspecification of the model for which they are derived (see, e.g., [
5,
18]).
We now discuss how our results relate to previous results. Most of the variable selection methods in high-dimensional case are studied for deterministic regressors; here, our results concern random regressors with subgaussian distributions. Note that random regressors scenario is much more realistic for experimental data than deterministic one. The stated results to the best of our knowledge are not available for random predictors even when the model is correctly specified. As to novelty of SS procedure, for its second stage we assume that the number of active predictors is bounded by a deterministic sequence
tending to infinity and we minimize GIC on family
of models with sizes satisfying also this condition. Such exhaustive search has been proposed in [
19] for linear models and extended to GLMs in [
20] (cf. [
21]). In these papers, GIC has been optimized on all possible subsets of regressors with cardinality not exceeding certain constant
. Such method is feasible for practical purposes only when
is small. Here, we consider a similar set-up but with important differences:
is a data-dependent small nested family of models and optimization of GIC is considered in the case when the original model is misspecified. The regressors are supposed random and assumptions are carefully tailored to this case. We also stress the fact that the presented results also cover the case when the regression model is correctly specified and Equation (
5) is satisfied.
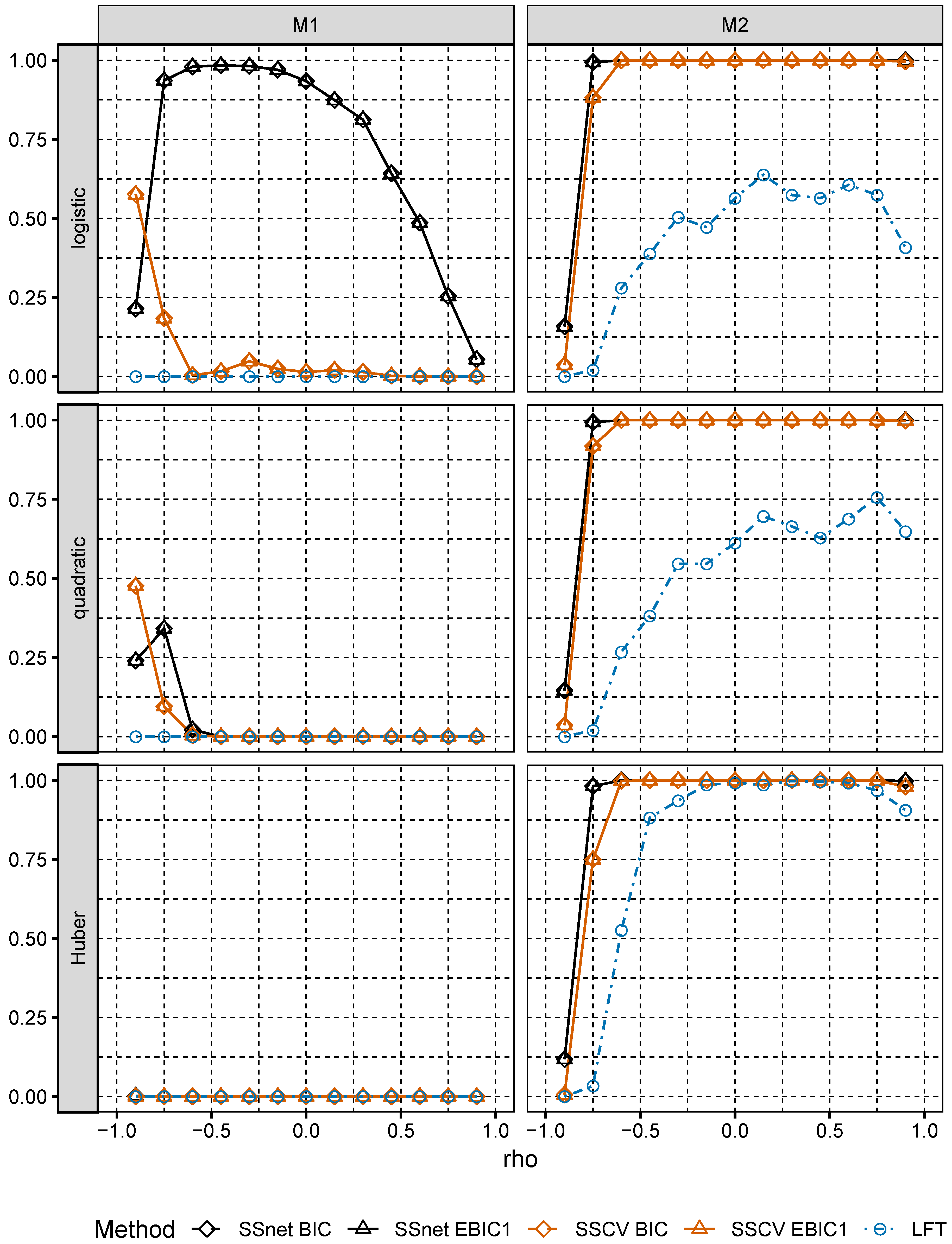
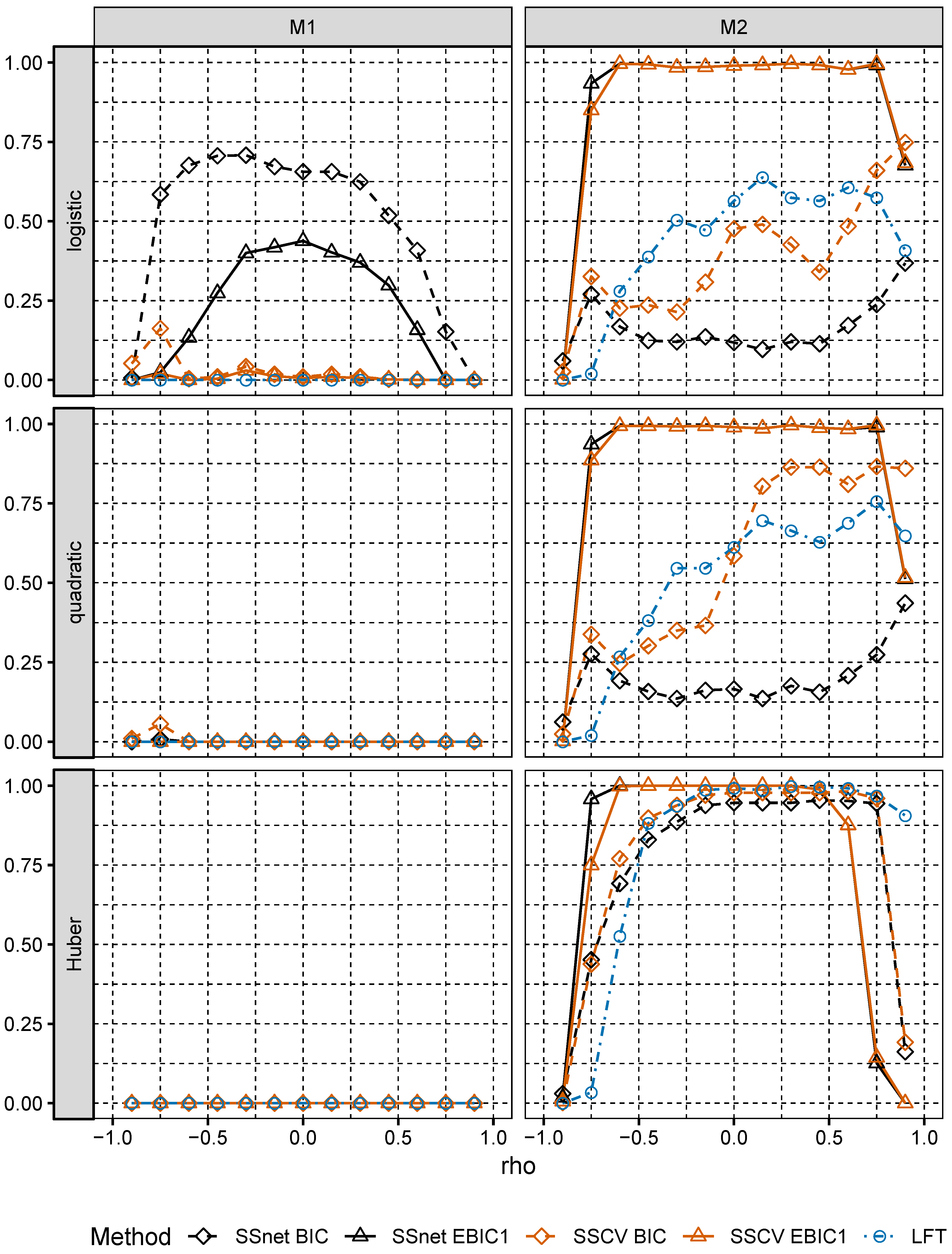
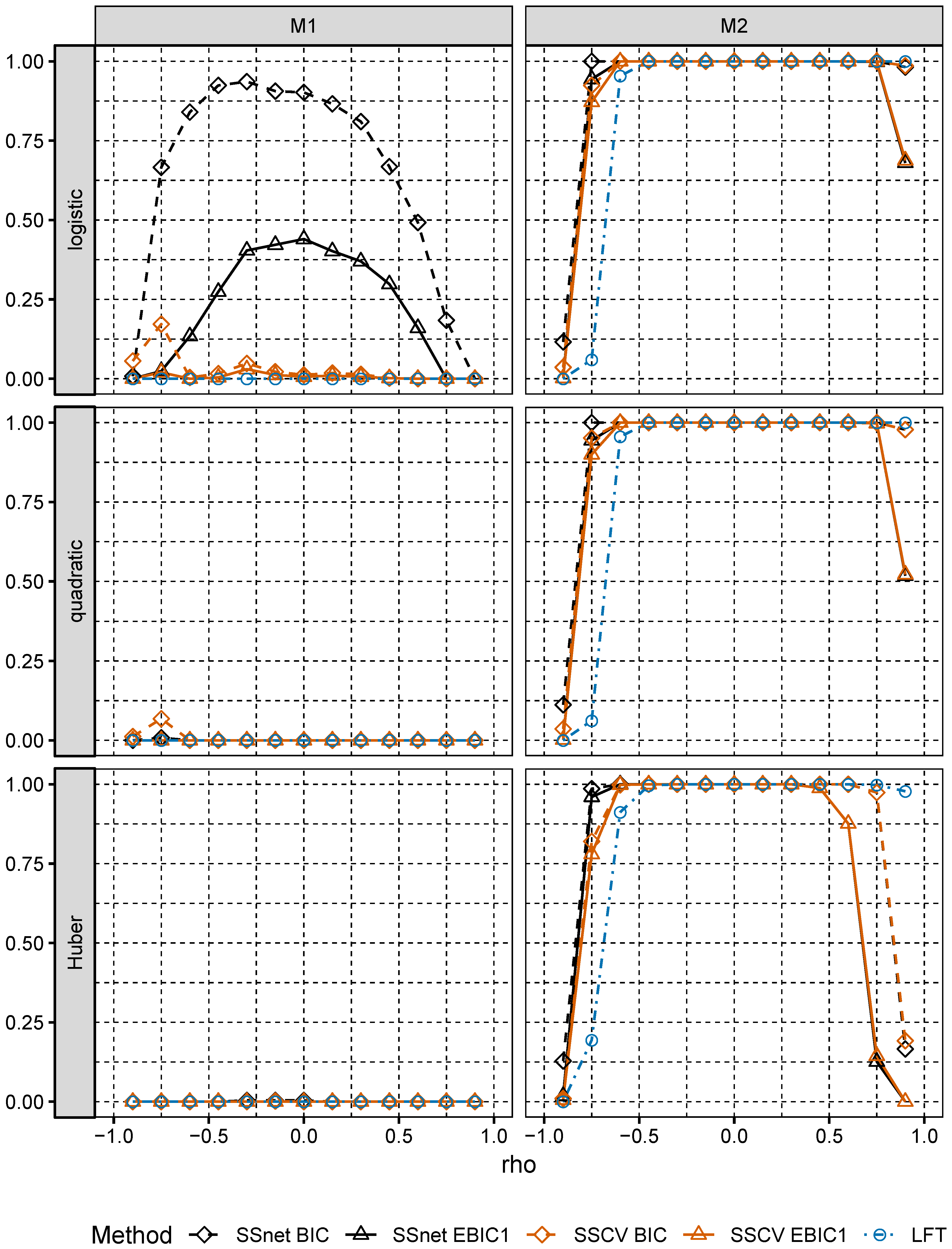
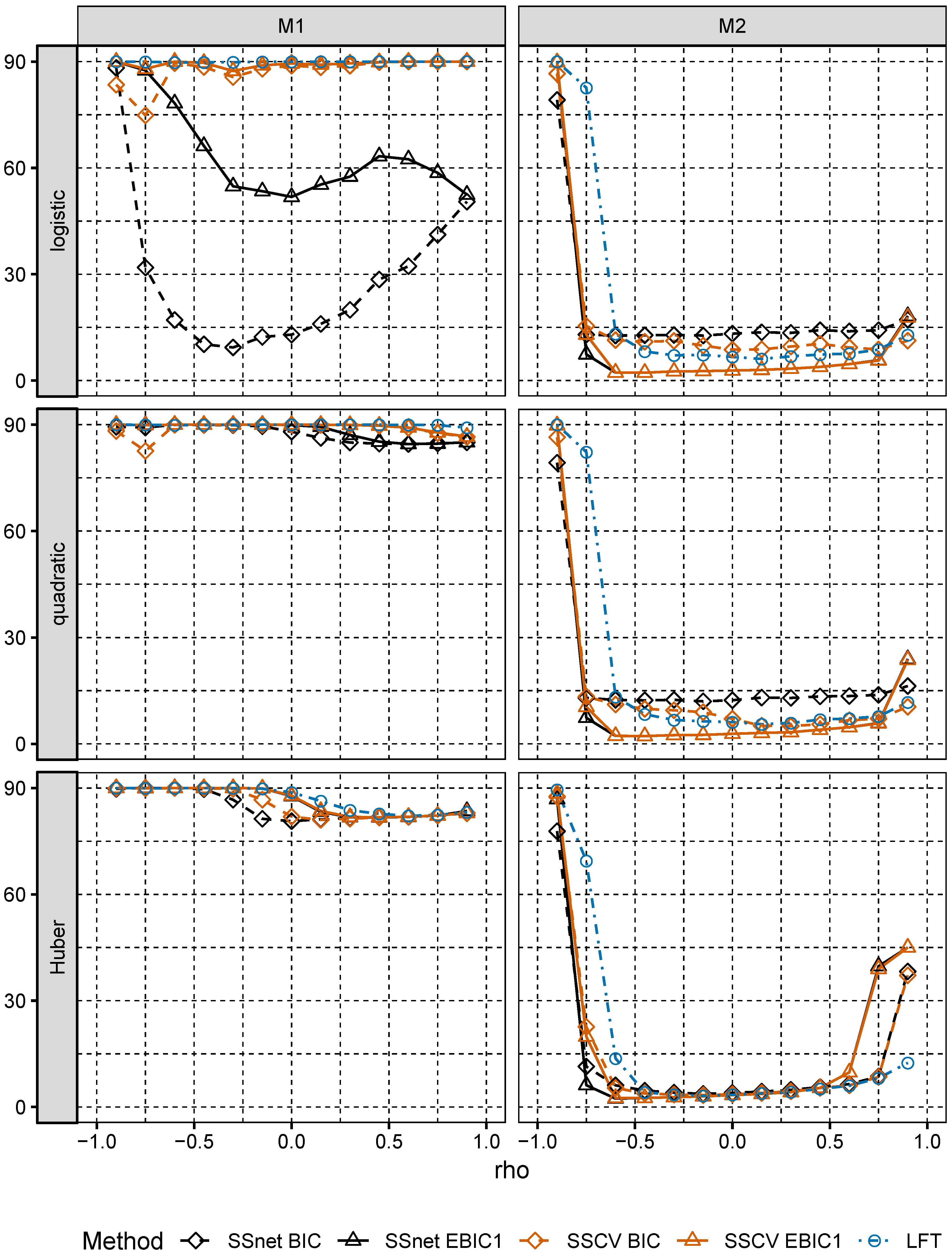
In numerical experiments, we study the performance of grid version of logistic and linear SOS and compare it to its several Lasso-based competitors.
The paper is organized as follows.
Section 2 contains auxiliaries, including new useful probability inequalities for empirical risk in the case of subgaussian random variables (Lemma 2). In
Section 3, we prove a bound on approximation error for Lasso when the loss function is convex and Lipschitz and regressors are random (Theorem 1). This yields separation property of Lasso. In Theorems 2 and 3 of
Section 4, we prove GIC consistency on nested family, which in particular can be built according to the order in which the Lasso coordinates are included in the fitted model. In
Section 5.1, we discuss consequences of the proved results for semi-parametric binary model when distribution of predictors satisfies linear regressions condition. In
Section 6, we numerically compare the performance of two-stage selection method for two closely related models, one of which is a logistic model and the second one is misspecified.
2. Definitions and Auxiliary Results
In the following, we allow random vector
,
, and
p to depend on sample size
n, i.e.,
and
. We assume that
n copies
of a random vector
in
are observed together with corresponding binary responses
. Moreover, we assume that observations
are independent and identically distributed (iid). If this condition is satisfied for each
n, but not necessarily for different
n and
m, i.e., distributions of
may be different from that of
or they may be dependent for
, then such framework is called a triangular scenario. A frequently considered scenario is the sequential one. In this case, when sample size
n increases, we observe values of new predictors additionally to the ones observed earlier. This is a special case of the above scheme as then
. In the following, we skip the upper index
n if no ambiguity arises. Moreover, we write
. We impose a condition on distributions of random predictors assume that coordinates
of
are subgaussian
with subgaussianity parameter
, i.e., it holds that (see [
22])
for all
. This condition basically says that the tails of of
do not decrease more slowly than tails of normal distribution
. For future reference, let
and assume in the following that
We assume moreover that
are linearly independent in the sense that their arbitrary linear combination is not constant almost everywhere. We consider a general form of response function
and assume that for the given loss function
, as defined in Equation (
7), exists and is unique. For
, let
be defined as in Equation (
7) when minimum is taken over
b with support in
s. We let
denote the support of
with
.
Let
for
and
. Let
be
restricted to its support
. Note that if
, then provided projections are unique (see
Section 2) we have
Note that this implies that for every superset
of
s the projection
on the model pertaining to
s is obtained by appending projection
with appropriate number of zeros. Moreover, let
We remark that
,
and
may depend on
n. We stress that
is an important quantity in the development here as it turns out that it may not decrease too quickly in order to obtain approximation results for
(see Theorem 1). Note that, when the parametric model is correctly specified, i.e.,
for some
with
l being an associated log-likelihood loss, if
s is the support of
, we have
.
First, we discuss quantities and assumptions needed for the first step of SS procedure.
We consider cones of the form:
where
,
and
for
. Cones
are of special importance because we prove that
(see Lemma 3). In addition, we note that since
-norm is decomposable in the sense that
the definition of the cone above can be stated as
Thus,
consists of vectors which do not put too much mass on the complement of
. Let
be a fixed non-negative definite matrix. For cone
, we define a quantity
which can be regarded as a restricted minimal eigenvalue of a matrix in high-dimensional set-up:
In the considered context,
H is usually taken as hessian
and, e.g., for quadratic loss, it equals
. When
H is non-negative definite and not strictly positive definite its smallest eigenvalue
and thus
. That is why we have to restrict minimization in Equation (
12) in order to have
in the high-dimensional case. As we prove that
and would use
it is useful to restrict minimization in Equation (
12) to
. Let
R and
be the risk and the empirical risk defined above. Moreover, we introduce the following notation:
Note that
. Thus,
corresponds to oscillation of centred empirical risk over ball
. We need the following Margin Condition (MC) in Lemma 3 and Theorem 1:
- (MC)
There exist
and non-negative definite matrix
such that for all
b with
we have
The above condition can be viewed as a weaker version of strong convexity of function
R (when the right-hand side is replaced by
) in the restricted neighbourhood of
(namely, in the intersection of ball
and cone
). We stress the fact that
H is not required to be positive definite, as in
Section 3 we use Condition (MC) together with stronger conditions than
which imply that right hand side of inequality in (MC) is positive. We also do not require here twice differentiability of
R. We note in particular that Condition (MC) is satisfied in the case of logistic loss,
X being bounded random variable and
(see [
23,
24,
25]). It is also easily seen that that (MC) is satisfied for quadratic loss,
X such that
and
. Similar condition to (MC) (called Restricted Strict Convexity) was considered in [
16] for empirical risk
:
for all
, some
, and tolerance function
. Note however that MC is a deterministic condition, whereas Restricted Strict Convexity has to be satisfied for random empirical risk function.
Another important assumption, used in Theorem 1 and Lemma 2, is the Lipschitz property of
- (LL)
.
Now, we discuss preliminaries needed for the development of the second step of SS procedure. Let
stand for dimension of
w. For the second step of the procedure we consider an arbitrary family
of models (which are identified with subsets of
and may be data-dependent) such that
a.e. and
is some deterministic sequence. We define Generalized Information Criterion (GIC) as:
where
is ML estimator for model
w as minimization above is taken over all vectors
b with support in
w. Parameter
is some penalty factor depending on the sample size
n which weighs how important is the complexity of the model described by the number of its variables
. Typical examples of
include:
AIC (Akaike Information Criterion): ;
BIC (Bayesian Information Criterion): ; and
EBIC(d) (Extended BIC): , where .
AIC, BIC and EBIC were introduced by Akaike [
26], Schwarz [
27], and Chen and Chen [
19], respectively. Note that for
BIC penalty is larger than AIC penalty and in its turn EBIC penalty is larger than BIC penalty.
We study properties of
for
, where:
and is the maximal absolute value of the centred empirical risk
and sets
for
are defined as follows:
The idea here is simply to consider sets
consisting of vectors having no more that
non-zero coordinates. However, for
, we need that for
, we have
, what we exploit in Lemma 2. This entails additional condition in the definition of
. Moreover, in
Section 4, we consider the following condition
for
,
and some
:
We observe also that, although Conditions (MC) and
are similar, they are not equivalent, as they hold for
belonging to different sets:
and
, respectively. If the minimal eigenvalue
of matrix
H in Condition (MC) is positive and Condition (MC) holds for
(instead of for
), then we have for
:
Furthermore, if
is the maximal eigenvalue of
H and Condition
holds for all
without restriction on
, then we have for
:
Thus, Condition (MC) holds in this case. A similar condition to Condition
for empirical risk
was considered by Kim and Jeon [
28] (formula (2.1)) in the context of GIC minimization. It turns out that Condition
together with
being convex for all
y and satisfying Lipschitz Condition (LL) are sufficient to establish bounds which ensure GIC consistency for
and
(see Corollaries 2 and 3). First, we state the following basic inequality.
and
are defined above the definition of Margin Condition.
Lemma 1. (Basic inequality). Let be convex function for all If for some we havethen The proof of the lemma is moved to the
Appendix A. It follows from the lemma that, as in view of decomposability of
-distance we have
, when
is small we have
is not large in comparison with
.
Quantities
are defined in Equation (
18). Recall that
is an oscillation taken over ball
, whereas
are oscillations taken over
ball with restriction on the number of nonzero coordinates.
Lemma 2. Let be convex function for all y and satisfy Lipschitz Condition (LL). Assume that for are subgaussian , where . Then, for :
- 1.
,
- 2.
,
- 3.
.
The proof of the Lemma above, which relies on Chebyshev inequality, symmetrization inequality (see Lemma 2.3.1 of [
29]), and Talagrand–Ledoux inequality ([
30], Theorem 4.12), is moved to the
Appendix A. In the case when
does not depend on
n and thus its support does not change, Part 3 implies in particular that
is of the order
in probability.