Analytic Expression of Quantum Discords in Werner States under LQCC
Abstract
1. Introduction
2. WLQCC State
3. Quantum Discord in the WLQCC State
4. Analyses and Discussions
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G.; Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Popescu, S.; Schumacher, B.; Smolin, J.A.; Wootters, W.K. Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels. Phys. Rev. Lett. 1996, 76, 722. [Google Scholar] [CrossRef]
- Raussendorf, R.; Briegel, H.J. A One-Way Quantum Computer. Phys. Rev. Lett. 2001, 86, 5188. [Google Scholar] [CrossRef] [PubMed]
- Cirac, J.I.; Ekert, A.K.; Huelga, S.F.; Macchiavello, C. Distributed quantum computation over noisy channels. Phys. Rev. A 1999, 59, 4249. [Google Scholar] [CrossRef]
- Gheorghiu, V.; Yu, L.; Cohen, S.M. Local cloning of entangled states. Phys. Rev. A 2010, 82, 022313. [Google Scholar] [CrossRef]
- Hillery, M.; Buzek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Gheorghiu, V.; Sanders, B.C. Accessing quantum secrets via local operations and classical communication. Phys. Rev. A 2013, 88, 022340. [Google Scholar] [CrossRef]
- DiVincenzo, D.P.; Mor, T.; Shor, P.W.; Smolin, J.A.; Terhal, B.M. Unextendible product bases, uncompletable product bases, and bound entanglement. Commun. Math. Phys. 2003, 238, 379. [Google Scholar] [CrossRef]
- Niset, J.; Cerf, N.J. Multipartite nonlocality without entanglement in many dimensions. Phys. Rev. A 2006, 74, 052103. [Google Scholar] [CrossRef]
- Cohen, S.M. Local distinguishability with preservation of entanglement. Phys. Rev. A 2007, 75, 052313. [Google Scholar] [CrossRef]
- Cohen, S.M. Local quantum protocols for separable measurements with many parties. Phys. Rev. A 2013, 87, 052135. [Google Scholar] [CrossRef]
- Chitambar, E.; Hsieh, M.H. Asymptotic state discrimination and a strict hierarchy in distinguishability norms. J. Math. Phys. 2014, 55, 112204. [Google Scholar] [CrossRef]
- Hebenstreit, M.; Spee, C.; Kraus, B. Maximally entangled set of tripartite qutrit states and pure state separable transformations which are not possible via local operations and classical communication. Phys. Rev. A 2016, 93, 012339. [Google Scholar] [CrossRef]
- Yamasaki, H.; Pirker, A.; Murao, M.; Dür, W.; Kraus, B. Multipartite entanglement outperforming bipartite entanglement under limited quantum system sizes. Phys. Rev. A 2018, 98, 052313. [Google Scholar] [CrossRef]
- Sauerwein, D.; Wallach, N.R.; Gour, G.; Kraus, B. Transformations among pure Multipartite entangled states via local operations are almost never possible. Phys. Rev. X 2018, 8, 031020. [Google Scholar] [CrossRef]
- Contreras-Tejada, P.; Palazuelos, C.; Vicente, J.I. Resource theory of entanglement with a unique multipartite maximally entangled state. Phys. Rev. Lett. 2019, 122, 120503. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Luo, S.L. Usingmeasurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 2008, 77, 022301. [Google Scholar] [CrossRef]
- Luo, S.L.; Fu, S.S. Geometric measure of quantum discord. Phys. Rev. A 2010, 82, 034302. [Google Scholar] [CrossRef]
- Zhou, T.; Cui, J.; Long, G.L. Measure of nonclassical correlation in coherence-vector representation. Phys. Rev. A 2011, 84, 062105. [Google Scholar] [CrossRef]
- Girolami, D.; Paternostro, M.; Adesso, G. Faithful nonclassicality indicators and extremal quantum correlations in two-qubit states. J. Phys. A Math. Theor. 2011, 44, 352002. [Google Scholar] [CrossRef][Green Version]
- Modi, K.; Paterek, T.; Son, W.; Vedral, V.; Williamson, M. Unified view of quantum and classical correlations. Phys. Rev. Lett. 2010, 104, 080501. [Google Scholar] [CrossRef] [PubMed]
- Dakic, B.; Vedral, V.; Brukner, C. Necessary and sufficient condition for nonzero quantum discord. Phys. Rev. Lett. 2010, 105, 190502. [Google Scholar] [CrossRef] [PubMed]
- Rulli, C.C.; Sarandy, M.S. Global quantum discord in multipartite systems. Phys. Rev. A 2011, 84, 042109. [Google Scholar] [CrossRef]
- Streltsov, A. Quantum Correlations beyond Entanglement and Their Role in Quantum Information Theory; Springer: Berlin, Germany, 2015. [Google Scholar]
- Werlang, T.; Souza, S.; Fanchini, F.F.; Villas Boas, C.J. Robustness of quantum discord to sudden death. Phys. Rev. A 2009, 80, 024103. [Google Scholar] [CrossRef]
- Maruyama, K.; Nori, F.; Vedral, V. The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1. [Google Scholar] [CrossRef]
- Francica, G.; Goold, J.; Plastina, F.; Paternostro, M. Daemonic ergotropy: Enhanced work extraction from quantum correlations. npj Quant. Inf. 2017, 3, 12. [Google Scholar] [CrossRef]
- Ciampini, M.A.; Mancino, L.; Orieux, A.; Vigliar, C.; Mataloni, P.; Paternostro, M.; Barbieri, M. Experimental extractable work-based multipartite separability criteria. npj Quant. Inf. 2017, 3, 10. [Google Scholar] [CrossRef]
- Celeri, L.C.; Maziero, J.; Serra, R.M. Theoretical and experimental aspects of quantum discord and related measures. Int. J. Quant. Inf. 2011, 9, 1837. [Google Scholar] [CrossRef]
- Datta, A.; Shaji, A.; Caves, C.M. Quantum discord and the power of one qubit. Phys. Rev. Lett. 2008, 100, 050502. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Barbieri, M.; Almeida, M.P.; White, A.G. Experimental quantum computing without entanglement. Phys. Rev. Lett. 2008, 101, 200501. [Google Scholar] [CrossRef] [PubMed]
- Madhok, V.; Datta, A. Interpreting quantum discord through quantum state merging. Phys. Rev. A 2011, 83, 032323. [Google Scholar] [CrossRef]
- Dakic, B.; Lipp, Y.O.; Ma, X.; Ringbauer, M.; Kropatschek, S.; Barz, S.; Paterek, T.; Vedral, V.; Zeilinger, A.; Brukner, C. Quantum discord as resource for remote state preparation. Nat. Phys. 2012, 8, 666. [Google Scholar] [CrossRef]
- Li, B.; Fei, S.M.; Wang, Z.X.; Fan, H. Assisted state discrimination without entanglement. Phys. Rev. A 2012, 85, 022328. [Google Scholar] [CrossRef]
- Xie, C.M.; Liu, Y.M.; Xing, H.; Chen, J.L.; Zhang, Z.J. Quantum correlation swapping. Quantum Inf. Process. 2015, 14, 653. [Google Scholar] [CrossRef]
- Xie, C.M.; Liu, Y.M.; Chen, J.L.; Zhang, Z.J. Study of quantum correlation swapping with relative entropy methods. Quantum Inf. Process. 2016, 15, 809. [Google Scholar] [CrossRef]
- Xie, C.M.; Liu, Y.M.; Chen, J.L.; Zhang, Z.J. Quantum correlation swapping in parallel and antiparallel two-qubit mixed states. Quantum Inf. Process. 2019, 18, 106. [Google Scholar] [CrossRef]
- Luo, S.L. Quantum discord for two-qubit systems. Phys. Rev. A 2008, 77, 042303. [Google Scholar] [CrossRef]
- Ali, M.; Rau, A.R.P.; Alber, G. Quantum discord for two-qubit X states. Phys. Rev. A 2010, 81, 042105. [Google Scholar] [CrossRef]
- Ye, B.L.; Liu, Y.M.; Chen, J.L.; Liu, X.S.; Zhang, Z.J. Analytic expressions of quantum correlations in qutrit Werner states. Quantum Inf. Process. 2013, 12, 2355. [Google Scholar] [CrossRef]
- Tang, H.J.; Liu, Y.M.; Chen, J.L.; Ye, B.L.; Zhang, Z.J. Analytic expressions of discord and geometric discord in Werner derivatives. Quantum Inf. Process. 2014, 13, 1331. [Google Scholar] [CrossRef]
- Li, G.F.; Liu, Y.M.; Tang, H.J.; Yin, X.F.; Zhang, Z.J. Analytic expression of quantum correlations in qutrit Werner states undergoing local and nonlocal unitary operations. Quantum Inf. Process. 2014, 14, 559. [Google Scholar]
- Werner, R. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277. [Google Scholar] [CrossRef] [PubMed]
- Kent, A.; Linden, N.; Massar, S. Optimal Entanglement Enhancement for Mixed States. Phys. Rev. Lett. 1999, 83, 13. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Liu, Y.M. Perfect teleportation of arbitrary n-qudit states using different quantum channels. Phys. Lett. A 2007, 372, 28. [Google Scholar] [CrossRef]
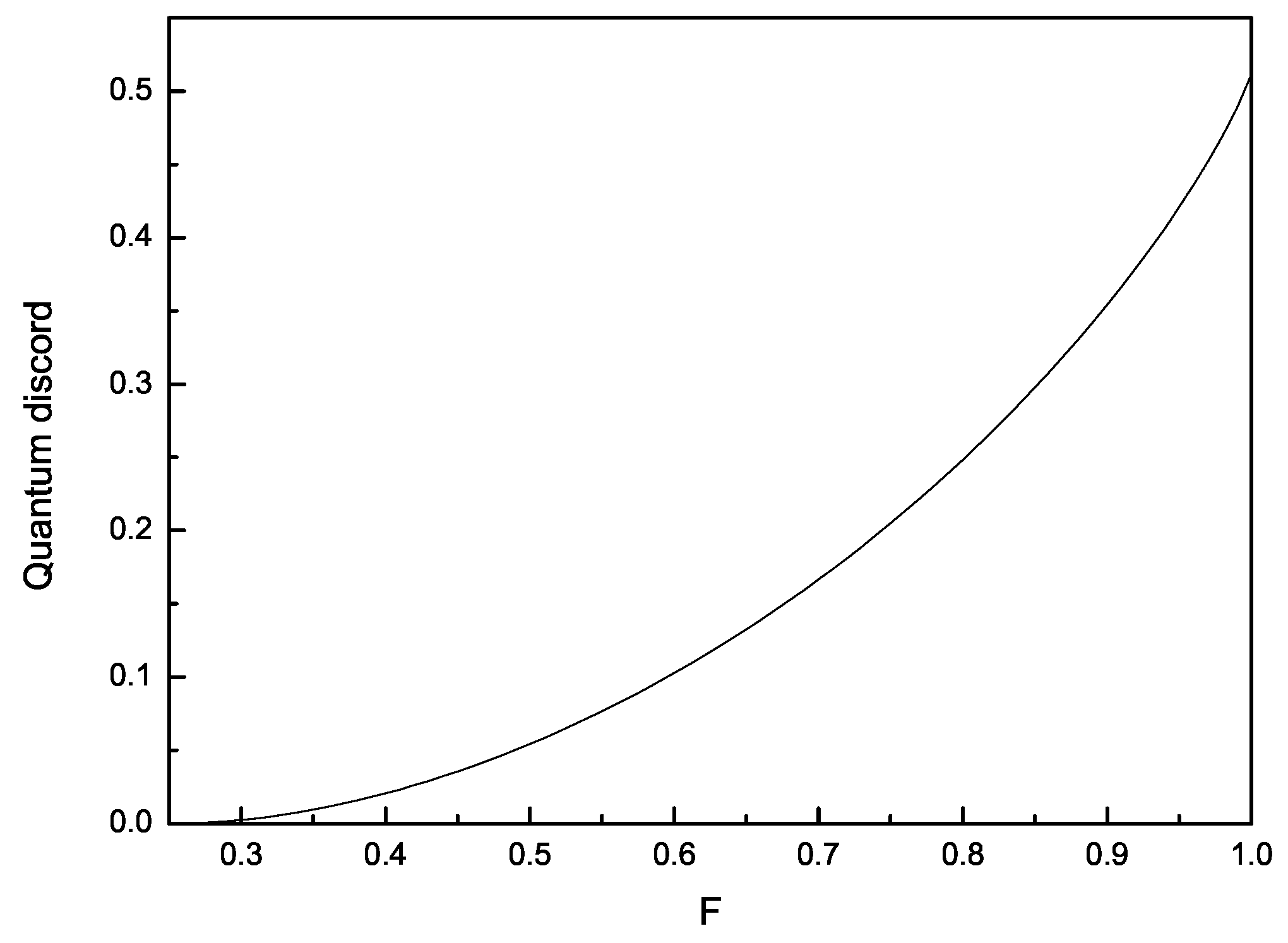
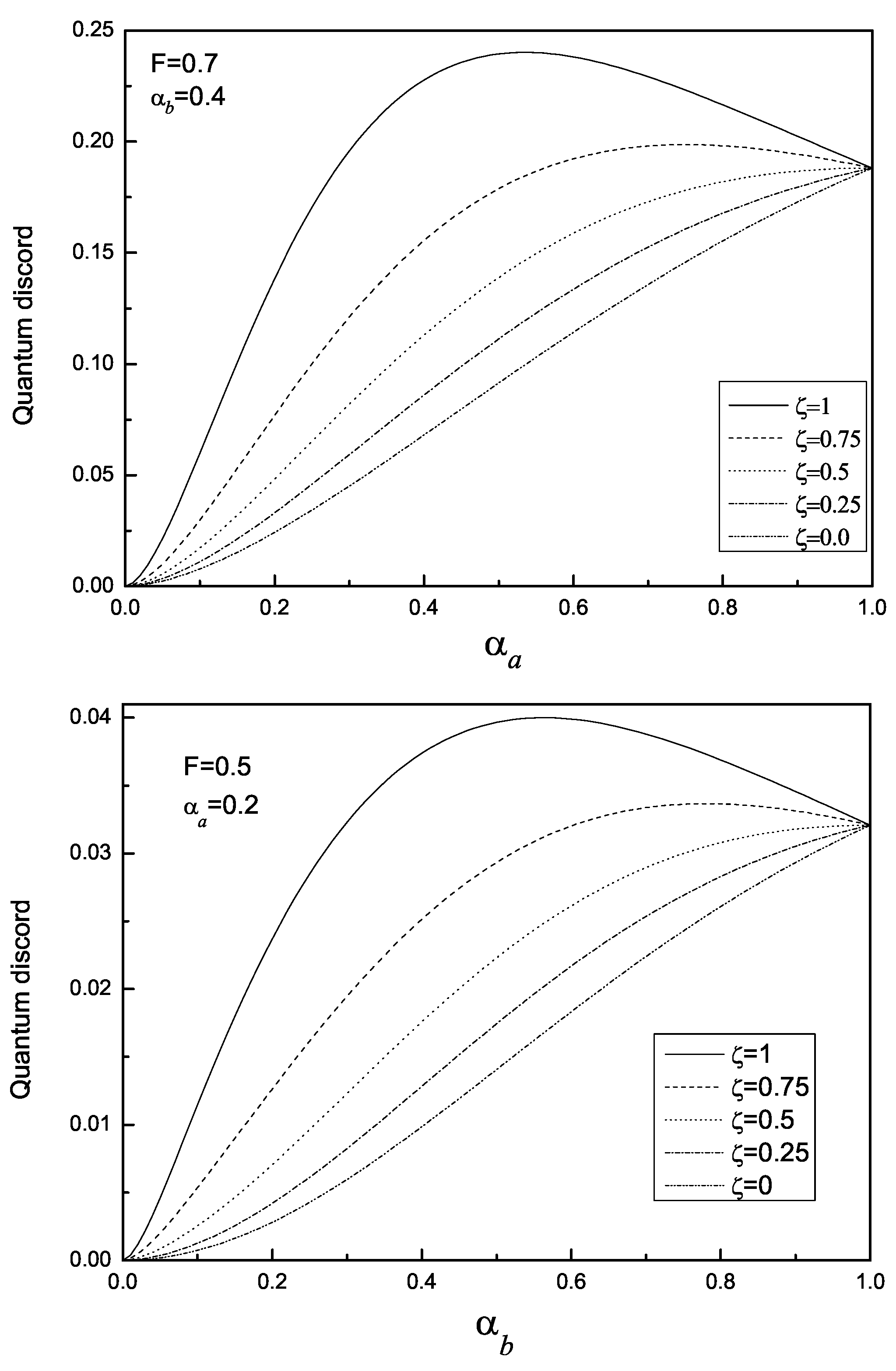
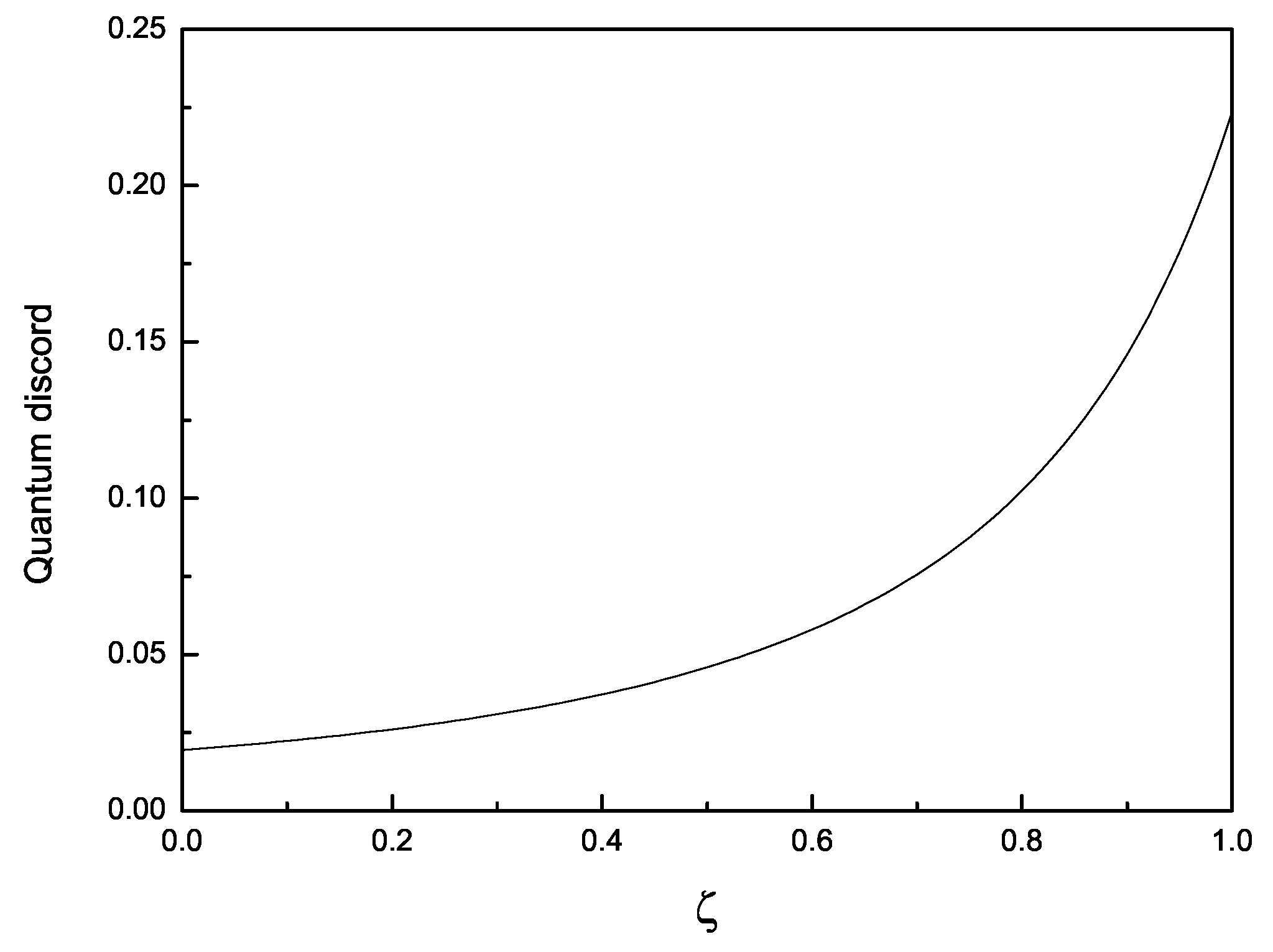
| (Equation (2)) | (Equation (7)) | ||
|---|---|---|---|
| N | 19 | 7 | 8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, C.; Zhang, Z.; Chen, J.; Yin, X. Analytic Expression of Quantum Discords in Werner States under LQCC. Entropy 2020, 22, 147. https://doi.org/10.3390/e22020147
Xie C, Zhang Z, Chen J, Yin X. Analytic Expression of Quantum Discords in Werner States under LQCC. Entropy. 2020; 22(2):147. https://doi.org/10.3390/e22020147
Chicago/Turabian StyleXie, Chuanmei, Zhanjun Zhang, Jianlan Chen, and Xiaofeng Yin. 2020. "Analytic Expression of Quantum Discords in Werner States under LQCC" Entropy 22, no. 2: 147. https://doi.org/10.3390/e22020147
APA StyleXie, C., Zhang, Z., Chen, J., & Yin, X. (2020). Analytic Expression of Quantum Discords in Werner States under LQCC. Entropy, 22(2), 147. https://doi.org/10.3390/e22020147




