Lottery and Auction on Quantum Blockchain
Abstract
1. Introduction
- Randomness. All tickets are equally likely to win.
- Unpredictability. No player can predict the winning ticket.
- Unforgeability. Tickets cannot be forged. Especially, it is impossible to create a winning ticket after the outcome of the random process is known.
- Verifiablity. The number and the revenue of winning tickets are publicly verifiable.
- Decentralization. The random process does not rely on a single authority.
- 6.
- Unconditional security. Even an adversary with an unlimited power of computation cannot rig the lottery.
- Bid privacy. The submitted bids are not visible to other buyers during the bidding phase.
- Posterior privacy. The losing bids are not revealed to the public. In other words, only the seller knows all losing bids and their corresponding buyers.
- Bids’ binding. Buyers cannot deny or change their bids once they are committed.
- 4.
- Decentralization. The process of the auction does not rely on a single trusted third party.
- 5.
- Unconditional security. Even an adversary with an unlimited power of computation cannot manipulate the process of auction.
2. Background
2.1. Quantum Blockchain
- Every node is a (small scale) quantum computer which can run some quantum computation on a small number of qubits. More specifically, nodes are capable of performing the quantum computation involved in at least one quantum bit commitment protocol.
- The communication between different nodes is unconditionally secure.
- There is a consensus algorithm which can be used by all miners to achieve consensus. The consensus mechanism is immune to attacks. A general definition of the consensus algorithm is given as the following.
2.2. Quantum Bit Commitment
- (1)
- Two finite-dimensional Hilbert spaces A and B.
- (2)
- A function .
- (3)
- Two pure states , in which is the commitment of i.
- (4)
- A quantum operation (i.e., completely positive, trace-preserving super operator) on such that .
3. Lottery on Quantum Blockchain
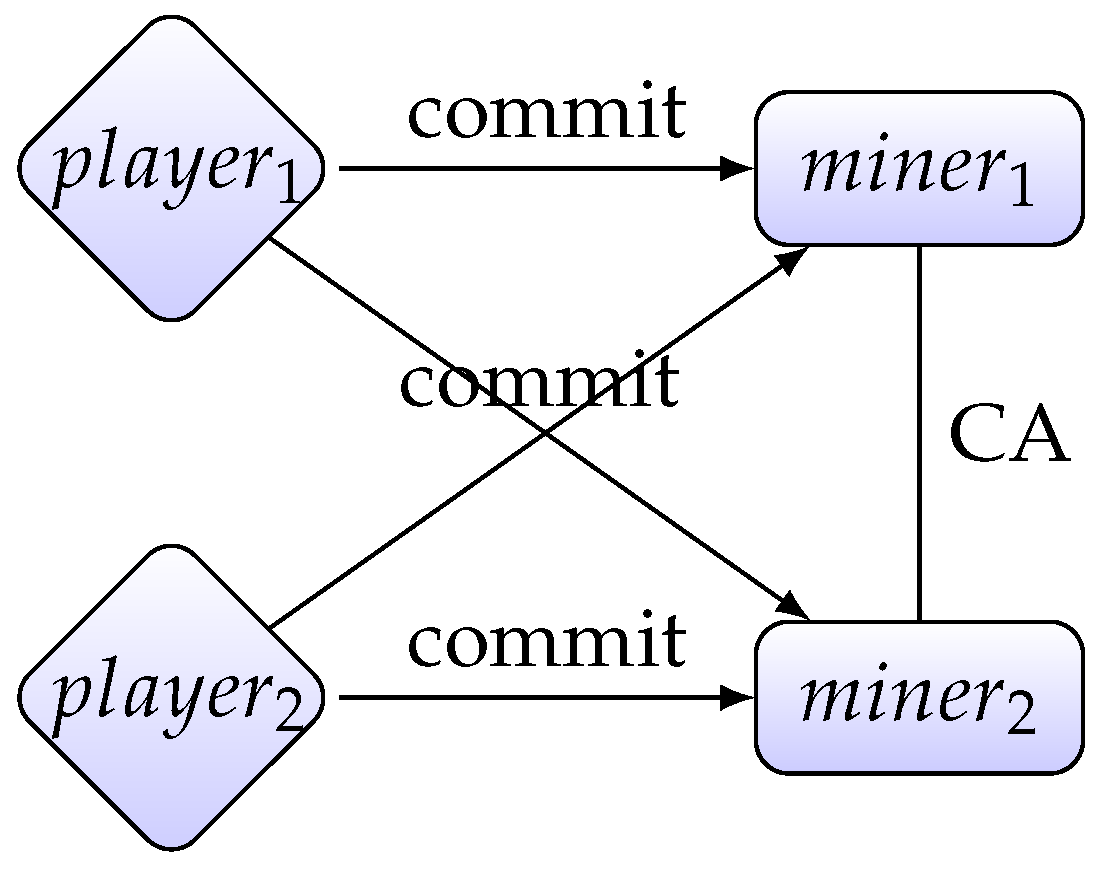
- Ticket purchasing:
- (a)
- For every player , to purchase a ticket , uses QBC to commit to all miners. At the end of this phase, every miner possesses a list of commitments .
- Ticket agreement:
- (a)
- Every player opens his commitment to every miner, so that the commitments in every miner’s possession change to , which essentially equals to .
- (b)
- All the miners run a consensus algorithm to achieve a consensus on the tickets purchased by players. Every miner adds to his local copy of the blockchain.
- Winner determination:
- (a)
- The winning ticket is calculated by bit-wise XOR: .
- (b)
- A player’s revenue is determined by the Hamming distance between his ticket and the winning ticket T. The closer his ticket is to the winning ticket, the higher is his revenue (a specific rule of revenue which satisfies this principle is beyond the scope of this paper and is left for future work).
Analysis
- Randomness.The winning ticket is calculated by bit-wise XOR. For every index in the winning ticket, iff . Therefore, the probability of is the same as .
- Unpredictability.To predict the winning ticket a player has to know all tickets before they are opened. The concealing property of QBC ensures that even miners cannot know the players’ tickets before they are opened. Since tickets are only sent to the miners by QBC, the probability that a player knows all tickets is even lower than the probability that a miner knows them.
- Unforgeability.The binding property of QBC ensures that it is impossible to change a ticket after the ticket purchasing phase.
- Verifiablity.This is because the quantum blockchain is a transparent database. After the ticket agreement phase, the list is added to the blockchain. Every player can read all the other players’ tickets and calculate the winning ticket by himself.
- Decentralization.The random process does not rely on a single authority. Every player’s ticket essentially affects the calculation of the winning ticket.Moreover, the calculation of the winning ticket does not rely on a single miner, but on all miners.
- Unconditional security.Even an adversary with an unlimited power of computation cannot manipulate the lottery protocol. The concealing and binding property of QBC does not rely on any computational assumption. Nor does the security of the consensus algorithm. The unconditional security of the ledger is further guaranteed by the unconditional security of the digital signature schemes adopted by quantum Blockchain.
4. Auction on Quantum Blockchain
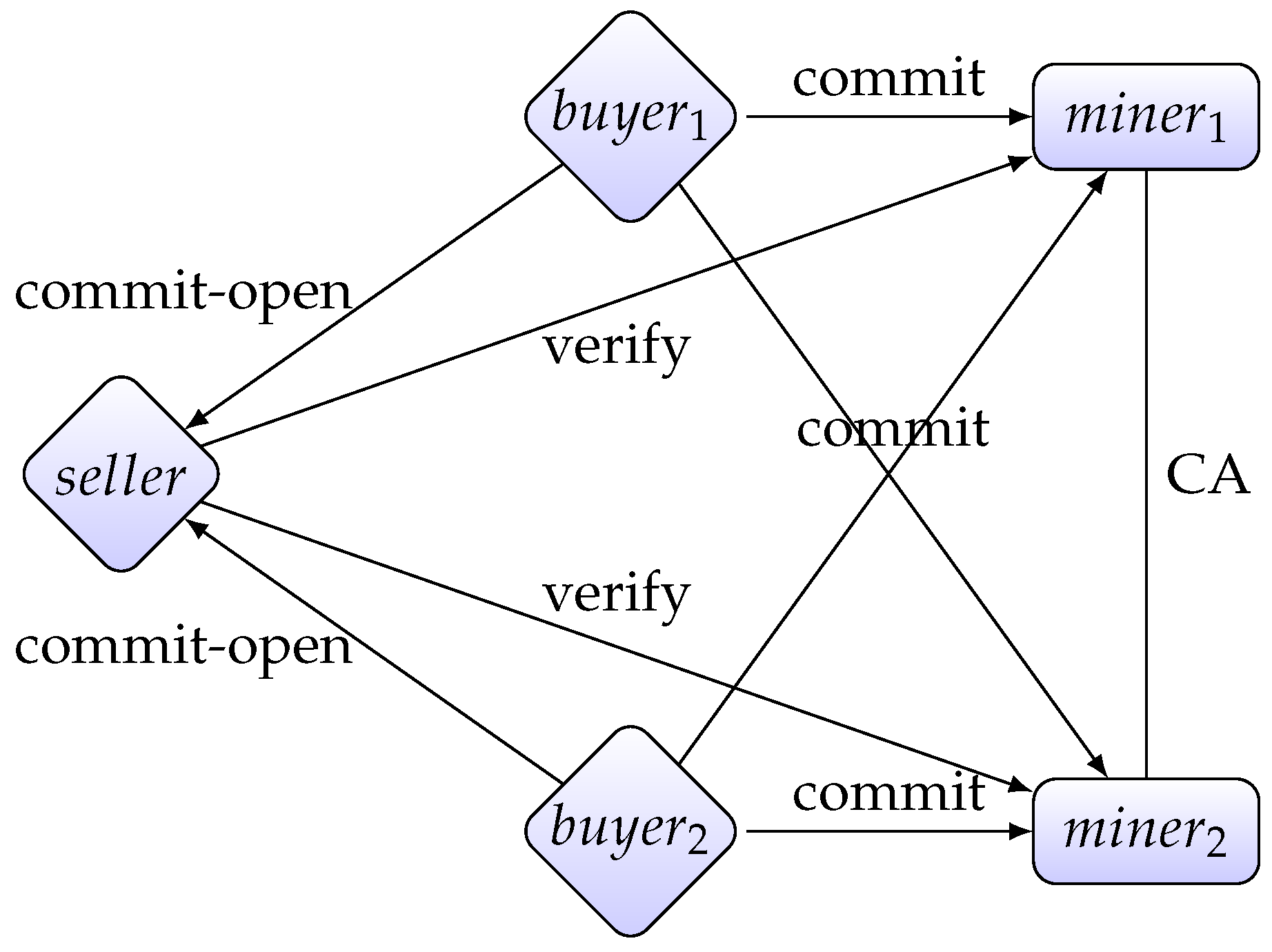
- The bidding phase: Every buyer commits his bid to the seller and to all miners , where is a positive integer.
- The opening phase: Every buyer opens his bid to the seller.
- Decision phase: The seller calculates the winning bid, which is the highest bid (if there is a tie, then one of the maximal bids is chosen randomly), and the winning buyer, who has offered the winning bid.
- Verification phase: In this phase, the seller S and every miner () run the following procedure to convince that S has chosen the valid winner:
- (a)
- S sends the information about the winning buyer and his bid to the miner .
- (b)
- S permutes losing bids to obtain a new list of bids .
- (c)
- S sends to .
- (d)
- first checks if for all . If yes, then sends to all buyers. Otherwise, sets S as a cheater by setting output to ⊥.
- (e)
- After receiving , every buyer checks if his bid is in the list, i.e., there is some . If yes, then sends the message “valid” to . Otherwise opens to . then sets S as a cheater by setting output to ⊥.
- (f)
- If does not output ⊥, then the seller passes the verification phase. The output of is now
- Publication phase: All miners run the consensus algorithm to achieve consensus on the output of the verification phase. The consensus is then added to the blockchain.
Analysis
- 1.
- Bid privacy.Every buyer only commits and opens his bids to the seller. Therefore, no buyer knows other buyers’ bids.
- 2.
- Posterior privacy.What is added to the blockchain is the winning buyer and his bid, as well as a permuted list of losing bids. Therefore, no losing buyer’s bid is revealed.
- 3.
- Bids’ binding.The binding property of quantum bit commitment ensures that buyers cannot deny or change their bids once they are committed.
- 4.
- Decentralization.There are in total n miners. The process of the auction does not rely on a single miner.
- 5.
- Unconditional security.As in the case of our lottery protocol, even an adversary with an unlimited power of computation cannot manipulate the auction protocol because the security of the quantum bit commitment and consensus algorithm does not depend on computational complexity. The unconditional security of the ledger relies on quantum Blockchain properties.
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 19 November 2020).
- Szabo, N. The Idea of Smart Contracts. 1997. Available online: https://nakamotoinstitute.org/the-idea-of-smart-contracts/ (accessed on 19 November 2020).
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Mosca, M. Cybersecurity in an Era with Quantum Computers: Will We Be Ready? IEEE Secur. Priv. 2018, 16, 38–41. [Google Scholar] [CrossRef]
- Fedorov, A.K.; Kiktenko, E.O.; Lvovsky, A.I. Quantum computers put blockchain security at risk. Nature 2018, 563, 465–467. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Pozhar, N.O.; Anufriev, M.N.; Trushechkin, A.S.; Yunusov, R.R.; Kurochkin, Y.V.; Lvovsky, A.I.; Fedorov, A.K. Quantum-secured blockchain. Quantum Sci. Technol. 2018, 3, 035004. [Google Scholar] [CrossRef]
- Aggarwal, D.; Brennen, G.; Lee, T.; Santha, M.; Tomamichel, M. Quantum Attacks on Bitcoin, and How to Protect Against Them. Ledger 2018, 3. [Google Scholar] [CrossRef]
- Stewart, I.; Ilie, D.; Zamyatin, A.; Werner, S.; Torshizi, M.; Knottenbelt, W. Committing to quantum resistance: A slow defence for Bitcoin against a fast quantum computing attack. R. Soc. Open Sci. 2018, 5, 180410. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Sopek, M.; Wang, Q.; Kulicki, P. Towards Quantum-Secured Permissioned Blockchain: Signature, Consensus, and Logic. Entropy 2019, 21, 887. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Q.; Kulicki, P.; Sopek, M. A Simple Voting Protocol on Quantum Blockchain. Int. J. Theor. Phys. 2019, 58, 275–281. [Google Scholar] [CrossRef]
- Isidore, C. Americans Spend More on the Lottery Than on. Available online: https://money.cnn.com/2015/02/11/news/companies/lottery-spending/ (accessed on 19 November 2020).
- Chow, S.S.M.; Hui, L.C.K.; Yiu, S.; Chow, K.P. An e-Lottery Scheme Using Verifiable Random Function. In Proceedings of the International Conference on Computational Science and its Applications, Singapore, 9–12 May 2005; pp. 651–660. [Google Scholar] [CrossRef]
- Bentov, I.; Kumaresan, R. How to Use Bitcoin to Design Fair Protocols. In Proceedings of the Advances in Cryptology—CRYPTO 2014—34th Annual Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2014; pp. 421–439. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Dziembowski, S.; Malinowski, D.; Mazurek, L. Secure Multiparty Computations on Bitcoin. In Proceedings of the 2014 IEEE Symposium on Security and Privacy, SP 2014, Berkeley, CA, USA, 18–21 May 2014; IEEE Computer Society: Washington, DC, USA, 2014; pp. 443–458. [Google Scholar] [CrossRef]
- Bartoletti, M.; Zunino, R. Constant-Deposit Multiparty Lotteries on Bitcoin. In International Conference on Financial Cryptography and Data Security; Springer: Cham, Switzerland, 2017; Volume 10323, pp. 231–247. [Google Scholar] [CrossRef]
- Grumbach, S.; Riemann, R. Distributed Random Process for a Large-Scale Peer-to-Peer Lottery. In Distributed Applications and Interoperable Systems; Chen, L.Y., Reiser, H.P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 34–48. [Google Scholar]
- Miller, A.; Bentov, I. Zero-Collateral Lotteries in Bitcoin and Ethereum. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy Workshops, EuroS&P Workshops 2017, Paris, France, 26–28 April 2017; pp. 4–13. [Google Scholar] [CrossRef]
- Goldenberg, L.; Vaidman, L.; Wiesner, S. Quantum Gambling. Phys. Rev. Lett. 1999, 82, 3356–3359. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Rudolph, T. Quantum Protocol for Cheat-Sensitive Weak Coin Flipping. Phys. Rev. Lett. 2002, 89, 227901. [Google Scholar] [CrossRef]
- Nayak, A.; Shor, P. Bit-commitment-based quantum coin flipping. Phys. Rev. A 2003, 67, 012304. [Google Scholar] [CrossRef]
- Ambainis, A.; Buhrman, H.; Dodis, Y.; Rohrig, H. Multiparty Quantum Coin Flipping. In Proceedings of the 19th IEEE Annual Conference on Computational Complexity, Amherst, MA, USA, 24 June 2004; IEEE Computer Society: Washington, DC, USA, 2004; pp. 250–259. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Frison, J.; Huy, K.P.; Massar, S. Experimental quantum tossing of a single coin. New J. Phys. 2008, 10, 083037. [Google Scholar] [CrossRef]
- Silman, J.; Chailloux, A.; Aharon, N.; Kerenidis, I.; Pironio, S.; Massar, S. Fully Distrustful Quantum Bit Commitment and Coin Flipping. Phys. Rev. Lett. 2011, 106, 220501. [Google Scholar] [CrossRef] [PubMed]
- Hänggi, E.; Wullschleger, J. Tight Bounds for Classical and Quantum Coin Flipping. Theory of Cryptography; Ishai, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 468–485. [Google Scholar]
- Nayak, A.; Sikora, J.; Tunçel, L. A search for quantum coin-flipping protocols using optimization techniques. Math. Program. 2016, 156, 581–613. [Google Scholar] [CrossRef]
- Brandt, F. Fully Private Auctions in a Constant Number of Rounds. In Financial Cryptography, Proceedings of the International Conference on Financial Cryptography, Guadeloupe, France, 27–30 January 2003; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2742, pp. 223–238. [Google Scholar] [CrossRef]
- Brandt, F. How to obtain full privacy in auctions. Int. J. Inf. Secur. 2006, 5, 201–216. [Google Scholar] [CrossRef]
- Montenegro, J.A.; Fischer, M.J.; Lopez, J.; Peralta, R. Secure sealed-bid online auctions using discreet cryptographic proofs. Math. Comput. Model. 2013, 57, 2583–2595. [Google Scholar] [CrossRef]
- Blass, E.O.; Kerschbaum, F. Strain: A Secure Auction for Blockchains. In Computer Security; Lopez, J., Zhou, J., Soriano, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 87–110. [Google Scholar]
- Galal, H.S.; Youssef, A.M. Succinctly Verifiable Sealed-Bid Auction Smart Contract. In Data Privacy Management, Cryptocurrencies and Blockchain Technology; Garcia-Alfaro, J., Herrera-Joancomartí, J., Livraga, G., Rios, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Liu, W.; Wang, H.; Yuan, G.; Xu, Y.; Chen, Z.; An, X.; Ji, F.; Gnitou, G.T. Multiparty quantum sealed-bid auction using single photons as message carrier. Quantum Inf. Process. 2016, 15, 869–879. [Google Scholar] [CrossRef]
- Zhang, R.; Shi, R.; Qin, J.; Peng, Z. An economic and feasible Quantum Sealed-bid Auction protocol. Quantum Inf. Process. 2018, 17, 35. [Google Scholar] [CrossRef]
- Bennetta, C.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Brassard, G.; Crépeau, C. Quantum Bit Commitment and Coin Tossing Protocols. In Conference on the Theory and Application of Cryptography; Menezes, A., Vanstone, S.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 49–61. [Google Scholar]
- Brassard, G.; Crépeau, C.; Jozsa, R.; Langlois, D. A Quantum Bit Commitment Scheme Provably Unbreakable by both Parties. In Proceedings of the 34th Annual Symposium on Foundations of Computer Science, Palo Alto, CA, USA, 3–5 November 1993; IEEE Computer Society: Washington, DC, USA, 1993; pp. 362–371. [Google Scholar] [CrossRef]
- Mayers, D. Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 1997, 78, 3414–3417. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Is Quantum Bit Commitment Really Possible? Phys. Rev. Lett. 1997, 78, 3410–3413. [Google Scholar] [CrossRef]
- Sun, X.; He, F.; Wang, Q. Impossibility of Quantum Bit Commitment, a Categorical Perspective. Axioms 2020, 9, 28. [Google Scholar] [CrossRef]
- Hardy, L.; Kent, A. Cheat Sensitive Quantum Bit Commitment. Phys. Rev. Lett. 2004, 92, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Buhrman, H.; Christandl, M.; Hayden, P.; Lo, H.K.; Wehner, S. Possibility, impossibility, and cheat sensitivity of quantum-bit string commitment. Phys. Rev. A 2008, 78, 1–10. [Google Scholar] [CrossRef]
- Shimizu, K.; Fukasaka, H.; Tamaki, K.; Imoto, N. Cheat-sensitive commitment of a classical bit coded in a block of m × n round-trip qubits. Phys. Rev. A 2011, 84, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Wen, Q.; Li, Z.; Qin, S.; Yang, Y. Cheat sensitive quantum bit commitment via pre- and post-selected quantum states. Quantum Inf. Process. 2014, 13, 141–149. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, X.; Su, C.; Liu, Z.; Choo, K.R. Game theoretic security of quantum bit commitment. Inf. Sci. 2019, 479, 503–514. [Google Scholar] [CrossRef]
- Kent, A. Unconditionally secure bit commitment with flying qudits. New J. Phys. 2011, 13, 1–16. [Google Scholar] [CrossRef]
- Kent, A. Unconditionally Secure Bit Commitment by Transmitting Measurement Outcomes. Phys. Rev. Lett. 2012, 109, 130501. [Google Scholar] [CrossRef]
- Lunghi, T.; Kaniewski, J.; Bussières, F.; Houlmann, R.; Tomamichel, M.; Kent, A.; Gisin, N.; Wehner, S.; Zbinden, H. Experimental Bit Commitment Based on Quantum Communication and Special Relativity. Phys. Rev. Lett. 2013, 111, 180504. [Google Scholar] [CrossRef]
- Adlam, E.; Kent, A. Device-independent relativistic quantum bit commitment. Phys. Rev. A 2015, 92, 1–9. [Google Scholar] [CrossRef]
- Lunghi, T.; Kaniewski, J.; Bussières, F.; Houlmann, R.; Tomamichel, M.; Wehner, S.; Zbinden, H. Practical Relativistic Bit Commitment. Phys. Rev. Lett. 2015, 115, 030502. [Google Scholar] [CrossRef] [PubMed]
- Verbanis, E.; Martin, A.; Houlmann, R.; Boso, G.; Bussières, F.; Zbinden, H. 24-Hour Relativistic Bit Commitment. Phys. Rev. Lett. 2016, 117, 140506. [Google Scholar] [CrossRef] [PubMed]
- He, G.P. Quantum key distribution based on orthogonal states allows secure quantum bit commitment. J. Phys. A Math. Theor. 2011, 44, 445305. [Google Scholar] [CrossRef]
- He, G.P. Simplified quantum bit commitment using single photon nonlocality. Quantum Inf. Process. 2014, 13, 2195–2211. [Google Scholar] [CrossRef]
- Sun, X.; He, F. A First Step to the Categorical Logic of Quantum Programs. Entropy 2020, 22, 144. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Kulicki, P.; Sopek, M. Lottery and Auction on Quantum Blockchain. Entropy 2020, 22, 1377. https://doi.org/10.3390/e22121377
Sun X, Kulicki P, Sopek M. Lottery and Auction on Quantum Blockchain. Entropy. 2020; 22(12):1377. https://doi.org/10.3390/e22121377
Chicago/Turabian StyleSun, Xin, Piotr Kulicki, and Mirek Sopek. 2020. "Lottery and Auction on Quantum Blockchain" Entropy 22, no. 12: 1377. https://doi.org/10.3390/e22121377
APA StyleSun, X., Kulicki, P., & Sopek, M. (2020). Lottery and Auction on Quantum Blockchain. Entropy, 22(12), 1377. https://doi.org/10.3390/e22121377




