Laminar–Turbulent Intermittency in Annular Couette–Poiseuille Flow: Whether a Puff Splits or Not
Abstract
1. Introduction
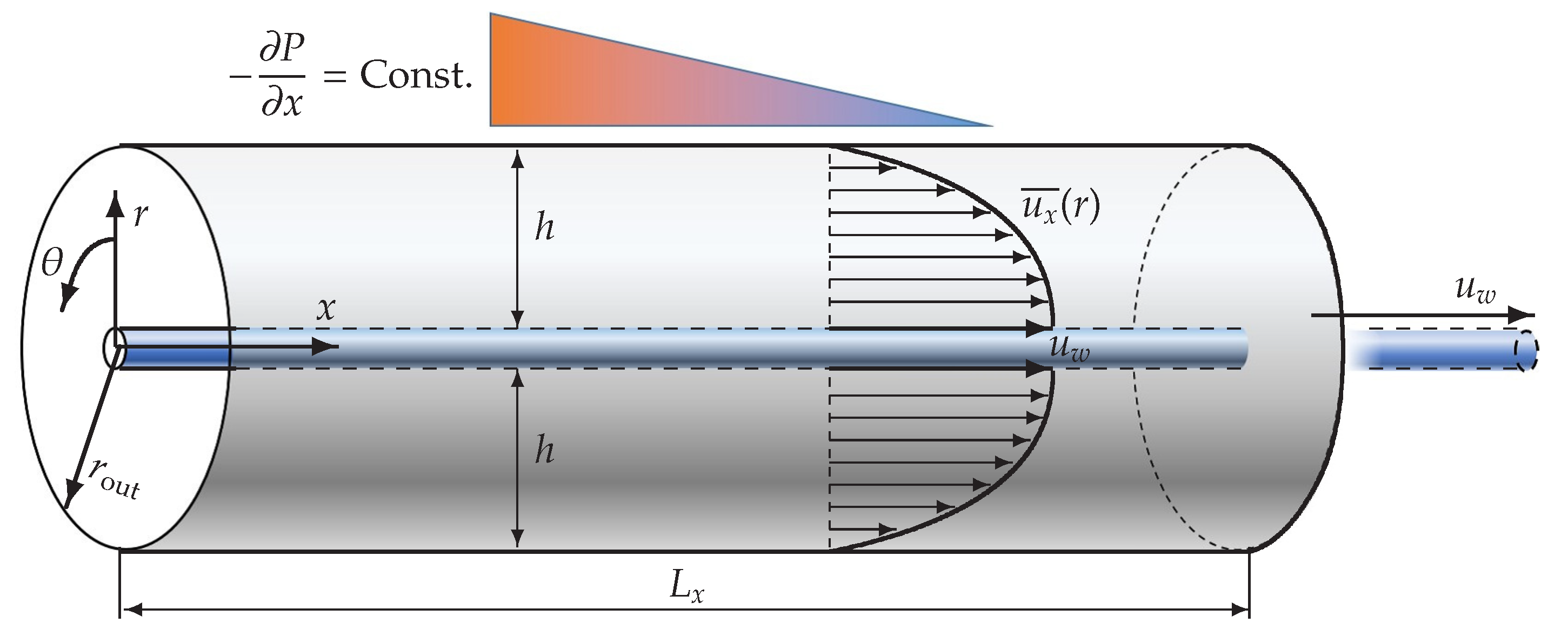
2. Problem Setup and Methods
3. Preliminary Simulations
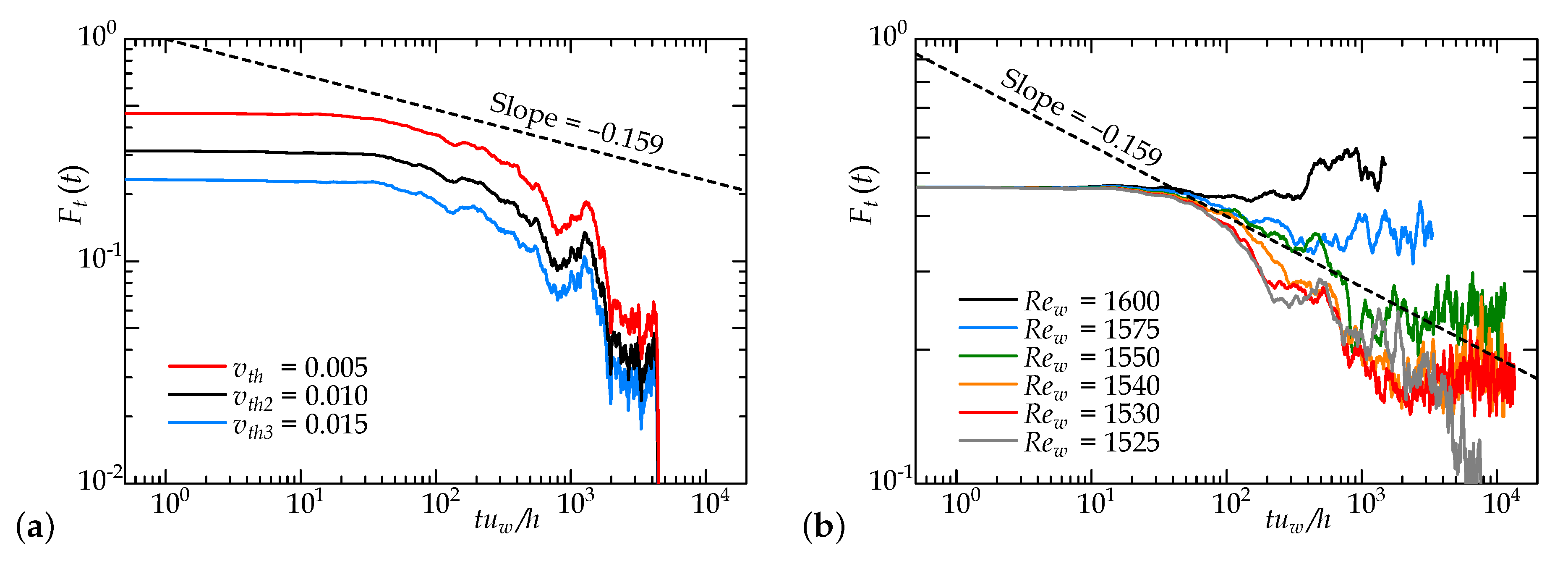
4. Results and Discussion
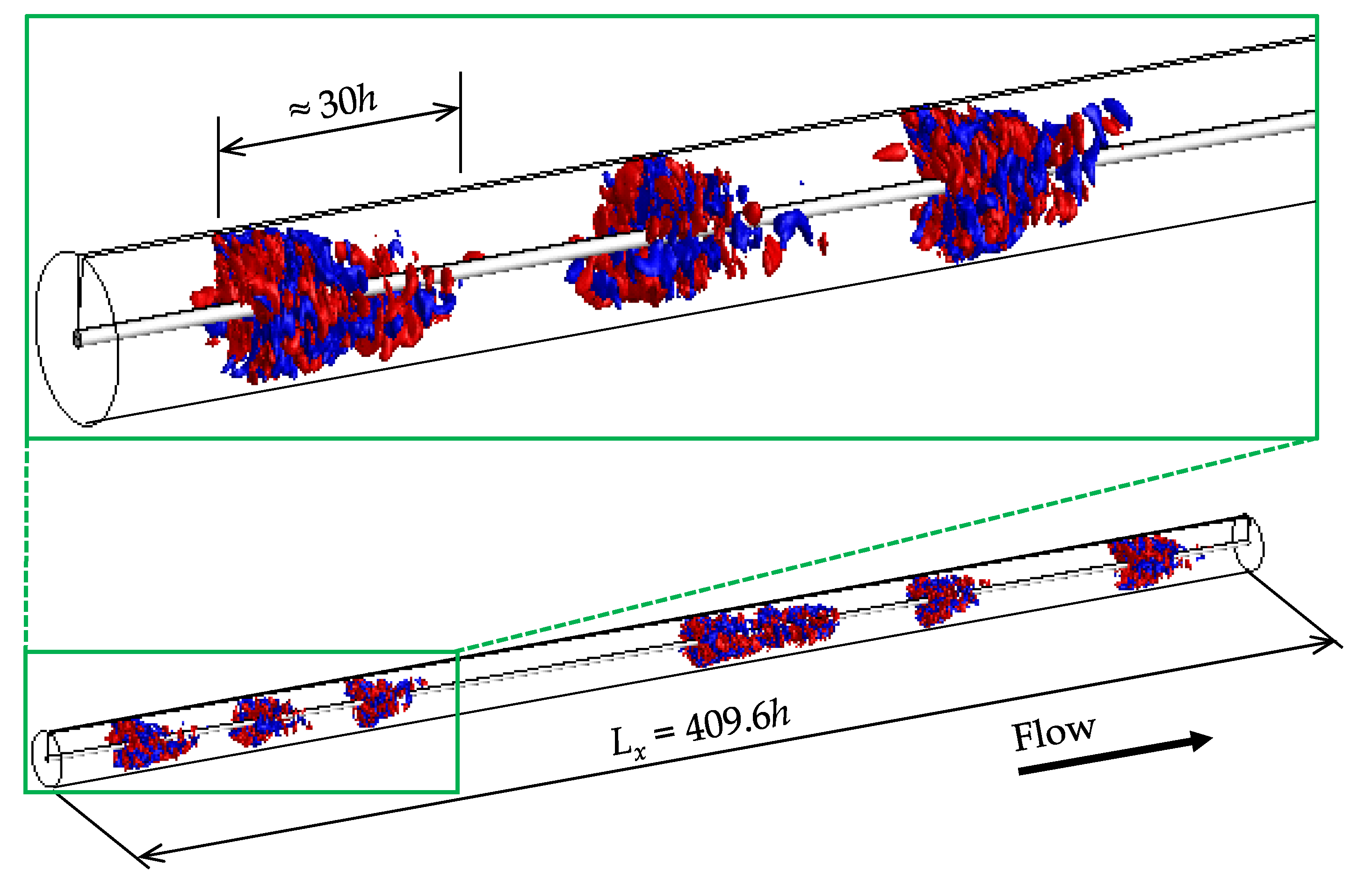
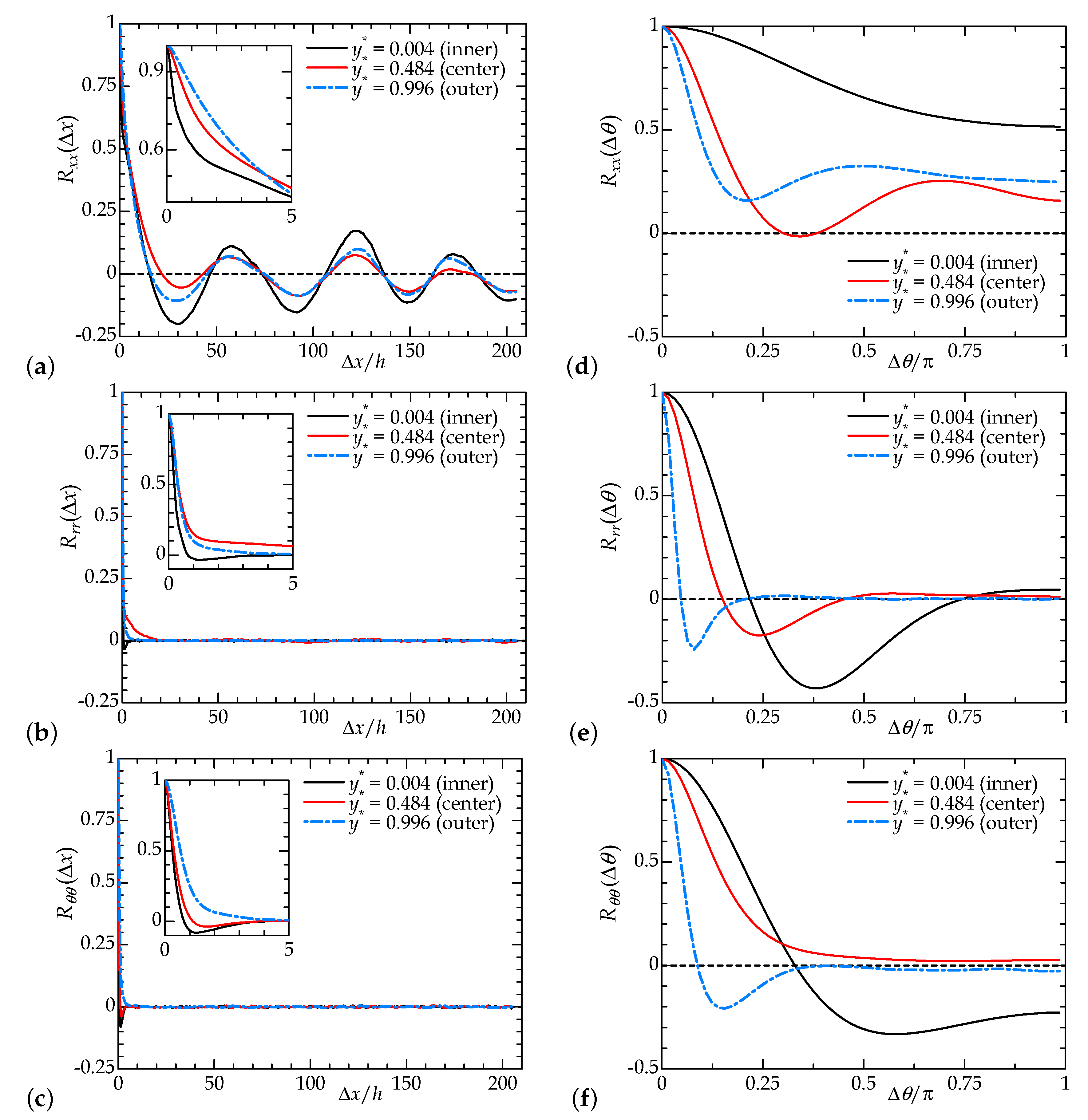
4.1. Puffs in Annular-Pipe Flow
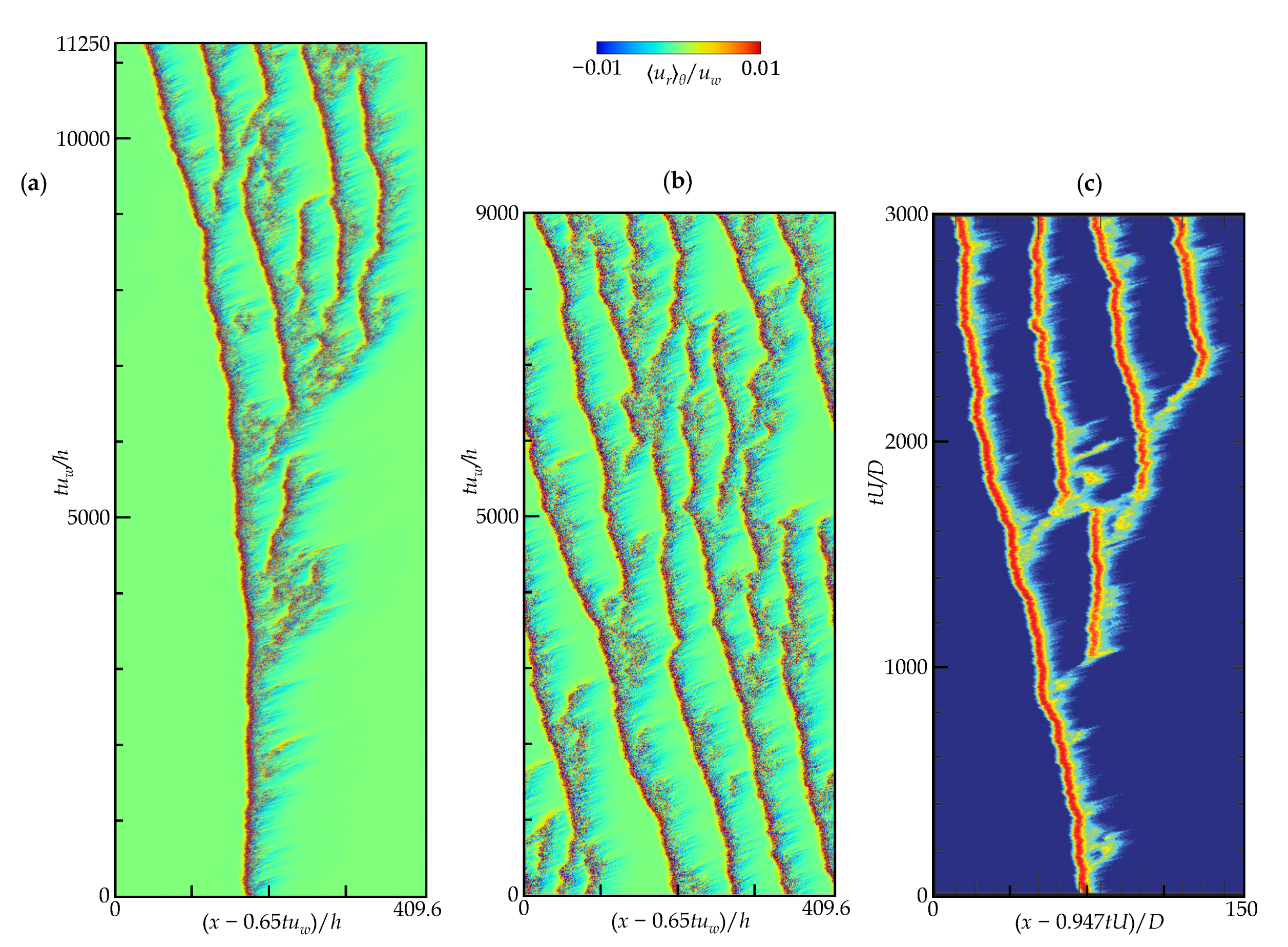
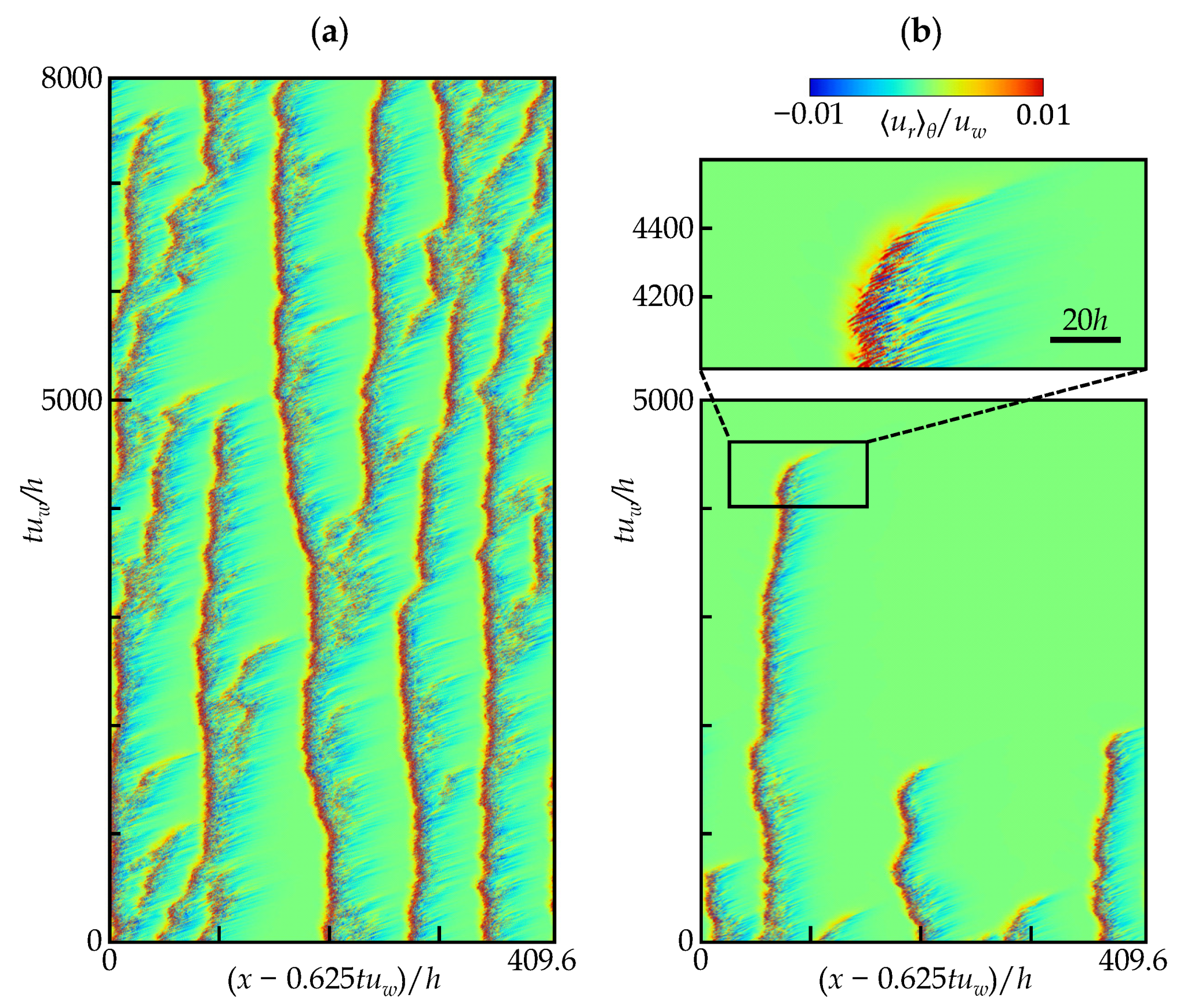
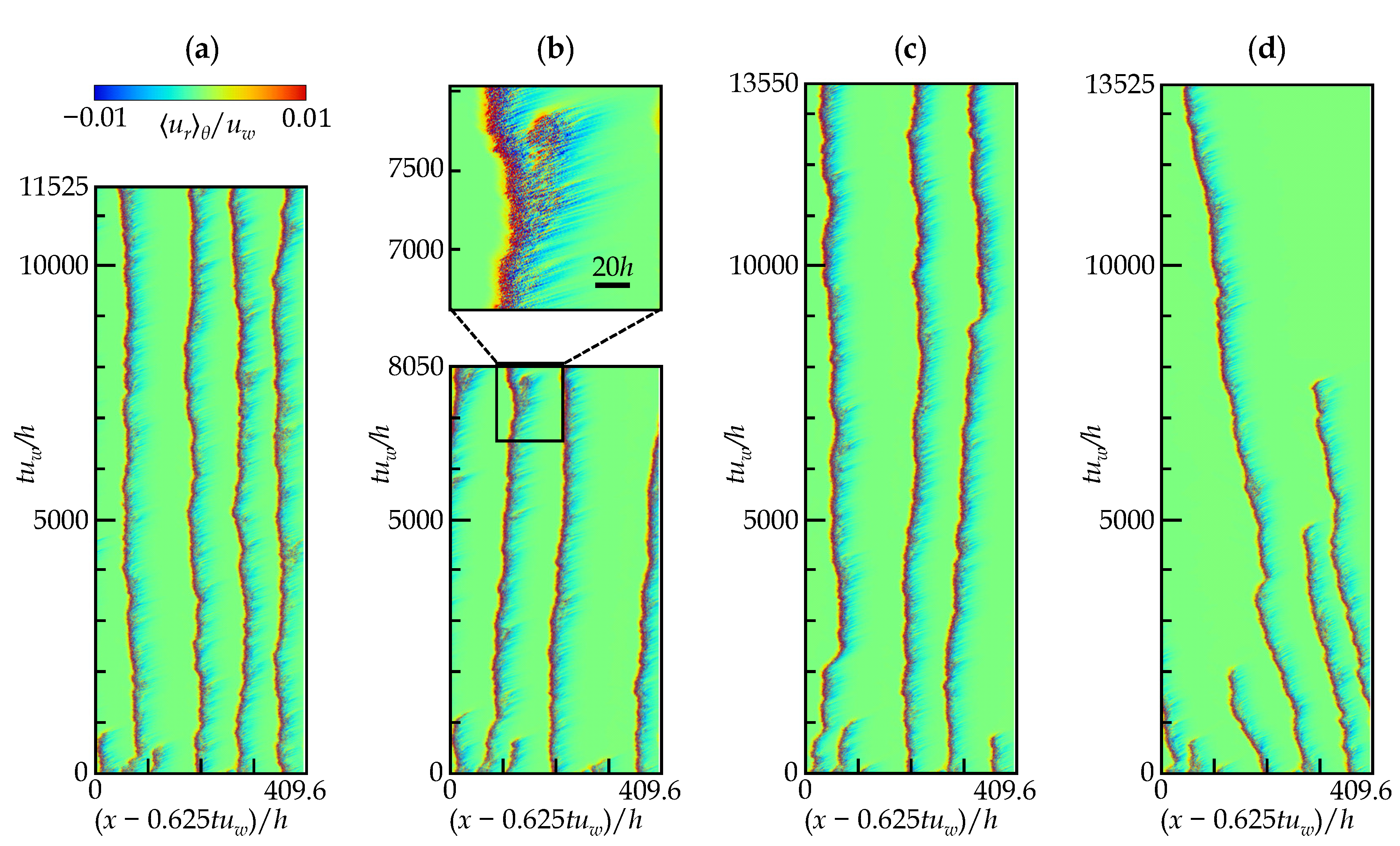
4.2. Space-Time Diagrams
5. Conclusions
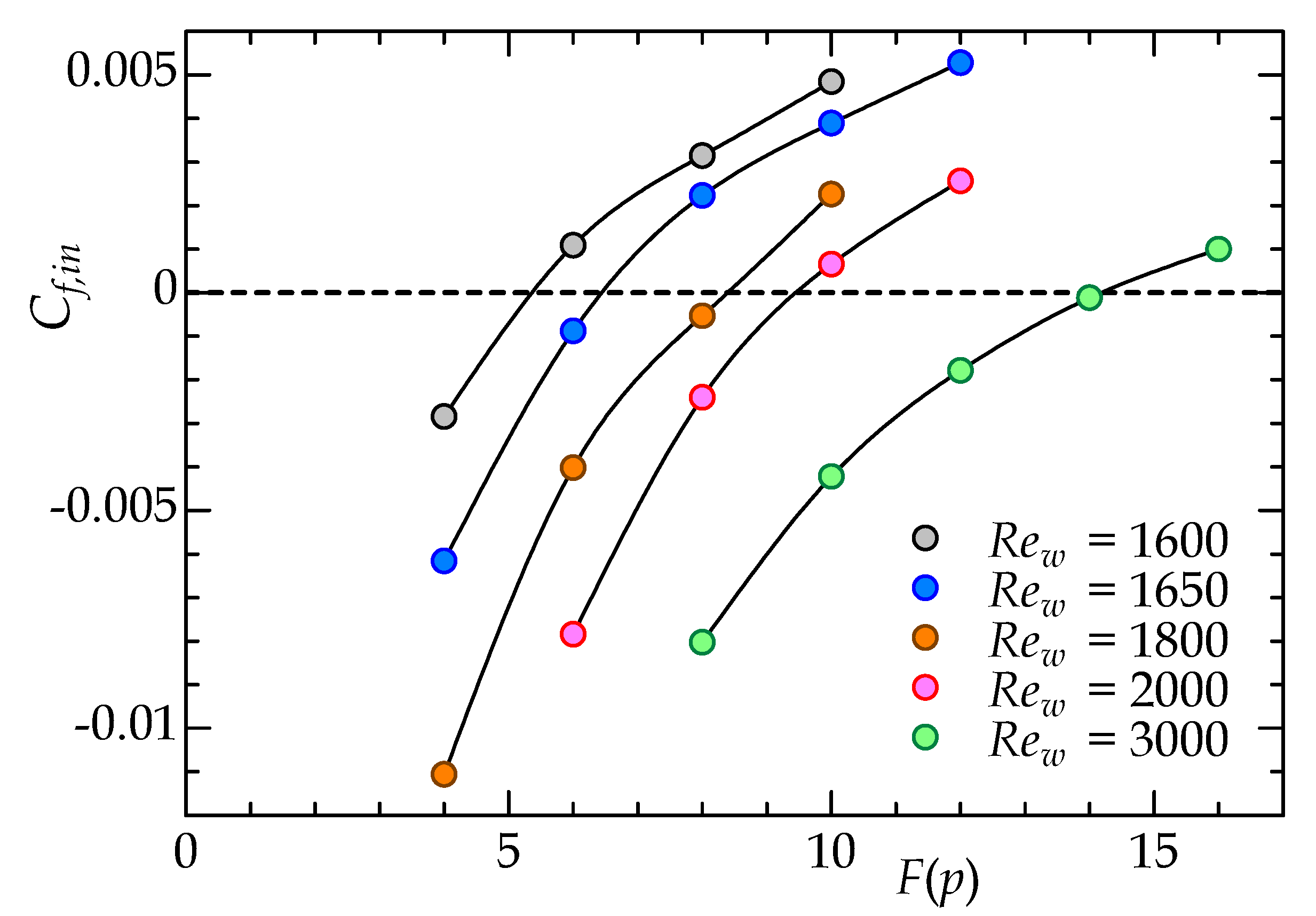
- At , puff-splitting events occur along with stochastic puff decay, resulting in wave-like fashion of multiple puffs with constant intervals.
- At , no puff-splitting event occurs, but initially given individual puffs survive over a present observation time of at least , maintaining the intervals among the puffs.
- At , a ‘spurious’ feature of (1+1)D-DP was detected during the quenching process even without puff splitting, and a lower deviates from the DP critical exponent.
- At , the flow becomes fully laminar after the non-trivial finite lifetime of the puff.
- The range of –1600 (with the accordingly changed ) corresponds to the bulk Reynolds-number range of –2190 based on the hydraulic diameter and bulk velocity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| aCf | annular Couette flow |
| aCPf | annular Couette–Poiseuille flow |
| aPf | annular Poiseuille flow |
| CPF | Circular pipe flow |
| DNS | direct numerical simulation |
| DP | direct percolation |
| pCPf | plane Couette–Poiseuille flow |
| pPf | plane Poiseuille flow |
| rms | root-mean-square value |
References
- Wygnanski, I.J.; Champagne, F.H. On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 1973, 59, 281–335. [Google Scholar] [CrossRef]
- Nishi, M.; Ünsal, B.; Durst, F. Laminar-to-turbulent transition of pipe flows through puffs and slugs. J. Fluid Mech. 2008, 614, 425–446. [Google Scholar] [CrossRef]
- Mukund, V.; Hof, B. The critical point of the transition to turbulence in pipe flow. J. Fluid Mech. 2018, 839, 76–94. [Google Scholar] [CrossRef]
- Priymak, V. Direct numerical simulation of quasi-equilibrium turbulent puffs in pipe flow. Phys. Fluids 2018, 30, 064102. [Google Scholar] [CrossRef]
- Avila, M.; Mellibovsky, F.; Roland, N.; Hof, B. Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 2013, 110, 224502. [Google Scholar] [CrossRef] [PubMed]
- Hof, B.; Van Doorne, C.W.; Westerweel, J.; Nieuwstadt, F.T.; Faisst, H.; Eckhardt, B.; Wedin, H.; Kerswell, R.R.; Waleffe, F. Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 2004, 305, 1594–1598. [Google Scholar] [CrossRef]
- Moxey, D.; Barkley, D. Distinct large-scale turbulent-laminar states in transitional pipe flow. Proc. Natl. Acad. Sci. USA 2010, 107, 8091–8096. [Google Scholar] [CrossRef]
- Shimizu, M.; Manneville, P.; Duguet, Y.; Kawahara, G. Splitting of a turbulent puff in pipe flow. Fluid Dyn. Res. 2014, 46, 061403. [Google Scholar] [CrossRef]
- Barkley, D. Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 2016, 803. [Google Scholar] [CrossRef]
- Avila, K.; Moxey, D.; de Lozar, A.; Avila, M.; Barkley, D.; Hof, B. The onset of turbulence in pipe flow. Science 2011, 333, 192–196. [Google Scholar] [CrossRef]
- Shimizu, M.; Kida, S. A driving mechanism of a turbulent puff in pipe flow. Fluid Dyn. Res. 2009, 41, 045501. [Google Scholar] [CrossRef]
- Barkley, D.; Song, B.; Mukund, V.; Lemoult, G.; Avila, M.; Hof, B. The rise of fully turbulent flow. Nature 2015, 526, 550–553. [Google Scholar] [CrossRef] [PubMed]
- Coles, D. Transition in circular Couette flow. J. Fluid Mech. 1965, 21, 385–425. [Google Scholar] [CrossRef]
- Prigent, A.; Grégoire, G.; Chaté, H.; Dauchot, O.; van Saarloos, W. Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 2002, 89, 014501. [Google Scholar] [CrossRef] [PubMed]
- Barkley, D.; Tuckerman, L.S. Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 2005, 94, 014502. [Google Scholar] [CrossRef]
- Duguet, Y.; Schlatter, P.; Henningson, D.S. Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 2010, 650, 119–129. [Google Scholar] [CrossRef]
- Couliou, M.; Monchaux, R. Large-scale flows in transitional plane Couette flow: A key ingredient of the spot growth mechanism. Phys. Fluids 2015, 27, 034101. [Google Scholar] [CrossRef]
- De Souza, D.; Bergier, T.; Monchaux, R. Transient states in plane Couette flow. J. Fluid Mech. 2020, 903, A33. [Google Scholar] [CrossRef]
- Tsukahara, T.; Seki, Y.; Kawamura, H.; Tochio, D. DNS of Turbulent Channel Flow at Very Low Reynolds Numbers; TSFP Digital Library Online; Begel House Inc.: Danbury, CT, USA, 2005; pp. 935–940. [Google Scholar]
- Hashimoto, S.; Hasobe, A.; Tsukahara, T.; Kawaguchi, Y.; Kawamura, H. An Experimental Study on Turbulent-Stripe Structure in Transitional Channel Flow; ICHMT Digital Library Online; Begel House Inc.: Danbury, CT, USA, 2009. [Google Scholar]
- Xiong, X.; Tao, J.; Chen, S.; Brandt, L. Turbulent bands in plane-Poiseuille flow at moderate Reynolds numbers. Phys. Fluids 2015, 27, 041702. [Google Scholar] [CrossRef]
- Tsukahara, T.; Tillmark, N.; Alfredsson, P. Flow regimes in a plane Couette flow with system rotation. J. Fluid Mech. 2010, 648, 5–33. [Google Scholar] [CrossRef]
- Brethouwer, G.; Duguet, Y.; Schlatter, P. Turbulent-laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 2012, 704, 137–172. [Google Scholar] [CrossRef]
- Reetz, F.; Kreilos, T.; Schneider, T.M. Exact invariant solution reveals the origin of self-organized oblique turbulent-laminar stripes. Nat. Commun. 2019, 10, 2277. [Google Scholar] [CrossRef] [PubMed]
- Paranjape, C.S.; Duguet, Y.; Hof, B. Oblique stripe solutions of channel flow. J. Fluid Mech. 2020, 897, A7. [Google Scholar] [CrossRef]
- Shimizu, M.; Manneville, P. Bifurcations to turbulence in transitional channel flow. Phys. Rev. Fluids 2019, 4, 113903. [Google Scholar] [CrossRef]
- Tsukahara, T.; Ishida, T. Lower bound of sub-critical transition in plane Poiseuille flow. Nagare 2014, 34, 383–386. (In Japanese) [Google Scholar]
- Takeda, K.; Tsukahara, T. Subcritical transition of plane Poiseuille flow as (2+1)d and (1+1)d DP universality classes. In Proceedings of the 8th Symposium on Bifurcations and Instabilities in Fluid Dynamics (BIFD2019), Limerick, Ireland, 16–19 July 2019. [Google Scholar]
- Xiao, X.; Song, B. Kinematics and dynamics of turbulent bands at low Reynolds numbers in channel flow. Entropy 2020, 22, 1167. [Google Scholar] [CrossRef]
- Kashyap, P.V.; Duguet, Y.; Dauchot, O. Flow statistics in the transitional regime of plane channel flow. Entropy 2020, 22, 1001. [Google Scholar] [CrossRef]
- Manneville, P. Transition to turbulence in wall-bounded flows: Where do we stand? Mech. Eng. Rev. 2016, 3, 15-00684. [Google Scholar] [CrossRef]
- Manneville, P. Laminar-turbulent patterning in transitional flows. Entropy 2017, 19, 316. [Google Scholar] [CrossRef]
- Tuckerman, L.S.; Chantry, M.; Barkley, D. Patterns in wall-bounded shear flows. Annu. Rev. Fluid Mech. 2020, 52, 343–367. [Google Scholar] [CrossRef]
- Ishida, T.; Duguet, Y.; Tsukahara, T. Transitional structures in annular Poiseuille flow depending on radius ratio. J. Fluid Mech. 2016, 794, R2. [Google Scholar] [CrossRef]
- Ishida, T.; Duguet, Y.; Tsukahara, T. Turbulent bifurcations in intermittent shear flows: From puffs to oblique stripes. Phys. Rev. Fluids 2017, 2, 073902. [Google Scholar] [CrossRef]
- Ishida, T.; Tsukahara, T. Friction factor of annular Poiseuille flow in a transitional regime. Adv. Mech. Eng. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Kunii, K.; Ishida, T.; Duguet, Y.; Tsukahara, T. Laminar–turbulent coexistence in annular Couette flow. J. Fluid Mech. 2019, 879, 579–603. [Google Scholar] [CrossRef]
- Takeda, K.; Duguet, Y.; Tsukahara, T. Intermittency and critical scaling in annular Couette flow. Entropy 2020, 22, 988. [Google Scholar] [CrossRef]
- Lemoult, G.; Shi, L.; Avila, K.; Jalikop, S.V.; Avila, M.; Hof, B. Directed percolation phase transition to sustained turbulence in Couette flow. Nat. Phys. 2016, 12, 254–258. [Google Scholar] [CrossRef]
- Sano, M.; Tamai, K. A universal transition to turbulence in channel flow. Nat. Phys. 2016, 12, 249–253. [Google Scholar] [CrossRef]
- Chantry, M.; Tuckerman, L.S.; Barkley, D. Universal continuous transition to turbulence in a planar shear flow. J. Fluid Mech. 2017, 824, R1. [Google Scholar] [CrossRef]
- Hiruta, Y.; Toh, S. Subcritical laminar–turbulent transition as nonequilibrium phase transition in two-dimensional Kolmogorov flow. J. Phys. Soc. Jpn. 2020, 89, 044402. [Google Scholar] [CrossRef]
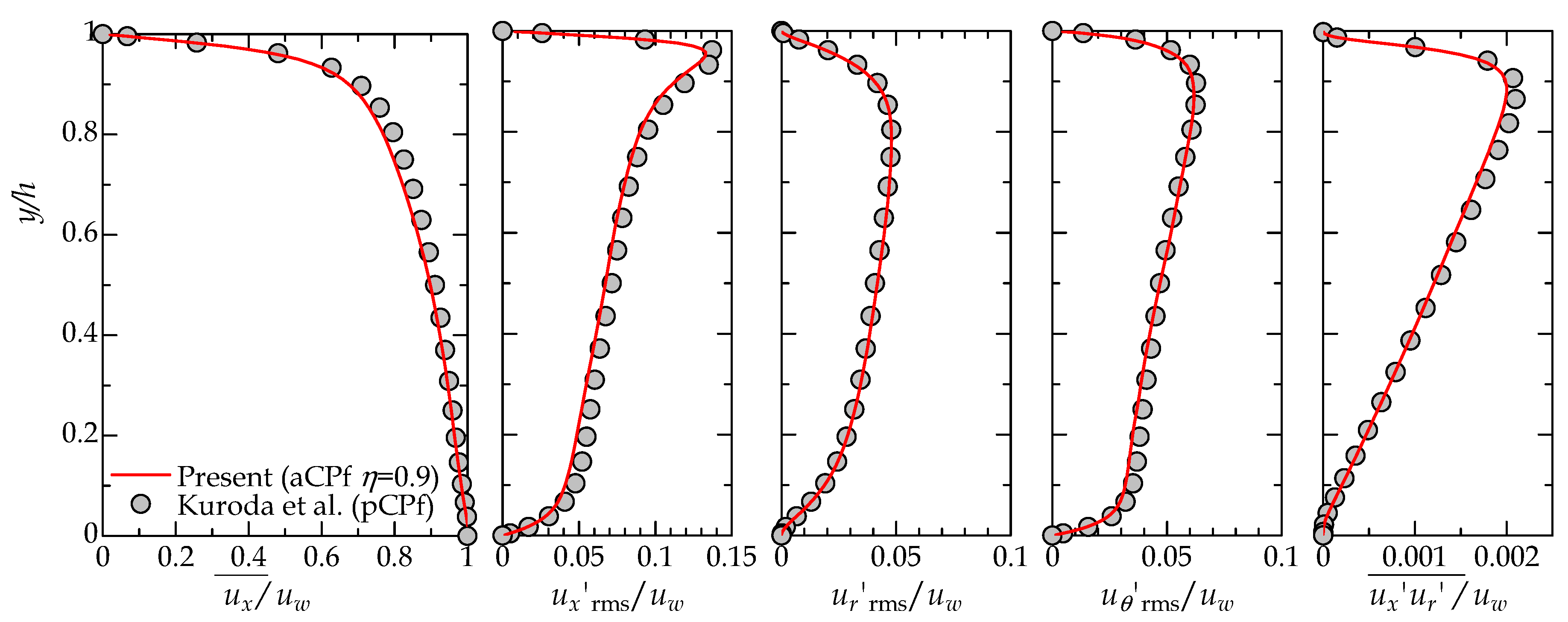
- Kuroda, A.; Kasagi, N.; Hirata, M. Direct numerical simulation of turbulent plane Couette-Poiseuille flows: Effect of mean shear rate on the near-wall turbulence structures. In Turbulent Shear Flows 9; Springer: Berlin/Heidelberg, Germany, 1995; pp. 241–257. [Google Scholar]
- Pirozzoli, S.; Bernardini, M.; Orlandi, P. Large-scale motions and inner/outer layer interactions in turbulent Couette–Poiseuille flows. J. Fluid Mech. 2011, 680, 534–563. [Google Scholar] [CrossRef]
- Orlandi, P.; Bernardini, M.; Pirozzoli, S. Poiseuille and Couette flows in the transitional and fully turbulent regime. J. Fluid Mech. 2015, 770, 424. [Google Scholar] [CrossRef]
- Kun, Y.; Lihao, Z.; Andersson, H.I. Turbulent Couette-Poiseuille flow with zero wall shear. Int. J. Heat Fluid Flow 2017, 63, 14–27. [Google Scholar]
- Nakabayashi, K.; Kitoh, O.; Katoh, Y. Similarity laws of velocity profiles and turbulence characteristics of Couette–Poiseuille turbulent flows. J. Fluid Mech. 2004, 507, 43–69. [Google Scholar] [CrossRef]
- Klotz, L.; Wesfreid, J.E. Experiments on transient growth of turbulent spots. J. Fluid Mech. 2017, 829. [Google Scholar] [CrossRef]
- Klotz, L.; Lemoult, G.; Frontczak, I.; Tuckerman, L.S.; Wesfreid, J.E. Couette-Poiseuille flow experiment with zero mean advection velocity: Subcritical transition to turbulence. Phys. Rev. Fluids 2017, 2, 043904. [Google Scholar] [CrossRef]
- Liu, T.; Semin, B.; Klotz, L.; Godoy-Diana, R.; Wesfreid, J.E.; Mullin, T. Anisotropic decay of turbulence in plane Couette–Poiseuille flow. arXiv 2020, arXiv:2008.08851. [Google Scholar]
- Wong, A.W.; Walton, A.G. Axisymmetric travelling waves in annular Couette–Poiseuille flow. Q. J. Mech. Appl. Math. 2012, 65, 293–311. [Google Scholar] [CrossRef]
- Kumar, R.; Walton, A. Self-sustaining critical layer/shear layer interaction in annular Poiseuille–Couette flow at high Reynolds number. Proc. R. Soc. 2020, 476, 20190600. [Google Scholar] [CrossRef]
- Abe, H.; Kawamura, H.; Matsuo, Y. Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. J. Fluids Eng. 2001, 123, 382–393. [Google Scholar] [CrossRef]
- Turbulence and Heat Transfer Laboratory (THTLAB; Nobuhide Kasagi Lab.); The University of Tokyo: Tokyo, Japan; Available online: http://thtlab.jp/ (accessed on 30 November 2020).
- Fukuda, T.; Tsukahara, T. Heat transfer of transitional regime with helical turbulence in annular flow. Int. J. Heat Fluid Flow 2020, 82, 108555. [Google Scholar] [CrossRef]
- Avila, M.; Willis, A.P.; Hof, B. On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 2010, 646, 127–136. [Google Scholar] [CrossRef]
- Shi, L.; Avila, M.; Hof, B. Scale invariance at the onset of turbulence in Couette flow. Phys. Rev. Lett. 2013, 110, 204502. [Google Scholar] [CrossRef] [PubMed]
| 0.1 | |
|---|---|
| Domain size | |
| Number of grids | |
| 1600–3000 | |
| 4.0–16.0 |
| 0.1 | ||||||||
| Domain Size | ||||||||
| Number of Grids | ||||||||
| 3000 | 1600 | 1575 | 1550 | 1540 | 1530 | 1525 | 1500 | |
| 70.2 | 36.0 | 34.1 | 33.4 | 33.1 | 32.7 | 32.4 | 31.5 | |
| 14.2 | 6.5 | 6.0 | 5.8 | 5.7 | 5.6 | 5.5 | 5.3 | |
| 14.1 | 7.14 | 6.82 | 6.68 | 6.61 | 6.53 | 6.47 | 6.30 | |
| 0.37 | 0.19 | 0.18 | 0.18 | 0.17 | 0.17 | 0.17 | 0.17 | |
| 4.44 | 2.26 | 2.16 | 2.11 | 2.09 | 2.07 | 2.05 | 1.99 | |
| 0.77 | 0.39 | 0.37 | 0.36 | 0.36 | 0.36 | 0.35 | 0.34 | |
| 7.66 | 3.89 | 3.72 | 3.64 | 3.61 | 3.56 | 3.53 | 3.44 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morimatsu, H.; Tsukahara, T. Laminar–Turbulent Intermittency in Annular Couette–Poiseuille Flow: Whether a Puff Splits or Not. Entropy 2020, 22, 1353. https://doi.org/10.3390/e22121353
Morimatsu H, Tsukahara T. Laminar–Turbulent Intermittency in Annular Couette–Poiseuille Flow: Whether a Puff Splits or Not. Entropy. 2020; 22(12):1353. https://doi.org/10.3390/e22121353
Chicago/Turabian StyleMorimatsu, Hirotaka, and Takahiro Tsukahara. 2020. "Laminar–Turbulent Intermittency in Annular Couette–Poiseuille Flow: Whether a Puff Splits or Not" Entropy 22, no. 12: 1353. https://doi.org/10.3390/e22121353
APA StyleMorimatsu, H., & Tsukahara, T. (2020). Laminar–Turbulent Intermittency in Annular Couette–Poiseuille Flow: Whether a Puff Splits or Not. Entropy, 22(12), 1353. https://doi.org/10.3390/e22121353






