Look at Tempered Subdiffusion in a Conjugate Map: Desire for the Confinement
Abstract
1. Introduction
- –
- Trapping, crowded environment (CTRW, FFPE, subordinated BM);
- –
- Labyrinthine environment (OD, percolation, RWRW);
- –
- Viscoelastic system (FBM, FLSM, FLE, ARFIMA);
- –
- System with time-dependent diffusion (scaled BM, scaled FBM, ARFIMA);
- –
- System with transient diffusion (BM with transient subordinators).
2. Conjugate Laplace Exponents and Stochastic Representation of Anomalous Diffusion
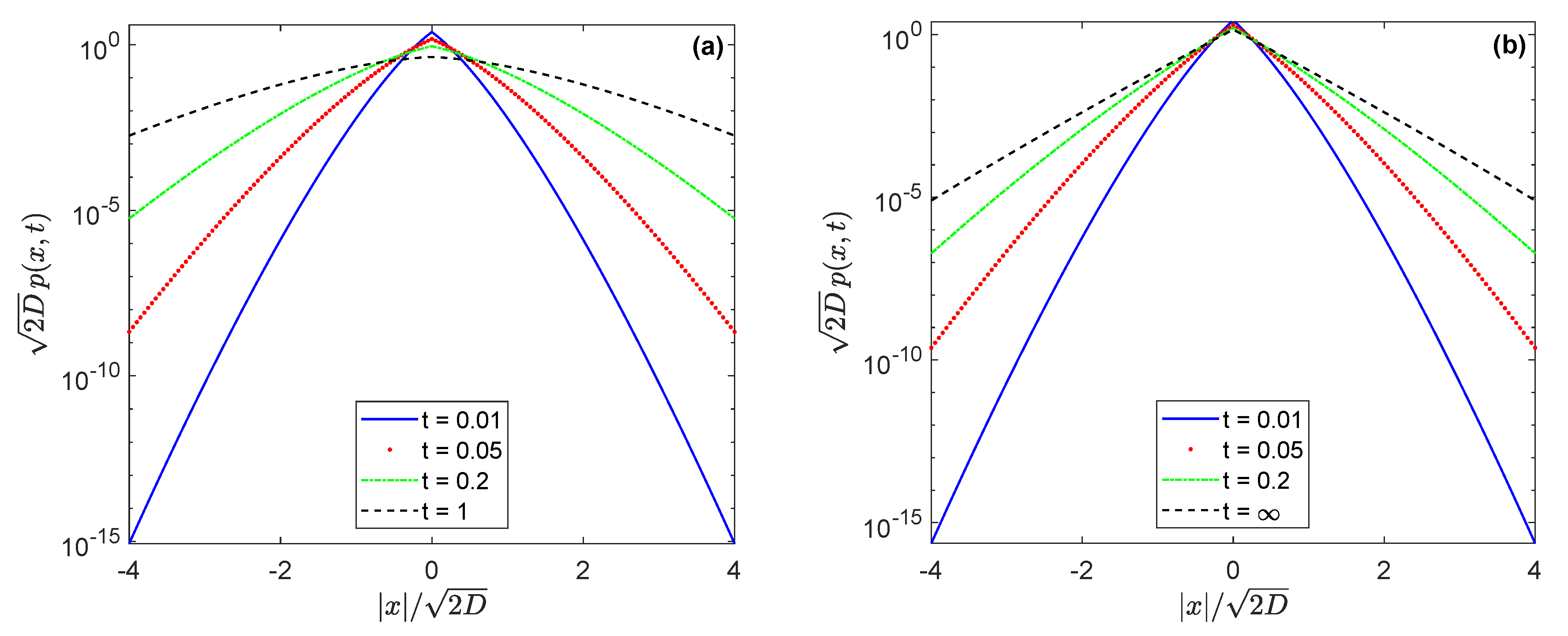
3. Tempered -Stable Process and Its Conjugate Partner
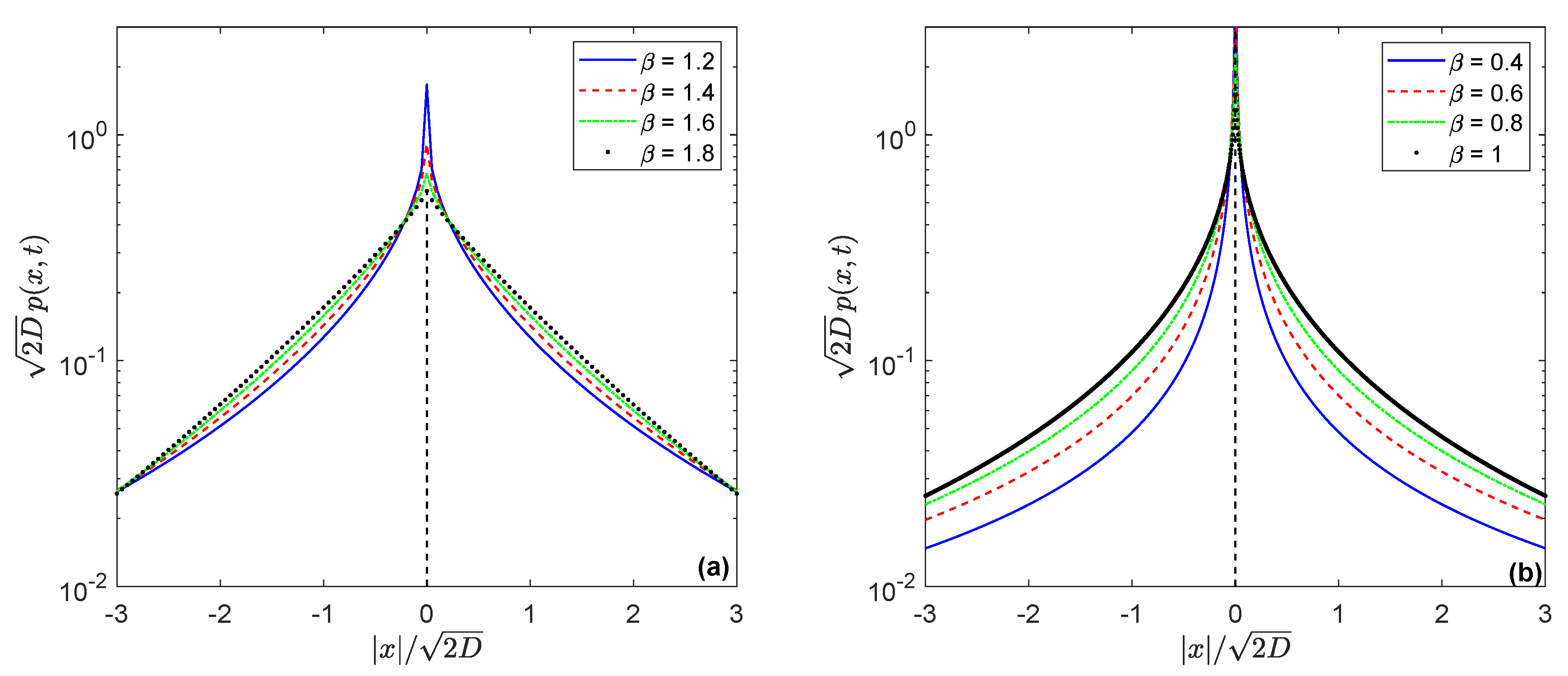
4. Confined Distributions for Infinitely Divisible Motion
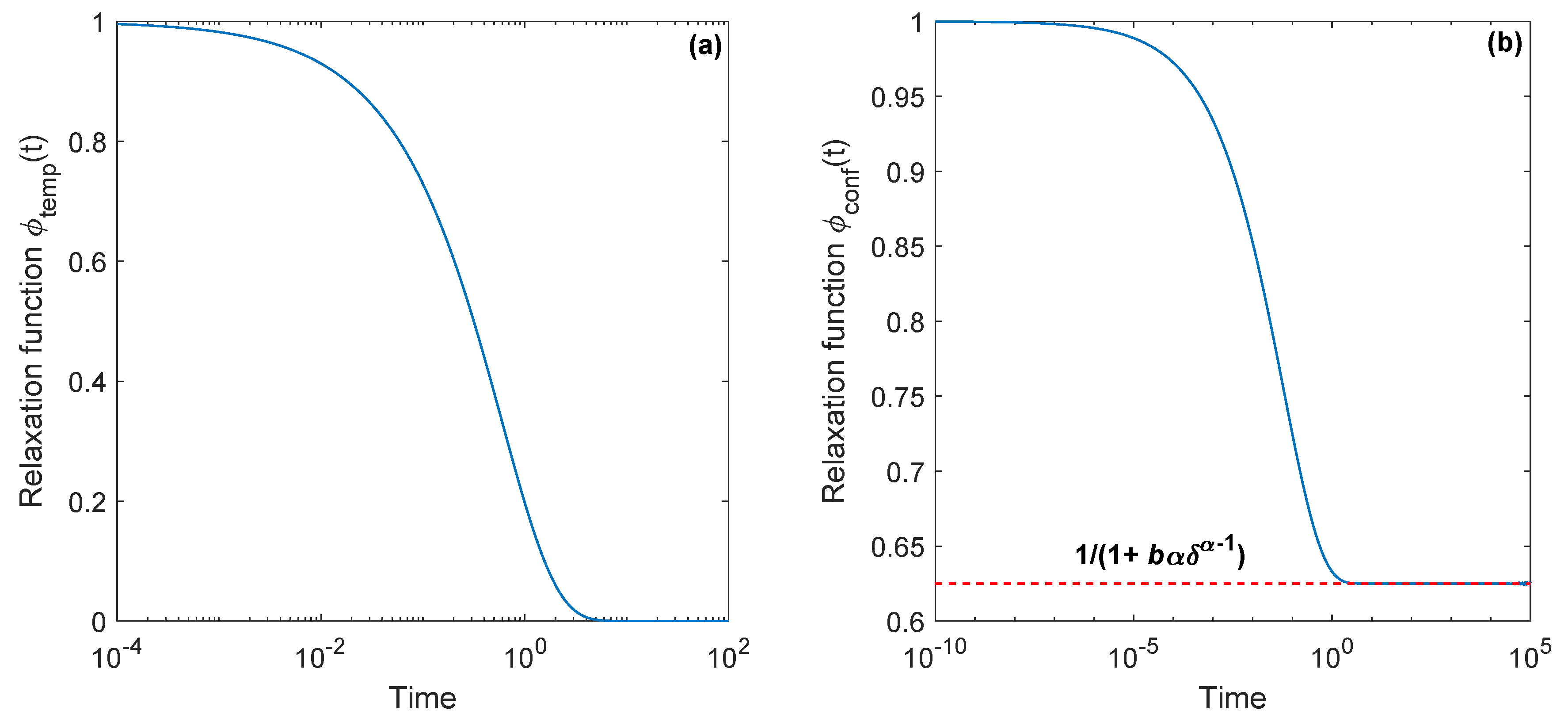
5. Conditionally Non-Exponential Decay of Relaxation
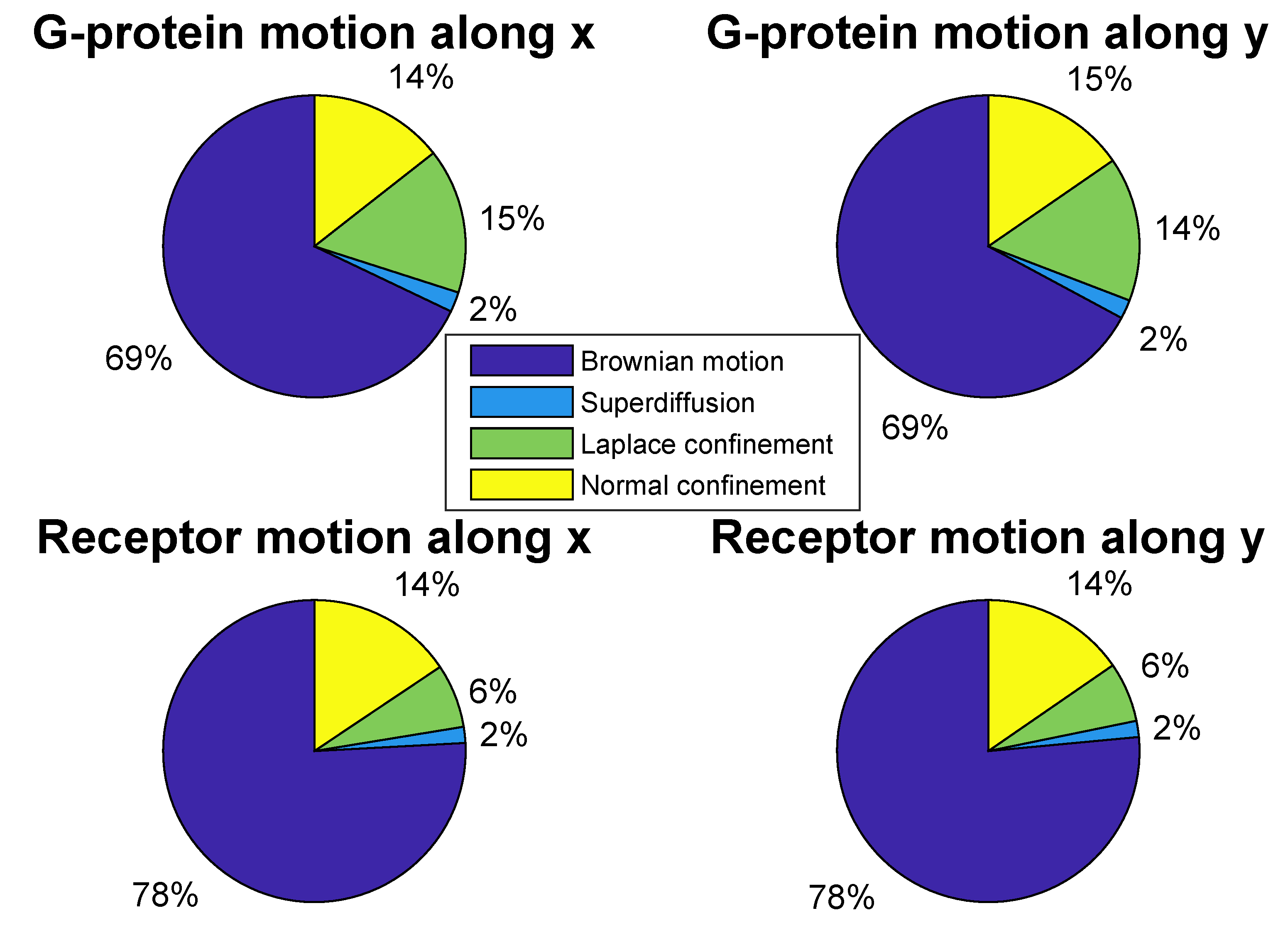
6. G-Proteins vs. a2AR Receptors from the Analysis of the SPT Data
- —an observed trajectory comes from Brownian motion,
- —the trajectory looks like a confined or directed diffusion.
7. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wigner, E.P. The unreasonable effectiveness of mathematics in the natural sciences. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Hamming, R.W. The unreasonable effectiveness of mathematics. Am. Math. Mon. 1980, 87, 81–90. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Manzo, C.; Garcia-Parajo, M.F. A review of progress insingle particle tracking: From methods to biophysical insights. Rep. Prog. Phys. 2015, 78, 124601. [Google Scholar] [CrossRef]
- Metzler, R.; Barkai, E.; Klafter, J. Anomalous diffusion and relaxation close to thermal equilibrium: A fractional Fokker–Planck equation approach. Phys. Rev. Lett. 1999, 82, 3563–3567. [Google Scholar] [CrossRef]
- Bel, G.; Barkai, E. Weak ergodicity breaking in the continuous-time random walk. Phys. Rev. Lett. 2005, 94, 240602. [Google Scholar] [CrossRef]
- Magdziarz, M.; Weron, A. Numerical approach to the fractional Klein–Kramers equation. Phys. Rev. E 2007, 76, 066708. [Google Scholar] [CrossRef] [PubMed]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 1987, 36, 695–798. [Google Scholar] [CrossRef]
- Saxton, M.J. Anomalous diffusion due to obstacles: A Monte Carlo study. Biophys. J. 1994, 66, 394–401. [Google Scholar] [CrossRef]
- Kehr, K.W.; Kutner, R. Random walk on a random walk. Phys. A 1982, 110, 535–549. [Google Scholar] [CrossRef]
- Schulz, J.H.P.; Barkai, E.; Metzler, R. Aging renewal theory and application to random walks. Phys. Rev. X 2014, 4, 011028. [Google Scholar] [CrossRef]
- Guigas, G.; Kalla, C.; Weiss, M. Probing the nanoscale viscoelasticity of intracellular fluids in living cells. Biophys. J. 2007, 93, 316–323. [Google Scholar] [CrossRef] [PubMed]
- Burnecki, K.; Kepten, E.; Janczura, J.; Bronshtein, I.; Garini, Y.; Weron, A. Universal algorithm for identification of fractional Brownian motion. A case of telomere subdiffusion. Biophys. J. 2012, 103, 1839–1847. [Google Scholar] [CrossRef]
- Manzo, C.; Torreno-Pina, J.A.; Massignan, P.; Lapeyre, G.J., Jr.; Lewenstein, M.; Garcia Parajo, M.F. Weak ergodicity breaking of receptor motion in living cells stemming from random diffusivity. Phys. Rev. X 2015, 5, 011021. [Google Scholar] [CrossRef]
- Bronstein, I.; Israel, Y.; Kepten, E.; Mai, S.; Shav-Tal, Y.; Barkai, E.; Garini, Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 2009, 103, 018102. [Google Scholar] [CrossRef]
- Burnecki, K.; Weron, A. Fractional Lévy stable motion can model subdiffusive dynamics. Phys. Rev. E 2010, 82, 021130. [Google Scholar] [CrossRef]
- Krapf, D.; Lukat, N.; Marinari, E.; Metzler, R.; Oshanin, G.; Selhuber-Unkel, C.; Squarcini, A.; Stadler, L.; Weiss, M.; Xu, X. Spectral content of a single non-Brownian trajectory. Phys. Rev. X 2019, 9, 011019. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Barkai, E.; Dubkov, A.A. Lévy flights versus Lévy walks in bounded domains. Phys. Rev. E. 2017, 95, 052102. [Google Scholar] [CrossRef]
- Kou, S.C.; Xie, X.S. Generalized Langevin equation with fractional Gaussian noise: Subdiffusion within a single protein molecule. Phys. Rev. Lett. 2004, 93, 180603. [Google Scholar] [CrossRef]
- Sadegh, S.; Higgins, J.L.; Mannion, P.C.; Tamkun, M.M.; Krapf, D. Plasma membrane is compartmentalized by a self-similar cortical actin meshwork. Phys. Rev. X 2017, 7, 011031. [Google Scholar] [CrossRef] [PubMed]
- Burnecki, K.; Sikora, G.; Weron, A. Fractional process as a unified model for subdiffusive dynamics in experimental data. Phys. Rev. E 2012, 86, 041912. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J.; Joyeux, R. An introduction to long memory time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R. Introduction to Time Series and Forecasting; Springer: New York, NY, USA, 2002. [Google Scholar]
- Beran, J. Statistics for Long-Memory Processes; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Magdziarz, M.; Weron, A. Fractional Langevin equation with α-stable noise. Stud. Math. 2007, 181, 47–60. [Google Scholar] [CrossRef]
- Crato, N.; Rothman, P. Fractional integration analysis of long-run behavior for US macroeconomic time series. Econom. Lett. 1994, 45, 287–291. [Google Scholar] [CrossRef]
- Fouskitakis, G.; Fassois, S. Pseudolinear estimation of fractionally integrated ARMA (ARFIMA) models with automatic applicatins. IEEE Trans. Signal Process. 1999, 47, 3365–3380. [Google Scholar] [CrossRef]
- Gil-Alana, L.A. A fractionally integrated model for the Spanish real GDP. Econom. Bull. 2004, 3, 1–6. [Google Scholar]
- Burnecki, K.; Weron, A. Algorithms for testing of fractional dynamics: A practical guide to ARFIMA modelling. J. Stat. Mech. 2014, 2014, P10036. [Google Scholar] [CrossRef]
- Schilling, R.L.; Song, R.; Vondraček, Z. Bernstein Functions: Theory and Applications; de Gruyter Studies: Berlin, Germany, 2010. [Google Scholar]
- Monroe, I. Processes that can be embedded in Brownian motion. Ann. Probab. 1978, 6, 42–56. [Google Scholar] [CrossRef]
- Weron, A.; Magdziarz, M. Anomalous diffusion and semimartingales. Europhys. Lett. 2009, 86, 60010. [Google Scholar] [CrossRef]
- Bochner, S. Diffusion equation and stochastic processes. Proc. Natl. Acad. Sci. USA 1949, 35, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Meerschaert, M.M.; Benson, D.A.; Scheffler, H.P.; Baeumer, B. Stochastic solution of space-time fractional diffusion equations. Phys. Rev. E 2002, 65, 041103. [Google Scholar] [CrossRef] [PubMed]
- Blumen, A.; Klafter, J.; White, B.S.; Zumofen, G. Continuous-time random walks on fractals. Phys. Rev. Lett. 1984, 53, 1301–1304. [Google Scholar] [CrossRef]
- Fogedby, H.C. Langevin equations for continuous time Lévy flights. Phys. Rev. E 1994, 50, 1657–1660. [Google Scholar] [CrossRef] [PubMed]
- Eule, S.; Friedrich, R. Subordinated Langevin equations for anomalous diffusion in external potentials—Biasing and decoupled external forces. Europhys. Lett. 2009, 86, 30008. [Google Scholar] [CrossRef][Green Version]
- Sokolov, I.M.; Klafter, J. From diffusion to anomalous diffusion: A century after Einstein’s Brownian motion. Chaos 2005, 15, 026103. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K.; Weron, A. Anomalous diffusion with transient subordinators: A link to compound relaxation laws. J. Chem. Phys. 2014, 140, 054113. [Google Scholar] [CrossRef]
- Barkai, E.; Burow, S. Packets of diffusing particles exhibit universal exponential tails. Phys. Rev. Lett. 2020, 124, 060603. [Google Scholar] [CrossRef]
- Saxton, M.J. Single Particle Tracking. In Fundamental Concepts in Biophysics. Handbook of Modern Biophysics; Jue, T., Ed.; Humana Press: Totowa, NJ, USA, 2009; pp. 147–179. [Google Scholar]
- Weron, A.; Burnecki, K.; Akin, E.J.; Solé, L.; Balcerek, M.; Tamkun, M.M.; Krapf, D. Ergodicity breaking on the neuronal surface emerges from random switching between diffusive states. Sci. Rep. 2017, 7, 5404. [Google Scholar] [CrossRef]
- Sungkaworn, T.; Jobin, M.-L.; Burnecki, K.; Weron, A.; Lohse, M.J.; Calebiro, D. Single-molecule imaging reveals receptor-G protein interactions at cell surface hot spots. Nature 2017, 550, 543–547. [Google Scholar] [CrossRef]
- Saxton, M.J. A biological interpretation of transient anomalous subdiffusion. I. Qualitative model. Biophys. J. 2007, 92, 1178–1191. [Google Scholar] [CrossRef] [PubMed]
- Magdziarz, M.; Klafter, J. Detecting origins of subdiffusion: P-variation test for confined systems. Phys. Rev. E 2010, 82, 011129. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J. Wanted: A positive control for anomalous subdiffusion. Biophys. J. 2012, 103, 2411–2422. [Google Scholar] [CrossRef] [PubMed]
- Stanislavsky, A.; Weron, A. Control of the transient subdiffusion exponent at short and long times. Phys. Rev. Res. 2019, 1, 023006. [Google Scholar] [CrossRef]
- Saxton, M.J.; Jacobson, K. Single-particle tracking: Applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 1997, 26, 373–399. [Google Scholar] [CrossRef]
- Saxton, M.J. Lateral diffusion in an archipelago. Single-particle diffusion. Biophys. J. 1993, 64, 1766–1780. [Google Scholar] [CrossRef]
- Schütz, G.J.; Kada, G.; Pastushenko, V.P.; Schindler, H. Properties of lipid microdomains in a muscle cell membrane visualized by single molecule microscopy. EMBO J. 2000, 19, 892–901. [Google Scholar] [CrossRef]
- Schmidt, T.; Schütz, G.J. Single-Molecule Analysis of Biomembranes. In Handbook of Single–Molecule Biophysics; Hinterdorfer, P., Oijen, A., Eds.; Springer: New York, NY, USA, 2009; pp. 19–42. [Google Scholar]
- Basak, S.; Sengupta, S.; Chattopadhyay, K. Understanding biochemical processes in the presence of sub-diffusive behavior of biomolecules in solution and living cells. Biophys. Rev. 2019, 11, 851–872. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K.; Weron, A. Diffusion and relaxation controlled by tempered α-stable processes. Phys. Rev. E 2008, 78, 051106. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Zhang, Y.; Baeumer, B. Tempered anomalous diffusion in heterogeneous systems. Geophys. Res. Lett. 2008, 35, L17403. [Google Scholar] [CrossRef]
- Flenner, E.; Das, J.; Rheinstädter, M.C.; Kosztin, I. Subdiffusion and lateral diffusion coefficient of lipid atoms and molecules in phospholipid bilayers. Phys. Rev. E 2009, 79, 011907. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.H.; Monne, H.M.S.; Javanainen, M.; Metzler, R. Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins. Phys. Rev. Lett. 2012, 109, 188103. [Google Scholar] [CrossRef] [PubMed]
- Molina Garcia, D.; Sandev, T.; Safdari, H.; Pagnini, G.; Chechkin, A.; Metzler, R. Crossover from anomalous to normal diffusion: Truncated power-law noise correlations and applications to dynamics in lipid bilayers. New J. Phys. 2018, 20, 103027. [Google Scholar] [CrossRef]
- Gajda, J.; Magdziarz, M. Fractional Fokker–Planck equation with tempered α-stable waiting times: Langevin picture and computer simulation. Phys. Rev. E 2010, 82, 011117. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K. Tempered relaxation with clustering patterns. Phys. Lett. A 2011, 375, 4244–4248. [Google Scholar] [CrossRef]
- Janczura, J.; Wyłomańska, A. Anomalous diffusion models: Different types of subordinator distribution. Acta Phys. Pol. B 2012, 43, 1001–1016. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K. Anomalous diffusion approach to dielectric spectroscopy data with independent low- and high-frequency exponents. Chaos Solitons Fractals 2012, 45, 909–913. [Google Scholar] [CrossRef]
- Wyłomańska, A. Arithmetic Brownian motion subordinated by tempered stable and inverse tempered stable processes. Physica A 2012, 391, 5685–5696. [Google Scholar] [CrossRef][Green Version]
- Wyłomańska, A. The tempered stable process with infinitely divisible inverse subordinators. J. Stat. Mech. 2013, 2013, P10011. [Google Scholar] [CrossRef][Green Version]
- Kumar, A.; Vellaisamy, P. Inverse tempered stable subordinators. Stat. Probab. Lett. 2015, 103, 134–141. [Google Scholar] [CrossRef]
- Sandev, T.; Chechkin, A.; Kantz, H.; Metzler, R. Diffusion and Fokker–Planck-Smoluchowski equations with generalized memory kernel. Fract. Calc. Appl. Anal. 2015, 18, 1006–1038. [Google Scholar] [CrossRef]
- Alrawashdeh, M.S.; Kelly, J.F.; Meerschaert, M.M. Applications of inverse tempered stable subordinators. Comput. Math. Appl. 2017, 73, 892–905. [Google Scholar] [CrossRef]
- Feller, W. Introduction to Probability Theory and Its Application; John Wiley & Sons Inc.: New York, NY, USA, 1967; Volume II. [Google Scholar]
- Song, R.; Vondraček, Z. Potential Theory of Subordinate Brownian Motion. In Potential Analysis of Stable Processes and Its Extensions; Graczyk, P., Stos, A., Eds.; Lecture Notes in Mathematics 1980; Springer: Berlin/Heidelberg, Germany, 2009; pp. 87–176. [Google Scholar]
- Magdziarz, M. Langevin picture of subdiffusion with infinitely divisible waiting times. J. Stat. Phys. 2009, 135, 763–772. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1964. [Google Scholar]
- Sandev, T.; Sokolov, I.M.; Metzler, R.; Chechkin, A. Beyond monofractional kinetics. Chaos Solitons Fractals 2017, 102, 210–217. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Chechkin, A. From continuous time random walks to the generalized diffusion equation. Fract. Calc. Appl. Anal. 2018, 21, 10–28. [Google Scholar] [CrossRef]
- Rosiński, J. Tempering stable processes. Stoch. Proc. Appl. 2007, 117, 677–707. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Special Functions for Applied Scientists; Springer: New York, NY, USA, 2008. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; John Wiley & Sons Inc.: New York, NY, USA, 1994. [Google Scholar]
- Kotz, S.; Kozubowski, T.; Podgórski, K. The Laplace Distribution and Generalizations: A Revisit with Applications to Communications, Economics, Engineering, and Finance; Birkhauser: Boston, MA, USA, 2001. [Google Scholar]
- Chubynsky, M.V.; Slater, G.W. Diffusing diffusivity: A model for anomalous, yet Brownian, diffusion. Phys. Rev. Lett. 2014, 113, 098302. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Seno, F.; Metzler, R.; Sokolov, I.M. Brownian yet non-Gaussian diffusion: From superstatistics to subordination of diffusing diffusivities. Phys. Rev. X 2017, 7, 021002. [Google Scholar] [CrossRef]
- Metzler, R. Superstatistics and non-Gaussian diffusion. Eur. Phys. J. Spec. Top. 2020, 229, 711–728. [Google Scholar] [CrossRef]
- Ślęzak, J.; Burov, S. From diffusion in compartmentalized media to non-Gaussian random walks. arXiv 2019, arXiv:1909.11395. [Google Scholar]
- Stanislavsky, A.; Weron, A. Accelerating and retarding anomalous diffusion: A Bernstein function approach. Phys. Rev. E 2020, 101, 052119. [Google Scholar] [CrossRef] [PubMed]
- Linnik, Y.V. Linear forms and statistical criteria, I, II. In English Translations in Mathematical Statistics and Probability, 3; American Mathematical Society: Providence, RI, USA, 1962; pp. 1–90. [Google Scholar]
- Pillai, R.N. Semi α-Laplace distributions. Commun. Stat. Theory Methods 1985, 14, 991–1000. [Google Scholar] [CrossRef]
- Kotz, S.; Ostrovskii, I.V.A. Hayfavi, Analytic and asymptotic properties of Linnik’s probability densities. J. Math. Anal. Appl. 1995, 193, 353–371. [Google Scholar] [CrossRef]
- Kozubowski, T.J. Geometric stable laws: Estimation and applications. Math. Comput. Model. 1999, 29, 241–253. [Google Scholar] [CrossRef]
- Kozubowski, T.J. Fractional moment estimation of Linnik and Mittag–Leffler parameters. Math. Comput. Model. 2001, 34, 1023–1035. [Google Scholar] [CrossRef]
- Kotz, S.; Ostrovskii, I.V. A mixture representation of the Linnik distribution. Statist. Probab. Lett. 1996, 26, 61–64. [Google Scholar] [CrossRef]
- Lukacs, E. Characteristic Functions, 2nd ed.; Charles Griffin and Co.: London, UK, 1970. [Google Scholar]
- Anderson, D.N.; Arnold, B.C. Linnik distributions and processes. J. Appl. Probab. 1993, 30, 330–340. [Google Scholar] [CrossRef]
- George, S.; Pillai, R.N. Multivariate α-Laplace distributions. J. Nat. Acad. Math. 1987, 5, 13–18. [Google Scholar]
- Devroye, L. A note on Linnik’s distribution. Stat. Prob. Let. 1990, 9, 305–306. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Wintner, A. The singularities of Cauchy’s distributions. Duke Math. J. 1941, 8, 678–681. [Google Scholar] [CrossRef]
- Pillai, R.N.; Sandhya, E. Distributions with complete monotone derivative and geometric infinite divisibility. Adv. Appl. Prob. 1990, 22, 751–754. [Google Scholar] [CrossRef]
- Weron, K. A probabilistic mechanism hidden behind the universal power law for dielectric relaxation: General relaxation equation. J. Phys. Condens. Matter 1991, 3, 9151–9162. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K. Stochastic tools hidden behind the empirical dielectric relaxation laws. Rep. Prog. Phys. 2017, 80, 036001. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Weron, K.; Jurlewicz, A. Two forms of self–similarity as a fundamental feature of the power–law dielectric response. J. Phys. A Math. Gen. 1993, 26, 395–410. [Google Scholar] [CrossRef]
- Jurlewicz, A. Frequency–independent rules for the dielectric susceptibility derived from two forms of self–similar dynamical behavior of dipolar system. J. Stat. Phys. 1995, 79, 993–1003. [Google Scholar] [CrossRef]
- Jurlewicz, A.; Weron, A.; Weron, K. Asymptotic behavior of stochastic systems with conditionally exponential decay property. Appl. Math. 1996, 23, 379–394. [Google Scholar]
- Briane, V.; Kervrann, C.; Vimond, M. Statistical analysis of particle trajectories in living cells. Phys. Rev. E 2018, 97, 062121. [Google Scholar] [CrossRef]
- Weron, A.; Janczura, J.; Boryczka, E.; Sungkaworn, T.; Calebiro, D. Statistical testing approach for fractional anomalous diffusion classification. Phys. Rev. E 2019, 99, 042149. [Google Scholar] [CrossRef]
- Kowalek, P.; Loch-Olszewska, H.; Szwabinski, J. Classification of diffusion modes in single-particle tracking data: Feature-based versus deep-learning approach. Phys. Rev. E 2019, 100, 032410. [Google Scholar] [CrossRef]
- Hubicka, K.; Janczura, J. Time-dependent classification of protein diffusion types: A statistical detection of mean-squared-displacement exponent transitions. Phys. Rev. E 2020, 101, 022107. [Google Scholar] [CrossRef]
- Wyłomańska, A.; Iskander, D.R.; Burnecki, K. Omnibus test for normality based on the Edgeworth expansion. PLoS ONE 2020, 15, e0233901. [Google Scholar] [CrossRef] [PubMed]
- Kundu, D. Discriminating between normal and Laplace distributions. In Advances in Ranking and Selection, Multiple Comparisons, and Reliability Statistics for Industry and Technology; Balakrishnan, N., Nagaraja, H.N., Kannan, N., Eds.; Birkhäuser: Boston, MA, USA, 2005; pp. 65–79. [Google Scholar]
- Lampo, T.J.; Stylianidou, S.; Backlund, M.P.; Wiggins, P.A.; Spakowitz, A.J. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys. J. 2017, 112, 532–542. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanislavsky, A.; Weron, A. Look at Tempered Subdiffusion in a Conjugate Map: Desire for the Confinement. Entropy 2020, 22, 1317. https://doi.org/10.3390/e22111317
Stanislavsky A, Weron A. Look at Tempered Subdiffusion in a Conjugate Map: Desire for the Confinement. Entropy. 2020; 22(11):1317. https://doi.org/10.3390/e22111317
Chicago/Turabian StyleStanislavsky, Aleksander, and Aleksander Weron. 2020. "Look at Tempered Subdiffusion in a Conjugate Map: Desire for the Confinement" Entropy 22, no. 11: 1317. https://doi.org/10.3390/e22111317
APA StyleStanislavsky, A., & Weron, A. (2020). Look at Tempered Subdiffusion in a Conjugate Map: Desire for the Confinement. Entropy, 22(11), 1317. https://doi.org/10.3390/e22111317





