1. Motivation and Overview
Among the distinctive features of quantum mechanics is that, in some regards, a quantum system acts as though it is simultaneously in multiple states of a given type. As an extreme example, a lattice Schrödinger particle in a momentum eigenstate is often said to reside at all positions, having an equal chance of being detected anywhere. However, how many of such “position identities” are effectively present in a generic state that can assign an arbitrarily varied relevance (probability) to different locations?
Variants of this counting problem appear in quantum physics quite often. One example arises in the context of Anderson localization [
1] (see, e.g., [
2,
3] for reviews). Indeed, the Fermi-level electron inside the band of extended states (Anderson conductor) is thought of as effectively present in most of the available position states. In contrast, such an electron inside the band of localized states (Anderson insulator) only resides in a drastically reduced subset of them. Hence, a well-founded effective counting of states could be used to quantitatively describe the transition between these regimes in a novel way.
Viewing an Anderson electron from a different perspective, the effective state counting could also be used to analyze the indeterminacy (quantum uncertainty) associated with the measurement of its position. In such an approach, uncertainty would be represented by the effective number of position states the electron collapses into upon repeating the experiment: the smaller this effective number, the smaller the uncertainty. Note that the general treatment of quantum indeterminacy this way (with respect to an arbitrary basis) would be very different in nature from, e.g., the classic spectral approach [
4,
5].
The above types of physics analyses may usefully materialize if the generic question [Q] below can be suitably formalized and meaningfully answered. In particular, if
is a state from an
N-dimensional Hilbert space and
its orthonormal basis (remark [
6]), it is desirable to ask:
[Q] How many states from is the system described by effectively in?
A well-founded resolution of this “quantum identity problem” is not readily available (remark [
7]). In this paper, we develop a theoretical framework (effective number theory) that gives the rationale to the following answer:
[A]
Let , be the probability vector assigned to quantum state and basis , and let . The system described by is effectively in states from , where:To arrive at [A], we start with the axiomatic definition of the effective number function (ENF)
, namely a function consistently assigning the effective totals. Solving [Q] then amounts to finding such an
and using it to specify the effective number of quantum identities in all situations. The subsequent analysis shows, however, that there exists an entire continuum of ENFs. This could render each fixed choice of
too arbitrary and its individual value uninformative on its own (remark [
8]). Interestingly, this is not the case because it turns out that
is an ENF with absolute meaning. Indeed, we will prove that
for all
C and all
, making
the unique minimum (least element) on the set of all ENFs. Having revealed that the system in state
has to be characterized as being simultaneously in at least
states from
, this result is used in [A] as a basis for the meaningful canonical choice of ENF (remark [
9]). It should be noted in this regard that a maximal ENF, whose interpretation would otherwise be on equal footing with
, does not exist (see Theorem 2).
A crucial novelty in our approach is the inclusion of additivity as a requirement for ENFs. This step is necessary since the effective number of states is an additive concept. However, a proper formulation requires some care. To that end, as well as to start invoking parallels with localization, consider the simple setting of a spinless Schrödinger particle on a finite lattice. In the position basis, its state
is represented by the
N-tuple
, with
being the probability of detection at the location
. Denoting by
the set of all counting weight vectors
,
, namely (remark [
10]):
the additivity property for
arises as follows. Assume that the particle is restricted to a lattice of
sites in a state generating the weight vector
. Separately, let it be restricted to a non-overlapping adjacent lattice of
sites and characterized by
. With symbol ⊞ representing the concatenation operation (remark [
11]), since:
there exists a state of the particle on the combined lattice, producing this composite
C. Given the additivity of numbers, the sum rule for the number of available states (
) has to hold for its effective counterpart as well (
). Consequently, the additivity property that we impose is:
(A) Additivity:
Here, the dimensions of vector arguments were made explicit to emphasize that represents N modified by distribution C. Notice that is evidently additive and that the above reasoning does not depend on the system, state, or basis in question.
Several decades ago, Bell and Dean [
12] dealt with a problem analogous to [Q] while analyzing the localization properties of vibrations in glassy silica. In particular, they asked how many atoms do these vibrations effectively spread over. Their quantifier, the participation number
, is given by:
and is still widely used in the analysis of localization. In other areas, it is common to exponentiate a suitable entropy, such as the Shannon [
13] or Rényi entropies [
14], and use it for analogous purposes. However, none of these quantifiers is (A)-additive. Their interpretation as effective totals is thus vague and they tend to be too arbitrary. In contrast, incorporating additivity into the definition of ENFs leads to the resolution of the quantum identity problem and suggests new possibilities both in physics and measure-related aspects of mathematics. The effective number theory, which we develop here as a tool to solve [Q], provides a theoretical starting point for such developments.
In the rest of this section, we describe the construction of ENFs and discuss the key results of effective number theory. The goal here is to provide a concise but rigorous overview, including the motivations for axiomatic properties, as well as the ramifications of deduced features. A fully mathematical treatment in the technically convenient dual form of effective complementary numbers (co-numbers) is then given in
Section 2. Various generalizations of the quantum identity problem are discussed in
Section 3. We then outline the use of effective numbers in quantum theory from a very broad perspective, namely as a general tool to characterize quantum states (
Section 4). Concluding remarks are given in
Section 5.
1.1. Effective Numbers
We now develop the notion of ENF as a function , assigning an effective total to each distribution of weights over the elements of a basis. Such a construction clearly does not depend on the fact that counted objects are quantum states, and we will thus use generic terms in that regard from now on. The underlying goal is to extend the “counting measure” for a collection of distinct, but otherwise equivalent objects (natural number ) to the situation when these objects acquire varied importance expressed by their counting weights (effective number ). The additivity property (A) is thus a basic consistency requirement for acceptable ENFs.
Like in ordinary counting, no specific relation among individual objects is assumed. Thus, in the same way the number of balls in a bag does not change upon their reshuffle, the effective number will not change upon the permutation of counting weights. In other words, ENFs are required to be totally symmetric in their arguments, namely (remark [
15]):
(S) Symmetry:
Extensions are by definition such that ordinary counting corresponds to all objects being equally important, and thus to a uniform distribution. More precisely:
(B1) Boundary Condition 1:
On the other hand, whenever all the weight is given to a single object, all others being irrelevant, the effective number is required to be one, namely:
(B2) Boundary Condition 2:
within each . Note that and are the opposite extremes in the cumulation of the weight. Hence, the effective number of objects with arbitrary weights has to fall between the corresponding extremal values, namely:
(B) Bounds:
The degree of weight cumulation plays a more detailed role in effective numbers than just determining the boundary properties. Indeed, the concept has to respect that increasing the cumulation in the distribution cannot increase the effective number. To formulate such monotonicity, consider two objects weighted by
with
. The deformation
leads to further cumulation in favor of the second object, and thus,
is imposed for all
. In a situation with an arbitrary
N, we require the same for each ordered pair
and deformation
, namely (remark [
16]):
(M) Monotonicity:
It is easy to check that (M
)-monotonic
attains its maximal value over
at
, while the minimum is at one or multiple fully cumulated vectors
. Conditions (B1), (B2), and (B) are thus compatible with (M
) (remark [
17]). Note that, although not an ENF, the participation number (
4) satisfies (M
)-monotonicity.
The final requirement in the definition of ENFs is continuity. The nature of problems with admitting discontinuities can be illustrated by:
which counts the number of non-zero weights in
C and will be relevant later in our analysis. Consider again two objects with
. When
c approaches zero, thus marginalizing the first object to an arbitrary degree, the effective number should approach one. However, this does not materialize in
due to its discontinuity. In general, we require that the ENF cannot jump upon an arbitrarily small change of weights, namely:
(C) Continuity:
The properties discussed above define the set of all effective number functions. However, there are dependencies among these requirements. In particular, it can be easily checked that the boundary condition (B1) is a consequence of (B2) and additivity. Similarly, (B) follows from (B1), (B2), symmetry and monotonicity. This leaves us with:
Definition 1. A real-valued function on is called an effective number function (belongs to set ) if it is simultaneously additive (A), symmetric (S), continuous (C), monotonic (M)and satisfies the boundary condition (B2).
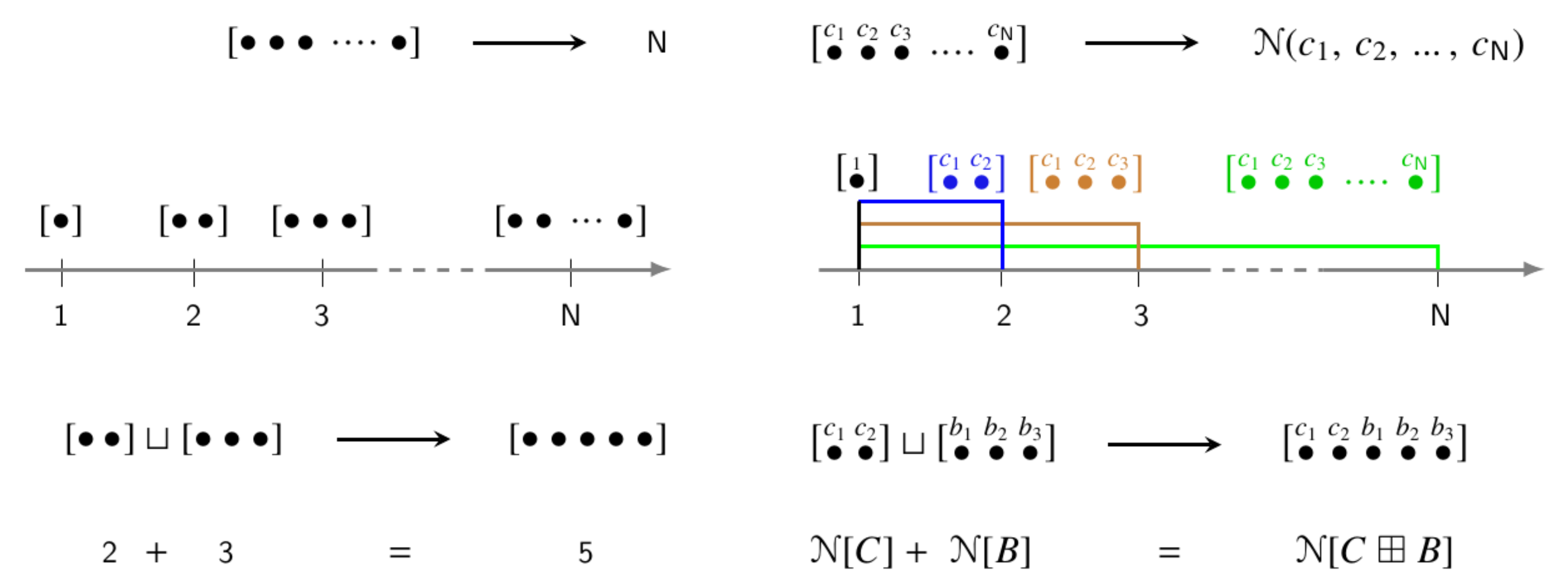
Some of the features imprinted on the corresponding notion of effective numbers are visualized in
Figure 1 (remark [
18]). On the left, natural numbers are shown as a theoretical model for expressing and manipulating the quantities of like objects (bags of balls) or of varied objects treated as equivalent. The bags containing differing amounts are assigned different discrete points on the real axis (natural numbers), with the operation of “merging the bags” (⊔) realized by ordinary addition. Extension to objects distinguished by counting weights is shown on the right. Here, the bags assigned equal amounts
N by ordinary counting may be assigned different effective numbers
, depending on the cumulation of their weight distributions. With maximal cumulation (
-function) producing
, the effective number continuously and monotonically increases as cumulation decreases, reaching
when cumulation is absent (uniform distribution). The operation of merging bags is represented by the additivity property (A). Each element of
, if any, implements a specific version of this scheme. Thus, to assess the conceptual value and practical impact of effective numbers, it is necessary to decipher the structure of
.
1.2. Effective Counting
It is not difficult to establish that ENFs do exist. For example, one can verify that the one parameter family of functions:
belongs to
, with
. However, it is rather remarkable that all
have the additively separable structure of (
6). Indeed, Theorem 3 (
Section 2) implies the following central result specifying
explicitly.
Theorem 1. Function on belongs to if and only if there exists a real-valued function on that is concave, continuous, , for , and:Such a function associated with is unique. Thus, there is a one-to-one correspondence between ENFs and functions of the single variable specified by Theorem 1 (remark [
19]). Such
associated with the given
will be referred to as its counting function.
The necessity of the additively separable form (
7) for ENFs is interesting conceptually. Indeed, it is common and familiar to represent the ordinary total (natural number) by a sequential process of adding a unit amount for each object in the collection. According to Theorem 1, this applies to every consistent extension to the effective total (effective number), albeit with objects contributing weight-dependent amounts specified by the counting function. It thus turns out that the construction of ENFs generalizes the process of ordinary counting to the process of effective counting.
1.3. Minimal Effective Number
A key insight into the nature of effective counting is provided by the following results concerning the structure of set
. They follow directly from Theorem 4 in
Section 2.
Theorem 2. Let and be functions on defined by (
1)
and (
5),
respectively. Then: To elaborate, first note that (a) is the refinement of defining condition (B). While the upper bound is intuitive ( counts the number of non-zero weights in ), the lower one is unexpected and consequential. In particular, the effective number of objects weighted by C cannot be smaller than . Since is an ENF, this feature is inherent to the concept itself: there is a meaningful notion of the minimal effective number. In technical terms, is the least element of function set with respect to partial order , and thus a unique ENF with this property.
Part (b) conveys that, for each fixed , effective counting can be adjusted so that assumes any desired value from the allowed range specified by (a). While reflecting a certain degree of arbitrariness built into the concept of effective numbers, the associated freedom of choice is in fact quite natural. To illustrate this, consider N objects with non-zero weights of very disparate magnitudes so that the collection is usefully characterized by an effective number. The insistence on the ordinary count in this situation constitutes a “large extrapolation” since it forces each object to contribute equally despite the disparity. According to (b), such an extrapolation can be realized by a sequence of ENFs that bring the effective total arbitrarily close to N. Accommodating the needed continuum of consistent schemes can thus be considered a useful feature in a framework describing the generalized aspects of counting.
Note that (b) also confirms an intuitive expectation that there is no maximal ENF since, although specifying a supremal value for each
C, function
does not belong to
. Taken together, the results of Theorem 2 form the basis for our canonical solution [A] of the quantum identity problem [Q]. The existence of minimal total
is particularly consequential in applications of effective numbers. One notable example is that it facilitates the notion of minimal (intrinsic) quantum uncertainty [
20].
3. Counting the General Quantum Identities
With the effective number theory in place, we now return to the topic that motivated its construction, namely the quantum identity problem. In particular, we will make explicit some of the straightforward, but useful and relevant, generalizations of [Q]. This serves, in part, as a stepping stone toward the most generic application of effective numbers in quantum theory, namely as a tool to characterize quantum states (
Section 4).
A conceptually important extension of [Q] and [A] is made possible by the additive separability of ENFs. Indeed, instead of an orthonormal basis, consider any collection
of
n orthonormal states from an
N-dimensional Hilbert space (
). How many states from
is a system described by
effectively in? Let
be an ENF and
the counting function uniquely associated with it by virtue of Theorem 1. We define:
for each
and
. This assignment is meaningful in the following sense. Given a fixed
, let
be its arbitrary completion into a basis of the Hilbert space. Then, owing to the additive separability of ENFs,
where “\” denotes the set subtraction. In other words, the contribution of
to
, defined by (
18), is independent of the completion
and is thus uniquely associated with
for fixed
. It is the effective number of states from
contained in
according to
. Moreover, it is straightforward to check that
minimizes the effective number so assigned, and we have:
[A
]
Let be a state vector from an N-dimensional Hilbert space and the set of n orthonormal states in this space. The physical system described by is effectively in states from , specified by (18) with .A few simple points regarding the above are worth emphasizing.
- (i)
The extension (
18) and the ensuing generalization of [A] to [A
] arise because the abundance of quantum identities is determined “locally”, namely without reference to basis elements orthogonal to the subspace in question. Apart from being natural for a measure-like characteristic, this feature has practical consequences in many-body applications where the dimension of the Hilbert space grows exponentially with the size of the system. Indeed, the above avoids such complexity in certain calculations, thus providing a computational benefit.
- (ii)
None of the above applies to the abundance of quantum identities determined by the participation number
of Equation (
4), since this value does not split into contributions from orthogonal subspaces generated by the partitioned basis. This is of course due to the lack of additivity and hence of additive separability.
- (iii)
The above considerations are clearly not limited to counting quantum identities. In a generic situation, the inquiry is concerned with the contribution to the effective number from a subset of weighted objects. To formalize such assignments directly in the effective number theory, one simply extends
from domain
of counting vectors to the domain of general weights:
by virtue of its counting function
, namely
.
While the effective number
specifies how many identities from basis
the state
can effectively take, it is frequently useful to inquire about a coarse-grained version of such an effective count. To formalize the corresponding generalization, consider the decomposition of Hilbert space
into
M mutually orthogonal subspaces
:
Subspaces
are implicitly treated as equivalent entities (remark [
27]). In how many subspaces from
is the system described by
effectively?
Given a state of the system, the rules of quantum mechanics assign a probability to each subspace of the associated Hilbert space. The effective number theory therefore provides an immediate answer to the above question. More specifically, let be the (unnormalized) projection of onto . Then, the probability vector is , where , and the corresponding counting vector is . Hence, given an ENF, we assign , which leads to the following generalization [A] of [A].
[A] Let C be the counting vector assigned by quantum mechanics to state and the orthogonal decomposition of the Hilbert space. Then, the system described by is effectively contained in subspaces from .
Applying the logic identical to the one producing [A], it is straightforward to generalize [A] into [A] for counting the identities from arbitrary sets (not necessarily full decompositions) of mutually orthogonal subspaces.
5. Concluding Remarks
When a quantum system is (strongly) probed, it emerges in one of many possible “identities”. This is among the key features of quantum behavior. Indeed, it underlies the notion of quantum uncertainty and is closely connected to a fruitful concept of localization. A well-founded prescription for the corresponding abundances is thus desirable. As a contemporary example, one may use it in the analysis of a quantum algorithm that produces the state as an output of a quantum run and follows up with a measurement involving a basis . The effective number of distinct collapsed states obtained upon repetition of these steps is relevant for the assessment of the algorithm’s efficiency.
In this work, we showed that requiring the desired characteristics to be measure-like (additive) is fruitful in identifying a meaningful quantifier. In particular, it results in the theoretical structure (effective number theory) revealing that a consistent assignment of totals to collections of objects with probability weights requires the existence of an inherent (minimal) amount
. The appearance of such a qualitative feature in basic measure considerations suggests the utility of the constructed framework already in contexts much less abstract than quantum mechanics. For example,
can be viewed as an extension of the ordinary counting measure into what can be referred to as a diversity measure with its wide range of contemporary applications (social sciences, ecosystems; see, e.g., [
29,
30]). Other viewpoints can cast it as a choice measure, facilitating a probabilistic notion of effective choices, or as a support measure, conveying the effective size of a function support (effective domain). Given this universality,
may find uses in multiple areas of quantitative science.
Finally, we wish to point out that the existence of a minimal amount is rooted in the simultaneous requirement of both monotonicity (Schur concavity) and additivity for ENFs. This combination is rather unusual from the mathematics standpoint. Indeed, while monotonicity is important for the theory of majorization [
31,
32], it has no role in the standard formalization of the measure. Conversely, additivity is crucial for the latter, but not native to the former. In fact, relaxing either (M
) or (A) in Definition 1 leaves the respective effective pseudo-number assignments too arbitrary. However, their combination, which is necessary on conceptual grounds, leads to
and the associated insights.