Time-Delay Characteristics of Complex Lü System and Its Application in Speech Communication
Abstract
1. Introduction
- The time-delay characteristics of complex Lü systems with different parameters are studied and a controller for realizing STDS is designed;
- The evolved STDS controller is applied to the encryption of speech communication using linear equations of state variables and its effect is verified by simulation experiments.
2. Characteristics of Complex Lü Chaotic Systems with Time-Delay
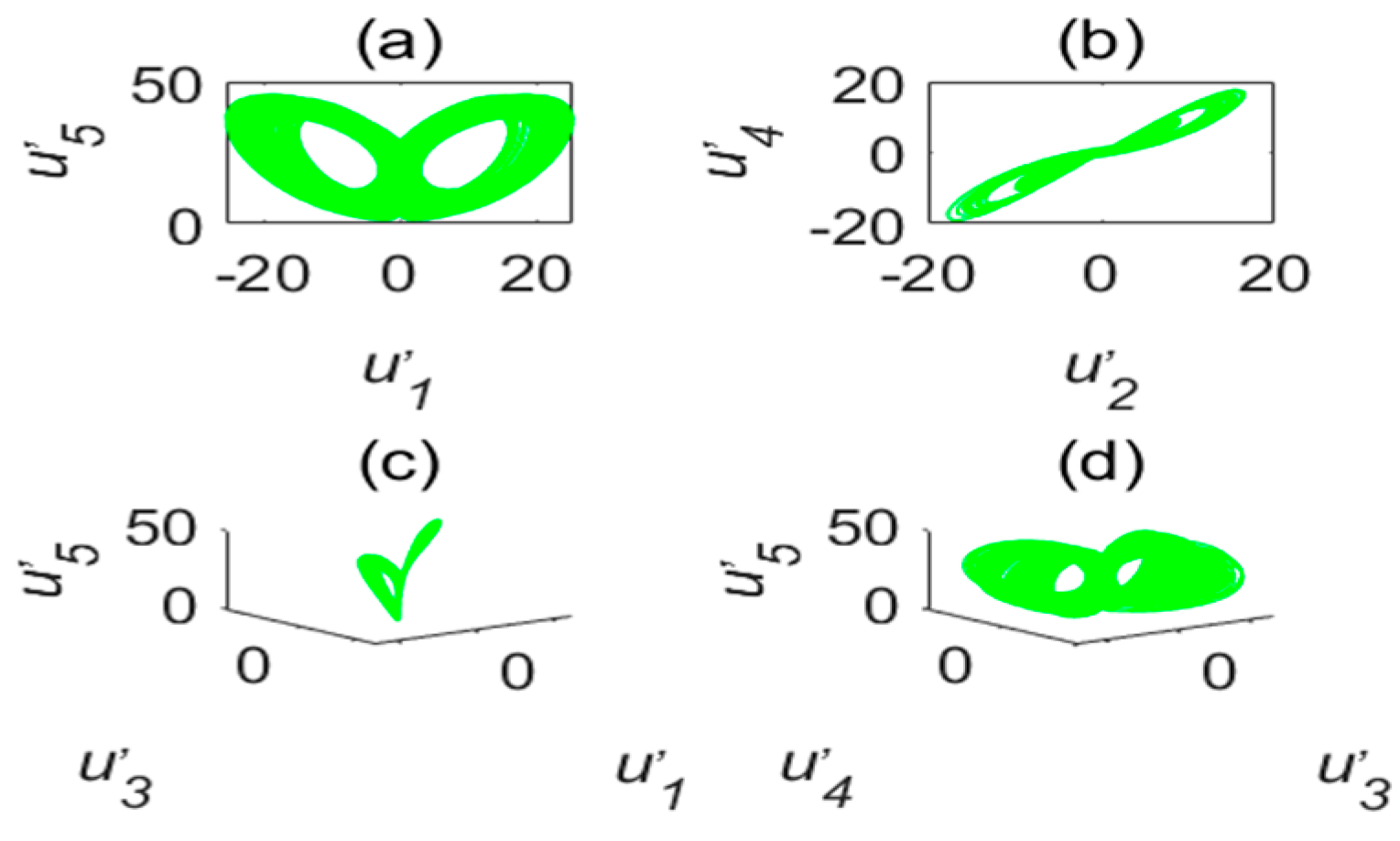
2.1. The Dissipation
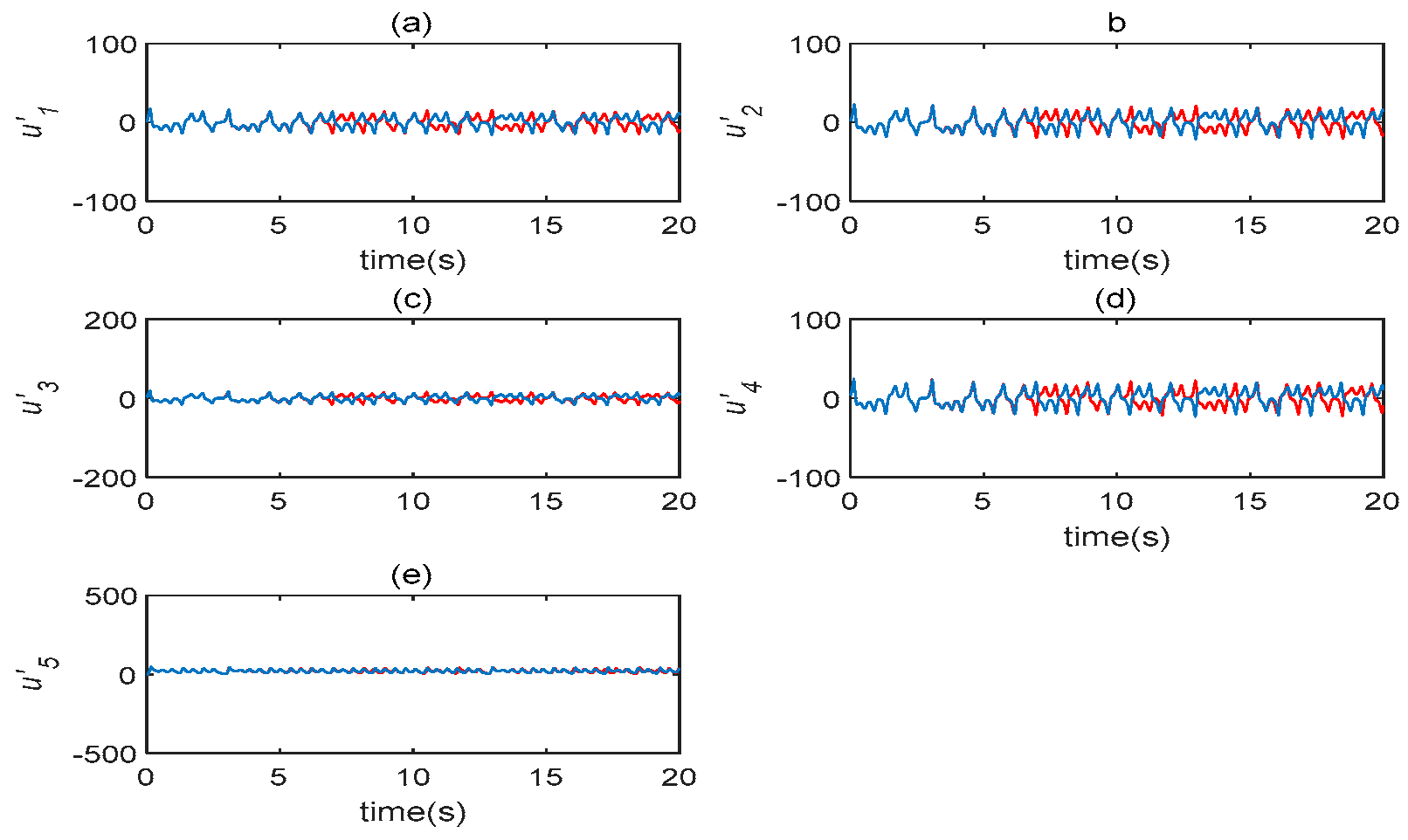
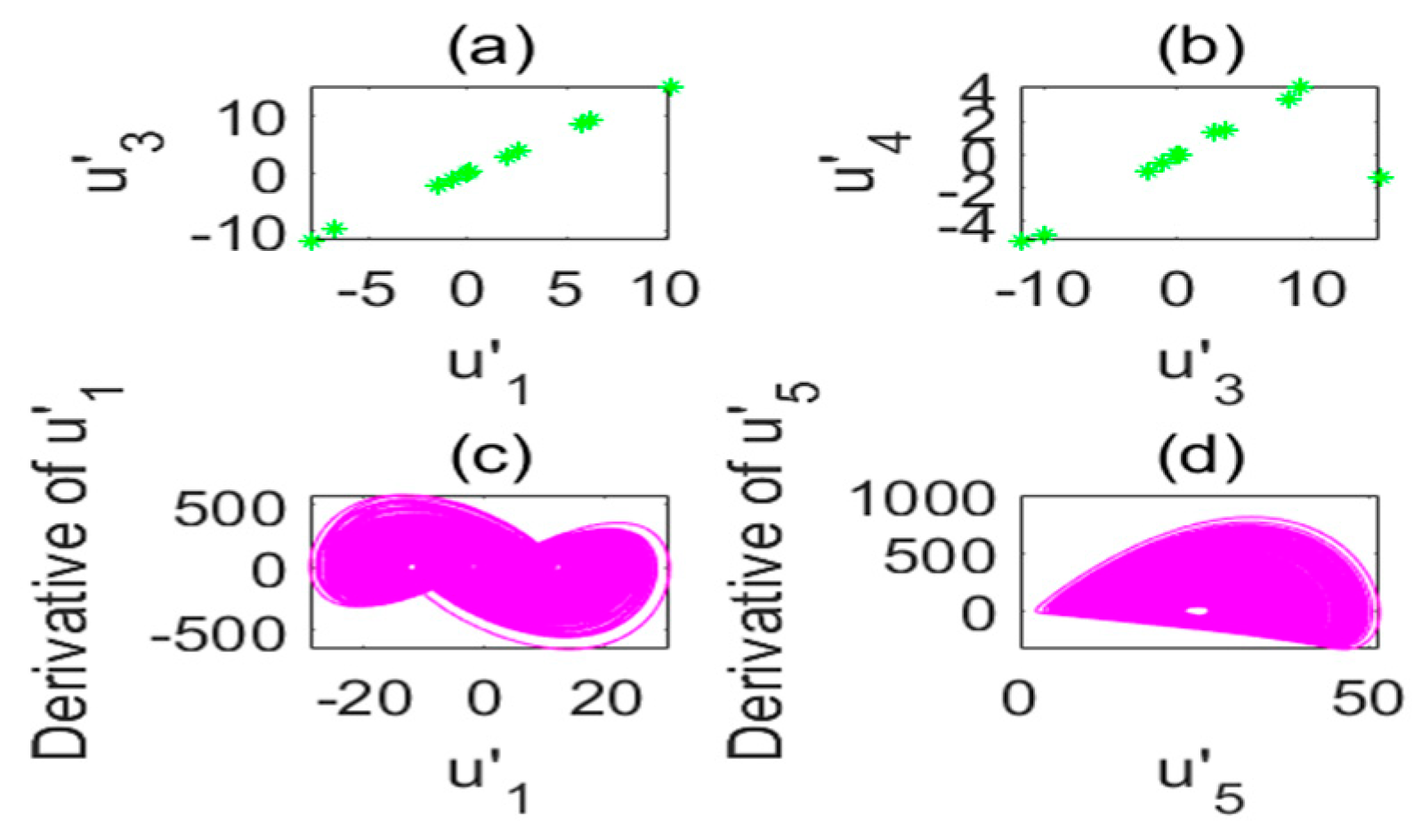
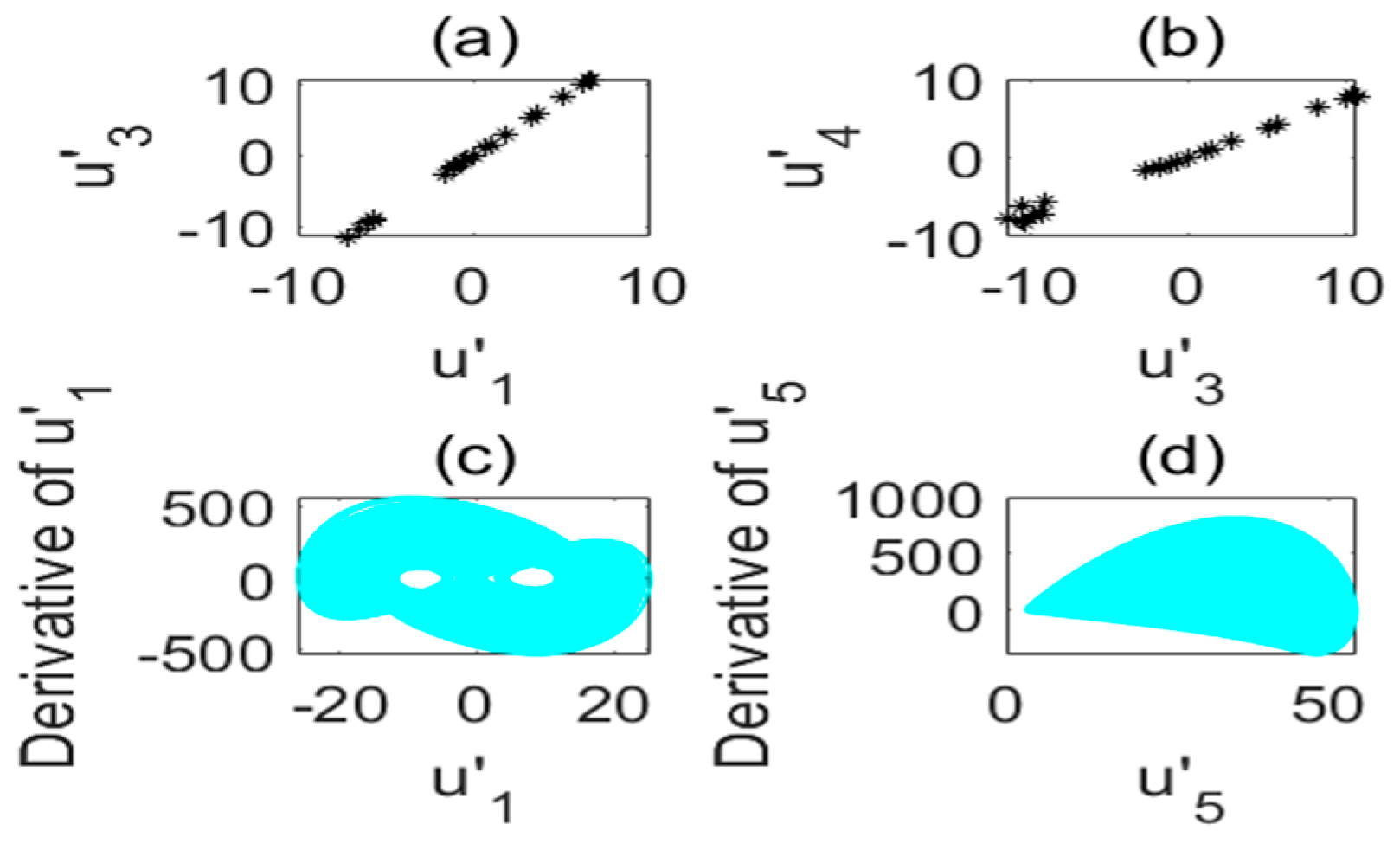
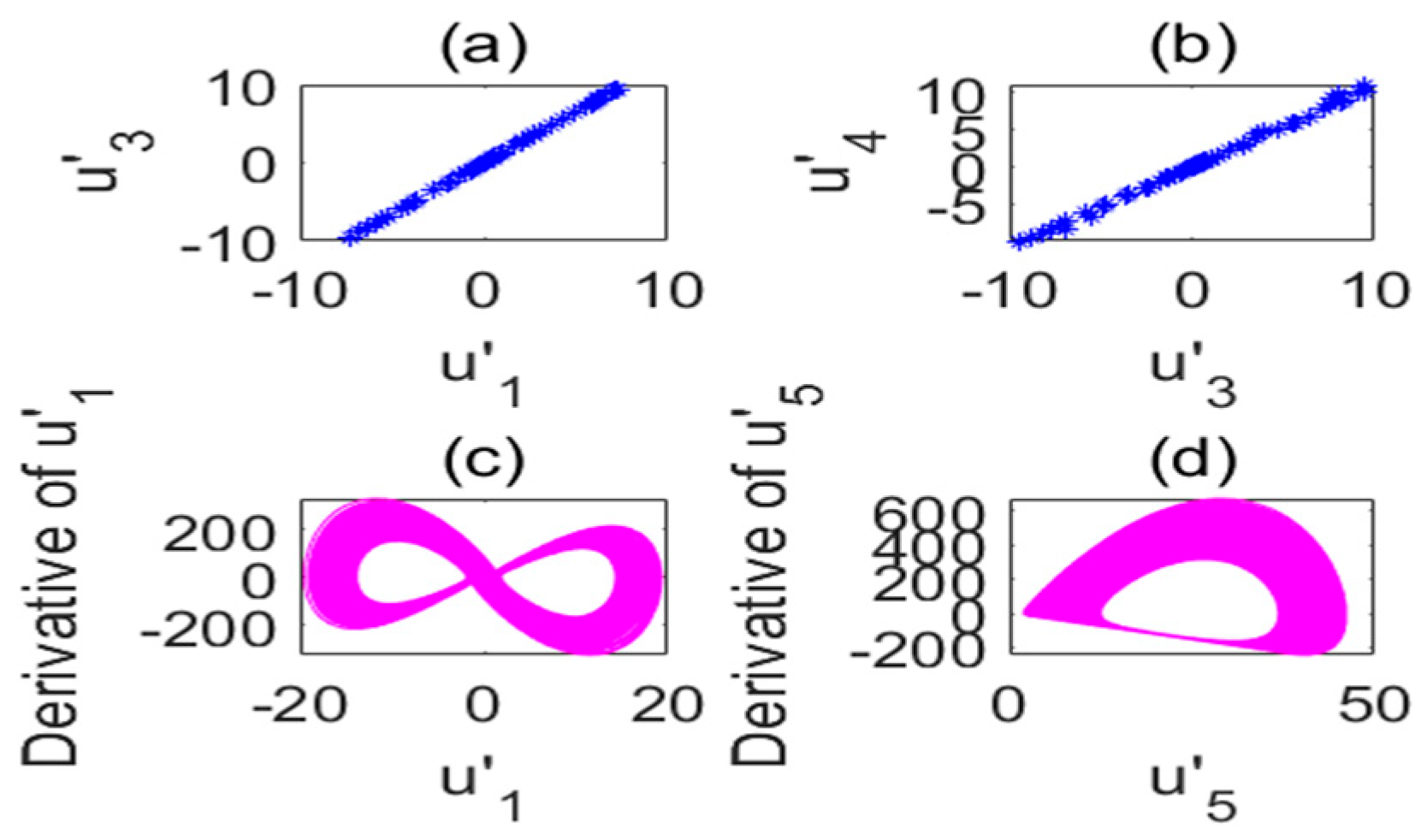
2.2. Sensitivity of Initial Values and Symmetry
2.3. Chaotic Characteristics under Different Time-Delay Factors
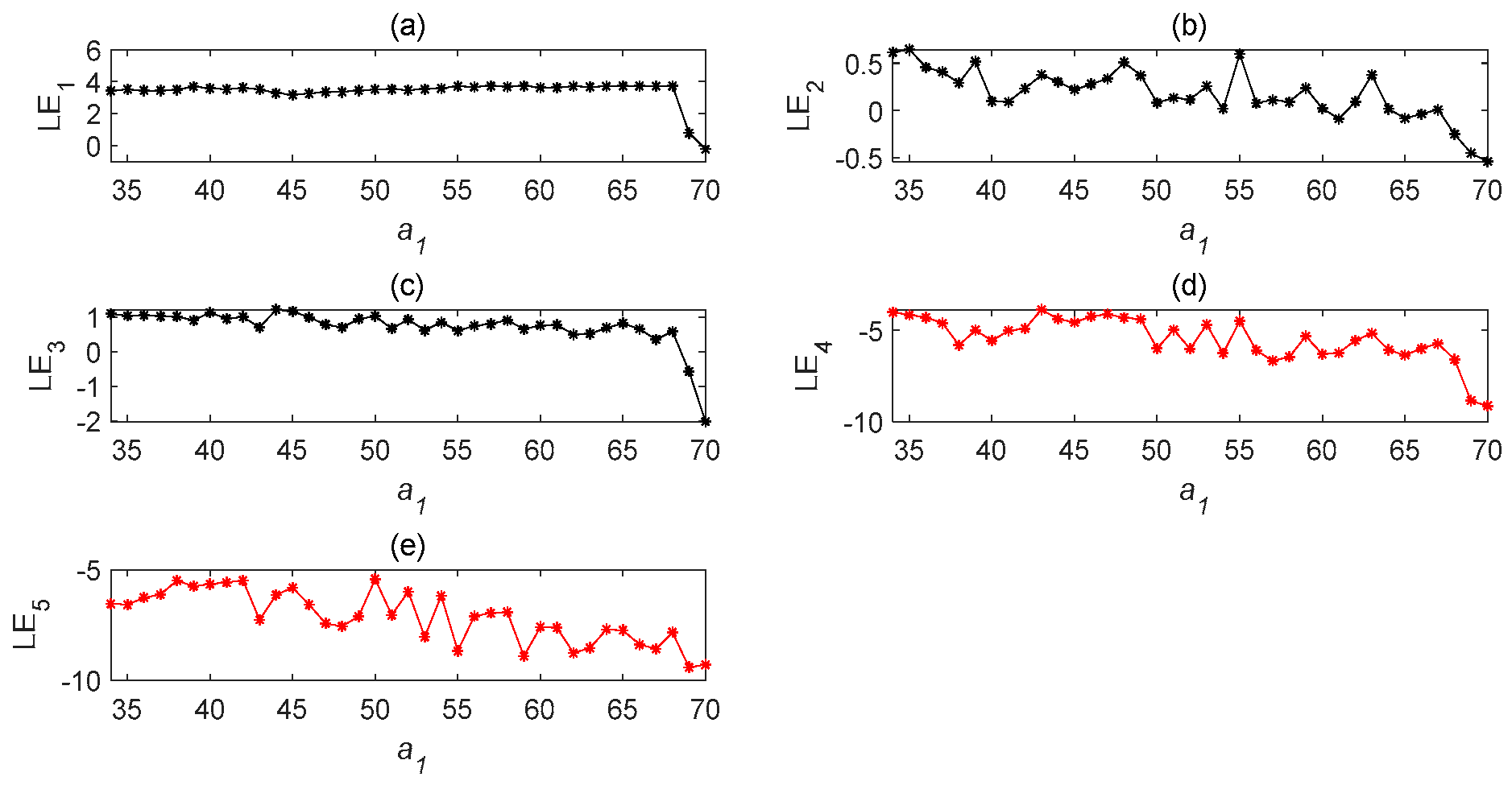
2.4. Chaotic Characteristics of Time-Delay Complex Lü Systems with Different Parameters
3. STDS of a Complex Lü System
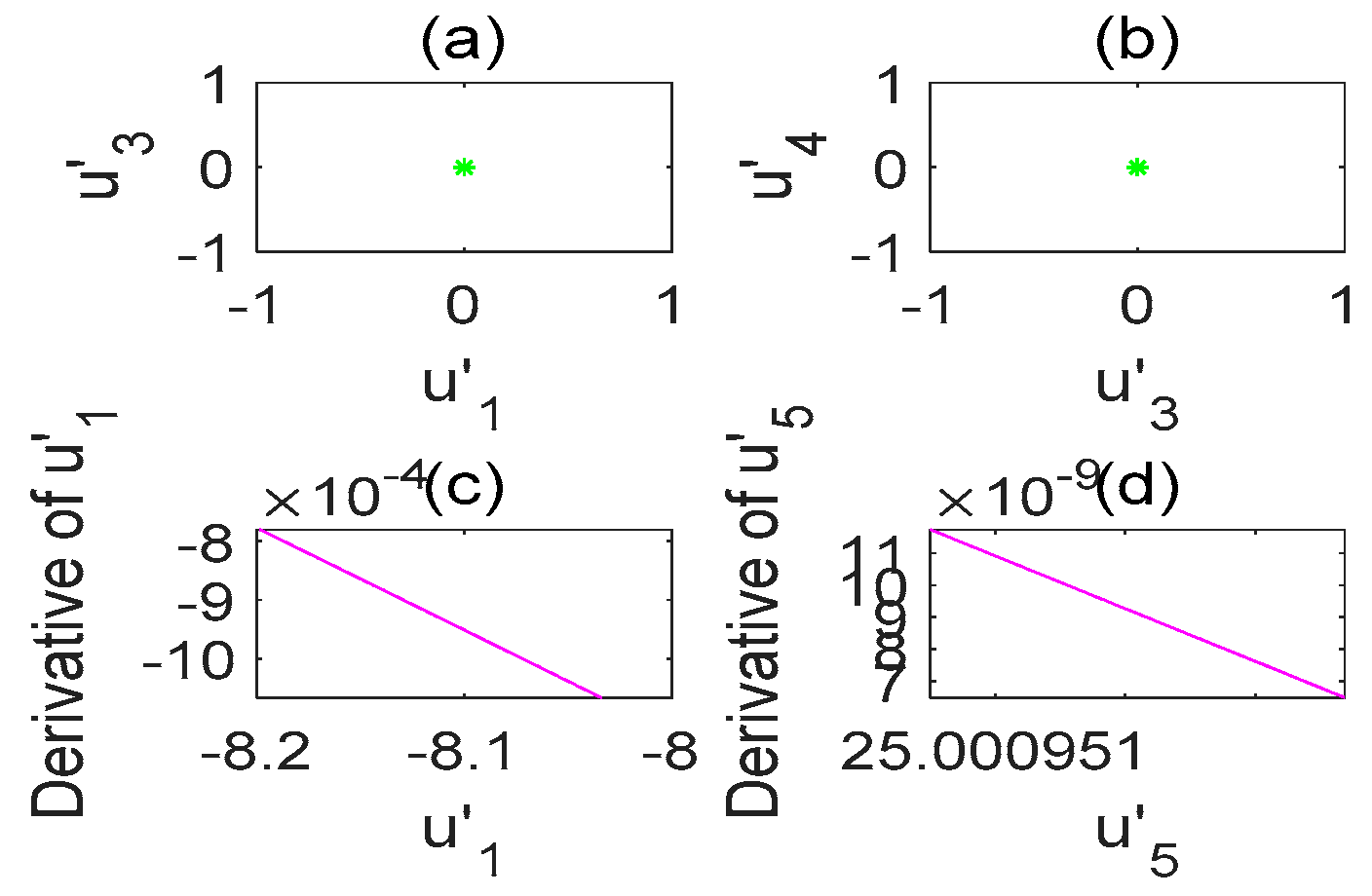
3.1. Definition of Self-Delay Synchronization
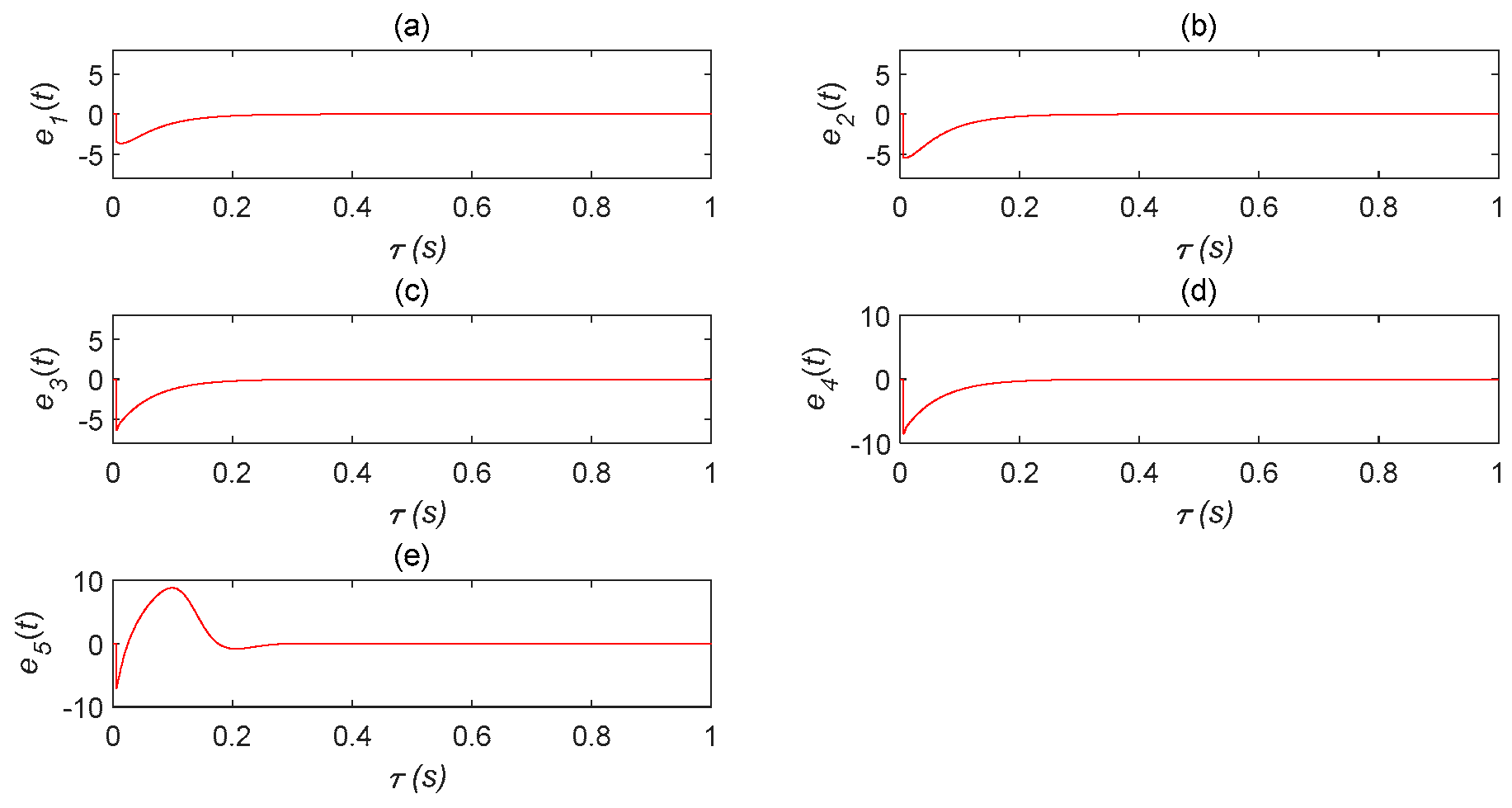
3.2. Design of the STDS Controller
4. Speech Secure Communication
- Due to the time lag in the transmission process, the synchronization phenomenon between the transmitter and the receiver is closer to the real situation;
- The STDS controller based on Lyapunov’s stability design is relatively simple and has strong stability. Equipped with double time-delay, the complex Lü system is safer;
- Encryption is performed using linear equations of state variables, which is quite different from previous encryption methods.
5. Simulation Experiment
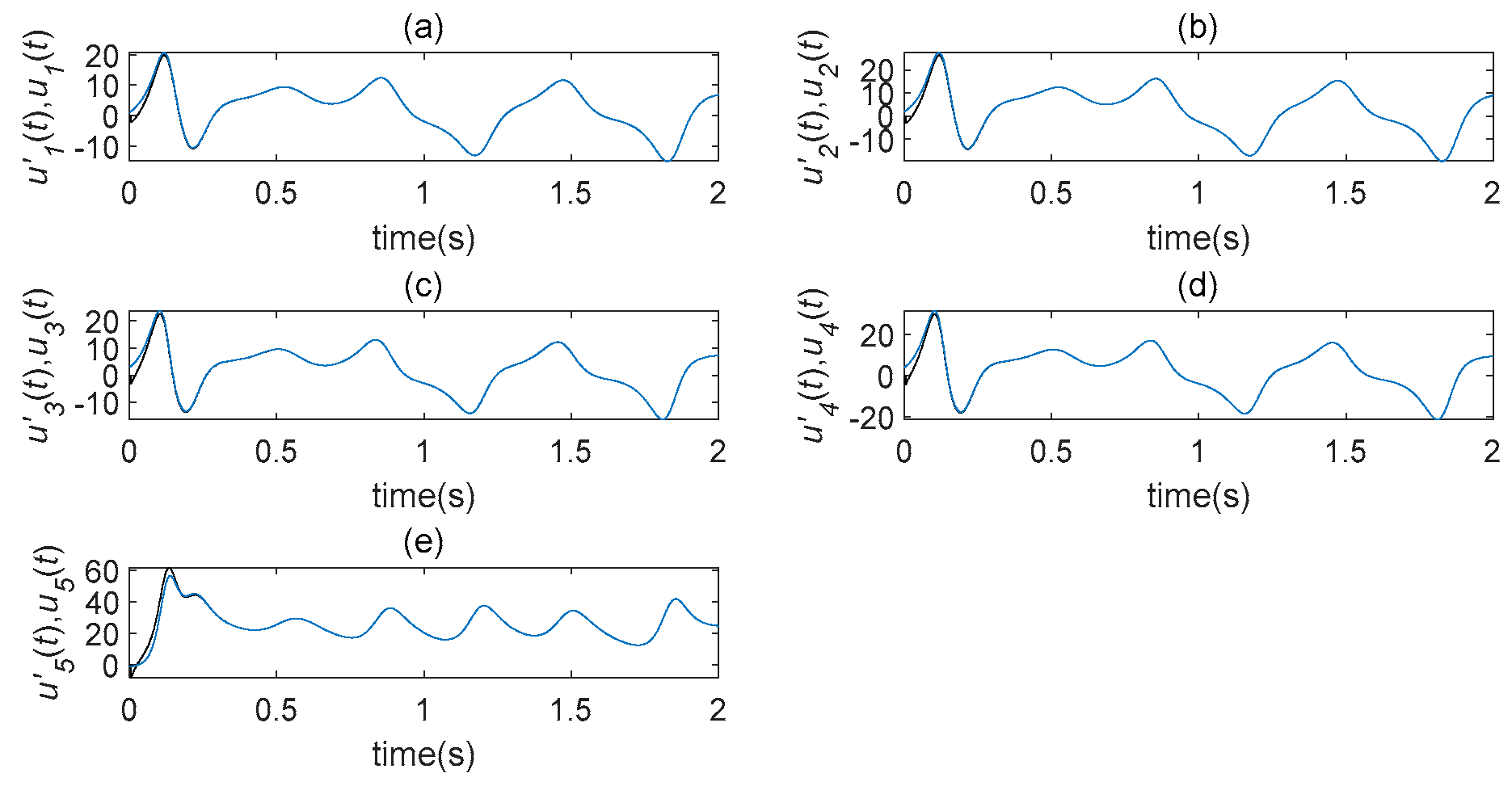
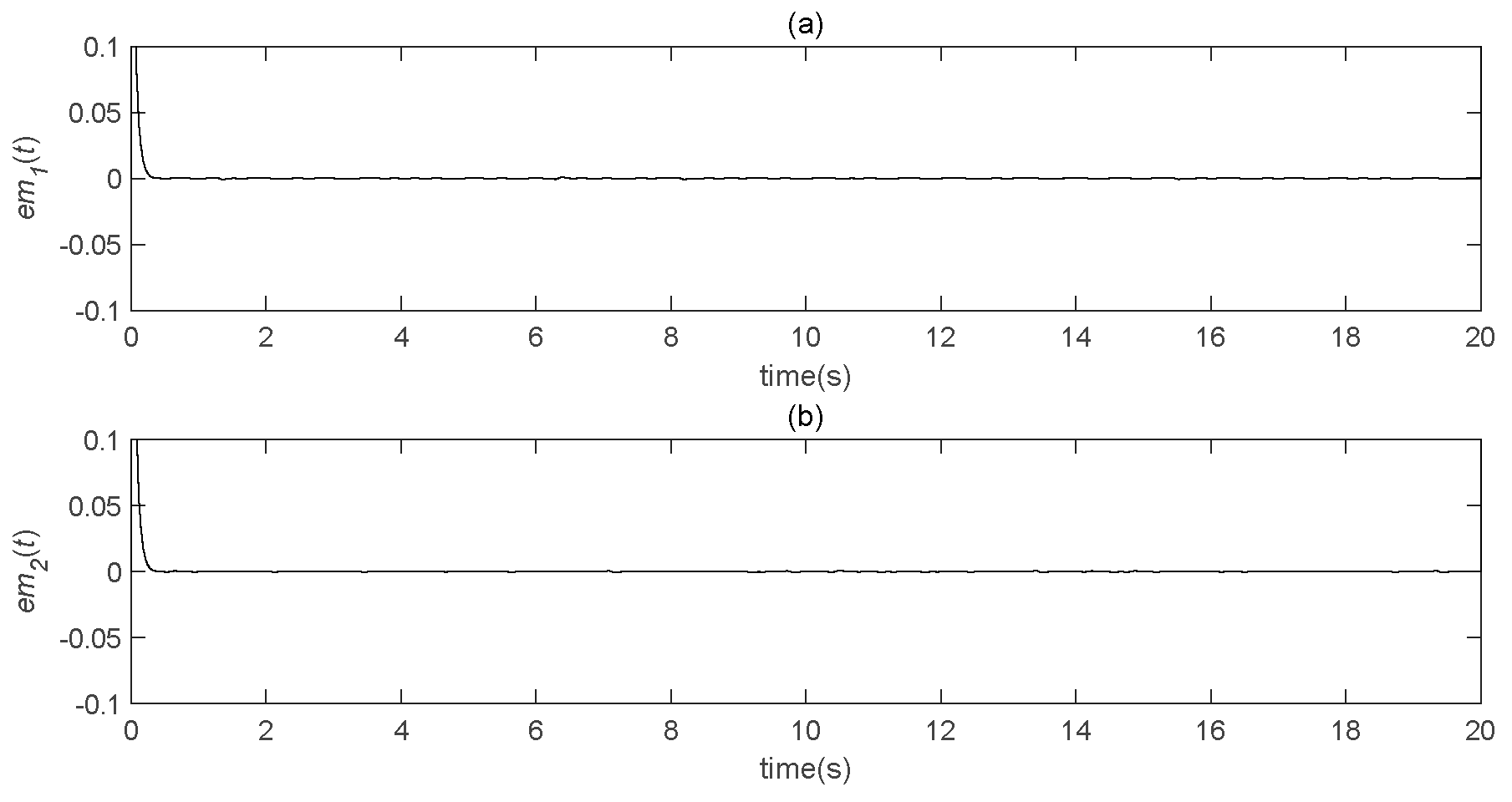
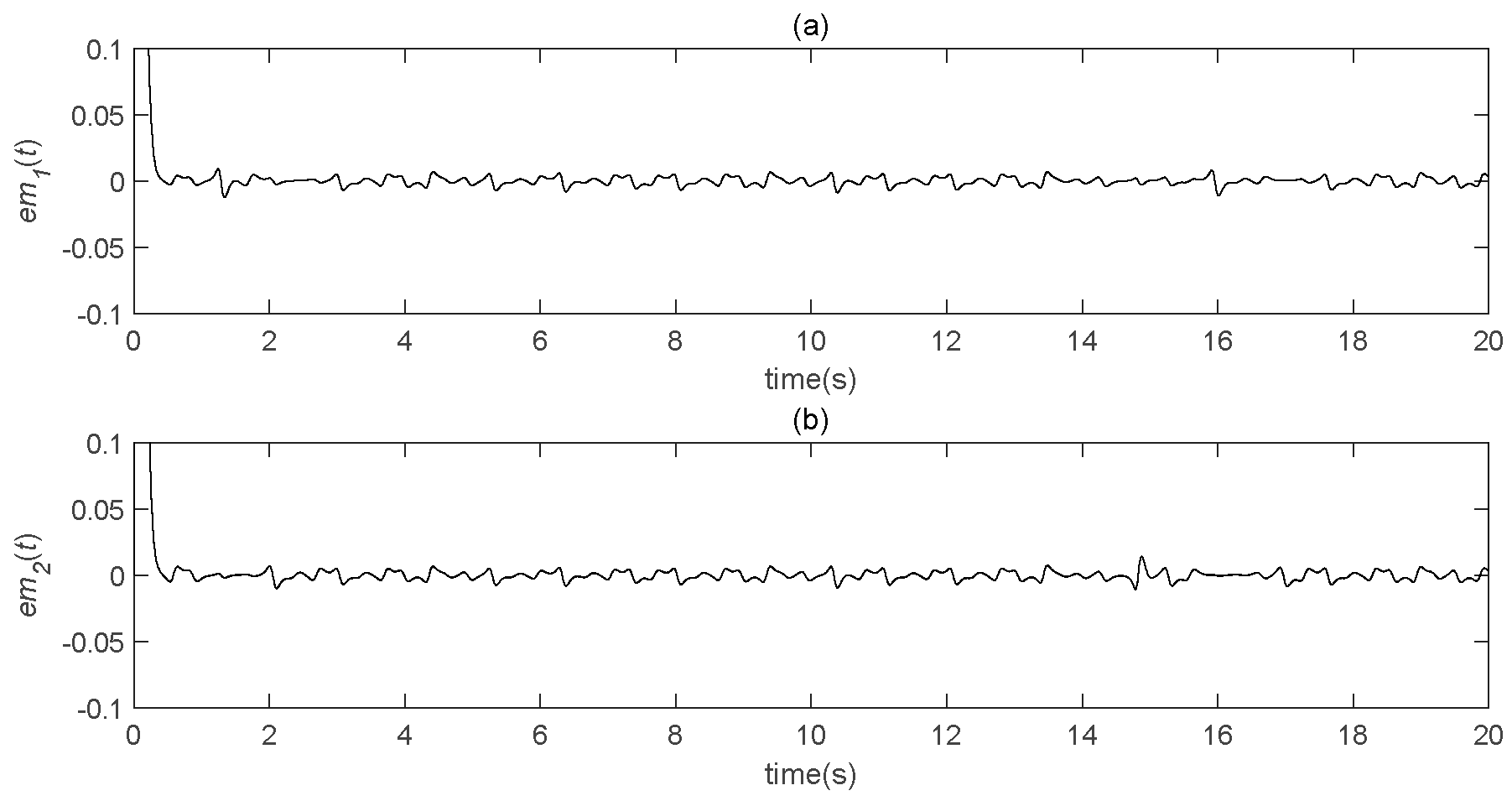
5.1. STDS Controller Simulation
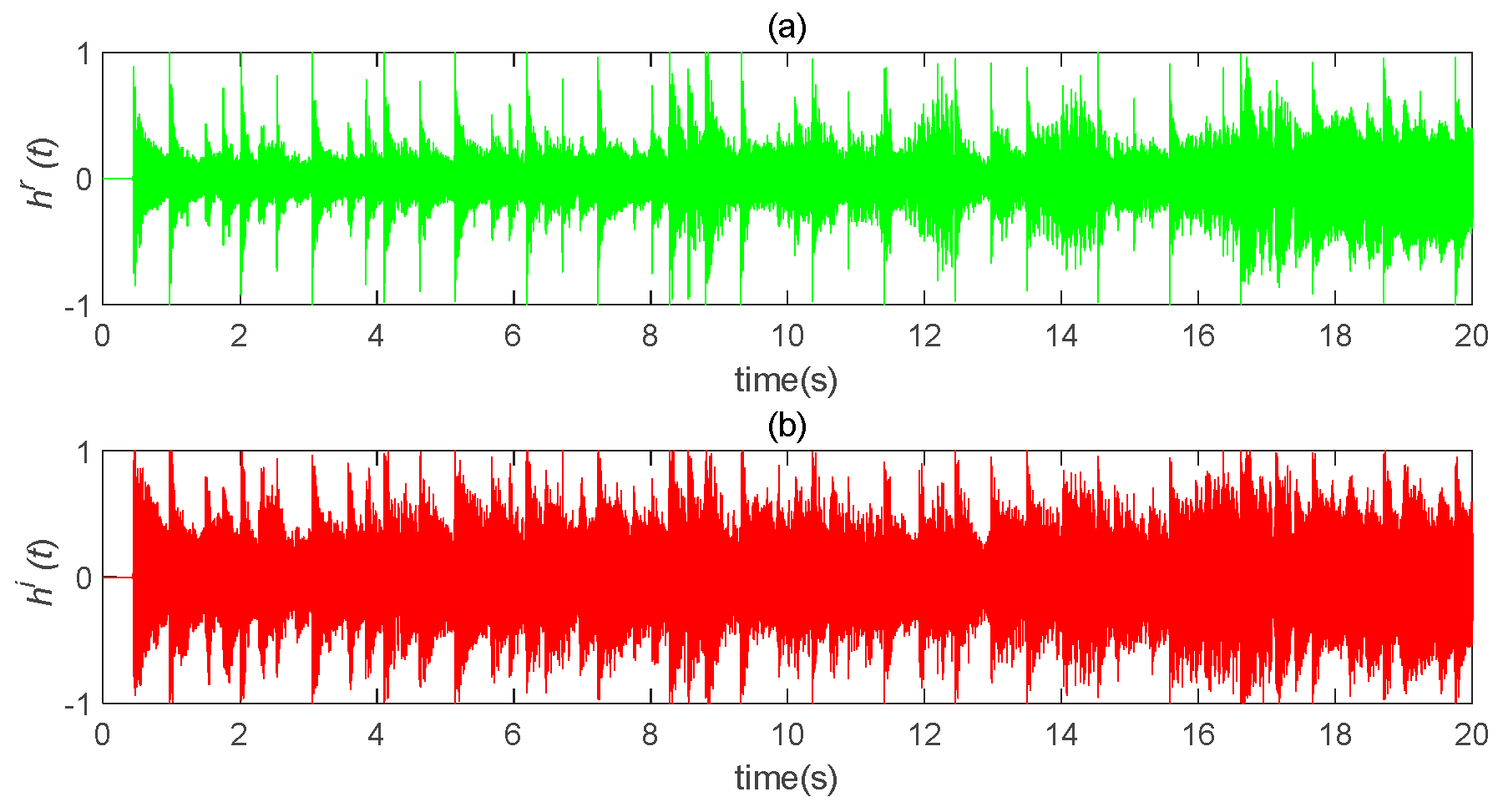
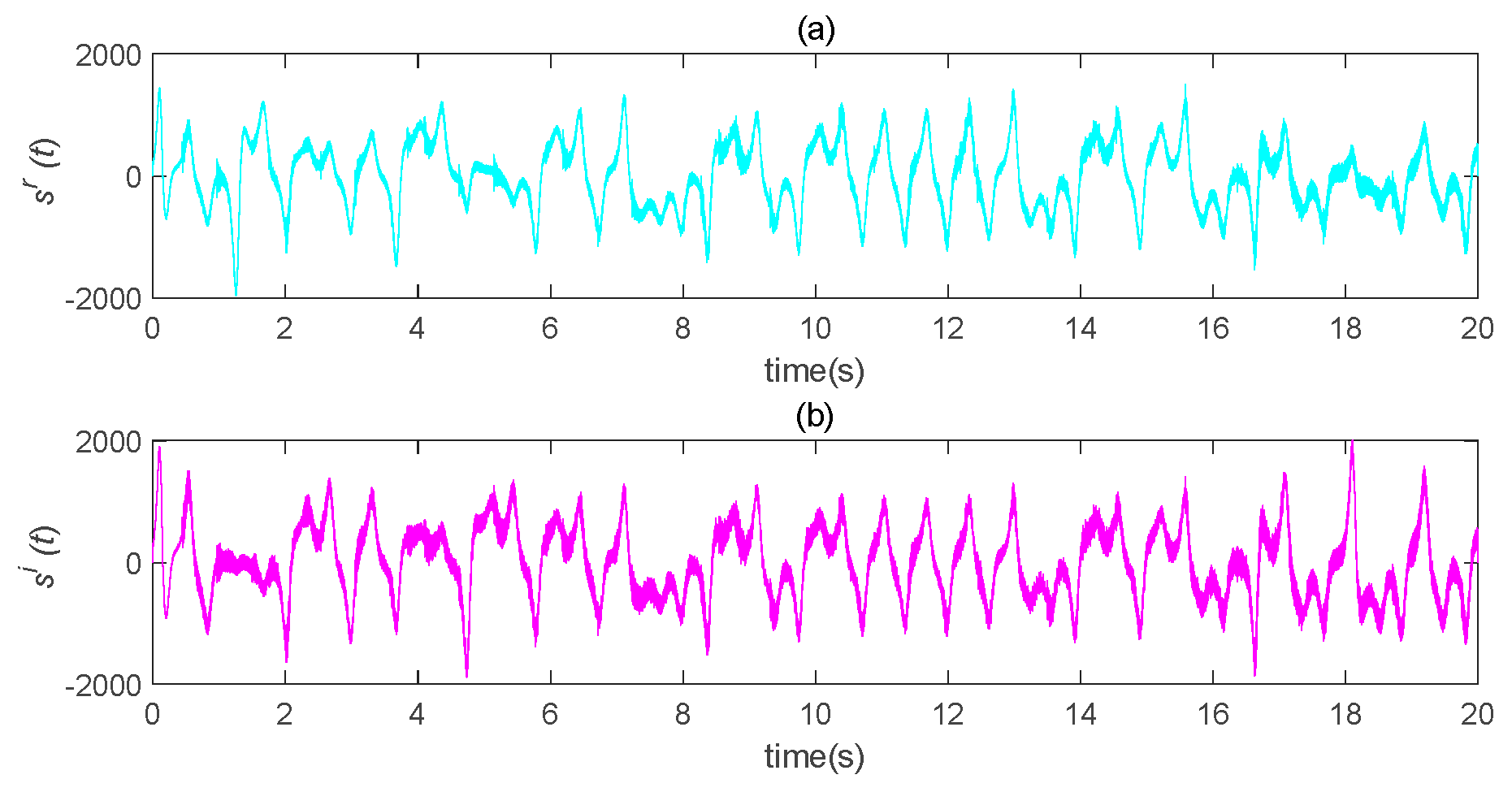
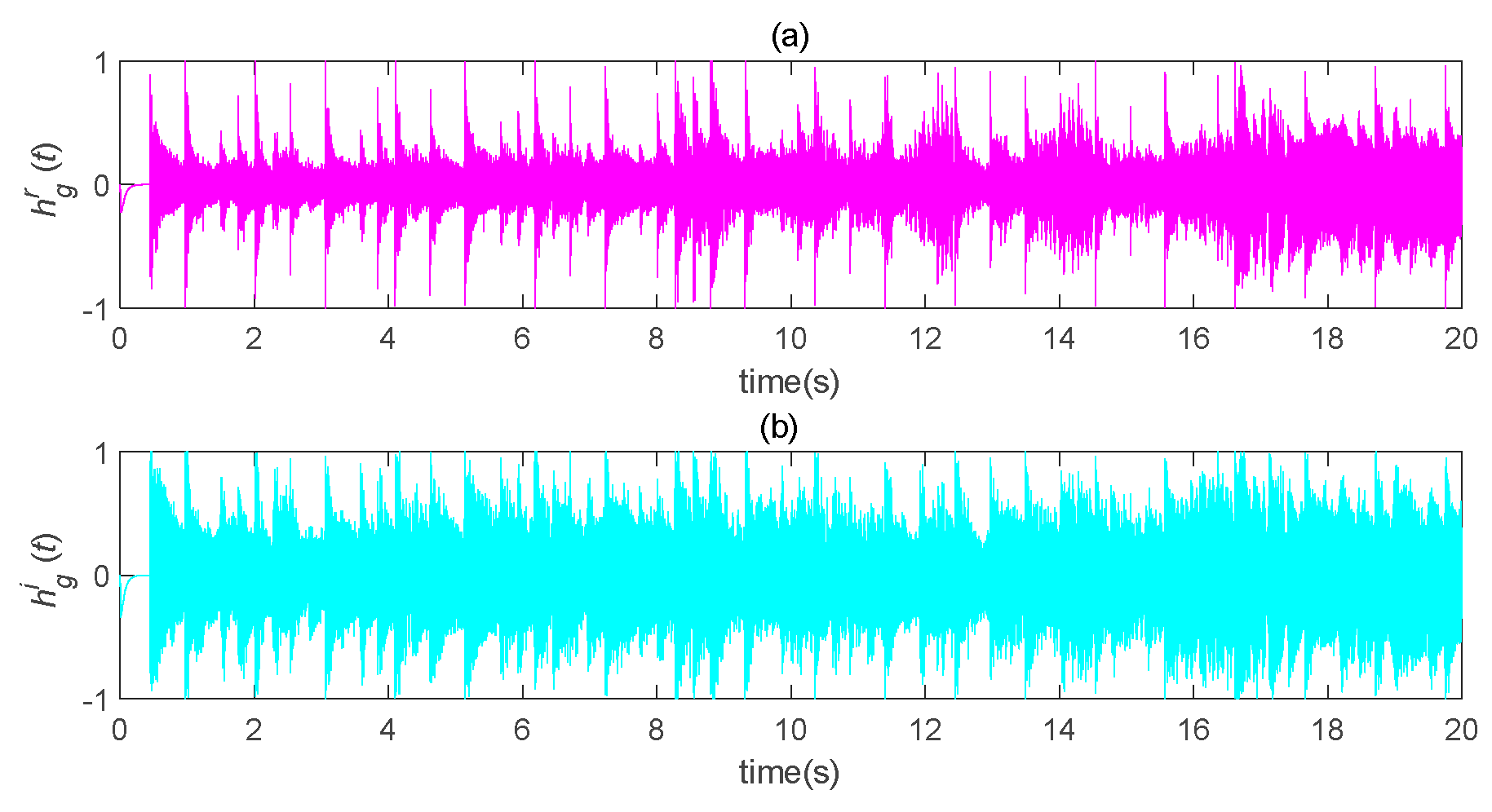
5.2. Speech Communication Simulation
5.3. Effect of the Parameter b
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Naderi, B.; Kheiri, H.; Heydari, A.; Mahini, R. Optimal Synchronization of Complex Chaotic T-Systems and Its Application in Secure Communication. J. Control Autom. Electr. Syst. 2016, 27, 379–390. [Google Scholar] [CrossRef]
- Rajagopal, K.; Kingni, S.T.; Khalaf, A.J.M.; Shekofteh, Y.; Nazarimehr, F. Coexistence of attractors in a simple chaotic oscillator with fractional-order-memristor component: Analysis, FPGA implementation, chaos control and synchronization. Eur. Phys. J. Spéc. Top. 2019, 228, 2035–2051. [Google Scholar] [CrossRef]
- Tolba, M.F.; Saleh, H.; Mohammad, B.; Al-Qutayri, M.; Elwakil, A.S.; Radwan, A.G. Enhanced FPGA realization of the fractional-order derivative and application to a variable-order chaotic system. Nonlinear Dyn. 2020, 99, 3143–3154. [Google Scholar] [CrossRef]
- Liu, H.; Yingqian, Z.; Kadir, A.; Xu, Y. Image encryption using complex hyper chaotic system by injecting impulse into parameters. Appl. Math. Comput. 2019, 360, 83–93. [Google Scholar] [CrossRef]
- Ge, B.; Luo, H. Image Encryption Application of Chaotic Sequences Incorporating Quantum Keys. Int. J. Autom. Comput. 2020, 17, 123–138. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Zhang, F.; Leng, S. Hidden Chaotic Attractors and Synchronization for a New Fractional-Order Chaotic System. J. Comput. Nonlinear Dyn. 2019, 14, 081010. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Zhang, F.; Yin, Y.; Ma, F. Special Characteristics and Synchronizations of Multi Hybrid-Order Chaotic Systems. Entropy 2020, 22, 664. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Alyami, M.A. Specialized study to perform complex phase synchronization of two chaotic complex systems including a similar structure of direct terms with modifying in nonlinear terms. Math. Methods Appl. Sci. 2019, 43, 1516–1529. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, S. Adaptive Complex Function Projective Synchronization of Uncertain Complex Chaotic Systems. J. Comput. Nonlinear Dynam. 2016, 11, 011013. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, J.; Wang, Z.; Jiang, C. N-Systems Function Projective Combination Synchronization—A Review of Real and Complex Continuous Time Chaos Synchronization. IEEE Access 2019, 7, 179320–179338. [Google Scholar] [CrossRef]
- Shi, J.; Zeng, Z. Global exponential stabilization and lag synchronization control of inertial neural networks with time delays. Neural Netw. 2020, 126, 11–20. [Google Scholar] [CrossRef]
- Wang, H.; Shen, X.H.; Zhang, X.L. Synchronization and Digital Circuit Implementation of Time-Delay Chaotic Systems based on Linear Controller. Dyn. Control 2012, 10, 142–146. [Google Scholar]
- Abd, M.H.; Tahir, F.R.; Al-Suhail, G.A.; Pham, V.-T. An adaptive observer synchronization using chaotic time-delay system for secure communication. Nonlinear Dyn. 2017, 90, 2583–2598. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Sun, J. Global synchronization criteria with channel time-delay for chaotic time-delay system. Chaos Solitons Fractals 2004, 21, 967–975. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, J. Adaptive synchronization between two different noise-perturbed chaotic systems with fully unknown parameters. Phys. A Stat. Mech. Its Appl. 2007, 376, 253–265. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, S.; Yu, W. Characteristics of Time-Delay Complex Lorenz Chaotic Systems and their Self-time-delay Synchronization. Acta Phys. Sin. 2013, 62, 64–72. [Google Scholar]
- Yu, J.; Wu, W.; Wang, C.; Luo, R.; Wen, H. A Stability Control Method of Fractional Complex Lorenz System with Time-Delay. In Proceedings of the 2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2015; pp. 464–467. [Google Scholar]
- Sun, B.; Li, M.; Zhang, F.; Wang, H.; Liu, J. The characteristics and self-time-delay synchronization of two-time-delay complex Lorenz system. J. Frankl. Inst. 2019, 356, 334–350. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E.; Arafa, A.A. On modified time delay hyperchaotic complex Lü system. Nonlinear Dyn. 2015, 80, 855–869. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Arafa, A.A.; Mahmoud, E.E. Bifurcations and chaos of time delay Lorenz system with dimension 2n+1. Eur. Phys. J. Plus 2017, 132, 461. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Mahmoud, E.E.; Arafa, A.A. Synchronization of time delay systems with non-diagonal complex scaling functions. Chaos Solitons Fractals 2018, 111, 86–95. [Google Scholar] [CrossRef]
- Farsana, F.J.; Gopakumar, K. Speech encryption based on four-dimensional hyperchaotic system. In Proceedings of the 2016 International Conference on Data Mining and Advanced Computing (SAPIENCE), Ernakulam, India, 16–18 March 2016; pp. 279–283. [Google Scholar]
- Sathiyamurthi, P.; Ramakrishnan, S. Speech encryption using chaotic shift keying for secured speech communication. EURASIP J. Audio Speech Music Process. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Sheu, L.J. A speech encryption using fractional chaotic systems. Nonlinear Dyn. 2011, 65, 103–108. [Google Scholar] [CrossRef]
- Mosa, E.; Messiha, N.W.; Zahran, O. Chaotic encryption of speech signals in transform domains. In Proceedings of the 2009 International Conference on Computer Engineering & Systems, Cairo, Egypt, 14–16 December 2009; pp. 300–305. [Google Scholar]
- Zhao, X.; Liu, J.; Liu, H.; Zhang, F.-F. Dynamic Analysis of a One-Parameter Chaotic System in Complex Field. IEEE Access 2020, 8, 28774–28781. [Google Scholar] [CrossRef]
- Huang, Y.; Yin, L.; Ding, W. Based-Parameter Adaptive Synchronization of Time-Delay Chaotic Systems. Comput. Vis. 2012, 7332, 431–439. [Google Scholar]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure Communication of Fractional Complex Chaotic Systems Based on Fractional Difference Function Synchronization. Complexity 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Zhang, F.-F.; Sun, K.; Chen, Y.; Zhang, H.; Jiang, C. Parameters identification and adaptive tracking control of uncertain complex-variable chaotic systems with complex parameters. Nonlinear Dyn. 2019, 95, 3161–3176. [Google Scholar] [CrossRef]
- Leng, S.; Liu, J.; Zhang, F.; Li, Z. The Characteristics of Complex Chen CHAOTIC Systems with Time-delay and It’s Self-delay Synchronization Control. In Proceedings of the 2019 International Conference on Big Data, Electronics and Communication Engineering (BDECE 2019), Beijing, China, 24–25 November 2019; pp. 51–54. [Google Scholar]
- Zhang, F.-F.; Liu, S. Self-time-delay synchronization of time-delay coupled complex chaotic system and its applications to communication. Int. J. Mod. Phys. C 2014, 25, 1350102. [Google Scholar] [CrossRef]
- Zhang, F. Lag Synchronization of Complex Lorenz System with Applications to Communication. Entropy 2015, 17, 4974–4985. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Zhu, Q. Asynchronous anti-noise hyper chaotic secure communication system based on dynamic delay and state variables switching. Phys. Lett. A 2011, 375, 2828–2835. [Google Scholar] [CrossRef]
- Azzaz, M.S.; Tanougast, C.; Sadoudi, S.; Bouridane, A. Synchronized hybrid chaotic generators: Application to real-time wireless speech encryption. Commun. Nonlinear Sci. 2013, 18, 2035–2047. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; An, X.; Luo, H.; Yao, K.E. Adaptive coupled synchronization among three coupled chaos systems and its application to secure communications. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 821. [Google Scholar] [CrossRef]
- Nwachioma, C.; Perez-Cruz, J.H.; Jimenez, A.; Ezuma, M.; Rivera-Blas, R. A New Chaotic Oscillator—Properties, Analog Implementation, and Secure Communication Application. IEEE Access 2019, 7, 7510–7521. [Google Scholar] [CrossRef]
- Sathiyamurthi, P.; Ramakrishnan, S. Speech encryption algorithm using FFT and 3D-Lorenz–logistic chaotic map. Multimed. Tools Appl. 2020, 79, 17817–17835. [Google Scholar] [CrossRef]
- Elsafty, A.H.; Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. Enhanced hardware implementation of a mixed-order nonlinear chaotic system and speech encryption application. AEU Int. J. Electron. Commun. 2020, 125, 153347. [Google Scholar] [CrossRef]
- Li, R.-G.; Wu, H.-N. Secure communication on fractional-order chaotic systems via adaptive sliding mode control with teaching–learning–feedback-based optimization. Nonlinear Dyn. 2018, 95, 1221–1243. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Ma, C.; Wang, Z.; Zhang, F. Time-Delay Characteristics of Complex Lü System and Its Application in Speech Communication. Entropy 2020, 22, 1260. https://doi.org/10.3390/e22111260
Guo J, Ma C, Wang Z, Zhang F. Time-Delay Characteristics of Complex Lü System and Its Application in Speech Communication. Entropy. 2020; 22(11):1260. https://doi.org/10.3390/e22111260
Chicago/Turabian StyleGuo, Junmei, Chunrui Ma, Zuoxun Wang, and Fangfang Zhang. 2020. "Time-Delay Characteristics of Complex Lü System and Its Application in Speech Communication" Entropy 22, no. 11: 1260. https://doi.org/10.3390/e22111260
APA StyleGuo, J., Ma, C., Wang, Z., & Zhang, F. (2020). Time-Delay Characteristics of Complex Lü System and Its Application in Speech Communication. Entropy, 22(11), 1260. https://doi.org/10.3390/e22111260




