Phytoplankton Temporal Strategies Increase Entropy Production in a Marine Food Web Model
Abstract
1. Introduction
2. Model Description
2.1. Entropy Production
2.2. Metabolic Reactions
2.3. Reaction Kinetics
2.4. Model Domain and Simulation Details
2.5. Optimize Trait-Based Model
2.6. Temporal Strategies
2.7. Optimization and Computational Approach
3. Results
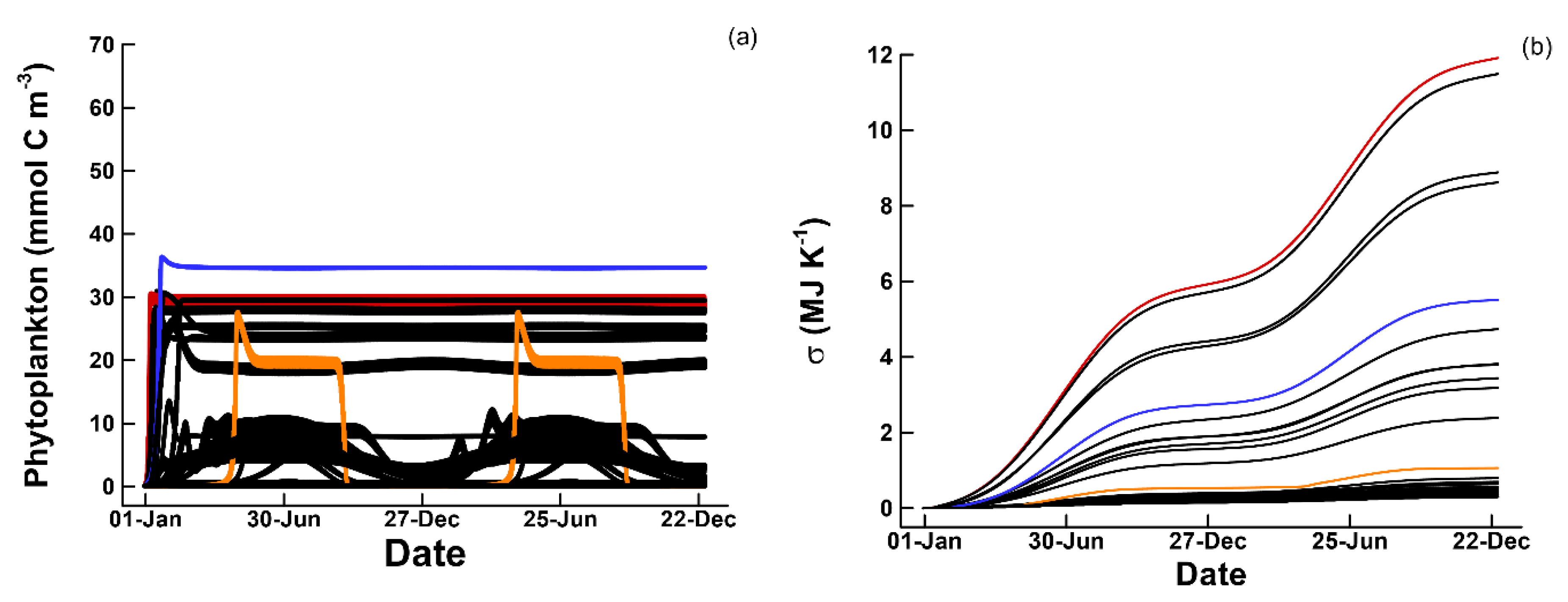
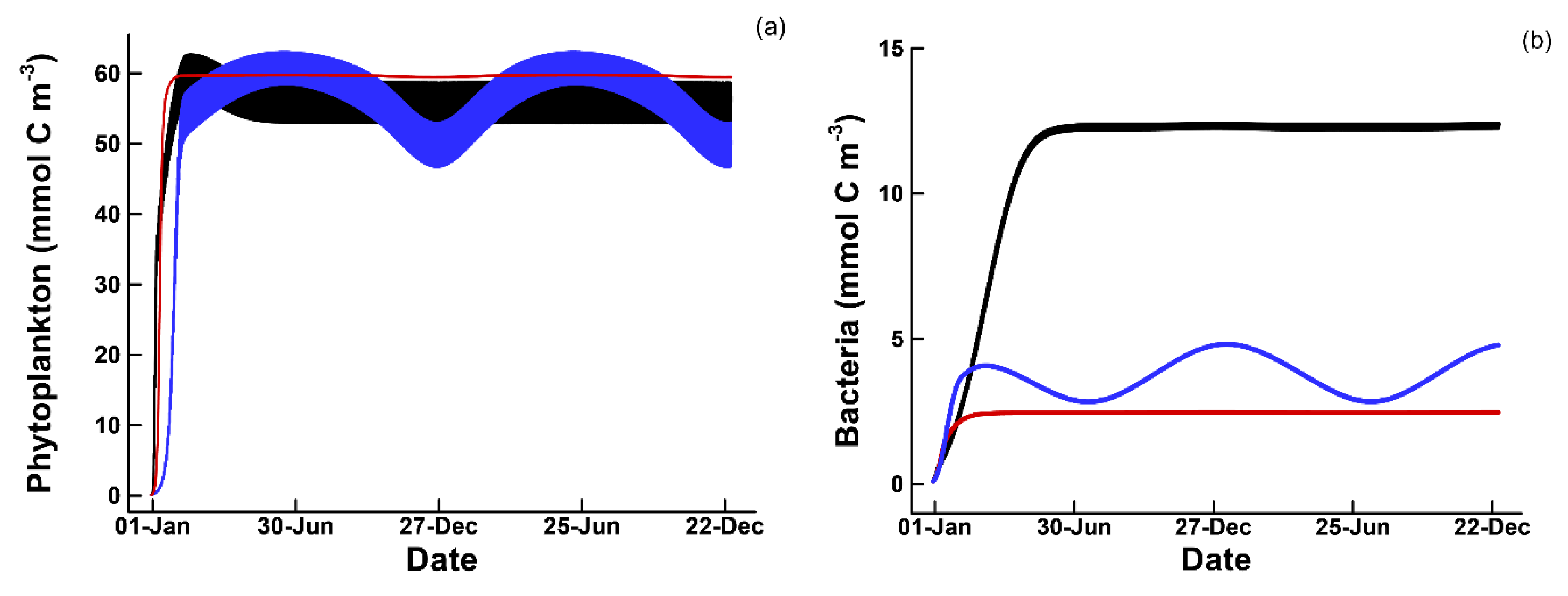
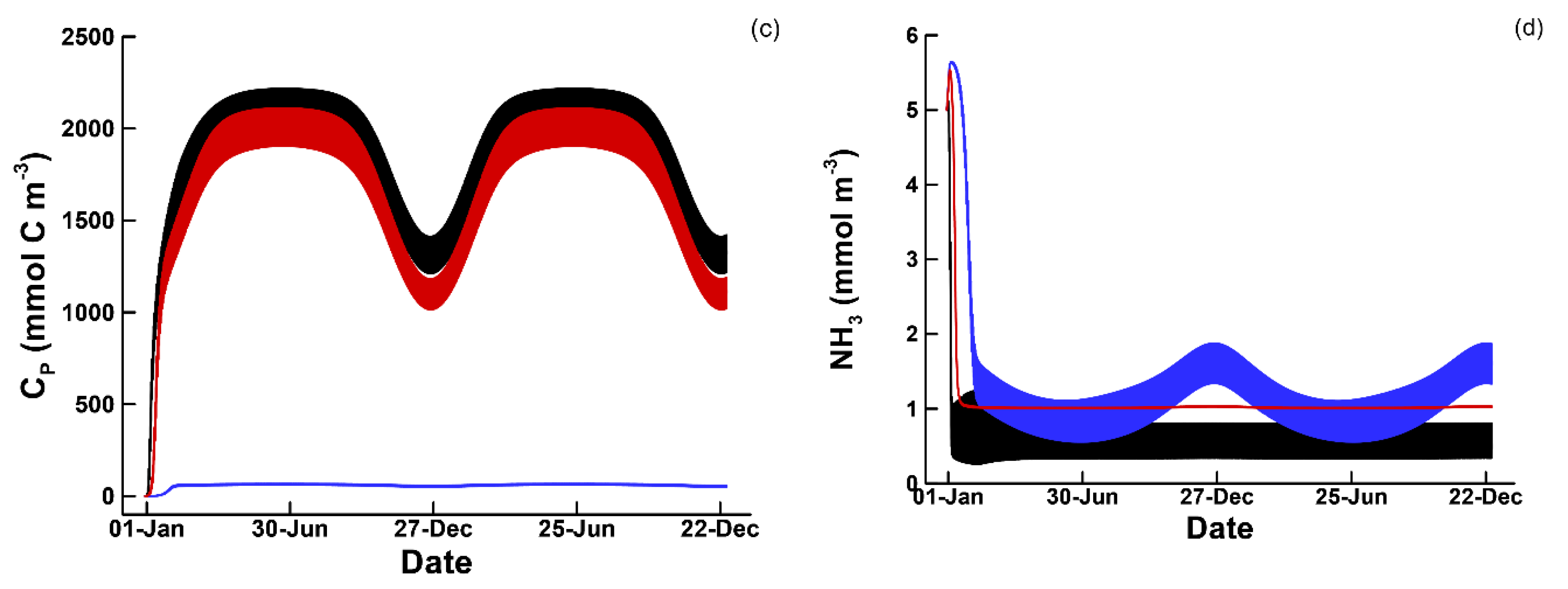
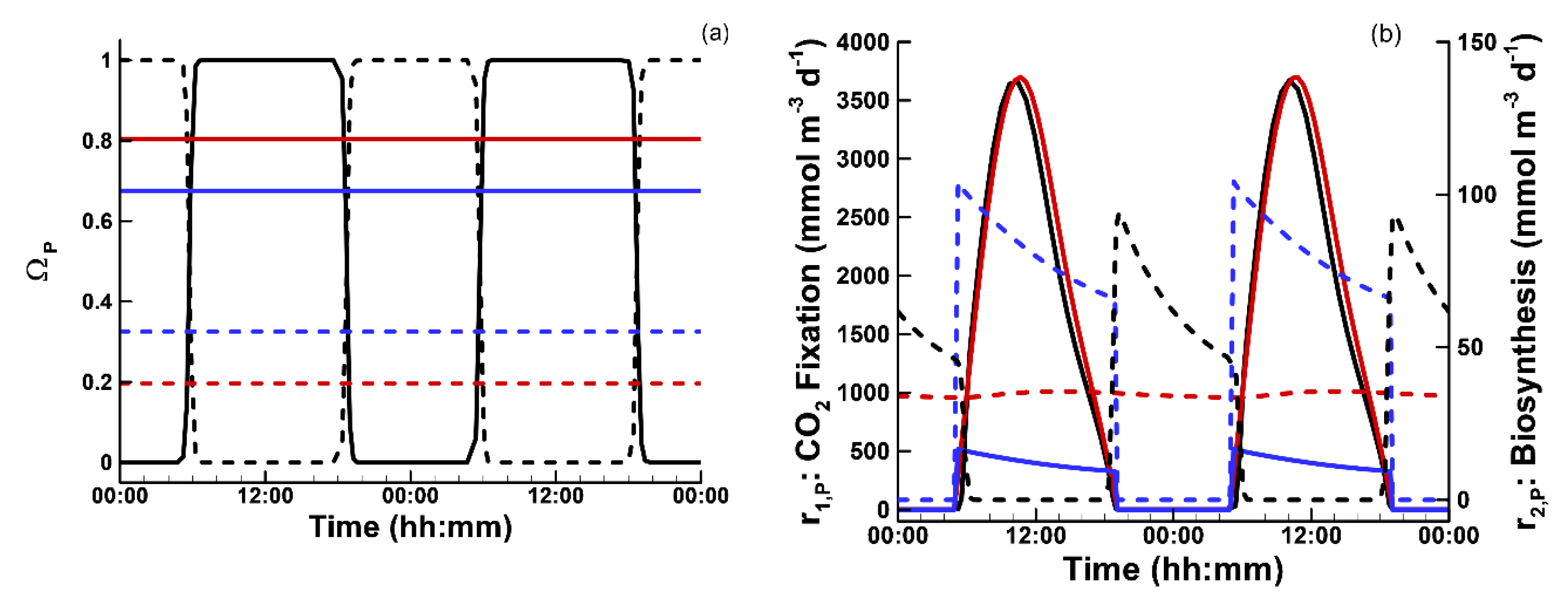
3.1. Phytoplankton Temporal Strategies and Entropy Production
3.2. Entropy Production and Food Web Complexity
3.3. Dissipation of Chemical versus Electromagnetic Free Energy
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36, 631–641. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A Math. Gen. 2005, 38, L371–L381. [Google Scholar] [CrossRef]
- Lorenz, R. Full Steam Ahead-Probably. Science 2003, 299, 837–838. [Google Scholar] [CrossRef] [PubMed]
- Paltridge, G.W. Global dynamics and climate-a system of minimum entropy exchange. Q. J. R. Met. Soc. 1975, 104, 927–945. [Google Scholar] [CrossRef]
- Vallino, J.J.; Algar, C.K. The Thermodynamics of Marine Biogeochemical Cycles: Lotka Revisited. Annu. Rev. Mar. Sci. 2016, 8, 333–356. [Google Scholar] [CrossRef]
- Ziegler, H. Chemical reactions and the principle of maximal rate of entropy production. Z. Angew. Math. Phys. 1983, 34, 832–844. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Kleidon, A.; Fraedrich, K.; Kunz, T.; Lunkeit, F. The atmospheric circulation and states of maximum entropy production. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Dewar, R.C.; Lineweaver, C.H.; Niven, R.K.; Regenauer-Lieb, K. (Eds.) Beyond the Second Law: Entropy Production and Non-Equilibrium Systems; Springer: Berlin, Germany, 2014. [Google Scholar] [CrossRef]
- Kleidon, A.; Lorenz, R.D. (Eds.) Non-Equilibrium Thermodynamics and the Production of Entropy; Springer: Berlin, Germany, 2005; p. 279. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production: Application to crystal growth and chemical kinetics. Curr. Opin. Chem. Eng. 2015, 7, 23–31. [Google Scholar] [CrossRef]
- Jia, C.; Jing, C.; Liu, J. The Character of Entropy Production in Rayleigh–Bénard Convection. Entropy 2014, 16, 4960–4973. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Konovalov, M.S. Thermodynamic model of nonequilibrium phase transitions. Phys. Rev. 2011, 84, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kleidon, A.; Renner, M. Thermodynamic limits of hydrologic cycling within the Earth system: Concepts, estimates and implications. Hydrol. Earth Syst. Sci. 2013, 17, 2873–2892. [Google Scholar] [CrossRef]
- Shimokawa, S.; Ozawa, H. On the thermodynamics of the ocean general circulation: Irrerversible transition to a state with higher rate of entropy production. Q. J. R. Met. Soc. 2002, 128, 2115–2128. [Google Scholar] [CrossRef]
- Skene, K.R. Thermodynamics, ecology and evolutionary biology: A bridge over troubled water or common ground? Acta Oecologica 2017, 85, 116–125. [Google Scholar] [CrossRef]
- Vallino, J.J.; Huber, J.A. Using Maximum Entropy Production to Describe Microbial Biogeochemistry over Time and Space in a Meromictic Pond. Front. Environ. Sci. 2018, 6, 100. [Google Scholar] [CrossRef]
- Annila, A.; Salthe, S. Physical foundations of evolutionary theory. J. Non Equilib. Thermodyn. 2010, 35, 301–321. [Google Scholar] [CrossRef]
- Beretta, G.P. The fourth law of thermodynamics: Steepest entropy ascent. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 1–17. [Google Scholar] [CrossRef]
- Paillard, D.; Herbert, C. Maximum Entropy Production and Time Varying Problems: The Seasonal Cycle in a Conceptual Climate Model. Entropy 2013, 15, 2846–2860. [Google Scholar] [CrossRef]
- Falkowski, P.G.; Fenchel, T.; DeLong, E.F. The Microbial Engines That Drive Earth’s Biogeochemical Cycles. Science 2008, 320, 1034–1039. [Google Scholar] [CrossRef]
- Sogin, M.L.; Morrison, H.G.; Huber, J.A.; Welch, D.M.; Huse, S.M.; Neal, P.R.; Arrieta, J.M.; Herndl, G.J. Microbial diversity in the deep sea and the underexplored “rare biosphere”. Proc. Natl. Acad. Sci. USA 2006, 103, 12115–12120. [Google Scholar] [CrossRef]
- Dewar, R. Maximum Entropy Production as an Inference Algorithm that Translates Physical Assumptions into Macroscopic Predictions: Don’t Shoot the Messenger. Entropy 2009, 11, 931–944. [Google Scholar] [CrossRef]
- Vallino, J.J. Modeling Microbial Consortiums as Distributed Metabolic Networks. Biol. Bull. 2003, 204, 174–179. [Google Scholar] [CrossRef][Green Version]
- Vallino, J.J. Ecosystem biogeochemistry considered as a distributed metabolic network ordered by maximum entropy production. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1417–1427. [Google Scholar] [CrossRef]
- Algar, C.K.; Vallino, J.J. Predicting microbial nitrate reduction pathways in coastal sediments. Aquat. Microb. Ecol. 2014, 71, 223–238. [Google Scholar] [CrossRef]
- Vallino, J.J.; Algar, C.K.; González, N.F.; Huber, J.A. Use of Receding Horizon Optimal Control to Solve MaxEP-Based Biogeochemistry Problems. In Beyond the Second Law—Entropy Production and Non-Equilibrium Systems; Dewar, R.C., Lineweaver, C.H., Niven, R.K., Regenauer-Lieb, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 337–359. [Google Scholar] [CrossRef]
- Sivak, D.A.; Thomson, M. Environmental Statistics and Optimal Regulation. PLoS Comput. Biol. 2014, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Vallino, J.J. Differences and implications in biogeochemistry from maximizing entropy production locally versus globally. Earth Syst. Dynam. 2011, 2, 69–85. [Google Scholar] [CrossRef]
- Kolody, B.C.; McCrow, J.P.; Allen, L.Z.; Aylward, F.O.; Fontanez, K.M.; Moustafa, A.; Moniruzzaman, M.; Chavez, F.P.; Scholin, C.A.; Allen, E.E.; et al. Diel transcriptional response of a California Current plankton microbiome to light, low iron, and enduring viral infection. ISME J. 2019, 13, 2817–2833. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.H.; Zhao, C.; Xu, Y.; Mori, T. Timing the day: What makes bacterial clocks tick? Nat. Rev. Micro 2017, 15, 232–242. [Google Scholar] [CrossRef]
- Grover, J.P. Resource Storage and Competition with Spatial and Temporal Variation in Resource Availability. Am. Nat. 2011, 178, E124–E148. [Google Scholar] [CrossRef]
- Schulz, H.N.; Brinkhoff, T.; Ferdelman, T.G.; Mariné, M.H.; Teske, A.; Jørgensen, B.B. Dense populations of a giant sulfur bacterium in Namibian shelf sediments. Science 1999, 284, 493–495. [Google Scholar] [CrossRef]
- Katz, Y.; Springer, M. Probabilistic adaptation in changing microbial environments. PeerJ 2016, 4, 1–28. [Google Scholar] [CrossRef]
- Mitchell, A.; Romano, G.H.; Groisman, B.; Yona, A.; Dekel, E.; Kupiec, M.; Dahan, O.; Pilpel, Y. Adaptive prediction of environmental changes by microorganisms. Nature 2009, 460, 220–224. [Google Scholar] [CrossRef]
- Lewis, K. Persister Cells. Annu. Rev. Microbiol. 2010, 64, 357–372. [Google Scholar] [CrossRef]
- Lloyd, K.G. Time as a microbial resource. Environ. Microbiol. Rep. 2020. [Google Scholar] [CrossRef] [PubMed]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Morrison, P. A Thermodynamic Characterization of Self-Reproduction. Rev. Mod. Phys. 1964, 36, 517–524. [Google Scholar] [CrossRef]
- Møller, E.F. Sloppy feeding in marine copepods: Prey-size-dependent production of dissolved organic carbon. J. Plankton Res. 2005, 27, 27–35. [Google Scholar] [CrossRef]
- Wozniak, B.; Dera, J. Light Absorption in Sea Water; Springer: Berlin/Heidelberg, Germany, 2007; Volume 33, p. 463. [Google Scholar]
- Jin, Q.; Bethke, C.M. Kinetics of electron transfer through the respiratory chain. Biophys. J. 2002, 83, 1797–1808. [Google Scholar] [CrossRef]
- LaRowe, D.E.; Dale, A.W.; Amend, J.P.; Van Cappellen, P. Thermodynamic limitations on microbially catalyzed reaction rates. Geochim. Cosmochim. Acta 2012, 90, 96–109. [Google Scholar] [CrossRef]
- Jin, Q.; Bethke, C.M. A New Rate Law Describing Microbial Respiration. Appl. Environ. Microbiol. 2003, 69, 2340–2348. [Google Scholar] [CrossRef]
- Follows, M.J.; Dutkiewicz, S.; Grant, S.; Chisholm, S.W. Emergent Biogeography of Microbial Communities in a Model Ocean. Science 2007, 315, 1843–1846. [Google Scholar] [CrossRef]
- Droop, M.R. Some thoughts on nutrient limitation in algae. J. Phycol. 1973, 9, 264–272. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. The BiM code for the numerical solution of ODEs. J. Comput. Appl. Math. 2004, 164, 145–158. [Google Scholar] [CrossRef]
- Powell, M.J. The BOBYQA Algorithm for Bound Constrained Optimization without Derivatives; Cambridge NA Report NA2009/06; University of Cambridge: Cambridge, UK, 2009; pp. 26–46. [Google Scholar]
- Reichert, P.; Omlin, M. On the usefulness of overparameterized ecological models. Ecol. Model. 1997, 95, 289–299. [Google Scholar] [CrossRef]
- Vallino, J.J. Improving marine ecosystem models: Use of data assimilation and mesocosm experiments. J. Mar. Res. 2000, 58, 117–164. [Google Scholar] [CrossRef]
- Friedrichs, M.A.M.; Dusenberry, J.A.; Anderson, L.A.; Armstrong, R.A.; Chai, F.; Christian, J.R.; Doney, S.C.; Dunne, J.; Fujii, M.; Hood, R.; et al. Assessment of skill and portability in regional marine biogeochemical models: Role of multiple planktonic groups. J. Geophys. Res. 2007, 112, C08001. [Google Scholar] [CrossRef]
- Edwards, C.A.; Moore, A.M.; Hoteit, I.; Cornuelle, B.D. Regional Ocean Data Assimilation. Annu. Rev. Mar. Sci. 2015, 7, 21–42. [Google Scholar] [CrossRef]
- Nielsen, S.N.; Müller, F.; Marques, J.C.; Bastianoni, S.; Jørgensen, S.E. Thermodynamics in Ecology. Entropy 2020, 22, 820. [Google Scholar] [CrossRef]
- Chapman, E.J.; Childers, D.L.; Vallino, J.J. How the Second Law of Thermodynamics Has Informed Ecosystem Ecology through Its History. BioScience 2016, 66, 27–39. [Google Scholar] [CrossRef]
- Ward, B.A.; Dutkiewicz, S.; Follows, M.J. Modelling spatial and temporal patterns in size-structured marine plankton communities: Top–down and bottom–up controls. J. Plankton Res. 2014, 36, 31–47. [Google Scholar] [CrossRef]
- Coles, V.J.; Stukel, M.R.; Brooks, M.T.; Burd, A.; Crump, B.C.; Moran, M.A.; Paul, J.H.; Satinsky, B.M.; Yager, P.L.; Zielinski, B.L.; et al. Ocean biogeochemistry modeled with emergent trait-based genomics. Science 2017, 358, 1149–1154. [Google Scholar] [CrossRef]
- Walworth, N.G.; Zakem, E.J.; Dunne, J.P.; Collins, S.; Levine, N.M. Microbial evolutionary strategies in a dynamic ocean. Proc. Natl. Acad. Sci. USA 2020. [Google Scholar] [CrossRef] [PubMed]
- Lineweaver, C.H.; Egan, C.A. Life, gravity and the second law of thermodynamics. Phys. Life Rev. 2008, 5, 225–242. [Google Scholar] [CrossRef]
- Wolf, D.M.; Arkin, A.P. Motifs, modules and games in bacteria. Curr. Opin. Microbiol. 2003, 6, 125–134. [Google Scholar] [CrossRef]
- Liu, J.; Martinez-Corral, R.; Prindle, A.; Lee, D.-Y.D.; Larkin, J.; Gabalda-Sagarra, M.; Garcia-Ojalvo, J.; Süel, G.M. Coupling between distant biofilms and emergence of nutrient time-sharing. Science 2017, 356, 638–642. [Google Scholar] [CrossRef]
- Boysen, A.K.; Carlson, L.T.; Durham, B.P.; Groussman, R.D.; Aylward, F.O.; Ribalet, F.; Heal, K.R.; DeLong, E.F.; Armbrust, E.V.; Ingalls, A.E. Diel Oscillations of Particulate Metabolites Reflect Synchronized Microbial Activity in the North Pacific Subtropical Gyre. bioRxiv 2020. [Google Scholar] [CrossRef]
- Vislova, A.; Sosa, O.A.; Eppley, J.M.; Romano, A.E.; DeLong, E.F. Diel Oscillation of Microbial Gene Transcripts Declines With Depth in Oligotrophic Ocean Waters. Front. Microbiol. 2019, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Hellweger, F.L.; Kianirad, E. Individual-based modeling of phytoplankton: Evaluating approaches for applying the cell quota model. J. Theor. Biol. 2007, 249, 554–565. [Google Scholar] [CrossRef]
- Basan, M.; Honda, T.; Christodoulou, D.; Hörl, M.; Chang, Y.-F.; Leoncini, E.; Mukherjee, A.; Okano, H.; Taylor, B.R.; Silverman, J.M.; et al. A universal trade-off between growth and lag in fluctuating environments. Nature 2020, 584, 470–474. [Google Scholar] [CrossRef]
- Tsakalakis, I.; Pahlow, M.; Oschlies, A.; Blasius, B.; Ryabov, A.B. Diel light cycle as a key factor for modelling phytoplankton biogeography and diversity. Ecol. Model. 2018, 384, 241–248. [Google Scholar] [CrossRef]
- Reimers, A.-M.; Knoop, H.; Bockmayr, A.; Steuer, R. Cellular trade-offs and optimal resource allocation during cyanobacterial diurnal growth. Proc. Natl. Acad. Sci. USA 2017, 114, E6457–E6465. [Google Scholar] [CrossRef]
- Bissinger, J.E.; Montagnes, D.J.S.; Harples, J.; Atkinson, D. Predicting marine phytoplankton maximum growth rates from temperature: Improving on the Eppley curve using quantile regression. Limnol. Oceanogr. 2008, 53, 487–493. [Google Scholar] [CrossRef]
- Eppley, R.W. Temperature and phytoplankton growth in the sea. Fish. Bull. 1972, 70, 1063–1085. [Google Scholar]
- Sekar, K.; Linker, S.M.; Nguyen, J.; Grünhagen, A.; Stocker, R.; Sauer, U. Bacterial Glycogen Provides Short-Term Benefits in Changing Environments. Appl. Environ. Microbiol. 2020, 86, 1–14. [Google Scholar] [CrossRef]
- Gilpin, L.C.; Davidson, K.; Roberts, E. The influence of changes in nitrogen: Silicon ratios on diatom growth dynamics. J. Sea Res. 2004, 51, 21–35. [Google Scholar] [CrossRef]
- Hecky, R.E.; Kilham, P. Nutrient limitation of phytoplankton in freshwater and marine environments: A review of recent evidence on the effects of enrichment1. Limnol. Oceanogr. 1988, 33, 796–822. [Google Scholar] [CrossRef]
- Wagner, H.; Jebsen, C.; Wilhelm, C. Monitoring cellular C:N ratio in phytoplankton by means of FTIR-spectroscopy. J. Phycol. 2019, 55, 543–551. [Google Scholar] [CrossRef]
- Downing, A.L.; Brown, B.L.; Perrin, E.M.; Keitt, T.H.; Leibold, M.A. Environmental fluctuations induce scale-dependent compensation and increase stability in plankton ecosystems. Ecology 2008, 89, 3204–3214. [Google Scholar] [CrossRef]
- Frost, T.M.; Carpenter, S.R.; Ives, A.R.; Kratz, T.K. Species compensation and complementarity in ecosystem function. In Linking Species and Ecosystems; Jones, G.C., Lawton, J.H., Eds.; Chapman and Hall: New York, NY, USA, 1995; pp. 224–239. [Google Scholar]
- Dutkiewicz, S.; Follows, M.J.; Bragg, J.G. Modeling the coupling of ocean ecology and biogeochemistry. Glob. Biogeochem. Cycles 2009, 23, 1–15. [Google Scholar] [CrossRef]
- Edwards, A.M.; Yool, A. The role of higher predation in plankton population models. J. Plankton Res. 2000, 22, 1085–1112. [Google Scholar] [CrossRef]
- Caswell, H.; Neubert, G. Chaos and closure terms in plakton food chain models. J. Plankton Res. 1998, 20, 1837–1845. [Google Scholar] [CrossRef]
- Mitra, A. Are closure terms appropriate or necessary descriptors of zooplankton loss in nutrient-phytoplankton-zooplankton type models? Ecol. Model. 2009, 220, 611–620. [Google Scholar] [CrossRef]
- Schmitz, O.J.; Hawlena, D.; Trussell, G.C. Predator control of ecosystem nutrient dynamics. Ecol. Lett. 2010, 13, 1199–1209. [Google Scholar] [CrossRef]
- Biagini, G.A.; Finlay, B.J.; Lloyd, D. Protozoan stimulation of anaerobic microbial activity: Enhancement of the rate of terminal decomposition of organic matter. FEMS Microbiol. Ecol. 1998, 27, 1–8. [Google Scholar] [CrossRef]
- Urabe, J.; Elser, J.J.; Kyle, M.; Yoshida, T.; Sekino, T.; Kawabata, Z. Herbivorous animals can mitigate unfavourable ratios of energy and material supplies by enhancing nutrient recycling. Ecol. Lett. 2002, 5, 177–185. [Google Scholar] [CrossRef]
- Mazancourt, D.C.; Loreau, M. Grazing optimization, nutrient cycling, and spatial heterogeneity of plant-herbivore interactions: Should a palatable plant evolve? Evolution 2000, 54, 81–92. [Google Scholar] [CrossRef]
- Cook, J.; Endres, R.G. Thermodynamics of switching in multistable non-equilibrium systems. J. Chem. Phys. 2020, 152, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ratajczak, Z.; D’Odorico, P.; Collins, S.L.; Bestelmeyer, B.T.; Isbell, F.I.; Nippert, J.B. The interactive effects of press/pulse intensity and duration on regime shifts at multiple scales. Ecol. Monogr. 2017. [Google Scholar] [CrossRef]
- Dakos, V.; Matthews, B.; Hendry, A.P.; Levine, J.; Loeuille, N.; Norberg, J.; Nosil, P.; Scheffer, M.; De Meester, L. Ecosystem tipping points in an evolving world. Nat. Ecol. Evol. 2019, 3, 355–362. [Google Scholar] [CrossRef]
- Gu, C.; Kim, G.B.; Kim, W.J.; Kim, H.U.; Lee, S.Y. Current status and applications of genome-scale metabolic models. Genome Biol. 2019, 20, 121. [Google Scholar] [CrossRef]
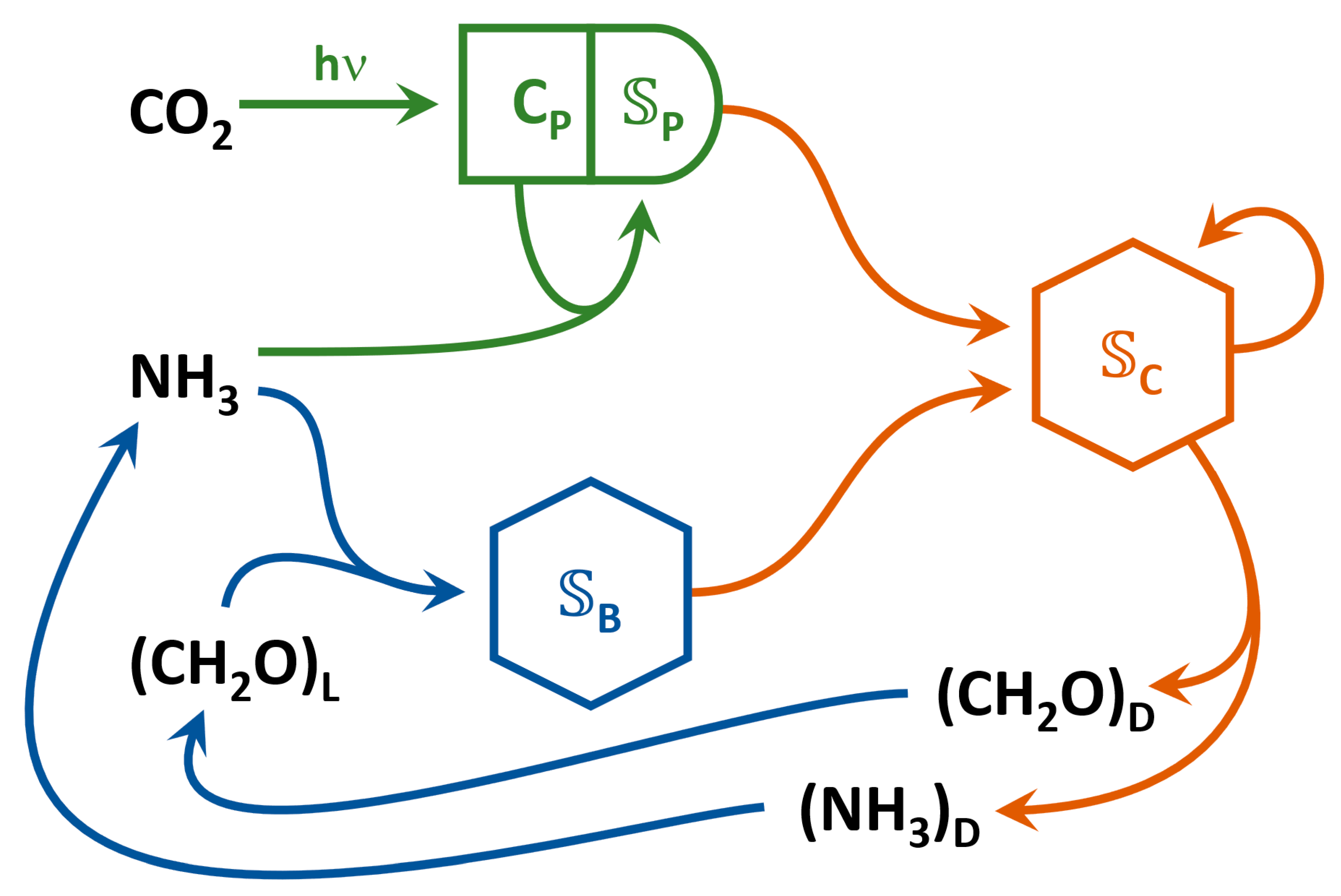


| Rxn. | Abbreviated Stoichiometry | Cat. |
|---|---|---|
| Input | Value | Input | Value |
|---|---|---|---|
| 406,000 | 10 | ||
| 293 | 100 | ||
| 8.1 | 7 | ||
| 0.72 | 0.1 | ||
| 2000 | 0.1 | ||
| 225 | 0.1 | ||
| 5 | 0.1 |
| Variable | Balanced Growth | Passive Storage | Circadian Allocation |
|---|---|---|---|
| 0.2536 | 0.3452 | 0.3788 | |
| 0.0000 * | 0.0000 * | 0.2389 | |
| 1.0000 * | 1.0000 * | 0.7799 | |
| 0.6746 | 0.8036 | 1.0000 | |
| 0.1686 | 0.1618 | 0.1628 | |
| 0.3351 | 0.3852 | 0.4349 | |
| 0.1997 | 0.1609 | 0.2869 | |
| 0.4651 | 0.4539 | 0.2782 | |
| 0.0001 | 0.9971 | 0.0001 | |
| 0.7288 | 0.0000 | 0.6547 | |
| 0.0729 | 0.3888 | 0.5809 | |
| 0.4396 | 0.5868 | 0.0963 | |
| 0.2826 | 0.9901 | 0.9787 | |
| 0.2751 | 1.687 | 1.616 | |
| 3.426 | 17.79 | 18.60 | |
| 3.984 | 18.95 | 19.74 |
| Strategy | |||
|---|---|---|---|
| Balanced | 3.9837 | 4.034 | 4.0811 |
| Passive | 18.9511 | 18.9976 | 19.0152 |
| Circadian | 19.7359 | 19.7844 | 19.7987 |
| Strategy | |||
|---|---|---|---|
| Balanced | 0.3226 | 0.3455 | 0.3684 |
| Passive | 1.3374 | 1.4995 | 1.6432 |
| Circadian | 3.0891 | 3.4000 | 3.6242 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallino, J.J.; Tsakalakis, I. Phytoplankton Temporal Strategies Increase Entropy Production in a Marine Food Web Model. Entropy 2020, 22, 1249. https://doi.org/10.3390/e22111249
Vallino JJ, Tsakalakis I. Phytoplankton Temporal Strategies Increase Entropy Production in a Marine Food Web Model. Entropy. 2020; 22(11):1249. https://doi.org/10.3390/e22111249
Chicago/Turabian StyleVallino, Joseph J., and Ioannis Tsakalakis. 2020. "Phytoplankton Temporal Strategies Increase Entropy Production in a Marine Food Web Model" Entropy 22, no. 11: 1249. https://doi.org/10.3390/e22111249
APA StyleVallino, J. J., & Tsakalakis, I. (2020). Phytoplankton Temporal Strategies Increase Entropy Production in a Marine Food Web Model. Entropy, 22(11), 1249. https://doi.org/10.3390/e22111249






