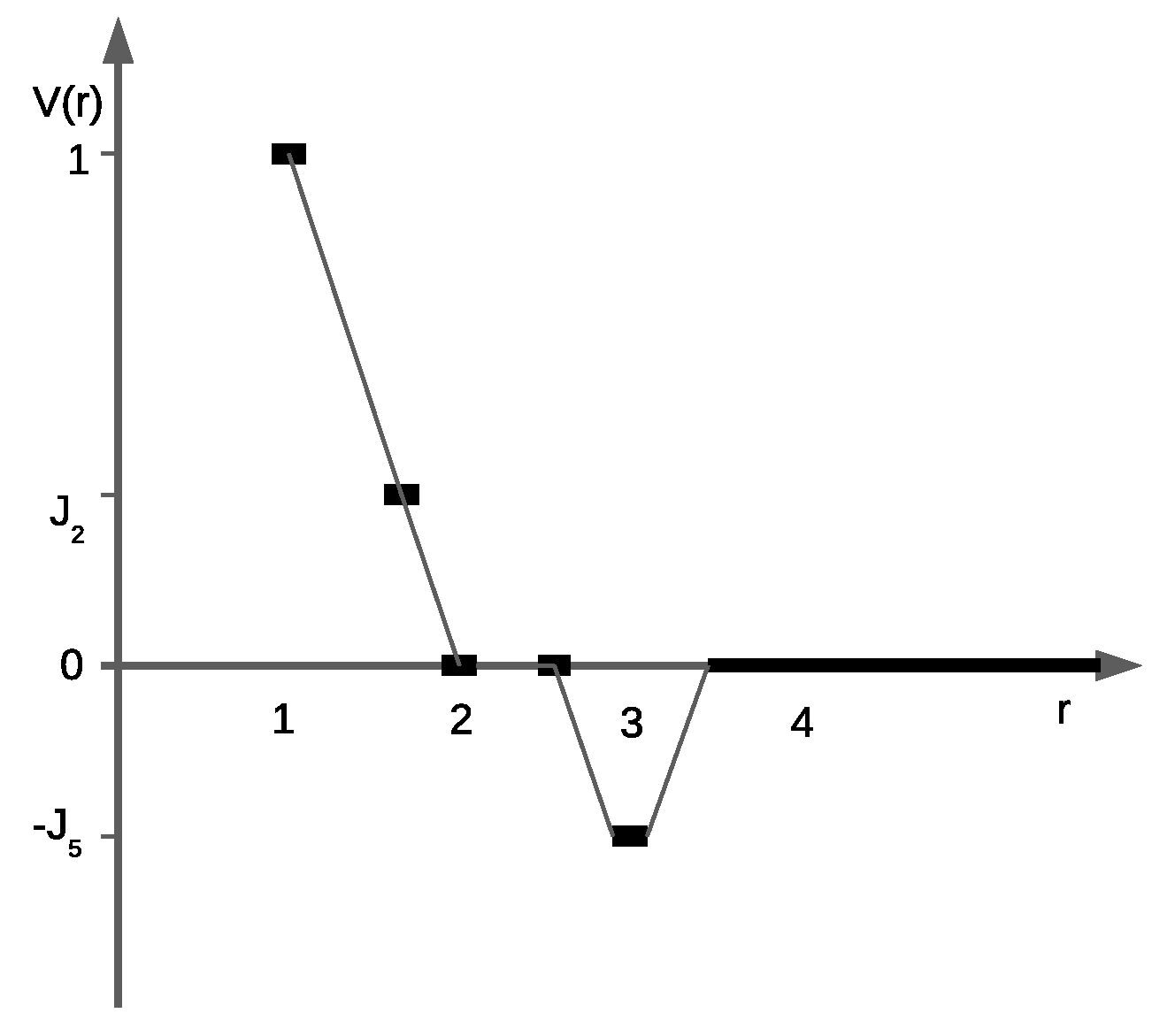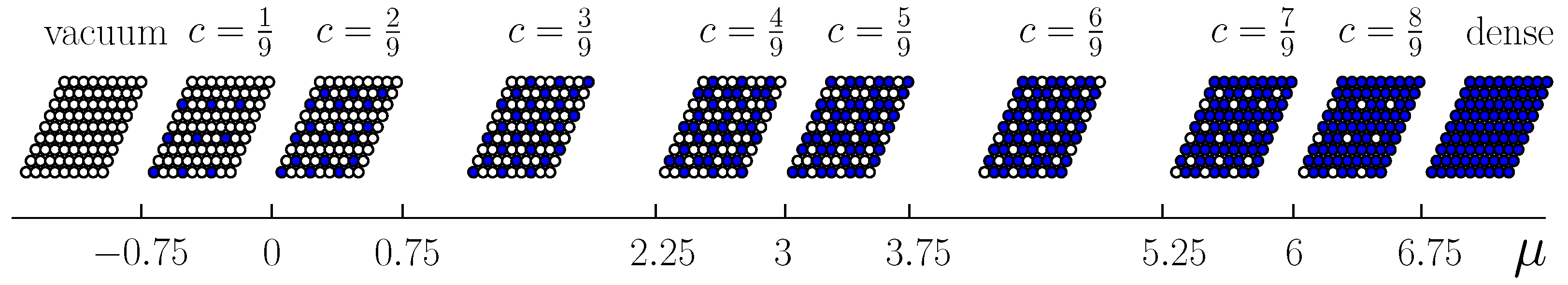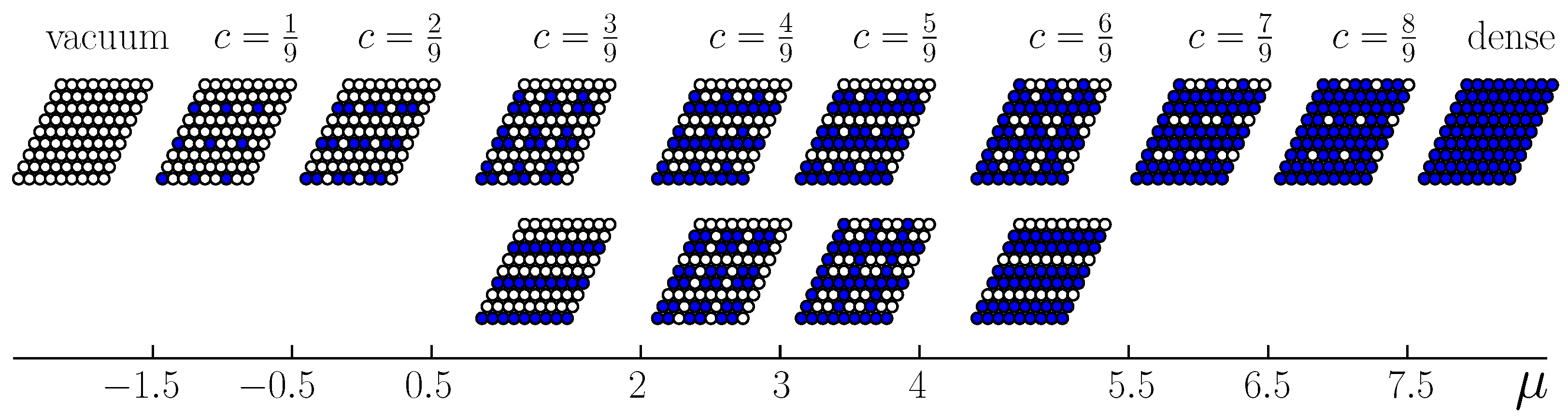1. Introduction
Metal or semiconducting nanoparticles find numerous applications in catalysis, optics, biomedicine, environmental science, and so forth. In order to prevent the charge-neutral nanoparticles from aggregation, recently, various types of core-shell nanoparticles (CSNPs) have been produced [
1,
2]. In the CSNPs, the hard, typically metal or semiconducting nanoparticle with a diameter ranging from a few tens to a few hundreds of nanometers is covered by a soft polymeric shell. The polymeric chains can interpenetrate, and the distance between the particles can become smaller than the shell diameter at some energetic cost. This energetic cost, or the softness of the shells, can be controlled in particular by the crosslinking of the polymeric chains. The shell-to-core diameter ratio in the majority of the experiments varies from about 1.1 to about 4 [
2,
3,
4,
5]. Since the shell thickness can be controlled independently of the core diameter, and the effective interactions between the CSNPs depend on the thickness and the architecture of the shells, the desired effective interactions can be obtained by choosing different protocols for the synthesis.
Properties of the CSNPs have been intensively studied not only in the bulk, but also at the fluid interfaces [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12]. It turned out that while in the bulk, the effective interaction consists of the hard core followed by the soft repulsive shoulder; at fluid interfaces, strong capillary attraction can be present for separations larger than the shell diameter, in addition to the above mentioned repulsive interactions at shorter distances [
2,
3,
4].
Experimental results show that the CSNPs at fluid interfaces can form interesting patterns, depending on the properties of the particles and on the fraction of the interface area covered by them [
2,
3,
4]. For a small area fraction, highly ordered arrays of hexagonally packed particles are typically observed. Compression may lead to the sudden formation of particle clusters [
1]. The surface pressure–area isotherms can have a characteristic shape of alternating segments with a very large and quite small slope, and the large compressibility signals structural changes [
2,
3]. The origin of these patterns and of the structural changes, their nature, and dependence on the properties of the CSNPs are not fully understood yet. The theory of CSNPs, that at fluid interfaces, they repel each other at short separations and attract each other at large separations, is much less developed than the experimental studies [
13,
14,
15]. This is in contrast to theoretical and simulation studies of patterns formed by particles with soft repulsive potentials [
16].
Because there are many factors controlling the core-and-shell diameter and the architecture of the shell, there is a need for a simplified, coarse-grained theory that could predict general trends in pattern formation for various ranges, strengths, and shapes of the effective potential. In Ref. [
13], a one-dimensional (1D) lattice model with repulsion between nearest neighbors and attraction between second or third neighbors was solved exactly. The obtained isotherms consist of alternating segments with very large and quite small slopes, as in experiments. The steep parts of the isotherms are associated with periodic patterns. The number of the steps, however, is larger in the case of third-neighbor attraction (i.e., thicker shell), and depends on the strengths of the repulsive and attractive parts of the potential. There are no phase transitions in the thermodynamic sense in 1D, but the correlation function shows oscillatory decay with the correlation length that for a strong attraction can be very large (
times the core diameter). These results show a strong dependence of the structure and mechanical properties of the monolayers of the CSNPs on the range, shape, and strength of the effective interactions and agree with the experimental observation of the more complex behavior of the CSNPs with thick shells. However, any 1D model cannot answer the question if different patterns correspond to different phases, and obviously only 1D patterns can be examined.
Particles with a size equal to or larger than a few tens of nanometers are practically irreversibly adsorbed at the interface, but can move freely in the interface area [
2]. For this reason, the particles trapped at the interface can be modeled as a two-dimensional system. Since closely packed CSNPs form a hexagonal pattern, triangular lattice models with the lattice constant
a equal to the diameter of the hard core (or the distance of the closest approach of the particles upon compression) are appropriate and convenient generic models for CSNPs at fluid interfaces. In Ref. [
15], lattice models for CSNPs with thin and thick shells were introduced and studied. Following Ref. [
16], we assumed that the shell-to-core ratio separating the thin and thick shells is
. According to this criterion, the shell is thin when the shells of the second neighbors of closely-packed particle-cores do not overlap, otherwise it is thick.
For thin shells, nearest-neighbor repulsion and second neighbor attraction between particle cores occupying sites of the triangular lattice were assumed. The shell-to-core ratio in this model is
. We have found four phases in this model—very dilute gas, hexagonal lattice of closely packed shells, hexagonal lattice of vacancies, and closely packed cores. We have calculated the surface tension between coexisting phases for different orientations of the interface and found that the particles at the stable interfaces corresponding to the smallest surface tension lie on straight lines. The interface lines meet at the angles 60° or 120°. When the fixed area fraction of the CSNPs is smaller than the area fraction of the hexagonal phase, large voids with a hexagonal shape are formed. The results are in good agreement with the experiment in Reference [
2,
3,
4].
In order to study the effect of the shell thickness, in the second model, we assume that the inner shell is covered by a much softer outer shell, and the nearest-neighbor repulsion is followed by vanishing interactions for the second, third, and fourth neighbors and by attraction between the fifth neighbors. The shell-to-core ratio in this model is equal to 3, as in the experiments of Refs. [
1,
3]. Six more phases, including honeycomb lattices of particles or vacancies and periodically ordered rough clusters were found, but these additional phases were stable only at the coexistence with the phases found for the thin-shell model. For the fixed area fraction of the particles, two phases with the closest area fraction to the mean one, and the interface between them, were present at low temperature. For increasing
T, islands of different phases in the sea of the hexagonally packed shells were observed in the course of simulations for the area fraction exceeding the value at the close packing of the shells. Such complex patterns, somewhat similar to the patterns observed in experiments [
2,
3,
4], occur because of the metastability of several ordered phases and large interface fluctuations in 2D.
The results of Reference [
15] concern CSNPs with composite shells with a stiff inner shell and very soft outer shell. In this work, we focus on the question of the role of the shape of the repulsive shoulder, associated with the architecture of the crosslinked polymeric chains. We assume first- and second-neighbor repulsion, and fifth-neighbor attraction, and consider different second- to first-neighbor repulsion ratios. The model is introduced in
Section 2. The ground state of an open system and of the system with a fixed number of particles is determined in
Section 3.1 and
Section 3.2, respectively. We find the same patterns as in Ref. [
15] for weak second-neighbor repulsion, but the patterns absent for thin shells are present for some intervals of the chemical potential. For the second-to-first neighbor repulsion ratio larger than
, the stable patterns are completely different. Moreover, for some ranges of the chemical potential, the ground state is degenerated, and two quite different patterns are stable. In
Section 4, thermodynamic properties obtained for
by Monte Carlo simulations are described. We present the chemical potential, compressibility, and specific heat as functions of the concentration.
Section 5 contains our conclusions.
2. The Model
The system that models the core-shall particles on a surface is described in Ref. [
15]. The thermodynamic Hamiltonian of the system is:
where
numerates the sites of the
k-th coordination sphere around the site
i,
is the coordination number,
is the interaction constant for the
k-th coordination sphere,
is the occupation number (0 or 1), and
is the chemical potential. The particles can occupy sites of a triangular lattice containing
lattice sites.
The lattice parameter
a is equal to the diameter of the hard core of the particles. It is supposed that the particles repel each other with the intensity
(
), if the particles occupy the nearest neighbor sites, and feel weaker repulsion on the next nearest sites with the intensity
. The intermediate third and fourth neighbors do not interact (
), while the fifth neighbors attract each other with the energy
. Thus,
and
are the dimensionless interaction energies (
,
, and
J has units of energy). The dimensionless chemical potential
and dimensionless temperature
will be used as well. In the terminology of Reference [
15], it is model II with an additional repulsive interaction of the second neighbors.
The interaction potential as a function of the distance between the particle cores is shown in
Figure 1. As is demonstrated below, the variation of the second and fifth neighbor interactions can lead to different symmetry-breaking (heterostructural) transitions in the system; it was recently attained using the augmented potential [
17]. Compared to conventional interaction potentials that are determined a priori, the augmented potentials adjust the effective interactions on the basis of the local environment of each particle and efficiently capture multi-body effects at a local level.
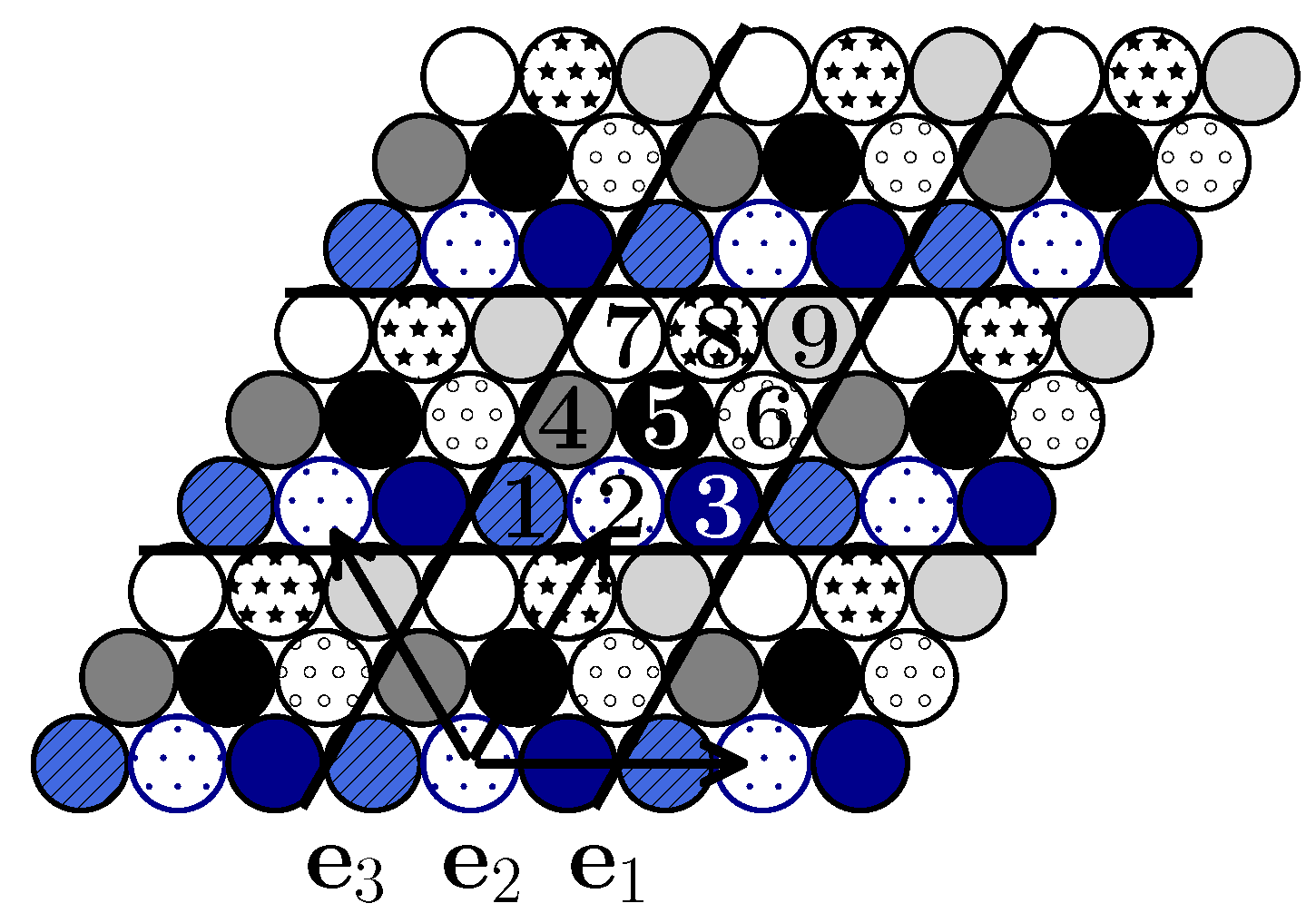
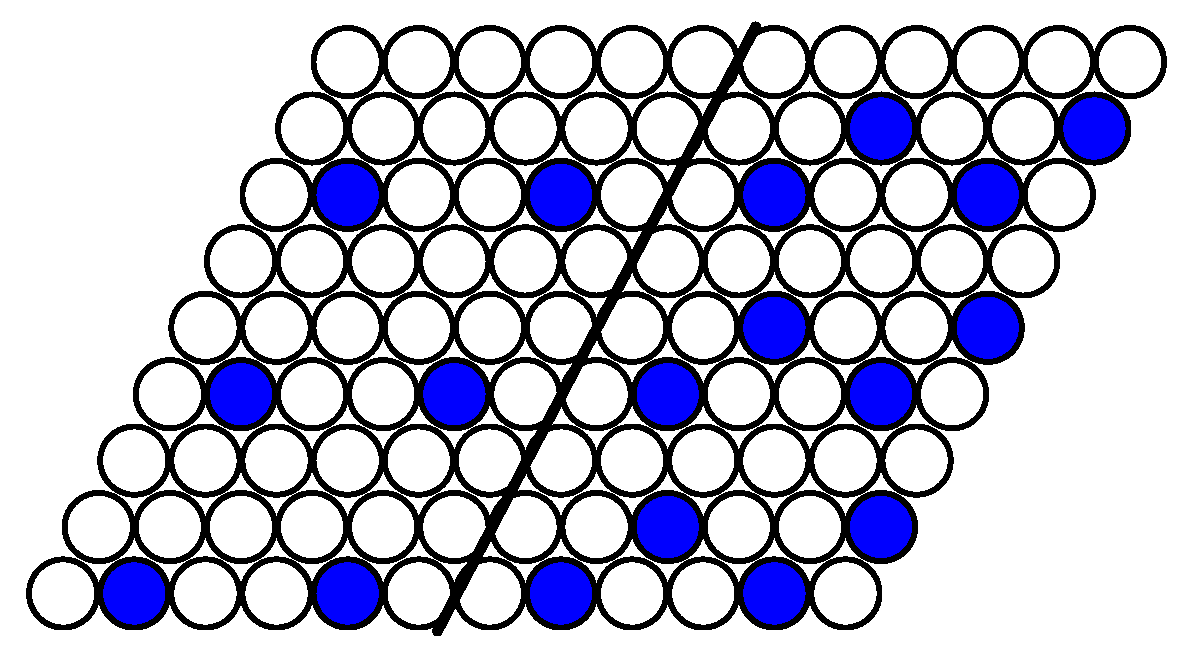
In accordance with the range of the interparticle interactions (up to the fifth neighbors), the unit cell contains nine (
) lattice sites. In this case, the fifth neighbors (that correspond to the largest interaction range) belong to the nearest unit cells and the distance between them determines the translation vector that preserves the symmetry of the system. The subsequent calculation (
Section 3) and simulation (
Section 4) shows that such a choice accounts for all possible ordered states of the system. For describing the ordered states, the lattice is decomposed in nine sublattices (
Figure 2).
4. Thermodynamics of the System at
At low dimensionless temperatures (where is the absolute temperature and the Boltzmann constant), the ordered states found in the ground state remain present in the system, while the ordering is destroyed gradually with the temperature increase, due to thermal fluctuations. In this section, the Monte Carlo (MC) simulation results for isotherms, isothermal compressibility, and specific heat are presented for the system at two values of the interaction parameter and below and above the crossover value . The Metropolis importance sampling simulations were performed with the chemical potential step for the system of lattice sites with periodic boundary conditions. one thousand Monte Carlo simulation steps (MCS) were used for equilibration. The subsequent 10 000 MCS were used for calculating the average values.
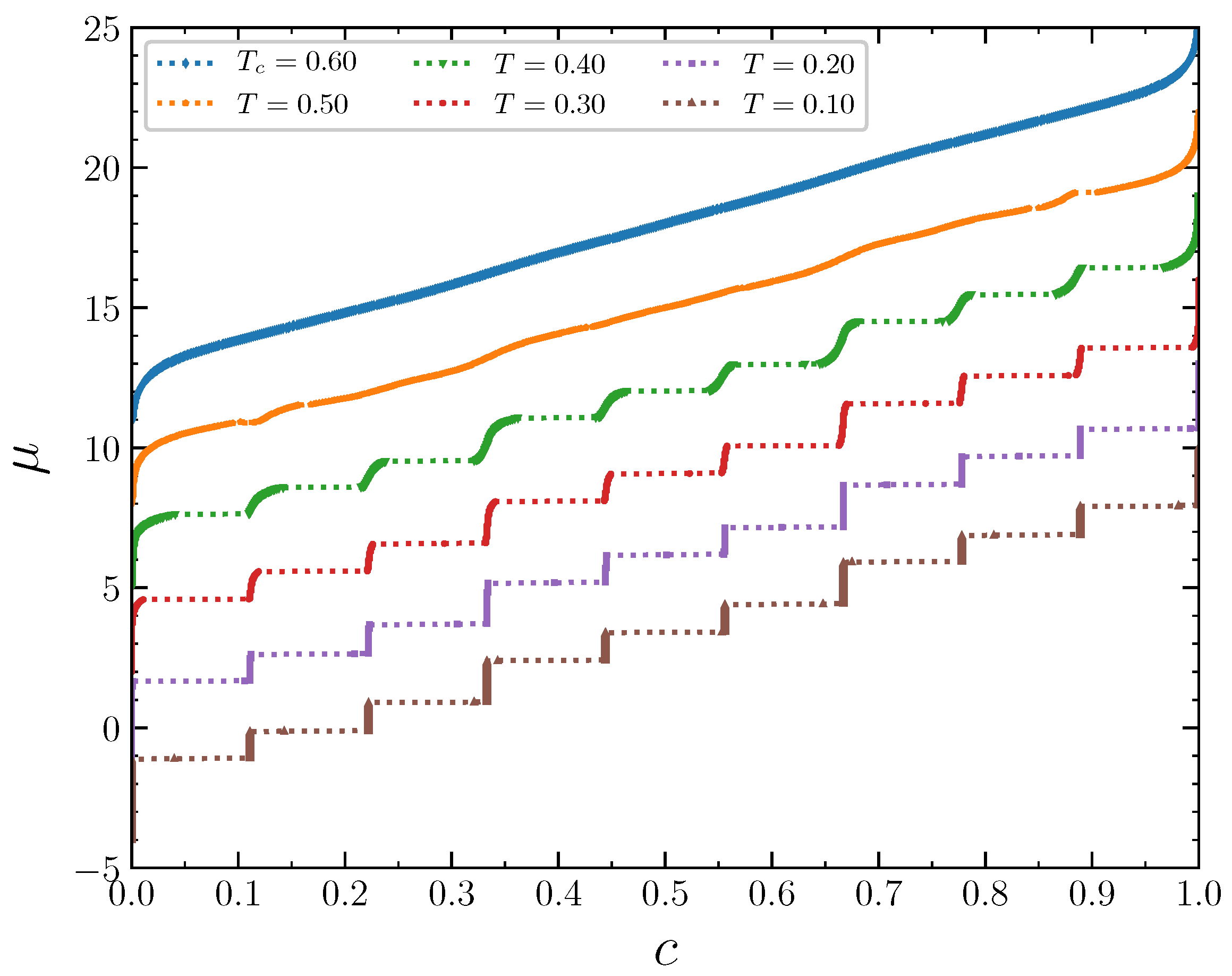
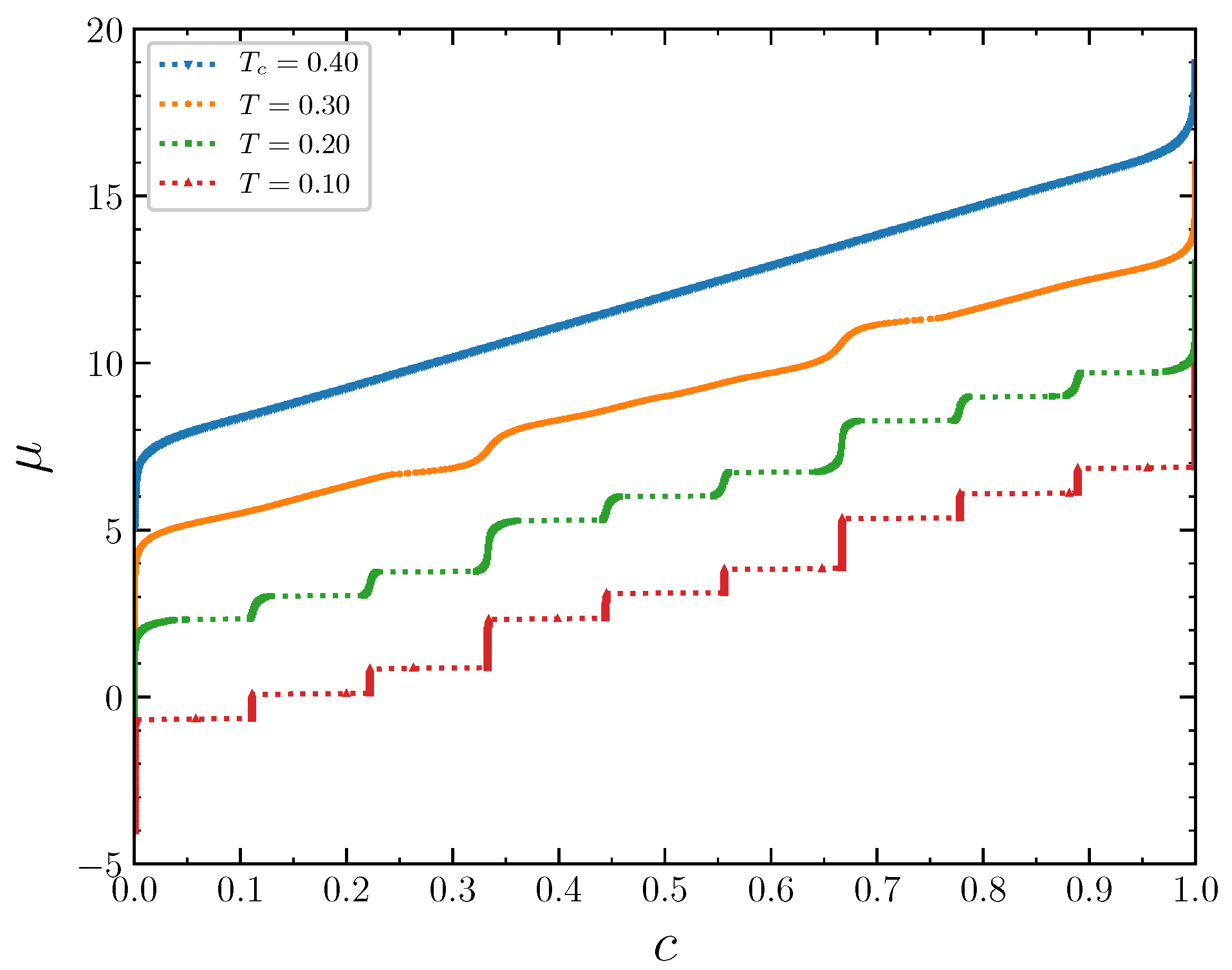
The isotherms displaying the concentration dependence on the chemical potential at
demonstrate typical behavior at low temperatures
, 0.2, and 0.3 (
Figure 11). The wide empty horizontal segments in the
plots indicate forbidden regions of concentrations. These two-phase segments are separated by very steep parts of the
plots, where
increases rapidly for very narrow range of
c, centered at
. These intervals of
c separating the horizontal segments expand with increasing temperature. The concentration intervals around
correspond to the ordered patterns discussed in the previous section in the case of the grand canonical ensemble. At larger temperature
, the horizontal regions in the
plot almost disappear. Thus, the critical temperature can be estimated as
. The concentration increases continuously as a function of the chemical potential at this temperature. The repulsion interaction between the second neighbors not only removes the degeneracy of the system states at the concentrations 1/3 and 2/3, but also significantly reduces the critical temperature, which is around 1.1 when the second neighbors do not interact [
15].
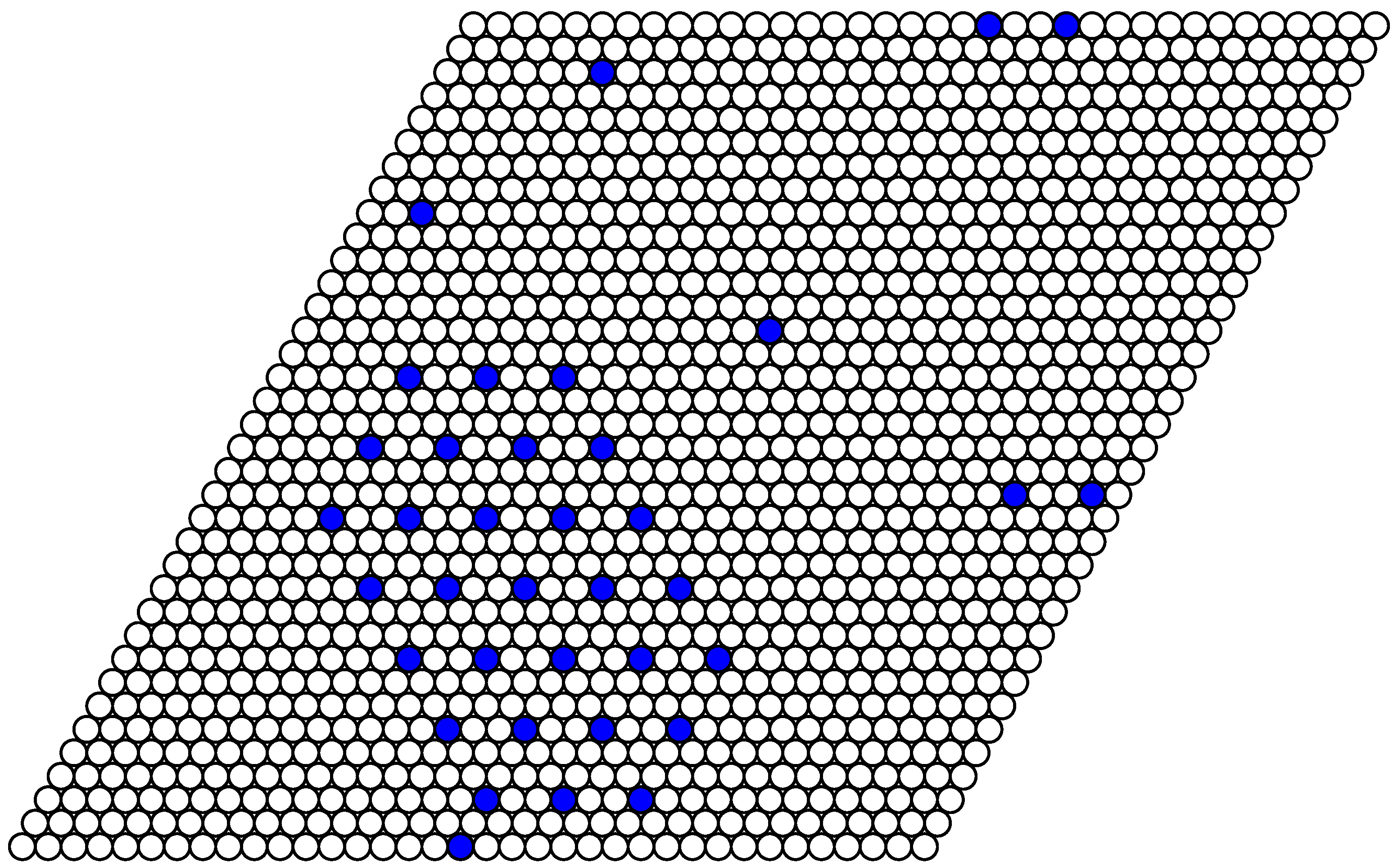
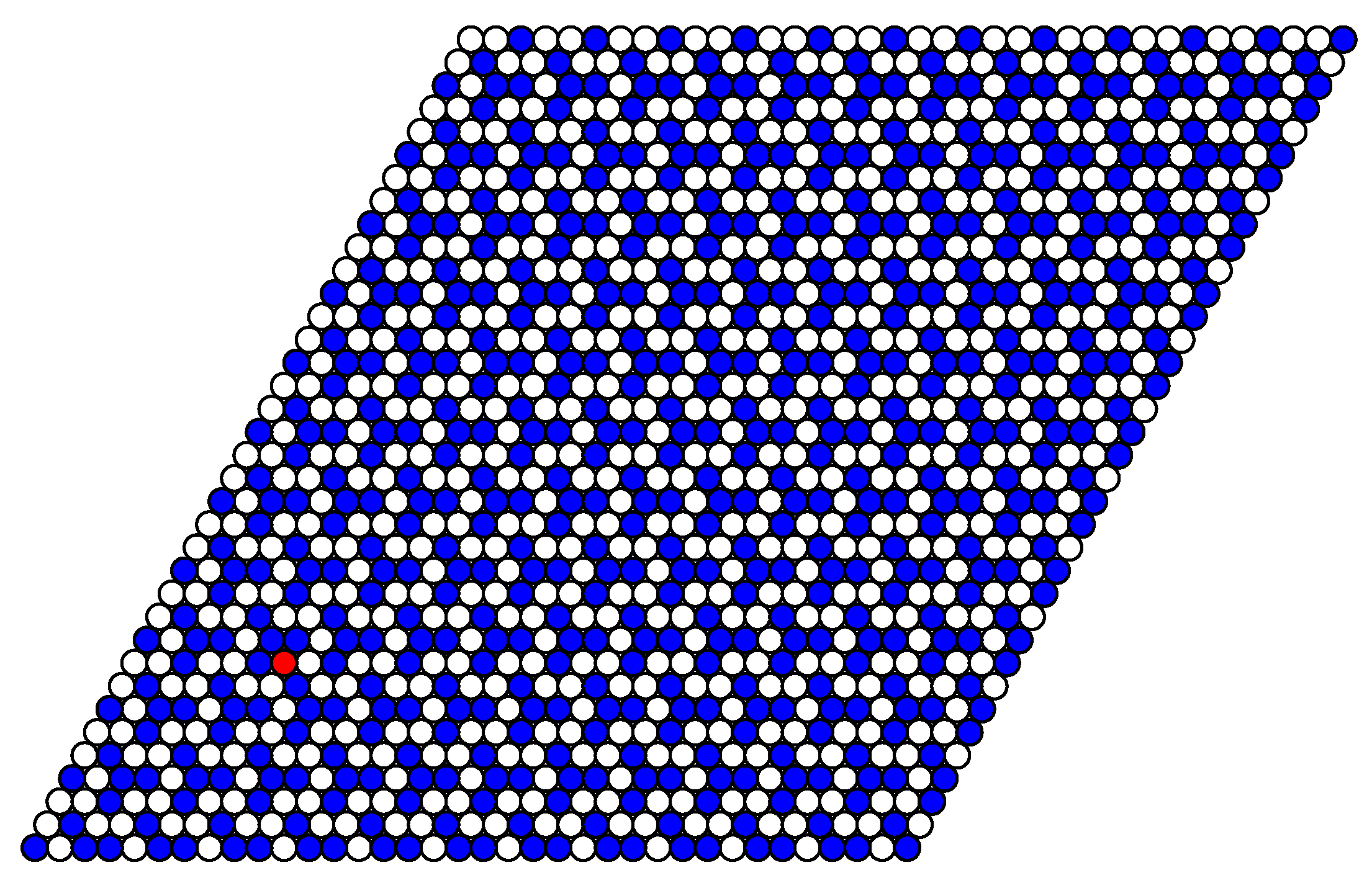
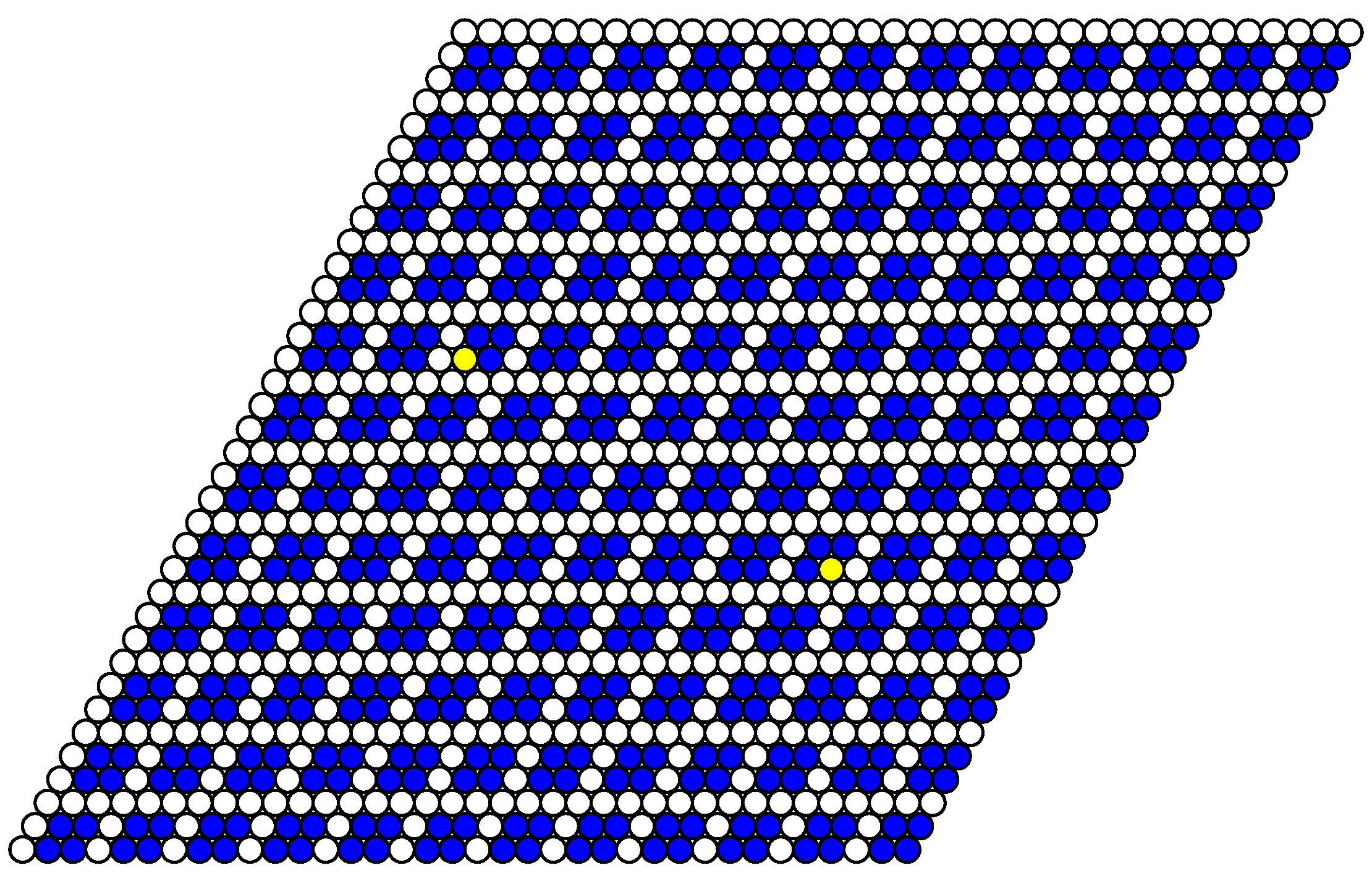
The structure of stable phases resembles the ground state configurations. In
Figure 12,
Figure 13 and
Figure 14 the snapshots of the system at the concentration close to 4/9 are shown as examples. At the interaction parameter
above its critical value 1/3, the system is degenerated and in different runs the final state
Figure 13 and
Figure 14 corresponds to the possible ground state configurations given in
Figure 8 with a few defects, due to thermal fluctuations.
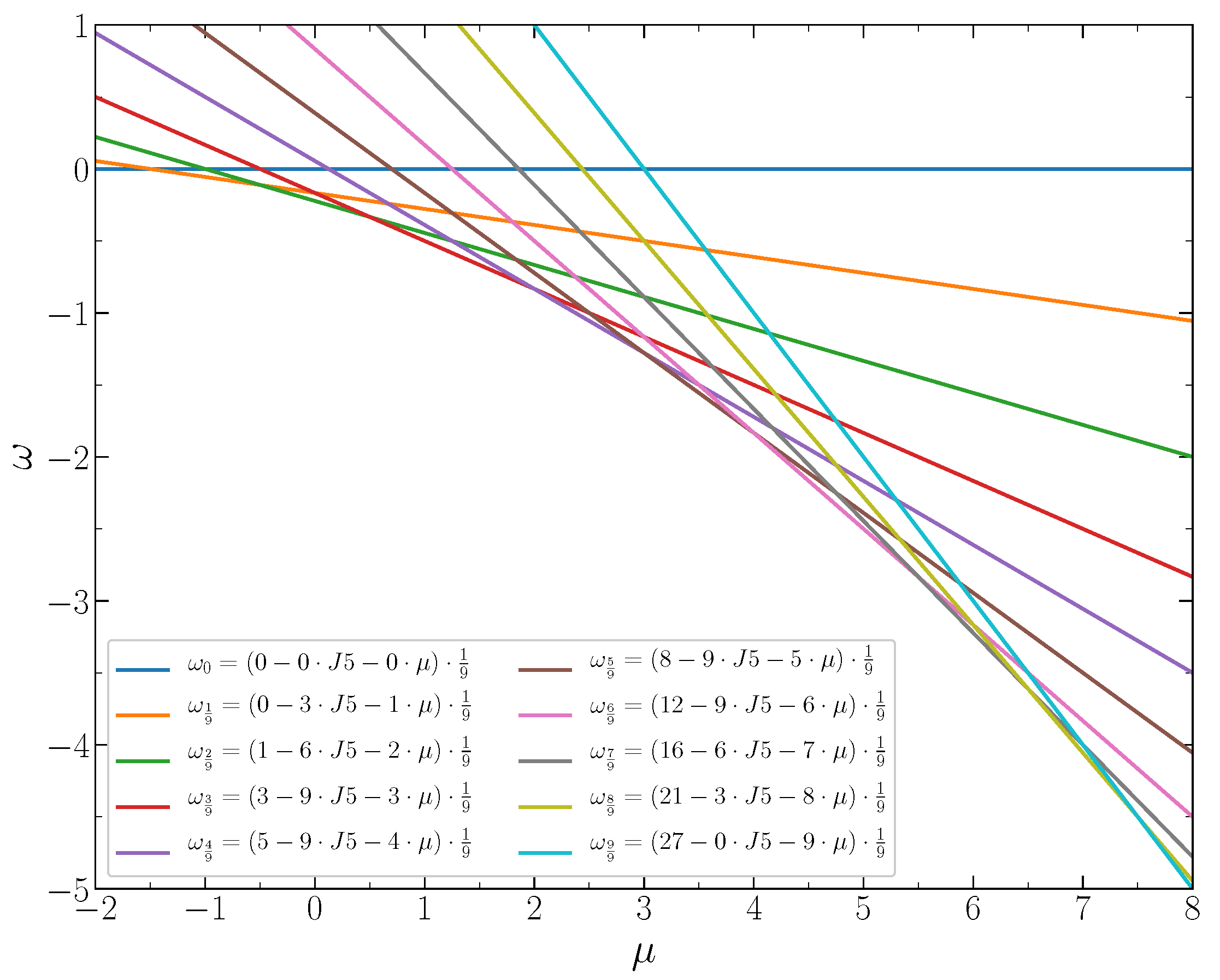
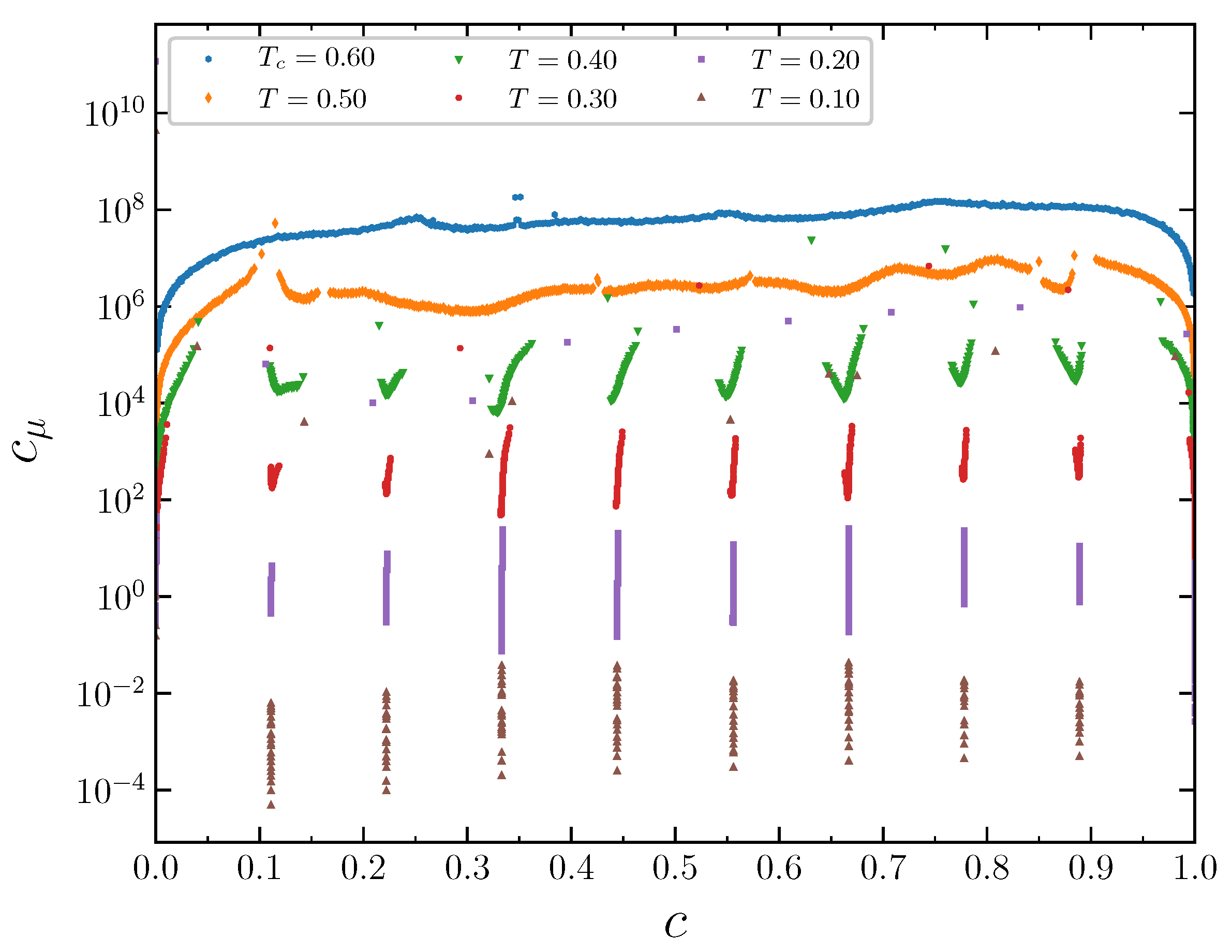
The phase transitions can be more clearly revealed by considering fluctuations (
Figure 15). The inverse value of the thermodynamic factor
is proportional to the concentration fluctuations
that in turn is proportional to the isothermal compressibility
,
, where the angular brackets
denote averaging over the grand canonical ensemble,
N is the number of particles in the system,
is the mean lattice concentration, and
p is the pressure.
At the lowest temperatures, and , the concentration fluctuations of each phase exist in narrow concentration regions. At the temperature , the minima of the concentration fluctuations are well distinguishable. They are attained at the most ordered system states with concentrations equal to a multiple 1/9. At , the concentration fluctuations span almost over the entire concentration range (0,1), indicating the approach to the critical temperature.
Similar behavior is observed for the dimensionless specific heat (
Figure 16), which is proportional to the energy fluctuations
where
is the dimensionless system energy (see the first term on the RHS in Equation (
1)), and
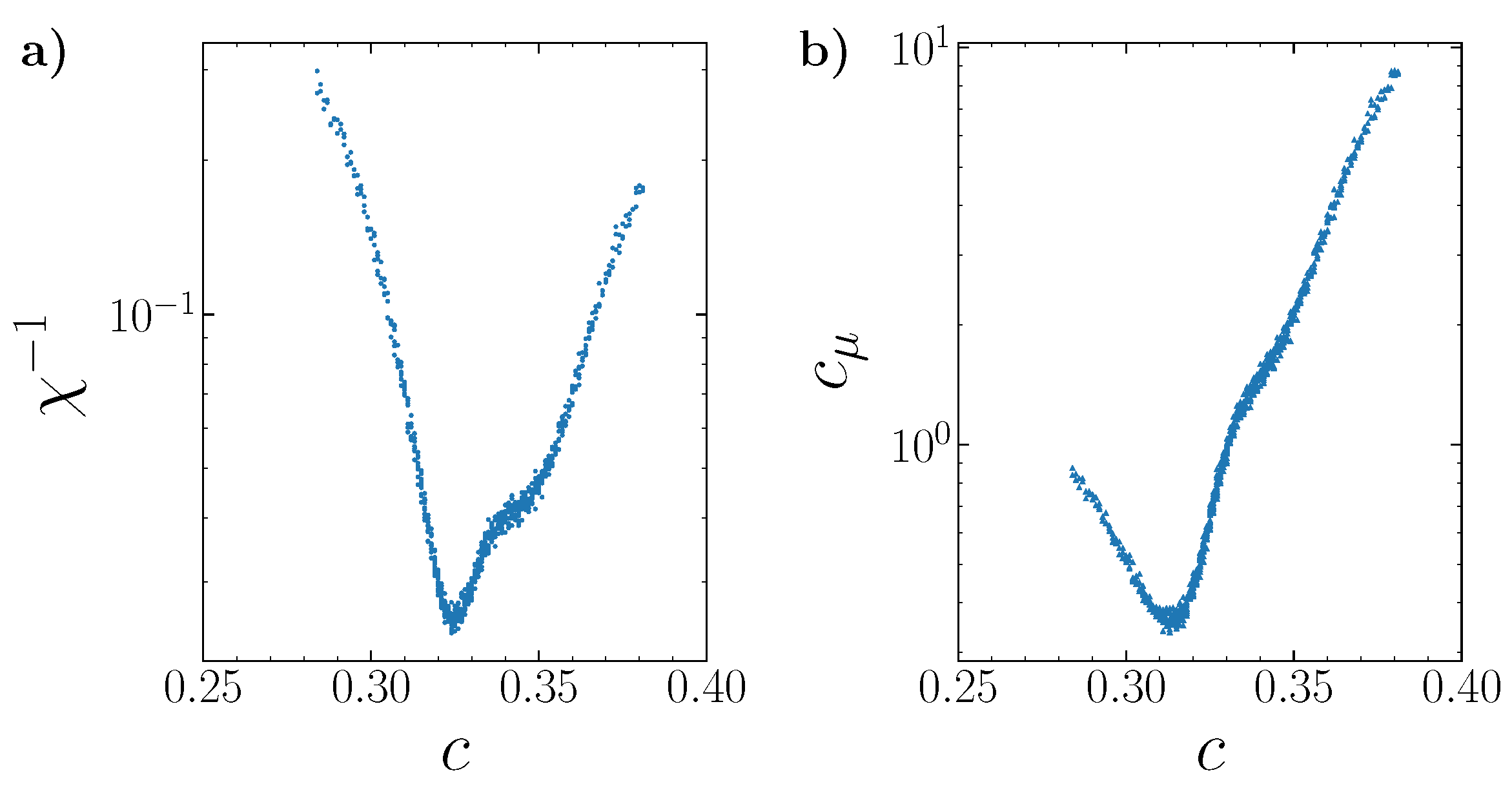
As an example, the fine structure of the concentration and energy fluctuations is shown in
Figure 17 and simulated with the reduced chemical potential step. The minima of these characteristics are close to the concentration
of the most ordered system state.
Structural peculiarities of the system can be tracked by considering the order parameters. The occupancy of particular sublattices (
Figure 2) represents nine such order parameters. At the lowest temperatures,
and
, the succession of the order parameters is in fact represented by the step functions rising from 0 to 1 when the concentration attains the value equal to a multiple of 1/9. The order parameters become smoother when the temperature increases.
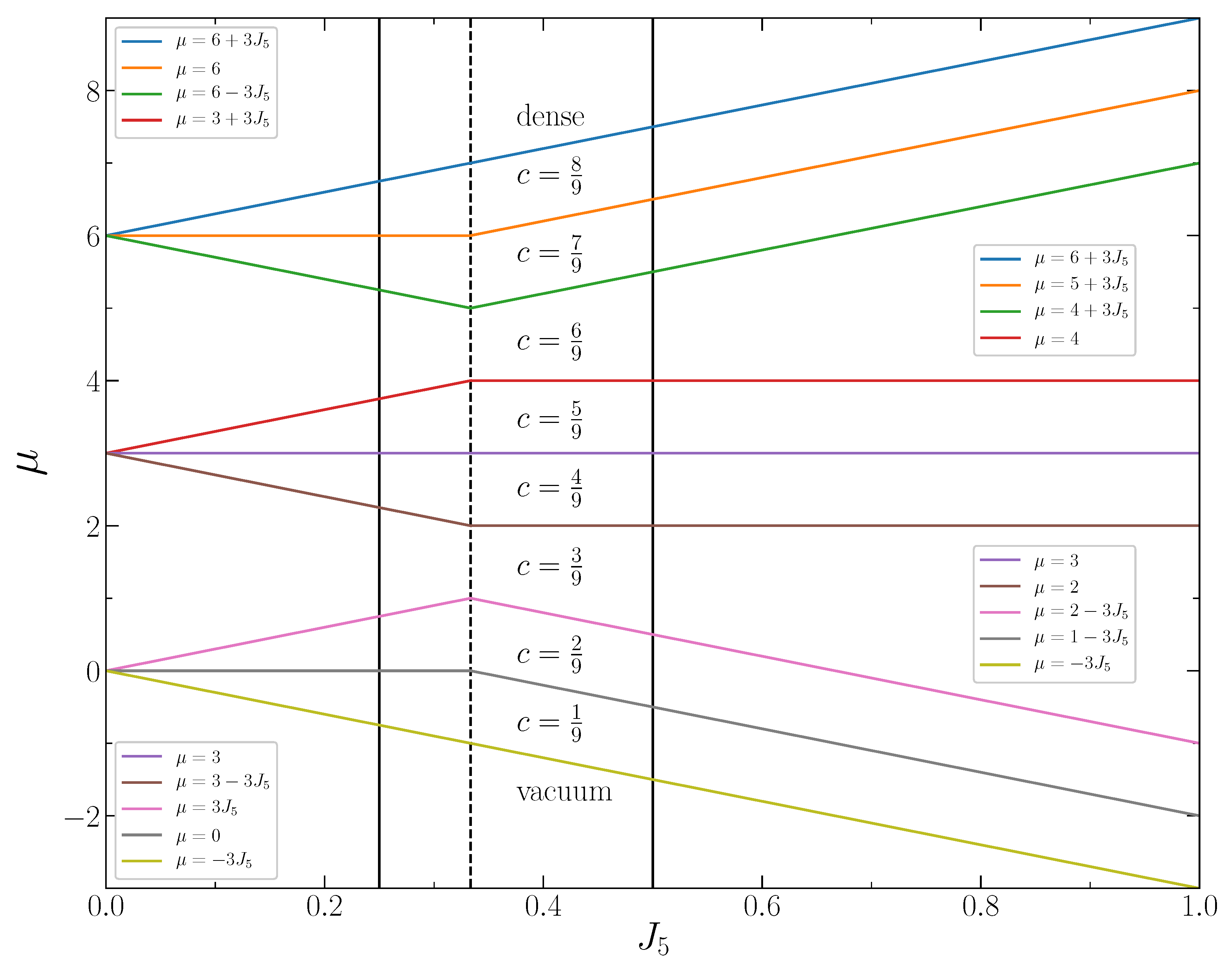
For the interaction parameter below its critical value 1/3, in particular for
, the chemical potential isotherms look like in the previous case (
Figure 18), but the critical temperature is even lower, around 0.4. At low temperatures, the inverse thermodynamic factor and the specific heat, as well as the order parameters, have the same prominent features at the concentrations around a multiple of 1/9. The rapid changes of the above quantities for
are smoothed out with the temperature increase.
Despite very similar thermodynamic properties of the systems with the interaction parameter
above and below its crossover value
, the structural characteristics are completely different above and below the crossover. The particle distribution over the lattice sites corresponds to the structures of
Figure 5 or
Figure 8 in the former and in the latter case, respectively. Due to thermal fluctuations at non-zero temperatures, the structures contain defects, which are particles on the sites that do not belonging to the ideal configurations or vacant sites on these configurations. The number of defects increases with the temperature increase, and the concentration range corresponding to the ordered phases increases as well.
5. Conclusions
We considered pattern formation by particles with hard cores covered by thick polymeric shells on a fluid interface. The structure of the shell can be designed in experimental studies, and it determines the effective repulsion between the particles. For this reason, the aim of our study was the determination of the effect of the shape of the repulsive potential on the patterns formed by the particles. We focused on the question how the rate at which the repulsion decreases with the distance influences the pattern formation. We considered a triangular lattice model with the lattice sites occupied by the particle cores. The nearest and next nearest neighbors repel each other, due to the overlapping polymeric shells, while the fifth neighbors attract each other because of the capillary forces.
The second neighbor repulsion in addition to the nearest and fifth neighbor interaction results in the significant enrichment of the ground state structures. Alongside with the concentrations equal to a multiple of 1/3, the states with the concentrations equal to a multiple of 1/9 are present for certain intervals of the chemical potential.
Importantly, the patterns formed for the concentration
, are completely different for the repulsion that shows a fast and a slow decrease with the interparticle separation (see
Figure 5 and
Figure 8 for the first and the second case, respectively). In the second case, two quite different patterns can occur with the same probability for given
. The crossover value of the second-neighbor repulsion (equal to the fifth neighbor attraction) separating the two types of patterns is
. Our model is suitable for thick composite shells, with a stiff inner part and soft outer part. The results show that by modifying the thickness and the structure of the stiff inner part, we can obtain completely different patterns on an interface.
In systems with a fixed number of particles, the energetically preferable interface lines are parallel to the lattice vectors for all stable interfaces. We have shown that in the case of the degenerated ground states, two types of patterns with lower density can coexist with two patterns with higher density, giving together four pairs of coexisting patterns. A stable interface, however, cannot be formed for one of these pairs.
At non-zero but not too large temperatures, the system passes through the structures corresponding to the ground states with thermally initiated defects. At low temperatures, the stable states exist in very narrow concentration intervals close to the concentrations equal to a multiple of 1/9. The concentration intervals enlarge with the temperature increase. At temperatures slightly above the critical one, the concentration versus chemical potential isotherms become continuous. The critical temperature depends strongly on the shape of the interaction potential too. In the case of
, i.e., when the intensity of the second neighbor repulsion is equal to the fifth neighbor attraction and twice as low as the first neighbor repulsion, the critical temperature is almost two times lower than in the system with vanishing interaction between the second neighbors [
15]. The critical temperature decreases with decreasing interaction between the second and the fifth neighbors.
The fluctuations of the number of particles and energy are maximal at the concentrations corresponding to the phase transition points, and minimal in the most ordered states at concentrations close to a multiple of 1/9. The order parameters determined as the mean concentrations on the sublattices demonstrate fast increase from 0 to 1, while the mean system concentration crosses a value equal to a multiple of 1/9.
Quantitative comparison of the predictions of our model with experimental results is not possible yet. Due to the sensitive dependence of the patterns formed by the particles on the interfaces on the details of the effective interactions, it is necessary to precisely design and control the crosslinking architecture of the polymeric shell, in order to obtain the desired shape of the effective interactions in experiment. On the theoretical side, it would be necessary to compute the pressure–area fraction isotherms that are measured in experiments. On the qualitative level, however, our predictions for the chemical potential—area fraction isotherms can be compared with the experimental pressure–area fraction isotherms for the CSNPs with the shell-to-core size ratio
, since the chemical potential and the pressure play similar roles. Indeed, steps in the isotherms are clearly seen in Ref. [
3], in qualitative agreement with our results. Moreover, structural evolution for increasing area fraction, in particular the formation of clusters, and the orientation of the interface between coexisting phases in our theory and in experiment are similar.
To summarize, we stress that our model indicates that by careful construction of the polymeric shell, one should be able to obtain core-shell nanoparticles forming a variety of different patterns on an interface.