Statistical Approach for Biologically Relevant Gene Selection from High-Throughput Gene Expression Data
Abstract
1. Background
2. Materials and Methods
2.1. Motivation
2.2. Data Source
2.3. Methods
2.3.1. Notations
2.3.2. Maximum Relevance and Minimum Redundancy (MRMR) Filter
2.3.3. Support Vector Machine (SVM)
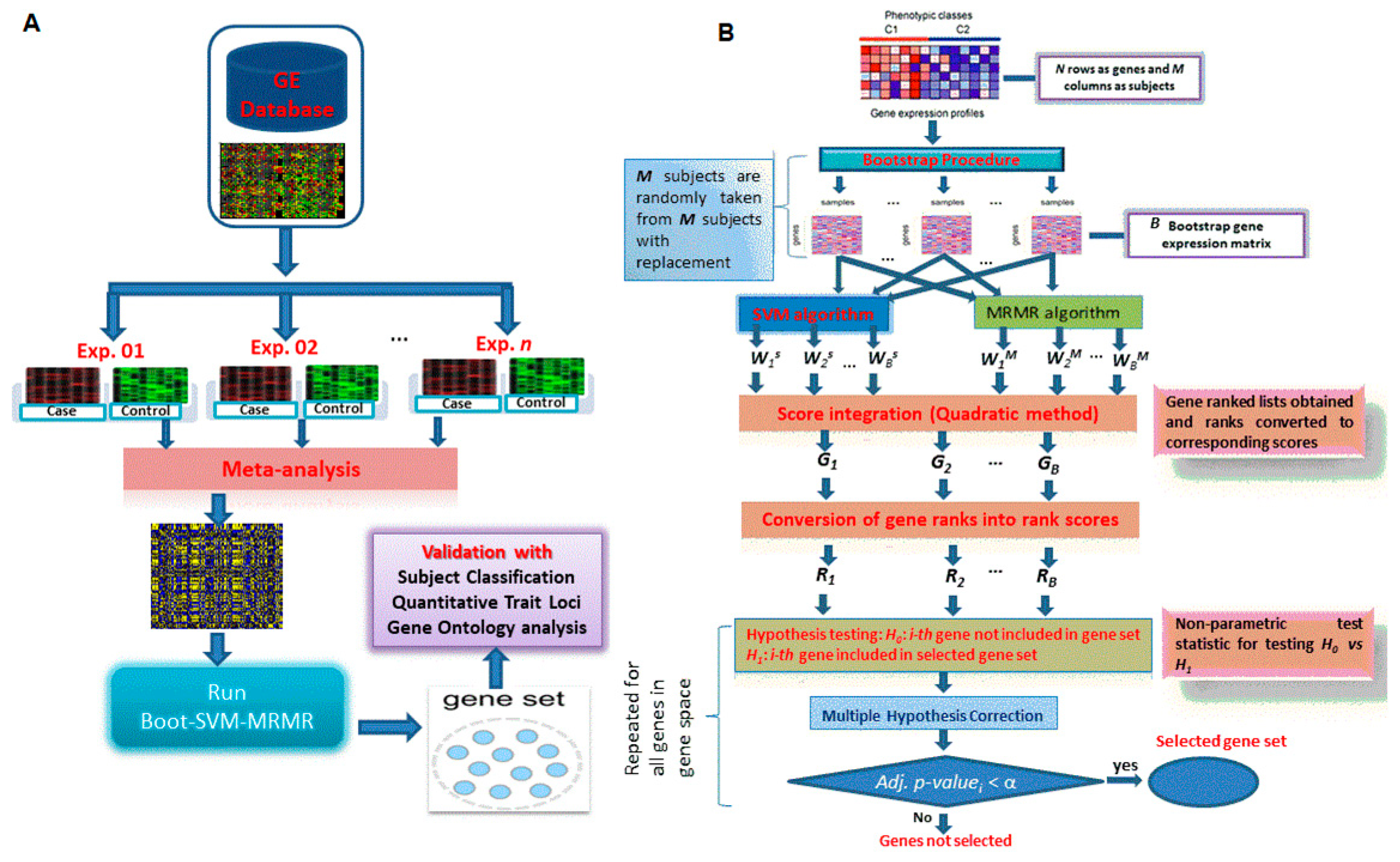
2.3.4. Proposed Hybrid Approach of Gene Selection
2.4. Comparative Performance Analysis of the Proposed Approach
2.4.1. Performance Analysis with Subject Classification
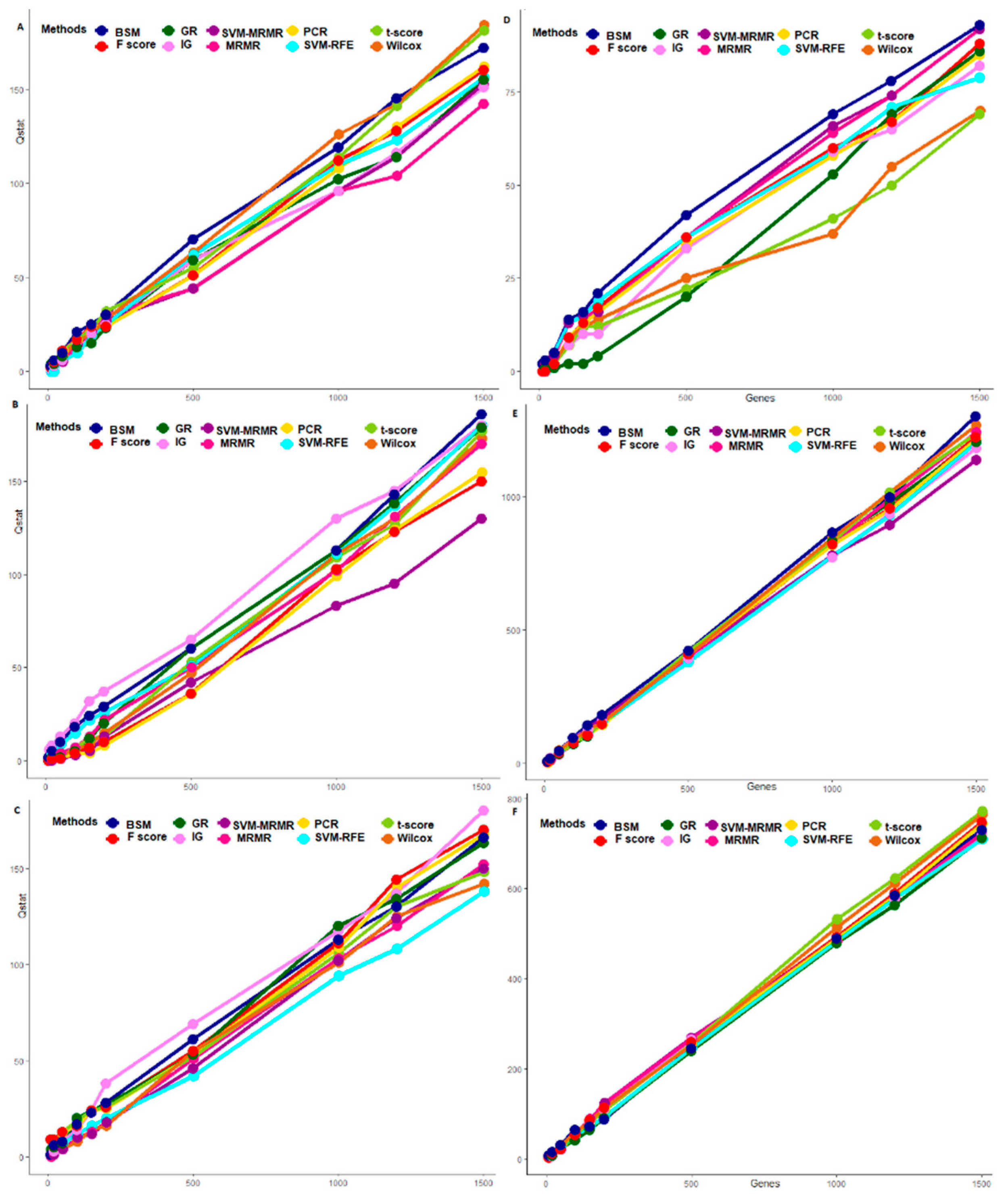
2.4.2. Performance Analysis with QTL Testing
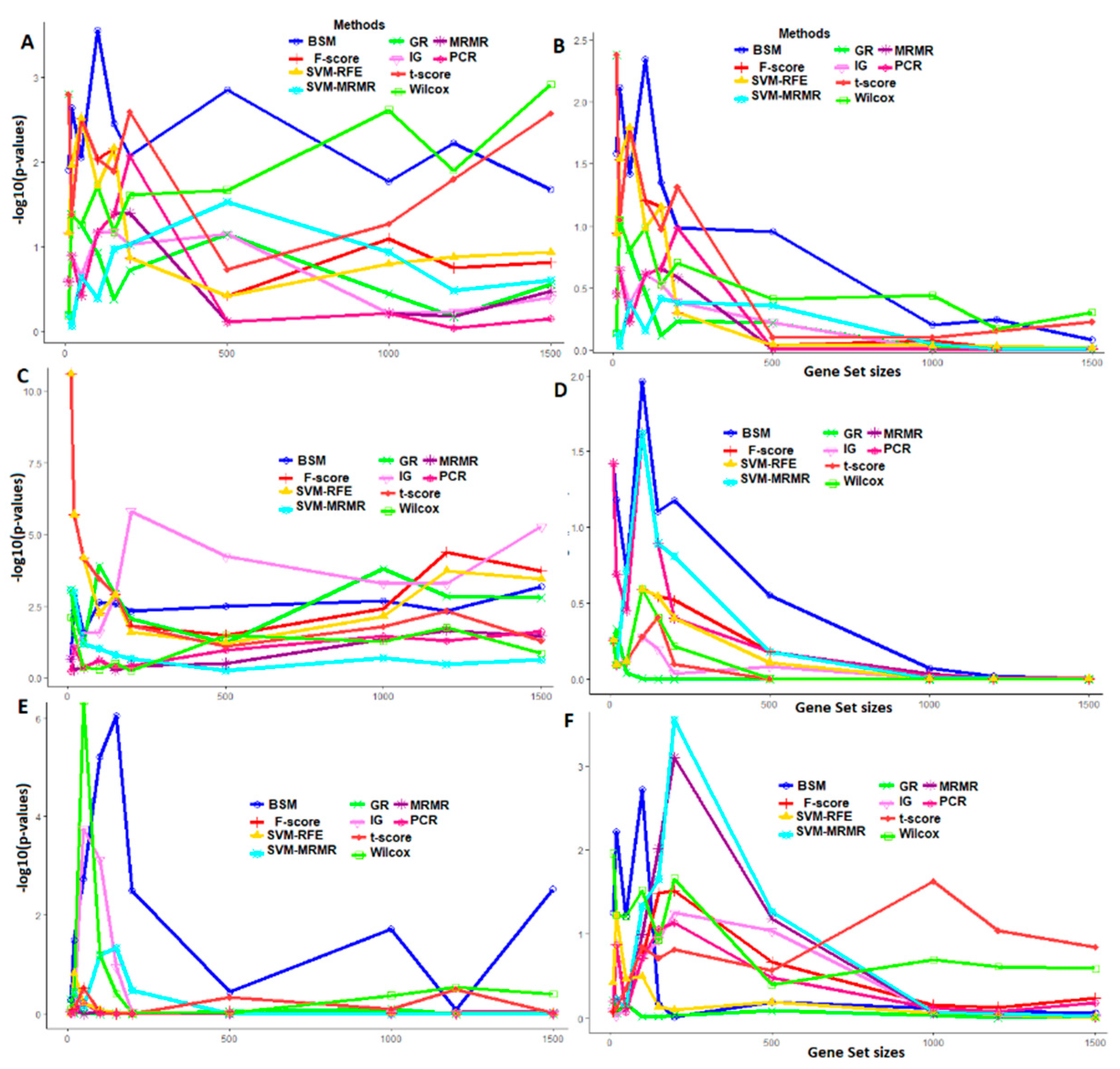
2.4.3. Performance Analysis with GO Enrichment
3. Results and Discussion
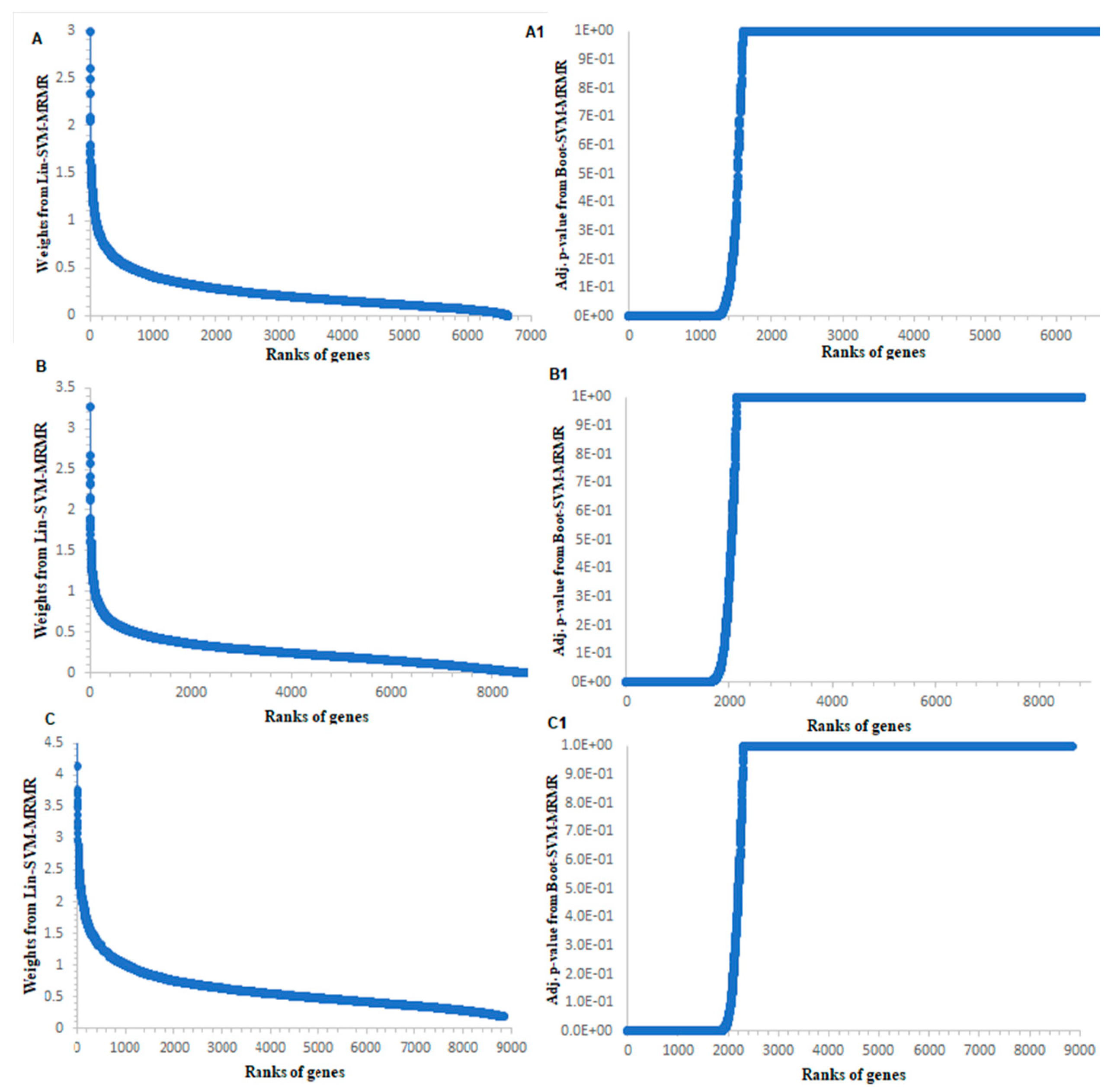
3.1. Computation of Genes Selection Criteria through Proposed Approach
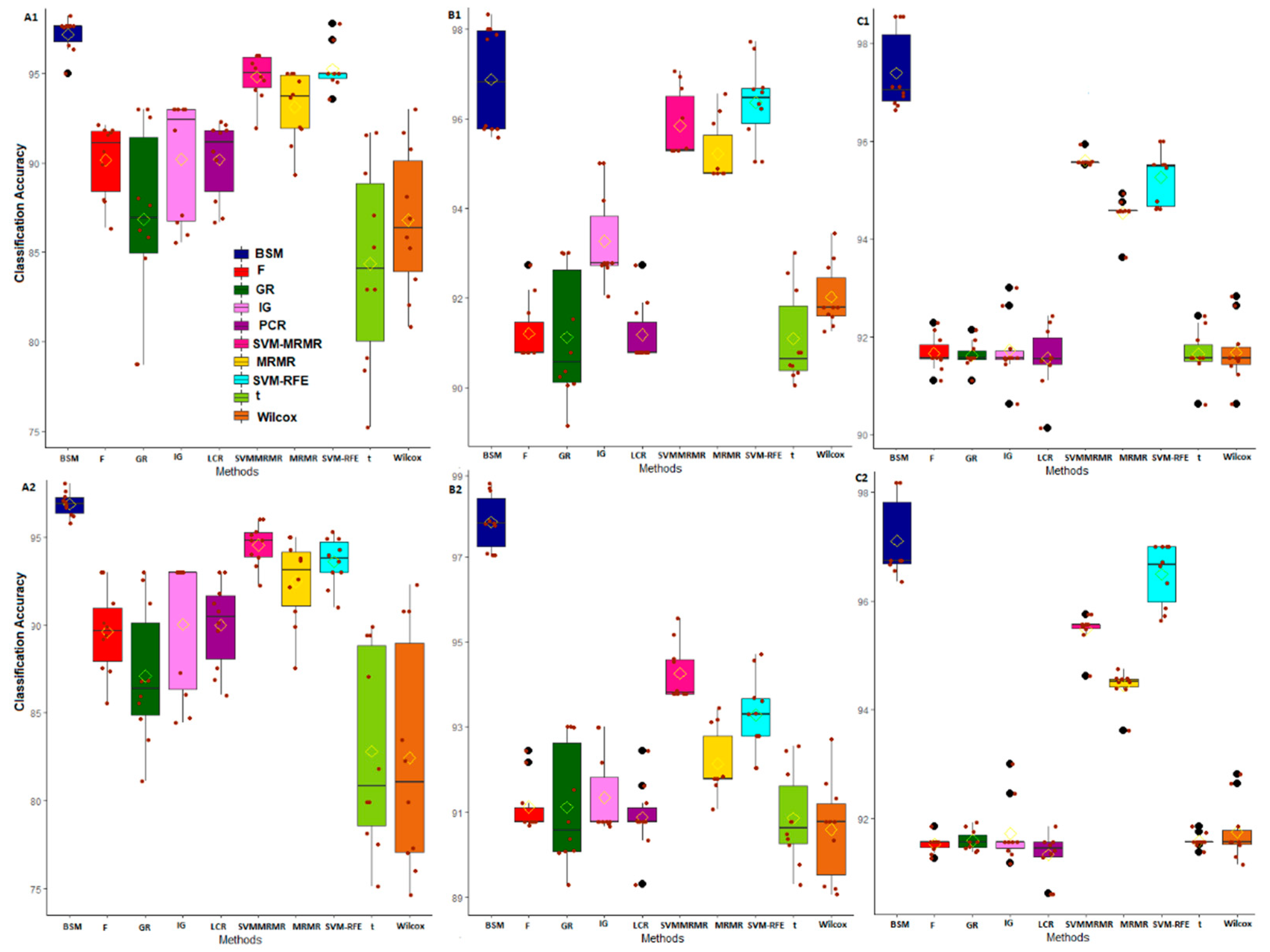
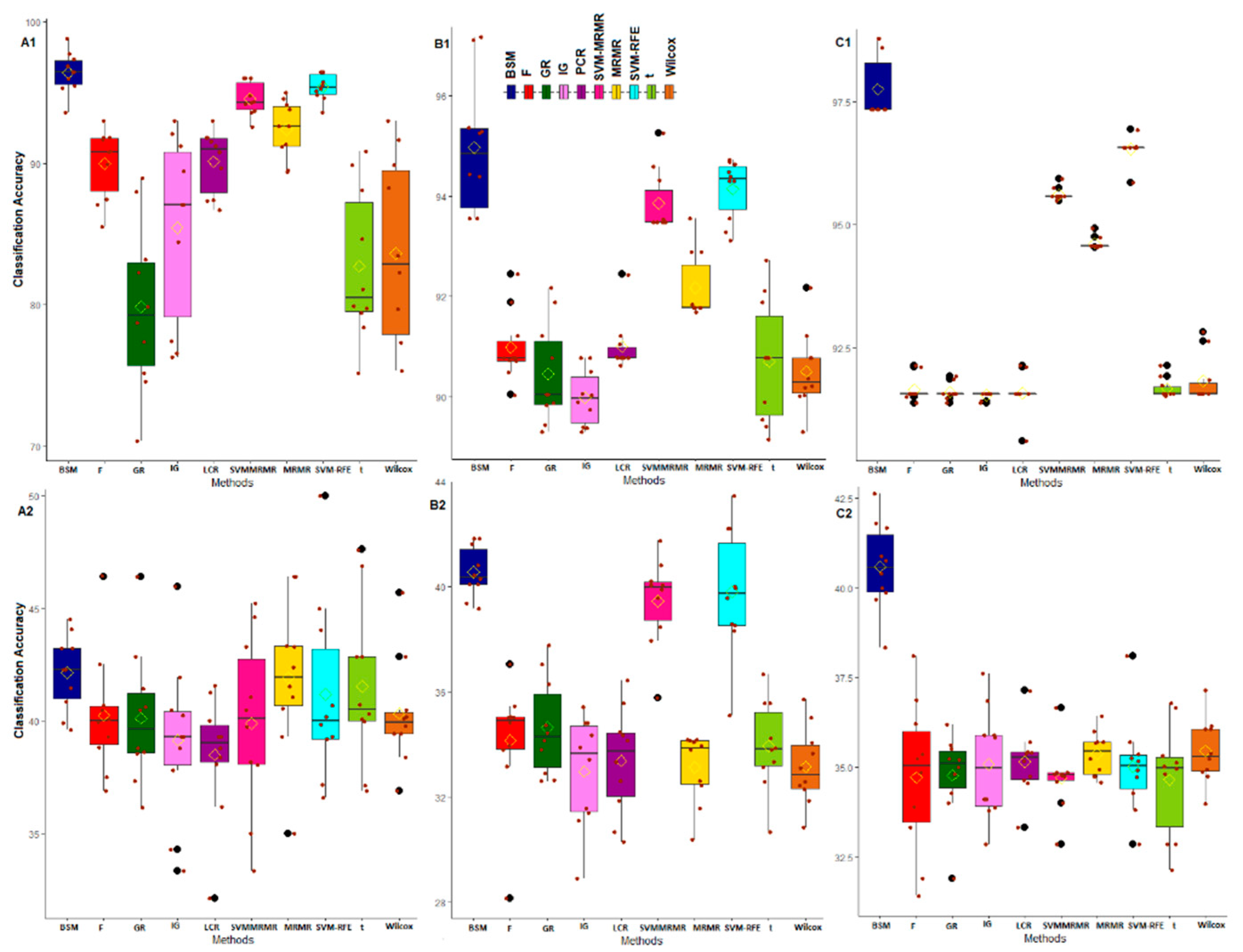
3.2. Comparative Performance Analysis Based on Subject Classification
3.3. Comparative Performance Analysis Based on QTL Testing
3.4. Comparative Performance Analysis Based on GO Analysis
3.5. Comparative Performance Analysis Based on Runtime
4. Developed R Software Package
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Availability of Data and Material
References
- Reuter, J.A.; Spacek, D.V.; Snyder, M.P. High-Throughput Sequencing Technologies. Mol. Cell 2015, 58, 586–597. [Google Scholar] [CrossRef] [PubMed]
- Trevino, V.; Falciani, F.; Barrera-Saldaña, H.A. DNA Microarrays: A Powerful Genomic Tool for Biomedical and Clinical Research. Mol. Med. 2007, 13, 527–541. [Google Scholar] [CrossRef] [PubMed]
- Charpe, A.M. DNA Microarray. In Advances in Biotechnology; Springer: New Delhi, India, 2014; pp. 71–104. [Google Scholar] [CrossRef]
- Barrett, T.; Wilhite, S.E.; Ledoux, P.; Evangelista, C.; Kim, I.F.; Tomashevsky, M. NCBI GEO: Archive for functional genomics data sets—Update. Nucleic Acids Res. 2012, 41, D991–D995. [Google Scholar] [CrossRef]
- Das, S.; Meher, P.K.; Rai, A.; Bhar, L.M.; Mandal, B.N. Statistical approaches for gene selection, hub gene identification and module interaction in gene co-expression network analysis: An application to aluminum stress in soybean (Glycine max L.). PLoS ONE 2017, 12, e0169605. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, L.; Wang, Y.; Zhang, J.; Liang, Y.; Xu, D. A Computational Systems Biology Study for Understanding Salt Tolerance Mechanism in Rice. PLoS ONE 2013, 8, e64929. [Google Scholar] [CrossRef] [PubMed]
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P. Molecular Classification of Cancer: Class Discovery and Class Prediction by Gene Expression Monitoring. Science 1999, 286, 531–537. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, F.; Wang, J.; Joshi, T.; Wang, Y.; Xu, D. Prediction of Drought-Resistant Genes in Arabidopsis thaliana Using SVM-RFE. PLoS ONE 2011, 6, e21750. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005. [Google Scholar] [CrossRef]
- Mundra, P.A.; Rajapakse, J.C. SVM-RFE with MRMR Filter for Gene Selection. IEEE Trans. Nanobioscience 2010, 9, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Pandey, P.; Rai, A.; Mohapatra, C. A computational system biology approach to construct gene regulatory networks for salinity response in rice (Oryza sativa). Indian J. Agric. Sci. 2015, 85, 1546–1552. [Google Scholar]
- Kursa, M.B. Robustness of Random Forest-based gene selection methods. BMC Bioinform. 2014. [Google Scholar] [CrossRef] [PubMed]
- Inza, I.; Larrañaga, P.; Blanco, R.; Cerrolaza, A.J. Filter versus wrapper gene selection approaches in DNA microarray domains. Artif. Intell. Med. 2004. [Google Scholar] [CrossRef] [PubMed]
- Lazar, C.; Taminau, J.; Meganck, S.; Steenhoff, D.; Coletta, A.; Molter, C. A survey on filter techniques for feature selection in gene expression microarray analysis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Churchill, G.A. Statistical tests for differential expression in cDNA microarray experiments. Genome Biol. 2003. [Google Scholar] [CrossRef]
- Das, S.; Meher, P.K.; Pradhan, U.K.; Paul, A.K. Inferring gene regulatory networks using Kendall’s tau correlation coefficient and identification of salinity stress responsive genes in rice. Curr. Sci. 2017, 112. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. Computational Systems Bioinformatics CSB2003 Proceedings of the 2003 IEEE Bioinformatics Conference CSB2003. IEEE Comput. Soc. 2003, 523–528. [Google Scholar] [CrossRef]
- Chen, Y.W.; Lin, C.J. Combining SVMs with various feature selection strategies. Stud. Fuzziness Soft Comput. 2006. [Google Scholar] [CrossRef]
- Hossain, A.; Willan, A.R.; Beyene, J. An improved method on wilcoxon rank sum test for gene selection from microarray experiments. Commun. Stat. Simul. Comput. 2013. [Google Scholar] [CrossRef]
- Troyanskaya, O.G.; Garber, M.E.; Brown, P.O.; Botstein, D.; Altman, R.B. Nonparametric methods for identifying differentially expressed genes in microarray data. Bioinformatics 2002. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Wang, Y.; Bryant, S.H. F Selector: A Ruby gem for feature selection. Bioinformatics 2012, 28, 2851–2852. [Google Scholar] [CrossRef][Green Version]
- Radovic, M.; Ghalwash, M.; Filipovic, N.; Obradovic, Z. Minimum redundancy maximum relevance feature selection approach for temporal gene expression data. BMC Bioinform. 2017, 18, 9. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Zhang, G.-L.; Pan, L.-L.; Huang, T.; Wang, J.-H. The transcriptome difference between colorectal tumor and normal tissues revealed by single-cell sequencing. J. Cancer 2019, 10, 5883–5890. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Duan, K.B.; Rajapakse, J.C.; Wang, H.; Azuaje, F. Multiple SVM-RFE for gene selection in cancer classification with expression data. IEEE Trans. Nanobioscience 2005. [Google Scholar] [CrossRef]
- Tao, X.; Wu, X.; Huang, T.; Mu, D. Identification and Analysis of Dysfunctional Genes and Pathways in CD8+ T Cells of Non-Small Cell Lung Cancer Based on RNA Sequencing. Front. Genet. 2020. [Google Scholar] [CrossRef] [PubMed]
- Ting, K.M.; Witten, I.H. Stacking bagged and dagged models. In ICML ′97: Proceedings of the Fourteenth International Conference on Machine Learning; Douglas, H., Fisher, E.D., Eds.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1997; pp. 367–375. [Google Scholar]
- Li, J.R.; Huang, T. Predicting and analyzing early wake-up associated gene expressions by integrating GWAS and eQTL studies. Biochim. Biophys. Acta Mol. Basis Dis. 2018. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Kong, X.; Xu, J.; Xue, Z.; Zhai, R.; Zhang, S. A Hybrid Gene Selection Method Based on ReliefF and Ant Colony Optimization Algorithm for Tumor Classification. Sci. Rep. 2019. [Google Scholar] [CrossRef]
- Mahi, M.; Baykan, Ö.K.; Kodaz, H. A new hybrid method based on Particle Swarm Optimization, Ant Colony Optimization and 3-Opt algorithms for Traveling Salesman Problem. Appl. Soft Comput. 2015, 30, 484–490. [Google Scholar] [CrossRef]
- Sohn, I.; Owzar, K.; George, S.L.; Kim, S.; Jung, S.H. A permutation-based multiple testing method for time-course microarray experiments. BMC Bioinform. 2009. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Phipson, B.; Wu, D.; Hu, Y.; Law, C.W.; Shi, W. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef]
- Knijnenburg, T.A.; Wessels, L.F.A.; Reinders, M.J.T.; Shmulevich, I. Fewer permutations, more accurate P-values. Bioinformatics 2009. [Google Scholar] [CrossRef]
- Das, S.; Rai, A.; Mishra, D.C.; Rai, S.N. Statistical approach for selection of biologically informative genes. Gene 2018, 655. [Google Scholar] [CrossRef]
- Lai, C.; Reinders, M.J.T.; van’t Veer, L.J.; Wessels, L.F.A. A comparison of univariate and multivariate gene selection techniques for classification of cancer datasets. BMC Bioinform. 2006. [Google Scholar] [CrossRef]
- Das, S.; Rai, A.; Mishra, D.C.; Rai, S.N. Statistical Approach for Gene Set Analysis with Trait Specific Quantitative Trait Loci. Sci. Rep. 2018, 8, 2391. [Google Scholar] [CrossRef]
- Tiwari, S.; Kumar, V.; Singh, B.; Rao, A.; Mithra, S.V.A. Mapping QTLs for Salt Tolerance in Rice (Oryza sativa L) by Bulked Segregant Analysis of Recombinant Inbred Lines Using 50K SNP Chip. Yadav RS, editor. PLoS ONE 2016, 11, e0153610. [Google Scholar] [CrossRef]
- Gene Ontology Consortium. The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 2004. [Google Scholar] [CrossRef]
- Gautier, L.; Cope, L.; Bolstad, B.M.; Irizarry, R.A. Affy—Analysis of Affymetrix GeneChip data at the probe level. Bioinformatics 2004. [Google Scholar] [CrossRef] [PubMed]
- Ware, D. Gramene: A resource for comparative grass genomics. Nucleic Acids Res. 2002. [Google Scholar] [CrossRef] [PubMed]
- Tian, T.; Liu, Y.; Yan, H.; You, Q.; Yi, X.; Du, Z. AgriGO v2.0: A GO analysis toolkit for the agricultural community, 2017 update. Nucleic Acids Res. 2017. [Google Scholar] [CrossRef]
- Sahani, M.; Linden, J. Advances in Neural Information Processing Systems, Processing Systems: Proceedings from the 2002, 2003; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Springer: Boston, MA, USA, 1993. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Multiple Hypotheses Testing with Weights. Scand. J. Stat. 1997, 24, 407–418. [Google Scholar] [CrossRef]
- Li, Q.; Brown, J.B.; Huang, H.; Bickel, P.J. Measuring reproducibility of high-throughput experiments. Ann. Appl. Stat. 2011, 5, 1752–1779. [Google Scholar] [CrossRef]
- Chen, S.-Y.; Feng, Z.; Yi, X. A general introduction to adjustment for multiple comparisons. J. Thorac. Dis. 2017, 9, 1725–1729. [Google Scholar] [CrossRef] [PubMed]
- Mazandu, G.K.; Mulder, N.J. Information content-based gene ontology functional similarity measures: Which one to use for a given biological data type? PLoS ONE 2014. [Google Scholar] [CrossRef]
- Lord, P.W.; Stevens, R.D.; Brass, A.; Goble, C.A. Investigating semantic similarity measures across the gene ontology: The relationship between sequence and annotation. Bioinformatics 2003. [Google Scholar] [CrossRef]
- Wang, J.Z.; Du, Z.; Payattakool, R.; Yu, P.S.; Chen, C.F. A new method to measure the semantic similarity of GO terms. Bioinformatics 2007. [Google Scholar] [CrossRef]
- Ouyang, S.; Zhu, W.; Hamilton, J.; Lin, H.; Campbell, M.; Childs, K. The TIGR Rice Genome Annotation Resource: Improvements and new features. Nucleic Acids Res. 2007. [Google Scholar] [CrossRef] [PubMed]
- Glazko, G.V.; Emmert-Streib, F. Unite and conquer: Univariate and multivariate approaches for finding differentially expressed gene sets. Bioinformatics 2009. [Google Scholar] [CrossRef] [PubMed]
| Sl. No. | Descriptions | #Series | Series ID | #Genes | #Samples | Stress Type |
|---|---|---|---|---|---|---|
| 1. | Salinity stress | 3. | GSE14403, GSE16108, GSE6901. | 6637 | 45 (23, 22) | Abiotic |
| 2. | Cold stress | 4. | GSE31077, GSE33204. GSE37940, GSE6901. | 8840 | 28 (15, 13) | Abiotic |
| 3. | Drought stress | 5. | GSE6901, GSE26280. GSE21651, GSE23211. GSE24048. | 9078 | 70 (35, 35) | Abiotic |
| 4. | Bacterial (xanthomonas) stress | 3. | GSE19239, GSE36093. GSE36272. | 8356 | 74 (37, 37) | Biotic |
| 5. | Fungal (blast) stress | 2. | GSE41798, GSE7256. | 7072 | 26 (13, 13) | Biotic |
| 6. | Insect (brown plant hopper) stress | 1. | GSE29967. | 7241 | 18 (12, 6) | Biotic |
| Methods | MRMR | SVM | SVM-MRMR | IG | GR | Wilcox | t | PCR | F | BSM |
|---|---|---|---|---|---|---|---|---|---|---|
| Salt stress in rice | ||||||||||
| 10 | 0.98 | 0.95 | 0.97 | 0.92 | 0.89 | 0.93 | 0.93 | 0.96 | 0.96 | 0.88 |
| 20 | 0.97 | 0.89 | 0.93 | 0.92 | 0.86 | 0.89 | 0.89 | 0.91 | 0.91 | 0.86 |
| 50 | 0.92 | 0.91 | 0.92 | 0.90 | 0.90 | 0.87 | 0.87 | 0.92 | 0.92 | 0.85 |
| 100 | 0.92 | 0.90 | 0.89 | 0.90 | 0.88 | 0.87 | 0.88 | 0.92 | 0.91 | 0.83 |
| 150 | 0.90 | 0.89 | 0.90 | 0.89 | 0.88 | 0.87 | 0.87 | 0.90 | 0.91 | 0.83 |
| 200 | 0.90 | 0.89 | 0.88 | 0.89 | 0.87 | 0.88 | 0.88 | 0.90 | 0.90 | 0.84 |
| 500 | 0.90 | 0.90 | 0.89 | 0.90 | 0.90 | 0.89 | 0.90 | 0.89 | 0.89 | 0.83 |
| Cold stress in rice | ||||||||||
| 10 | 0.82 | 0.84 | 0.82 | 0.92 | 0.99 | 0.92 | 0.87 | 0.77 | 0.77 | 0.75 |
| 20 | 0.93 | 0.88 | 0.93 | 0.95 | 0.93 | 0.88 | 0.90 | 0.91 | 0.88 | 0.71 |
| 50 | 0.91 | 0.88 | 0.91 | 0.93 | 0.90 | 0.91 | 0.91 | 0.92 | 0.92 | 0.73 |
| 100 | 0.91 | 0.90 | 0.91 | 0.90 | 0.88 | 0.91 | 0.91 | 0.91 | 0.91 | 0.74 |
| 150 | 0.90 | 0.89 | 0.90 | 0.89 | 0.89 | 0.89 | 0.90 | 0.91 | 0.91 | 0.72 |
| 200 | 0.90 | 0.89 | 0.90 | 0.89 | 0.88 | 0.89 | 0.90 | 0.90 | 0.90 | 0.73 |
| 500 | 0.90 | 0.88 | 0.90 | 0.90 | 0.89 | 0.88 | 0.89 | 0.88 | 0.89 | 0.73 |
| Drought stress in rice | ||||||||||
| 10 | 0.82 | 0.86 | 0.81 | 0.90 | 0.93 | 0.65 | 0.76 | 0.76 | 0.76 | 0.71 |
| 20 | 0.79 | 0.86 | 0.78 | 0.91 | 0.90 | 0.80 | 0.81 | 0.81 | 0.81 | 0.75 |
| 50 | 0.88 | 0.84 | 0.87 | 0.88 | 0.90 | 0.84 | 0.88 | 0.89 | 0.89 | 0.75 |
| 100 | 0.89 | 0.89 | 0.88 | 0.89 | 0.89 | 0.88 | 0.88 | 0.88 | 0.88 | 0.76 |
| 150 | 0.88 | 0.88 | 0.87 | 0.89 | 0.88 | 0.88 | 0.88 | 0.88 | 0.88 | 0.76 |
| 200 | 0.88 | 0.88 | 0.87 | 0.88 | 0.89 | 0.89 | 0.88 | 0.88 | 0.88 | 0.74 |
| 500 | 0.88 | 0.88 | 0.87 | 0.88 | 0.88 | 0.89 | 0.88 | 0.87 | 0.87 | 0.73 |
| Methods | MRMR | SVM | SVM-MRMR | IG | GR | Wilcox | t | PCR | F | BSM |
|---|---|---|---|---|---|---|---|---|---|---|
| Salt stress in rice | ||||||||||
| 10 | 0.86 | 0.94 | 0.86 | 0.92 | 0.97 | 0.90 | 0.90 | 0.88 | 0.88 | 0.83 |
| 20 | 0.90 | 0.91 | 0.90 | 0.89 | 0.91 | 0.92 | 0.92 | 0.84 | 0.85 | 0.84 |
| 50 | 0.89 | 0.90 | 0.88 | 0.88 | 0.90 | 0.88 | 0.89 | 0.88 | 0.88 | 0.82 |
| 100 | 0.88 | 0.89 | 0.86 | 0.89 | 0.89 | 0.85 | 0.86 | 0.89 | 0.87 | 0.82 |
| 150 | 0.87 | 0.89 | 0.90 | 0.88 | 0.89 | 0.85 | 0.85 | 0.89 | 0.89 | 0.83 |
| 200 | 0.87 | 0.89 | 0.86 | 0.88 | 0.89 | 0.84 | 0.85 | 0.89 | 0.88 | 0.82 |
| 500 | 0.87 | 0.89 | 0.87 | 0.87 | 0.89 | 0.86 | 0.86 | 0.86 | 0.86 | 0.82 |
| Cold stress in rice | ||||||||||
| 10 | 0.79 | 0.82 | 0.79 | 0.86 | 0.94 | 0.91 | 0.90 | 0.79 | 0.79 | 0.79 |
| 20 | 0.93 | 0.89 | 0.93 | 0.90 | 0.88 | 0.86 | 0.88 | 0.90 | 0.86 | 0.82 |
| 50 | 0.88 | 0.89 | 0.88 | 0.90 | 0.88 | 0.88 | 0.87 | 0.89 | 0.90 | 0.71 |
| 100 | 0.88 | 0.89 | 0.88 | 0.89 | 0.87 | 0.90 | 0.88 | 0.89 | 0.89 | 0.74 |
| 150 | 0.89 | 0.88 | 0.89 | 0.88 | 0.88 | 0.88 | 0.87 | 0.88 | 0.88 | 0.73 |
| 200 | 0.89 | 0.87 | 0.89 | 0.87 | 0.87 | 0.87 | 0.87 | 0.88 | 0.84 | 0.73 |
| 500 | 0.88 | 0.86 | 0.88 | 0.86 | 0.86 | 0.84 | 0.86 | 0.87 | 0.83 | 0.71 |
| Drought stress in rice | ||||||||||
| 10 | 0.86 | 0.79 | 0.85 | 0.81 | 0.89 | 0.62 | 0.83 | 0.83 | 0.83 | 0.73 |
| 20 | 0.84 | 0.79 | 0.83 | 0.89 | 0.90 | 0.80 | 0.84 | 0.84 | 0.84 | 0.72 |
| 50 | 0.88 | 0.81 | 0.87 | 0.88 | 0.88 | 0.81 | 0.88 | 0.88 | 0.88 | 0.72 |
| 100 | 0.87 | 0.84 | 0.86 | 0.88 | 0.88 | 0.84 | 0.86 | 0.87 | 0.87 | 0.72 |
| 150 | 0.86 | 0.84 | 0.85 | 0.88 | 0.88 | 0.84 | 0.87 | 0.87 | 0.87 | 0.71 |
| 200 | 0.86 | 0.84 | 0.85 | 0.87 | 0.87 | 0.85 | 0.86 | 0.86 | 0.86 | 0.72 |
| 500 | 0.87 | 0.85 | 0.86 | 0.86 | 0.87 | 0.87 | 0.86 | 0.85 | 0.83 | 0.72 |
| MRMR | SVM | SVM-MRMR | IG | GR | Wilcox | t | PCR | F | BSM | |
|---|---|---|---|---|---|---|---|---|---|---|
| Salt stress in rice | ||||||||||
| 10 | 0.77 | 0.71 | 0.70 | 0.94 | 0.97 | 0.93 | 0.93 | 0.95 | 0.95 | 0.78 |
| 20 | 0.88 | 0.87 | 0.85 | 0.92 | 0.90 | 0.91 | 0.91 | 0.88 | 0.88 | 0.81 |
| 50 | 0.88 | 0.89 | 0.86 | 0.92 | 0.92 | 0.90 | 0.90 | 0.89 | 0.89 | 0.84 |
| 100 | 0.88 | 0.90 | 0.8 | 0.91 | 0.89 | 0.86 | 0.86 | 0.88 | 0.88 | 0.83 |
| 150 | 0.87 | 0.90 | 0.87 | 0.90 | 0.89 | 0.86 | 0.87 | 0.88 | 0.88 | 0.83 |
| 200 | 0.87 | 0.89 | 0.85 | 0.90 | 0.90 | 0.88 | 0.89 | 0.88 | 0.88 | 0.83 |
| 500 | 0.88 | 0.90 | 0.88 | 0.89 | 0.90 | 0.88 | 0.89 | 0.87 | 0.87 | 0.82 |
| Cold stress in rice | ||||||||||
| 10 | 0.78 | 0.80 | 0.78 | 0.96 | 0.81 | 0.87 | 0.86 | 0.70 | 0.70 | 0.70 |
| 20 | 0.88 | 0.86 | 0.88 | 0.96 | 0.87 | 0.87 | 0.89 | 0.81 | 0.83 | 0.71 |
| 50 | 0.86 | 0.89 | 0.86 | 0.90 | 0.85 | 0.84 | 0.85 | 0.89 | 0.90 | 0.73 |
| 100 | 0.88 | 0.90 | 0.88 | 0.90 | 0.81 | 0.83 | 0.84 | 0.87 | 0.87 | 0.74 |
| 150 | 0.88 | 0.89 | 0.88 | 0.90 | 0.82 | 0.82 | 0.86 | 0.87 | 0.88 | 0.74 |
| 200 | 0.87 | 0.90 | 0.87 | 0.90 | 0.84 | 0.85 | 0.86 | 0.87 | 0.85 | 0.73 |
| 500 | 0.88 | 0.89 | 0.88 | 0.89 | 0.86 | 0.97 | 0.86 | 0.88 | 0.87 | 0.73 |
| Drought stress in rice | ||||||||||
| 10 | 0.82 | 0.86 | 0.81 | 0.91 | 0.89 | 0.83 | 0.87 | 0.87 | 0.87 | 0.74 |
| 20 | 0.89 | 0.85 | 0.88 | 0.93 | 0.90 | 0.87 | 0.89 | 0.89 | 0.89 | 0.74 |
| 50 | 0.86 | 0.88 | 0.85 | 0.91 | 0.87 | 0.87 | 0.88 | 0.88 | 0.88 | 0.73 |
| 100 | 0.87 | 0.87 | 0.86 | 0.89 | 0.86 | 0.87 | 0.88 | 0.88 | 0.88 | 0.74 |
| 150 | 0.87 | 0.87 | 0.86 | 0.90 | 0.85 | 0.85 | 0.87 | 0.87 | 0.87 | 0.74 |
| 200 | 0.87 | 0.87 | 0.86 | 0.89 | 0.86 | 0.86 | 0.87 | 0.87 | 0.87 | 0.73 |
| 500 | 0.87 | 0.86 | 0.86 | 0.89 | 0.87 | 0.88 | 0.87 | 0.86 | 0.85 | 0.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.; Rai, S.N. Statistical Approach for Biologically Relevant Gene Selection from High-Throughput Gene Expression Data. Entropy 2020, 22, 1205. https://doi.org/10.3390/e22111205
Das S, Rai SN. Statistical Approach for Biologically Relevant Gene Selection from High-Throughput Gene Expression Data. Entropy. 2020; 22(11):1205. https://doi.org/10.3390/e22111205
Chicago/Turabian StyleDas, Samarendra, and Shesh N. Rai. 2020. "Statistical Approach for Biologically Relevant Gene Selection from High-Throughput Gene Expression Data" Entropy 22, no. 11: 1205. https://doi.org/10.3390/e22111205
APA StyleDas, S., & Rai, S. N. (2020). Statistical Approach for Biologically Relevant Gene Selection from High-Throughput Gene Expression Data. Entropy, 22(11), 1205. https://doi.org/10.3390/e22111205






