Shape Effect of Nanosize Particles on Magnetohydrodynamic Nanofluid Flow and Heat Transfer over a Stretching Sheet with Entropy Generation
Abstract
1. Introduction
2. Mathematical Formulation
3. Solution via Homotopy Analysis Method
4. Entropy Generation
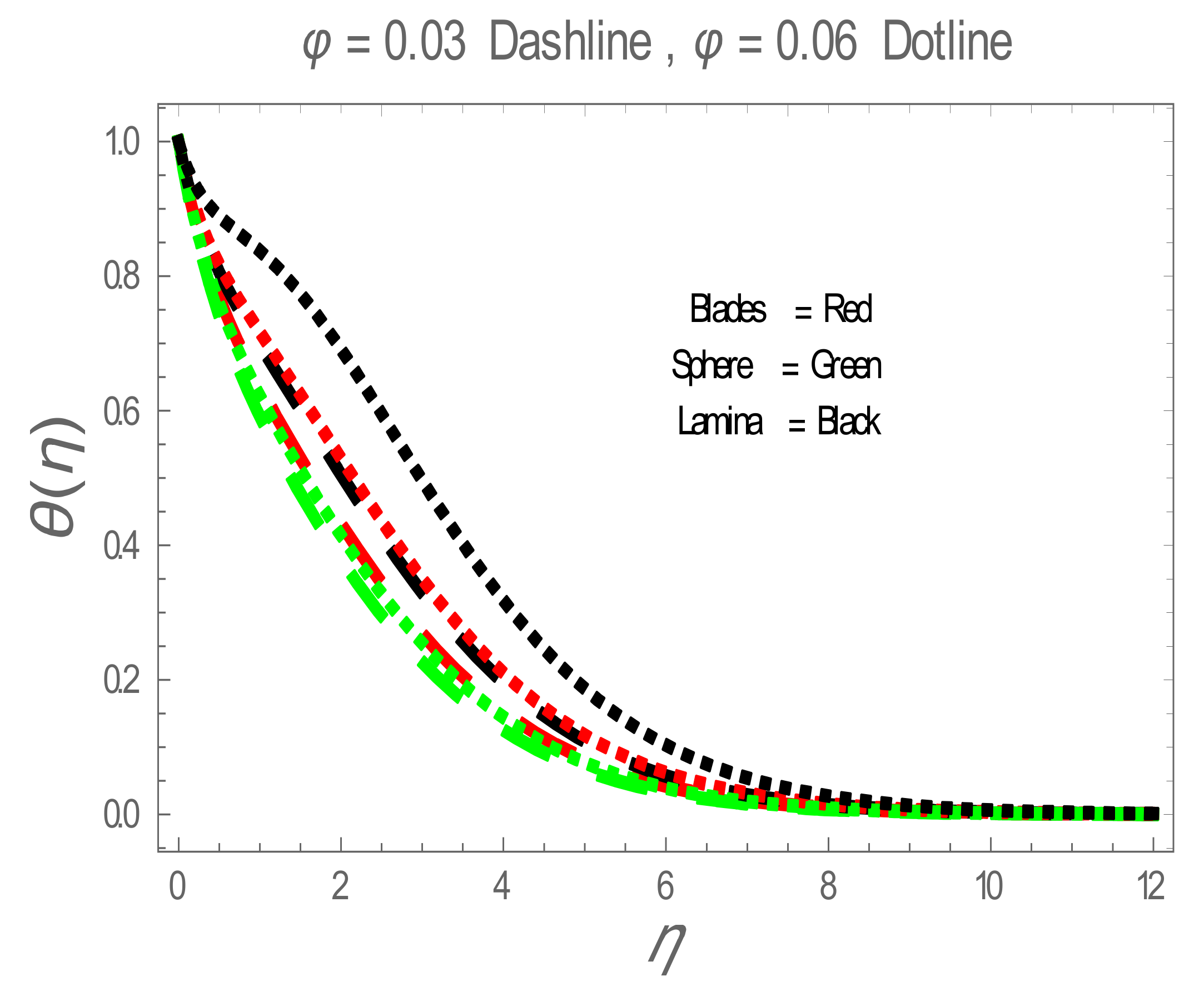
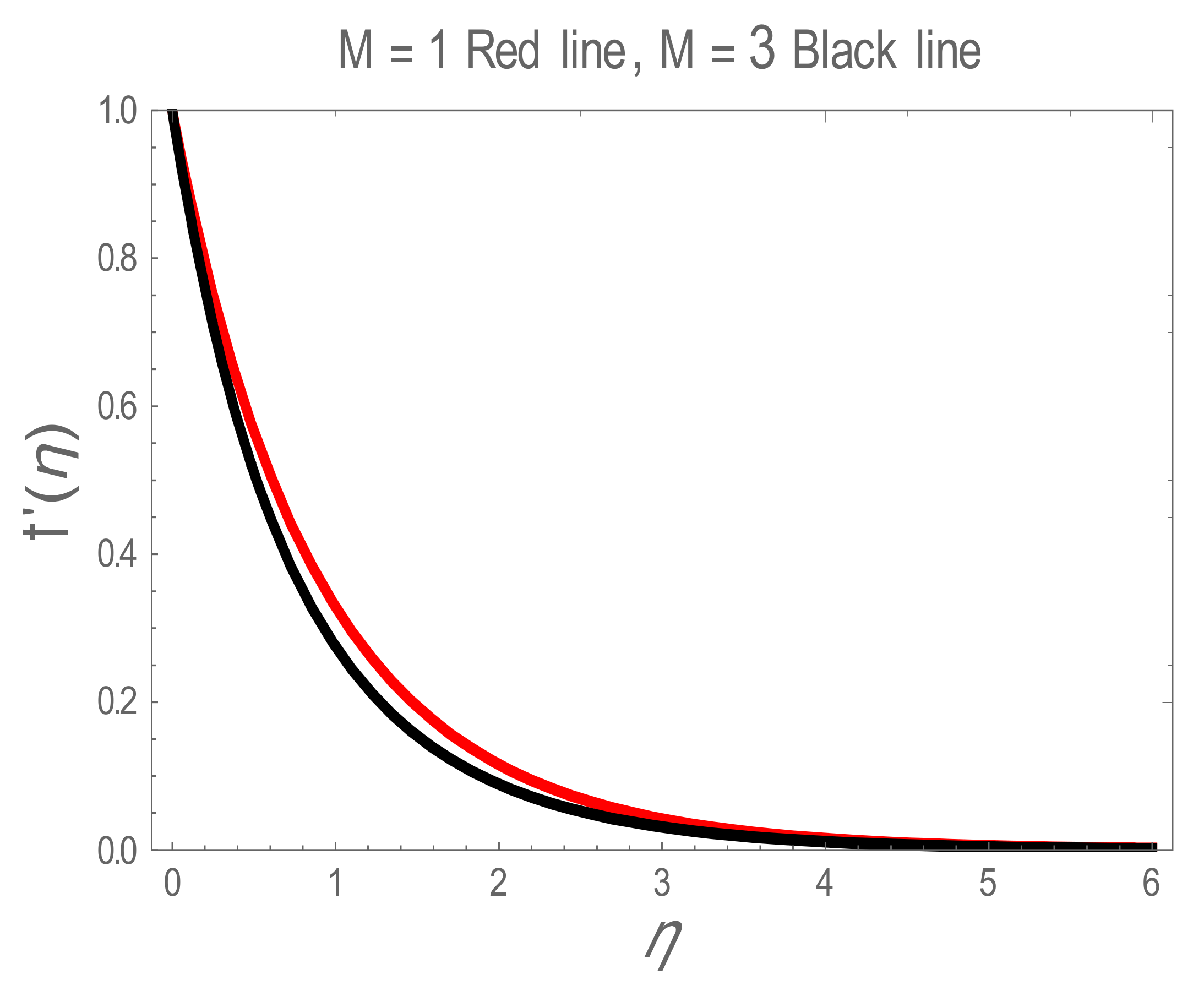
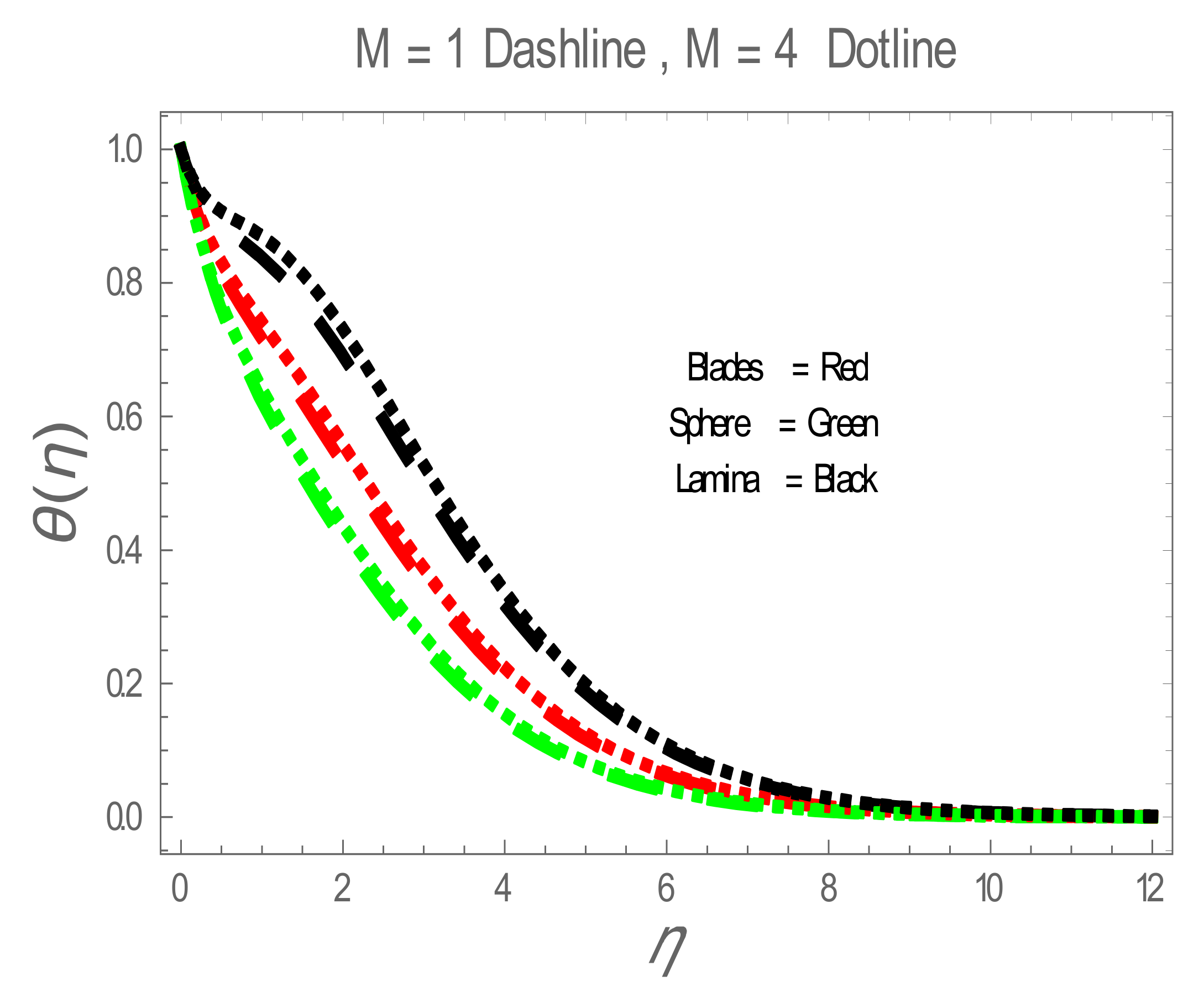
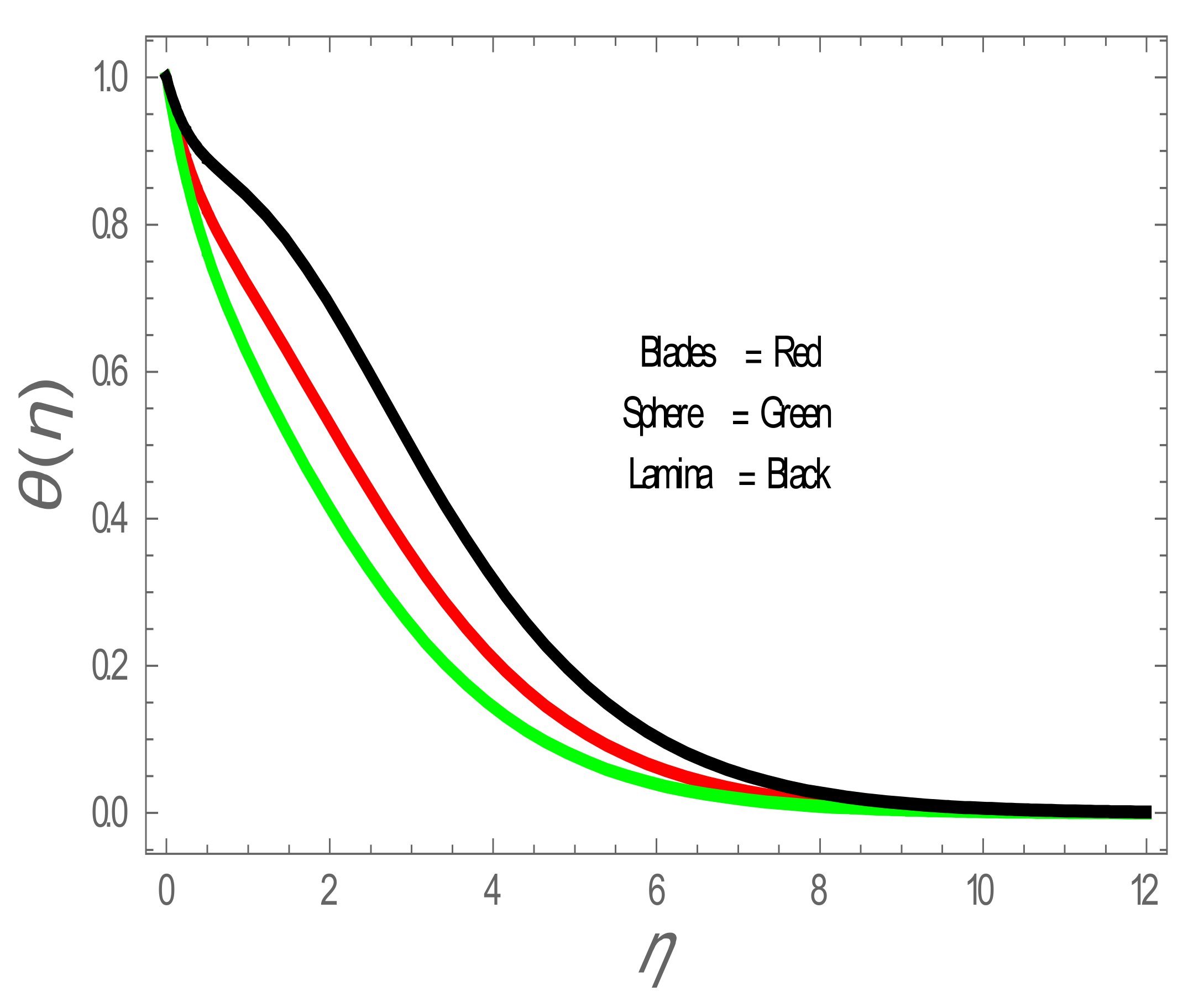
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| T | Temperature of nanofluid (k) |
| u, v | The velocity components (m/s) |
| Stream function (m2/s) | |
| Thermal conductivity of the nanofluid (W/m K) | |
| Thermal conductivity of the fluid (W/m K) | |
| Thermal conductivity of the solid (W/m K) | |
| Specific heat capacity of the nanofluid (J/kg K) | |
| Specific heat capacity of the fluid (J/kg K) | |
| Specific heat capacity of the solid (J/kg K) | |
| Density of the nanofluid (kg/m3) | |
| Density of the fluid (kg/m3) | |
| Density of the solid (kg/m3) | |
| Solid volume fraction | |
| Dynamic viscosity of the nanofluid (Ns/m2) | |
| Ratio of volumetric entropy (W/m3K) | |
| Characteristic entropy generation rate | |
| Electric conductivity of nanofluid (S/m) | |
| Dimensionless temperature difference | |
| The imposed magnetic strength (kg/s2 A) | |
| Brinkman number | |
| Hartman number | |
| Prandtl number | |
| Shape variable | |
| Nanofluid | |
| Liquid | |
| Solid |
Abbreviations
| MHD | Magnetohydrodynamic |
| PDEs | Partial differential equations |
| ODEs | Ordinary differential equations |
| HAM | Homotopy analysis method |
References
- Govindaraju, M.; Vishnu Ganesh, N.; Ganga, B.; Abdul Hakeem, A.K. Entropy generation analysis of magneto hydrodynamic flow of a nanofluid over a stretching sheet. J. Egypt Math. Soc. 2015, 23, 429–434. [Google Scholar] [CrossRef]
- Govindaraju, M.; Akilesh, M.; Abdul Hakeem, A.K. Analysis of entropy generation for nanofluid flow over a stretching sheet with an inclined magnetic field and uniform heat source/sink. J. Phys. Conf. Ser. 2018, 1139, 012010. [Google Scholar] [CrossRef]
- Sheikhzadeh, G.; Aghaei, A.; Ehteram, H.; Abbaszadeh, M. Analytical study of parameters affecting entropy generation of nanofluid turbulent flow in channel and micro-channel. Therm. Sci. 2016, 20, 2037–2050. [Google Scholar] [CrossRef]
- Ko, T.H.; Cheng, C.S. Numerical investigation on developing laminar forced convection and entropy generation in a wavy channel. Int. Commun. Heat Mass Transf. 2007, 34, 924–933. [Google Scholar] [CrossRef]
- Mahian, O.; Mahmud, S.; Heris, S.Z. Analysis of entropy generation between co-rotating cylinders using nanofluids. Energy 2012, 44, 438–446. [Google Scholar] [CrossRef]
- Tshehla, M.S.; Makinde, O.D. Analysis of entropy generation in a variable viscosity fluid flow between two concentric pipes with a convective cooling at the surface. Int. J. Phys. Sci. 2011, 6, 6053–6060. [Google Scholar] [CrossRef]
- Govindaraju, M.; Saranya, S.; Abdul Hakeem, A.K.; Jayaprakash, R.; Ganga, B. Analysis of slip MHD nanofluid flow on entropy generation in a stretching sheet. Procedia Eng. 2015, 127, 501–507. [Google Scholar] [CrossRef]
- Berrehal, H.; Maougal, A. Entropy generation analysis for multi-walled carbon nanotube (MWCNT) suspended nanofluid flow over wedge with thermal radiation and convective boundary condition. J. Mech. Sci. Technol. 2019, 33, 459–464. [Google Scholar] [CrossRef]
- Malvandi, A.; Ganji, D.D.; Hedayati, F.; Yousefi Rad, E. An analytical study on entropy generation of nanofluids over a flat plate. Alexandria Eng. J. 2013, 52, 595–604. [Google Scholar] [CrossRef]
- Acharya, N.; Das, K.; Kundu, P.K. On the heat transport mechanism and entropy generation in a nozzle of liquid rocket engine using ferrofluid: A computational framework. J. Comput. Des. Eng. 2019, 6, 739–750. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Gorji-Bandpy, M.; Soleimani, S. Magnetic field effect on nanofluid flow and heat transfer using KKL model. J. Taiwan Inst. Chem. Eng. 2014, 45, 795–807. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Rudraiah, N.; Barron, R.M.; Venkatachalappa, M.; Subbaraya, C.K. Effect of a magnetic field on free convection in a rectangular enclosure. Int. J. Eng. Sci. 1995, 33, 1075–1084. [Google Scholar] [CrossRef]
- Abbas, Z.; Javed, T.; Sajid, M.; Ali, N. Unsteady MHD flow and heat transfer on a stretching sheet in a rotating fluid. J. Taiwan Inst. Chem. Eng. 2010, 41, 644–650. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; pp. 99–105. [Google Scholar]
- De Freitas Rosa, P.; Rodrigues Cirqueira, S.S.; Aguiar, M.L.; Bernardo, A. Synthesis and characterization of silver nanoparticles. Mater. Sci. Forum 2014, 802, 135–139. [Google Scholar]
- Atashafrooz, M. Effects of Ag-water nanofluid on hydrodynamics and thermal behaviors of three-dimensional separated step flow. Alexandria Eng. J. 2018, 57, 4277–4285. [Google Scholar] [CrossRef]
- Upreti, H.; Pandey, A.K.; Kumar, M. MHD flow of Ag-water nanofluid over a flat porous plate with viscous-Ohmic dissipation, suction/injection and heat generation/absorption. Alexandria Eng. J. 2018, 57, 1839–1847. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Ahmad, S.; Lu, D.; Muhammad, T.; Chung, J.D. A numerical simulation of silver-water nanofluid flow with impacts of Newtonian heating and homogeneous-heterogeneous reactions past a nonlinear stretched cylinder. Symmetry 2019, 11. [Google Scholar] [CrossRef]
- Rashid, U.; Ibrahim, A. Impacts of nanoparticle shape on Al2O3-water nanofluid flow and heat transfer over a non-linear radically stretching sheet. Adv. Nanopart. 2020, 09, 23–39. [Google Scholar] [CrossRef]
- Wang, C.Y. Free Convection on a Vertical Stretching Surface. ZAMM Z. Angew. Math. Mech. 1989, 69, 418–420. [Google Scholar] [CrossRef]

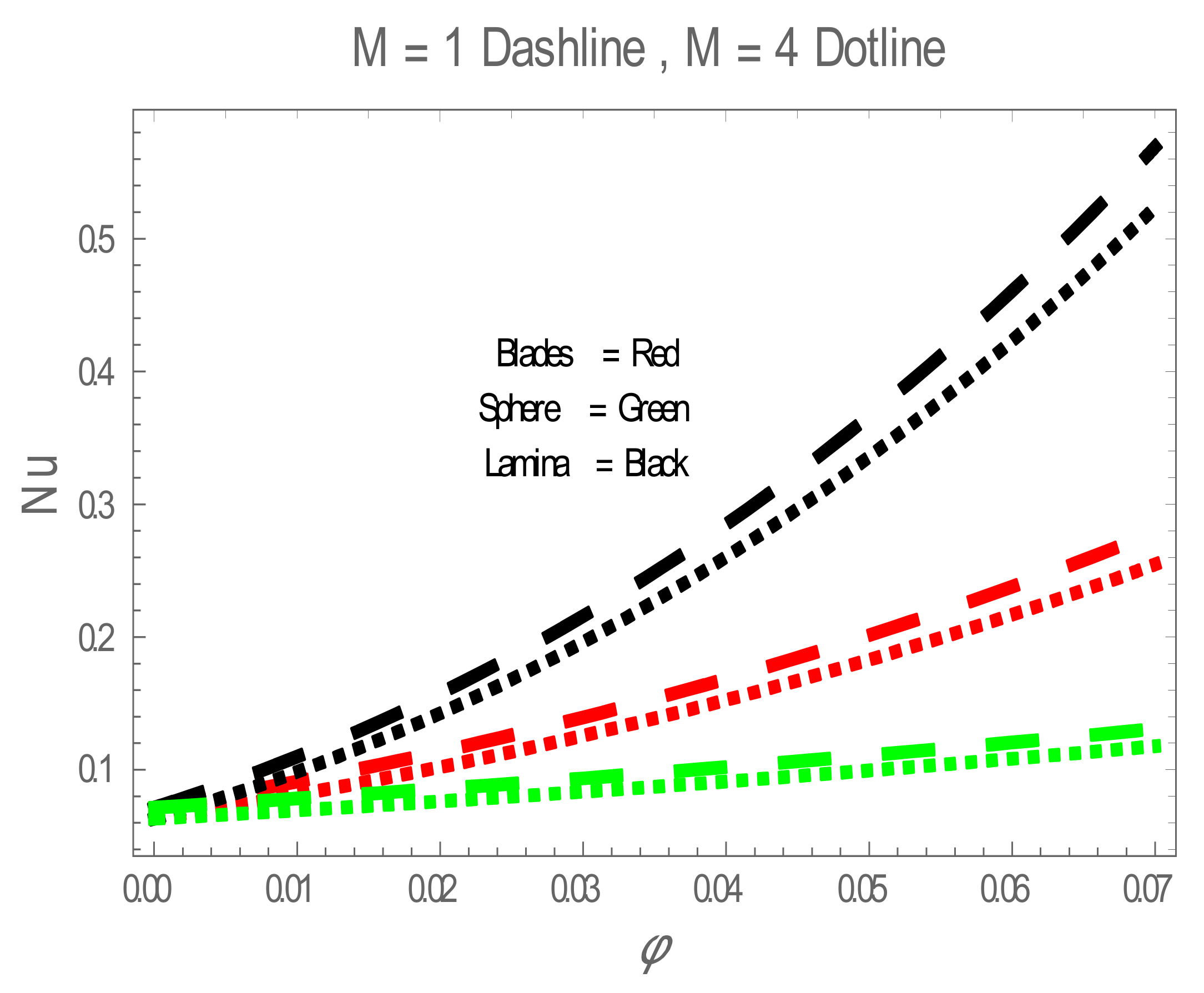
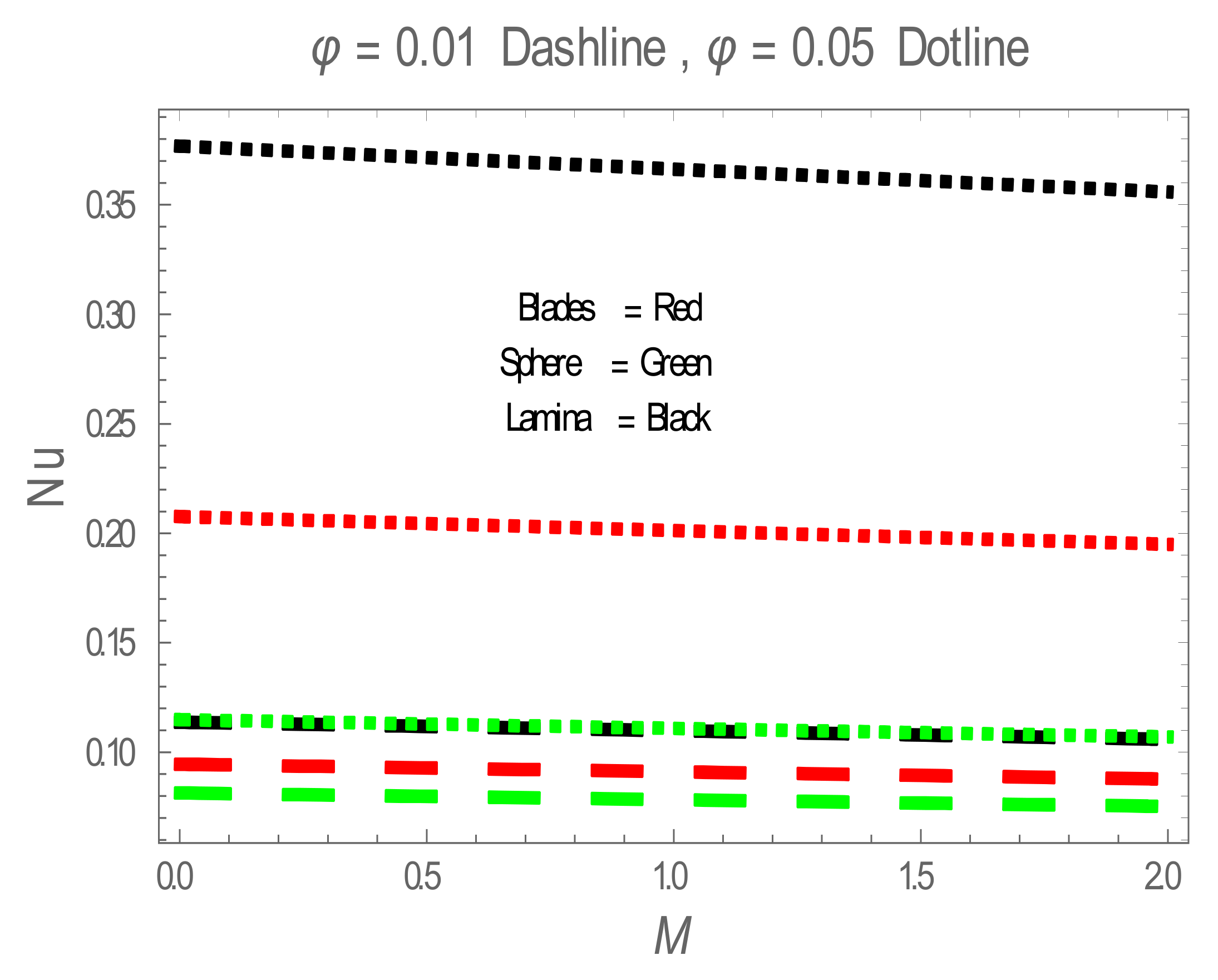
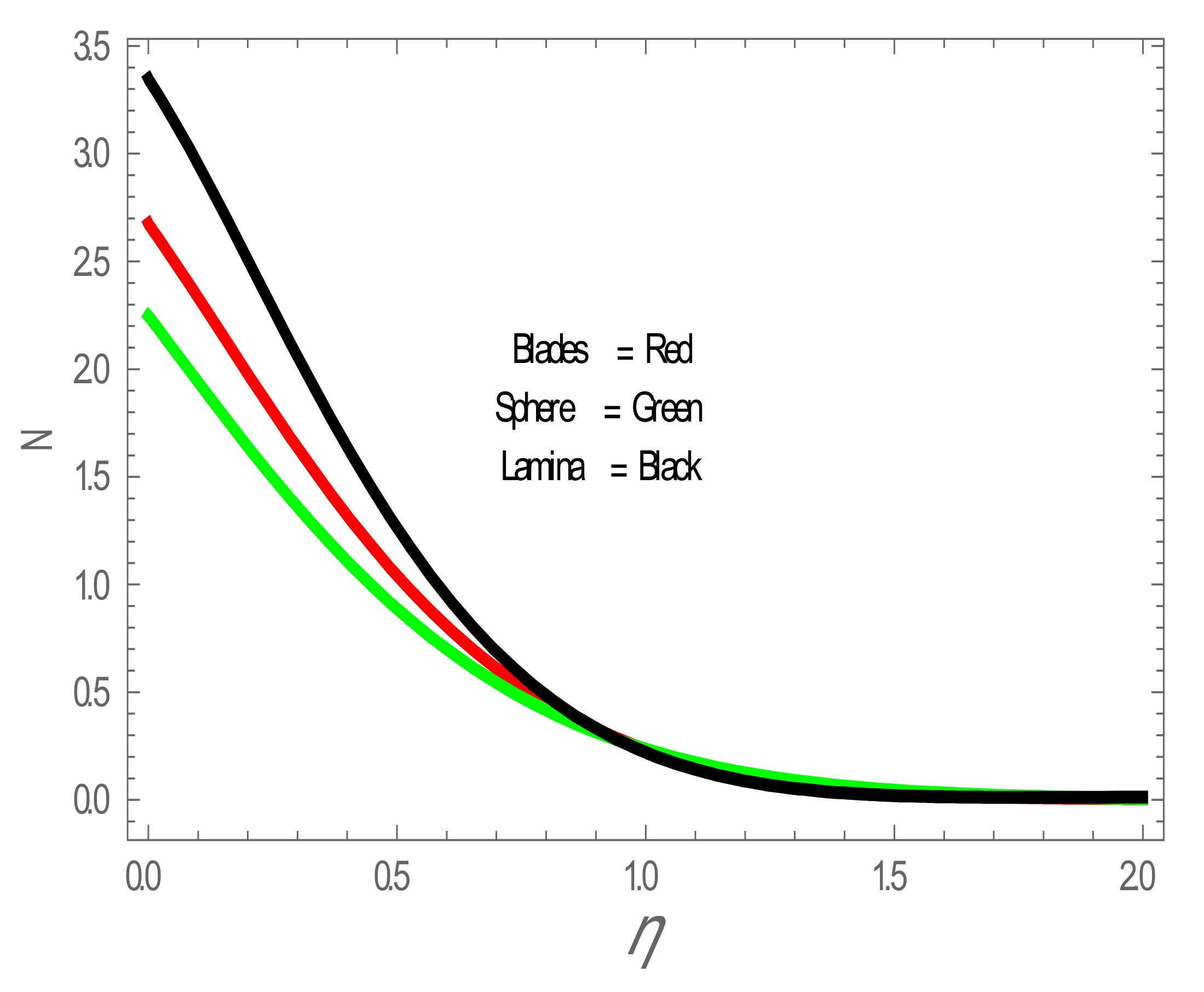
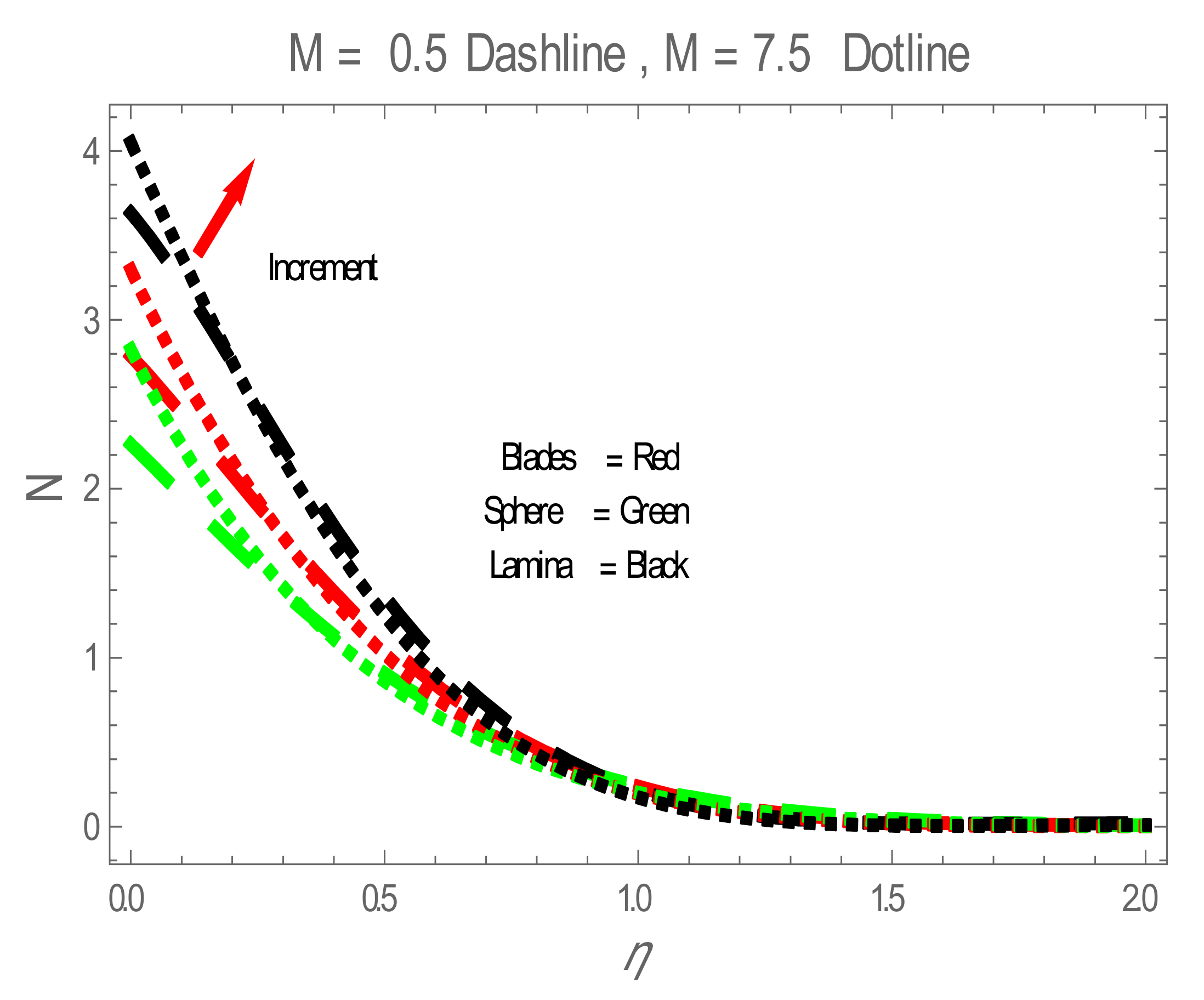
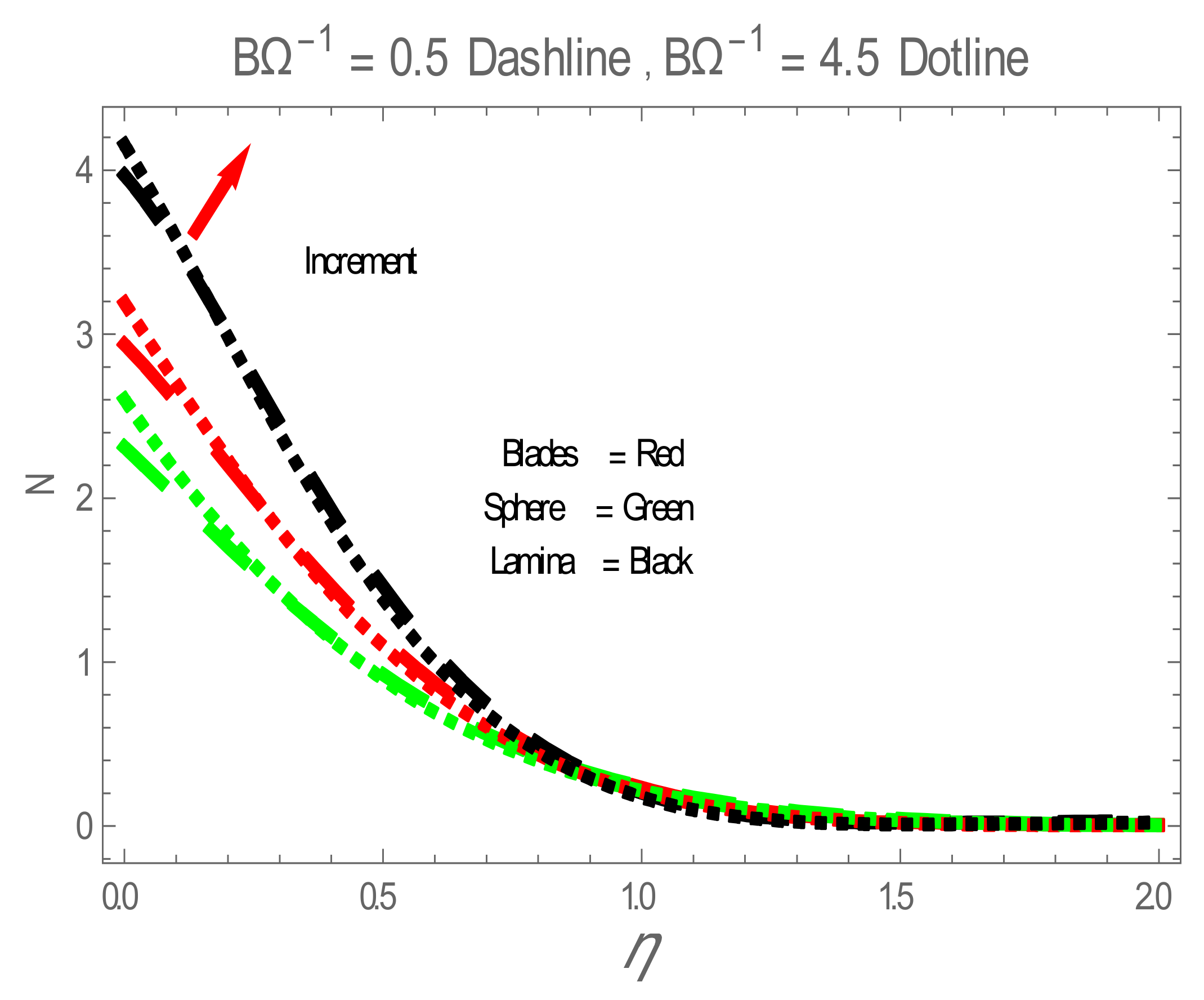
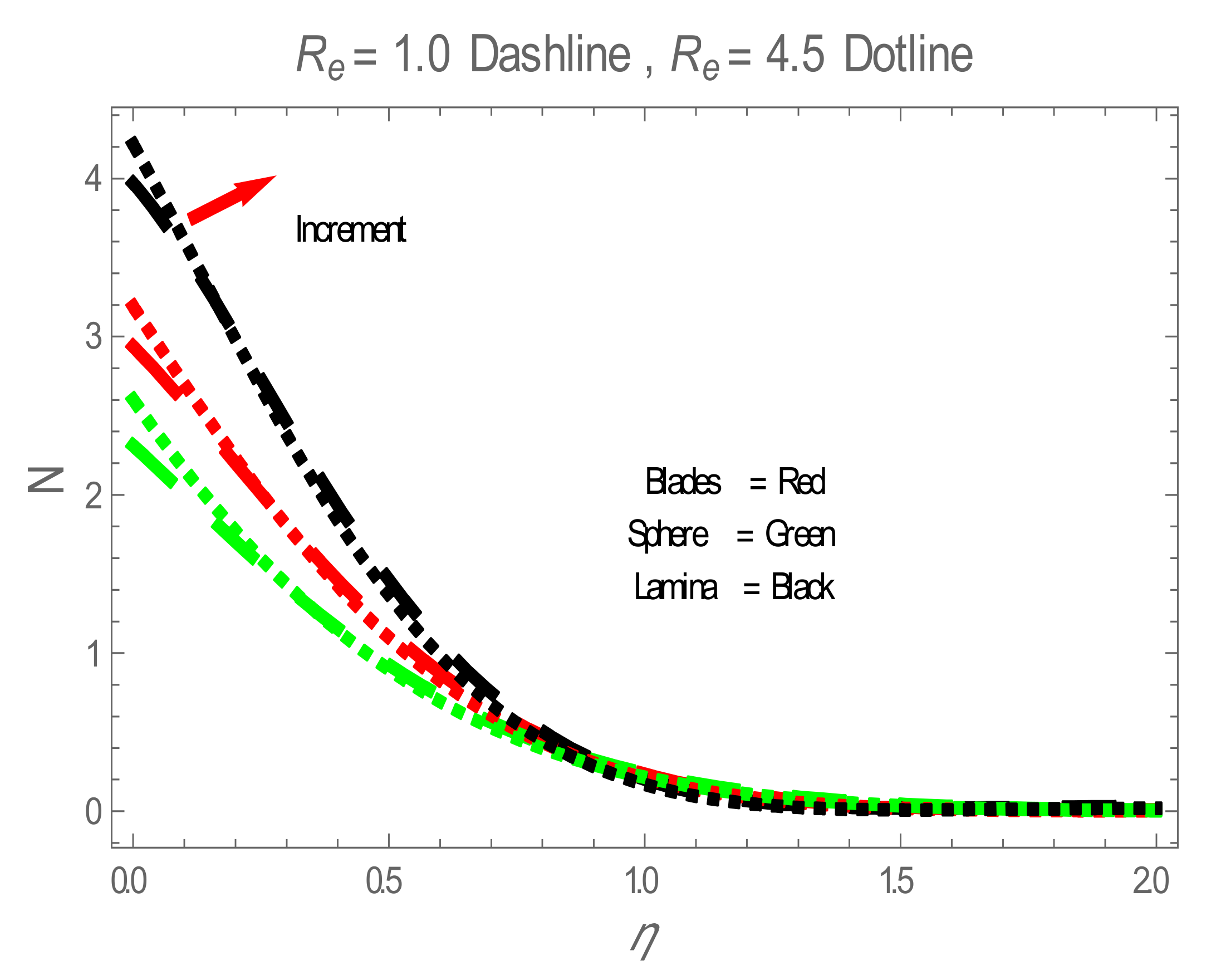
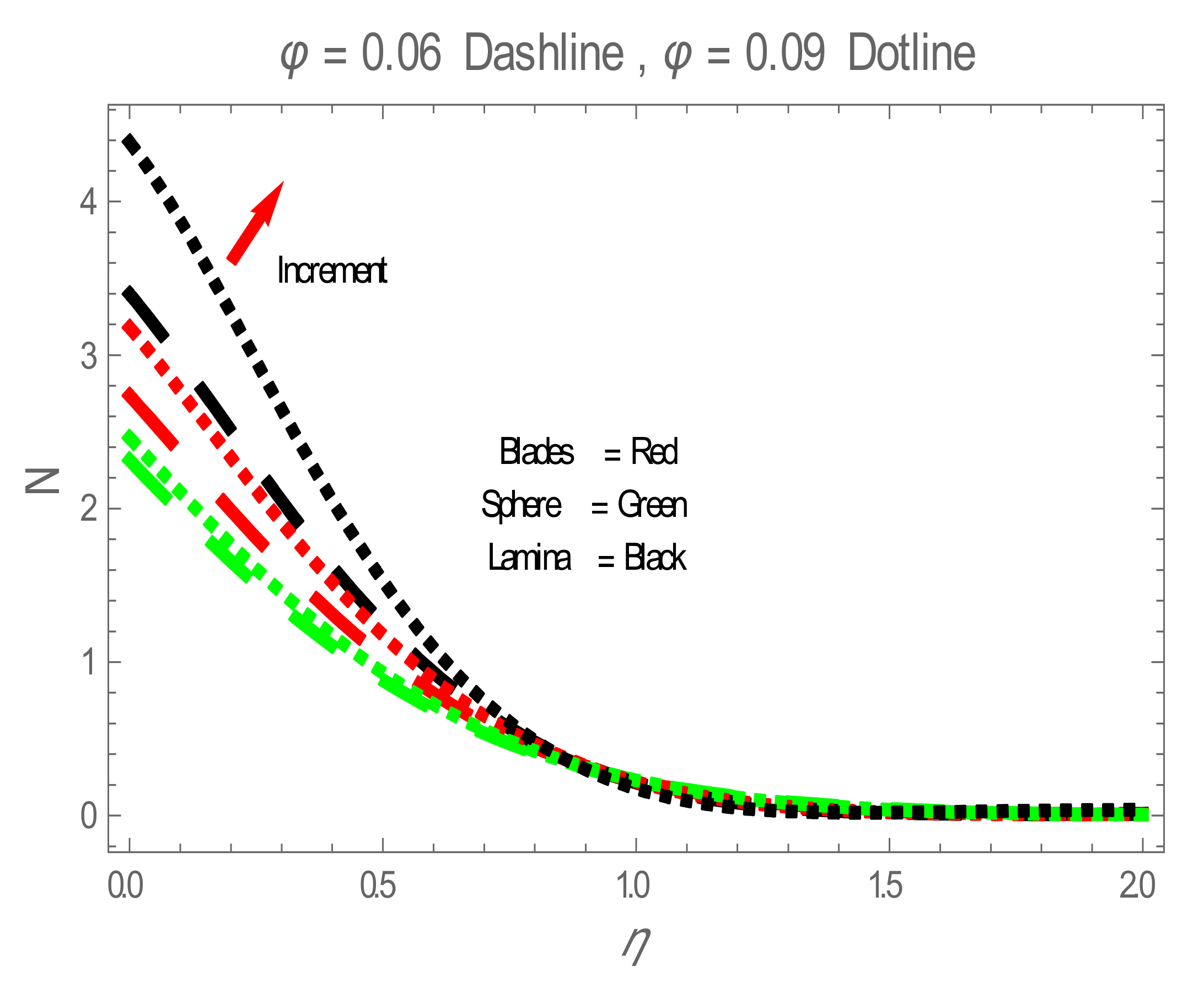
| Physical Properties | Ag | Water |
|---|---|---|
| (kg/m3) | 10,500 | 997.1 |
| (J/kg K) | 235 | 4179 |
| k (W/m K) | 429 | 0.60 |
| Shapes | Blades | Sphere | Lamina |
|---|---|---|---|
| m | 8.6 | 3 | 16.1576 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, U.; Baleanu, D.; Iqbal, A.; Abbas, M. Shape Effect of Nanosize Particles on Magnetohydrodynamic Nanofluid Flow and Heat Transfer over a Stretching Sheet with Entropy Generation. Entropy 2020, 22, 1171. https://doi.org/10.3390/e22101171
Rashid U, Baleanu D, Iqbal A, Abbas M. Shape Effect of Nanosize Particles on Magnetohydrodynamic Nanofluid Flow and Heat Transfer over a Stretching Sheet with Entropy Generation. Entropy. 2020; 22(10):1171. https://doi.org/10.3390/e22101171
Chicago/Turabian StyleRashid, Umair, Dumitru Baleanu, Azhar Iqbal, and Muhammd Abbas. 2020. "Shape Effect of Nanosize Particles on Magnetohydrodynamic Nanofluid Flow and Heat Transfer over a Stretching Sheet with Entropy Generation" Entropy 22, no. 10: 1171. https://doi.org/10.3390/e22101171
APA StyleRashid, U., Baleanu, D., Iqbal, A., & Abbas, M. (2020). Shape Effect of Nanosize Particles on Magnetohydrodynamic Nanofluid Flow and Heat Transfer over a Stretching Sheet with Entropy Generation. Entropy, 22(10), 1171. https://doi.org/10.3390/e22101171







