The Topp-Leone Generalized Inverted Exponential Distribution with Real Data Applications
Abstract
1. Introduction
2. The Topp-Leone Generalized Inverted Exponential Distribution
Some Ideal Sub Models as Special Cases from Our Proposed Distribution
- For , the proposed distribution in (5) converts to Topp-Leone Inverted Exponential (TLIE) distribution.
- For and , the proposed distribution reduces to Topp-Leone Standard Inverted Exponential (TLSIE) distribution.
- For and , the proposed distribution reduces to Inverted Exponential (IE) distribution.
- For , the proposed distribution reduces to Topp-Leone Generalized Standard Inverted Exponential (TLGSIE) distribution.
- If we replace in Equation (5), we obtain: the cdf of Exponentiated Generalized Inverted Exponential (EGIE) distribution with three parameters ().
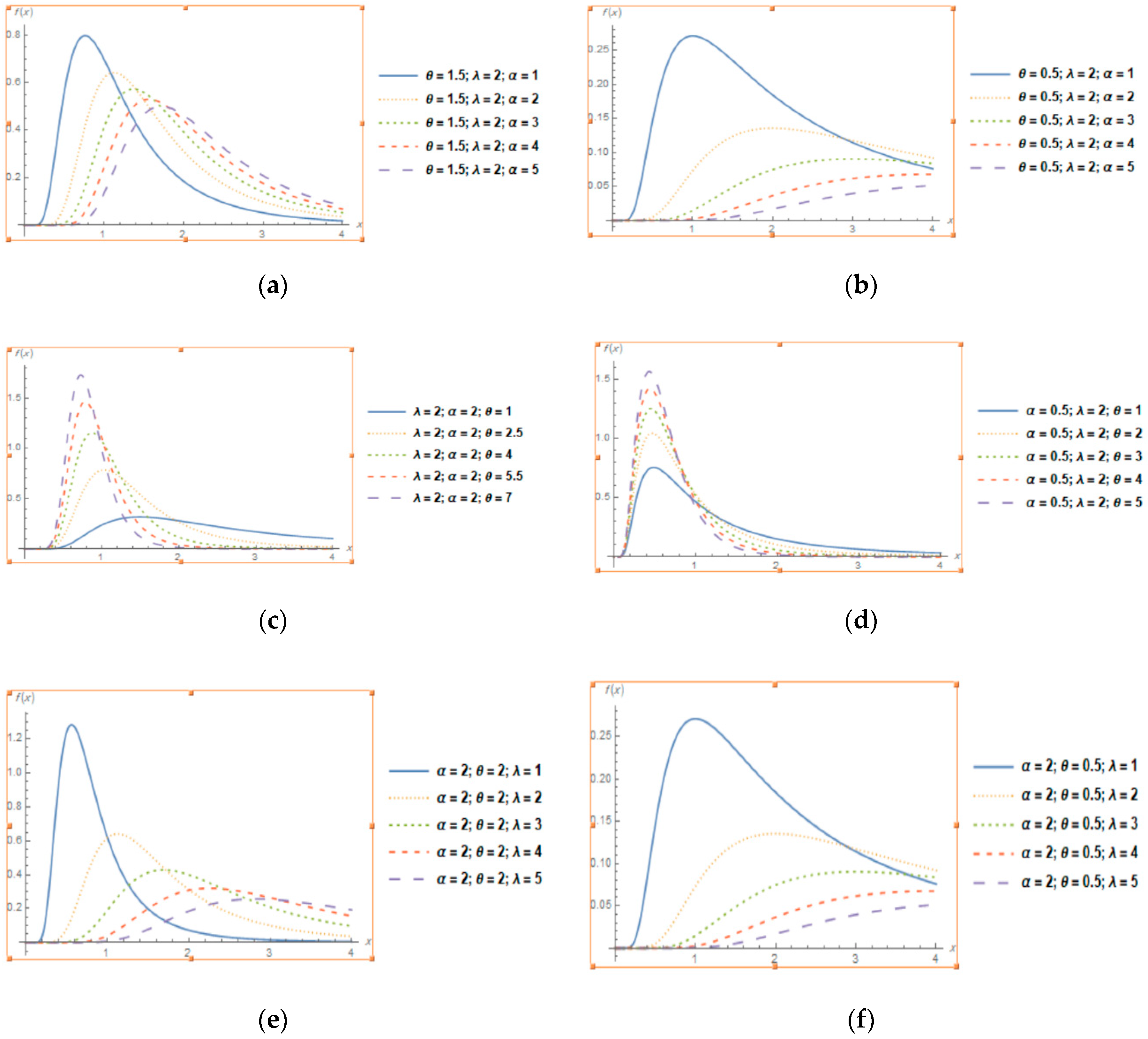
3. Properties of TLGIE Distribution
3.1. Quantile and Median
3.2. Moments
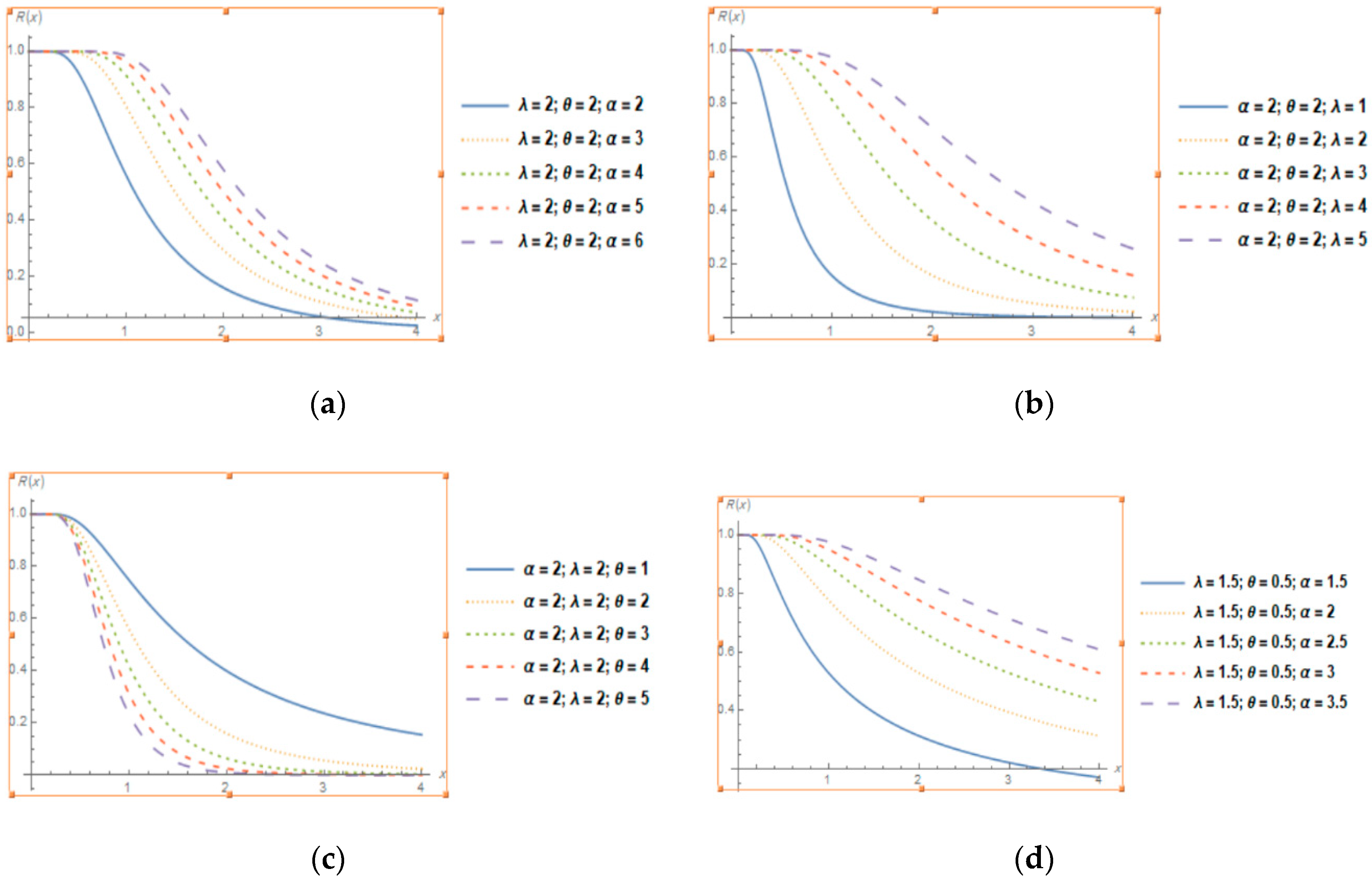
3.3. Reliability Function
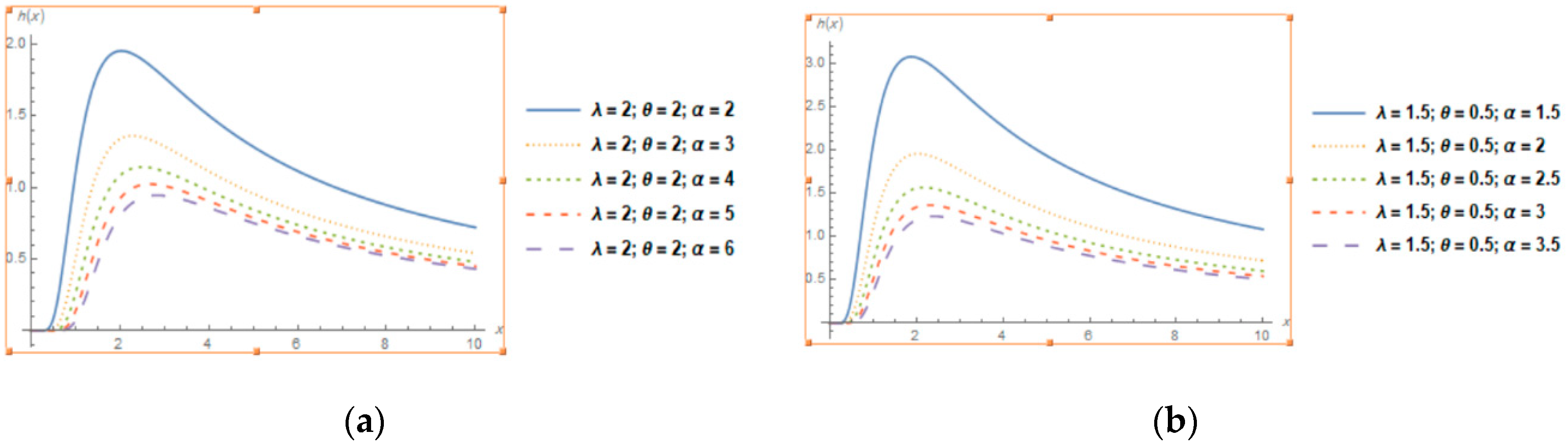
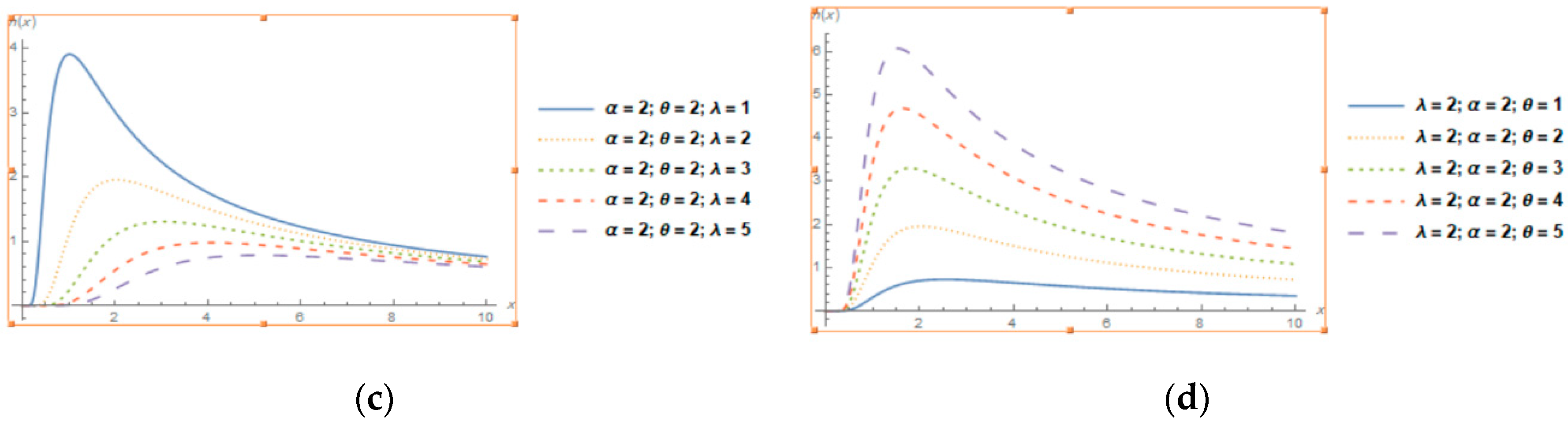
3.4. Hazard Rate Function
3.5. Mode
3.6. The Mean Deviation and the Median Deviation
4. Rényi Entropy of TLGIE
5. Parameters Estimation
5.1. Maximum Likelihood Estimation
5.2. Fisher Information
6. Simulation Study
7. Applications
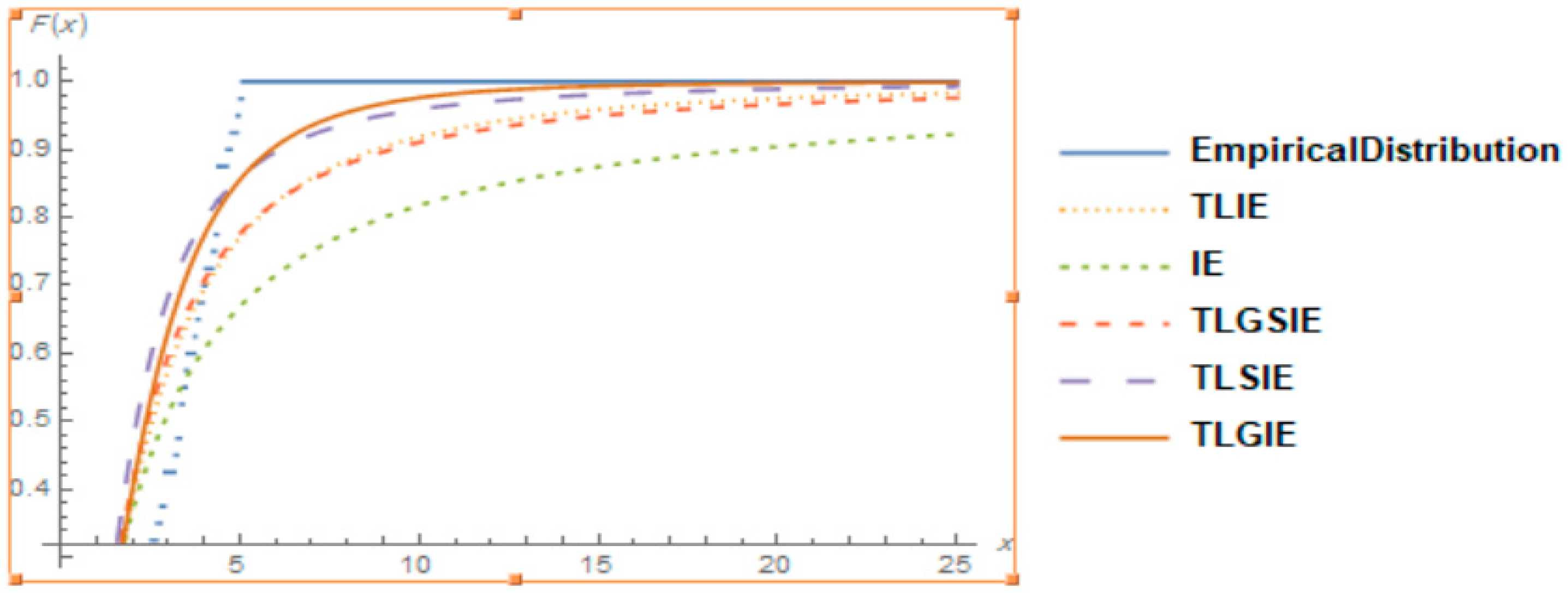
7.1. Data Set 1
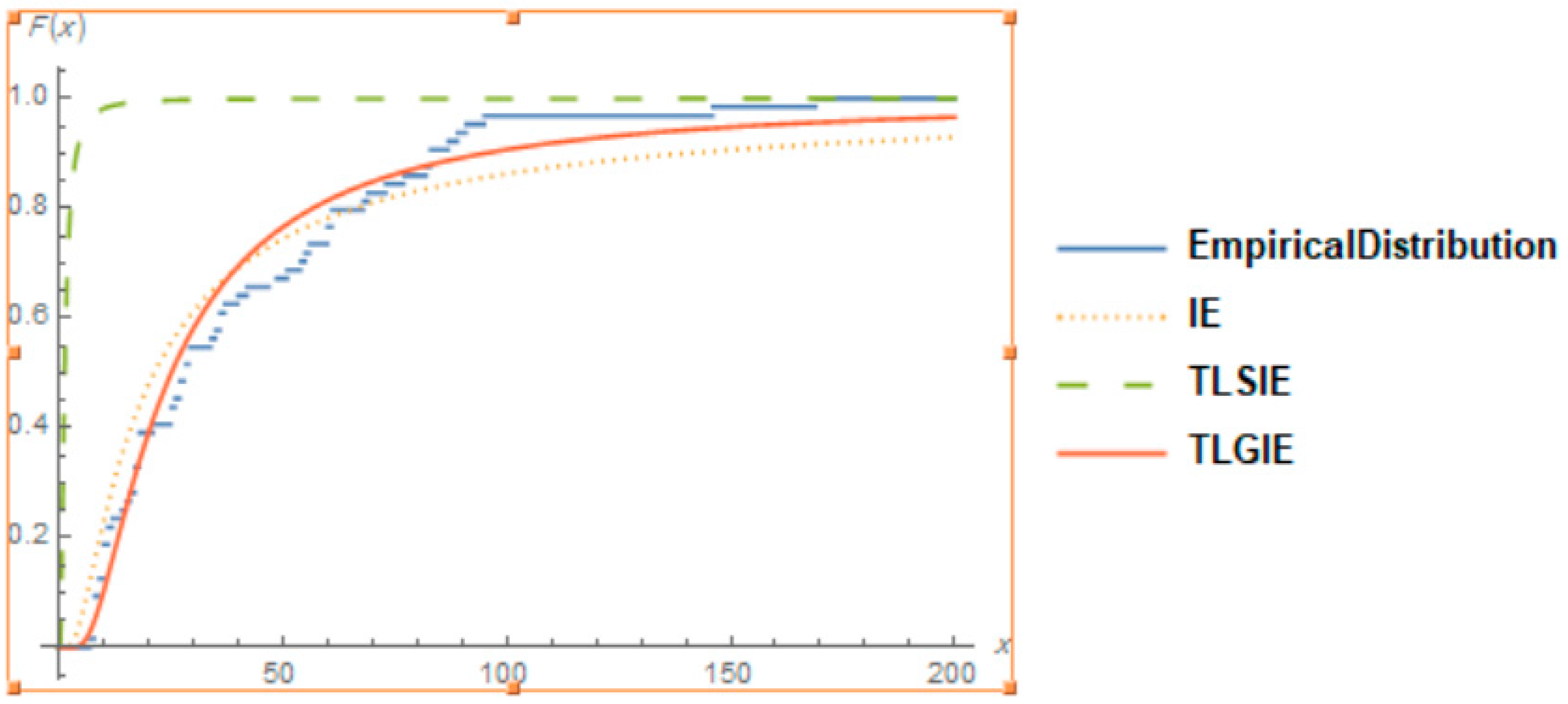
7.2. Data Set 2
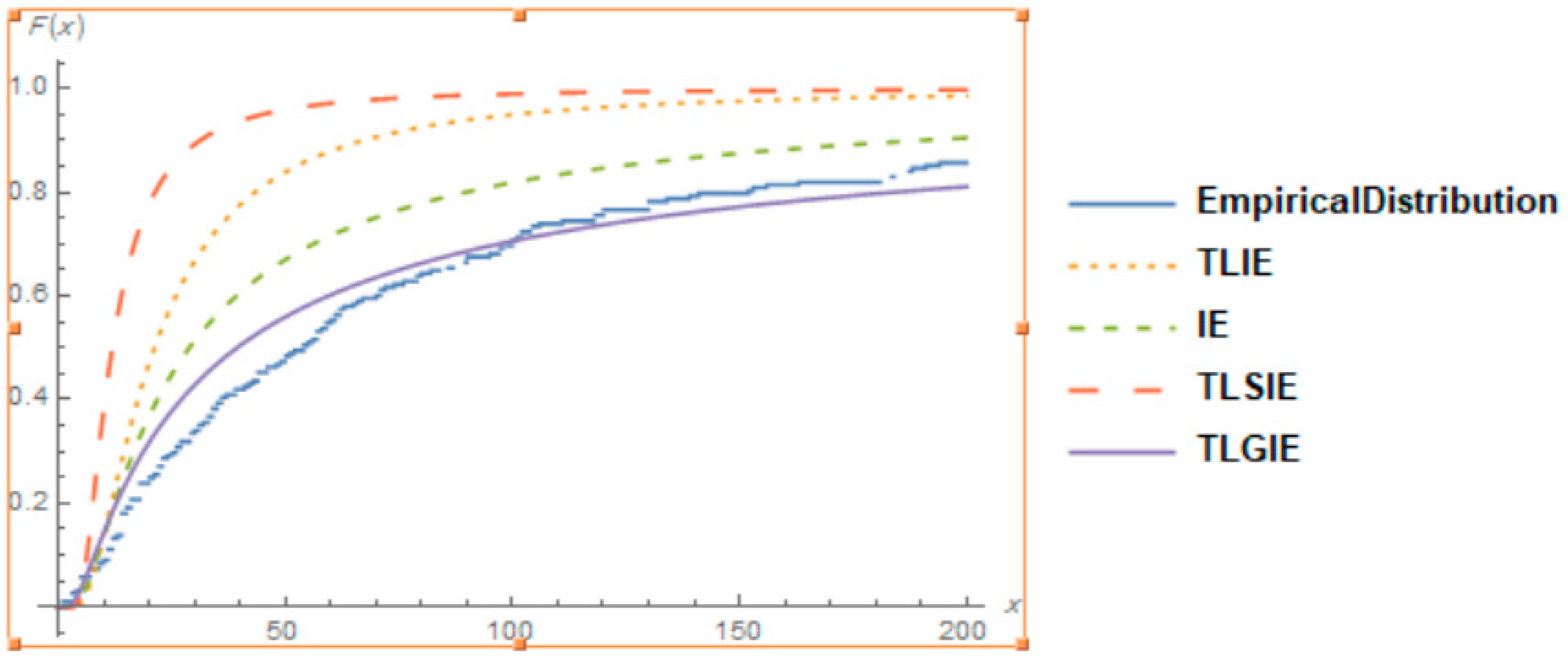
7.3. Data Set 3
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TLGIE | Topp-Leon Generalized Inverted Exponential |
| GIE | Generalized Inverted Exponential |
| TL | Topp-Leone |
| cdf | cumulative distribution function |
| probability distribution function | |
| TLIE | Topp-Leone Inverted Exponential |
| TLSIE | Topp-Leone Standard Inverted Exponential |
| IE | Inverted Exponential |
| TLGSIE | Topp-Leone Generalized Standard Inverted Exponential |
| EGIE | Generalized Inverted Exponential |
| the integration exponential function | |
| CV | coefficient of variation |
| CS | coefficient of skewness |
| CK | coefficient of kurtosis |
| MLE | maximum likelihood estimate |
| MSE | mean squared error |
| AIC | Akaike information criterion |
| CAIC | consistent Akaike information criterion |
| HQIC | Hannan-Quinn information criterion |
| MLEs | the maximum likelihood estimates |
| L | The likelihood function |
| the log-likelihood function | |
| BIAS | bias |
| LL | log-likelihood |
| pdf of GIE | |
| Cdf of GIE | |
| Cdf of TL distribution | |
| Pdf of TL distribution | |
| R (x) | The reliability or survival function |
| h(y) | The hazard function |
| The mean deviation | |
| The median deviation |
References
- Abouammoh, A.M.; Alshingiti, A.M. Reliability estimation of generalized inverted exponential distribution. J. Stat. Comput. Simul. 2009, 79, 1301–1315. [Google Scholar] [CrossRef]
- Zografos, K.; Balakrishnan, N. On families of beta- and generalized gamma- generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Alexander, C.; Cordeiro, G.M.; Ortega, E.M.M.; Sarabia, J.M. Generalized Beta-generated distributions. Comput. Stat. Data Anal. 2012, 56, 1880–1897. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar]
- Alizadeh, M.; Emadiz, M.; Doostparast, M.; Cordeiro, G.M.; Ortega, E.M.M.; Pescim, R.R. A new family of distributions: The Kumaraswamy odd log-logistic, properties and applications. Hacet. J. Math. Stat. 2015, 44, 1491–1512. [Google Scholar] [CrossRef]
- Alizadeh, M.; Altun, E.; Cordeiro, G.M.; Rasekhi, M. The odd power Cauchy family of distributions: Properties, regression models and applications. J. Stat. Comput. Simul. 2018, 88, 785–805. [Google Scholar] [CrossRef]
- Topp, C.W.; Leone, F.C. A family of J-shaped frequency functions. J. Amer. Stat. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Moments of some J-shaped distributions. J. Appl. Stat. 2003, 30, 311–317. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Kotz, S.; Xie, M. On some reliability measures and their stochastic orderings for the Topp- Leone distribution. J. Appl. Stat. 2005, 32, 715–722. [Google Scholar] [CrossRef]
- Kotz, S.; Seier, E. Kurtosis of the Topp-Leone distributions. Interstat 2007, 1–15. [Google Scholar]
- Vicaria, D.; Dorpb, J.R.V.; Kotzb, S. Two-sided generalized Topp and Leone (TS-GTL) distributions. J. Appl. Stat. 2008, 35, 1115–1129. [Google Scholar] [CrossRef]
- Al-Zahrani, B. Goodness-of-fit for the Topp-Leone distribution with unknown parameters. Appl. Math. Sci. 2012, 6, 6355–6363. [Google Scholar]
- Sangsanit, Y.; Bodhisuwan, W. The Topp-Leone generator of distributions: Properties and inferences. Songklanakarin J. Sci. Technol. 2016, 38, 537–548. [Google Scholar]
- Al-Shomrani, A.; Arif, O.; Shawky, A.; Hanif, S.; Shahbaz, M.Q. Topp leone family of distributions: Some properties and application. Pak. J. Stat. Oper. Res. 2016, 2, 443–451. [Google Scholar] [CrossRef]
- Abbas, S.; Taqi, S.A.; Mustafa, F.; Murtaza, M.; Shahbaz, M.Q. Topp-Leone Inverse Weibull distribution: Theory and Application. Eur. J. Pure Appl. Math. 2017, 10, 1005–1022. [Google Scholar]
- Elgarhy, M.; Nasir, M.A.; Jamal, F.; Ozel, G. The type II Topp-Leone generated family of distributions: Properties and applications. J. Stat. Manag. Syst. 2018, 21, 1529–1551. [Google Scholar] [CrossRef]
- Arshad, M.; Jamal, Q.A. Statistical Inference for Topp–Leone-generated Family of Distributions Based on Records. J. Stat. Theory Appl. 2019, 18, 65–78. [Google Scholar]
- Ibrahim, S.; Doguwa, I.S.; Audu, I.; Muhammad, H.J. On the Topp Leone Exponentiated-G Family of Distributions: Properties and Applications. Asian J. Probab. Stat. 2020, 7, 1–15. [Google Scholar] [CrossRef]
- Ibrahim, S.; Doguwa, I.S.; Audu, I.; Muhammad, H.J. On the Flexibility of Topp Leone Exponentiated Inverse Exponential Distribution. Int. J. Data Sci. Anal. 2020, 6, 83–89. [Google Scholar] [CrossRef]
- Bantan, R.A.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II Power Topp-Leone Generated Family of Distributions with Statistical Inference and Applications. Symmetry 2020, 12, 75. [Google Scholar] [CrossRef]
- Al-Marzouki, S.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II Topp Leone Power Lomax Distribution with Applications. Mathematics 2020, 8, 4. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon and Breach Science Publishers: New York, NY, USA, 1986; Volume 3. [Google Scholar]
- Rényi, A. On the dimension and entropy of probability distributions. Acta Math. Hung. 1959, 10, 193–215. [Google Scholar] [CrossRef]
- Shannon, C.E. A note on the concept of entropy. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Song, K.S. Rényi information, loglikelihood and an intrinsic distribution measure. J. Stat. Plan. Inference 2001, 93, 51–69. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. A corrected Akaike information criterion for vector autoregressive model selection. J. Time Ser. Anal. 1994, 14, 271–279. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. Ser. B. 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Atallah, M.; Mahmoud, M.; Al-Zahrani, B. A new test for exponentiality versus nbumgf life distributions based on laplace transform. Qual. Reliab. Eng. Int. 2014, 30, 1353–1359. [Google Scholar] [CrossRef]
- Proschan, F. Theoretical explanation of observed decreasing failure rate. Technometrics 1963, 5, 375–383. [Google Scholar] [CrossRef]
- Pinho, L.G.; Cordeiro, G.M.; Nobre, J.S. The Harris extended exponential distribution. Commun. Stat. Theory Methods 2015, 44, 3486–3502. [Google Scholar] [CrossRef]
| Mode | Median | Mean | Skewness | Kurtosis | |
|---|---|---|---|---|---|
| = 2 | |||||
| 1 | 0.883857 | 1.62873 | 2.77259 | 0.329501 | 1.01815 |
| 1.5 | 1.21014 | 2.13383 | 3.53576 | 0.323435 | 0.998774 |
| 2 | 1.49385 | 2.56696 | 4.18599 | 0.320047 | 0.988074 |
| = 2 | |||||
| 1 | 0.813107 | 1.26708 | 1.72609 | 0.266825 | 0.783853 |
| 1.5 | 1.06167 | 1.58027 | 2.10295 | 0.260112 | 0.764511 |
| 2 | 1.26368 | 1.83326 | 2.40667 | 0.25654 | 0.754304 |
| = 2 | |||||
| 1 | 0.763937 | 1.08802 | 1.35919 | 0.230164 | 0.66022 |
| 1.5 | 0.96812 | 1.32112 | 1.6177 | 0.223727 | 0.642568 |
| 2 | 1.12748 | 1.50317 | 1.81971 | 0.220472 | 0.63372 |
| Mode | Median | Mean | Skewness | Kurtosis | |
|---|---|---|---|---|---|
| = 1.5 | |||||
| 1 | 0.572953 | 0.816016 | 1.01939 | 0.230164 | 0.66022 |
| 1.5 | 0.72609 | 0.990843 | 1.21328 | 0.223727 | 0.642568 |
| 2.5 | 0.944791 | 1.24077 | 1.49067 | 0.218523 | 0.628463 |
| = 2 | |||||
| 1 | 0.763937 | 1.08802 | 1.35919 | 0.230164 | 0.66022 |
| 1.5 | 0.96812 | 1.32112 | 1.6177 | 0.223727 | 0.642568 |
| 2.5 | 1.25972 | 1.65436 | 1.98757 | 0.218523 | 0.628463 |
| = 2.5 | |||||
| 1 | 0.954922 | 1.36003 | 1.69899 | 0.230164 | 0.66022 |
| 1.5 | 1.21015 | 1.65141 | 2.02213 | 2.02213 | 0.642568 |
| 2.5 | 1.57465 | 2.06794 | 2.48446 | 0.218523 | 0.628463 |
| n | ||||
|---|---|---|---|---|
| 50 | MLE | 1.64944 | 1.3656 | 1.63393 |
| MSE | 2.54294 | 0.935221 | 2.53382 | |
| BIAS | 0.649439 | 0.365595 | 0.633934 | |
| 100 | MLE | 1.53764 | 1.2062 | 1.481 |
| MSE | 2.04645 | 0.312122 | 1.76203 | |
| BIAS | 0.537636 | 0.2062 | 0.481003 | |
| 200 | MLE | 1.48996 | 1.09878 | 1.28113 |
| MSE | 1.72886 | 0.0987432 | 0.980768 | |
| BIAS | 0.489958 | 0.0987782 | 0.281133 | |
| 500 | MLE | 1.28438 | 1.03796 | 1.11058 |
| MSE | 0.888928 | 0.0282187 | 0.34375 | |
| BIAS | 0.284384 | 0.0379592 | 0.110576 | |
| 1000 | MLE | 1.12872 | 1.02304 | 1.0703 |
| MSE | 0.359509 | 0.0125671 | 0.168361 | |
| BIAS | 0.12872 | 0.0230431 | 0.0703043 | |
| Model | Parameters | LL | AIC | CAIC | HQIC | ||
|---|---|---|---|---|---|---|---|
| TLGIE | 0.418685 | 2.19025 | 7.26267 | −82.2875 | 170.575 | 171.242 | 172.407 |
| TLIE | 0.589171 | 4.55247 | −85.5231 | 175.046 | 175.37 | 176.267 | |
| TLSIE | 4.55482 | −90.3942 | 182.788 | 182.894 | 183.399 | ||
| IE | 2.00825 | −91.1589 | 184.318 | 184.423 | 184.929 | ||
| TLGSIE | 3.2155 | 0.755551 | −88.1251 | 180.25 | 180.575 | 181.472 | |
| Model | Parameters | LL | AIC | CAIC | HQIC | ||
|---|---|---|---|---|---|---|---|
| TLGIE | 8.84653 | 0.361313 | 1.11353 | −1065.13 | 2136.25 | 2136.38 | 2140.18 |
| TLIE | 1.20401 | 22.9514 | −1164.41 | 2332.83 | 2332.89 | 2335.45 | |
| TLSIE | 106.161 | −1379.43 | 2762.86 | 2762.92 | 2765.4 | ||
| IE | 19.9992 | −1082.51 | 2167.01 | 2167.03 | 2168.32 | ||
| Model | Parameters | LL | AIC | CAIC | HQIC | ||
|---|---|---|---|---|---|---|---|
| TLGIE | 2.06861 | 0.77448 | 14.7643 | −295.07 | 596.14 | 596.54 | 598.691 |
| TLSIE | 283.888 | −304.914 | 611.828 | 611.893 | 612.679 | ||
| IE | 20.4134 | −299.175 | 600.351 | 600.415 | 601.201 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Saiary, Z.A.; Bakoban, R.A. The Topp-Leone Generalized Inverted Exponential Distribution with Real Data Applications. Entropy 2020, 22, 1144. https://doi.org/10.3390/e22101144
Al-Saiary ZA, Bakoban RA. The Topp-Leone Generalized Inverted Exponential Distribution with Real Data Applications. Entropy. 2020; 22(10):1144. https://doi.org/10.3390/e22101144
Chicago/Turabian StyleAl-Saiary, Zakeia A., and Rana A. Bakoban. 2020. "The Topp-Leone Generalized Inverted Exponential Distribution with Real Data Applications" Entropy 22, no. 10: 1144. https://doi.org/10.3390/e22101144
APA StyleAl-Saiary, Z. A., & Bakoban, R. A. (2020). The Topp-Leone Generalized Inverted Exponential Distribution with Real Data Applications. Entropy, 22(10), 1144. https://doi.org/10.3390/e22101144





