Topological constraints among polymers determine the viscoelastic properties of complex fluids and soft materials such as creams, oils, gels and plastics that we use everyday. During the last decades several theories have been proposed to connect the macroscopic and rheological behaviour of complex fluids with the microscopic properties of entangled polymers. Among the most successful, there are the reptation and tube theories and their extensions, such as constraint release or double-reptation [
1]. One of the strongest assumption of these theories is that polymer chains do not change their architecture, length or topology within experimental or practical timescales. One important class of systems that do not obey this constraint is the family of so-called “living” polymers [
2,
3,
4].
Living polymers are different from their non-living counterparts as random architectural changes such as breakage, fusion and reconnections alter the architecture and topology of the polymers on timescales shorter than, or comparable to, their relaxation. Models of living polymers have been successfully applied to explain the behaviour of certain surfactants that form worm-like micelles [
5]. One crucial feature of living polymers is that they are fundamentally in equilibrium (unless external forces are applied) and that the architectural re-arrangements occur randomly at any point and time along the polymers’ contours. Importantly, changing the structure of the polymers on timescales shorter than their own (reptation) relaxation brings about intriguing rheological behaviours such as dramatic shear thinning, banding or even thickening [
6,
7].
1.1. Review of Equilibrium Living Polymers
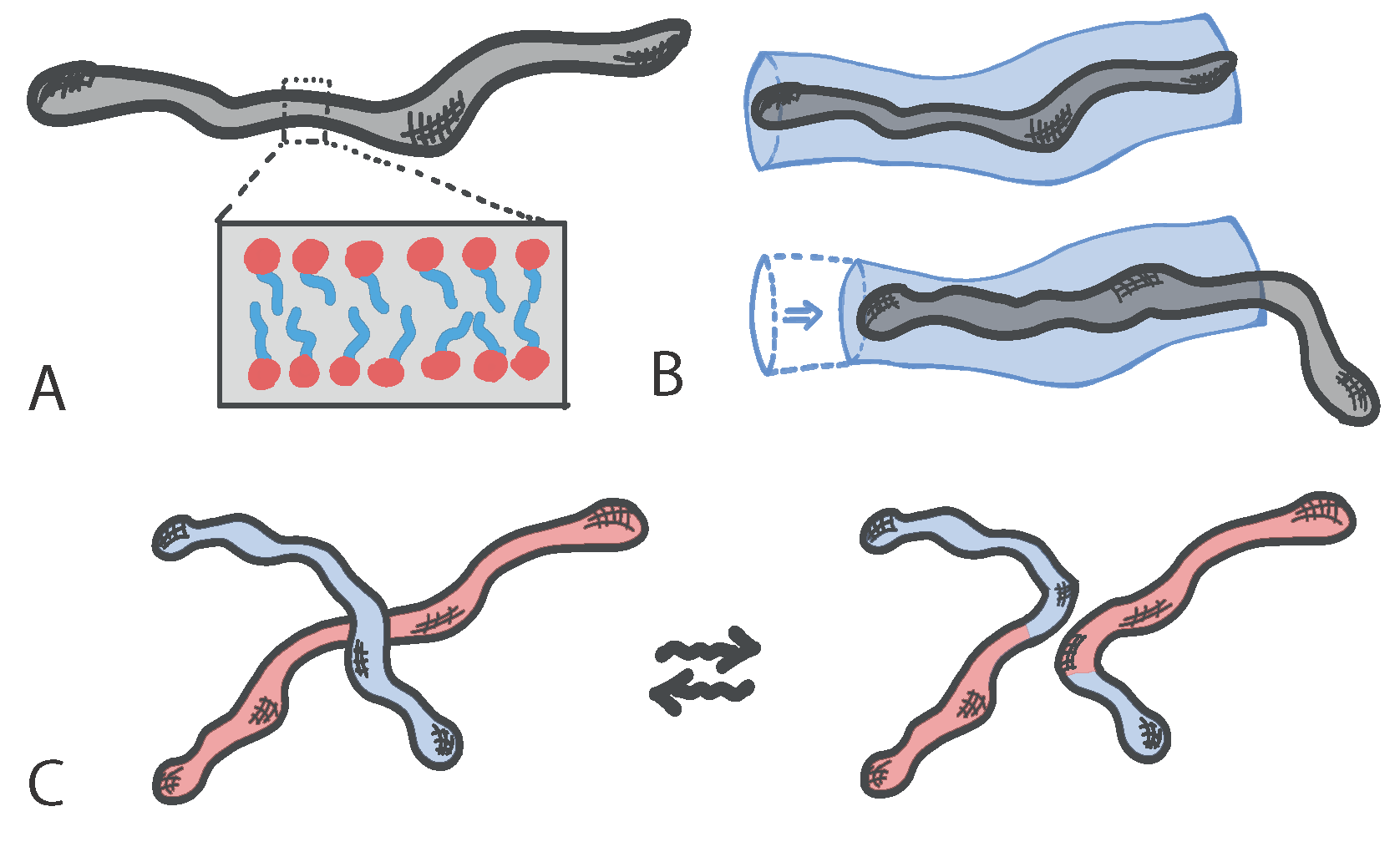
Living polymers with dynamic architecture can be realised using certain surfactants that create micelles: structures made of amphiphilic molecules that combine a water-loving, or hydrophilic, part with a water-hating, or hydrophobic, parts. When embedded in aqueous solutions amphiphilic molecules form hollow structures (the micelles) in which the hydrophobic part is shielded from the water. In certain regimes of surfactant and salt concentrations, micelles can self-assemble to form elongated structures with a self-explanatory name of “worm-like” micelles (
Figure 1A). These structures take the form of effective polymers, which can become entangled with each other and hence confer viscoelasticity to the solution. Standard polymers relax mainly by reptation, i.e., a slithering motion of the polymer within the tube formed by neighbouring polymers (
Figure 1B); instead, worm-like micelles can also break, fuse and reconnect with neighbours and hence form a “living” network of entanglements with unique rheological properties (
Figure 1C).
The stress relaxation of a chain can be computed as the survival probability of the average tube segment. A segment of the tube that is present at time
disappears when the chain travels far enough and one of its termini crosses one of the boundaries of the tube (
Figure 1B). This problem can be recast into that of a diffusing tube along a static polymer and the monitored segment can be represented as a 1D Brownian walk on a domain of length
L with absorbing boundary conditions [
1,
2]. For standard, monodisperse polymer systems relaxing by reptation, the stress relaxation function, i.e., the response of the system to an infinitesimal perturbation, is essentially the survival probability of a diffusing particle placed at random on a 1D interval of length
L and with absorbing boundaries; it can be written as [
1]
where
is the relaxation (or “reptation”) time,
is the diffusion coefficient of the centre of mass of the polymer (and that of the particle) and
a microscopic diffusion constant.
A theory for the relaxation of “living polymers” must also account for the reversible breakage and fusion and it was first proposed by Cates and co-authors [
2,
3,
4,
10]. This theory assumes that the system is in equilibrium with respect to the breakage/fusion process and that breakage can occur at any point along the polymer contour. Because of this morphological process the system attains polydispersity in lengths with mean
. For exponentially polydisperse polymers, the stress relaxation function is proportional to the following survival function
where
is the distribution of polymer lengths with mean
and
is the longest contribution (
component) of the reptative relaxation for a polymer of length
L. The solution to Equation (
2) can be found via a saddle-point approximation to be a stretched exponential with exponent
, with
for reptation dynamics [
2,
11,
12].
From the survival function
, the stress relaxation can be found as
, with
an instantaneous shear modulus. In turn, the zero-shear viscosity (which will be used later on) can be computed as
One of the key timescales in the system is the breakage timescale
where
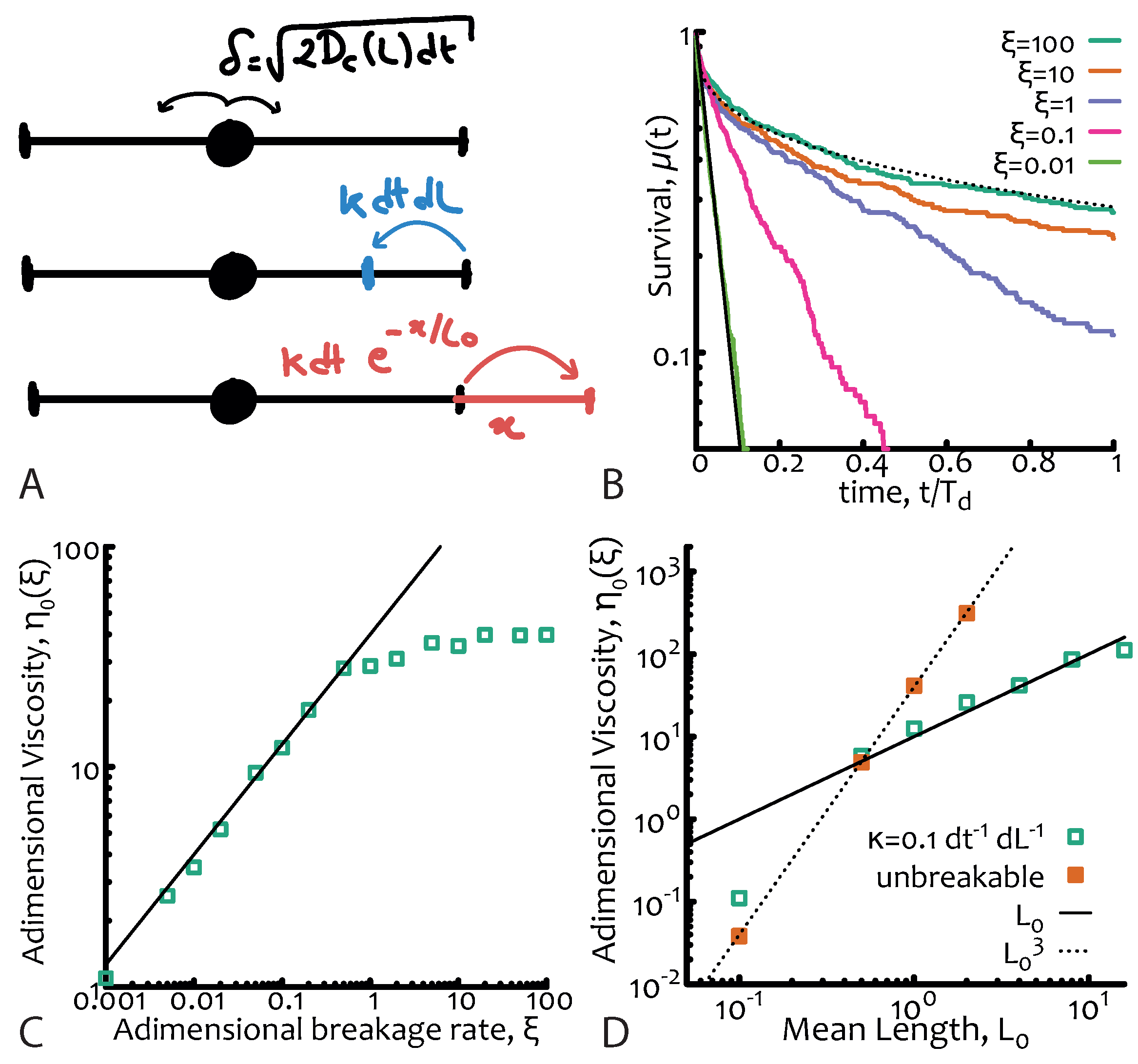
is the number of breaks per unit time per unit length. Since the system is also in morphological equilibrium, the timescale for the fusion process must be the same as the breakage one. The kinetics of breakage and fusion are effectively implemented by introducing dynamical and discontinuous changes in the positions of the absorbing boundaries at a certain rate (see
Figure 2A). This stochastic process can no longer be mapped to a diffusive equation and it cannot be exactly solved analytically [
2]. The relevant adimensional quantity is now the ratio of the breakage and reptation timescales, i.e.,
If
the breakage dynamics is slower than the relaxation of the chains and hence reptation dominates, whereas if
the breakage dynamics occurs on timescales comparable, or shorter than, the reptative ones. In this case the reaction process—which can take place anywhere along the polymers—has the net effect of “democratising” the stress relaxation of the micelles and forces it to become closer to a simple exponential (rather than a stretched one) in spite of the sample polydispersity. The explanation for this near-Maxwellian, or simple exponential, stress relaxation of polydisperse micelles is one of the fundamental results of this theory (see
Figure 2B).
In this regime, one may then ask what is the typical relaxation timescale, accounting for the architectural change. To compute this, one should notice that for a breakage to be “useful” in accelerating the relaxation of the chain it has to happen within a distance
from the current position of the diffusing particle (representing the relaxing tube segment) such that the particle will on average cross the new boundary (and hence be absorbed) before a new fusion event occurs. This can be calculated simply as
The rate limiting step thus involves waiting for a breakage to happen within a distance
from the relaxing segment, which happens on average at a rate
or at timescale
We can then find that the viscosity depends on the parameters of the system as
which depends only linearly on the average chain length, rather as
valid for unbreakable chains (see
Figure 2D).
A numerical algorithm to simulate equilibrium living polymers is detailed in Reference [
2] and also implemented as a C
++ code by the author and shared in a git repository (see acknowledgement section); briefly, one should simulate the diffusion of a particle deposited at random along a 1D interval with exponentially distributed length (and mean
). The diffusion depends on the instantaneous length as
and breakages or fusions of an
l-long segment can occur at rate
per unit time and unit length and at rate
per unit time and per each end, respectively (see also
Figure 2A). The survival function
is computed as the probability of a particle to have not reached one of the two ends of the interval by time
t. Examples of this function for different values of
are given in
Figure 2B. The adimensional viscosity is the suitably normalised integral of
and is plotted in
Figure 2C as a function of
for fixed
—thus confirming Equation (
7)—and in
Figure 2D as a function of the mean length
for unbreakable chains and living polymers thereby confirming Equation (
8).
1.3. Non-Equilibrium DNA Digestion and Ligation
Systems of non-equilibrium living polymers may be realised using DNA functionalised by certain classes of proteins. For instance, using restriction enzymes (RE) it is possible to cut—or “digest”—DNA thereby generating irreversible breakages along the contour. More specifically, (type II) REs recognise specific DNA sequences and break the sugar-phosphate DNA backbone in correspondence of those sequences [
13]. This process is akin to the “breakage-only” process described above with the caveat that typically DNA molecules are (i) initially monodisperse in length and (ii) have a finite number of restriction sites along their contour. For this reason at large times one expects the viscosity to reach a plateau at about
, where
is the number of restriction sites and if the large time regime is still well described by reptation.
It should also be noted that the time for a typical digestion experiment is about 15 min in optimal conditions and high-fidelity enzymes or ∼ hours for less ideal conditions [
13]. At this time all the restriction sites available have been cleaved. Thus, the typical cutting time of one restriction site is of the order of minutes or tens of minutes, considering that a typical RE has between 1 and 10 sites per DNA molecule (of course this number depends on the specific combination of DNA sequence and RE considered). This cutting time should be compared with the typical relaxation time of, for example,
DNA in moderately entangled conditions, which is of the order to 1–10 s (at 0.5–5 mg/mL) [
14]. Thus, the regime that can be attained in experiments that can be performed with moderately entangled
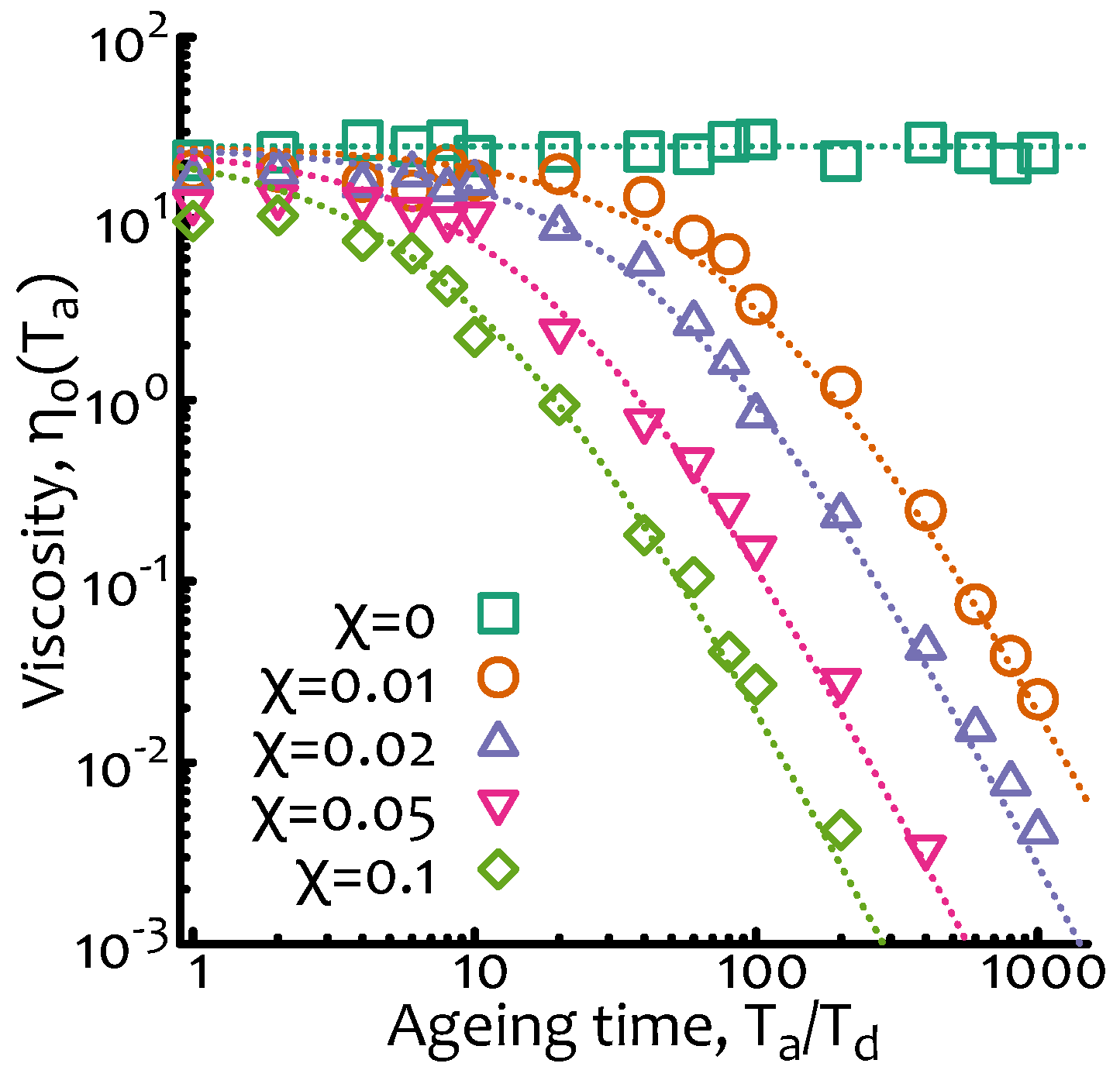
—DNA is that in which
(as the one numerically reported in
Figure 3) so that at small ageing times the solution should behave as a standard complex fluid and display deviations from this behaviour only at large ageing times (following the scaling of Equation (
10)).
It is also worth noting that type II REs leave so-called “sticky ends” in correspondence of the cleaved sequences. These sticky ends can in principle re-anneal by thermal fluctuations but can never permanently fuse back two segments. In order to achieve irreversible fusion of DNA molecules one needs ligase enzymes (and ATP) [
15]. Using this family of proteins one can in principle also reproduce the condition of irreversible fusion described above and so induce a gelling by exponential growth of the polymers in solution.
Finally, it should be highlighted that enzymes such as restriction and ligase are commonly found in vivo where they fulfil important biological functions. For instance, restriction enzymes are found in bacteria and used as a defence mechanism against viral infection of phages. At the same time, ligases catalyse the formation of a phosphodiester bond and are required to repair DNA single or double-strand breaks in vivo. Other proteins that change the architecture and topology of DNA, such as Topoisomerase [
16] or Structural Maintenance of Chromosome (SMC) complexes [
17,
18], may also be used to create new viscoelastic regimes of entangled DNA in vitro. Understanding these regimes will also shed light into how the topology of genomes are regulated in vivo, where DNA is stored under extreme conditions of confinement and crowding.