Complexity as Causal Information Integration
Abstract
1. Introduction
Therefore Integrated Information can be seen as a measure of the systems complexity. In this context it belongs to the class of theories that define complexity as to what extent the whole is more than the sum of its parts.In short, integrated information captures the information generated by causal interactions in the whole, over and above the information generated by the parts.
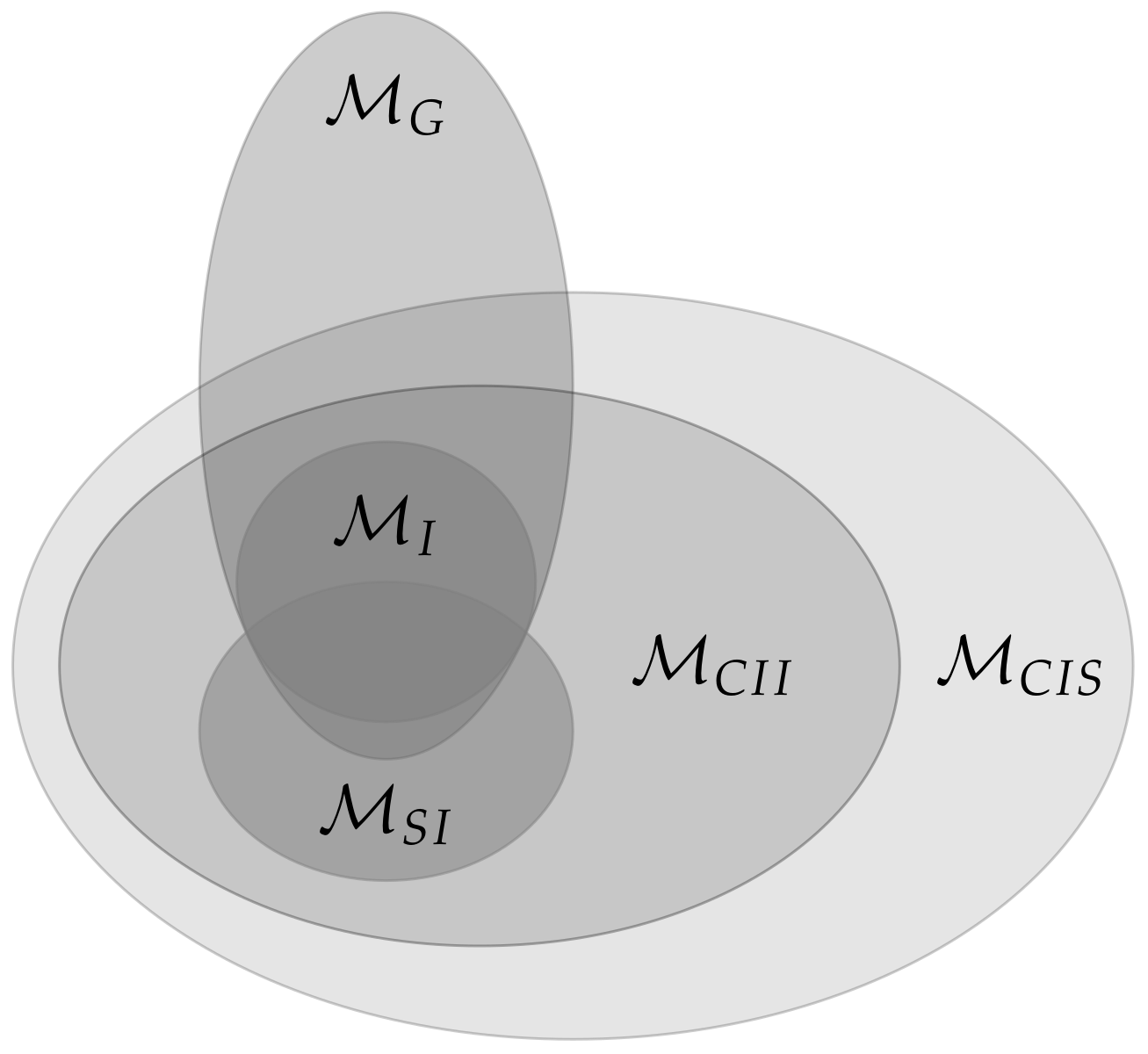
Integrated Information Measures
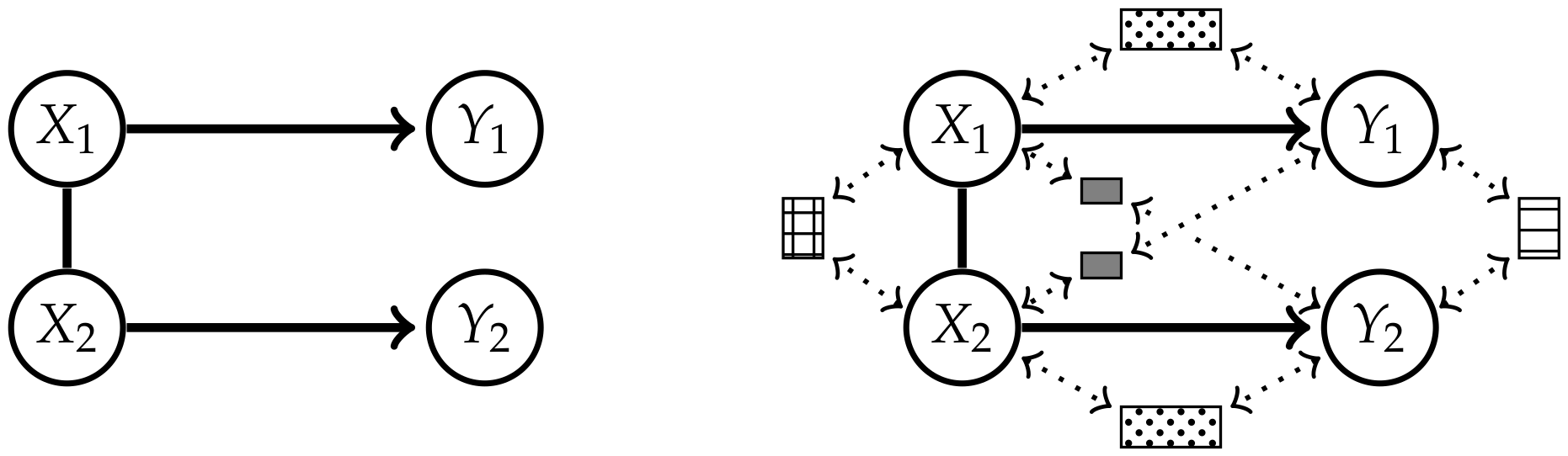
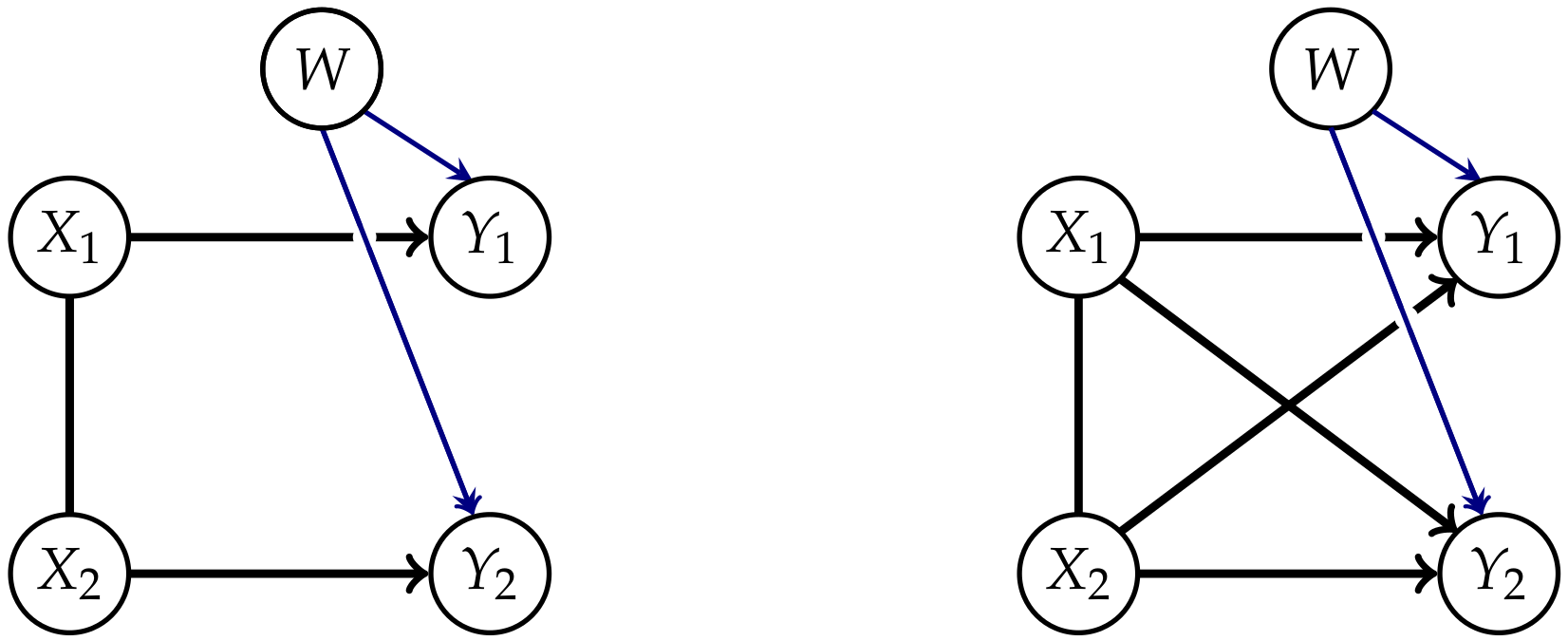
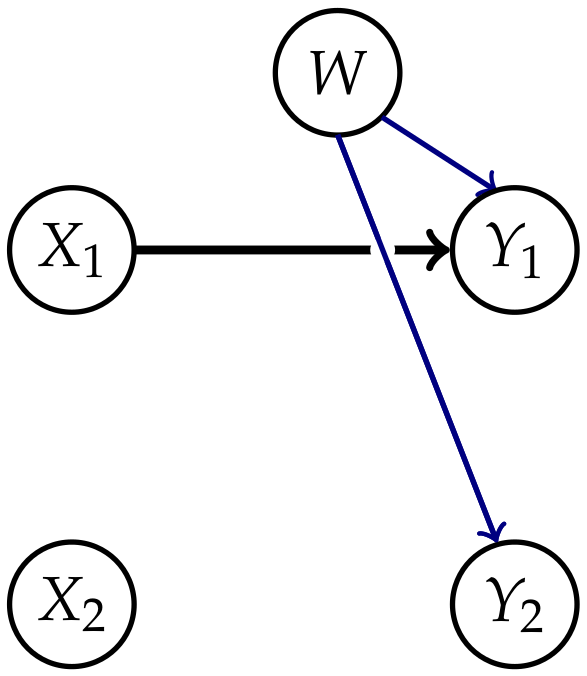
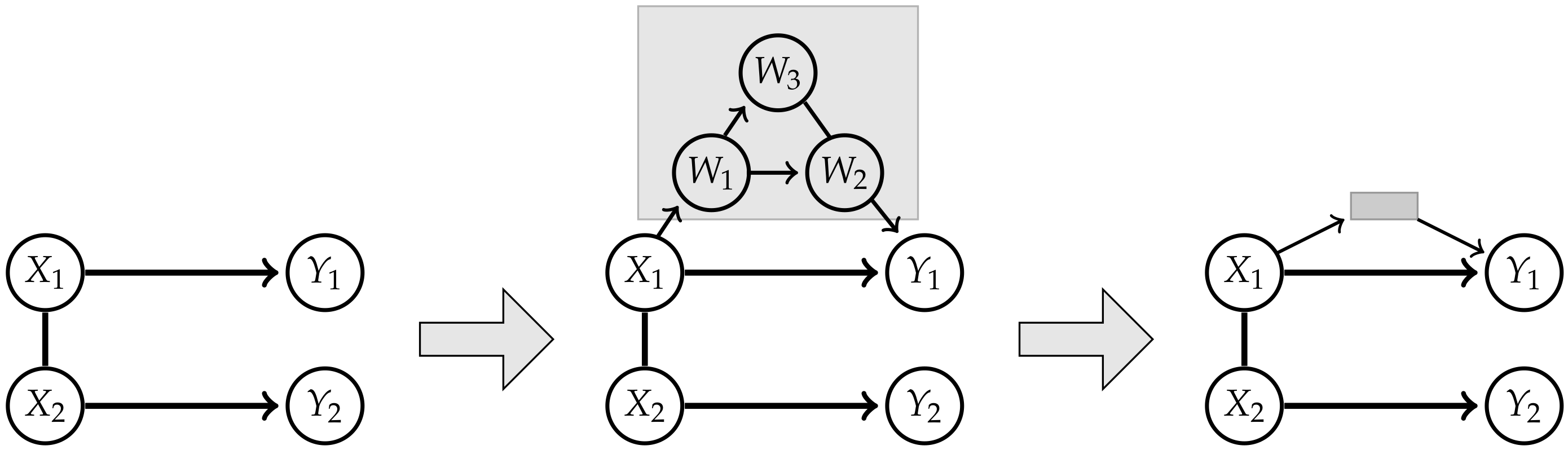
Therefore, measures of the strength of causal cross-connections should be based on split models, that have a graphical representation.It seems that if conditional independence judgments are by-products of stored causal relationships, then tapping and representing those relationships directly would be a more natural and more reliable way of expressing what we know or believe about the world. This is indeed the philosophy behind causal Bayesian networks.
2. Causal Information Integration
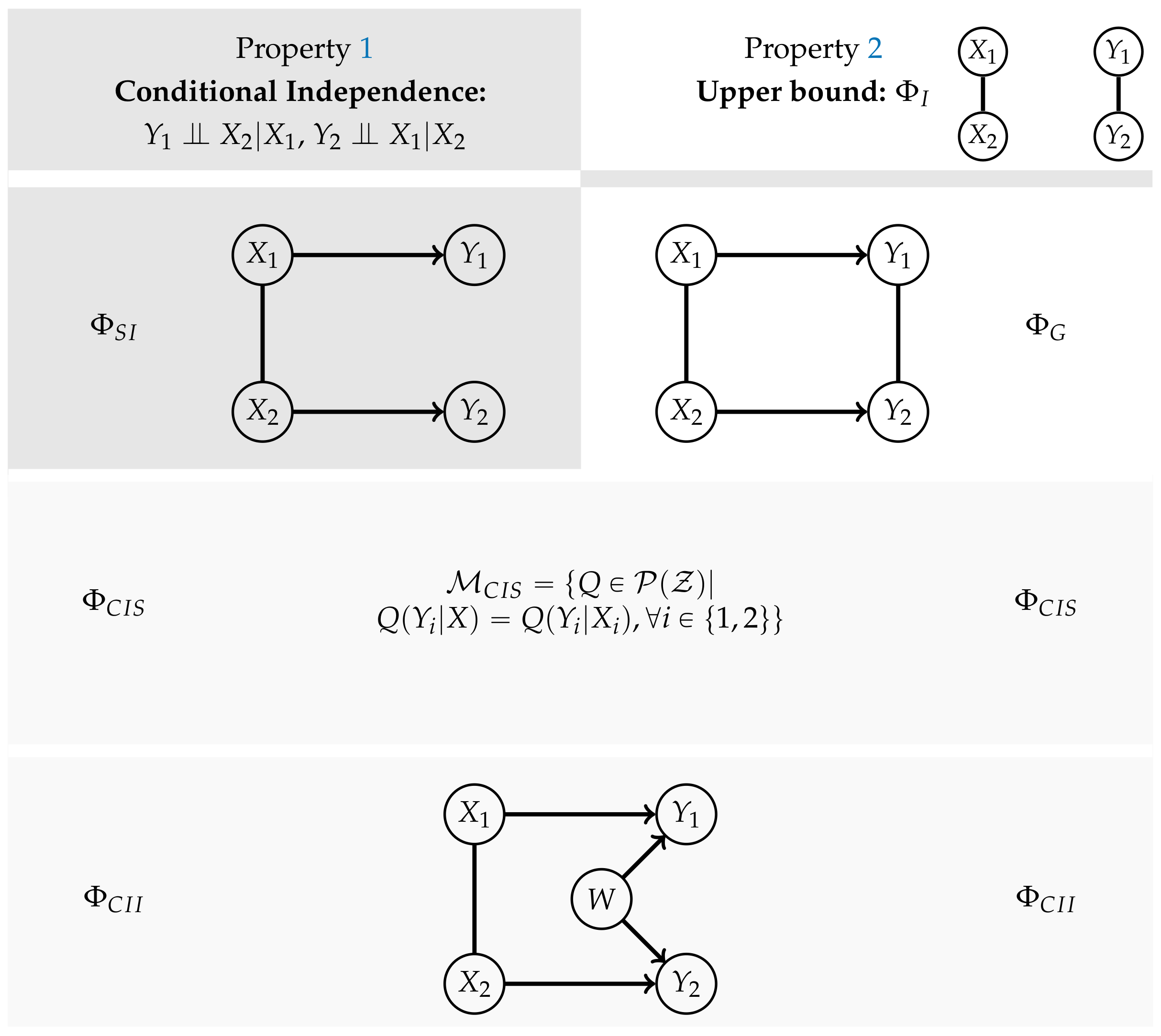
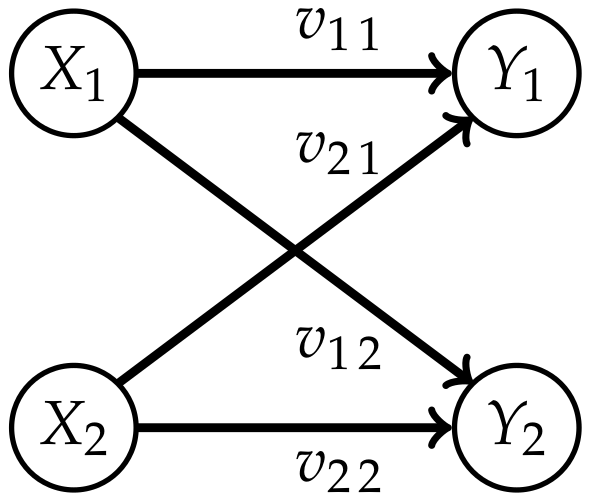
2.1. Definition
- 1.
- 2.
- For every there exists a distribution that has marginals equal toAdditionally factors according to the graph corresponding to the split system
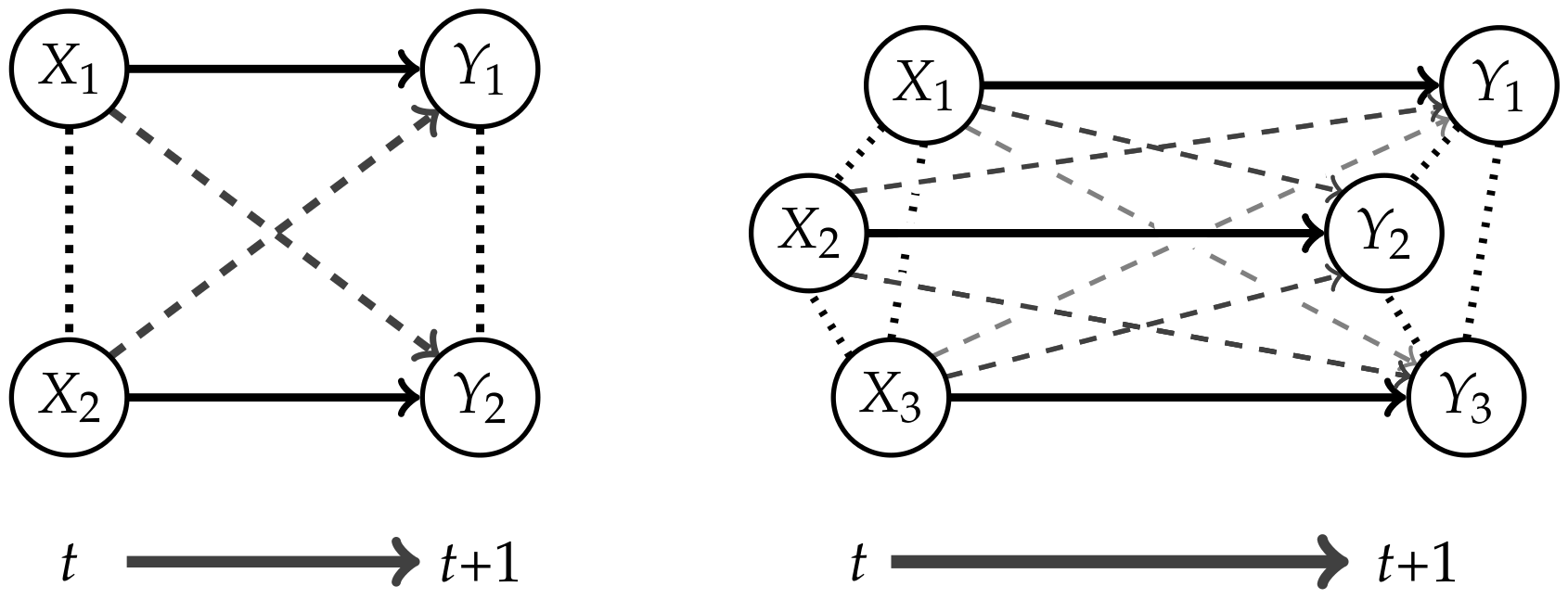
2.1.1. Ground Truth
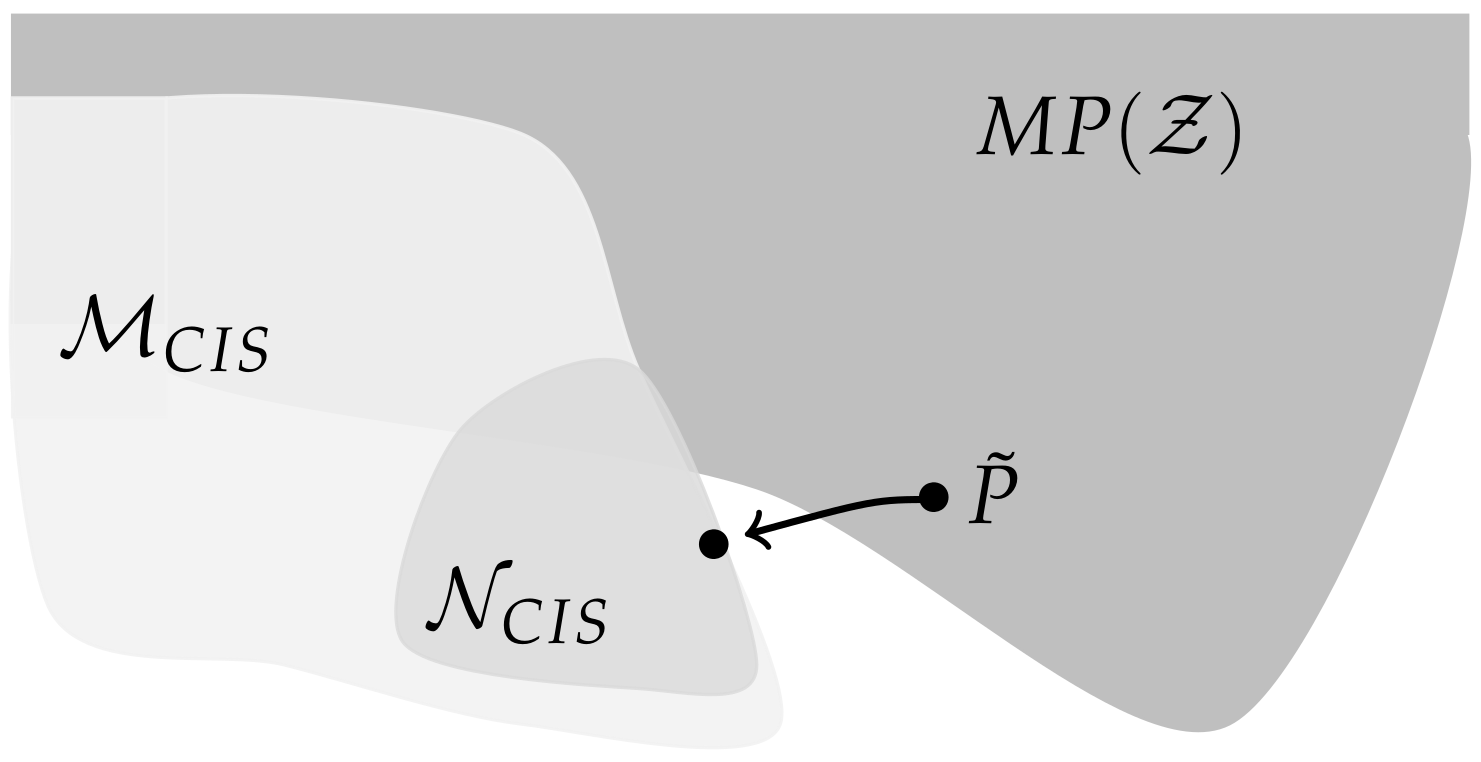
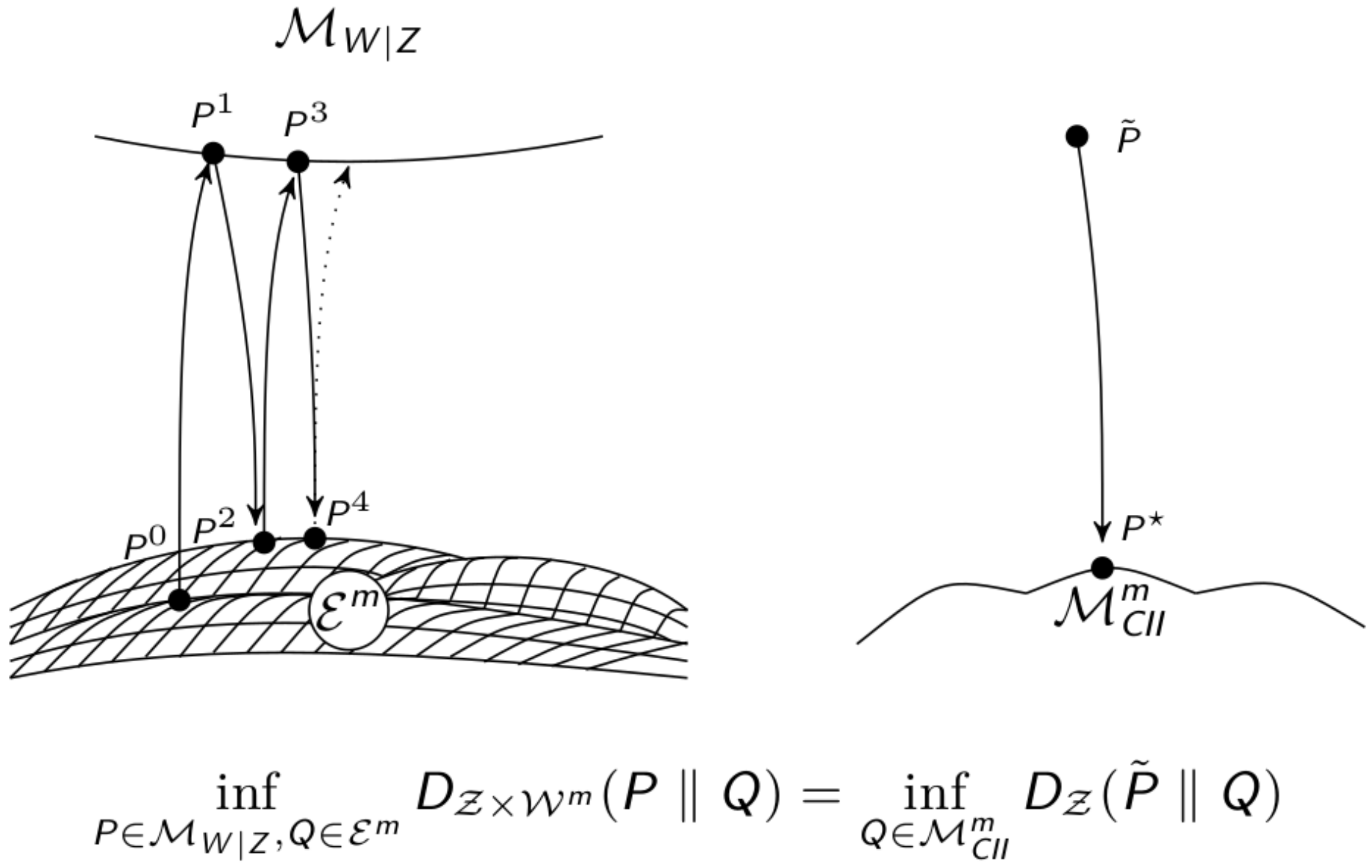
2.1.2. Relationships between the Different Measures
2.1.3. em-Algorithm
2.2. Comparison
2.2.1. Ising Model
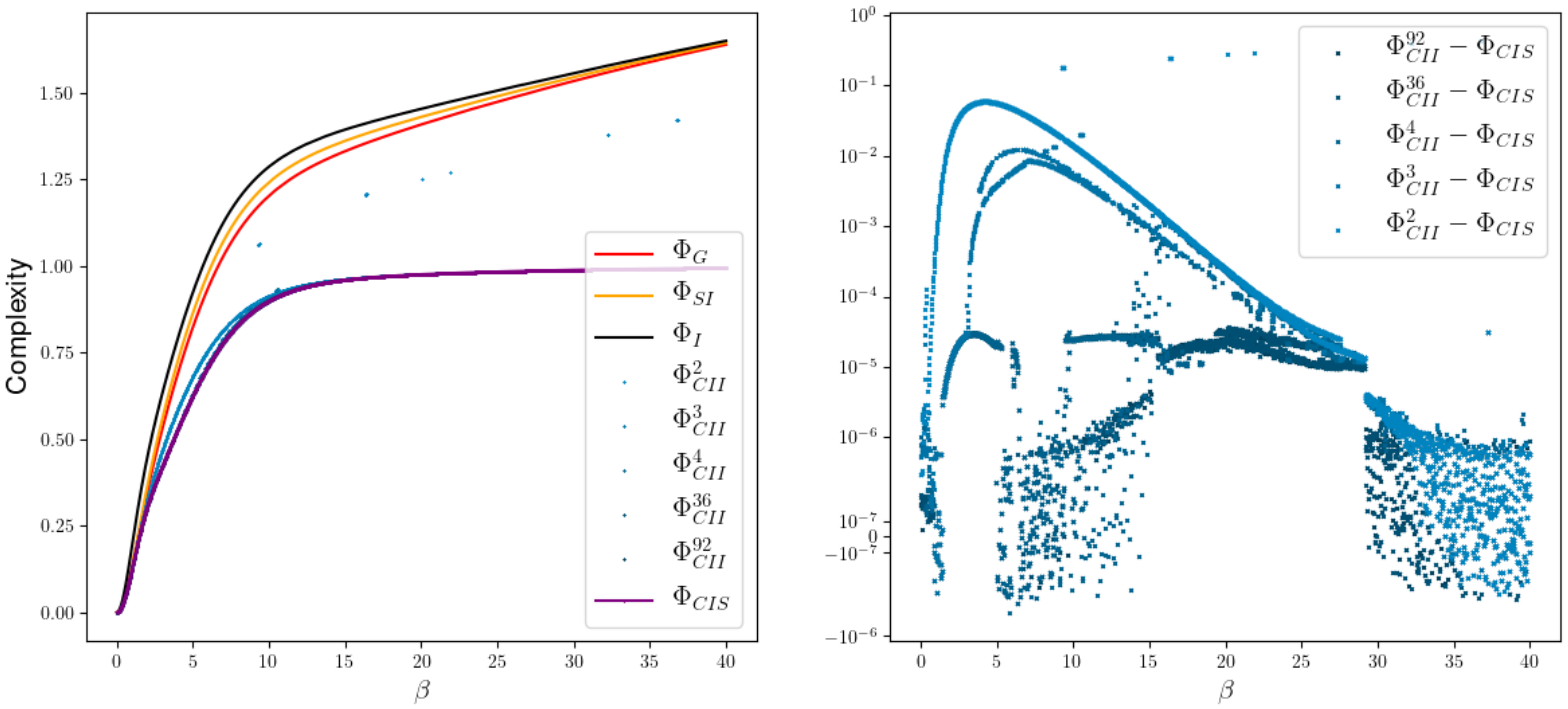
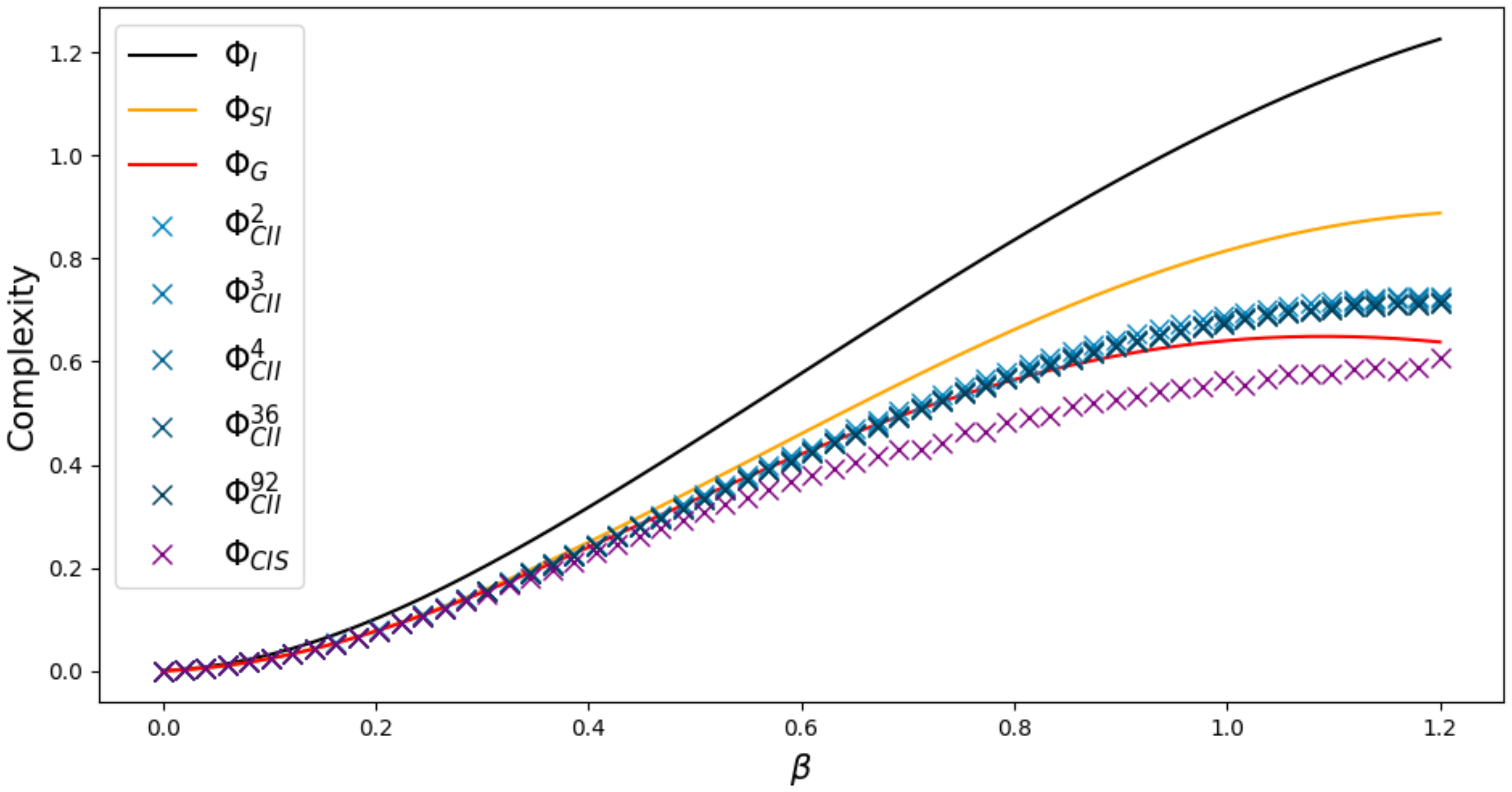
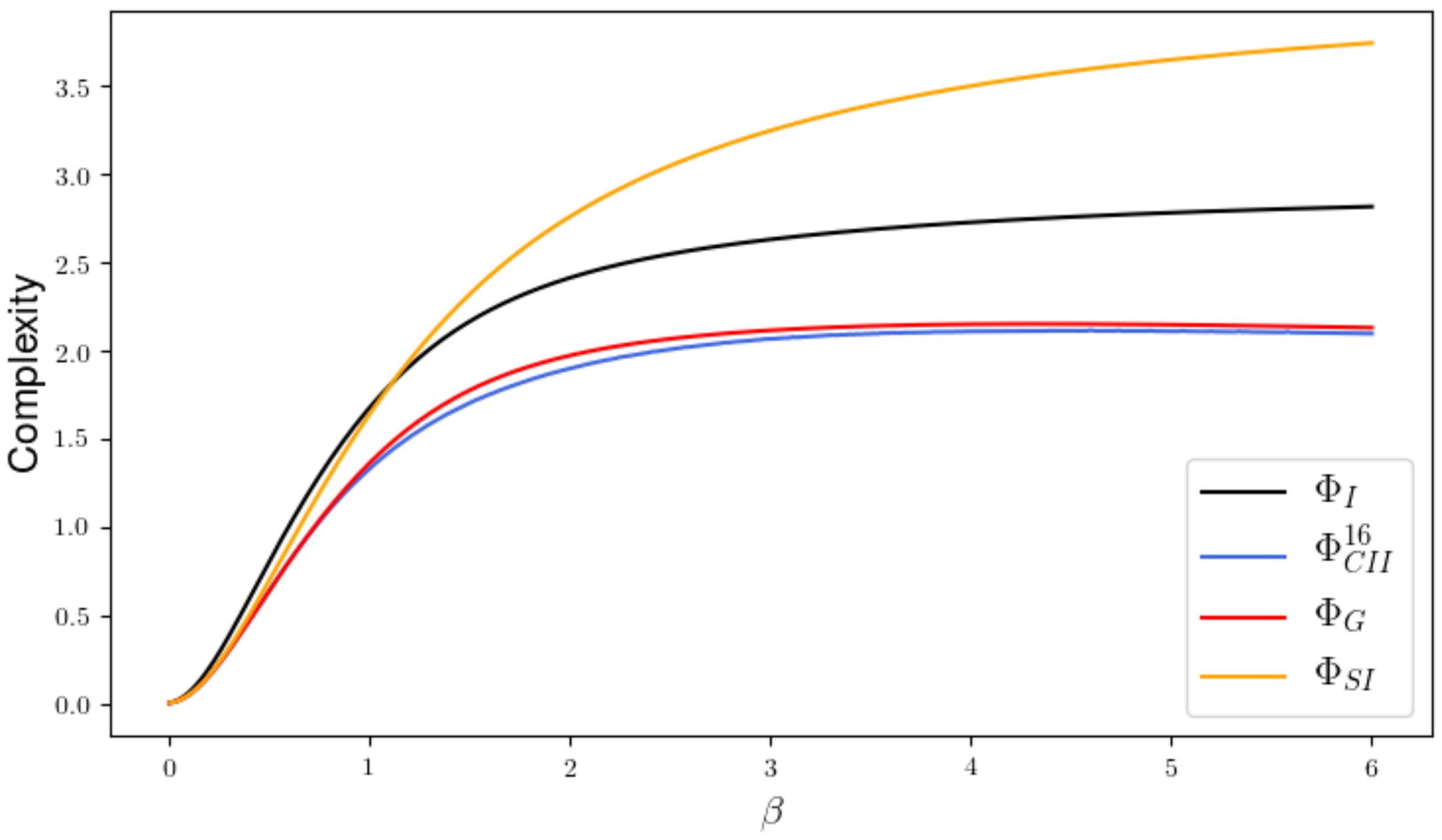
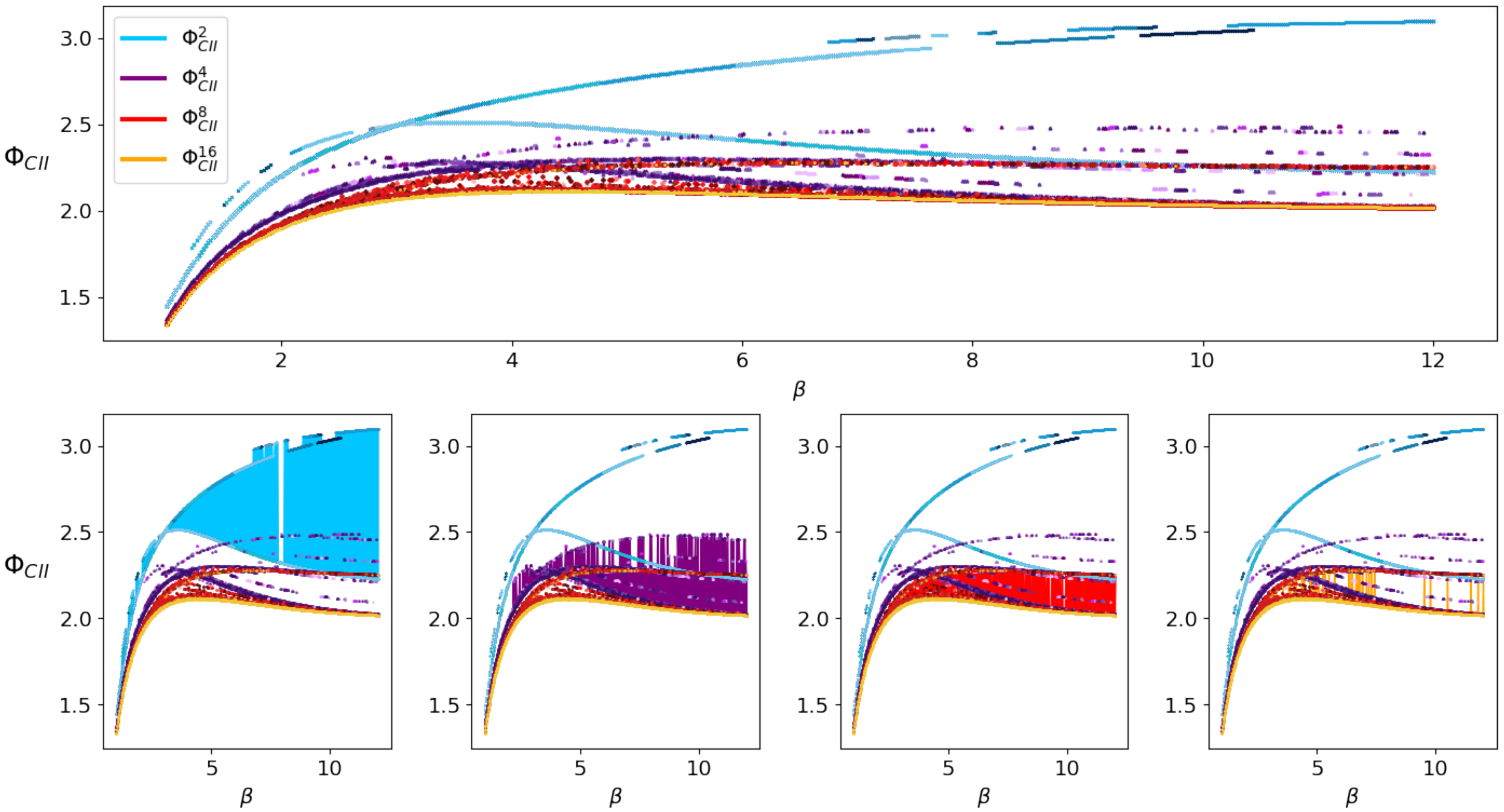
2.2.2. Results
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Conflicts of Interest
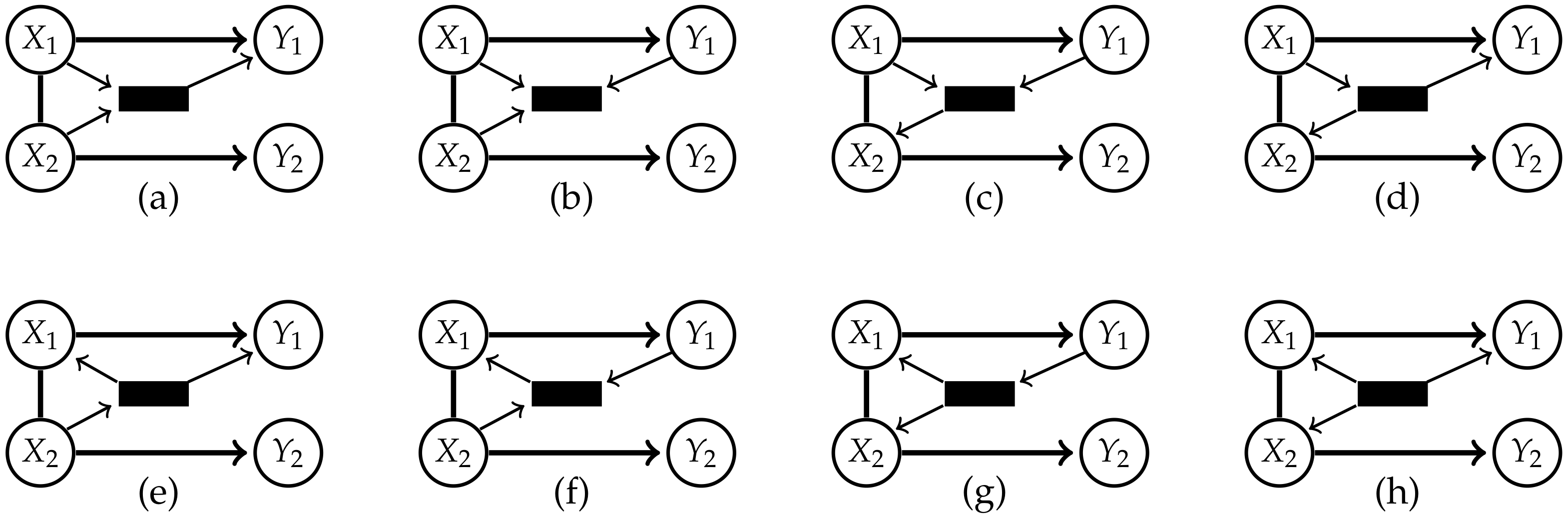
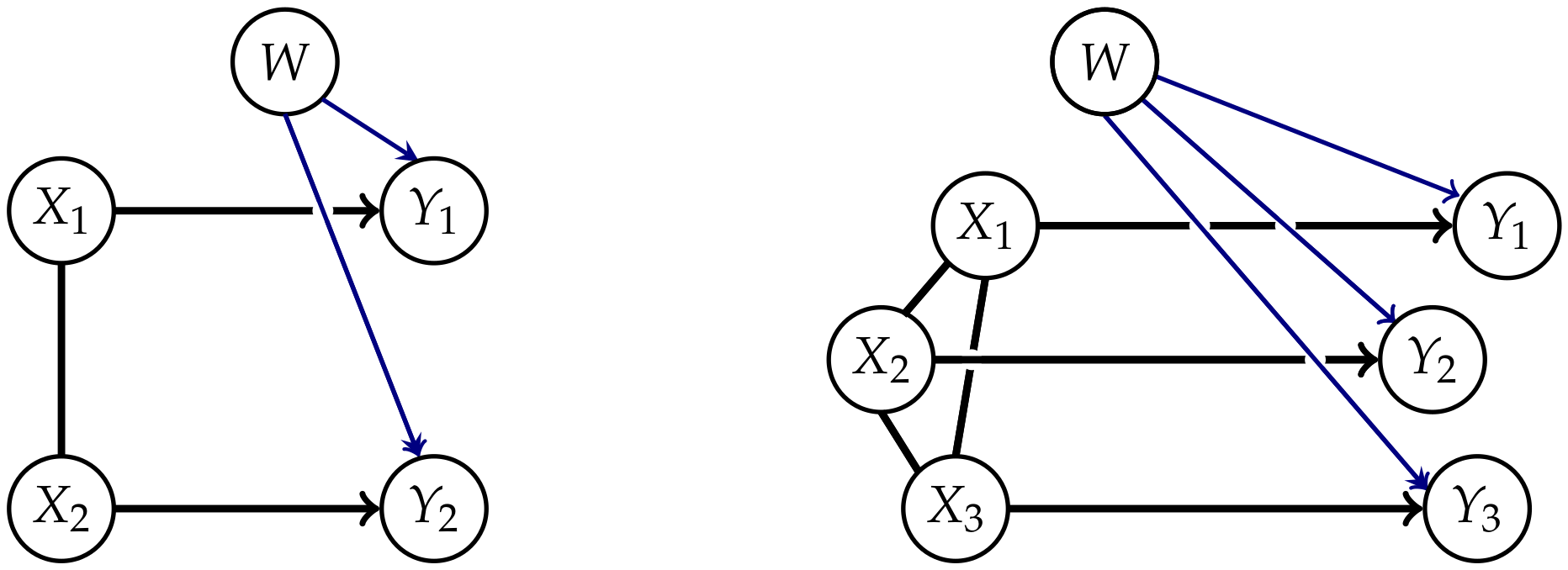
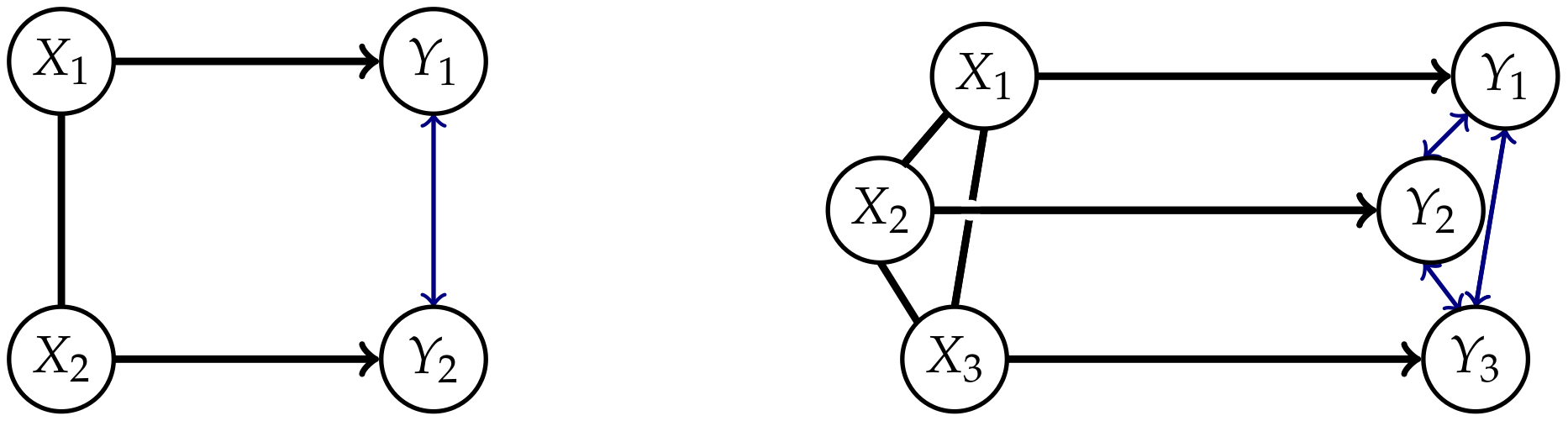
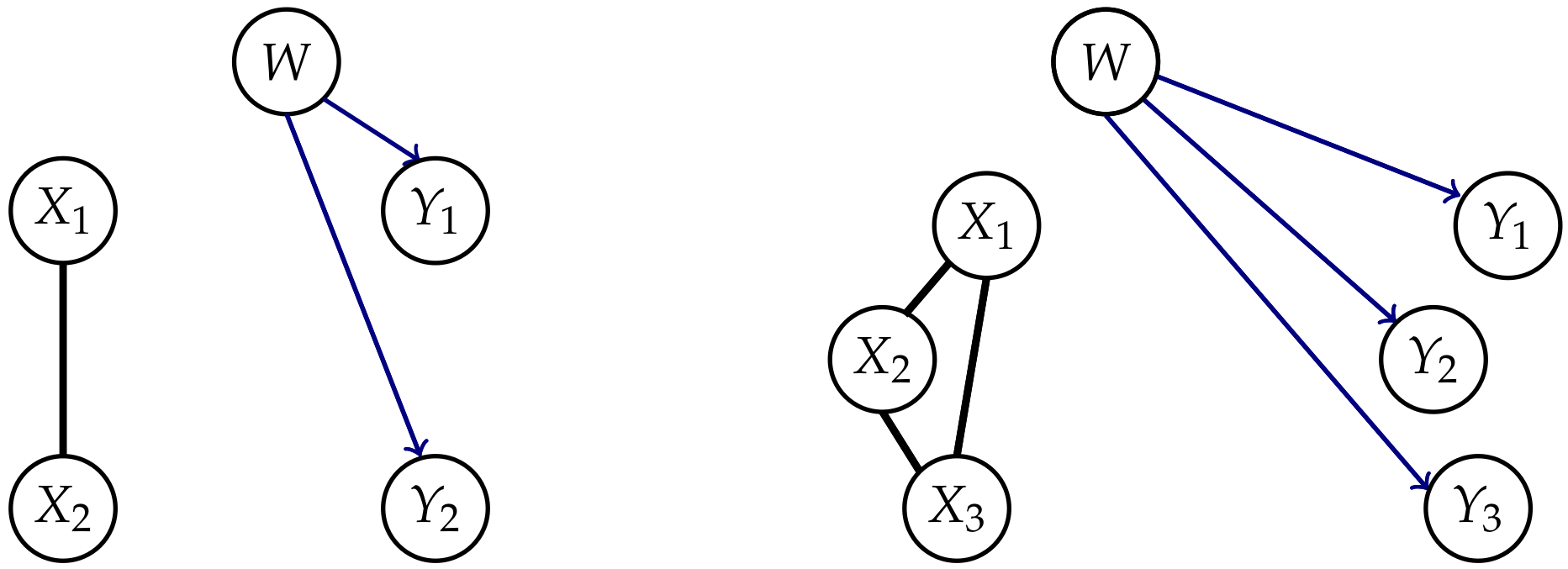
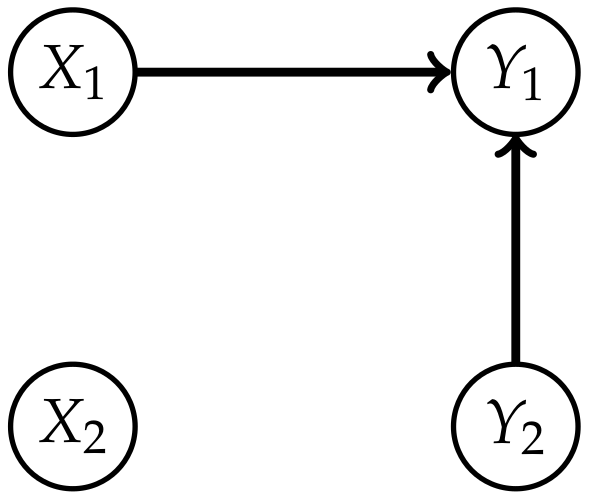
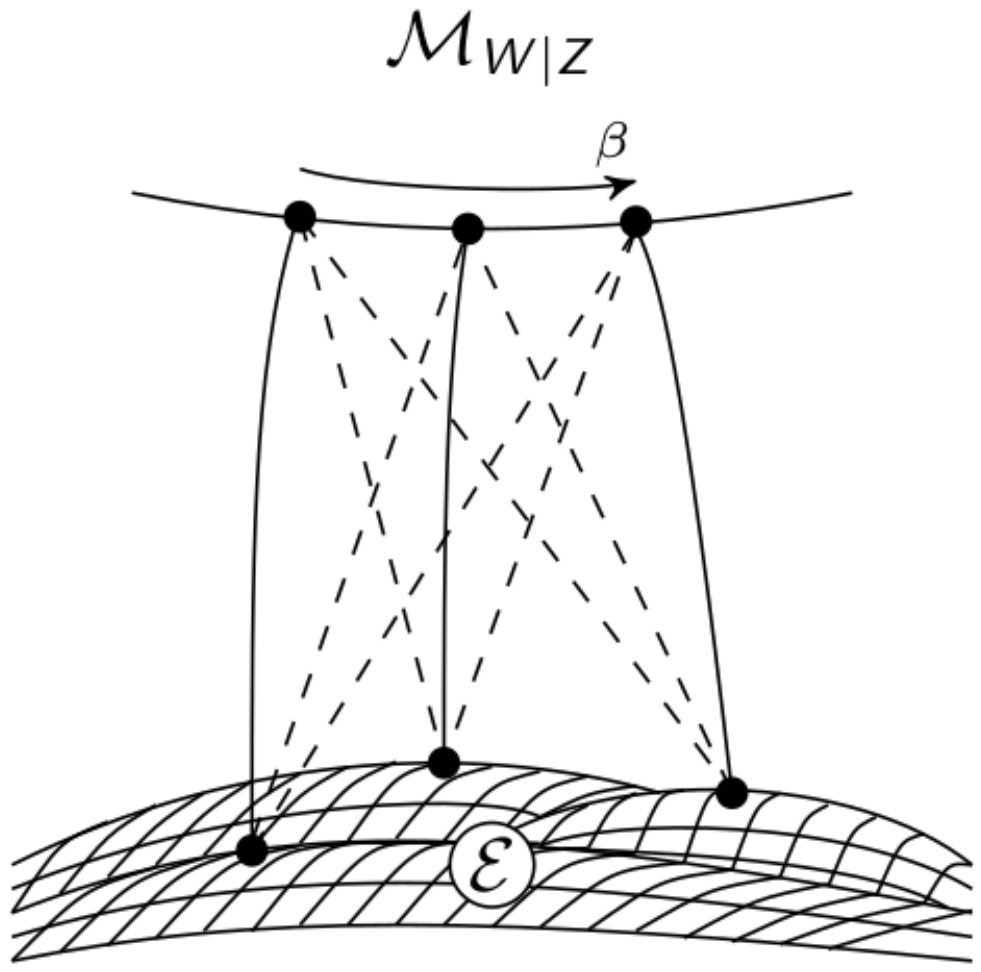
Appendix A. Graphical Models
- 1.
- Generate an ij edge as in Table A1, steps 8 and 9, between i and j on a collider trislide with an endpoint j and an endpoint in M if the edge of the same type does not already exist.
- 2.
- Generate an appropriate edge as in Table A1, steps 1 to 7, between the endpoints of every tripath with inner node in M if the edge of the same type does not already exist. Apply this step until no other edge can be generated.
- 3.
- Remove all nodes in M.
| 1 | i ← m ← j | generates | i ← j |
| 2 | i ← m – j | generates | i ← j |
| 3 | i ↔ m —j | generates | i ↔ j |
| 4 | i ← m → j | generates | i ↔ j |
| 5 | i ← m ↔ j | generates | i ↔ j |
| 6 | i – m ← j | generates | i ← j |
| 7 | i – m – j | generates | i–j |
| 8 | m → i – ⋯ – j | generates | i ← j |
| 9 | mj | generates | i ↔ j |
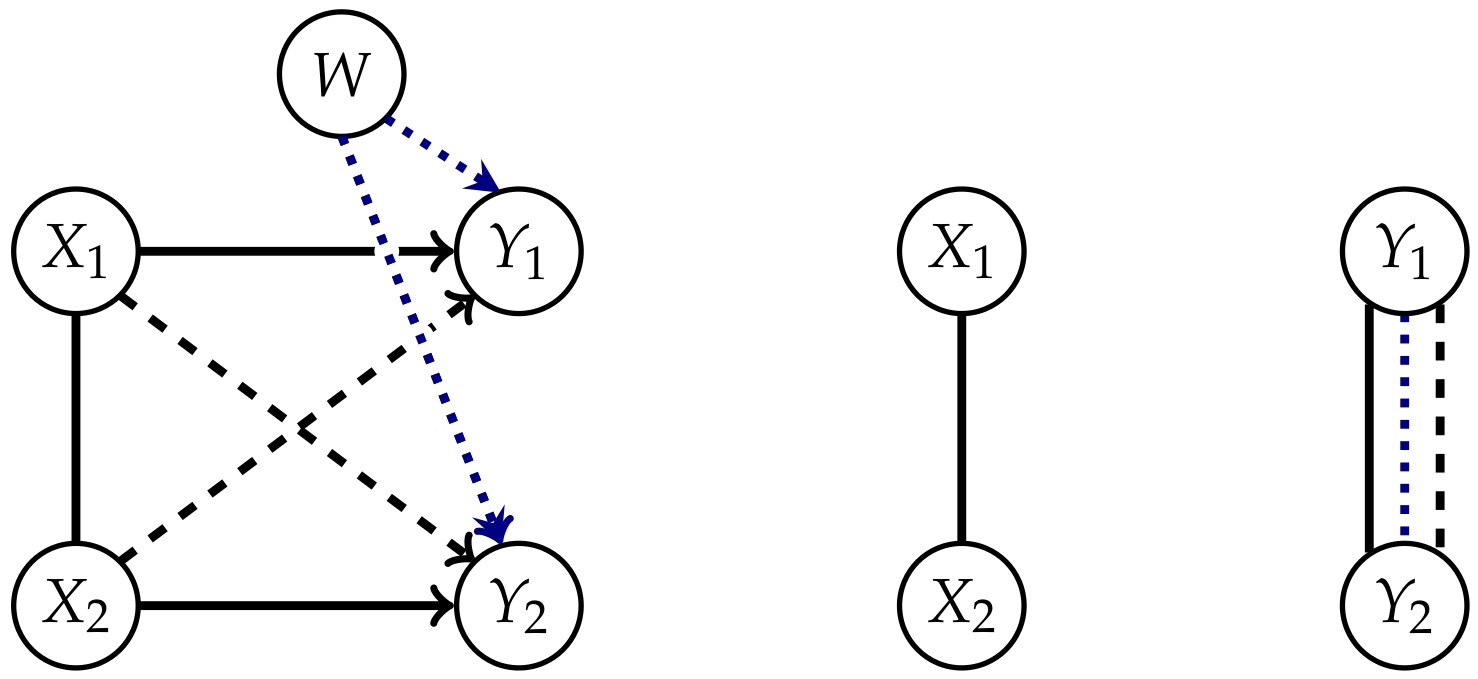
Appendix B. Proofs
- they form an undirected path between A and B,
- they can form a directed path from A to B,
- they can form a directed path form B to A,
- there exists a collider,
- A and B have a common exterior influence.
References
- Tononi, G.; Edelman, G.M. Consciousness and Complexity. Science 1999, 282, 1846–1851. [Google Scholar] [CrossRef]
- Tononi, G. Consciousness as Integrated Information: A Provisional Manifesto. Biol. Bull. 2008, 215, 216–242. [Google Scholar] [CrossRef]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 2014, 10, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Tsuchiya, N.; Amari, S. Unified framework for information integration based on information geometry. Proc. Natl. Acad. Sci. USA 2016, 113, 14817–14822. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.; Tsuchiya, N.; Oizumi, M. Geometry of Information Integration. In Information Geometry and Its Applications; Ay, N., Gibilisco, P., Matúš, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–17. [Google Scholar]
- Ay, N. Information Geometry on Complexity and Stochastic Interaction. MPI MIS PREPRINT 95. 2001. Available online: https://www.mis.mpg.de/preprints/2001/preprint2001_95.pdf (accessed on 28 September 2020).
- Ay, N. Information Geometry on Complexity and Stochastic Interaction. Entropy 2015, 17, 2432–2458. [Google Scholar] [CrossRef]
- Ay, N.; Olbrich, E.; Bertschinger, N.A. Geometric Approach to Complexity. Chaos 2011, 21. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Amari, S.; Yanagawa, T.; Fujii, N.; Tsuchiya, N. Measuring Integrated Information from the Decoding Perspective. PLoS Comput. Biol. 2016, 12. [Google Scholar] [CrossRef] [PubMed]
- Amari, S. Information Geometry and Its Applications; Springer Japan: Tokyo, Japan, 2016. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kanwal, M.S.; Grochow, J.A.; Ay, N. Comparing Information-Theoretic Measures of Complexity in Boltzmann Machines. Entropy 2017, 19, 310. [Google Scholar] [CrossRef]
- Barrett, A.B.; Seth, A.K. Practical Measures of Integrated Information for Time- Series Data. PLoS Comput. Biol. 2011, 7. [Google Scholar] [CrossRef] [PubMed]
- Csiszár, I.; Shields, P. Foundations and Trends in Communications and Information Theory. In Information Theory and Statistics: A Tutorial; Now Publishers Inc.: Delft, The Netherlands, 2004; pp. 417–528. [Google Scholar]
- Studený, M. Probabilistic Conditional Independence Structures; Springer: London, UK, 2005. [Google Scholar]
- Lauritzen, S.L. Graphical Models; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Sadeghi, K. Marginalization and conditioning for LWF chain graphs. Ann. Stat. 2016, 44, 1792–1816. [Google Scholar] [CrossRef]
- Montúfar, G. On the expressive power of discrete mixture models, restricted Boltzmann machines, and deep belief networks—A unified mathematical treatment. Ph.D. Thesis, Universität Leipzig, Leipzig, Germany, 2012. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Csiszár, I.; Tusnády, G. Information geometry and alternating minimization procedures. Stat. Decis. 1984, Supplemental Issue Number 1, 205–237. [Google Scholar]
- Amari, S.; Kurata, K.; Nagaoka, H. Information geometry of Boltzmann machines. IEEE Trans. Neural Netw. 1992, 3, 260–271. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. 1977, 39, 2–38. [Google Scholar]
- Amari, S. Information Geometry of the EM and em Algorithms for Neural Networks. Neural Netw. 1995, 9, 1379–1408. [Google Scholar] [CrossRef]
- Winkler, G. Image Analysis, Random Fields and Markov Chain Monte Carlo Methods; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Choromanska, A.; Henaff, M.; Mathieu, M.; Arous, G.B.; LeCun, Y. The Loss Surfaces of Multilayer Networks. PMLR 2015, 38, 192–204. [Google Scholar]
- Langer, C. Integrated-Information-Measures GitHub Repository. Available online: https://github.com/CarlottaLanger/Integrated-Information-Measures (accessed on 18 August 2020).
- Frydenberg, M. The Chain Graph Markov Property. Scand. J. Stat. 1990, 17, 333–353. [Google Scholar]
- Ay, N.; Jost, J.; Lê, H.V.; Schwachhöfer, L. Information Geometry; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
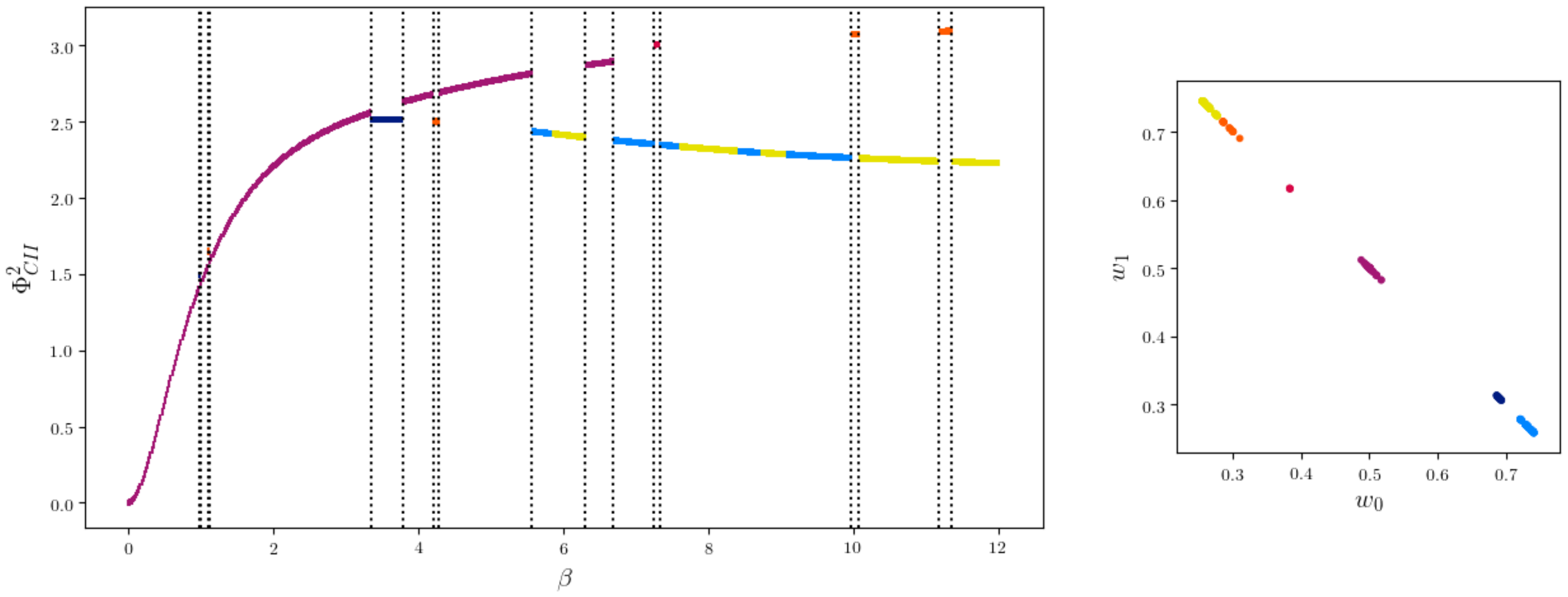
| Minimum | Maximum | Arithmetic Mean | |
|---|---|---|---|
| 2 | 0.011969035529826939 | 0.5028091152589176 | 0.15263592877594967 |
| 3 | 0.021348311360946 | 0.5499395859771526 | 0.1538653506807848 |
| 4 | 0.014762084688030863 | 0.3984635189946462 | 0.15139198568055212 |
| 8 | 0.017334311629729246 | 0.4383731978333986 | 0.15481967618112732 |
| 16 | 0.024306996171092318 | 0.4238222051787452 | 0.1490336847067273 |
| 300 | 0.016524177216064712 | 0.47733473380366764 | 0.15493896625208842 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Langer, C.; Ay, N. Complexity as Causal Information Integration. Entropy 2020, 22, 1107. https://doi.org/10.3390/e22101107
Langer C, Ay N. Complexity as Causal Information Integration. Entropy. 2020; 22(10):1107. https://doi.org/10.3390/e22101107
Chicago/Turabian StyleLanger, Carlotta, and Nihat Ay. 2020. "Complexity as Causal Information Integration" Entropy 22, no. 10: 1107. https://doi.org/10.3390/e22101107
APA StyleLanger, C., & Ay, N. (2020). Complexity as Causal Information Integration. Entropy, 22(10), 1107. https://doi.org/10.3390/e22101107





