Performance Analysis of Identification Codes
Abstract
1. Introduction
2. Preliminaries
2.1. Identification
2.1.1. Types of Errors
- A transmission error (the same reason as for the missed identification) happens; and the channel gives an output of message j although having received the message i.
- The scheme uses a randomized identification code (see Section 2.1.2), and the randomly selected codeword lies in the overlapping section of the decoding sets of message i and message j.
2.1.2. Identification Codes
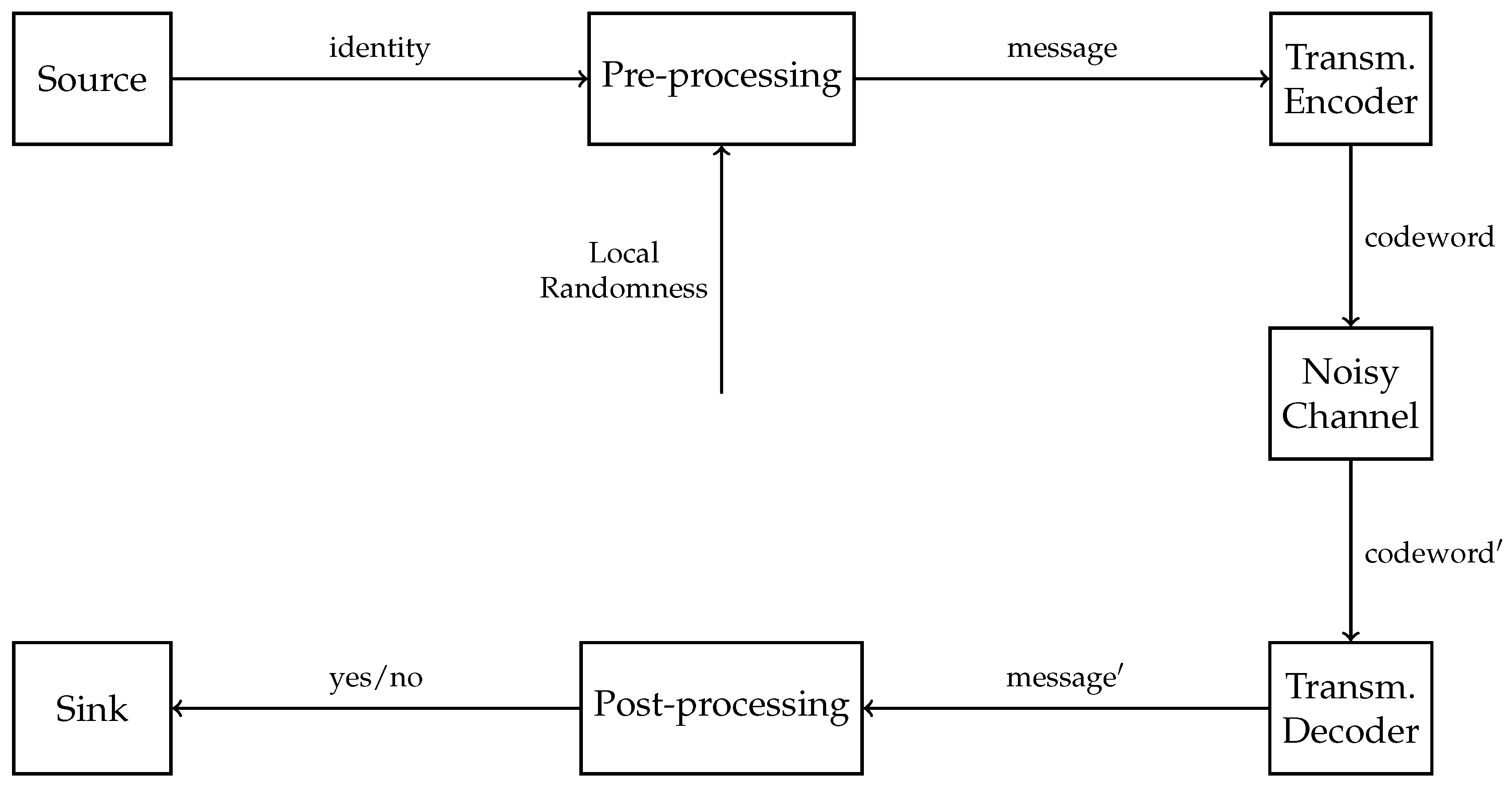
2.1.3. Identification Codes from Transmission Codes
2.2. Error-Correction Codes
2.2.1. Reed-Solomon Codes
2.2.2. Concatenated Codes
2.3. Error-Correction Codes Achieving Identification Capacity
- The size of the block code, and thus the size of the identification code, must be exponential in the size of the randomness:
- The size of the tag in bits must be negligible in the size of the randomness in bits:
- The distance of the code must grow as the blocklength, so that the error of the second kind goes to zero:
2.4. Example
3. Comparison of Identification and Transmission
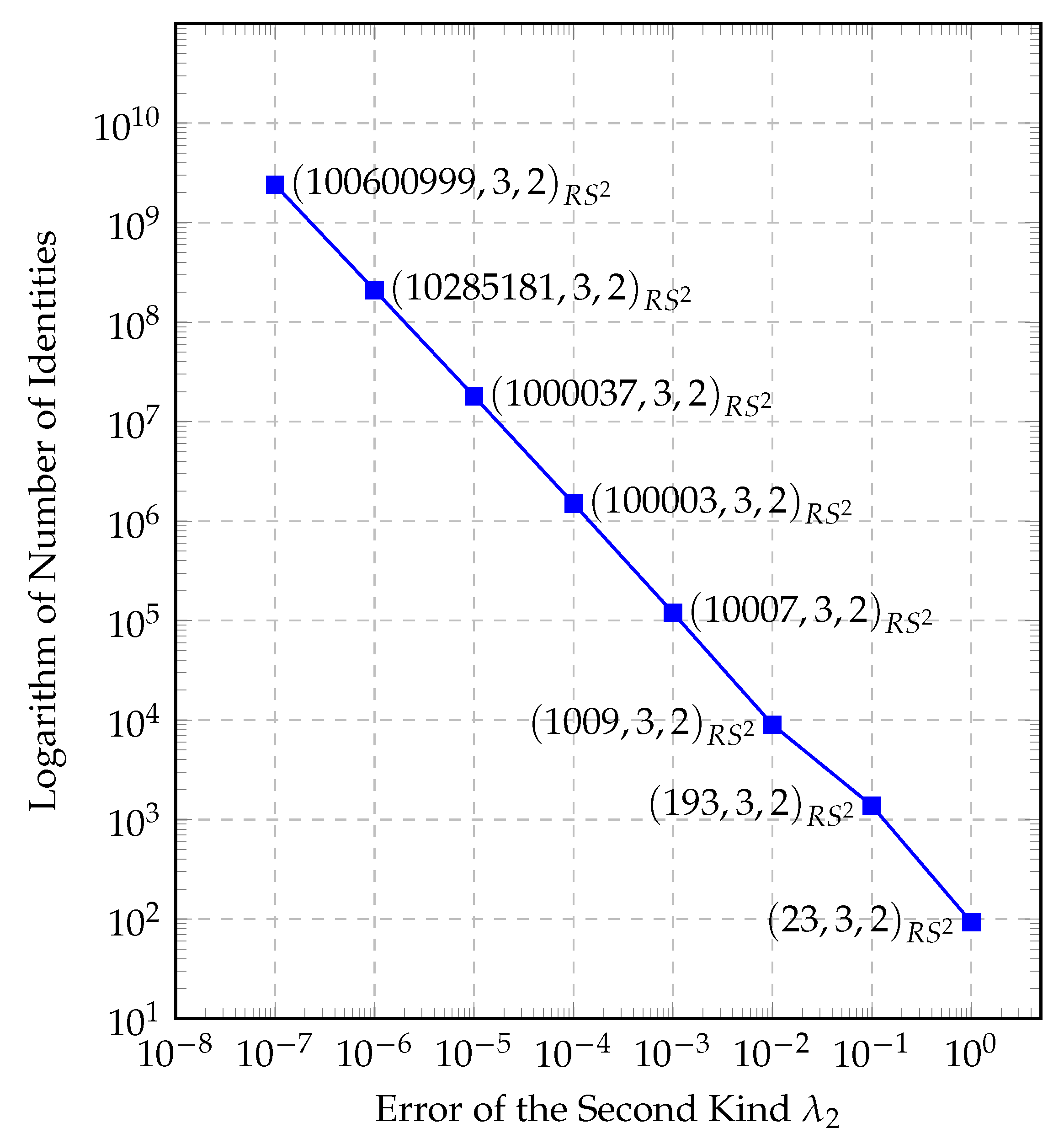
3.1. Single Reed-Solomon Code
3.2. Double Reed-Solomon Code
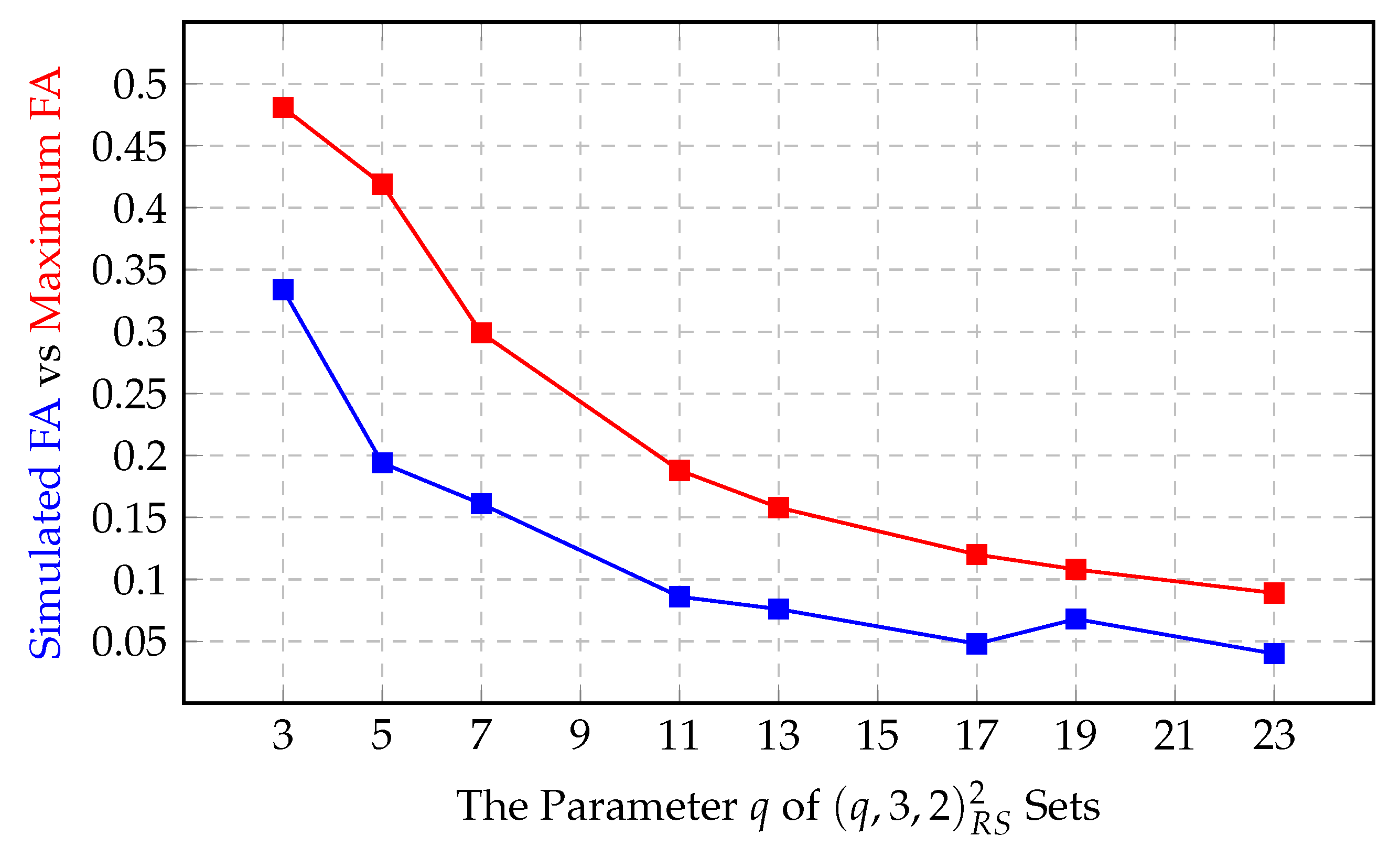
3.3. Implementation and Simulation
- Divide the randomness j, ranging from 0 to by q. The quotient shows us which column of the generator matrix of the we need to use. We do not need the other columns to calculate the necessary tag. Using only that column, we will get one symbol in the alphabet of size . The remainder of the division, is used later.
- Expand the symbol into k symbols of size q. The list of these q elements will be called the expanded codeword.
- Find the column - or the code locator - in the generator matrix of with the index as the remainder and multiply the expanded codeword with that column scalarly, or simply evaluate it with the picked code locator.
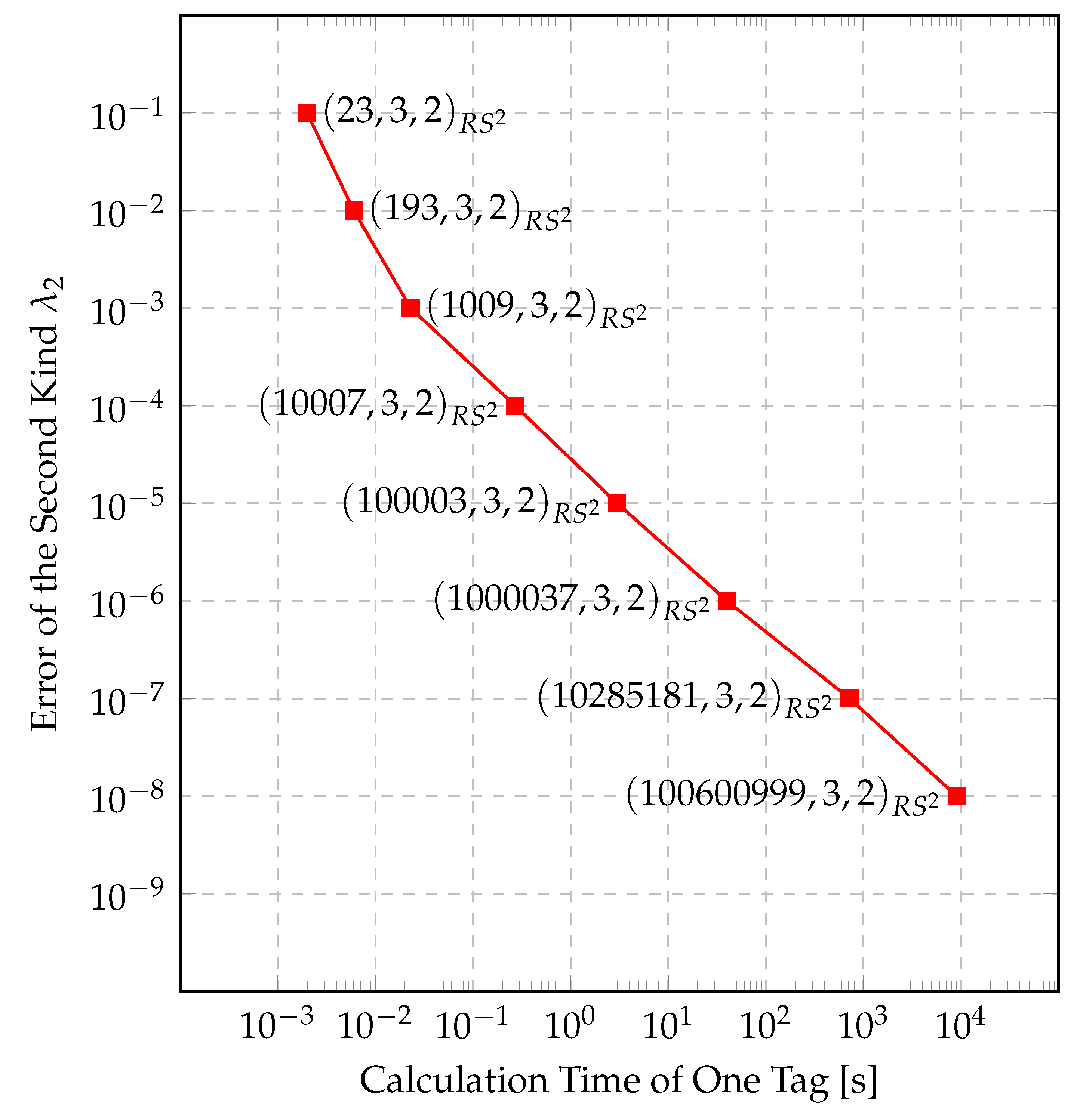
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ahlswede, R.; Dueck, G. Identification via channels. IEEE Trans. Inf. Theory 1989, 35, 15–29. [Google Scholar] [CrossRef]
- Ahlswede, R.; Dueck, G. Identification in the presence of feedback-a discovery of new capacity formulas. IEEE Trans. Inf. Theory 1989, 35, 30–36. [Google Scholar] [CrossRef]
- Boche, H.; Deppe, C. Secure Identification for Wiretap Channels; Robustness, Super-Additivity and Continuity. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1641–1655. [Google Scholar] [CrossRef]
- Verdu, S.; Wei, V.K. Explicit construction of optimal constant-weight codes for identification via channels. IEEE Trans. Inf. Theory 1993, 39, 30–36. [Google Scholar] [CrossRef]
- Ahlswede, R.; Zhang, Z. New directions in the theory of identification via channels. IEEE Trans. Inf. Theory 1995, 41, 1040–1050. [Google Scholar] [CrossRef]
- Ahlswede, A.; Althöfer, I.; Deppe, C.; Tamm, U. Identification and Other Probabilistic Models, Rudolf Ahlswede’s Lectures on Information Theory 6, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Ahlswede, R.; Wolfowitz, J. The structure of capacity functions for compound channels. In Probability and Information Theory; Behara, M., Krickeberg, K., Wolfowitz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1969; pp. 12–54. [Google Scholar]
- Han, T.S.; Verdu, S. New results in the theory of identification via channels. IEEE Trans. Inf. Theory 1992, 38, 14–25. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N. Transmission, Identification and Common Randomness Capacities for Wire-Tape Channels with Secure Feedback from the Decoder. In General Theory of Information Transfer and Combinatorics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 258–275. [Google Scholar] [CrossRef]
- Boche, H.; Deppe, C. Secure Identification Under Passive Eavesdroppers and Active Jamming Attacks. IEEE Trans. Inf. Forensics Secur. 2019, 14, 472–485. [Google Scholar] [CrossRef]
- Boche, H.; Deppe, C.; Winter, A. Secure and Robust Identification via Classical-Quantum Channels. IEEE Trans. Inf. Theory 2019, 65, 6734–6749. [Google Scholar] [CrossRef]
- Kurosawa, K.; Yoshida, T. Strongly universal hashing and identification codes via channels. IEEE Trans. Inf. Theory 1999, 45, 2091–2095. [Google Scholar] [CrossRef]
- Reed, I.S.; Solomon, G. Polynomial Codes Over Certain Finite Fields. J. Soc. Ind. Appl. Math. 1960, 8, 300–304. [Google Scholar] [CrossRef]
- Eswaran, K. Identification via Channels and Constant-Weight Codes. Available online: https://people.eecs.berkeley.edu/~ananth/229BSpr05/Reports/KrishEswaran.pdf (accessed on 23 September 2020).
- Moulin, P.; Koetter, R. A framework for the design of good watermark identification codes. In Security, Steganography, and Watermarking of Multimedia Contents VIII; Delp, E.J., III, Wong, P.W., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2006; Volume 6072, pp. 565–574. [Google Scholar] [CrossRef]
- The Sage Developers. SageMath, the Sage Mathematics Software System (Version 8.1). Available online: https://www.sagemath.org (accessed on 23 September 2020).
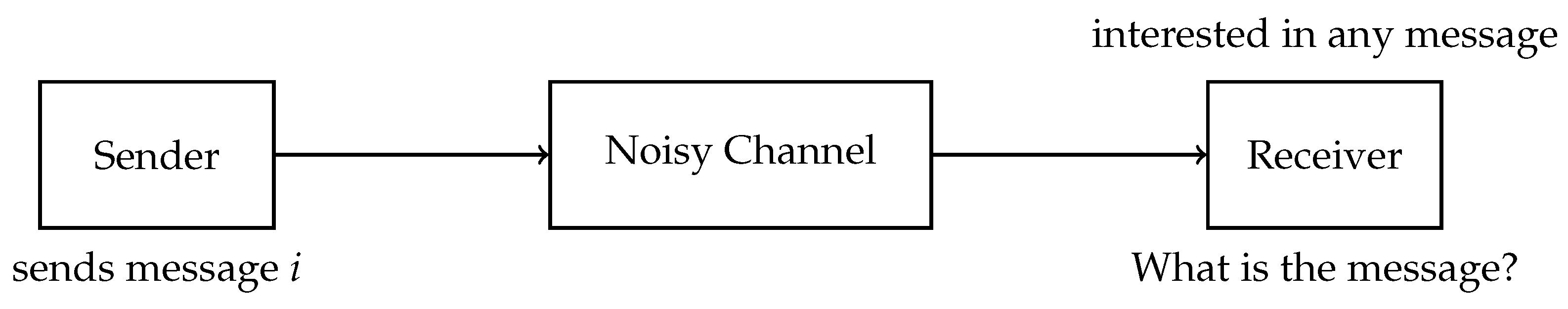
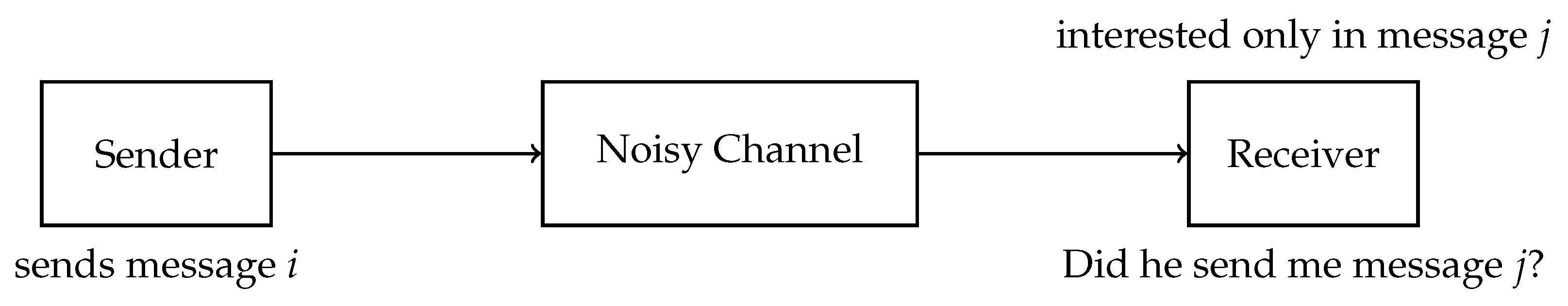




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derebeyoğlu, S.; Deppe, C.; Ferrara, R. Performance Analysis of Identification Codes. Entropy 2020, 22, 1067. https://doi.org/10.3390/e22101067
Derebeyoğlu S, Deppe C, Ferrara R. Performance Analysis of Identification Codes. Entropy. 2020; 22(10):1067. https://doi.org/10.3390/e22101067
Chicago/Turabian StyleDerebeyoğlu, Sencer, Christian Deppe, and Roberto Ferrara. 2020. "Performance Analysis of Identification Codes" Entropy 22, no. 10: 1067. https://doi.org/10.3390/e22101067
APA StyleDerebeyoğlu, S., Deppe, C., & Ferrara, R. (2020). Performance Analysis of Identification Codes. Entropy, 22(10), 1067. https://doi.org/10.3390/e22101067






