Detection of Hypoglycemia Using Measures of EEG Complexity in Type 1 Diabetes Patients
Abstract
1. Introduction
2. Materials and Methods
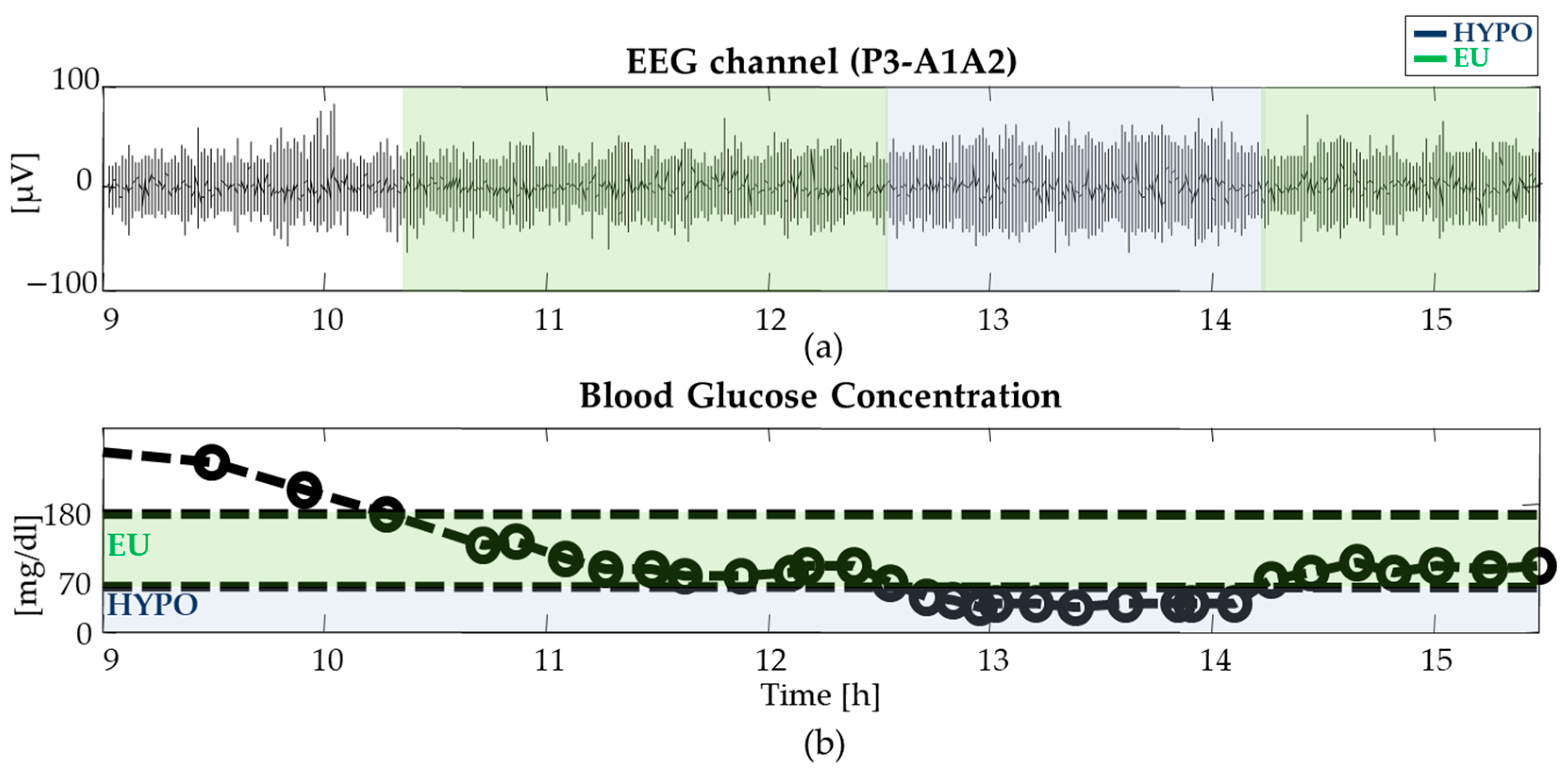
2.1. Database and Experimental Protocol
2.2. EEG Pre-Processing
2.3. Assessment of EEG Complexity in Euglycemia and Hypoglycemia
2.3.1. Entropy Measures
2.3.2. Fractal Dimension Measures
2.3.3. Criteria for Statistical Analysis
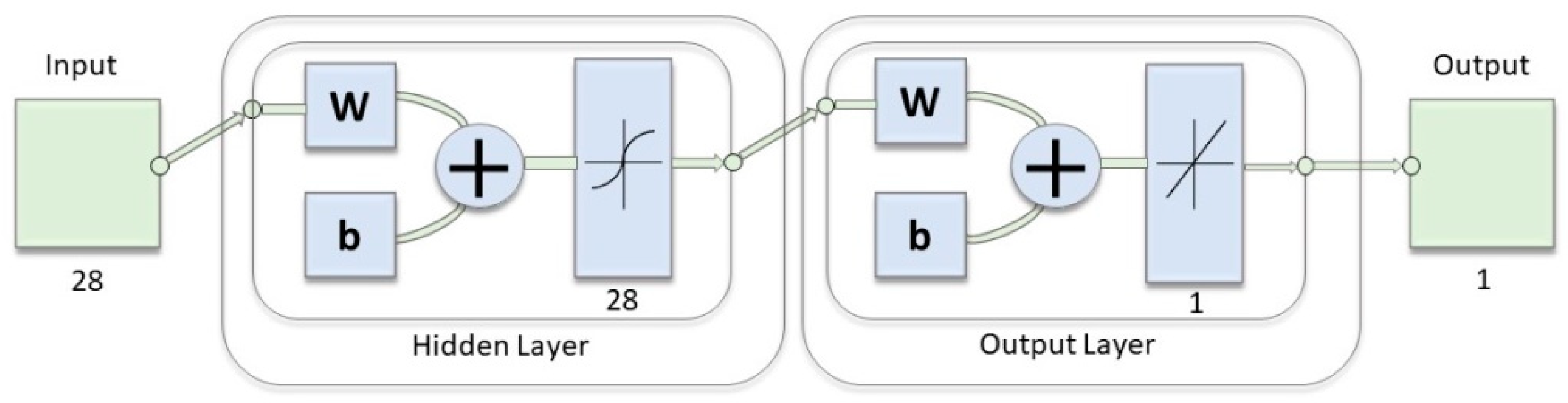
2.4. Hypoglycemia Detection through Indices of EEG Complexity
3. Results
3.1. Assessment of EEG Complexity in Euglycemia and Hypoglycemia
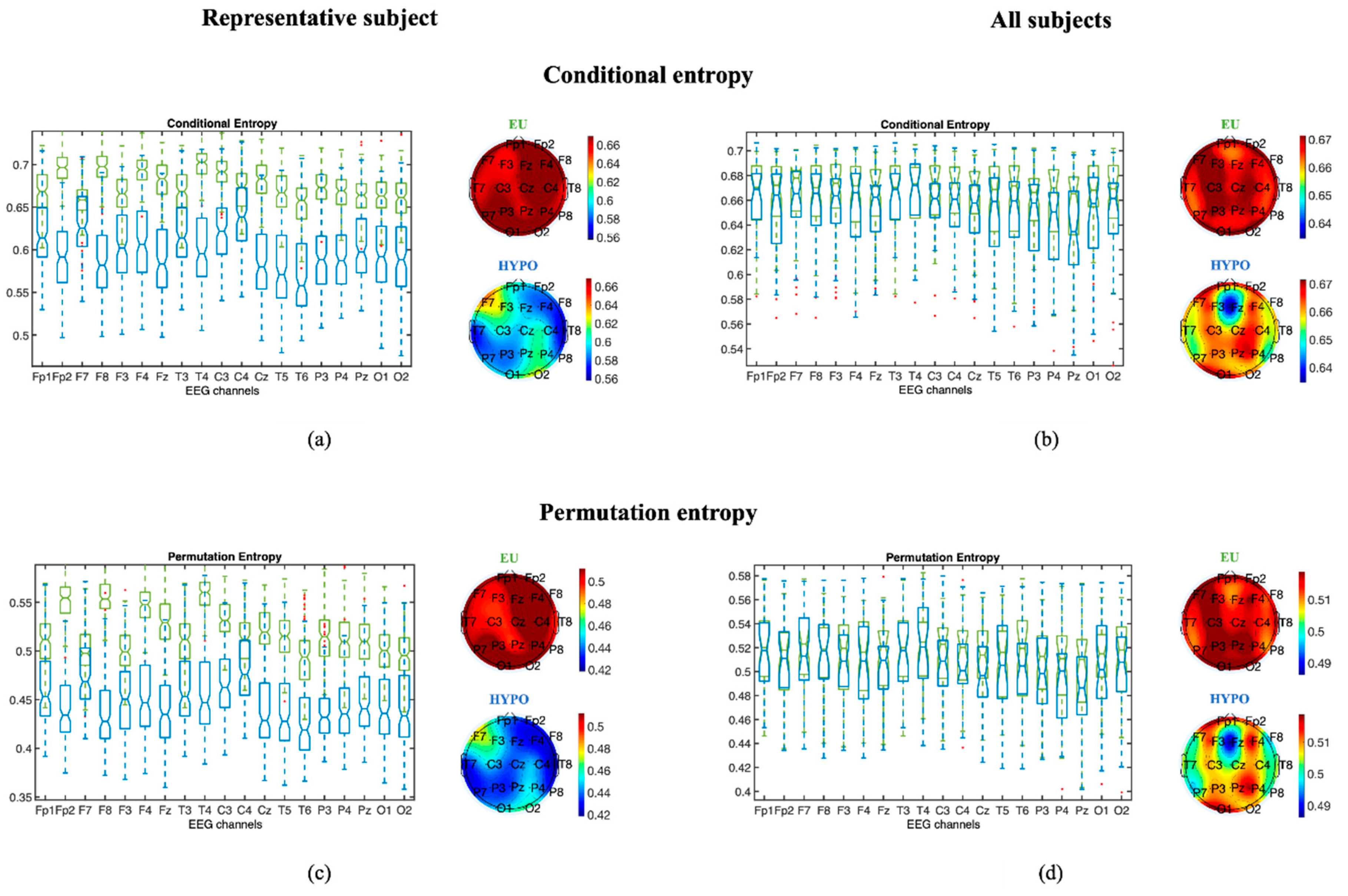
3.1.1. Entropy Measures
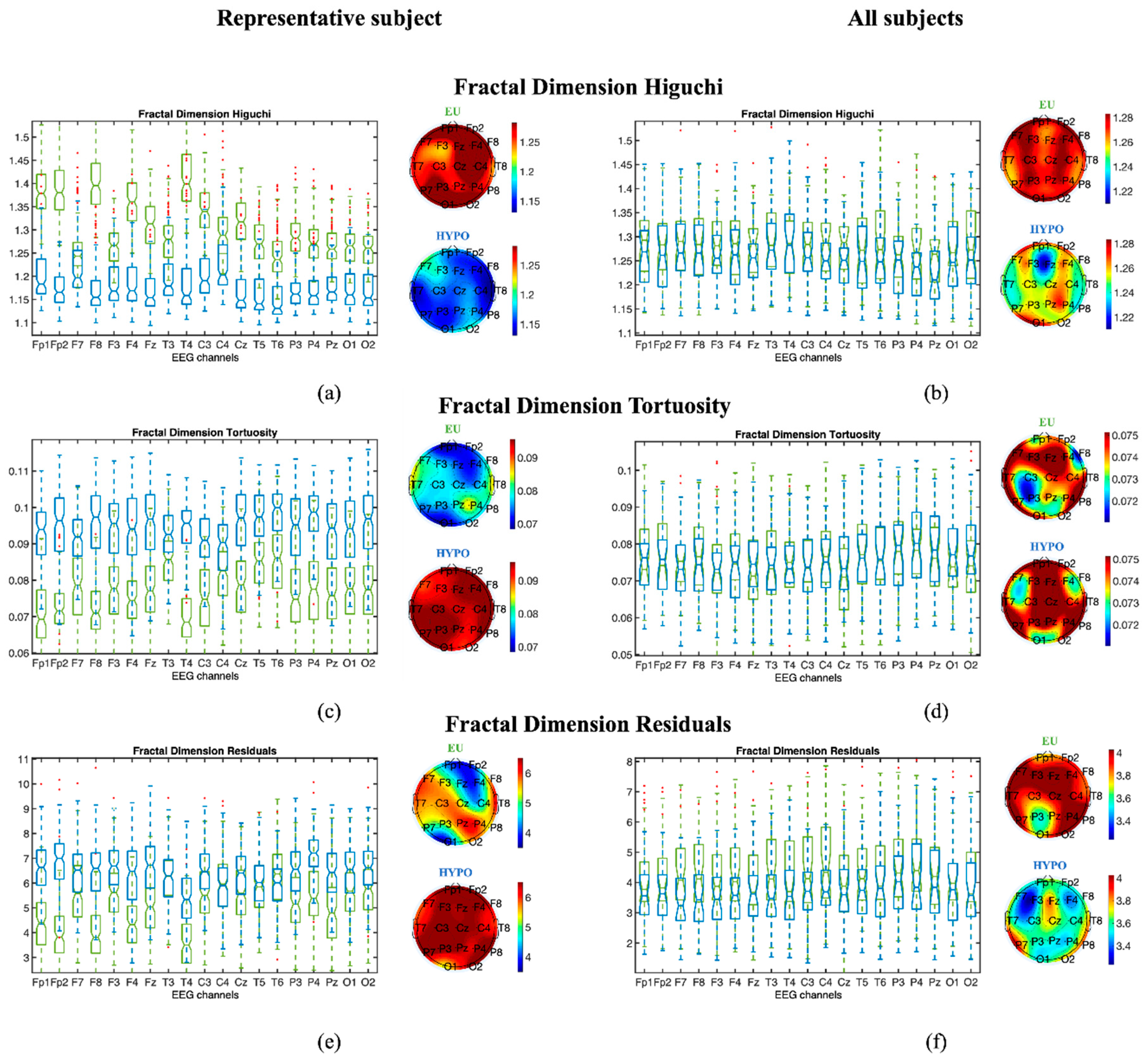
3.1.2. Fractal Dimension Measures
3.1.3. Statistical Analysis
3.2. Hypoglycemia Detection through Indices of EEG Complexity
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- American Diabetes Association. Defining and reporting hypoglycemia in diabetes: A report from the American Diabetes Association Workgroup on Hypoglycemia. Diabetes Care 2005, 28, 1245–1249. [Google Scholar] [CrossRef] [PubMed]
- Mergenthaler, P.; Lindauer, U.; Dienel, G.A.; Meisel, A. Sugar for the brain: The role of glucose in physiological and pathological brain function. Trends Neurosci. 2013, 36, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Erbsloh, F.; Bernsmeier, A.; Hillesheim, H. The glucose consumption of the brain its dependence on the liver. Arch. Psychiatr. Nervenkrankh. 1958, 196, 611–626. [Google Scholar]
- Sokoloff, L. Energetics of Functional Activation in Neural Tissues. Neurochem. Res. 1999, 24, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Asvold, B.O.; Sand, T.; Hestad, K.; Bjorgaas, M.R. Cognitive Function in Type 1 Diabetic Adults with Early Exposure to Severe Hypoglycemia. Diabetes Care 2010, 33, 1945–1947. [Google Scholar] [CrossRef]
- Sejling, A.S.; Kjaer, T.W.; Pedersen-Bjergaard, U.; Diemar, S.S.; Frandsen, C.S.; Hilsted, L.; Faber, J.; Holst, J.J.; Tarnow, L.; Nielsen, M.V.; et al. Hypoglycemia-associated changes in electroencephalogram in patients with type 1 diabetes and normal hypoglycemia awareness or unawareness. Diabetes 2015, 64, 1760–1769. [Google Scholar] [CrossRef]
- Rubega, M.; Sparacino, G. Neurological changes in hypoglycemia. Diabetes Technol. Ther. 2017, 19, 73–75. [Google Scholar] [CrossRef]
- Fabrykant, M.; Pacella, B.L. Association of spontaneous hypoglycemia with hypocalcemia and electrocerebral dysfunction. Arch. Intern. Med. 1948, 81, 184–202. [Google Scholar] [CrossRef]
- Ross, I.S.; Loeser, L.H. Electroencephalographic findings in essential hypoglycemia. Electroencephalogr. Clin. Neurophysiol. 1951, 3, 141–148. [Google Scholar] [CrossRef]
- Pramming, S.; Thorsteinsson, B.; Bendtson, I.; Binder, C. The relationship between symptomatic and biomechanical hypoglycemia in insulin-dependent diabetic patients. J. Int. Med. 1990, 228, 641–646. [Google Scholar] [CrossRef]
- Tribl, G.; Howorka, K.; Heger, G.; Anderer, P.; Thoma, H.; Zeitlhofer, J. EEG Topography during Insulin-Induced Hypoglycemia in Patients with Insulin-Dependent Diabetes mellitus. Eur. Neurol. 1996, 36, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, D.Y.; Baccala, L.A.; Sameshima, K. Information partial directed coherence. Biol. Cybern. 2010, 103, 463–469. [Google Scholar] [CrossRef] [PubMed]
- Rubega, M.; Sparacino, G.; Sejling, A.S.; Juhl, C.B.; Cobelli, C. Decrease of EEG coherence during hypoglycemia in type 1 diabetic subjects. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015. [Google Scholar]
- Rubega, M.; Sparacino, G.; Sejling, A.S.; Juhl, C.B.; Cobelli, C. Hypoglycemia-Induced Decrease of EEG Coherence in Patients with Type 1 Diabetes. Diabetes Technol. Ther. 2016, 18, 178–184. [Google Scholar] [CrossRef] [PubMed]
- Fabris, C.; Sparacino, G.; Sejling, A.S.; Goljahani, A.; Duun-Henriksen, J.; Remvig, L.S.; Juhl, C.B.; Cobelli, C. Hypoglycemia related electroencephalogram changes assessed by multiscale entropy. Diabetes Technol. Ther. 2014, 16, 688–694. [Google Scholar] [CrossRef]
- Scarpa, F.; Rubega, M.; Zanon, M.; Finottello, F.; Sejling, A.S.; Sparacino, G. Hypoglycemia-induced EEG complexity changes in Type 1 diabetes assessed by fractal analysis algorithm. Biomed. Signal Process. Control 2017, 38, 168–173. [Google Scholar]
- Accardo, A.; Affinito, M.; Carrozzi, M.; Bouquet, F. Use of the fractal dimension for the analysis of electroencephalographic time series. Biol. Cybern. 1997, 77, 339–350. [Google Scholar]
- Finotello, F.; Scarpa, F.; Zanon, M. EEG signal features extraction based on fractal dimension. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4154–4157. [Google Scholar]
- Facchinetti, A.; Sparacino, G.; Cobelli, C. Online denoising method to handle intraindividual variability of signal-to-noise ratio in continuous glucose monitoring. IEEE Trans. Biomed. Eng. 2011, 58, 2664–2671. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Henry, M.; Judge, G. Permutation Entropy and Information Recovery in Nonlinear Dynamic Economic Time Series. Econometrics 2019, 7, 10. [Google Scholar] [CrossRef]
- Cao, Y.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. 2004, 70, 046217. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEg recordings during sevourane anesthesia. J. Neural Eng. 2010, 7, 046010. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.; Unakafov, A.; Unakafova, V. Ordinal patterns, entropy and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Bian, C.; Qin, C.; Ma, Q.D.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. 2012, 85, 021906. [Google Scholar] [CrossRef]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation Entropy: New Ideas and Challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Unakafov, A.M.; Karsten, K. Conditional entropy of ordinal patterns. Phys. D 2014, 269, 94–102. [Google Scholar] [CrossRef]
- Klinkenberg, B. A review of methods used to determine the fractal dimension of linear features. Math Geol. 1994, 26, 23–46. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Polychronaki, G.E.; Ktonas, P.Y.; Gatzonis, S.; Siatouni, A.; Asvestas, P.A.; Tsekou, H.; Sakas, D.; Nikita, K.S. Comparison of fractal dimension estimation algorithms for epileptic seizure onset detection. J. Neural. Eng. 2010, 7, 46007. [Google Scholar] [CrossRef]
- Scarpa, F.; Zheng, X.; Ohashi, Y.; Ruggeri, A. Automatic evaluation of corneal nerve tortuosity in images from in vivo confocal microscopy. Investig. Ophthalmol. Vis. Sci. 2011, 52, 6404–6408. [Google Scholar] [CrossRef]
- Ngo, C.G.; Chai, R.; Nguyen, T.V.; Jones, T.W.; Nguyen, H.T. Electroencephalogram Spectral Moments for the Detection of Nocturnal Hypoglycemia. IEEE J. Biomed. Health Inform. 2019. [Google Scholar] [CrossRef]
- Yeh, C.; Fang, Y.; Shi, W.; Hong, Y. A novel method of visualizing q-complexity-entropy curve in the multiscale fashion. Nonlinear Dyn. 2019, 97, 2813–2828. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Zunino, L.; Mendes, R.S.; Lenzi, E.K. Complexity–Entropy causality plane: A useful approach for distinguishing songs. Phys. A 2012, 391, 2421–2428. [Google Scholar] [CrossRef]
- Rubega, M.; Carboni, M.; Seeber, M.; Pascucci, D.; Tourbier, S.; Toscano, G.; van Mierlo, P.; Hagmann, P.; Plomp, G.; Vulliemoz, S.; et al. Estimating EEG source dipole orientation based on singular-value decomposition for connectivity analysis. Brain Topogr. 2019, 32, 704–719. [Google Scholar] [CrossRef] [PubMed]
- Vettoretti, M.; Cappon, G.; Acciaroli, G.; Facchinetti, A.; Sparacino, G. Continuous Glucose Monitoring: Current Use in Diabetes Management and Possible Future Applications. J. Diabetes Sci. Technol. 2018, 12, 1064–1071. [Google Scholar] [CrossRef] [PubMed]
- Cappon, G.; Acciaroli, G.; Vettoretti, M.; Sparacino, G.; Facchinetti, A. Wearable continuous glucose monitoring sensors: A revolution in diabetes treatment. Electronics 2017, 6, 65. [Google Scholar] [CrossRef]
- Juhl, C.B.; Hojlund, K.; Elsborg, R.; Poulsen, M.K.; Selmar, P.E.; Holst, J.J.; Christiansen, C.; Beck-Nielsen, H. Automated detection of hypoglycemia-induced EEG changes recorded by subcutaneous electrodes in subjects with type 1 diabetes—The brain as a biosensor. Diabetes Res. Clin. Pract. 2010, 88, 22–28. [Google Scholar] [CrossRef]
| Accuracy | Sensitivity | Specificity | Precision | |||||
|---|---|---|---|---|---|---|---|---|
| Testing Set | Training Set | Testing Set | Training Set | Testing Set | Training Set | Testing Set | Training Set | |
| All | 87.66 ± 0.80 1 | 91.44 ± 0.67 | 86.81 ± 1.41 | 90.74 ± 1.06 | 88.51 ± 1.28 | 92.14 ± 0.86 | 88.33 ± 1.19 | 92.03 ± 0.80 |
| Fractal Dimension indices | 86.73 ± 0.86 | 89.91 ± 0.64 | 85.84 ± 1.52 | 89.10 ± 1.11 | 87.63 ± 1.37 | 90.72 ± 0.92 | 87.43 ± 1.27 | 90.57 ± 0.83 |
| Higuchi | 71.52 ± 1.46 | 72.50 ± 1.14 | 72.92 ± 3.66 | 73.92 ± 3.27 | 70.13 ± 3.24 | 71.08 ± 2.90 | 71.03 ± 2.01 | 71.93 ± 1.50 |
| Residuals | 68.44 ± 1.21 | 69.39 ± 0.83 | 63.71 ± 3.07 | 64.71 ± 2.64 | 73.18 ± 2.39 | 74.06 ± 1.97 | 70.43 ± 1.76 | 71.41 ± 1.05 |
| Tortuosity | 66.67 ± 1.13 | 67.73 ± 0.62 | 63.19 ± 3.15 | 64.24 ± 2.70 | 70.18 ± 2.88 | 71.21 ± 2.49 | 67.99 ± 1.83 | 69.10 ± 1.15 |
| ePE | 56.51 ± 0.98 | 56.79 ± 0.34 | 64.74 ± 3.33 | 64.96 ± 2.94 | 48.31 ± 3.08 | 48.61 ± 2.72 | 55.61 ± 1.33 | 55.84 ± 0.39 |
| Computational Time | Storage | |
|---|---|---|
| SampEn | O(N2) | O(N) |
| ePE | O(N) | O((d + 1)!(d + 1)) |
| eCE | O(N) | O((d + 1)!(d + 1)) |
| Fractal dimension measures | O(kN) | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubega, M.; Scarpa, F.; Teodori, D.; Sejling, A.-S.; Frandsen, C.S.; Sparacino, G. Detection of Hypoglycemia Using Measures of EEG Complexity in Type 1 Diabetes Patients. Entropy 2020, 22, 81. https://doi.org/10.3390/e22010081
Rubega M, Scarpa F, Teodori D, Sejling A-S, Frandsen CS, Sparacino G. Detection of Hypoglycemia Using Measures of EEG Complexity in Type 1 Diabetes Patients. Entropy. 2020; 22(1):81. https://doi.org/10.3390/e22010081
Chicago/Turabian StyleRubega, Maria, Fabio Scarpa, Debora Teodori, Anne-Sophie Sejling, Christian S. Frandsen, and Giovanni Sparacino. 2020. "Detection of Hypoglycemia Using Measures of EEG Complexity in Type 1 Diabetes Patients" Entropy 22, no. 1: 81. https://doi.org/10.3390/e22010081
APA StyleRubega, M., Scarpa, F., Teodori, D., Sejling, A.-S., Frandsen, C. S., & Sparacino, G. (2020). Detection of Hypoglycemia Using Measures of EEG Complexity in Type 1 Diabetes Patients. Entropy, 22(1), 81. https://doi.org/10.3390/e22010081






