Abstract
In this paper, we obtain upper bounds on the minimum distance for turbo codes using fourth degree permutation polynomial (4-PP) interleavers of a specific interleaver length and classical turbo codes of nominal 1/3 coding rate, with two recursive systematic convolutional component codes with generator matrix . The interleaver lengths are of the form or , where is a product of different prime numbers greater than three. Some coefficient restrictions are applied when for a prime , condition is fulfilled. Two upper bounds are obtained for different classes of 4-PP coefficients. For a 4-PP , , the upper bound of 28 is obtained when the coefficient of the equivalent 4-permutation polynomials (PPs) fulfills or when and , , for any values of the other coefficients. The upper bound of 36 is obtained when the coefficient of the equivalent 4-PPs fulfills and , , for any values of the other coefficients. Thus, the task of finding out good 4-PP interleavers of the previous mentioned lengths is highly facilitated by this result because of the small range required for coefficients and . It was also proven, by means of nonlinearity degree, that for the considered inteleaver lengths, cubic PPs and quadratic PPs with optimum minimum distances lead to better error rate performances compared to 4-PPs with optimum minimum distances.
1. Introduction
Error correcting codes with very good performances are an essential component for modern digital communications systems [1,2]. There are three classes of capacity approaching codes—turbo codes [3], low density parity check codes [4], and polar codes [5]. As a class of capacity approaching error correcting codes, turbo codes have gained much interest since their invention. One of the important research directions is increasing their minimum distances by different approaches. For example, recent works that deal with this topic are [6,7,8,9]. In [6], some upper bounds on the minimum distance for 3-dimensional turbo codes (conventional turbo codes with an additional patch) with quadratic permutation polynomial (QPP) interleavers were derived. Some example of QPPs found by random search that lead to significantly improved minimum distances are given. In [7], 4-dimensional (4-D) turbo codes are proposed and upper bounds on bit error rate (BER) performances are derived. These upper bounds imply weight enumerating functions and are derived by a simplified, augmented state-diagram-based method. This method is used to select different parameters of 4-D turbo codes so that they lead to lower BER values or higher minimum distances. In [8], a moment based augmented state diagram method was proposed to derive tighter upper bounds on BER performance for 4-D turbo codes. It was used to design 4-D turbo codes in order to achieve improved BER performances. In [9], a modified interleaver for a new structure of 4-D turbo codes, based on superposition modulation and grouped power allocation, has been proposed to improve the minimum distance. An appropriate design of interleavers for turbo codes considers the approaches that can lead to higher minimum distances. In this respect, knowing the upper bounds on the minimum distances for different classes of interleavers is important from the perspective of the measurements of their performances or limitations.
Permutation polynomial (PP) interleavers for turbo codes were introduced by Sun and Takeshita in 2005 [10]. They are very attractive because of their fully algebraic description, low memory, and high performance if they are appropriately chosen. Other very high-performing interleavers that are not fully algebraic described, are dithered relative prime (DRP) interleavers [11] and almost regular permutation interleavers [12]. Many results have been obtained regarding QPP interleavers. They have been chosen as interleavers for turbo codes in the long term evolution (LTE) standard [13]. The most notable results regarding QPP interleavers are those from [14,15]. In the last years, analysis and design of PP interleavers of degree greater than two have gained interest. For example, good interleavers based on PPs of degree greater than two have been obtained in [16,17,18].
In [15], upper bounds of the minimum distance for turbo codes with QPP interleavers and different interleaver lengths were obtained. Some upper bounds for PP interleavers of any degree were obtained in [19]. Recently, some results regarding upper bounds of the minimum distance for turbo codes with cubic permutation polynomial (CPP) interleavers have been acquired [20,21]. In this paper, for the first time, upper bounds of the minimum distance for turbo codes with fourth degree permutation polynomial (4-PP) interleavers of a specific type of interleaver length and for classical turbo codes of nominal 1/3 coding rate, with two recursive systematic convolutional component codes with generator matrix , were obtained. Specifically, for interleaver lengths of the form or , with , a product of prime numbers greater than three, the minimum distance is upper bounded by the value of 36 or 28, depending on the 4-PP coefficients. Some coefficient restrictions are applied when for a prime , condition is fulfilled. If is a product of prime numbers so that , the result in the paper is fully general.
2. Preliminaries
2.1. Notation
In the paper we use the following notation:
- , with L a positive integer, denotes modulo L operation;
- , with a and b positive integers, denotes a dividing b;
- , with a and b positive integers, denotes that a does not divide; b
- , with a and b positive integers, denotes the greatest common divisor of a and b;
- denotes base 10 logarithm;
- is the natural exponential function of variable x.
2.2. Results Regarding 4-PPs
A 4-PP modulo L is a fourth degree polynomial
so that for , values perform a permutation of the set .
A 4-PP is true if the permutation it performs cannot be performed by a permutation polynomial of degree smaller than four.
Two 4-PPs with different coefficients are different if they lead to different permutations.
Conditions on coefficients , , , and so that the fourth degree polynomial in (1) is a 4-PP modulo L have been obtained in [22]. Because we are interested in interleaver lengths of the form or , with a positive integer, in Table 1 we give the coefficient conditions only for the primes 2, 3, and , , when the interleaver length is of the form

3. Main Results
In this section, we consider the interleaver lengths of the form
with different prime numbers so that , , and .
For a prime so that , , we will consider only the 4-PPs with coefficients fulfilling conditions
In the following, we denote
The reason for which we focus on the interleaver lengths of the form given in (5) is as follows. In [17], 4-PPs of several lengths that lead to the best minimum distance of 36 were reported. We wanted to see if this minimum distance is a general upper bound for a general form of interleaver lengths. From the lengths in [17] for which the best minimum distance of 4-PPs is 36, we restrict ourselves to those of the form given in (5) and also we restrict ourselves to the coefficients fulfilling conditions (6) when because, in this case, the possible coefficients of a true 4-PP are limited to a few values (see Lemma 1). This simplifies finding the coefficients of the inverse 4-PPs, and thus, the proofs for upper bounds on minimum distance for 4-PPs of the focal interleaver lengths. We note that increasing the power of primes in the product leads to more values of the possible coefficients of 4-PPs, and thus, finding the inverse 4-PPs is more complicated.
3.1. Methodology
The research methodology is similar to that from [20,21] and it is described in this subsection. To find upper bounds on the minimum distance for turbo codes that have 4-PP interleavers of lengths of the form given in (5), the research methodology assumes the following steps:
- (1)
- For the interleaver lengths of the form given in (5), we found all possible values for the coefficients of true different 4-PPs. Thus, every 4-PP will have the coefficients equivalent to these found values.
- (2)
- We proved that for the interleaver lengths in question, every true 4-PP has an inversely true 4-PP, extending the result from [23].
- (3)
- For some 4-PPs with particular minimum distances, we found the interleaver patterns that lead to these minimum distances. There are several methods to find minimum distance of turbo codes with particular interleavers. The method from [24] or its improved version from [25] allow the determination of the true minimum distance (), but their complexity increases rapidly when increasing . Methods based on impulses of high amplitude inserted in the all-zero codeword and then decoding this perturbed codeword to give a decoded codeword of low weigth, are faster for high values of and useful for finding interleaver patterns. Double impulse method (DIM) and triple impulse method (TIM) [26] are more reliable among the impulse based methods. An alternative method of TIM is the full range double impulse method from [27] (denoted DIMK in [28]), wherein the reliability of DIM is improved by a full range for the second impulse, instead of a limited range search. The complexity of impulse based methods can be reduced for structured interleavers (such as 4-PP ones) [29]. We have made use of DIMK method for finding the interleaver patterns from Theorems 1 and 2.
- (4)
- Finally, we proved that these critical interleaver patterns always appear for 4-PPs of the interleaver lengths in question and classes of their coefficients.
3.2. Coefficients of 4-PPs for the Interleaver Lengths of the Form or
In [23], we derived a pure mathematical result. For interleaver lengths of the form , in Lemma 3.1 from [23], the possible values of the coefficients of a true 4-PP were obtained. Lemma 3.2 provides an equation to determine the coefficients of an inverse true 4-PP without giving all its possible solutions. The next two lemmas are extensions of Lemmas 3.1 and 3.2 from [23]. Lemma 1 gives the coefficients of a true 4-PP and Lemma 2 gives the coefficients of an inverse true 4-PP of a true 4-PP, fulfilling conditions (6) when , the modulo of an integer of the form given in (5). These two lemmas are necessary to derive the upper bounds on the minimum distance from Section 3.3. We note that because of coefficient conditions 2) from Table 1, the extension of the results from [23] to the interleaver lengths of the form is not straightforward. Because , we can have any of the following combinations of and coefficients’ conditions: (1) , ; (2) , , with any of the following combinations of and coefficients conditions: (1) and ; (2) , ; (3) , . Therefore, we will have more different cases to determine the coefficients of an inverse 4-PP, as Tables 5–8 show show.
Lemma 1.
Proof.
For the interleaver length of the form , a true 4-PP is equivalent to a 4-PP for which , , and . For the interleaver length of the form , a true 4-PP is equivalent to a 4-PP for which , , and . Taking into account the coefficient conditions for a 4-PP given in Table 1 and that is odd, coefficients , , and from Table 2 follows.
We note that when or , (from condition 1 in Table 1) becomes odd. □
Lemma 2.






Let the interleaver length be of the form , with and Ψ given in (7). Then, a true 4-PP , fulfilling conditions (6) when , has an inverse true 4-PP , with
is the unique modulo L solution of the congruence . k, , and are given in Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, according to the values of , , and .

Table 3.
Coefficients of an inverse 4-PP for a 4-PP (Part I) ( and ). For , .

Table 4.
Coefficients of an inverse 4-PP for a 4-PP (Part II) ( and ). For , .

Table 5.
Coefficients of an inverse 4-PP for a 4-PP (Part I). For , .

Table 6.
Coefficients of an inverse 4-PP for a 4-PP (Part II). For , .

Table 7.
Coefficients of an inverse 4-PP for a 4-PP (Part III). For , .

Table 8.
Coefficients of an inverse 4-PP for a 4-PP (Part IV). For , .
Proof.
is an inverse 4-PP of if
Because and are true 4-PPs, from Lemma 1 it results that , , , with , , and , with , . Because is odd , from (7) is also odd. Then, we can have , , , or . Then, or . Because every is odd and , we can have , , , , , , , or . Then, , , , or .
Because , from (13) we have
Equation (14) is equivalent to
We note that when , we have . According to Theorem 57 from [30], in this case congruence (15) has only one solution in variable . When , we can have . Thus, congruence (15) has three solutions, but as we will see, only one solution from the three will be valid.
We note that the values of and are given by the interleaver length.
Because is odd, when we can have .
For we denote and .
In this case, the variables from Equation (16) are , , , k, and . The values of , , and are given by the true 4-PP, for which we want to find the inverse 4-PP; and is given by the interleaver length. Given the values of , , , and , we can find the coefficients of the inverse 4-PP by exhaustive searching for the rest of variables, , , , and k. For each , , , and , we test if the left hand side term from (16), evaluated modulo 16, is equal to 0 for each . For a combination of variables , , , and , only a combination of , , , and k results in a solution of (16). In this way, using Matlab environment we found all the solutions of Equation (16). Solutions in variables k, , , and are the same , and also solutions in the previously mentioned variables are the same . For every , solutions of Equation (16) in variables k, , and are the same , or , or , or . If the solution of Equation (16) in variable for and the other variables with fixed values, is , then solution of the same equation in variable , for , is . Thus, for , we can summarize the solutions of (16) for every and for every . These solutions are given in Table 3 and Table 4.
When , because , we can have . We note that in this case, because of condition , we can have only some values for , not every odd number. Because , we can have . Because , with , we can have:
- (1)
- , when and ;
- (2)
- , when and or when and ;
- (3)
- , when and or when and .
Solutions of Equation (16) for were found in the same way as for , as it was previously explained. Solutions in variables k, , , and are the same , or , or , or . For every , solutions of Equation (16) in variables k, , and are the same and for . If the solution of Equation (16) in variable for and with the other variables with fixed values, is , then solution of the same equation in variable , for , is . Thus, for , we can summarize the solutions of (16) for every and for every . These solutions, found by means of Matlab software, are given in Table 5, Table 6, Table 7 and Table 8. □
We note that the inverse 4-PP from Lemma 2 is a true 4-PP, and thus the 4-PP does not admit an inverse QPP or CPP.
3.3. Upper Bounds on the Minimum Distances for 4-PP-Based Turbo Codes for Interleaver Lengths of the Form or
In this subsection, we prove that for the interleaver lengths of the form given in Equation (5), a true 4-PP leads to a minimum distance which is upper bounded by the value of 36 or 28, depending on the classes of coefficients, for a classical 1/3 rate turbo code with two recursive systematic convolutional (RSC) component codes having generator matrix in octal form.
Theorem 1.
Let the interleaver length be of the form given in (5). Then, the minimum distance of the classical nominal 1/3 rate turbo code with two RSC codes parallel concatenated having the generator matrix (in octal form) and 4-PP interleavers—fulfilling conditions (6) when , with coefficients , , , , , and —is upper bounded by the value of 36.
Proof.
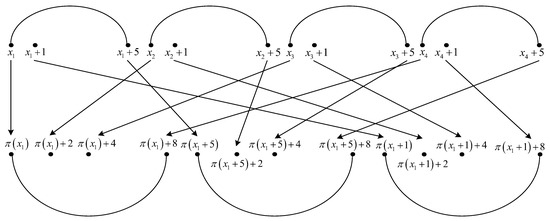
We consider the interleaver pattern of size twelve shown in Figure 1.

Figure 1.
Critical interleaver pattern of size twelve for 4-PP-based interleavers.
The twelve elements of permutation indicated in Figure 1 are written in detail below.
Writing in the fifth and sixth equations from (17), in the eighth and ninth equations from (17), and in the eleventh and twelfth equation from (17), with , we have
For , , , , , , , equations from (21) become
Equations from (22) are fulfilled if and only if
Equations from (28) are fulfilled if and only if and , or and .
With , , and , we have
and
By exhaustive searching by means software programs, it can be verified that equations from (33) are fulfilled if and only if and , or and .
For , equations from (20) become
For , , , , , , , equations from (34) become
Equations from (35) are fulfilled if and only if
For and , equations from (36) are fulfilled if and only if
We have
The third equation from (45) is fulfilled if and only if and , or and . It can be verified that these values also fulfill the first two equations from (45).
For , equations from (36) are fulfilled if and only if
With
we have
Taking into account Equations (47)–(56), it can be verified, by exhaustive searching by means of Matlab that equations from system (46) are fulfilled if and only if and , or and .
From solutions of (28), (33), (45), and (46), it results that the interleaver pattern from Figure 1 always appears for or , when and . For an interleaver pattern as in Figure 1, the weight of the codeword for classical nominal 1/3 rate turbo codes with two RSC codes having generator matrix , is equal to , because each of the four error patterns with a weight of three leads to a parity weight of three, and each of the three error patterns with a weight of four leads to a parity weight of four. Because the interleaver pattern from Figure 1 always appears in the previous conditions, it results that the minimum distance is upper bounded by the value of 36. □
Theorem 2.
Let the interleaver length be of the form given in (5). Then, the minimum distance of the classical nominal 1/3 rate turbo code—with two RSC codes concatenated in parallel, having the generator matrix (in octal form), 4-PP interleavers, and fulfilling conditions (6) when , with coefficients , , , , when and or when and —is upper bounded by the value of 28.
Proof.
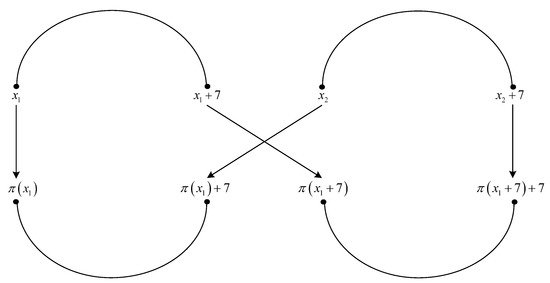
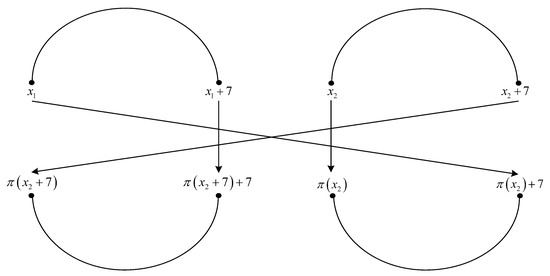



Figure 2.
Critical interleaver pattern of size four for 4-PP-based interleavers.

Figure 3.
Critical interleaver pattern of size four for 4-PP-based interleavers.
The four elements of permutation indicated in Figure 2 are written in detail below.
Writing in the fourth equation from (57), with , we have
For , and , Equation (63) becomes
and Equations (64)–(66) become
where
where
and
where
respectively.
The four elements of permutation indicated in Figure 3 are written in detail below
Writing in the fourth equation from (81), with , we have
For , , and , Equation (84) becomes
and Equations (85)–(87) become
where
where
and
where
respectively.
Solutions of Equations (68), (70), (72), (89), (91), and (93) for variables , , and , which fulfill the results from Lemma 2, are given in Table 9 and Table 10. It can be observed that they can be summarized as in Table 11.

Solutions of equations (75), (77), (79), (96), (98), and (100) in variables , , , which fulfill the results from Lemma 2, are given in Table 12 and Table 13. It can be observed that they can be summarized as in Table 14.

From Table 11 and Table 14, it results that an interleaver pattern as in Figure 2 or Figure 3 always appears for or or , when and or when and . For an interleaver pattern as in Figure 2 or Figure 3, the weight of the codeword for classical nominal 1/3 rate turbo codes with two RSC codes having generator matrix , is equal to , because each of the four error patterns with weight of 2 lead to parity weight of 6. Because an interleaver pattern as in Figure 2 or Figure 3 always appears in the previous conditions, it results that the minimum distance is upper bounded by the value of 28. □
Combining the results from Theorems 1 and 2, it results that the upper bound of 36 is reached only for and , . Thus, the task for finding good 4-PPs is facilitated with this result, because coefficients , , and have only four possible combinations.
We note that from the LTE interleaver lengths [13], there exist 25 lengths of the form (5); namely 48, 80, 112, 176, 208, 240, 272, 304, 336, 368, 464, 496, 528, 560, 592, 624, 656, 688, 752, 816, 848, 880, 912, 944, and 976. From these, for the lengths 40, 208, 304, 496, 592, 624, 688, 912, and 976, restriction conditions (6) on coefficients are not required, and thus, the result in the paper is fully general. Examples of 4-PP interleavers that reach the upper bound of 36 are those from [17] for the interleaver lengths 368, 464, and 496, when dual trellis termination [31] is used.
4. Remarks and Examples
4.1. Remarks
In this subsection, we make some remarks regarding the upper bounds on the minimum distance derived in [19] and those on the minimum distance derived in this paper. From Lemma 3.2 and Table 2 in [19], it results that an upper bound on minimum distance for turbo codes with any degree PP interleavers is equal to 36 in the following conditions:
- (1)
- The PPs can be represented by a parallel linear PP (PLPP) with the minimum number of linear PPs (LPPs) from the PLPP representation equal to two or 14.
- (2)
- The coefficients of the first degree term of LPPs from the PLPP representation are all equal to each other. We denote by the minimum number of LPPs from the PLPP representation fulfilling this condition.
In the following, we prove that 4-PPs fulfilling the conditions from Theorem 1 can be represented by PLPPs with the value of greater than two. For this task, it is enough to prove that these 4-PPs do not allow a PLPP representation with LPPs. A 4-PP allows a PLPP representation with component LPPs if and only if the following condition is fulfilled
With from (1) fulfilling conditions (6) when and with L as in (5), Equation (102) is equivalent to
or
For the coefficients of 4-PPs given in Theorem 1 we have when and when . Thus (107) is equivalent to
when , and to
when .
It is clear that equalities (108) and (109) are not fulfilled for . Therefore, it results that the 4-PPs given in Theorem 1 do not allow a PLPP representation with component LPPs.
Because there is no cubic null polynomial modulo 8 with the coefficient of the third term degree equal to six, it results that the 4-PPs from Theorem 1 can not be represented by a PLPP with three component LPPs.
It can be easily verified that the equality from (114) is fulfilled for .
To show that the 4-PPs established in Theorem 1 can be represented by a PLPP with LPPs, we still have to prove that all the coefficients of the first term degree of the four LPPs are equal to each other. For that, we have to show that
For the 4-PPs established in Theorem 1, we have and , . Then, for and , Equation (117) becomes
and
respectively. It can be easily verified that the equalities from (118) and (119) are fulfilled for . Thus, the 4-PPs established in Theorem 1 always allow a PLPP representation with LPPs. Therefore, from Table 2 in [19] it results that the tightest upper bound derived in [19] is equal to 52. Thus, the upper bound of 36, derived in Theorem 1, is much tighter. The examples of 4-PPs given in the next subsection show that this upper bound can be reached.
4.2. Examples
Table 15 shows some CPPs and 4-PPs with optimum minimum distance for several LTE interleaver lengths of the form given in (5). We note that for all these 4-PPs we have , and thus, the best upper bound derived in [19] is equal to 52. Minimum distances () and corresponding multiplicities (), spread factors (D), nonlinearity degrees (), and refined nonlinearity degrees () for each CPP and each 4-PP are also given in Table 15. As it can be observed, CPPs have optimum distances greater than those of 4-PPs (38 compared to 36) and the corresponding multiplicities for CPPs are equal to about a half of those for 4-PPs. These relation between the multiplicities for CPPs and 4-PPs with optimum distances is explained by means of nonlinearity degrees. In [21], it was proven that CPPs with optimum distance have the nonlinearity degree equal to . In Appendix A, it is proven that the nonlinearity degree of 4-PPs for interleaver lengths of the form (5), fulfilling conditions (6) when , is equal to
where the coefficient of the third term of 4-PP is . Because 4-PPs with optimum distance have , it results that their nonlinearity degree is equal to . Thus, the result for the multiplicities is explained.

Table 15.
Minimum distances () and corresponding multiplicities (), spread factors (D), nonlinearity degrees (), and refined nonlinearity degrees () for cubic permutation polynomials (CPPs) and for fourth degree permutation polynomials (4-PPs) with optimum minimum distance.
We also note that the good QPPs reported in Table XIII from [21] have the minimum distance equal to 38 and the corresponding multiplicities are approximately equal to those for 4-PPs from Table 15 in this paper. The results for multiplicities are explained by the fact that QPPs given in [21] have the nonlinearity degree .
Taking into account the above, it is expected that CPPs and QPPs for these interleaver lengths to lead to better error rate performances compared to 4-PPs.
An estimation of asymptotic improvement in terms of the error rate for CPP and QPP interleavers compared to 4-PP interleavers can be given if we compare the upper bounds on error rates for distance spectra of the turbo codes truncated at the first term. For an additive white Gaussian noise (AWGN) channel with the signal to noise ratio , the frame error rate () for a block code with coding rate , minimum distance , and the corresponding multiplicity , is upper bounded by
where
and
From Table 15 it results that the multiplicity of the codewords of weight is approximately equal to L for CPP interlevears and to for 4-PP interleavers. From the QPPs reported in Table XIII from [21], it results that for QPPs, the best minimum distance is equal to 38 and the corresponding multiplicity is approximately equal to . Thus, if we use the upper bounds with from (123), the for QPP, CPP, and 4-PP interleavers, is approximately upper bounded by
and
respectively.
From (124)–(126), it results that when considering the interleaver lengths of the form given in (5) and turbo codes of nominal 1/3 coding rate with RSC component codes with generator matrix , the asymptotic coding gain for QPPs compared to 4-PPs, is equal to
and the asymptotic coding gain for CPPs compared to 4-PPs, for a given value, is equal to
For example, for a target and for interleaver length , the coding gain from (128) becomes dB. Increasing the interleaver length, resulting from (128) decreases easily. For an increase of interleaver length with a factor of approximately 25 compared to 656, the coding gain from (128) decreases with about 0.023 dB.
In Figure 4, the , , and curves for 4-PP, CPP, and QPP of interleaver length L = 656 are shown. The 4-PP and the CPP are those from Table 15, and the QPP is given in [21]. For curves, the Max-Log-MAP algorithm with a scaling coefficient of the extrinsec information of 0.75 was used. We note that the considered multiplicities for and curves are the estimated ones; i.e., , L, and , for 4-PP, CPP, and QPP, respectively. For , from Figure 4, it results that
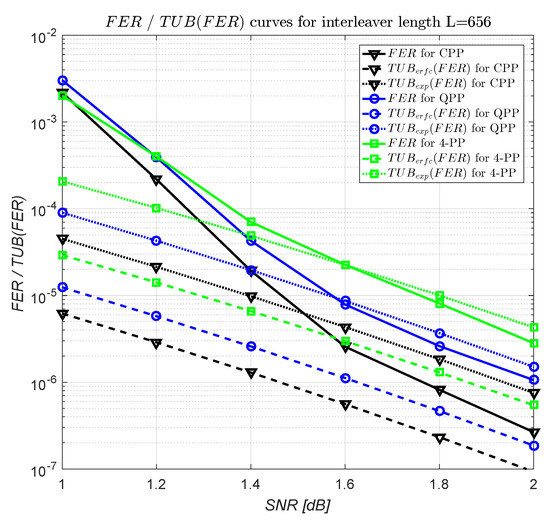
Figure 4.
Frame error rate () and truncated upper bound of () curves for interleaver length L = 656.
- (1)
- The coding gains resulting from FER curves are dB and dB and
- (2)
- The coding gains resulting from curves are dB and dB.
We observe that these coding gains are very close to those previously estimated by the upper bounds.
5. Conclusions
In this paper, we obtained the upper bounds of the minimum distance for turbo codes when using 4-PP interleavers. The component RSC codes were those from the LTE standard and 1/3 nominal coding rate. The interleaver lengths in question were of the form (5), and condition (6) was applied for 4-PP coefficients when for a prime , . The two obtained upper bounds have the values of 28 and 36 for different classes of 4-PP coefficients. The result obtained in this paper has theoretical importance. The highest upper bound for 4-PPs (i.e., 36) is smaller than that for CPPs or QPPs (i.e., 38), while the corresponding multiplicities are about twice as high as those for CPPs and approximately equal to those for QPPs. Thus, it is expected that CPPs and QPPs for the interleaver lengths in question are better compared to 4-PPs.
Author Contributions
Conceptualization, D.T.; data curation, L.T.; investigation, J.R.; methodology, L.T. and D.T.; project administration, L.T.; software, A.-M.R.; validation, J.R.; writing—original draft, L.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a National Research Grant—ARUT of the TUIASI, project number GnaC2018_39.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In [32], an efficient algorithm for the computing nonlinearity degree of a 4-PP was given. We remember that for interleaver lengths of the form (5), the coefficients of 4-PPs fulfilling conditions (6) when , are equivalent to the following ones: , , with , , with and . Then, we have
For
we have
Then condition is equivalent to
or
or
and condition is equivalent to
or
or
Because , we have , . Then, with Equations (A1)–(A11), Algorithm 2 from [32] becomes Algorithm A1 in this paper. Run Algorithm A1 for every , , and , (120) result.
| Algorithm 1: Algorithm for computing the nonlinearity degree for a 4-PP for interleaver lengths of the form (5) and the coefficients of 4-PP fulfilling conditions (6) when . |
| input: Values for the interleaver length, and , for the 4-PP. output: Nonlinearity degree for the 4-PP. 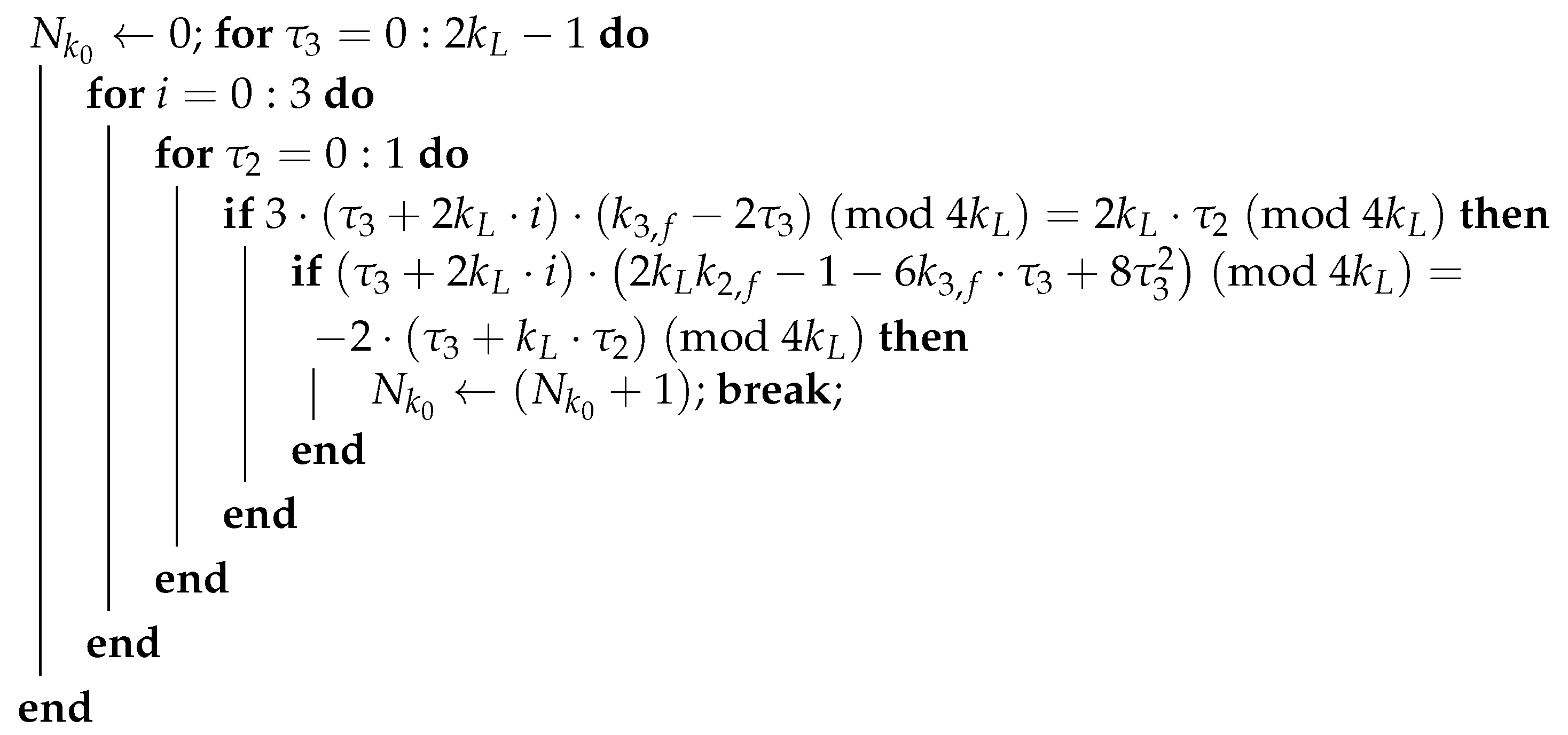 ; |
References
- Shao, S.; Hailes, P.; Wang, Y.-Y.; Wu, J.-Y.; Maunder, R.G.; Al-Hashimi, B.M.; Hanzo, L. Survey of turbo, LDPC, and polar decoder ASIC implementations. IEEE Commun. Surv. Tutor. 2019, 21, 2309–2333. [Google Scholar] [CrossRef]
- Arora, K.; Singh, J.; Randhawa, Y.S. A survey on channel coding techniques for 5G wireless networks. Telecommun. Syst. 2019. [Google Scholar] [CrossRef]
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. In Proceedings of the IEEE International Conference on Communications (ICC 1993), Geneva, Switzerland, 23–26 May 1993; pp. 1064–1070. [Google Scholar]
- MacKay, D.J.C.; Neal, R.M. Near Shannon limit performance of low density parity check codes. Electron. Lett. 1996, 32, 457–458. [Google Scholar] [CrossRef]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inform. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Rosnes, E.; i Amat, A.G. Performance analysis of 3-D turbo codes. IEEE Trans. Inform. Theory 2011, 57, 3707–3720. [Google Scholar] [CrossRef]
- Banerjee, S.; Chattopadhyay, S. Evaluation of system performance by adding a fourth dimension to turbo code. Int. J. Commun. Syst. 2018, 31, e3450. [Google Scholar] [CrossRef]
- Banerjee, S.; Chattopadhyay, S. Performance analysis of four dimensional turbo code (4D-TC) using moment based simplified augmented state diagram (MSASD) approach: Extension to LTE system. Wirel. Person. Commun. 2019, 108, 2077–2102. [Google Scholar] [CrossRef]
- Banerjee, S.; Chattopadhyay, S. Superposition modulation-based new structure of four-dimensional turbo code (4D-TC) using modified interleaver and its application in WiMAX & LTE systems. Person. Ubiquitous Comput. 2019, 23, 943–959. [Google Scholar]
- Sun, J.; Takeshita, O.Y. Interleavers for turbo codes using permutation polynomials over integer rings. IEEE Trans. Inform. Theory 2005, 51, 101–119. [Google Scholar]
- Crozier, S.; Guinand, P. High-performance low-memory interleaver banks for turbo-codes. In Proceedings of the IEEE 54th Vehicular Technology Conference, VTC Fall 2001, Atlantic City, NJ, USA, 7–11 October 2001; pp. 2394–2398. [Google Scholar]
- Berrou, C.; Saoter, Y.; Douillard, C.; Kerouedan, S.; Jezequel, M. Designing good permutations for turbo codes: Towards a single model. In Proceedings of the 2004 IEEE International Conference on Communications, Paris, France, 20–24 June 2004; pp. 341–345. [Google Scholar]
- 3GPP TS 36.212 V8.3.0, 3rd Generation Partnership Project, Multiplexing and channel coding (Release 8). 2008. Available online: http://www.etsi.org (accessed on 23 July 2009).
- Takeshita, O.Y. Permutation polynomial interleavers: An algebraic-geometric perspective. IEEE Trans. Inform. Theory 2007, 53, 2116–2132. [Google Scholar] [CrossRef]
- Rosnes, E. On the minimum distance of turbo codes with quadratic permutation polynomial interleavers. IEEE Trans. Inform. Theory 2012, 58, 4781–4795. [Google Scholar] [CrossRef]
- Ryu, J. Permutation polynomials of higher degrees for turbo code interleavers. IEICE Trans. Commun. 2012, E95-B, 3760–3762. [Google Scholar] [CrossRef]
- Trifina, L.; Ryu, J.; Tarniceriu, D. Up to five degree permutation polynomial interleavers for short length LTE turbo codes with optimum minimum distance. In Proceedings of the 13th IEEE International Symposium on Signals, Circuits and Systems (ISSCS), Iasi, Romania, 13–14 July 2017. [Google Scholar]
- Trifina, L.; Tarniceriu, D. On the equivalence of cubic permutation polynomial and ARP interleavers for turbo codes. IEEE Trans. Commun. 2017, 65, 473–485. [Google Scholar] [CrossRef]
- Ryu, J.; Trifina, L.; Balta, H. The limitation of permutation polynomial interleavers for turbo codes and a scheme for dithering permutation polynomials. AEU Int. J. Electron. Commun. 2015, 69, 1550–1556. [Google Scholar] [CrossRef]
- Trifina, L.; Tarniceriu, D.; Ryu, J.; Rotopanescu, A.-M. Some Lengths for Which CPP Interleavers Have Weaker Minimum Distances Than QPP Interleavers. Available online: http://telecom.etti.tuiasi.ro/tti/papers/PDFs/Some%20lengths%20for%20which%20CPPs%20have%20weaker%20minimum%20distances%20than%20QPPs.pdf (accessed on 7 December 2019).
- Trifina, L.; Tarniceriu, D.; Ryu, J.; Rotopanescu, A.-M. Upper Bounds on the Minimum Distance for Turbo Codes Using CPP Interleavers. Available online: http://telecom.etti.tuiasi.ro/tti/papers/PDFs/UB%20of%20dmin%20for%20CPPs%20of%20L_16p_48p.pdf (accessed on 7 December 2019).
- Trifina, L.; Tarniceriu, D. A coefficient test for fourth degree permutation polynomials over integer rings. AEU Int. J. Electron. Commun. 2016, 70, 1565–1568. [Google Scholar] [CrossRef]
- Trifina, L.; Tarniceriu, D.; Rotopanescu, A.-M.; Ursu, E. The inverse of a fourth degree permutation polynomial. In Proceedings of the Fifth Conference of Mathematical Society of Moldova, Chisinau, Moldova, 28 September–1 October 2019; pp. 255–260. [Google Scholar]
- Garello, R.; Pierleoni, P.; Benedetto, S. Computing the free distance of turbo codes and serially concatenated codes with interleavers: Algorithms and applications. IEEE J. Sel. Areas Commun. 2001, 19, 800–812. [Google Scholar] [CrossRef]
- Rosnes, E.; Ytrehus, Y. Improved algorithms for the determination of turbo-code weight distributions. IEEE Trans. Commun. 2005, 53, 20–26. [Google Scholar] [CrossRef]
- Crozier, S.; Guinand, P.; Hunt, A. Computing the minimum distance of turbo-codes using iterative decoding techniques. In Proceedings of the 22th Biennial Symposium on Communications, Kingston, ON, Canada, 31 May–3 June 2004; pp. 306–308. [Google Scholar]
- Ould-Cheikh-Mouhamedou, Y.; Crozier, S.; Guinand, P.; Kabal, P. Comparison of distance measurement methods for turbo codes. In Proceedings of the 9th Canadian Workshop on Information Theory (CWIT-05), Montreal, QC, Canada, 5–8 June 2005; pp. 36–39. [Google Scholar]
- Crozier, S.; Guinand, P.; Hunt, A. Estimating the minimum distance of large-block turbo codes using iterative multiple-impulse methods. In Proceedings of the 4th International Symposium on Turbo Codes and Related Topics, Munich, Germany, 3–7 April 2006. [Google Scholar]
- Ould-Cheikh-Mouhamedou, Y. Reducing the complexity of distance measurement methods for circular turbo codes that use structured interleavers. Int. J. Commun. Syst. 2015, 28, 1572–1579. [Google Scholar] [CrossRef]
- Hardy, G.H.; Wright, E.M. An Introduction to the Theory of Numbers; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Guinand, P.; Lodge, J. Trellis termination for turbo encoders. In Proceedings of the 17th Biennial Symposium on Communications, Kingston, ON, Canada, 29 May–1 June 1994; pp. 389–392. [Google Scholar]
- Trifina, L.; Tarniceriu, D.; Rotopanescu, A.-M. Nonlinearity degree for CPP, 4-PP, and 5-PP interleavers for turbo codes. In Proceedings of the 11th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 27–29 June 2019. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).