Spatiotemporal Evolution of a Landslide: A Transition to Explosive Percolation
Abstract
1. Introduction
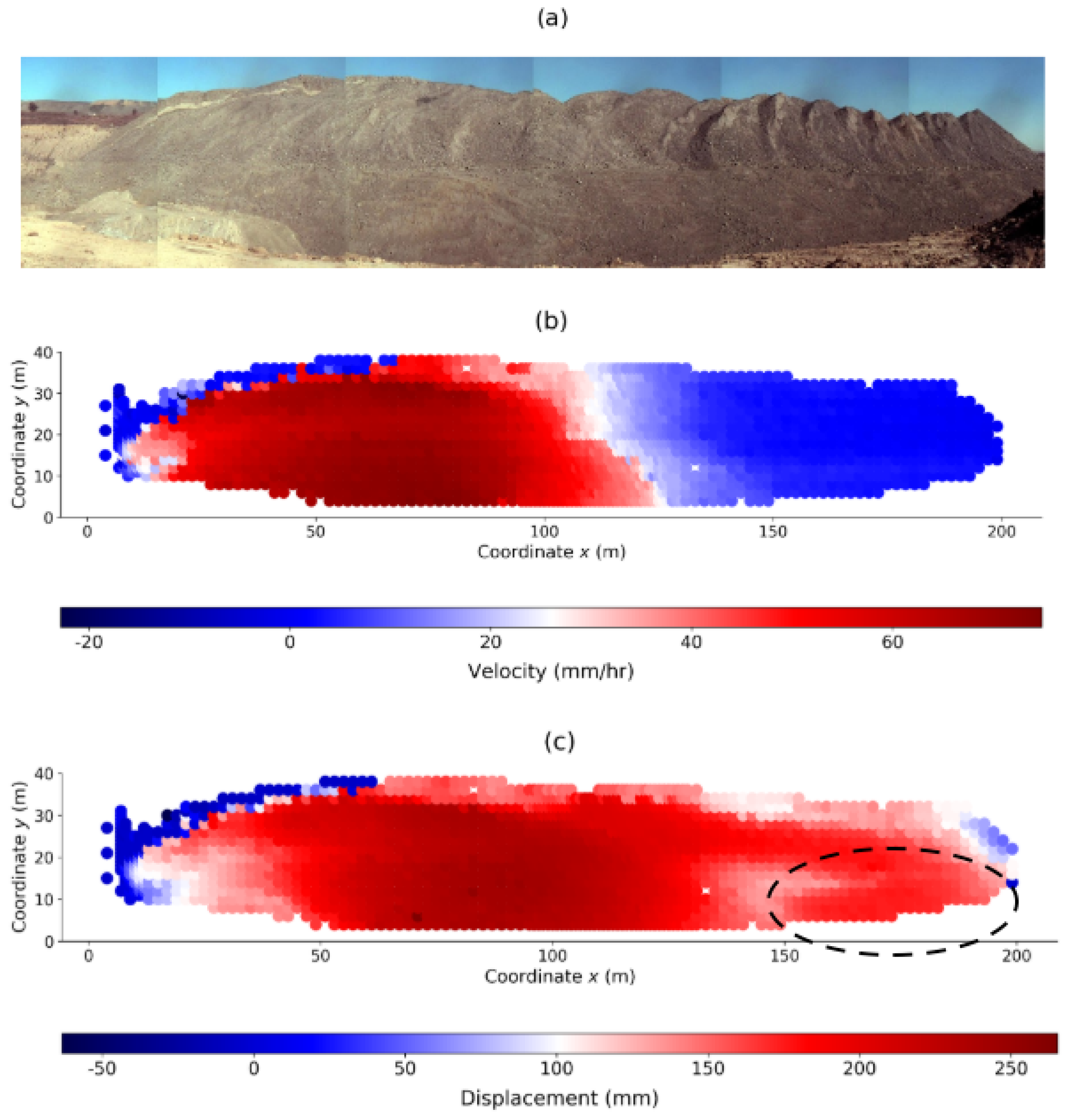
2. Data
3. Methodology
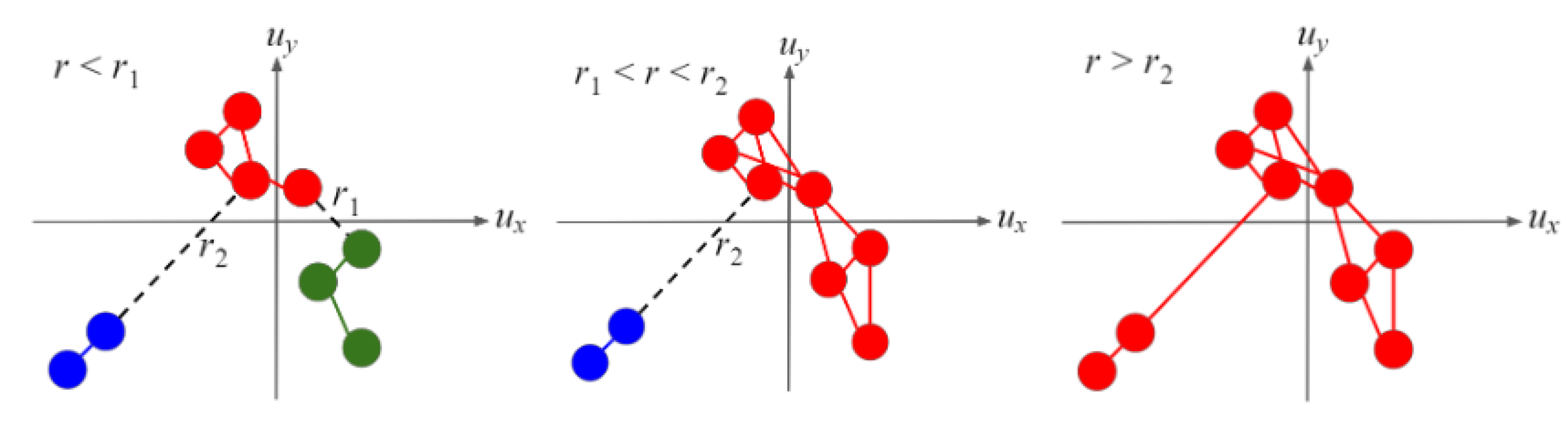
3.1. Algorithm Input and Network Construction
3.2. Algorithm Outputs
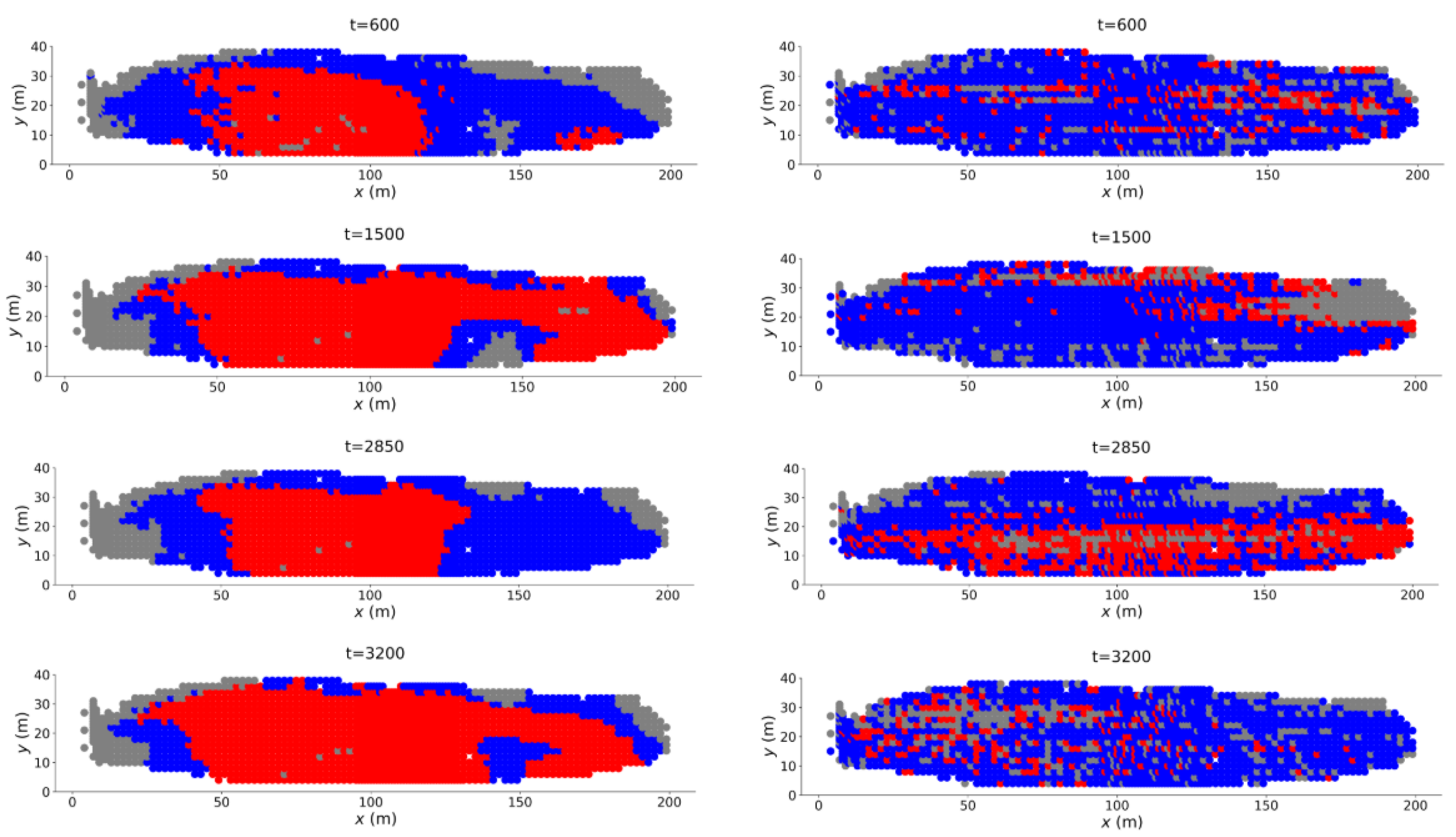
4. Results
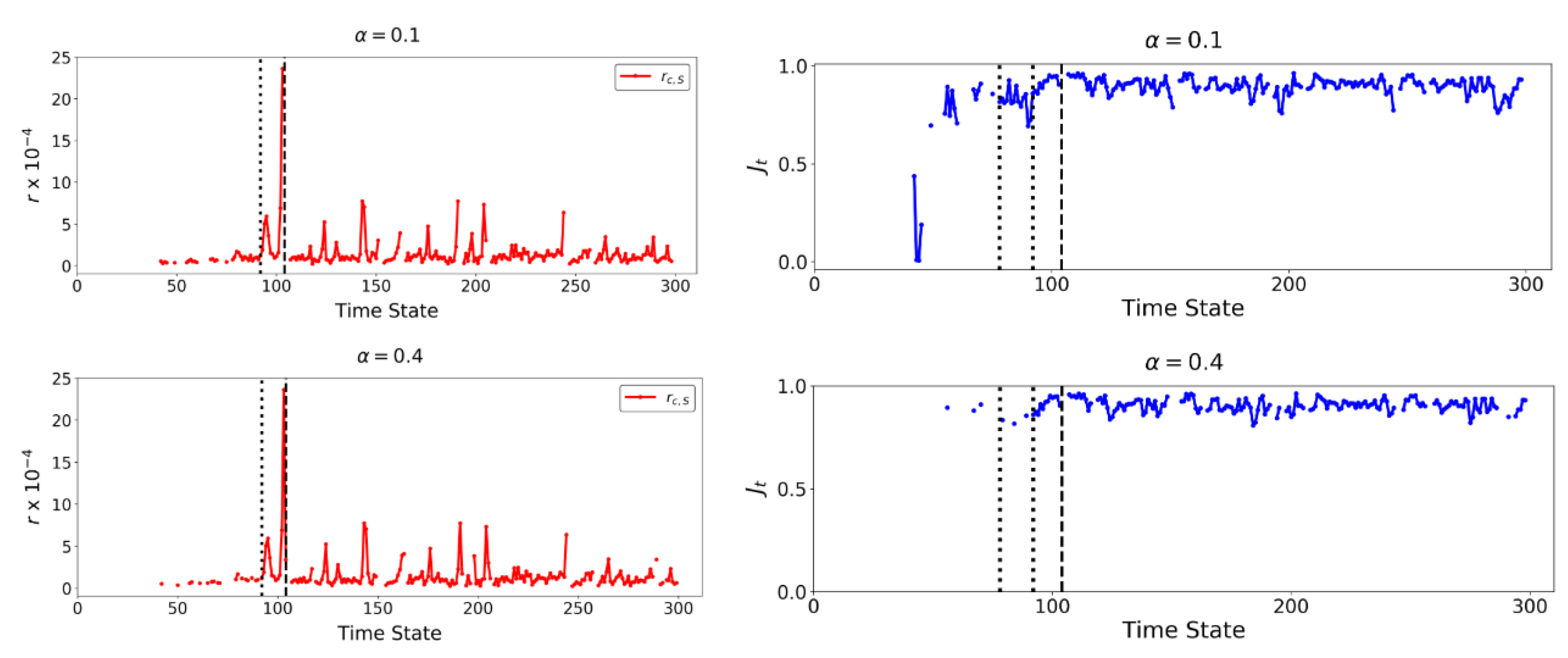
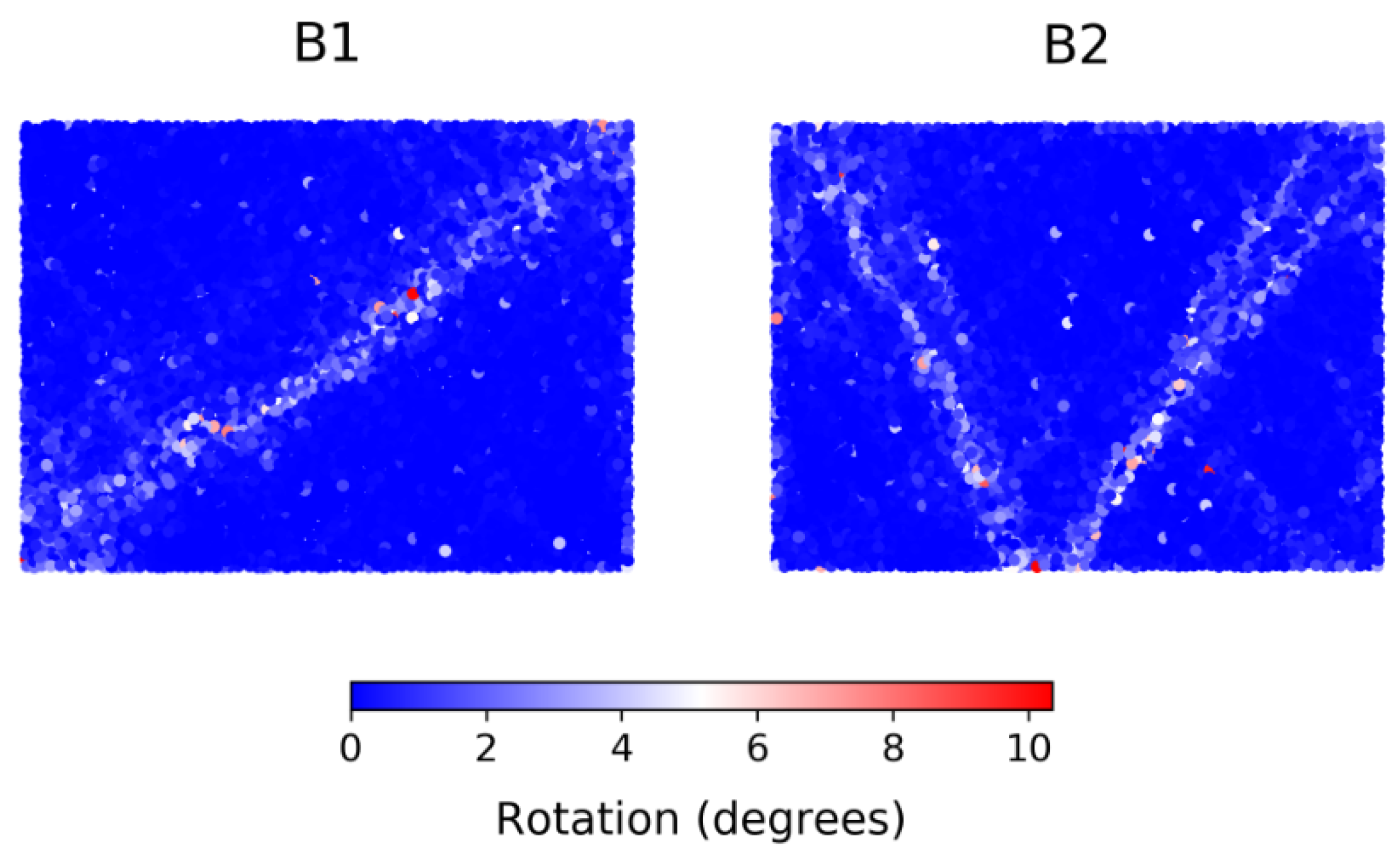
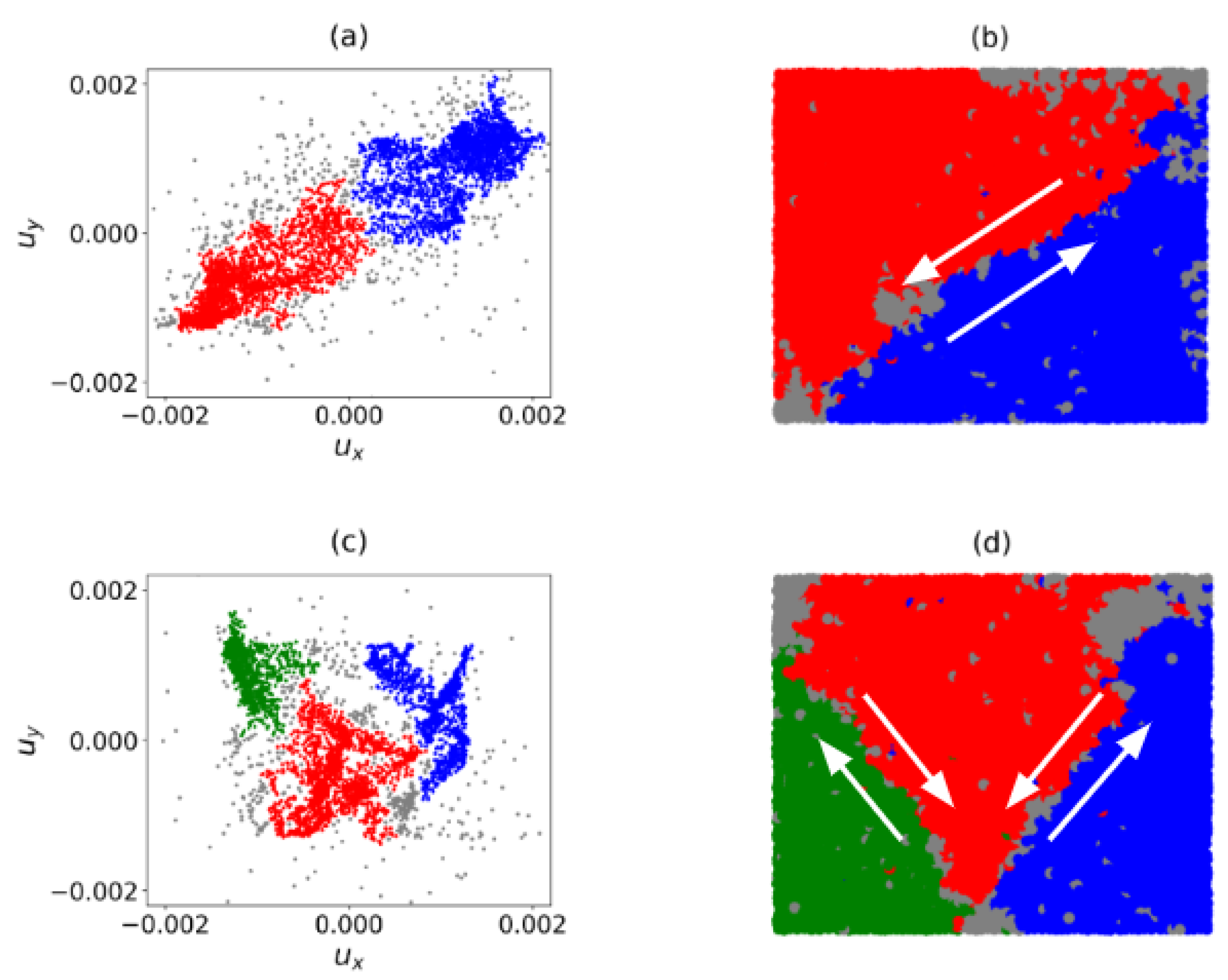
4.1. Prediction of Location of Failure for B1 and B2
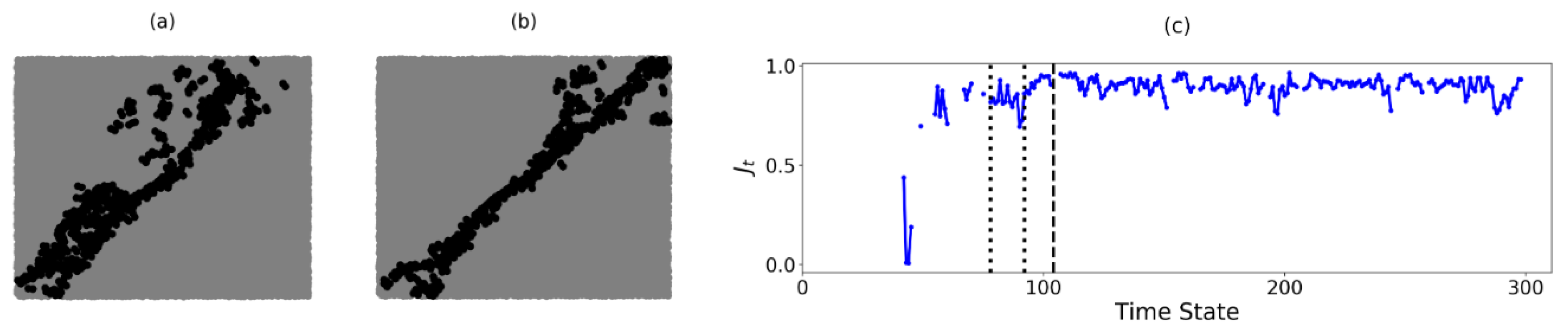
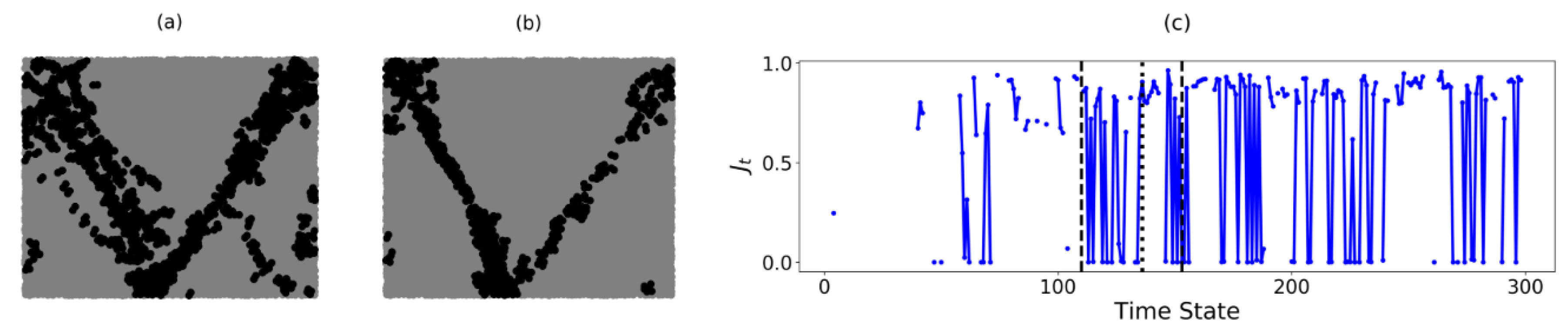
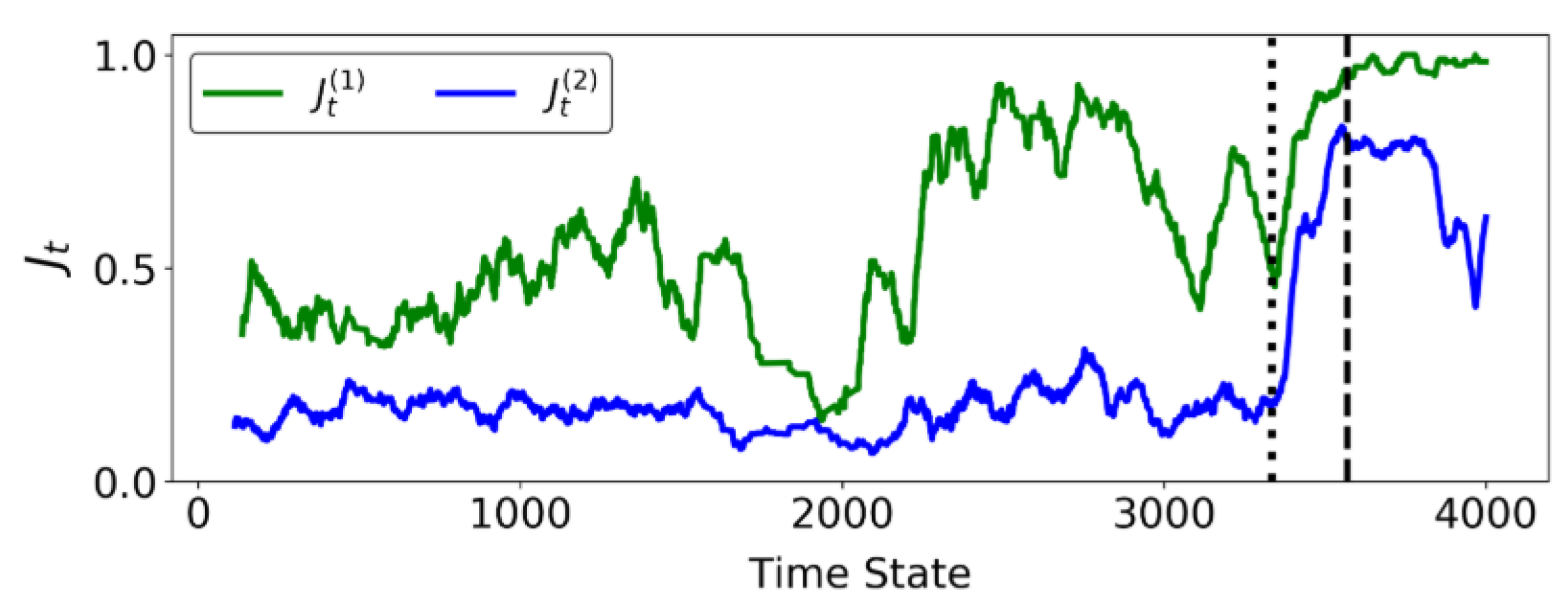
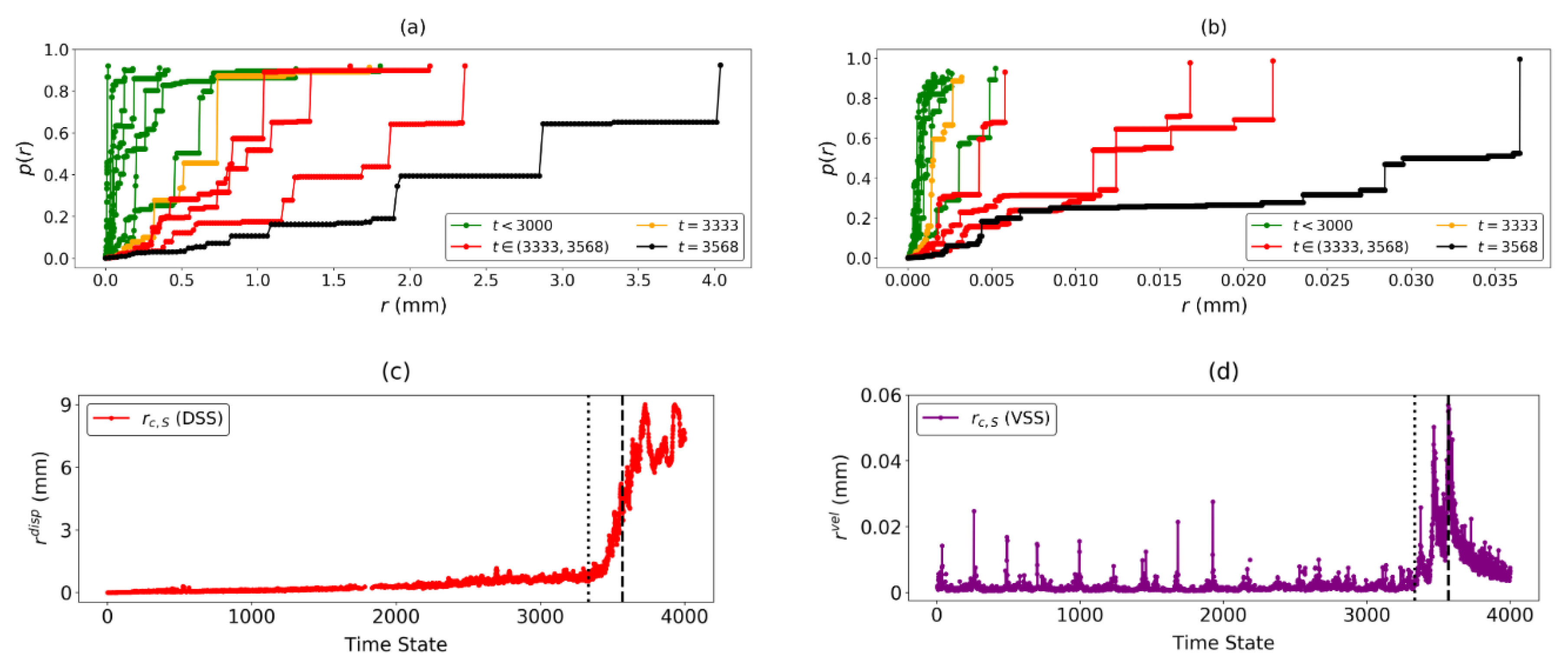
4.2. Identification of Regime Change Point for B1 and B2
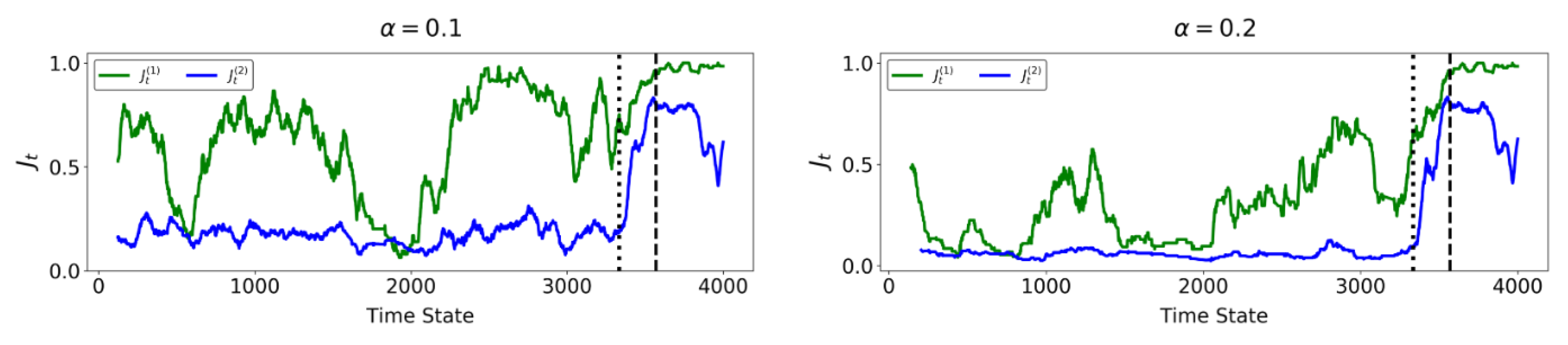
4.3. Prediction of Location of Failure for the Mine
4.4. Identification of Regime Change Point for the Mine
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Glossary of Terms
| Term | Definition |
|---|---|
| Physical state space (PSS) | The space defined by the geographical coordinates () of the pixels (grains). |
| Network state space (NSS) | The space in which the network is constructed. |
| Largest component | The component in the network that consists of the most number of nodes. |
| System-spanning component | A component that spans the network (greater than of N). |
| Feature state space | The space defined by some feature of the pixels/grains in the system. It is n-dimensional depending on the feature chosen. |
| Displacement state space (DSS) | The space defined by the displacement of pixels (grains) in the system. |
| Velocity state space (VSS) | The space defined by the velocity of pixels (grains) in the system. |
| The minimum distance between a node in one component, and a node in another component, , in a feature state space. | |
| The minimum inter-component distance of the component, , which measures the separation of the component in the feature state space. | |
| The critical radius or maximum separation across all components in the network. | |
| The maximally separated component, i.e., . | |
| Regime change point or time of imminent failure. | |
| Time of failure or onset of failure regime. | |
| or | Similarity of failure pattern across consecutive time states using the same feature state space. The term is used if a secondary similarity measure () is considered. |
| Similarity of failure pattern across two feature state spaces, e.g., DSS and VSS, at the same time state. | |
| Shared boundary | A collection of pairs of points, one from each of two distinct groups, that are in contact with each other in the physical state space. |
| A tuning parameter used to determine the minimum size for a component to be considered. | |
| Discontinuous jump | A jump in the order parameter, characterised by the merger of a component to the current largest component in the network. We limit our attention to components that are of size greater than of N. |
Appendix B. Component Sizes

References
- Walker, D.; Tordesillas, A.; Pucilowski, S.; Lin, Q.; Rechenmacher, A.; Abedi, S. Analysis of grain-scale measurements of sand using kinematical complex networks. Int. J. Bifurc. Chaos 2013, 22, 1230042. [Google Scholar] [CrossRef]
- Tordesillas, A.; Walker, D.M.; Rechenmacher, A.L.; Abedi, S. Discovering community structures and dynamical networks from grain-scale kinematics of shear bands in sand. In Advances in Bifurcation and Degradation in Geomaterials; Springer: Dordrecht, The Netherlands, 2011; pp. 67–73. [Google Scholar]
- Ma, G.; Regueiro, R.A.; Zhou, W.; Liu, J. Spatiotemporal analysis of strain localization in dense granular materials. Acta Geotech. 2019, 14, 973–990. [Google Scholar] [CrossRef]
- Nitka, M.; Tejchman, J.; Kozicki, J.; Leśniewska, D. DEM analysis of micro-structural events within granular shear zones under passive earth pressure conditions. Granul. Matter 2015, 17, 325–343. [Google Scholar] [CrossRef]
- Tordesillas, A.; Walker, D.M.; Andò, E.; Viggiani, G. Revisiting localized deformation in sand with complex systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20120606. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Scaringi, G.; Dai, L.; Li, W.; Dong, X.; Zhu, X.; Pei, X.; Dai, K.; Havenith, H.B. Failure mechanism and kinematics of the deadly June 24th 2017 Xinmo landslide, Maoxian, Sichuan, China. Landslides 2017, 14, 2129–2146. [Google Scholar] [CrossRef]
- Delacourt, C.; Allemand, P.; Berthier, E.; Raucoules, D.; Casson, B.; Grandjean, P.; Pambrun, C.; Varel, E. Remote-sensing techniques for analysing landslide kinematics: A review. Bulletin de la Société Géologique de France 2007, 178, 89–100. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, J.; Ding, X.; Mingzhou, W. Elevation extraction and deformation monitoring by multitemporal InSAR of Lupu Bridge in Shanghai. Remote Sens. 2017, 9, 897. [Google Scholar] [CrossRef]
- Tordesillas, A.; Zhou, Z.; Batterham, R. A data-driven complex systems approach to early prediction of landslides. Mech. Res. Commun. 2018, 92, 137–141. [Google Scholar] [CrossRef]
- Mistretta, F.; Sanna, G.; Stochino, F.; Vacca, G. Structure from motion point clouds for structural monitoring. Remote Sens. 2019, 11, 1940. [Google Scholar] [CrossRef]
- Hu, W.; Hicher, P.Y.; Scaringi, G.; Xu, Q.; Van Asch, T.W.J.; Wang, G. Seismic precursor to instability induced by internal erosion in loose granular slopes. Géotechnique 2018, 68, 989–1001. [Google Scholar] [CrossRef]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth-Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Dick, G.J.; Eberhardt, E.; Cabrejo-Liévano, A.G.; Stead, D.; Rose, N.D. Development of an early-warning time-of-failure analysis methodology for open-pit mine slopes utilizing ground-based slope stability radar monitoring data. Can. Geotech. J. 2015, 52, 515–529. [Google Scholar] [CrossRef]
- Harries, N.; Noon, D.; Rowley, K. Case Studies of Slope Stability Radar Used in Open Cut Mines; The South African Institute of Mining and Metallurgy: Johannesburg, South Africa, 2006. [Google Scholar]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Stähli, M.; Sättele, M.; Huggel, C.; McArdell, B.W.; Lehmann, P.; Van Herwijnen, A.; Berne, A.; Schleiss, M.; Ferrari, A.; Kos, A.; et al. Monitoring and prediction in early warning systems for rapid mass movements. Nat. Hazards Earth Syst. Sci. 2015, 15, 905–917. [Google Scholar] [CrossRef]
- Casagli, N.; Catani, F.; Del Ventisette, C.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Intrieri, E.; Bardi, F.; Fanti, R.; Gigli, G.; Fidolini, F.; Casagli, N.; Costanzo, S.; Raffo, A.; Di Massa, G.; Capparelli, G.; et al. Big data managing in a landslide early warning system: Experience from a ground-based interferometric radar application. Nat. Hazards Earth Syst. Sci. 2017, 17, 1713–1723. [Google Scholar] [CrossRef]
- Zhou, Z.; Tordesillas, A. Powder keg divisions in the critical state regime: Transition from continuous to explosive percolation. EPJ Web Conf. 2017, 140, 10006. [Google Scholar] [CrossRef]
- Achlioptas, D.; D’Souza, R.M.; Spencer, J. Explosive percolation in random networks. Science 2009, 323, 1453–1455. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–61. [Google Scholar]
- D’Souza, R.M.; Gómez-Gardeñes, J.; Nagler, J.; Arenas, A. Explosive phenomena in complex networks. Adv. Phys. 2019, 68, 123–223. [Google Scholar] [CrossRef]
- Pan, R.K.; Kivelä, M.; Saramäki, J.; Kaski, K.; Kertész, J. Using explosive percolation in analysis of real-world networks. Phys. Rev. E 2011, 83, 046112. [Google Scholar] [CrossRef] [PubMed]
- Rozenfeld, H.D.; Gallos, L.K.; Makse, H.A. Explosive percolation in the human protein homology network. Eur. Phys. J. B 2010, 75, 305–310. [Google Scholar] [CrossRef]
- Friedman, E.J.; Landsberg, A.S. Construction and analysis of random networks with explosive percolation. Phys. Rev. Lett. 2009, 103, 255701. [Google Scholar] [CrossRef] [PubMed]
- Tordesillas, A. Force chain buckling, unjamming transitions and shear banding in dense granular assemblies. Philos. Mag. 2007, 87, 4987–5016. [Google Scholar] [CrossRef]
- Tordesillas, A.; O’Sullivan, P.; Walker, D.M.; Paramitha. Evolution of functional connectivity in contact and force chain networks: Feature vectors, k-cores and minimal cycles. Comptes Rendus Mécanique 2010, 338, 556–569. [Google Scholar] [CrossRef]
- Tordesillas, A.; Pucilowski, S.; Walker, D.M.; Peters, J.F.; Walizer, L.E. Micromechanics of vortices in granular media: Connection to shear bands and implications for continuum modelling of failure in geomaterials. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1247–1275. [Google Scholar] [CrossRef]
- Walker, D.M.; Tordesillas, A.; Froyland, G. Mesoscale and macroscale kinetic energy fluxes from granular fabric evolution. Phys. Rev. E 2014, 89, 032205. [Google Scholar] [CrossRef]
- Tordesillas, A.; Pucilowski, S.; Lin, Q.; Peters, J.F.; Behringer, R.P. Granular vortices: Identification, characterization and conditions for the localization of deformation. J. Mech. Phys. Solids 2016, 90, 215–241. [Google Scholar] [CrossRef]
- Das, S.; Tordesillas, A. Near real-time characterization of spatio-temporal precursory evolution of a rockslide from radar data: Integrating statistical and machine learning with dynamics of granular failure. Remote Sens. 2019, 11, 2777. [Google Scholar] [CrossRef]
- Tordesillas, A.; Muthuswamy, M.; Walsh, S.D. Mesoscale measures of nonaffine deformation in dense granular assemblies. J. Eng. Mech. 2008, 134, 1095–1113. [Google Scholar] [CrossRef]
- D’Souza, R.M.; Nagler, J. Anomalous critical and supercritical phenomena in explosive percolation. Nat. Phys. 2015, 11, 531–538. [Google Scholar] [CrossRef]
- Bohman, T.; Frieze, A.; Wormald, N.C. Avoidance of a giant component in half the edge set of a random graph. Random Struct. Algorithms 2004, 25, 432–449. [Google Scholar] [CrossRef]
- Chen, W.; Cheng, X.; Zheng, Z.; Chung, N.N.; D’Souza, R.M.; Nagler, J. Unstable supercritical discontinuous percolation transitions. Phys. Rev. E 2013, 88, 042152. [Google Scholar] [CrossRef] [PubMed]
- Ben-Hur, A.; Elisseeff, A.; Guyon, I. A stability based method for discovering structure in clustered data. Pac. Symp. Biocomput. 2002, 2002, 6–17. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, K.; Tordesillas, A. Spatiotemporal Evolution of a Landslide: A Transition to Explosive Percolation. Entropy 2020, 22, 67. https://doi.org/10.3390/e22010067
Singh K, Tordesillas A. Spatiotemporal Evolution of a Landslide: A Transition to Explosive Percolation. Entropy. 2020; 22(1):67. https://doi.org/10.3390/e22010067
Chicago/Turabian StyleSingh, Kushwant, and Antoinette Tordesillas. 2020. "Spatiotemporal Evolution of a Landslide: A Transition to Explosive Percolation" Entropy 22, no. 1: 67. https://doi.org/10.3390/e22010067
APA StyleSingh, K., & Tordesillas, A. (2020). Spatiotemporal Evolution of a Landslide: A Transition to Explosive Percolation. Entropy, 22(1), 67. https://doi.org/10.3390/e22010067





