Stochastic SIS Modelling: Coinfection of Two Pathogens in Two-Host Communities
Abstract
1. Introduction
2. Materials and Methods
2.1. Continuous Time Markov Chain Model
- The rate at which the two infectious classes, and , can be recovered are and respectively,and .
- The two susceptible classes, and , can move to infectious classes, and , at the disease transmission rates , and , such that,,,.
2.2. Basic Reproduction Number
2.3. Multi-Type Branching Process
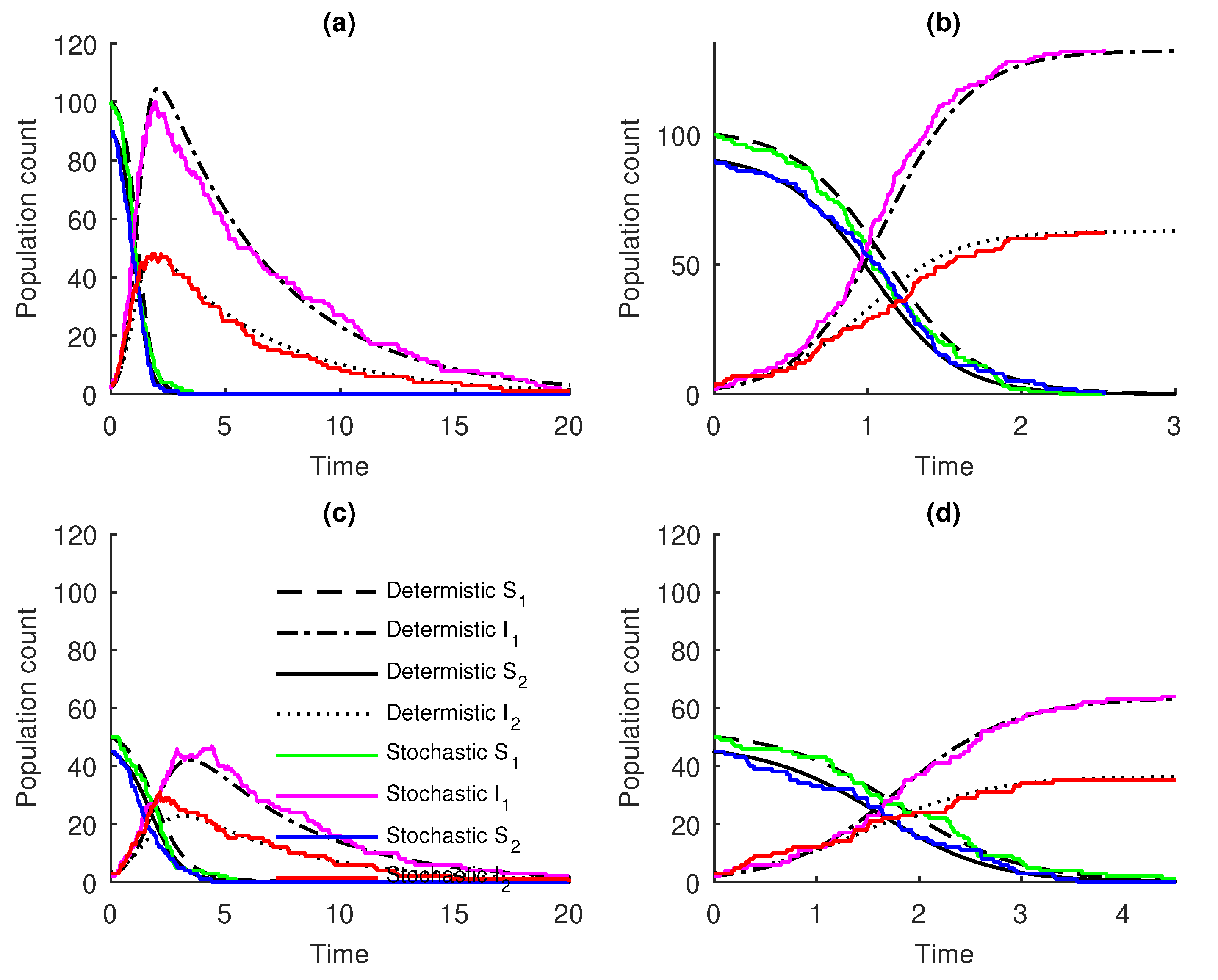
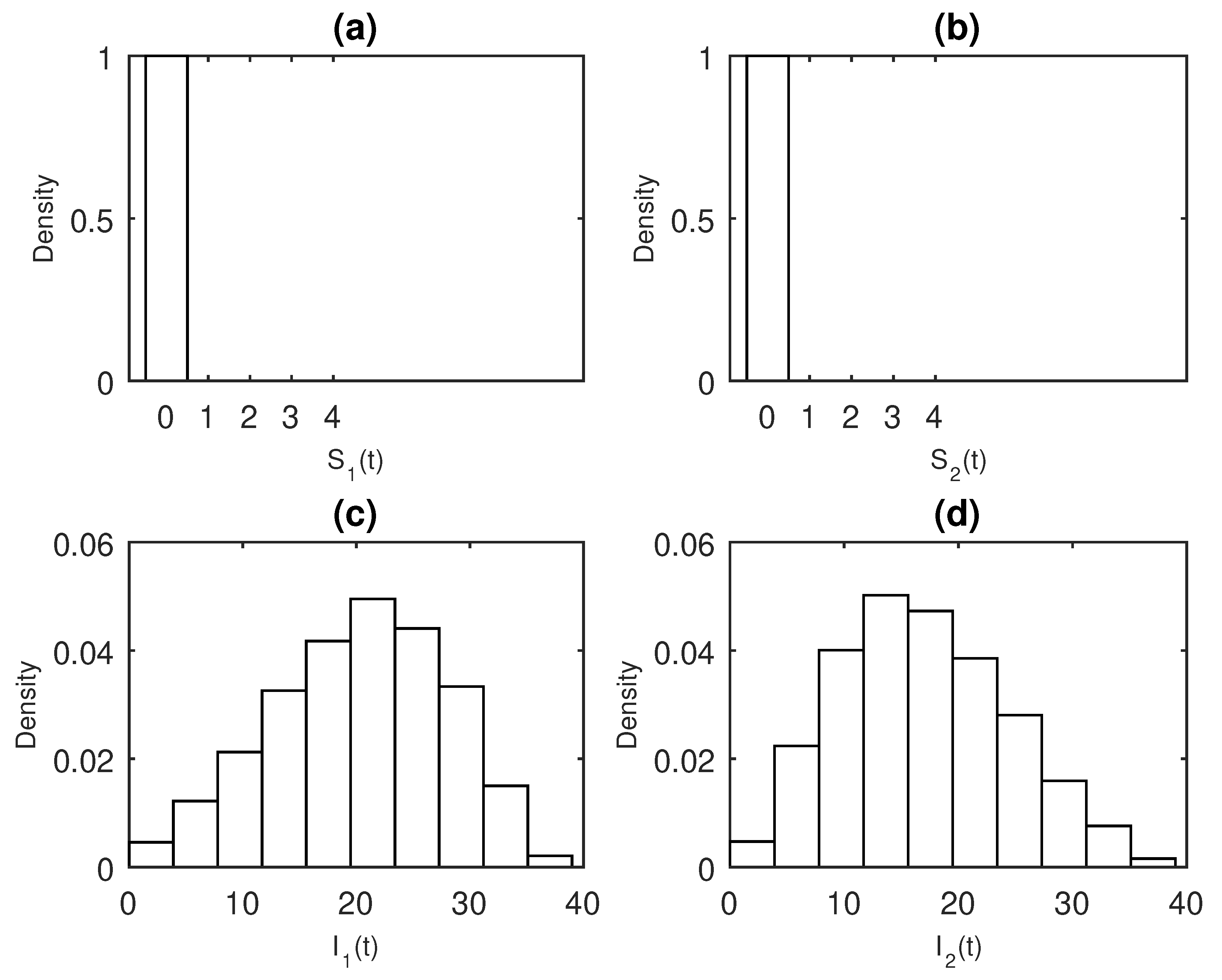
3. Results
Numerical Examples
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, B.A.; Schmidt, J.P.; Bowden, S.E.; Drake, J.M. Rodent reservoirs of future zoonotic diseases. Proc. Natl. Acad. Sci. USA 2015, 112, 7039–7044. [Google Scholar] [CrossRef]
- McCormack, R.K.; Allen, L.J. Stochastic SIS and SIR multihost epidemic models. In Proceedings of the Conference on Differential and Difference Equations and Applications, New York, NY, USA, 1–5 August 2005; pp. 775–786. [Google Scholar]
- Haydon, D.T.; Cleaveland, S.; Taylor, L.H.; Laurenson, M.K. Identifying reservoirs of infection: A conceptual and practical challenge. Emerg. Infect. Dis 2002, 8, 1468–1473. [Google Scholar] [PubMed]
- Gao, D.; Porco, T.C.; Ruan, S. Coinfection dynamics of two diseases in a single host population. J. Math. Anal. Appl. 2016, 442, 171–188. [Google Scholar] [CrossRef] [PubMed]
- Alemu, A.; Shiferaw, Y.; Addis, Z.; Mathewos, B.; Birhan, W. Effect of malaria on HIV/AIDS transmission and progression. Parasites Vectors 2013, 6, 18. [Google Scholar] [CrossRef] [PubMed]
- Vapalahti, O.; Mustonen, J.; Lundkvist, Å.; Henttonen, H.; Plyusnin, A.; Vaheri, A. Hantavirus infections in Europe. Lancet. Infect. Dis. 2003, 3, 653–661. [Google Scholar] [CrossRef]
- Bhunu, C.P.; Garira, W.; Mukandavire, Z. Modeling HIV/AIDS and tuberculosis coinfection. Bull. Math. Biol. 2009, 71, 1745–1780. [Google Scholar] [CrossRef] [PubMed]
- Sharomi, O.; Podder, C.; Gumel, A.; Song, B. Mathematical analysis of the transmission dynamics of HIV/TB coinfection in the presence of treatment. Math. Biosci. Eng. 2008, 5, 145. [Google Scholar]
- Nwankwo, A.; Okuonghae, D. Mathematical analysis of the transmission dynamics of HIV syphilis co-infection in the presence of treatment for syphilis. Bull. Math. Biol. 2018, 80, 437–492. [Google Scholar] [CrossRef]
- Müller, J.; Kretzschmar, M.; Dietz, K. Contact tracing in stochastic and deterministic epidemic models. Math. Biosci. 2000, 164, 39–64. [Google Scholar] [CrossRef]
- Ball, F. Stochastic and deterministic models for SIS epidemics among a population partitioned into households. Math. Biosci. 1999, 156, 41–67. [Google Scholar] [CrossRef]
- Allen, L.J.; Lahodny, G.E., Jr. Extinction thresholds in deterministic and stochastic epidemic models. J. Biol. Dyn. 2012, 6, 590–611. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. J. Biol. Dyn. 2017, 2, 128–142. [Google Scholar] [CrossRef] [PubMed]
- Erten, E.; Lizier, J.; Piraveenan, M.; Prokopenko, M. Criticality and information dynamics in epidemiological models. Entropy 2017, 19, 194. [Google Scholar] [CrossRef]
- Britton, T. Stochastic epidemic models: A survey. Math. Biosci. 2010, 225, 24–35. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J.; Jang, S.R.; Roeger, L.I. Predicting population extinction or disease outbreaks with stochastic models. In Letters in Biomathematics; Taylor & Francis Group: Abingdon-on-Thames, UK, 2017; Volume 4, pp. 1–22. [Google Scholar]
- Lahodny, G.E.; Allen, L.J. Probability of a disease outbreak in stochastic multipatch epidemic models. Bull. Math. Biol. 2013, 75, 1157–1180. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J.; Burgin, A.M. Comparison of deterministic and stochastic SIS and SIR models. Dept. Math. Stat. Tech. Rep. Ser. 1998, 98–103. [Google Scholar]
- Cooper, B.S. Confronting models with data. J. Hosp. Infect. 2007, 65, 88–92. [Google Scholar] [CrossRef]
- Dorman, K.S.; Sinsheimer, J.S.; Lange, K. In the garden of branching processes. SIAM Rev. 2004, 46, 202–229. [Google Scholar] [CrossRef]
- Allen, L.J.; van den Driessche, P. Relations between deterministic and stochastic thresholds for disease extinction in continuous-and discrete-time infectious disease models. Math. Biosci. 2013, 243, 99–108. [Google Scholar] [CrossRef]
- Brightwell, G.; House, T.; Luczak, M. Extinction times in the subcritical stochastic SIS logistic epidemic. J. Math. Biol. 2018, 77, 455–493. [Google Scholar] [CrossRef]
- Tritch, W.; Allen, L.J. Duration of a minor epidemic. Infect. Dis. 2018, 3, 60–73. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; Chapman and Hall: London, UK, 2010; pp. 159–196. [Google Scholar]
- Almaraz, E.; Gómez-Corral, A. Number of infections suffered by a focal individual in a two-strain SIS model with partial cross-immunity. Math. Meth. Appl. Sci. 2019, 42, 4318–4330. [Google Scholar] [CrossRef]
- Allman, E.S.; Allman, E.S.; Rhodes, J.A. Mathematical Models in Biology: An Introduction; Cambridge University Press: Cambridge, UK, 2004; pp. 1–39. [Google Scholar]
- Cao, B.; Shan, M.; Zhang, Q.; Wang, W. A stochastic SIS epidemic model with vaccination. Physica A 2017, 486, 127–143. [Google Scholar] [CrossRef]
- Miao, A.; Wang, X.; Zhang, T.; Wang, W.; Pradeep, B.S.A. Dynamical analysis of a stochastic SIS epidemic model with nonlinear incidence rate and double epidemic hypothesis. Adv. Differ. Equ. 2017, 2017, 226. [Google Scholar] [CrossRef]
- Zhou, Y.; Yuan, S.; Zhao, D. Threshold behavior of a stochastic SIS model with Lévy jumps. Appl. Math. Comput. 2016, 275, 255–267. [Google Scholar]
- Zhang, X.; Jiang, D.; Hayat, T.; Ahmad, B. Dynamics of a stochastic SIS model with double epidemic diseases driven by Lévy jumps. Physica A 2017, 471, 767–777. [Google Scholar] [CrossRef]
- Economou, A.; Gómez-Corral, A.; López-Garcĺa, M. A stochastic SIS epidemic model with heterogeneous contacts. Physica A 2015, 421, 78–97. [Google Scholar] [CrossRef]
- Grimmett, G.; Grimmett, G.R.; Stirzaker, D. Probability and Random Processes; Oxford University Press: Oxford, UK, 2001; pp. 213–296. [Google Scholar]
- Nåsell, I. Stochastic models of some endemic infections. Math. Biosci. 2002, 179, 1–19. [Google Scholar] [CrossRef]
- Bailey, N.T. The Elements of Stochastic Processes with Applications to the Natural Sciences; John Wiley & Sons: Chichester, UK, 1990; Volume 25, pp. 84–105. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Further Notes on the Basic Reproduction Number. In Mathematical Epidemiology; Springer: Berlin/Heidelberger, Germany, 2008; pp. 159–178. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Allen, L.J. Introduction to Mathematical Biology; Prentice Hall: Upper Saddle River, NJ, USA, 2007; pp. 37–70. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
| Event | Transition Between t and | Probability |
|---|---|---|
| Mortality of | → | |
| Mortality of | → | |
| infects | → | |
| infects | → | |
| infects | → | |
| infects | → |
| P | Approx 1 | P | Approx 2 | ||
|---|---|---|---|---|---|
| 1 | 1 | ||||
| 2 | 1 | ||||
| 1 | 2 | ||||
| 2 | 2 | ||||
| 3 | 2 | ||||
| 2 | 3 | ||||
| 3 | 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullahi, A.; Shohaimi, S.; Kilicman, A.; Hafiz Ibrahim, M.; Salari, N. Stochastic SIS Modelling: Coinfection of Two Pathogens in Two-Host Communities. Entropy 2020, 22, 54. https://doi.org/10.3390/e22010054
Abdullahi A, Shohaimi S, Kilicman A, Hafiz Ibrahim M, Salari N. Stochastic SIS Modelling: Coinfection of Two Pathogens in Two-Host Communities. Entropy. 2020; 22(1):54. https://doi.org/10.3390/e22010054
Chicago/Turabian StyleAbdullahi, Auwal, Shamarina Shohaimi, Adem Kilicman, Mohd Hafiz Ibrahim, and Nader Salari. 2020. "Stochastic SIS Modelling: Coinfection of Two Pathogens in Two-Host Communities" Entropy 22, no. 1: 54. https://doi.org/10.3390/e22010054
APA StyleAbdullahi, A., Shohaimi, S., Kilicman, A., Hafiz Ibrahim, M., & Salari, N. (2020). Stochastic SIS Modelling: Coinfection of Two Pathogens in Two-Host Communities. Entropy, 22(1), 54. https://doi.org/10.3390/e22010054






